Topology design of two-fluid heat exchange

Abstract

Heat exchangers are devices that typically transfer heat between two fluids. The performance of a heat exchanger such as heat transfer rate and pressure loss strongly depends on the flow regime in the heat transfer system. In this paper, we present a density-based topology optimization method for a two-fluid heat exchange system, which achieves a maximum heat transfer rate under fixed pressure loss. We propose a representation model accounting for three states, i.e., two fluids and a solid wall between the two fluids, by using a single design variable field. The key aspect of the proposed model is that mixing of the two fluids can be essentially prevented. This is because the solid constantly exists between the two fluids due to the use of the single design variable field. We demonstrate the effectiveness of the proposed method through three-dimensional numerical examples in which an optimized design is compared with a simple reference design, and the effects of design conditions (i.e., Reynolds number, Prandtl number, design domain size, and flow arrangements) are investigated.

1 Introduction

Heat exchangers are devices that transfer heat between two or more fluids. Recently, designing high-performance heat exchangers has been prioritized owing to an increased demand for such systems with low energy consumption. Most heat exchangers involve two-fluid heat exchange with indirect contact; i.e., there are two fluids separated by a wall. In such heat exchangers, the performances depend on the flow regime. For instance, the curving and branching of the flow channels of each fluid and the adjacency of the flow channels to each other have a significant effect on the heat transfer rate and the pressure loss. Therefore, consideration of such characteristics is significant in heat exchanger design.

Generally, in heat exchanger design, a type is first selected from the existing ones, and the details, e.g., size, shape, and fin type, are determined (Shah and Sekulic 2003). Optimization methods for the existing types of heat exchangers have been well researched in previous works. For instance, Hilbert et al. (2006) studied a multiobjective optimization method concerning the blade shape of a tubular heat exchanger via a genetic algorithm. Kanaris et al. (2009) applied a response surface method to optimization problems for a plate heat exchanger with undulated surfaces. Guo et al. (2018) proposed a design method to simultaneously determine the fin types and their optimal sizes in plate fin heat exchangers.

The existing types of heat exchangers are typically manufactured through traditional processes such as pressing of plates and bending of tubes. This implies that the typical heat exchangers are designed under strict constraints pertaining to their manufacturability. However, there is an increasing demand to produce heat exchangers more efficient and compact, as the traditional manufacturing techniques are usually too inefficient to satisfy this demand. To produce innovative heat exchangers, these constraints pertaining to their manufacturability should be eliminated. In this regard, using additive manufacturing is a promising option, and has been employed for manufacturing innovative heat exchangers (e.g., Scheithauer et al. 2018) in instances where traditional techniques cannot be easily be applied. According to such progression of additive manufacturing technologies, revealing and understanding the ideal flow regime of the two fluids in heat exchange systems become increasingly important. However, the ideal flow regime is not obvious in most cases. For such a problem, topology optimization is a promising methodology, as it enables shape and topological changes of the structure.

Topology optimization was first proposed by Bendsøe and Kikuchi (1988). It essentially comprises introduction of a fixed design domain and replacement of the original optimization problem with a material distribution problem. A characteristic function is introduced to represent either solid material or void at the appropriate points in the design domain. Although topology optimization was originally applied to solid mechanics problems, it has been developed for application in various physical problems (Bendsøe and Sigmund 2003; Sigmund and Maute 2013; Deaton and Grandhi 2014).

For fluid flow problems, Borrvall and Petersson (2003) proposed a topology optimization method for solid/fluid distribution problems in Stokes flow. The critical feature in their method is the introduction of a fictitious body force term, which can discriminate fluid and solid at points in the design domain, according to each design variable value. Their method was extended for Navier–Stokes equations (Gersborg-Hansen et al. 2005; Olesen et al. 2006), and design problems of fluidic devices, such as microreactors (Okkels and Bruus 2007), micromixers (Andreasen et al. 2009; Deng et al. 2018), Tesla valves (Lin et al. 2015; Sato et al. 2017), and flow batteries (Yaji et al. 2018b; Chen et al. 2019). The thermal-fluid problems that have been studied include forced convection problems (Matsumori et al. 2013; Koga et al. 2013; Yaji et al. 2015), natural convection problems (Alexandersen et al. 2014; Coffin and Maute 2016), and large-scale three-dimensional problems involving cluster computing (Alexandersen et al. 2016; Yaji et al. 2018a). In addition, Dilgen et al. (2018) applied density-based topology optimization to turbulent heat transfer problems. For practical approaches in utilizing topology optimization in complex fluid problems, simplified models have recently been studied for solving turbulent heat transfer problems (Zhao et al. 2018; Yaji et al. 2020; Kambampati and Kim 2020), natural convection problems (Asmussen et al. 2019; Pollini et al. 2020), and heat exchanger design problems (Haertel and Nellis 2017; Kobayashi et al. 2019). The history and the state-of-the-art of topology optimization for fluid problems including heat transfer problems are summarized in the recently published review paper (Alexandersen and Andreasen 2020).

Many studies regarding topology optimization of thermal-fluid problems dealt with solid/fluid distribution; i.e., only one fluid is considered. A topology optimization method for two-fluid and one-solid distribution problems is essential to generate an innovative design of a two-fluid heat exchanger. Papazoglou (2015) first explored topology optimization for designing two-fluid heat exchangers. The results indicated that a multi-material model, which uses two types of design variable fields, is more effective than a tracking model, which uses an advection equation for identifying two fluids. However, the utility of the results is limited by the assumption of a zero thickness wall, which provides an unrealistic situation. Saviers et al. (2019) reported numerical and empirical investigations on a topology-optimized heat exchanger. However, the detailed formulation was withheld as proprietary information. Based on a multi-material model, Tawk et al. (2019) proposed a topology optimization method for two-dimensional heat transfer problems involving two-fluid and one-solid domains. In their method, a penalty function is used to prevent the mixing of the two fluids by introducing a non-zero thickness wall. The authors, however, stated that the solution search becomes unstable in certain conditions because of the penalty scheme.

In the general framework of multi-material topology optimization, three states (two types of materials and a void) are accounted for by using multiple design variable fields. Conversely, in topology optimization of two-fluid heat exchange, the two fluids should be separated by a non-zero thickness wall. For two-fluid problems, solving the multi-material topology optimization typically requires a penalty scheme as with the previous work (Tawk et al. 2019), since the representation model for the multiple states has an excessive degree of freedom. There arises a possibility that a simpler representation model can be obtained by focusing on the characteristics of the two-fluid problems. Haertel (2018) proposed a two-dimensional representation model for designing cross-flow heat exchangers, in which three states—two fluids and a wall—are represented using a single design variable field with the design field gradient (Clausen et al. 2015).

In this study, we propose a simple representation model for topology optimization of two-fluid heat exchange. We introduce two types of fictitious force terms, one in each flow field, for representing a wall between the two types of fluid, which essentially cannot mix. This idea is related to the previous work of Papazoglou (2015). However, our model can handle a non-zero thickness wall by using a single design variable field.

We emphasize that the two-fluid heat exchange problems should be treated as three-dimensional problems since the topological change is significantly restricted in the case of two-dimensional problems. Thus, we apply the proposed method to three-dimensional heat exchange problems and examine the effects of several design conditions, such as Reynolds number, Prandtl number, design domain size, and flow arrangements.

The remaining sections of this paper are organized as follows. In Section 2, the design problem of two-fluid heat exchange is presented, as well as the method to represent two fluids and one solid by the single design variable field is briefly discussed. In Section 3, the analysis model and the proposed representation model are presented, and the topology optimization problem is formulated. Furthermore, the numerical implementation is presented. In Section 4, several three-dimensional numerical examples¹ are provided to validate the proposed method and to discuss the ideal flow regime of the two-fluid heat exchange. Finally, Section 5 concludes this study.

2 Topology optimization for two-fluid heat exchange

2.1 Design problem

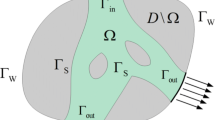
A simple heat exchanger, in which flow channels of the two fluids are separated by a wall as presented in Fig. 1, is considered. An inlet and an outlet of each fluid are respectively set, and each fluid flows independently. The heat is transferred between the two fluids in the design domain D. The hot and cold fluids are denoted by “fluid 1” and “fluid 2,” respectively.

Fig. 1

Schematic diagram of two-fluid heat exchange

In this study, we consider a topology optimization problem for designing the shape and topology of the flow channels and the separating wall in the design domain D. The objectives of the heat exchanger design are the maximization of the heat transfer rate and minimization of the pressure loss. This multi-objective design problem is transformed into a single-objective design problem by fixing the pressure loss. The detailed formulation is provided in Section 3.

2.2 Basic concept of topology optimization

Topology optimization essentially involves the replacement of the original structural optimization problem with a material distribution problem in a fixed design domain D that contains the original design domain Ω. Bendsøe and Kikuchi (1988) introduced a characteristic function χ_Ω that assumes a discrete value 0 and 1, as follows:

$$ \chi_{\Omega} (\mathbf{x}) = \begin{cases} 1\quad \text{if}\quad \mathbf{x} \in {\Omega}\\ 0\quad \text{if}\quad \mathbf{x} \in D\backslash {\Omega}, \end{cases} $$

(1)

where x represents the position in the fixed design domain D. Since the characteristic function χ_Ω is a discontinuous function, a relaxation technique is required for gradient-based optimization. In the density-based method (Bendsøe and Sigmund 2003), the characteristic function χ_Ω is replaced with a continuous scalar function 0 ≤ γ(x) ≤ 1, which corresponds to the raw design variable field in the topology optimization problem.

To ensure the spatial smoothness of the material distribution in D, the filtering technique is generally applied in topology optimization. In this study, Helmholtz-type filter (Kawamoto et al. 2011; Lazarov and Sigmund 2011) is employed, as follows:

$$ -R^{2} \nabla^{2} \tilde{\gamma} +\tilde{\gamma} = \gamma, $$

(2)

where $\tilde {\gamma }$ is a smoothed design variable field, and R is a filtering radius. By solving (2), γ is mapped to $\tilde {\gamma }$, thus ensuring a spatial smoothness in D.

To elucidate the physical phenomena more accurately, intermediate values of the design variable field need to be eliminated. Therefore, a projection function is used as follows (Wang et al. 2011):

$$ \hat{\tilde{\gamma}} = \frac{\tanh (\upbeta \eta) + \tanh (\upbeta(\tilde{\gamma}-\eta))}{\tanh (\upbeta \eta) + \tanh (\upbeta (1-\eta))}, $$

(3)

where $\hat {\tilde {\gamma }}$ is the design variable field after the projection, and β and η are the tuning parameters that control the function shape.

2.3 Representation model

For the topology optimization of two-fluid heat exchange, the design variable field should represent the two fluids and the one solid, as shown in Fig. 1. Here, we discuss the method to represent the two fluids and the one solid by the design variable field.

Table 1 shows the state represented by the design variable field. The design variable field γ assumes 1 in fluid 1 and 0 in fluid 2. The two fluids can consistently be separated by the solid when the spatial smoothness of the design variable field is preserved in the design domain D. It should be noted that a filtering technique (2) is essential in the proposed representation model. In addition, as the solid domain is defined as the intermediate value of the design variable field, a projection function (3) is used to represent a thin wall precisely.

Table 1 Representation model of two fluids and one solid in the proposed method

The method of incorporating $\hat {\tilde {\gamma }}$ into the governing equations for a two-fluid heat exchange system is discussed in Section 3.1, and the numerical verification of the proposed model is provided in Section 4.2.

3 Formulation

3.1 Governing equations and boundary conditions

The governing equations of an incompressible steady flow are given as follows:

$$ \nabla \cdot \mathbf{u} = 0, $$

(4)

$$ \rho (\mathbf{u} \cdot \nabla) \mathbf{u} = - \nabla p + \mu \nabla^{2} \mathbf{u} + \mathbf{F}, $$

(5)

where u is the velocity, ρ is the density, p is the pressure, μ is the viscosity, and F is a body force. In the fluid topology optimization, F is a fictitious body force caused by the solid objects in the flow (Borrvall and Petersson 2003). The energy equation without the heat source is defined as follows:

$$ \rho C_{p} (\mathbf{u} \cdot \nabla) T - k \nabla^{2} T = 0, $$

(6)

where C_p is the specific heat at constant pressure, T is the temperature, and k is the thermal conductivity.

The boundary conditions are defined as follows:

$$ \begin{array}{@{}rcl@{}} p=p_{\mathrm{in, 1}}, \quad T=T_{\mathrm{in,1}} \quad &\text{on}& \quad {\Gamma}_{\text{in},1}, \end{array} $$

(7)

$$ \begin{array}{@{}rcl@{}} p=p_{\mathrm{out, 1}}, \quad \nabla T \cdot \mathbf{n} = 0 \quad &\text{on}& \quad {\Gamma}_{\text{out},1}, \end{array} $$

(8)

$$ \begin{array}{@{}rcl@{}} p=p_{\mathrm{in, 2}}, \quad T=T_{\mathrm{in,2}} \quad &\text{on}& \quad {\Gamma}_{\text{in},2}, \end{array} $$

(9)

$$ \begin{array}{@{}rcl@{}} p=p_{\mathrm{out, 2}}, \quad \nabla T \cdot \mathbf{n} = 0 \quad &\text{on}& \quad {\Gamma}_{\text{out},2}, \end{array} $$

(10)

$$ \begin{array}{@{}rcl@{}} \mathbf{u}=\mathbf{0}, \quad \nabla T \cdot \mathbf{n} = 0 \quad &\text{on}& \quad {\Gamma}_{\text{wall}}, \end{array} $$

(11)

where subscripts 1 and 2 represent the fluid 1 and fluid 2, respectively. As mentioned in Section 2.1, the constant pressure loss is assumed by fixing the pressure at the inlet and outlet.

3.2 Proposed interpolation scheme

In this study, the different fictitious forces in the governing equations for fluid 1 and fluid 2 are imposed separately to realize the state represented by the design variable field indicated in Table 1. Therefore, the governing equations are separated for fluid 1 and fluid 2, as follows:

$$ \nabla \cdot \mathbf{u}_{1} = 0, $$

(12)

$$ \rho_{1} (\mathbf{u}_{1} \cdot \nabla) \mathbf{u}_{1} = - \nabla p_{1} + \mu_{1} \nabla^{2} \mathbf{u}_{1} + \mathbf{F}_{1}, $$

(13)

$$ \nabla \cdot \mathbf{u}_{2} = 0, $$

(14)

$$ \rho_{2} (\mathbf{u}_{2} \cdot \nabla) \mathbf{u}_{2} = - \nabla p_{2} + \mu_{2} \nabla^{2} \mathbf{u}_{2} + \mathbf{F}_{2}. $$

(15)

The last terms in (13) and (15) are crucial in the proposed method. These fictitious body forces are defined as follows:

$$ \mathbf{F}_{1} = - \alpha_{1} \mathbf{u}_{1}, $$

(16)

$$ \mathbf{F}_{2} = - \alpha_{2} \mathbf{u}_{2}, $$

(17)

where α₁(x) and α₂(x) are the inverse permeability of the porous media at position x (Borrvall and Petersson 2003). The fluid hardly flows when α₁ or α₂ assumes a large value. Consequently, the fluid can flow freely when α₁ or α₂ assumes a zero value. The inverse permeabilities α₁ and α₂ are defined as follows:

$$ \alpha_{1}(\hat{\tilde{\gamma}}) = \alpha_{\max} \frac{q(1-\hat{\tilde{\gamma}})}{q + \hat{\tilde{\gamma}}}, $$

(18)

$$ \alpha_{2}(\hat{\tilde{\gamma}}) = \alpha_{\max} \frac{q \hat{\tilde{\gamma}}}{q + 1 - \hat{\tilde{\gamma}}}, $$

(19)

where $\alpha _{\max \limits }$ is the maximum inverse permeability and q is the parameter that controls the convexity of α. Both inverse permeabilities are defined based on the interpolation function by Borrvall and Petersson (2003). However, these two interpolation functions are symmetrical with respect to $\hat {\tilde {\gamma }}$. Figure 2 displays the graph of the interpolation functions at $\alpha _{\max \limits }= 10^{4}$ and q = 0.01 in (18) and (19), and β = 8 and η = 0.5 in (3). As revealed in Fig. 2, if $\hat {\tilde {\gamma }}=0$, α₁ assumes a large value $\alpha _{\max \limits }$ and α₂ assumes a zero value. For this reason, only fluid 2 can flow whereas fluid 1 cannot flow. Conversely, if $\hat {\tilde {\gamma }}=1$, only fluid 1 can flow since α₁ assumes a zero value and α₂ assumes $\alpha _{\max \limits }$. In the intermediate value of $\hat {\tilde {\gamma }}$, both fluids hardly flow because both α₁ and α₂ are not zero. Therefore, the flow characteristics of Table 1 can be achieved via these interpolation functions of the inverse permeability.

Fig. 2

Interpolation functions for fluid 1 and fluid 2 at $\alpha _{\max \limits }= 10^{4}$ and q = 0.01 in (18) and (19), and β = 8 and η = 0.5 in (3)

To simplify the numerical implementation, the governing equations are replaced with dimensionless form, and the dimensionless quantities, i.e., the Reynolds number and the Péclet number, are introduced.

The dimensionless equations of (12)–(15) are defined as follows:

$$ \nabla^{*} \cdot \mathbf{u}_{1}^{*} = 0, $$

(20)

$$ (\mathbf{u}_{1}^{*} \cdot \nabla^{*}) \mathbf{u}_{1}^{*} = - \nabla^{*} p_{1}^{*} + \frac{1}{Re_{1}} \nabla^{*2} \mathbf{u}_{1}^{*} - \alpha_{1}^{*} \mathbf{u}_{1}^{*}, $$

(21)

$$ \nabla^{*} \cdot \mathbf{u}_{2}^{*} = 0, $$

(22)

$$ (\mathbf{u}_{2}^{*} \cdot \nabla^{*}) \mathbf{u}_{2}^{*} = - \nabla^{*} p_{2}^{*} + \frac{1}{Re_{2}} \nabla^{*2} \mathbf{u}_{2}^{*} - \alpha_{2}^{*} \mathbf{u}_{2}^{*}, $$

(23)

where ∇^∗ = L∇. The superscript asterisk represents dimensionless variables, defined by a characteristic length L and characteristic speeds U₁ and U₂, as follows:

$$ \begin{array}{@{}rcl@{}} \begin{aligned} &{\mathbf{u}}_{1}^{*} = \frac{{\mathbf{u}_{1}}}{{U}_{1}},\quad {p}_{1}^{*} = \frac{{p}_{1} - p_{\mathrm{out, 1}}}{{\rho}_{1} {U}_{1}^{2}},\\ &{\alpha}_{1}^{*} = \frac{{L} {\alpha}_{1}}{{\rho}_{1} {U}_{1}},\quad \mathit{{Re}}_{1} = \frac{{\rho}_{1} {U}_{1} {L}}{{\mu}_{1}}, \end{aligned} \end{array} $$

(24)

$$ \begin{array}{@{}rcl@{}} \begin{aligned} &{\mathbf{u}}_{2}^{*} = \frac{{\mathbf{u}_{2}}}{{U}_{2}},\quad {p}_{2}^{*} = \frac{{p}_{2} - p_{\mathrm{out, 2}}}{{\rho}_{2} {U}_{2}^{2}},\\ &{\alpha}_{2}^{*} = \frac{{L} {\alpha}_{2}}{{\rho}_{2} {U}_{2}},\quad \mathit{{Re}}_{2} = \frac{{\rho}_{2} {U}_{2} {L}}{{\mu}_{2}}. \end{aligned} \end{array} $$

(25)

The characteristic speeds U₁ and U₂ cannot be defined using the magnitude of the inlet velocity because the inlet pressure is fixed, as mentioned in Section 3.1. Therefore, U₁ and U₂ are defined using the pressure loss (Yaji et al. 2015), as follows:

$$ {U}_{1}=\sqrt{\frac{{p}_{\mathrm{in, 1}}-{p}_{\mathrm{out, 1}}}{{\rho}_{1}}}, $$

(26)

$$ {U}_{2}=\sqrt{\frac{{p}_{\mathrm{in, 2}}-{p}_{\mathrm{out, 2}}}{{\rho}_{2}}}. $$

(27)

As a result, the proposed interpolation functions $\alpha _{1}^{*}(\hat {\tilde {\gamma }})$ and $\alpha _{2}^{*}(\hat {\tilde {\gamma }})$ in the dimensionless form are given as:

$$ \alpha_{1}^{*} (\hat{\tilde{\gamma}}) = \alpha_{\max}^{*} \frac{q(1-\hat{\tilde{\gamma}})}{q + \hat{\tilde{\gamma}}}, $$

(28)

$$ \alpha_{2}^{*} (\hat{\tilde{\gamma}}) = \alpha_{\max}^{*} \frac{q \hat{\tilde{\gamma}}}{q + 1 - \hat{\tilde{\gamma}}}, $$

(29)

where $\alpha _{\max \limits }^{*}$ is the maximum inverse permeability.

The dimensionless equation of (6) is defined as follows:

$$ \mathbf{u}^{*} \cdot \nabla^{*} T^{*} - \frac{1}{Pe} \nabla^{*2} T^{*} = 0. $$

(30)

Here, Pe is the Péclet number Pe = PrRe, in which Pr is the Prandtl number given for the three states, i.e., fluid 1, fluid 2, and the solid. The dimensionless temperature T^∗ and these Prandtl numbers, Pr₁, Pr₂, and Pr_s, are respectively defined as follows:

$$ \begin{array}{@{}rcl@{}} \begin{aligned} &{T}^{*} = \frac{{T} - {T}_{\mathrm{in, 2}}}{{T}_{\mathrm{in, 1}} - {T}_{\mathrm{in, 2}}},\\ &\mathit{{Pr}}_{\text{1}} = \frac{\mu_{1} C_{p,1}}{k_{\text{1}}},\quad \mathit{{Pr}}_{\text{2}} = \frac{\mu_{2} C_{p,2}}{k_{\text{2}}},\quad \mathit{{Pr}}_{\text{s}} = \frac{\bar{\mu} C_{p,\text{s}}}{k_{\text{s}}}, \end{aligned} \end{array} $$

(31)

where $\bar {\mu }=(\mu _{1}+\mu _{2})/2$, and subscript s represents the solid. In (30), since the dimensional parameters of thermal-fluid properties are integrated into the dimensionless parameter, Pe, an interpolation function should be introduced so that Pe depends on the states, i.e., fluid 1, fluid 2, or the solid. Therefore, we propose an interpolation function based on the Gaussian function, as follows:

$$ \begin{array}{@{}rcl@{}} \begin{aligned} Pe(\hat{\tilde{\gamma}}) = &\left( Pe_{\mathrm{s}}-\frac{Pe_{\mathrm{1}}+Pe_{\mathrm{2}}}{2}\right) \exp \left( -\frac{(\hat{\tilde{\gamma}}-0.5)^{2}}{2s^{2}} \right) \\ &+Pe_{\mathrm{2}}+(Pe_{\mathrm{1}}-Pe_{\mathrm{2}})\hat{\tilde{\gamma}} , \end{aligned} \end{array} $$

(32)

where s is the parameter that controls the shape of the Gaussian function. Pe₁ = Pr₁Re₁, Pe₂ = Pr₁Re₁, and Pe_s = Pr_s(Re₁ + Re₂)/2 are the Péclet numbers of fluid 1, fluid 2, and the solid, respectively. As shown in Fig. 3, Pe in the intermediate region corresponding to the solid can be smaller than that of the two fluids. This indicates that the solid has larger thermal conductivity than that of the two fluids, under the condition that the remaining parameters of thermal-fluid properties are fixed.

Fig. 3

Interpolation function at Pe₁ = 700, Pe₂ = 700, Pe_s = 350, and s = 0.1 in (18) and (19), and β = 8 and η = 0.5 in (3)

3.3 Optimization formulation

As discussed in Section 2.1, the objective of the design problem is to maximize the total heat transfer with a fixed pressure loss. The total heat transfer is given as follows:

$$ Q=\dot{m} C_{p} (\overline{T}_{\text{in}} - \overline{T}_{\text{out}}), $$

(33)

where $\dot {m}$ is the mass flow, and $\overline {T}$ is the mean temperature. Introducing the boundary integral form, the equation for total heat transfer can be rewritten as:

$$ Q= C_{p} {\int}_{{\Gamma}_{\text{out}}} \rho \mathbf{u} \cdot \mathbf{n} d{\Gamma} \left( \frac{{\int}_{{\Gamma}_{\text{in}}} (\mathbf{u}\cdot \mathbf{n}) T d{\Gamma}}{{\int}_{{\Gamma}_{\text{in}}} \mathbf{u}\cdot \mathbf{n} d{\Gamma}} - \frac{{\int}_{{\Gamma}_{\text{out}}} (\mathbf{u}\cdot \mathbf{n}) T d{\Gamma}}{{\int}_{{\Gamma}_{\text{out}}} \mathbf{u}\cdot \mathbf{n} d{\Gamma}} \right). $$

(34)

Since incompressible flow is assumed in this study, the density is constant and the volume flows at the inlet and outlet are equal. In addition, the inlet temperature T is constant as defined in (7) and (9). Thus, the equation can be further rewritten as:

$$ Q= \rho C_{p} {\int}_{{\Gamma}_{\text{out}}} (\mathbf{u}\cdot \mathbf{n}) (T_{\text{in}} -T) d{\Gamma}. $$

(35)

To replace the objective function with dimensionless form, a total heat transfer Q is nondimensionalized as follows:

$$ Q^{*} = \frac{Q}{\rho C_{p} U L^{2} (T_{\mathrm{in, 1}} - T_{\mathrm{in, 2}})}. $$

(36)

Based on (36), we define the objective function in this study as the sum of the total heat transfer in fluid 1 and fluid 2, as follows:

$$ J = {\int}_{{\Gamma}_{\text{out},1}} (\mathbf{u}^{*} \cdot \mathbf{n}^{*}) (1-T^{*}) d{\Gamma} + {\int}_{{\Gamma}_{\text{out},2}} (\mathbf{u}^{*} \cdot \mathbf{n}^{*}) T^{*} d{\Gamma}. $$

(37)

For brevity, the asterisk symbol of the dimensionless variables is dropped henceforth.

Finally, the topology optimization problem is formulated as follows:

$$ \begin{array}{@{}rcl@{}} \begin{aligned} & \underset{\gamma({\mathbf{x}})}{\text{maximize}}\quad {J} = {\int}_{{\Gamma}_{\text{out},1}} (\mathbf{u} \cdot \mathbf{n}) (1-T) d{\Gamma} + {\int}_{{\Gamma}_{\text{out},2}} (\mathbf{u} \cdot \mathbf{n}) T d{\Gamma}, \\ & \mathrm{subject\ to}\quad 0 \leq \gamma({\mathbf{x}}) \leq 1\quad \text{for} \ \forall {\mathbf{x}} \in D, \end{aligned} \end{array} $$

(38)

where the thermal-fluid field is governed by (20)–(23), and (30).

3.4 Numerical implementation

The numerical solution of the governing (20)–(23) and (30) is obtained using COMSOL Multiphysics 5.5. The analysis domain is discretized using tetrahedral finite elements. The design variable field γ(x) is transformed into a discrete form γ_i (i = 1,…,n), where n is the total number of nodal points in the design domain D. The initial values of γ_i are set to 0.5 uniformly. For the sensitivity analysis, we employ the adjoint method based on the discrete formulation described in the literature (Bendsøe and Sigmund 2003).

The optimization procedure in this study is described as follows:

Step 1. :

The initial values of γ_i are set in D.

Step 2. :

The smoothed design variables $\tilde {\gamma }_{i}$ are derived using the Helmholtz-type filter (2), and are projected to $\hat {\tilde {\gamma }}_{i}$ using the projection function (3). black

Step 3. :

The objective function in (38) is calculated by solving the governing (20)–(23), and (30).

Step 4. :

If the value of J is converged, the optimization process ends. Otherwise, the sensitivity is calculated using the adjoint method.

Step 5. :

The design variables are updated using sequential linear programming (SLP), and the optimization procedure then returns to Step 2.

4 Numerical examples

4.1 Analysis model

Figure 4 shows the three-dimensional analysis domain and its dimensions. The dimensions L_x, L_y, and L_z are set to 4L, 2L, and 4L, respectively. A symmetrical boundary condition is imposed in the ZX plane. Hence, the computational domain is only half of that shown in Fig. 4, with the symmetrical boundary condition.

Fig. 4

Analysis domain and its dimensions for two-fluid heat exchange. The rectangular parallelepiped domain is the design domain, and the cubic domains are the non-design domain. (0,0,0) is the coordinate origin

The analysis domain is discretized using 5.3 × 10⁵ tetrahedral elements. The inlets and outlets of the two fluids are set as shown in Fig. 5, which outlines the counter flow. The dimensionless quantities are set to Re₁ = 100, Re₂ = 100, Pr₁ = 7, Pr₂ = 7, and Pr_s = 3.5. Note that, in this paper, these dimensionless parameter values are not supposed to those of practical heat exchangers.

Fig. 5

Schematic diagram of counter flow

The parameters regarding the interpolation functions are $\alpha _{\max \limits }=1\times 10^{4}$, q = 0.01, and s = 0.1. The filtering radius R in (2) is set to L/12 and the parameters for the projection function in (3) are set to β = 8, and η = 0.5, respectively.

4.2 Verification on a simple plate model

To verify the applicability of the proposed representation model, we evaluate its accuracy with a simple plate model. As shown in Fig. 6, the plate corresponding to the wall between the two fluids is placed at z = L_z/2. To represent the plate, γ = 1 (z ≥ L_z/2) and γ = 0 (z < L_z/2) are set, respectively. Besides, γ is projected to $\hat {\tilde {\gamma }}$ via using the PDE filter and the projection function.

Fig. 6

Simple plate model for verification of the proposed method. The plate is represented as the isosurface of $\hat {\tilde {\gamma }}=0.5$. The evaluation line is located at (L_x/2,L_y/4,z)

Figure 7a shows the distributions of $\hat {\tilde {\gamma }}$, α, and Pe along the evaluation line shown in Fig. 6, where it can be confirmed that $\hat {\tilde {\gamma }}$ sharply increases from 0 to 1 between L_z/2 ±Δd/2, with Δd ≈ 0.08L. It should be noted that Δd is related to the thickness of the plate, which can be controlled by changing the parameters such as R and β. However, explicit control of the plate thickness is difficult in the proposed representation model, as many parameters are implicitly dependent upon the thickness. Therefore, the thickness is determined via comparison with a high-fidelity model that has an exact solid plate, as shown in the leftmost panel of Fig. 7b.

Fig. 7

Numerical results for the verification of the simple plate model: a distribution of $\hat {\tilde {\gamma }}$, α and Pe; b comparison with a high-fidelity model. In the high-fidelity model, a plate, with a thickness of 0.08L, is located at z = L_z/2. The evaluation line is located at (L_x/2,L_y/4,z)

Table 2 shows the objective function J of the high-fidelity model and its discrepancy for the three cases of different resolutions. As the discrepancy between the case of 5.2 × 10⁵ and 1.3 × 10⁶ elements is 2.3%, the analysis domain is discretized using 5.2 × 10⁵ elements. By conducting the preliminary experiments, the thickness of the high-fidelity model is set to 0.08L. From Fig. 7b, it can be confirmed that the velocity and the temperature of the proposed representation model are in good agreement with those of the high-fidelity model.

Table 2 Mesh dependency in the numerical result of the high-fidelity model in Fig. 7b

4.3 Optimized design

Figure 8 shows the isosurface of $\hat {\tilde {\gamma }}=0.5$. Note that only half of the domain is optimized with the symmetrical boundary condition on ZX plane. Besides, the half sectional view is shown in Fig. 9, where the separating wall is colored with orange on fluid 1 side, and light blue on fluid 2 side. The color of the arrows represents the temperature of the fluids.

Fig. 8

Isosurface of $\hat {\tilde {\gamma }}=0.5$ of the optimized result. The half domain is optimized with the symmetrical boundary condition on ZX plane

Fig. 9

Optimized result with velocity vectors, where the colors represent the temperature of the fluids. Objective function value: J = 0.321

The optimization history of $\hat {\tilde {\gamma }}$ is illustrated in Fig. 10, in which fluid 1 and fluid 2 domains appear as the optimization proceeds. In this study, the maximum iteration number of the optimization is set to 100.

Fig. 10

Optimization history of $\hat {\tilde {\gamma }}$ in YZ slices

Figure 11 shows the results for the accuracy check as with the case of the simple plate model shown in Fig. 7. The analysis domain of the high-fidelity model is discretized using 5.9 × 10⁵ tetrahedral elements, which are chosen in a similar way to the values in Table 2. The high-fidelity model in the leftmost panel of Fig. 11b is constructed from the result in Fig. 9 so that the thickness of the solid domain is approximately equal to 0.08L. For this, the solid domain is defined as $0.1\leq \hat {\tilde {\gamma }}\leq 0.9$. Note that the range of $\hat {\tilde {\gamma }}$ for representing the solid is dependent of the parameters such as R and β, as discussed in Section 4.2.

Fig. 11

Numerical results for the verification of the optimized result: a distribution of $\hat {\tilde {\gamma }}$, α and Pe; b comparison with a high-fidelity model. In the high-fidelity model, a solid domain is defined as $0.1\leq \hat {\tilde {\gamma }}\leq 0.9$ so that the thickness is approximately equal to 0.08L. The evaluation line is located at (L_x/2,L_y/4,z)

From the results in Fig. 11b, the velocity and the temperature along the evaluation line in the optimized design are in good agreement with those of the high-fidelity model, while a slight error is observed. Besides, Fig. 12 shows the results of the two-dimensional slice at y = L_y/4, with an error is also observed in Fig. 12b. This discrepancy can be reduced by increasing β during the optimization process. However, such a technique typically causes numerical oscillation in terms of the objection function, and is therefore omitted in this study for simplicity. The values of the objective function J in the optimized design and its high-fidelity model are 0.321 and 0.326, respectively. Hence, the error of the optimized design using the proposed representation model over the high-fidelity model is 1.6%.

Fig. 12

Numerical results of ZX plane at y = L_y/4 for the verification of the optimized result: a distribution of $\hat {\tilde {\gamma }}$, α and Pe; b comparison with the high-fidelity model

As shown in Figs. 8 and 9, geometrically complex flow channels are obtained. The flow channels are gradually curved and branched to circulate the fluids in the whole heat exchange domain, and fluid 1 and fluid 2 are placed alternately. This is because increasing the heat transfer area without the sharp bend is effective for improving the total heat transfer with low pressure loss. In addition, it is found that the outlet temperature of fluid 1 is lower than that of fluid 2. As illustrated in Fig. 9, the downstream region of fluid 1 adjoins the upstream region of fluid 2 and vice versa. Thus, the fluids can exchange heat in the downstream region, whereas the heat is already transferred in the upstream branched region. This feature is unique to the counter flow and can enhance the heat transfer.

4.4 Performance comparison with a reference design

We now verify the performance of the optimized design, shown in the leftmost panel of Fig. 11b, by comparison with a reference design shown in Fig. 13, which refers to a simple configuration of a multiple plate heat exchanger (Shah and Sekulic 2003). Note that the volume of the solid in the reference model is equal to that of the optimized design.

Fig. 13

Reference design. The thickness of the solid domain is 0.08L. The volume of the solid domain is equal to that of the high-fidelity model of the optimized design in Fig. 11b

Table 3 shows the comparison of the total heat transfer J, the flow rate of fluid 1 and fluid 2, i.e., $\dot {V}_{1}$ and $\dot {V}_{2}$, and the mean outlet temperature of fluid 1 and fluid 2, i.e., $\bar {T}_{\mathrm {out, 1}}$ and $\bar {T}_{\mathrm {out, 2}}$. The flow rate of the reference design is approximately equal to that of the optimized design. However, there is not a large difference between each mean outlet temperature and each inlet temperature in the reference design. Consequently, the total heat transfer of the optimized design is approximately three times higher than that of the reference design. Therefore, it is observed that the optimized design enhances heat transfer under the investigated operating condition.

Table 3 Thermal fluid performance of the optimized design and reference design, where J is the total heat transfer, $\dot {V}_{1}$ and $\dot {V}_{2}$ are the flow rates of fluid 1 and fluid 2, and $\bar {T}_{\mathrm {out, 1}}$ and $\bar {T}_{\mathrm {out, 2}}$ are the mean outlet temperature of fluid 1 and fluid 2

4.5 Effects of design conditions

4.5.1 Effect of Reynolds number

Here, we investigate the effect of Reynolds number, Re, settings on the optimized configuration. In this study, the Reynolds number represents the pressure loss because the characteristic speed is based on the pressure loss as defined in (26). Figure 14 illustrates the optimized results in the case of Re₁ = 50, Re₂ = 50, and the case of Re₁ = 200, Re₂ = 200. The parameters except for the Reynolds number are identical to the case of Re₁ = 100, Re₂ = 100 presented in Section 4.3.

Fig. 14

Optimized result for different Reynolds numbers: a Re₁ = 50, Re₂ = 50; b Re₁ = 200, Re₂ = 200. Objective function values: a J = 0.271; b J = 0.329

From Figs. 9 and 14, the number of branches increases as the Reynolds number increases. In Fig. 14, a relatively simple structure is obtained in low Re. The heat transfer surface is approximately planar instead of the circular channels. Conversely, narrow branched channels are obtained for high Re. This is because the heat transfer area can be increased when the high pressure loss is allowed.

Table 4 shows the crosscheck of J for the different optimized designs and Re settings. Here, the optimized designs are analyzed across the different Re settings, and it can be confirmed that the optimized design for a certain Re setting performs better than the alternative designs for that setting. These results indicate that the ideal topology of the two fluids varies by the Reynolds number setting.

Table 4 Cross-check of J with respect to Re

Figure 15 shows the optimized design in which a different Reynolds number, Re₁ = 200 and Re₂ = 50, is set for each fluid. As the Reynolds number is defined using the pressure loss in this study, a higher Reynolds number can lead to a larger flow rate. Furthermore, the flow rates of fluid 1 and fluid 2 are $\dot {V}_{1}=0.340$ and $\dot {V}_{2}=0.260$, respectively, which are significantly different from the case using the same Re settings, as shown in Table 3. Consequently, it is observed that the flow channel of fluid 1 is relatively thinner and more deviant than the flow channel of fluid 2.

Fig. 15

Optimized result for Reynolds number Re₁ = 200, Re₂ = 50. Objective function value: J = 0.310

4.5.2 Effect of Prandtl number

Figure 16 shows the optimized results in a case of Pr₁ = 14, Pr₂ = 14. The parameters except for the Prandtl number are similar to the case of Pr₁ = 7, Pr₂ = 7 presented in Section 4.3. The Prandtl number shown in (31) is defined as the ratio of momentum diffusivity to thermal diffusivity. Hence, high Prandtl number results in low total heat transfer.

Fig. 16

Optimized result for Prandtl number Pr₁ = 14, Pr₂ = 14. Objective function value: J = 0.265

In Fig. 16, complex flow channels are obtained, which is similar to the case of Re₁ = 200, Re₂ = 200 shown in Fig. 14b. The reason for this similarity is related to the trade-off between the total heat transfer and the pressure loss. Increasing the Reynolds number corresponds with the eased pressure loss limit. In contrast, increasing the Prandtl number corresponds with the strict requirement for total heat transfer. This can be explained by the fact that Péclet numbers of both cases in Figs. 14b and 16 are identical; Pe₁ = 1400, Pe₂ = 1400. In addition, this similarity can be explained in the same way as the tendency of the temperature change of the fluids through the inlet to the outlet. That is, a higher Re prevents any decrease in the temperature, due to a higher flow rate. This feature is also observed in a higher Pr due to a smaller heat conductivity.

4.5.3 Effect of design domain size

To investigate the effect of the design domain size, the optimization is performed in various L_x, L_y, and L_z. Figure 17 shows the optimized results for L_x = 2L, L_y = 2L, and L_z = 4L, as well as for L_x = 4L, L_y = 4L, and L_z = 4L. The parameters are similar to the case of L_x = 4L, L_y = 2L, and L_z = 4L presented in Section 4.3.

Fig. 17

Optimized result for different design domain size: a L_x = 2L, L_y = 2L, L_z = 4L; b L_x = 4L, L_y = 4L, L_z = 4L. Objective function values: a J = 0.213; b J = 0.433

Although the flow channels are placed alternately regardless of the design domain size, different features are obtained in each case. For Fig. 17a, the branched channels are in the z direction instead of the x direction as found in the cases of Figs. 9 and 17b. Since the length in x direction is short and the heat exchange domain is small, a relatively sharp bend is obtained. From Fig. 17b, thick and flat flow channels are realized when the length in y direction is large. This is because the narrow flow channels are not necessary in case of a large heat exchange domain.

4.5.4 Effect of flow arrangement

Finally, the effect of the flow arrangement, i.e., the arrangement of the inlet and the outlet in each fluid, is investigated. Figure 18 displays the schematic diagram and the optimized results. We denote the arrangement of Fig. 18b and c by “U-counter” and “U-parallel,” respectively. The aim of this numerical example is to demonstrate that the proposed method can generate appropriate optimized configurations for each flow arrangement, whereas it is widely known that counter flow arrangements, as shown in Fig. 5, are generally more effective than other arrangements.

Fig. 18

Schematic diagram and optimized result of several flow arrangements: a parallel flow; b U-counter flow; c U-parallel flow. Objective function values: aJ = 0.289; b J = 0.294; c J = 0.263

From Fig. 18a, the flow channels of each fluid are placed alternately at right angles in parallel flow. It is discovered that the heat is mainly exchanged in the upstream region, and the temperature is nearly unchanged in the downstream region. This is because both fluids have approximately the same temperature after passing the branched section, and downstream fluid 1 cannot be adjacent to the upstream fluid 2, and vice versa, unlike in the case of counter flow. Similar features are found in Fig. 18c, U-parallel flow. In Fig. 18b, the high temperature difference can be maintained in the whole heat exchange surface, which is similar to counter flow. Based on these results, it can be confirmed that the outlet of the fluid 1 should be close to the inlet of the fluid 2, and vice versa, for efficient heat exchange.

5 Conclusions

In this paper, we proposed a density-based topology optimization method for two-fluid heat exchange problems. The novel aspect of the paper is that a representation model involving three states (two types of fluids and a solid wall) is defined using a single design variable field. To this end, we introduced two types of fictitious force terms, one in each flow field so that, essentially, the two fluids cannot mix.

We formulated the optimization problem as a maximization problem of the heat transfer rate under the fixed pressure loss. Based on the formulation, we investigated the effectiveness of the proposed method through three-dimensional numerical examples.

In the numerical examples, we first conducted the verification of the proposed representation model in a simple analysis model that has a flat plate between fluid 1 and fluid 2. We then demonstrated the performance of an optimized design in comparison with a reference design. We demonstrated the dependency of the optimized design with respect to the design conditions, i.e., Reynolds number, Prandtl number, design domain size, and flow arrangements. Accordingly, it was found that the proposed method can generate effective optimized designs for optimization problem concerning the two-fluid heat exchange system.

Conversely, one aspect of the proposed representation model has an issue, namely, control of the solid wall thickness is difficult due to the use of the simple model for representing the three states. This is an unresolved issue, which we plan to study in future work. In addition, we hope to apply the proposed method to practical designs of heat exchangers (Webb and Kim 2005).

In the review process of this paper after the first original submission, we identified a related reference (Høghøj et al. 2020), which was recently uploaded to arxiv.org as a preprint. This reference also used a single design variable field for designing two-fluid heat exchangers via topology optimization, and provided three-dimensional numerical examples. Including this reference, as research focusing on topology optimization for two-fluid heat exchange is a developing field, as mentioned in Section 1, future work would need to comprehensively investigate the effectiveness of each method under the same design conditions.