Nature-inspired optimization of tubular joints for metal 3D printing

Abstract

Steel tubular frames are often used to build a variety of structures because of their optimal mechanical properties and attractive forms. However, their joint fabrication involves a vast quantity of cutting and welding works, which induces high labour costs, material waste, and environmental pollution. The construction industry dominates the global carbon footprint, and it needs more sustainable products. Nature’s structures are also often tubular, and their joints (e.g. the knees of a human body, the nodes of trees and plants) are intrinsically optimized to maximize stiffness, resistance, and robustness. The 3D metal printing technology can enable a nature-inspired optimization of steel tubular joints, saving material waste and decreasing fabrication costs as well as the carbon footprint of the sector, since it is free from the constraints of traditional manufacturing. In this study, we designed new tubular joint shapes using solid isotropic material with the penalization (SIMP) method. The objective of the optimization was to maximize the structural performance of the node. The optimized node that used to be achieved after a complex manufacturing process composed of numerous cutting and welding operations, can now be 3D printed and then connected to the rest of the joint leading to a shorter fabrication time. We quantified the joints’ structural performance with different grades of optimization using non-linear finite element analysis. Compared with the conventional joint shapes, the new geometries offered a higher stiffness, resistance, and robustness. We performed a powder bed fusion simulation to analyze the residual stresses after production, and estimated the cost of the new solutions.

Introduction

Steel tubular structures are often used in the built environment (e.g. offshore wind platforms, bridges, stadiums) because of their mechanical qualities and elegant forms. The hollow cross-sections of the tubular steel profiles present a high multidirectional axial and bending inertia, which makes them an excellent choice to achieve a high strength and stability with minimum weight (Duarte et al. 2017). Furthermore, the steel tubular frames require less corrosion and fire protection materials than other frames types with similar mechanical properties. Apart from these mechanical advantages, their aesthetic appeal influences positively the choice of the decision makers (e.g. architect, building owner), since the tubes are more attractive and look more “natural” with respect to the open profiles. However, the fabrication of the tubular joints is problematic and expensive, because it contains a vast quantity of cutting, drilling, and welding works. The joint fabrication has a major impact on the overall project budget (Kanyilmaz 2019).

Mainly, three methods are adopted to fabricate tubular joints:

• a) Directly welding the profiles: Welded local stiffeners and gusset plates transfer the load among the profiles (Kurobane et al. 2004; Wardenier 1982). This method requires extensive quality controls to prevent the brittle failures caused by metallurgic reasons (e.g. the formation of cracks, hot and cold cracking, lamellar tearing, and hydrogen embrittlement).

• b) Steel casting (De Oliveira 2015), (Wang et al. 2013): Complex joint shapes can be produced by using a mould. They are useful to fabricate a single joint topology in series using the same mould. The shapes are limited by the mould availability; an entirely “free-form” shape is not possible.

• c) Space frames connectors (e.g. “bolt ball” or “Mero” connection) (Stephan et al. 2004), (Ghasemi et al. 2010). The discontinuities given by the multiple parts of such systems make the load transfer difficult.

These existing solutions involve a vast quantity of cutting, drilling, and welding works, which results in high fabrication costs, material waste, work-place safety problems, and a large carbon-print in the environment. Construction sector dominates the global carbon footprint with a 40% share among all sectors (IEA 2018). Half of this share is due to the embodied CO₂ that is in the building elements, and one third is covered by the structural system (Kaethner and Burridge 2012). Since the operational energy emissions are dropping down thanks to the passive building design and decarbonization of electricity grids, the contribution of the structural system to the carbon footprint will gain even more portion (Arnold 2020). With the global population estimated to increase by 2.5 billion by 2050, 230 billion square meters of new construction is expected (LETI 2020) (UN Environment 2017). Therefore, the operations involved in developing new structural systems can have a vital role in reducing the global CO₂ emissions. The need for the development of advanced assembling technologies to optimize the use of steel in buildings and infrastructure is explicitly mentioned as a “building block” (BB12: innovative steel applications for low CO2 emissions) in the document “Clean Steel Partnership Roadmap” developed by the European Steel Technology Platform (ESTEP) in the context of the EU goal and policies to achieve climate neutrality by 2050—the European Green Deal, the Clean Planet for All strategy, and the Paris Agreement (European Commission 2020).

A complex architectural design often requires the connection of asymmetric elements in the joints, which leads to a complex and lengthy fabrication process. Consequently, the joints also become more prone to extreme loads such as fatigue and seismic, due to the large stress concentrations at their connections and residual stresses at the welds. Several collapses have been reported in the literature related to these problems (Imam and Chryssanthopoulos 2010; Moan 1985; Vayas et al. 2006; Gulf and Mehr 2016). The construction industry needs more efficient solutions with reduced costs, person-hours and energy consumption (EU-Agency 2016; EU 2016). Simplifying the joint fabrication process can have a strong impact in that direction. Indeed, a significant research effort has been invested worldwide to improve the efficiency of tubular steel joints. A review article by the author (Kanyilmaz 2019) summarizes most of these studies; some of them are listed in Table 1.

Table 1 Summary of research efforts for the tubular joints

This article presents a new approach to design complex tubular joints, which is nature-inspired. Tubular structures of nature such as bones, trunks, branches have excellent mechanical properties thanks to their minimized weight and maximized moments of inertia (achieved by removing material from the cross-section centre) (Taylor 2015). Yet, nature does not have any of the above-mentioned “joint fabrication” issues. As a result of a billion years of evolution, it succeeded in the creation of flawless tube geometries and joints with minimized stress concentrations and maximized stiffness, resistance, and robustness. In many living beings (humans, animals, insects, trees), we can note outstanding examples of such tubular structures (Mattheck et al. 2018).

A bamboo hollow-section “culm” is an example of the naturally strengthened tubular joints, as described in Fig. 1a. Internal diaphragm elements resist the extra loads of the growing leaves and branches (Fig. 1b) at the nodes. Topology optimization methods and the quickly growing 3D printing technology (Delgado Camacho et al. 2018; Yakout et al. 2018) can allow us to “mimic” such examples in nature to design new tubular joints with higher stiffness, resistance, and robustness combined with easy fabrication.

Fig. 1

Anatomy of a bamboo culm (photo credits: Matt Truong, http://www.bamboobotanicals.ca)

In the literature, design optimization usually aims for the minimum weight. In the aerospace industry, this is called as “buy-to-fly” ratio (Siegel 1975), and it quantifies the weight ratio between the raw material and final component. The “buy-to-fly” approach does not fully apply to the built-environment. For building structures, most of the costs are hidden in the fabrication stage rather than weight. Indeed, this can also be observed in the static structures of nature: A tree body is not weight minimized; if a part of it is removed for any accidental action, it still stands (“optimized” for robustness). Therefore, in this study, the optimization is not limited to the “weight reduction”; we also aim to maximize the strength and robustness. The “robustness” property emerges when we accept a slightly heavier part weight to have a margin for exceptional loading. The solution is achieved by setting the topology optimization objective to design customized tubular joint node geometries (shape and wall thickness) locally to the internal stresses. Normally such a tubular joint is fabricated using numerous cutting and welding operations. Our optimized nodes can be 3D printed, and orthogonally bolted or welded to the conventional steel profiles of the frame, and this can reduce the fabrication difficulties.

Design approach and methodology

As a case study, a steel tubular structure fabricated by CIMOLAI SPA is considered (Fig. 2). It is a 67 × 124-m double-layer steel space frame structure with hollow cross-section elements of different shapes and sizes. Due to the unusual shape of the structure, the members intersect in several ways. There is a consequent development of complex joint geometries with a high density of welded connections. The present analysis focuses on a typical joint with the scope of developing a general methodology, which can also be applied to other joints with different configurations.

Fig. 2

The relevant portion of a steel tubular structure example, courtesy: CIMOLAI Spa

Two conventional joint fabrication methods of this structure are schematized in Fig. 3. In the conventional solution 1, there are many welding and cutting points to connect the various elements and to add stiffeners inside the circular hollow steel section (HSS). The profiles had to be cut and welded to insert the internal stiffeners. In conventional solution 2, the connection is fabricated using thread pre-stressed bolts and milled surfaces welded to the HSS elements. In this case, a removable access panel was necessary to apply the bolts, weakening the members.

Fig. 3

Conventional joint solutions for HSS tubes requiring significant work of cutting and welding

We propose an alternative to these highly complex and time/resource-consuming fabrication methods. Our design idea is to customize the complex node geometries at each joint with a free-form geometry optimized for high stiffness, resistance, and robustness. The result is a sort of “natural” stiffener inside the tubular joint. The optimized joints can be 3D printed and then welded (or bolted) to the rest of the structure made of conventional steel profiles, as described in Figs. 4 and 5.

Fig. 4

Parametric customization of the nodes of the structure

Fig. 5

Hybrid tubular joint concept

We call this approach “Structural Design for Additive Manufacturing (SDfAM)”, and its advantages can be listed as follows:

• The optimized joint is “naturally” strengthened and stiffened. This eliminates most of the operations described above for the two conventional solutions.

• The joint can be welded perpendicularly to the tube profiles with a smoother transition in the welded region.

• The orthogonal welding removes the joint region from the node core to a less stressed area, reducing the stress concentrations and residual stresses.

• Lower stress concentrations may result in higher static and fatigue performance of the joint.

• Reduced stress concentrations and force eccentricities will result in a decreased weld size in the joint (with an extra possibility to decrease the tube wall thickness).

• The welded zone becomes more accessible for periodic inspection and maintenance during the service life of the structure.

• All these can result in less shop-welding time and consumption and hence, less environmental impact.

This paper focuses on the design and development of the “optimized joint” rather than the welded region. The latter will be the subject of a future paper. The final design is achieved after several steps:

• 1^st step: Computer-aided design (CAD) for the concept and geometric design.

• 2^nd step: Computer-aided engineering (CAE) to construct the finite element model (FEM) from CAD geometry. Mesh, loads, and boundary conditions are defined.

• 3^rd step: Topology optimization starting with a “solid” body for design space (DS). The objective function and constraints are defined. The minimum compliance design with a volume fraction and stress constraints are considered.

• 4^th step: Finite element analysis (FEA) is performed for all the cases using Optistruct-Hyperworks 2017 (Altair University 2017).

Definition of the design space

To build-up the 3D model of the joint, a parametric joint builder tool was developed (Fig. 6). The original structure consists of four different groups of joints with similar geometry (170 types of joint geometries in total). For this article, two representative versions are generated: a symmetric (S) and an asymmetric case (A) (Fig. 7a and b).

Fig. 6

Parametric joint builder tool developed in Grasshopper

Fig. 7

Typical connection model in Rhinoceros

An unstiffened and a benchmark model have been simulated for each case (Fig. 8). The benchmark presents a conventionally cut-weld solution similar to the ones shown in Fig. 3. The design space is highlighted in Fig. 9. Boundary conditions (loads and support constraint) are linked to the non-design spaces that are constant volumes.

Fig. 8

Unstiffened and benchmark models

Fig. 9

CAD process of the typical symmetric joint (dimensions are in mm)

The new joint shapes are designed with the SDfAM approach. To analyze the new shapes, stainless steel 316 L (EN_6892–1 2009) has been chosen. Among the metal powder alloys available in the metal 3D printing market, this material has appropriate strength, durability, and weldability characteristics (Stratasys 2020) for the structure under investigation. The unstiffened and the benchmark shapes represent joints to be produced by traditional fabrication techniques. Therefore, for those shapes, a common steel material available in the market is selected (AISI, 1080), which has similar mechanical characteristics with SS 316 L. The yield strength of both materials is equal, while SS-316 L presents lower ultimate strength than the traditional steel, which keeps our results on the safe side. Figure 10 and Table 2 present the material properties used in the simulations.

Fig. 10

Material properties

Table 2 Material properties

As boundary conditions, a simple support at the bottom and axial loads on top and four lateral faces have been applied. Four different loading conditions were considered to make sure the worst-case scenario is present in the stress analysis: full compression, full tension, and two asymmetric loadings (Fig. 11).

Fig. 11

Loading conditions used in the simulations

The finite element model consisted of a solid discretized in a tetra-mesh generated by solidThinking Inspire. Its algorithms use a combination of HyperMesh and Simlab for meshing. The tetra-mesh configuration created in solidThinking Inspire presents first-order elements, which were fair and accurate for the initial set of analysis performed in this study. More advanced analysis has been performed using Hyperworks (Altair Engineering 2017).

Topology optimization of the tubular joint design space

Figure 12 shows our SDfAM process using a truss-optimization analogy: the removal of material from a solid body where it is not needed, based on stress analysis. This approach is well-established in high-tech industries, such as automotive and aerospace. In our case, the inner material distribution is considered as a design variable. The solid isotropic material with penalization (SIMP) method (Bendsøe and Sigmund 2004) is used.

Fig. 12

Topology optimization scheme process following the (SIMP) method

The design domain is discretized so that only the material densities equal to one remain and those equal to zero are cancelled. The topology optimization is performed with the Optistruct/Hyperworks software (Altair Engineering 2017) using the following inputs:

• Definitions of design and non-design spaces

• Minimum compliance, as objective

• Material density distribution, as variable

• Volume fraction and maximum stress, as constraints

Our objective of topology optimization is to minimize the compliance under volume and stress constraints (the joint stiffness is maximized when the compliance is minimum). For this reason, as constraints, we used different volume fractions of the design space (DS) that is described in Fig. 9. The optimized solution was found by the SIMP method when the objective function and the constraints reached the convergence. Material density is cancelled in the zones where the stresses are low and placed for high stress concentration zones according to the loading path. Thus, the full solid core of the joint is transformed into a sort of internal truss, resulting in “internal natural stiffeners”. These joints with new shapes are then validated through finite element analysis. Moreover, some authors have demonstrated the possibility to also improve the fracture resistance at an increasing volume fraction during the topology optimization process (Da et al. 2018) and to obtain a desired overall stiffness of the joints (Kang and Li 2017).

Table 3 shows the loading conditions considered for different shapes characterized by the degree of volume and stress constraints (σ_{Von Mises} < σ_yielding): full compression, full tension, asymmetric. “Robust”, “Medium-weight”, and “Light-weight” solutions are called respectively “DS-R”, “DS-M”, and “DS-L”, where the volume fractions of the design space (DS) are, respectively, 50%, 40%, and 30%.

Table 3 Topology optimization cases (The percentages refer to the volume fractions of the design space—DS)

The entire structure is analyzed using SAP2000 (Computer and Structures 2017) to estimate the design loads for the joints (Fig. 13). Ultimate limit state (ULS) and service limit state (SLS) combinations are considered under code permanent and accidental loads for the structure considering Milan, Italy, as the location of the construction site. The joints were mainly loaded in different combinations of compression and tension actions. Multiple combinations of axial loads observed in this analysis are considered during topology optimization.

Fig. 13

Structural analysis to decide the design load for the topology optimization

The weighted compliance C_W approach was considered as the objective function. This global response is the weighted sum of the compliance of each subcase or load case (Altair University 2017), and it is defined by the following equation:

$$ {C}_W={\sum}_i{W}_i{C}_i=\frac{1}{2}{\sum}_i{W}_i\ {u}_i^T\ {f}_i $$

where W_i is scale factor per each load case,${u}_i^T$is displacement vector per each load case, and f_i: applied force per each load case.

The shapes obtained from the topology optimization process require a further post-processing. Before the 3D printing stage, it is necessary to smoothen and clean the part surfaces to achieve uniform shapes. The control of parameters, such as thickness and voids in the joints, is also essential to produce regular geometries. For this reason, a parametric post-processing tool is developed using Grasshopper (https://www.grasshopper3d.com/) (Fig. 14). The geometry was intersected with cutting planes to generate the required number of control points, and from these, the new and smoother surfaces were built up with the original thicknesses.

Fig. 14

Thickness and smoothing control tool on Grasshopper

Finally, the stress values and distributions have been calculated through finite element analysis. An “envelope load combination” is created by linear superposition of results to find the maximum stress values. The different alternatives (DS-R, DS-M, DS-L, and a Benchmark) have been compared. The structural performance was monitored by a common reference point (RP) that is set at the intersection of structural profiles. This location showed the highest stress concentrations in the joint. The densities are plot as a scale of colours in Optistruct (Hyperworks solver) to interpret the results. The range of values is from 0 to 1 (Fig. 15) as an iso-contour plot. It represents the absence or presence of material, respectively. An intermediate value of 0.5 is selected because it shows defined shapes. Consequently, the values above 0.5 are displayed, and the other ones below 0.5 are filtered from the iso-contour plot.

Fig. 15

Density scale of colours

Each one of the TO solutions reached the convergence after several iterations (in the range of 25 to 28 iterations) to obtain the minimum compliance and the lowest percentage of violated constraints. The optimization resulted in stiffening the hollow section joint. A higher percentage of DS results in more internal stiffeners. For the DS-R case, two sets of stiffeners are formed: two vertical and two horizontal ones, creating an internal void in the joint. For the DS-M case, just two horizontal stiffeners are generated. This also occurs to the DS-L case, differing only on the thickness, because the two resulting horizontal stiffeners are thinner compared to those of the DS-M case. The trend of results can be observed in both symmetric and asymmetric joint cases (Figs. 16, and 17). Although the new solutions (DS-R, DS-M) slightly weigh more than the benchmark, they are expected to have a significantly better structural performance with easier fabrication.

Fig. 16

TO results for symmetric joint case (S)

Fig. 17

TO results for asymmetric joint case (A)

The first estimation of stresses with a lower computational time was obtained by linear analysis. For this initial part, two solutions were analyzed considering the weight: the robust case DS-R (50% DS) and the light case DS-L (30% DS) for the symmetric and asymmetric joints. Regarding the unstiffened symmetric joint cases (cross-section views are shown in Fig. 18), the most stressed regions correspond to the intersection zones where the structural profiles converge. In that case, the material reached yield stresses because of the high concentration of stresses. In current practice, the traditional (and costly) way of preventing this situation is to use welded stiffeners inside the geometry to decrease the stress concentrations in the critical zones. On the other hand, the new solutions provide much better performance with their “naturally” stiffened shapes thanks to the material distribution, which was optimized according to the different load paths.

Fig. 18

FEA results for symmetric joint case

The yielding stress was not exceeded in the proposed solutions. Figure 19 compares the structural performance in terms of maximum stresses and weight information among different topologies. The DS-R solution, with a slightly higher weight, significantly drops the maximum stresses in the joint. The light and benchmark joints perform similarly; however, the fabrication of the benchmark joint would require many cuts and welding operations.

Fig. 19

FEA results for symmetric joint case

In the asymmetric joint case (A), a similar trend of results is obtained (Fig. 20). The unstiffened joint presented the highest stress concentrations along the members’ intersection zone. As in the previous cases, the topology optimized joints with the “natural stiffener” formations represent a vast drop of the stress values and an improved distribution (Fig. 21).

Fig. 20

FEA results for asymmetric joint case

Fig. 21

FEA results for asymmetric joint case

A comparison of the linear analysis results of symmetric (S) and asymmetric (A) cases is presented in Table 4. Their optimized shapes presented a similar stress decrease against their respective unstiffened cases. Both DS-R solutions achieved a large percentage of reduction with respect to the corresponding unstiffened cases: 81% and 82% less, respectively, for the symmetric and asymmetric cases. Both DS-L cases reached an important stress decrease compared with the unstiffened cases: 76% and 78% less, respectively, for the symmetric and asymmetric. Despite the similarities in terms of shape and weight, the DS-L solutions presented an improved linear behaviour with respect to the benchmark joint: For example, the unstiffened joint stress reduction reaches 76%, with the symmetric symmetric (S) Vol = 30% DS case and 69% with the benchmark symmetric (S) case.

Table 4 Symmetric and asymmetric joints: stress reduction with respect to the unstiffened benchmark

Tests by non-linear failure analysis

The new joint proposals have been tested using non-linear failure analysis. Their behaviour has been compared among them and with the benchmark joint. Plastic deformations were induced in the joints under different loading conditions by loading them until failure. Hence, the collapse situation was predicted by determining which zones would be the first to reach the ultimate strain. From the four load cases used in the previous FEA analysis, the compression-tension (1) combination produced the highest stress values. Therefore, we chose this case for the non-linear analysis. The plastic strain curves were obtained from the Ramberg-Osgood criteria (Ramberg and Osgood 1934) for true stress-strain curves and respectively converted into effective plastic strain (Total strain–Elastic strain). The benchmark and light joints (from both symmetric and asymmetric groups) displayed the same plasticity scenarios. The central part of the stiffeners first exceeded the characteristic strain at rupture values for the benchmark and light shapes. Moreover, some local points at the level of the intersection zone reached plastic strains. Compared with the benchmark and DS-L shapes, the maximum stress values are much lower, and the stress distribution is smoother in DS-M and DS-R solutions. The DS-R and DS-M joints reduced the stresses, respectively, by 73% and 51%, compared with the unstiffened joint. Figure 22 and Fig. 24 display the stress and strain contour plots of all joints. Only for the non-linear analysis of the symmetrical cases, the intermediate volume fraction DS-M (40%DS) was introduced. This slight additional weight stiffed the joint, and it reduced the strain values with respect to the benchmark case, as it is shown in Fig. 22.

Fig. 22

Non-linear FEA results for symmetric joint cases

Metal additive manufacturing (MAM) alloys present lower ultimate strength than the conventional steel (used in the benchmark case). On the other hand, the strain at rupture for SS-316 L is higher than conventional steel (30% vs 25%). For this reason, DS-L case achieved slightly higher plastic strain value and a stress reduction, with respect to the benchmark case. Table 5 shows a comparison of non-linear performance between the benchmark solution and the optimized joints for the symmetric case. The analyzed values belong to the reference point (RP) when the joint was loaded at 1700 kN; at this value the unstiffened case reaches the ultimate strain.

Table 5 Stress and strain reduction with respect to the unstiffened joint-symmetric

Figure 23a shows the force versus displacement curves of all the symmetric cases. Figure 23b zooms in the linear portion of the force displacement graph to compare the initial stiffness in different cases. The optimized joints were able to develop higher resistance and stiffness and stiffness values thanks to the extra material distributed as a sort of “natural” stiffeners. The “robustness” property emerges in the case of DS-R joint, which is optimized accepting a slightly heavier weight to have a margin for exceptional loading. The DS-R joint (V = 50%) required much higher load values to reach the collapse, besides having the highest initial stiffness values. Under a load value of 1700 kN, the unstiffened benchmark case has already reached the ultimate strain and the highest values of displacements. The inclusion of stiffeners reduced the displacements, and higher load values can be applied. The DS-M and DS-L solutions (V = 40% and V = 30% DS) leave the linear region and reach the ultimate strain at a very close loading value with the benchmark case Fig. 24.

Fig. 23

Force vs. displacement non-linear curves of symmetric joints

Fig. 24

Non-linear FEA results for asymmetric joint cases

Fig. 25

Force vs displacement non-linear curves of asymmetric joints

Fig. 26

Metal additive manufacturing simulation process workflow

Fig. 27

Residual stresses (Von Mises) [MPa]

Fig. 28

Cost reduction forecast per piece manufactured by SLM for the next years based on literature studies

The asymmetric cases had a similar trend as well (Table 6). In DS-L, there is a reduction of stresses around 49% compared with 36% of the benchmark case. The strains in the (A) DS-L solution are three times lower than the benchmark joint. It presents an improved non-linear behaviour and similar percentages of stress decrease with the ones achieved by the symmetric cases. For the non-linear analysis of the asymmetric joints, it was not necessary to introduce the intermediate volume fraction DS-M (40%DS) because the lighter solution DS-L (30%DS) presented an enhanced non-linear performance with respect to the benchmark case. The (A) DS-R joint shows a significant reduction of stresses and strains, in the order of 73% and 100%. The natural stiffeners along the horizontal and vertical direction decrease the plastic strain values sharply. Figure 25a shows the force versus displacement curves of all the asymmetric cases and Fig. 25b zooms in the initial linear portion. The same trend of the behaviour as the symmetric cases is observed. These analyses highlight two general conclusions:

• A joint shape can be optimized to provide the same structural performance with the conventionally stiffened joint without the need for cutting and internal welding operations (“DS-L” joint proves this).

• With a slight increase of the joint weight, much more stiff, resistant and robust joints can be obtained (“DS-M”, and “DS-R” solutions prove this).

  Table 6 Stress and strain reduction with reference to the unstiffened joint asymmetric

Simulation of additive manufacturing process and preliminary cost estimations

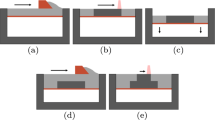
A simulation of the additive manufacturing process has been performed using the software Amphyon (Additive Works GmbH 2018). The powder bed fusion (PBF) process is considered. The main objective was to understand how the 3D printing stages can affect the mechanical properties of the connection. The selected case was the DS-R solution-symmetric with a volume fraction = 50% DS. The first three steps of the workflow include importing a tessellation file (STL), the orientation selection and the support generation (Fig. 26). The typical problems during the build-up of metal powder layers have been studied, such as residual stresses and distortions.

Post-process treatments can largely eliminate the residual stresses formed during the process. The orientation assessment is essential to evaluate the feasibility of a specific part to be printed within the build chamber. This process considers the deformation tendency and possible cracks that could be generated from a specific orientation (Additive Works GmbH 2018). In this case, a maximum overhang angle of 45° was selected. It requires a minimal amount of support density of 40% and 10% under overhanging and down faces, respectively. This is done by normalizing the value for the needed volume of supports for each orientation.

During the MAM process, high residual stresses are induced. For this reason, stress relief treatments are added most of the time. The simulations were performed under the assumptions of homogeneity of the material properties and thermal field. The base plate and the MAM part are assumed to be made of the same material. The thermal expansion and volume variation occur simultaneously along the part during the phase changes. For this reason, the plastic deformation after the annealing process is not affected by the expansion and contraction induced by additional stresses. Due to insufficient experimental data, the material models of Amphyon are restricted to be isotropic and ideally plastic. In the AM process, the yield strength restricts the residual stress, defining its maximum value and the deformation of the printed part after being released. Furthermore, an ideal plasticity mechanism is considered to describe the material behaviour (Additive Works GmbH 2018). The steel alloy SS316L used in the simulations contains the Young’s modulus and the maximum equivalent stress corresponding to the values obtained at annealing temperature. The mentioned properties were used referring to the experimental data presented by (Alberg 2003), where different heat treatment processes were carried out on stainless steel samples. For this study, Young’s modulus is expected to be around 50% of the value at room temperature with the correspondent temperature and maximum stress.

Figure 27 displays the effect of the simulated heat treatment before the removal from the base stage. During the first simulation without heat treatment, the stress values were close to the yielding threshold. This undesirable result tends to produce deformations and consequent distortions on the piece.

On the other hand, when the heat treatment is applied after the build-up of all layers and the support removal stage, the residual stresses reduce significantly. Thus, the risk of potential cracking throughout the piece or failures on the supports structure can be reduced. The distortions and the respective compensation are consequences of high displacements during the build-up process. It derives into the warping of the part and its deformation. The supports have a significant role in preserving the original shape under the stresses arising from the process. If the part geometry is regular, the original geometry of the pieces may be preserved without heat treatment.

Since metal additive manufacturing is still at the beginning of becoming a massive fabrication method, the initial production costs are relatively high. Nevertheless, projections show that in the next years, the costs will start to be fair competition with traditional technologies. In the literature, different cost modelling approaches are available (Zistl 2014; Piili et al. 2015; Liu 2017; Costabile et al. 2017; Previtali et al. 2017). Previtali et al. showed that, in the case of tube-forming tools, the selective laser melting (SLM) system and productivity were the main factors to define the production cost. They predicted a major reduction in the production costs due to the higher productivity expected from the next generation machines and a decrease in the machine costs (Previtali et al. 2017). In our study, the cost of building one piece of the topology-optimized connections is estimated with reference to the results obtained from the study done by (Liu 2017; Zistl 2014) using SLM method, which is classified under PBF process. The cost of the SLM part was divided into five main sections: machine (26.9%), auxiliary (38.2%), material (29.8%), energy (1.4%), and labour cost (3.6%). Under such observations, Fig. 28 shows the possible future cost of the joints studied in this work, when printed one piece a time. It is also noted that the SLM costs can decrease in relation with the production volume. This is because the machine cost and auxiliary costs are amortized over the number of parts manufactured. It is estimated that producing a high-volume series can imply savings of up to 80% with respect to printing a small number of pieces (Piili et al. 2015). The cost values are approximate and show a possible reduction trend in the process costs of the joints studied in this article, based on the current literature.

Conclusions

Typical connection details of steel structural joints involve a vast quantity of cutting, drilling, and welding works. This conventional way of fabrication results in high labour costs and material waste, safety problems, and pollution to the environment. Smarter joint shapes are needed to decrease the carbon footprint and costs hidden in the fabrication process of structures. Shapes from “nature” have not been exploited so far, because of the limits of conventional manufacturing techniques. Now, more than ever, there is a colossal chance to mimic nature to obtain near-perfect engineering solutions, thanks to the new manufacturing techniques that removed geometric limits (e.g. additive manufacturing).

In this study, we proposed new tubular joint shapes that can already be stiffened during their additive production. We achieved the solutions using solid isotropic material with the penalization (SIMP) method. The objective of the optimization was to maximize the structural performance of the node, which is normally achieved after a complex manufacturing process composed of numerous cutting and welding operations. In our case, the optimized nodes can be 3D-printed and then connected to the rest of the joint, following an easier manufacturing process. The new shapes are tested, and their performance is quantified by non-linear finite element analysis.

The optimized (new) solutions offer superior structural performance with similar or less weight without cutting and welding operations typically needed to stiffen and strengthen the conventional tubular joints. Under extreme loads of built environment, such an increase in structural performance merged with the fast and simple fabrication can be much more valuable than saving a few kilogrammes of material. At the fabrication stage, such joints can be welded perpendicularly to the tube profiles with a smoother transition in the welded region. This orthogonal welding would remove the joint region from the node core to a less stressed area, reducing the stress concentrations and residual stresses. Reduced stress concentrations and force eccentricities would result in a decreased weld size in the joint (with an extra possibility of decreasing the tube wall thickness). All of these can result in less shop-welding time and consumption and hence, less environmental impact.

Regarding the metal additive manufacturing (MAM), a simulation of the SLM process has been performed. In this way, we confirmed that the parameters of the 3D printing process that come from previous researches in SLM SS316L were appropriate. The built orientation of 45° was needed. The distortions, which can be induced by the presence of residual stresses, were decreased significantly by adding proper supports during the process and post-process heat treatment. Therefore, the final shape remained almost the same compared with the first CAD design in terms of distortion.

Metal 3D printing may be still expensive currently for structural engineering applications for their sizes. However, future projections show that the cost of the process will be much lower in 5 to 10 years. In that case, the solutions provided in this study may be alternatives to traditional joint fabrication methods. The design procedure used in this research can also be applied to other joints with different forms.

Outlook

Metal additive manufacturing (MAM) is currently at an early stage of development, and mainly concentrated at the level of research and prototyping in high-tech sectors such as automotive and aerospace. A significant market for the construction sector is expected to appear in the next decades. But once MAM technology allows larger-scale applications, National and European regulations will still represent a barrier to turn metal printed parts into commercial products.

Building code regulations are explicitly needed for the construction sector. They need to be general and commonly applicable in all countries (e.g. Provision of EN proposals to be accepted and introduced by the National Bodies). For instance, in Europe, EN 1090 (EN_1090 2011) specifies requirements for structural steel and aluminium elements as well as for components placed on the market as construction products. EN1090 regulates essential requirements such as mechanical resistance and stability, safety in case of fire, hygiene, health and the environment, safety and accessibility in use, protection against noise, energy economy, and heat retention and sustainable use of natural resources. Although the nature of EN1090 is open for innovative components, there is currently no specific reference to the metal additive manufacturing.

This article introduced a new idea of joint fabrication for steel structures, and it focused on the design and topology optimization stage. This is the primary crucial step to offer new products in the market.

To use such innovative solutions in the construction market, experimental studies must be performed, aiming to develop general design rules and procedures in compliance with the building codes. The focus must be given to the structural integrity between the design space and the rest of the structure, welding process parameters, and additive manufacturing process (material models, microstructure characteristics, anisotropy, and post-treatment).