Skip to main content
SpringerLink
Log in

An efficient method for time-dependent reliability prediction using domain adaptation

  • Research Paper
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

Due to dynamic uncertainties presence in service and performance conditions, time-dependent reliability prediction of a component or structure is a challenging problem. In this research, a transfer learning-based technique is proposed to predict the reliability in the future. The complete time interval is divided into two sub-intervals namely, present interval and future interval. It is assumed that the performance function information is available for the present interval only. Transfer learning, specifically domain adaptation is used to transform the stochastic processes to be represented in a way that their sample spaces in different time durations are made closer while maintaining some of their statistical properties such as variance. In order to transform the stochastic processes, correlated samples of stochastic processes are generated using a space-filling sampling technique for the complete time interval. An adaptive Kriging surrogate model is then built using the performance information available for the present interval only using transformed stochastic process samples. The built Kriging model is employed to estimate and predict the reliability for present and future intervals without retraining it using future data. Results show that the proposed method can predict the failure probability in present and future intervals accurately with significant efficiency improvement.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  • Andrieu-Renaud C, Sudret B, Lemaire M (2004) The PHI2 method: a way to compute time-variant reliability. Reliab Eng Syst Saf 84:75–86

    Article  Google Scholar 

  • Bataleblu AA (2019) Computational intelligence and its applications in uncertainty-based design optimization. Bridge Optimization-Inspection and Condition Monitoring. IntechOpen, In

    Google Scholar 

  • Dellino G, Meloni C (2015) Uncertainty management in simulation-optimization of complex systems. Springer

  • Du X (2014) Time-dependent mechanism reliability analysis with envelope functions and first-order approximation. J Mech Des 136:81010

    Article  Google Scholar 

  • Dubourg V, Sudret B, Bourinet J-M (2011) Reliability-based design optimization using kriging surrogates and subset simulation. Struct Multidiscip Optim 44:673–690

    Article  Google Scholar 

  • Echard B, Gayton N, Lemaire M (2011) AK-MCS: an active learning reliability method combining Kriging and Monte Carlo simulation. Struct Saf 33:145–154

    Article  Google Scholar 

  • Gretton A, Bousquet O, Smola A, Schölkopf B (2005) Measuring statistical dependence with Hilbert-Schmidt norms. International conference on algorithmic learning theory. Springer, In, pp 63–77

    MATH  Google Scholar 

  • Hu Z, Du X (2013a) Time-dependent reliability analysis with joint upcrossing rates. Struct Multidiscip Optim 48:893–907

    Article  MathSciNet  Google Scholar 

  • Hu Z, Du X (2013b) A sampling approach to extreme value distribution for time-dependent reliability analysis. J Mech Des 135:071003

    Article  Google Scholar 

  • Hu Z, Du X (2015) Mixed efficient global optimization for time-dependent reliability analysis. J Mech Des 137:051401

    Article  Google Scholar 

  • Hu Z, Mahadevan S (2016) A single-loop kriging surrogate modeling for time-dependent reliability analysis. J Mech Des 138:61406

    Article  Google Scholar 

  • Jiang M, Huang Z, Qiu L et al (2017) Transfer learning-based dynamic multiobjective optimization algorithms. IEEE Trans Evol Comput 22:501–514

    Article  Google Scholar 

  • Jones DR, Schonlau M, Welch WJ (1998) Efficient global optimization of expensive black-box functions. J Glob Optim 13:455–492

    Article  MathSciNet  Google Scholar 

  • Li C-C, Der Kiureghian A (1993) Optimal discretization of random fields. J Eng Mech 119:1136–1154

    Article  Google Scholar 

  • Lophaven SN, Nielsen HB, Søndergaard J (2002) DACE: a Matlab kriging toolbox. Citeseer

    Google Scholar 

  • Lu J, Behbood V, Hao P et al (2015) Transfer learning using computational intelligence: a survey. Knowledge-Based Syst 80:14–23

    Article  Google Scholar 

  • Lutes LD, Sarkani S (2004) Random vibrations: analysis of structural and mechanical systems. Butterworth-Heinemann

  • Matasci G, Volpi M, Kanevski M et al (2015) Semisupervised transfer component analysis for domain adaptation in remote sensing image classification. IEEE Trans Geosci Remote Sens 53:3550–3564

    Article  Google Scholar 

  • Min ATW, Sagarna R, Gupta A et al (2017) Knowledge transfer through machine learning in aircraft design. IEEE Comput Intell Mag 12:48–60

    Article  Google Scholar 

  • Pan SJ, Yang Q (2009) A survey on transfer learning. IEEE Trans Knowl Data Eng 22:1345–1359

    Article  Google Scholar 

  • Pan SJ, Tsang IW, Kwok JT, Yang Q (2010) Domain adaptation via transfer component analysis. IEEE Trans Neural Netw 22:199–210

    Article  Google Scholar 

  • Rasmussen CE (2003) Gaussian processes in machine learning. Summer School on Machine Learning. Springer, In, pp 63–71

    MATH  Google Scholar 

  • Rice SO (1945) Mathematical analysis of random noise. Bell Syst Tech J 24:46–156

    Article  MathSciNet  Google Scholar 

  • Roshanian J, Bataleblu AA, Ebrahimi M (2018) A novel evolution control strategy for surrogate-assisted design optimization. Struct Multidiscip Optim 58:1255–1273

    Article  Google Scholar 

  • Roshanian J, Bataleblu AA, Ebrahimi M (2020) A novel metamodel management strategy for robust trajectory design of an expendable launch vehicle. Proc Inst Mech Eng Part G J Aerosp Eng 234:236–253

    Article  Google Scholar 

  • Schneider R, Thöns S, Straub D (2017) Reliability analysis and updating of deteriorating systems with subset simulation. Struct Saf 64:20–36

    Article  Google Scholar 

  • Shawe-Taylor J, Cristianini N (2004) Kernel methods for pattern analysis. Cambridge University Press

  • Shi Y, Lu Z, Xu L, Chen S (2019) An adaptive multiple-Kriging-surrogate method for time-dependent reliability analysis. Appl Math Model 70:545–571

    Article  MathSciNet  Google Scholar 

  • Singh A, Mourelatos ZP (2010) On the time-dependent reliability of non-monotonic, non-repairable systems. SAE Int J Mater Manuf 3:425–444

    Article  Google Scholar 

  • Stein M (1987) Large sample properties of simulations using Latin hypercube sampling. Technometrics 29:143–151

    Article  MathSciNet  Google Scholar 

  • Sun H (2005) Mercer theorem for RKHS on noncompact sets. J Complex 21:337–349

    Article  MathSciNet  Google Scholar 

  • Tenne Y, Goh C-K (2010) Computational intelligence in expensive optimization problems. Springer Science & Business Media

    Book  Google Scholar 

  • Vennell R (2011) Estimating the power potential of tidal currents and the impact of power extraction on flow speeds. Renew Energy 36:3558–3565

    Article  Google Scholar 

  • Wang Z, Chen W (2017) Confidence-based adaptive extreme response surface for time-variant reliability analysis under random excitation. Struct Saf 64:76–86

    Article  Google Scholar 

  • Wang Z, Wang P (2015) A double-loop adaptive sampling approach for sensitivity-free dynamic reliability analysis. Reliab Eng Syst Saf 142:346–356

    Article  Google Scholar 

  • Wang Z, Mourelatos ZP, Li J et al (2014) Time-dependent reliability of dynamic systems using subset simulation with splitting over a series of correlated time intervals. J Mech Des 136:061008

    Article  Google Scholar 

  • Wang Z, Cheng X, Liu J (2018) Time-dependent concurrent reliability-based design optimization integrating experiment-based model validation. Struct Multidiscip Optim 57:1523–1531

    Article  Google Scholar 

  • Wang Z, Liu J, Yu S (2019) Time-variant reliability prediction for dynamic systems using partial information. Reliab Eng Syst Saf 106756

  • Yan K, Kou L, Zhang D (2017) Learning domain-invariant subspace using domain features and independence maximization. IEEE Trans Cybern 48:288–299

    Article  Google Scholar 

  • Yu S, Wang Z (2018) A novel time-variant reliability analysis method based on failure processes decomposition for dynamic uncertain structures. J Mech Des 140:51401

    Article  Google Scholar 

  • Yu S, Wang Z (2019) A general decoupling approach for time-and space-variant system reliability-based design optimization. Comput Methods Appl Mech Eng 357:112608

    Article  MathSciNet  Google Scholar 

  • Yu S, Wang Z, Zhang K (2018) Sequential time-dependent reliability analysis for the lower extremity exoskeleton under uncertainty. Reliab Eng Syst Saf 170:45–52

    Article  Google Scholar 

  • Zafar T, Wang Z (2020) Time-dependent reliability prediction using transfer learning. Struct Multidiscip Optim:1–12

  • Zhang D, Han X (2020) Kinematic reliability analysis of robotic manipulator. J Mech Des 142

  • Zhao H, Yue Z, Liu Y et al (2015) An efficient reliability method combining adaptive importance sampling and Kriging metamodel. Appl Math Model 39:1853–1866

    Article  MathSciNet  Google Scholar 

  • Zhou X-Y, Gosling PD, Ullah Z, Pearce CJ (2016) Exploiting the benefits of multi-scale analysis in reliability analysis for composite structures. Compos Struct 155:197–212

    Article  Google Scholar 

Download references

Acknowledgements

This research was partially supported by National Key R&D Program of China under the Contract No. 2017YFB1302301 and the National Natural Science Foundation of China under the Contract No. 11472075.

Author information

Authors and Affiliations

  1. School of Mechanical and Electrical Engineering, University of Electronic Science and Technology of China, Chengdu, 611731, People’s Republic of China

    Tayyab Zafar & Zhonglai Wang

  2. Center for System Reliability and Safety, University of Electronic Science and Technology of China, Chengdu, 611731, People’s Republic of China

    Tayyab Zafar & Zhonglai Wang

  3. National University of Sciences and Technology (NUST), Islamabad, Pakistan

    Tayyab Zafar

Authors
  1. Tayyab Zafar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhonglai Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhonglai Wang.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Replication of results

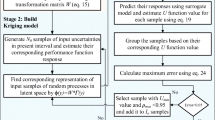
The results presented in this work are based on the flowchart in Fig. 1. In order to replicate the results, a series of Matlab code is provided as supplementary material. The attached Matlab file is named as “Main.m” and other function files can be utilized to compute the time-dependent reliability in case 4.2. For replication of the results of other cases in the proposed work, information of input variables and the random process can be modified in the corresponding source codes. It should be noted that the results presented in the paper are an average of 20 individual runs.

Additional information

Responsible Editor Shapour Azarm

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Highlights of the paper

• A transformation matrix is built to transform the stochastic process samples in the present and the future interval using domain adaptation.

• A domain adaptation based Kriging surrogate model is used to predict the time-dependent reliability for the future interval.

• A time-dependent reliability prediction method is proposed with improved efficiency and ensured accuracy.

• The proposed method can predict the time-dependent reliability for the performance function involving stationary as well as non-stationary stochastic processes.

Electronic supplementary material

ESM 1

(M 246 bytes)

ESM 2

(M 755 bytes)

ESM 3

(M 882 bytes)

ESM 4

(M 1 kb)

ESM 5

(M 1 kb)

ESM 6

(M 8 kb)

ESM 7

(M 538 bytes)

ESM 8

(M 1 kb)

ESM 9

(M 5 kb)

ESM 10

(M 868 bytes)

ESM 11

(M 859 bytes)

ESM 12

(M 767 bytes)

ESM 13

(M 814 bytes)

ESM 14

(M 592 bytes)

ESM 15

(M 2 kb)

ESM 16

(M 490 bytes)

ESM 17

(M 4 kb)

ESM 18

(M 377 bytes)

ESM 19

(DOCX 16 kb)

ESM 20

(DOCX 17 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zafar, T., Wang, Z. An efficient method for time-dependent reliability prediction using domain adaptation. Struct Multidisc Optim 62, 2323–2340 (2020). https://doi.org/10.1007/s00158-020-02707-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-020-02707-z

Keywords

Search

Navigation