1 Introduction

When passing through highly populated areas, the noise emitted by railway vehicles can cause severe nuisance and prejudice to nearby inhabitants. It is estimated that about 12 million people during the day and 6 million during the night are affected daily in Europe by this phenomenon (Clausen et al. 2012) and it is well known that a prolonged exposure to the levels emitted by railway vehicles is associated with major health problems, such as cardiovascular diseases and difficulties when falling asleep (WHO 2011). This makes it a necessity to adopt expensive measures to mitigate noise that limit the growth of the railway network, a problem that is increasingly relevant with the advance of climate change, the railway being the least polluting mass transport system (de Vos 2016). Among the types of noise emitted by railway vehicles, squeal, aerodynamic and rolling noise are considered as the most relevant (Thompson 2010). This work will focus on the latter, as it is predominant for the usual operating conditions of railway vehicles in urban areas.

Rolling noise is generated by the vibration of the wheel and rail induced by the interaction force generated due to the irregularities present in their surfaces, the so-called combined roughness. Thus, together with the rail, the wheel is one of the main sources of rolling noise generation, especially above \(\sim 1-2\) kHz depending on the wheel diameter (Thompson 1988; Remington 1987; Thompson et al. 2018). It is for this reason that the study of possible methods for the acoustic radiation attenuation of this component has been, and is nowadays, an active field of research. Previous works have covered various mitigation measures applied in the wheel for rolling noise, such as the implementation of bogie shrouds (Jones et al. 1996), retrofitting of freights with composite brake blocks (Bühler 2006), damping solutions developments like friction damping rings (Wang et al. 2019), resilient wheels (Bouvet et al. 2000; Cigada et al. 2008) and sandwich-type dampers (Merideno et al. 2014).

In particular, the present work is focused on optimization techniques to address the wheel noise issue. These have been applied in the past to some components involved in rolling noise generation, such as the track (Nielsen 1994; Vincent et al. 1996) and sleepers (Nielsen 2000). In regard to the wheel, there are different works that have applied optimization approaches with different purposes. For example, in Lee et al. (2019) it is presented a process centred on optimizing the web curvature with the intention of reducing wear damage and in Cui et al. (2019) the goal is to find the wheel profile that reduces the flange/rail gauge corner wear while ensuring an adequate vehicle dynamic behaviour. Considering those publications aiming to diminishing the rolling noise, first, a wheel shape optimization by means of genetic algorithms (GA) was presented in Efthimeros et al. (2002) with the objective of reducing the sound power emission, implementing a simplified methodology for the calculation of the SWL which did not include the interaction between wheel and track neither the radiation efficiencies, therefore not considering fundamental aspects of wheel noise radiation as the surface velocity of vibration. Later, in Nielsen and Fredö (2006) a response surface methodology (RSM) was used with the same purpose, considering wheels with a constrained damping layer. The scope of the work was to develop a methodology capable of minimizing, under high-speed operation, both dynamic wheel-rail contact loads and rolling noise, the latter calculated with the software TWINS (Janssens et al. 2014a, b), thus ensuring a full SWL calculation methodology (Thompson et al. 1996a, b; Jones and Thompson 2003) that includes wheel/track interaction. The study was limited to a 3-level full factorial design of experiments, with a total of 81 wheel designs tested.

Following these previous publications, the present work describes a railway wheel cross sectional geometric optimization by means of a GA with two different methodologies: a first one based on the direct minimization of the SWL, named LA, W-min methodology, and a second one based on the maximization of the natural frequencies (NF) of the wheel, named NF-max methodology. GAs, developed for the first time in Holland (1975), are part of the derivative-free optimization methods, which allow an effective approach for optimization in complex non-linear problems where no analytical expression of the objective function exists and no derivative information is available (Rios and Sahinidis 2013), as the one addressed in this paper. Since GAs do not require gradient information, they can be successful regardless of the nature of the objective functions and constraints and, as a global optimization technique, there is a greater chance of convergence to a global solution rather than to a local one (Marler and Arora 2004). In addition, they are suited for large-scale problems, as the number of function evaluations required can be scaled independent of the problem dimension (Hare et al. 2013). This way, due to the combination of a GA-based optimizer with the TWINS model for the SWL calculation, the proposed LA, W-min methodology offers a direct, accurate and potentially effective way of minimizing the railway wheel noise taking into account the whole dynamic process. Moreover, since this approach may imply a high computational cost, the second methodology presented, NF-max, attempts to indirectly minimize the radiated SWL with less computational cost and mathematical complexity. The main development areas of the work are the implementation of the vibro-acoustic behaviour of the wheel and rail, the geometrical parametrization of the wheel, its structural analysis and the integration of these parts within an optimization workflow. The optimization algorithm used is thought to be modular, the rest of the methodology still being applicable if another algorithm is chosen by the user.

Following this introduction, the dynamic and acoustic models are detailed in Section 2. Then, the optimization algorithm implemented is further described in Section 3. Later, results are discussed in Section 4. Conclusive remarks are presented in Section 5.

2 Theoretical model

In the present section, the calculations made during the optimization process are detailed. First, the system composed by the rail and the wheel as well as the associated dynamics is described, followed by the derivation of the railway wheel response. Afterwards, the formulation for calculating its radiated sound power and the implemented high-cycle fatigue analysis is presented. For further details related to the dynamic and acoustic radiation models, the reader is referred to the source of the models used in this paper, the work of D. J. Thompson and co-authors, implemented in the commercial software TWINS (Thompson 2010; Janssens et al. 2014b).

2.1 Dynamic model

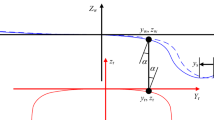
The system describing rolling noise generation mechanism is composed by a continuously supported rail and a wheel interacting at the contact point. The rail is described as a Timoshenko beam (Timoshenko and Gere 1963) and the wheel/rail interaction in the radial and axial directions is modelled by a contact spring, as presented in Fig. 1. In regard to the excitation of the system, it is generated by the introduction of a roughness amplitude which is assumed to act only in the vertical direction (Thompson 1993a). The roughness is defined by the standard prEN13979-1 (DIN 2017) for a train moving at the speed of V = 80 km/h, as seen in Fig. 2, and expressed in one-third octave bands. Therefore, when the wheel travels along the rail, this roughness amplitude generates a relative movement between the wheel/rail system which produces a contact force \(\bar {F_{c}}\). In addition, a contact filter (Thompson 2010; Remington 1976) is applied in order to consider the attenuation effect of the contact patch size in the force.

Fig. 1
figure 1

Wheel/rail interaction model

Full size image
Fig. 2
figure 2

Frequency spectrum of the roughness defined by prEN13979-1 (DIN 2017) for a vehicle moving at 80 km/h and cast-iron block brakes

Full size image

Then, assuming a roughness amplitude r, the contact force \(\bar {F_{c}}\) would be derived through

$$ \bar{r} = \boldsymbol{H}_{sys} \bar{F_{c}} , $$
(1)

where \(\bar {r}\) is a vector with amplitude r in the vertical direction and Hsys is the combined receptance of the system defined as (Thompson 2010)

$$ \boldsymbol{H}_{sys} = \boldsymbol{H}_{w} + \boldsymbol{H}_{r} + \boldsymbol{H}_{c} , $$
(2)

with Hw, Hr and Hc being the receptances in matrix form of the wheel, rail and contact, respectively, which are defined later.

Once the contact force \(\bar {F_{c}}\) has been derived, it is immediate to obtain the response of the wheel for the j th degree of freedom (d.o.f.)

$$ u_{w,j} = -\sum\limits_{i=1}^{3} H_{w,ji} F_{c,i} , $$
(3)

where Hw, ji is the receptance of the wheel for the j th d.o.f. when the force is applied at the contact point in the i th direction and Fc, i is the value of the contact force in the i th direction; directions 1, 2 and 3 representing directions x, y and z, respectively.

In the following sections, the receptances corresponding to each component of the system necessary to build the global receptance and to solve the dynamic interaction problem will be explained with further detail.

2.1.1 Wheel receptance

The description of the dynamics of the wheel is given from its modeshapes, which are previously calculated using a FEM approach. These modeshapes are classified with the (n, m) notation according to the number of nodal diameters n and nodal circumferences m (Cigada et al. 2008; Thompson 1993b). For illustration purposes, Fig. 3 shows several modeshapes and their respective classification.

Fig. 3
figure 3

Example of modeshapes of a railway wheel and its corresponding (n, m) classification. a (n = 0, m = 1). b (n = 4, m = 0). c (n = 2, m = 1). d (n = 4, m = 2)

Full size image

In the case of a stationary wheel, the receptance is derived from modal superposition as Thompson (1993b)

$$ H_{w,jk} (\omega)= \sum\limits_{n=0}^{\infty} \sum\limits_{m=0}^{\infty} \frac{{\Psi}_{nmj} {\Psi}_{nmk}}{m_{nm} ({\omega}_{nm}^{2} - \omega^{2} + 2i \xi_{nm} \omega_{nm}\omega)} , $$
(4)

where Ψnmj and Ψnmk are the modal amplitudes of the modeshape (n, m) for direction j and k, respectively; mnm is the modal mass of the corresponding modeshape, ξnm is the modal damping ratio, ωnm is the NF of the corresponding modeshape and ω the angular frequency at which the receptance is calculated. It should be noted that both radial and axial modeshapes are included in the modal superposition.

2.1.2 Rail receptance

The rail behaviour is modelled using a Timoshenko beam (Timoshenko and Gere 1963) on a continuous foundation and, therefore, takes into account shear deformation and rotational inertia. The continuous foundation, where rail pads, sleepers and ballast are included, is described by a spring-mass-spring system (Thompson et al. 1996b). A brief schematic of such system can be seen in Fig. 4.

Fig. 4
figure 4

Rail on continuous foundation represented by spring-mass-spring system

Full size image

In the present case, the direct receptance of the rail in the contact point for a given direction is defined by (Grassie et al. 1982)

$$ H_{r,jj} (\omega) = \frac{1}{2\pi i} {\int}_{-i \infty}^{i \infty} -\frac{1}{\tilde{G}A\kappa} \frac{s^{2}+C_{1}(\omega)}{s^{4}+C_{2}(\omega) s^{2} + C_{3}(\omega)} ds , $$
(5)

with

$$ \begin{array}{@{}rcl@{}} C_{1} (\omega) &=& \frac{-\tilde{G}A\kappa + \rho I \omega^{2}}{\tilde{E}I} , \end{array} $$
(6)
$$ \begin{array}{@{}rcl@{}} C_{2} (\omega) &=& \frac{\rho I \omega^{2}}{\tilde{E}I} - \frac{1}{\tilde{G}A\kappa} \left( \frac{\tilde{k}_{p}^{\prime} (\tilde{k}_{b}^{\prime} - m_{s}^{\prime} \omega^{2})}{\tilde{k}_{p}^{\prime} + \tilde{k}_{b}^{\prime}-m_{s}^{\prime}\omega^{2}} - \rho A \omega^{2} \right) , \end{array} $$
(7)
$$ \begin{array}{@{}rcl@{}} C_{3} (\omega) &=& \frac{\tilde{G}A\kappa - \rho I \omega^{2}}{\tilde{G}A\kappa \tilde{E}I} \left( \frac{\tilde{k}_{p}^{\prime}(\tilde{k}_{b}^{\prime} - m_{s}^{\prime} \omega^{2})}{\tilde{k}_{p}^{\prime} + \tilde{k}_{b}^{\prime} - m_{s}^{\prime} \omega^{2}} - \rho A \omega^{2} \right) , \end{array} $$
(8)

where \(\tilde {k}_{p}^{\prime } = k_{p}^{\prime } (1 + i \eta _{p})\) and \(\tilde {k}_{b}^{\prime } = k_{b}^{\prime } (1 + i \eta _{b})\). \(k_{p}^{\prime }\), \(k_{b}^{\prime }\) and \(m_{s}^{\prime }\) are the rail pad stiffness, ballast stiffness and sleeper mass, respectively, divided by the spacing between sleepers (stiffness and mass per unit length); ηb and ηp represent the ballast and pad damping loss factor; κ is the Timoshenko shear coefficient; I the area moment of inertia of the rail cross section; A is the cross section area; ρ the rail density and s is a complex propagation factor. Structural damping is included in the definition of the Young modulus as \(\tilde {E} = E (1+i\eta _{r})\) and in the shear modulus \(\tilde {G} = G (1+i\eta _{r})\), ηr being the loss factor of the rail (Thompson 2010). Depending on which set of characteristics values are used, the direct receptance in the x direction Hr, xx or in the y direction Hr, yy is derived.

Then, (5) is integrated in the complex domain by means of the theory of residues (Lang 1985), which yields

$$ H_{r,jj} (\omega) = \underset{\substack{k with \\ Res(s_{k}) <0}}{\sum} Res(s_{k}) , $$
(9)

with

$$ Res(s_{k}) = \frac{-1}{\tilde{G}A\kappa} \frac{{s}_{k}^{2} + C_{1}(\omega)}{4 {s}_{k}^{3} + 2 C_{2}(\omega) s_{k}} $$
(10)

where sk corresponds to the permissible complex propagation constants of free vibration for a given excitation frequency ω.

The rail cross receptance Hr, xy cannot be predicted directly using the Timoshenko beam model, because the vertical and lateral motion are uncoupled. In practice, this cross-coupling between a vertical force and a lateral response is not negligible, and the cross receptance Hr, xy is derived from the geometrical average of vertical receptance Hr, xx and lateral receptance Hr, yy (Thompson et al. 1996b)

$$ H_{r,xy} (\omega) = X \sqrt{H_{r,xx}(\omega) H_{r,yy}(\omega)} , $$
(11)

where X is an empirically estimated parameter from track characterization tests as

$$ L_{X} = 20 \log|X| $$
(12)

LX = − 15 dB being the best value to fit the numerical and experimental results in the track type used in the present work (bibloc track) (Thompson et al. (1996a, b)).

It should be noted that there is a frequency limit for the application of the described model, defined by that frequency where the condition ρIω2 ≥ GAκ is met, from which the Timoshenko beam formulation is not valid. The frequency range used in the present work lies completely within this range.

2.1.3 Contact receptance

The interaction between wheel and rail is described by means of a contact spring which allows modelling the contact receptance through a stiffness caused by local contact deformations. Using Hertz theory, if small displacement amplitudes produced through the interaction are considered, a contact receptance in the vertical direction can be defined as (Thompson 1993c)

$$ H_{c,xx} = \frac{1}{K_{H}} , $$
(13)

where

$$ K_{H} = \frac{2}{\xi} \left( \frac{3 E^{\ast^{2}} r_{e} F_{0}}{2} \right)^{1/3} $$
(14)

is the contact stiffness for the vertical direction and E∗ is the plain strain elastic modulus, re is the effective radius of curvature of the surfaces in contact, F0 is the normal load and ξ is a dimensionless factor which depends on the radii of curvature of the surfaces in contact and is derived with Kalker’s methodology (Kalker 1967).

For the receptance in the lateral direction, the lateral contact stiffness is combined with the creep forces present in the low frequency region (Knothe and Gross-Thebing 1986). A simplified equivalent formulation (Thompson 1991) is used where the lateral receptance is defined as

$$ H_{c,yy} = \frac{1}{K_{L}} - i \frac{V}{G c^{2} C_{22} \omega } , $$
(15)

V being the train speed, G is the shear modulus, C22 is the corresponding non-dimensional creep coefficient developed by Kalker (1967),

$$ K_{L} = K_{H} \left[1 + \frac{\nu}{1-\nu}\left( \frac{1}{4} + \frac{1}{\pi}\tan^{-1}(\frac{a}{b})\right)^{1/3}\right]^{-1} $$
(16)

is the transverse contact stiffness in the lateral direction, ν is the Poisson ratio, parameters a and b are the semi-axes of the ellipse that conforms the contact patch and c2 = ab.

2.2 Acoustic radiation

The main purpose of the present work is achieving less sound radiating designs for railway wheels and so it is necessary to explicitly compute the radiated sound power of the wheel. To this end, firstly the wheel surface is divided in six concentric rings, the areas and velocities of which are used for calculating the axial contribution to the sound radiation (Janssens et al. 2014b). Figure 5 shows the geometry parameters used in the wheel radiation model, where the radius rj defines the six axial ring areas Sa, j, each one with its axial vibration velocity \(\tilde {v}_{a,j}\). The radial surface area Sr combines the surfaces of the external and internal side of the tyre and is derived from the radius of the wheel r, the inner radius of the tyre rin, and the width of the web and tyre wweb and wtyre, respectively, \(\tilde {v}_{r}\) being the radial vibration velocity in the contact point. The corresponding surface areas are:

$$ \begin{array}{@{}rcl@{}} S_{a,j} &=& 2(\pi r^{2}_{j+1} - \pi {r^{2}_{j}}), \text{with } j=1 ... 6 , \end{array} $$
(17)
$$ \begin{array}{@{}rcl@{}} S_{r} &=& 2\pi r w_{tyre} + 2\pi r_{in} (w_{tyre} - w_{web}). \end{array} $$
(18)
Fig. 5
figure 5

Cross-sectional illustration of geometry parameters used in wheel radiation model

Full size image

Once the wheel/rail system dynamics has been solved using the methodology described in Section 2.1, the velocity for each of the concentric rings and for the contact point is calculated as

$$ \tilde{v} = i \omega \tilde{u} , $$
(19)

where \(\tilde {u}\) refers to the wheel vibration displacement.

After that, it is possible to extend the sound power W formulation (Thompson 2010) into the wheel through

$$ W = \rho c_0 \sum\limits_l^{N_m} \left( {\sigma}_{l}^{a} \sum\limits_j (S_{a,j} \langle\overline{\tilde{v}_{a,jl}^2}\rangle ) + \sigma_{l}^{r} S_r \langle\overline{\tilde{v}_{r,l}^2}\rangle \right) , $$
(20)

where index l refers to each the Nm modeshapes, \(\langle \overline {\tilde {v}_{a,jl}^{2}}\rangle \) and \(\langle \overline {\tilde {v}_{r,l}^{2}}\rangle \) to the mean squared vibration velocity averaged over time and surface area for the axial and radial directions, respectively, associated with lth modeshape and surface ring j; ρ is the air density, c0 the speed of sound, Sa, j the axial area of the jth ring, Sr the area used for the radial radiation and \({\sigma }_{l}^{a}\) and \({\sigma }_{l}^{r}\) are the radiation efficiencies for the lth mode for the axial and radial contribution of the whole wheel, respectively. Radiation efficiencies are defined as the ratio expressing the amount of acoustic power radiated to that of a piston of the same area on an infinite wall vibrating uniformly with the same average quadratic velocity at a frequency such that the diameter of the piston considerably exceeds the acoustic wavelength, or in other words, that the Helmholtz number ka >> 1 (Fahy and Gardonio 2007).

In this work, the formulation developed explicitly for railway wheels in Thompson and Jones (2002) is used, allowing a fast method to calculate each of the acoustic efficiencies with the required accuracy by defining them as a function of the frequency, the radius of the wheel and the number of nodal diameters.

In the case of the axial acoustic radiation, the formulation applied is

$$ \sigma^{a} = \frac{1}{1 + \left( \frac{{f}_{1}^{a}}{f}\right)^{2n+4}} , $$
(21)

where n is the number of nodal diameters of the modeshape and \({f}_{1}^{a}\) is a transition frequency defined as

$$ {f}_{1}^{a} = \frac{c_{0} \mu}{2\pi x_{1}} , $$
(22)

in which x1 is the wheel radius, as explained in Section 3.3 and μ is a scaling parameter with value:

$$ \mu = 1.90 + 1.015 n - 0.0189 n^{2} . $$
(23)

For the radial case, the acoustic efficiency is defined by

$$ \sigma^{r} = \left\lbrace \begin{array}{ll} \frac{\Gamma}{1 + \left( \frac{{f}_{2}^{r}}{f}\right)^{2}} & \textup{ if } n = 0\\ \textup{ }\\ \frac{\Gamma}{1 + \left( \frac{{f}_{1}^{r}}{f}\right)^{2n}} \frac{1}{1 + \left( \frac{{f}_{2}^{r}}{f}\right)^{2}} & \textup{ if } n > 0 \end{array} \right. , $$
(24)

with

$$ {\Gamma} = \left\lbrace \begin{array}{ll} \sqrt{\frac{S_{ext} - S_{int}}{S_{ext} +S_{int}}} & \textup{ for } f < {f}_{3}^{r}\\ \textup{ }\\ 1 & \textup{ for } f \geq {f_{3}^{r}} \end{array} \right. $$
(25)

and

$$ \begin{array}{@{}rcl@{}} {f}_{1}^{r} &=& \frac{120 n }{\sqrt{x_{1}/0.42}} , \end{array} $$
(26)
$$ \begin{array}{@{}rcl@{}} {f}_{2}^{r} &=& \frac{800}{\sqrt{x_{1}/0.42}} , \end{array} $$
(27)
$$ \begin{array}{@{}rcl@{}} {f}_{3}^{r} &=& \frac{280 + 150 n}{\sqrt{x_{1} / 0.42}} , \end{array} $$
(28)

where Sint and Sext are the areas of the inner and outer surfaces of the tyre, respectively.

2.3 Structural analysis

To assess the mechanical behaviour of each wheel design, a high-cycle fatigue analysis is performed following the standard EN13979-1 (UNE 2011) through which the risk of fatigue cracking in the railway wheel is computed by comparing the principal stresses resulting of three load cases that correspond to different vehicle operating conditions with an established threshold in each case. As it can be seen in Fig. 6, each load case is associated with a point of application of the forces Fz = 75 kN, Fy2 = 42 kN and Fy3 = 25.2 kN. By using a FEM software, the stress tensor is calculated in all nodes of the mesh for each load case, and the variation between the maximum and minimum stress

$$ {\Delta} \sigma = \sigma^{max} - \sigma^{min} $$
(29)

is derived in all nodes, obtaining a maximum variation Δσc. Those candidate wheels which meet Δσc < ΔAm are considered as feasible. ΔAm is defined as the maximum permissible range of dynamic stresses and, for the type of wheel studied in the present work, the standard fixes a value of ΔAm = 360 MPa.

Fig. 6
figure 6

Load cases defined by the standard EN13979-1 (UNE 2011). Distances are defined in metres

Full size image

3 Optimization procedure

In this work, GAs are used for the optimization procedure of a railway wheel cross section with the aim of finding designs that directly or indirectly minimize its radiated acoustic power. Throughout the present section, the different approximations applied for such purpose, together with the general algorithm used, are explained.

First the general algorithm used during the optimization process is described, then, the different objective functions considered in the work are explained in more detail and finally, the parametrization adopted for the wheel cross section is shown.

3.1 Optimization workflow

A flow diagram with the procedure described above is represented in Fig. 7. The first step of the algorithm implemented is to provide an initial set of wheel candidates X0, conforming the first generation. Then, for every candidate \(\bar {x}_{j}\) in Xi, a cross section is defined with the use of its corresponding geometric parameters. In the first generation candidates, these parameters are randomly generated inside the design domain defined by the selected lower and upper boundaries. In the subsequent generations, the information of the previous evaluations is then considered for the initialization of new candidates.

Fig. 7
figure 7

Flow diagram describing the optimization procedure

Full size image

Next to the proposal of a candidate wheel geometry, a structural analysis is computed to check whether the design is feasible or not from an endurance point of view, acting as a “death penalty” constraint (Coello 2002). This analysis is made following the standard EN13979-1 (UNE 2011), as it was previously explained. If the candidate is feasible, its evaluation process goes on; otherwise, it is discarded and the next candidate proceeds to be tested.

The next step is to perform a modal analysis to obtain the Nm modeshapes Φ and natural frequencies \(\bar {\omega }\) used to compute the selected objective function. Such analysis is carried out by the FEM software ANSYS®; APDLFootnote 1 using general axisymmetric elements of size h and a number of Fourier terms nf (Petyt 2010). Following this computation, modeshapes are identified and classified according to their number of nodal diameters and nodal circumferences (n, m). Then, the objective function Obj is evaluated and the GA feeded with this information. After computing Obj for each iteration of the generation, the stopping criteria ΔObj < tolm is checked, where ΔObj corresponds to the maximum change in the objective function in 50 generations, and tolm is a convergence tolerance, set in this work to tolm = 10− 6. If the stopping condition is fulfilled, the optimization procedure ends and the wheel design with the best fitness \(\bar {x}^{*}\) is selected as the Best Found Solution (BFS). Otherwise, the optimization procedure continues and a new set of geometric parameters Xi is initialized, taking into account the geometrical information of the previous generations candidates.

3.2 Objective functions

In this work, two different objective functions are implemented: one based on the SWL calculation explained in the previous section (LA, W-min) and another one based on the maximization of the natural frequencies of the wheel (NF-max). The main features of these objective functions are explained with further detail in the next paragraphs.

3.2.1 LA, W-min methodology

The LA, W-min methodology aims to directly minimize the radiated noise emission by the wheel, for what the SWL is calculated as explained in Section 2. Later, in order to take into account human perception of the noise, the radiated power is expressed as the sound power level in dB(A) (Beranek 2007)

$$ \text{SWL} = 10 \log_{10}(\frac{W}{W_{ref}}) + A_{filter} , $$
(30)

where W is the sound power, Wref = 10− 12 W and Afilter is the A-weighting filter for dB.

Finally, the summation of the radiated power in each frequency band after having taken into account the effect of the A-weighting filter is used as the objective function. Therefore, Obj is defined in this case as

$$ Obj_{L_{A,W}} = 10 \log_{10}(\sum\limits_{i = 1}^{n_{cf}} 10^{\frac{\text{SWL}_{i}}{10}}) , $$
(31)

where SWLi is the SWL of the i th one-third octave band and ncf the number of bands in the studied frequency region.

3.2.2 NF-max methodology

As seen in (1), the excitation of the wheel is highly influenced by the wheel-rail combined roughness, whose content is lower in the high frequency region. This is illustrated in Fig. 2, where the roughness defined by prEN13979-1 (DIN 2017) used in the present work is represented. Consequently, the assumption is that maximizing the natural frequencies of the modeshapes of the wheel, that is, shifting its natural frequencies to a higher frequency region where the roughness frequency content is lower, should generally lead to wheel candidates whose vibration modes are less excited, and therefore to quieter wheel designs. This trend has been observed before in Thompson (2010, 1993b) where more rigid wheel designs having smaller wheel radius, larger fillets and a thicker web are associated with noise reduction. To the best of the authors’ knowledge, the concept of a NF maximization–driven shape optimization procedure in railway wheels has not been reported in literature. To this end, the objective function Obj for the present methodology is defined as

$$ Obj_{NF} = \frac{1}{\hat{\omega}_{m}} , $$
(32)

where \(\hat {\omega }_{m}\) is the mean of all the Nm extracted natural frequencies of the wheel. It is obvious that this methodology only requires the performing of a modal analysis for each candidate wheel, thus highly simplifying the algorithmic complexity and reducing computational cost.

3.3 Geometric parametrization

In order to achieve an efficient way of generating and testing the different designs proposed by the GA, a parametric FE model based on that described by Nielsen and Fredö (2006) is implemented. There, the most influential geometric parameters for the acoustic radiation (Nielsen and Fredö 2006; Thompson and Jones 2002) are chosen in order to parametrize the wheel cross section, which is defined by four variables related to wheel radius x1, fillet radius x2, web thickness x3 and web offset x4. This parametrization is illustrated in Fig. 8 while the respective design boundaries, as selected for this work, are shown in Table 1. It should be specified that, although x1, x2 and x4 are absolute parameters whose value directly correspond to the wheel radius, fillet radius and the wheel offset, respectively, x3 is defined as a proportionality factor of the reference web thickness at each point. Therefore, x3 value does not directly reflect the web thickness, this being variable along the web. Instead, the physical magnitude of the thickness at each point of the web is derived according to

$$ w_{thick} = k_{thick} (1 + x_{3}) $$
(33)
Table 1 Design domain for the optimization methodologies
Full size table

where wthick represents the web thickness and kthick is the base magnitude, which ranges from kthick = 0.028 m at the beginning of the web to kthick = 0.024 m at its end.

Fig. 8
figure 8

Geometric design variables of the wheel parametrization with an explanatory scheme (shaded) of the reference wheel with x1, x2, x3 and x4 parameters. Cross sections corresponding to a wheel with upper (shaded) and lower (white) boundary parameters showed in Table 1

Full size image

The FE model considers the use of general axisymmetric quadratic elements for the wheel cross section discretization. These elements allow to perform a full three-dimensional eigenanalysis of the wheel through a two dimensional meshing of its cross section by considering Fourier series in the shape functions, whose purpose is describing the displacement field in the circumferential direction.

4 Results and discussion

After introducing the theoretical framework and methodology used through the work, in this section the results obtained for the optimizations under different configurations together with the study of its behaviour are described. First, a comparison of the results of the reference wheel with TWINS computations is shown. Afterwards, the optimized designs obtained with LA, W-min and NF-max methodologies are explained for two different wheel parametrizations: one keeping the radius constant and another treating it as an additional design variable. Lastly, the most relevant response surfaces obtained are displayed and their outcomes are discussed.

Regarding SWL simulations, the following elements are considered: UIC54 rail with concrete bibloc sleeper separated 0.6 m (track parameters are shown in Table 2), roughness defined by standard (DIN 2017), train speed of V = 80 km/h and contact filter applied to the roughness (which takes into account the force attenuation due to the contact patch size (Thompson 2010)). In relation to the wheel modal analysis, a rigid constraint is applied at the nodes on the inner surface of the wheel hub, thus providing better accuracy for those modeshapes with high contribution on rolling noise generation (Thompson 2010). The number of wheel modeshapes considered is Nm = 48 and the maximum element size for the FE mesh is h= 0.007 m. Moreover, the reference wheel used as a guideline to compare the changes in wheel designs during the optimization processes is based on a simplified monoblock wheel with typical dimensions. The frequency range used in dynamic calculations varies from 50 to 5000 Hz with a resolution of 1 Hz, and SWL curves are represented until the last full one-third octave band (36th band).

Table 2 Track parameters used in SWL calculations
Full size table

4.1 Acoustic model validation

To ensure the correct implementation of the acoustic calculation embedded in the optimization procedure, the resulting SWL for the reference wheel is compared in Fig. 9 with the results provided by the commercial package TWINS. For the wheel/rail interaction, a two-dimensional contact model is considered (as detailed in the Section 2), and for the SWL calculation, the acoustic efficiencies are directly extracted from TWINS in order to ensure the compatibility of the data compared (TWINS software uses a more simplified formulation of efficiencies than previously described in Section 2.2). The maximum discrepancy between both curves, with a value of 0.75 dB(A), is thought to be related with differences in the contact implementation. In terms of the total SWL, the difference between methods is just ΔLA, W = 0.018 dB(A), so it can be stated that the vibro-acoustic model implemented in the optimization procedure presents no significant discrepancies and provides satisfactory results from a practical point of view.

Fig. 9
figure 9

SWL of the reference wheel produced by the algorithm used in this work ( ) and the commercial software TWINS ( )

Full size image

4.2 Optimization with fixed radius

Due to constraints in the design process of a railway wheel, it is often not possible to treat the radius as a parameter that can be freely modified independently of the other geometric attributes that define the wheel. For this reason, in this first optimization, the parameter x1 corresponding to the radius has been kept constant with a value x1 = 0.45 m.

The values for the reference wheel are shown in Table 3, and the outcomes of this study are detailed in Table 4. It is clearly seen that in all cases the final LA, W is lower than the reference wheel, obtaining a reduction of ΔLA, W = − 3.94 dB(A) with the LA, W-min methodology. Instead, the NF-max methodology presents a more modest reduction of ΔLA, W = − 1.11 dB(A). In return, the computational effort of the GA to perform an optimization with the NF-max approach is considerably lower, since the number of generations ngen needed to achieve convergence is reduced by Δngen = − 24. Therefore, although the LA, W reduction achieved is smaller, its higher computational efficiency could represent an advantage in some situations (e.g. fast conceptual design). Furthermore, in both methodologies, a maximization of the mean of the natural frequencies \(\hat {\omega }_{m}\) is produced and NF are moderately shifted towards a higher frequency region, as it can be observed in Fig. 10. Although a certain correlation between both objective functions exists, this trend is not followed by some candidates with high rigidity but also greater noise generation (for example, the BFS of the NF-max methodology in comparison with that of the LA, W-min one). Also, note that if the noise-rigidity relationship was totally monotonical, the BFS for the LA, W-min approach will possibly present the lower bound for the wheel radius design variable x1 (0.40 m) when considered for optimization, and not the value actually obtained (x1 = 0.42 m). Finally, it is important to comment that, when compared with the optimization with all the geometric parameters, for a fixed radius and due to the great influence of x1 over NF, the modal shifting is hindered. This observation is later discussed.

Table 3 Parameters of the reference wheel
Full size table
Table 4 BFS values for the optimization considering a fixed wheel radius. x1, x2 and x4 are expressed in m. The mass of the wheel is expressed in kg. All LA values are expressed in dB(A)
Full size table
Fig. 10
figure 10

Comparison of NF distributions in the different wheel designs: continuous line for the fixed radius case (LA, W-min methodology, NF-max methodology); discontinuous for the optimization with all parameters allowed to change (LA, W-min methodology, NF-max methodology); —∙— reference wheel

Full size image

In both BFS, the mass increase, about \({\Delta } m = \sim 7\) kg, is negligible compared with the full weight of sprung masses (bogie frame and car body), representing around 2.4% of the wheel mass, while the safety factor obtained suggests the structural integrity of the solutions according to actual standards. Concerning a possible transfer of radiated noise from the wheel to other components of the system, the SWL of each subcomponent (as shown in Table 4) has been derived using TWINS for each BFS wheel together with the simulation parameters described earlier. As seen, the LA, W corresponding to the rail LA, R, sleeper LA, Sl and train superstructure LA, Ss are calculated, together with the LA, W corresponding to the total SWL radiated by all components LA, T. Here, it is observed how the rail provided moderately lower SWL values with respect to the ones of the reference wheel, while the sleeper and superstructure components present higher values, with a ΔLA, Sl ≈ 0.5 dB(A) in both methodologies for the sleeper and a maximum variation for the superstructure of ΔLA, Ss = 3.23 dB(A). It is important to note that, although the increase in some components like the superstructure is not negligible, the values of LA, T corresponding to the total SWL radiated by all the components together have also decreased for each optimal design, what allows to state that the optimization has accomplished its aim even without considering the coupled system model in the optimization procedure.

Table 4 shows that there are common patterns for the geometrical parameters in both methodologies which are consistent with literature (Thompson 2010; Nielsen and Fredö 2006; Garcia-Andrés et al. 2019). It is shown how fillet radius x2 and the factor determining web thickness x3 are maximized in all the designs. For the web offset x4, the BFS presents values corresponding to straighter wheels, specially in the LA, W-min method. In order to illustrate the geometrical parameters in the BFS obtained and its comparison with the reference wheel, these are represented in Fig. 11. x2 and x3 values are in the solution space boundary, that could indicate a global optimum outside the solution space. As the boundaries are strongly fixed by the wheel design and manufacturing process, it is not possible to broaden them and the search of a minimum beyond these limits is out of the scope of the present work.

Fig. 11
figure 11

Cross sections of the BFS of each methodology for the fixed radius case compared with the cross section of the reference wheel (in black). a NF-max methodology and bLA, W-min methodology

Full size image

In Fig. 12, where the SWL curves of each wheel BFS are represented, it is possible to appreciate how the biggest part of SWL reduction is focused on the mid and higher frequency regions, with the greatest improvements with respect to the reference wheel above the 28th band (562–708 Hz). Specially remarkable are bands as the 29th and 31st (708–891 and 1120–1410 Hz, respectively), where reductions of up to 12 dB(A) with respect to the reference wheel are obtained. On contrast, an increase on the SWL can be detected in the region from 75 to 600 Hz for all methodologies but nevertheless this range has a low energy contribution. As expected, the LA, W-min methodology improves the results with respect to the NF-max methodology in almost all one-third octave bands considered.

Fig. 12
figure 12

SWL of BFS wheels for an optimization considering the fixed wheel radius and the reference wheel (LA, W-min, NF-max, — ref. wheel)

Full size image

In order to understand the causes for local SWL variations in shape optimized wheel designs, their receptances and the resulting contact forces are studied, since the main mechanism that causes the wheel noise variation is the relocation of modeshapes in different one-third bands or frequencies where the excitation received is lower. Representative examples of such phenomena are shown in Fig. 13, by means of comparing the contact force \(|\bar {F_{c}}|\) and contact point receptance of the wheel Hw for the axial direction Hw, yy of the reference wheel and the BFS of the LA, W-min method in the fixed radius case. As it can be observed, Fig. 13 (left) reflects how the axial mode (1,0) present in the band B for the reference wheel shifts towards band A in the optimized wheel, and since no other modeshapes are present in both the reference and optimized cases, the SWL increase in this band is justified. In band C, the SWL increase in the optimized wheel is explained by the displacement of the axial (0,2) modeshape to a point with higher excitation content. Another example can be found in Fig. 13 (right), where axial modes (2,1) in band D and (3,1) in band E shift after optimization to points in the frequency domain with less excitation inside their original one-third octave bands. Again, since there are no additional modeshape influence in those respective bands and for the receptance considered, the SWL of the BFS design lowers in relation to the reference wheel levels in both D and E one-third octave bands. Such shift influence is especially significant for the ΔLA, W difference, as the axial modeshapes (2,1) and (3,1) are the most radiating modeshapes of the reference wheel, contributing from \(\sim \)55% of the emitted energy to just \(\sim \)4% in the BFS design. In addition, the effects described previously are also combined with the straightening of the web produced by the web offset x4 variation, decreasing the coupling between axial and radial displacements. Thus, if the more relevant modeshapes of the reference wheel (from an acoustic point of view) are observed, some degree of coupling effect can be found in all of them, unlike what happens in the LA, W-min BFS where the most influential modeshape set is entirely composed by uncoupled radial modeshapes. In any case, it is important to note that in order to carry out a quantitative study about the influence of the modeshape shifting mechanism over the SWL, it would be necessary to analyse more wheel receptances at different locations.

Fig. 13
figure 13

Receptance Hw, yy and contact force \(|\bar {F_{c}}|\) comparison between the BFS with LA, W-min method ( ) for the fixed radius case and the reference wheel (—) for different frequency ranges. Black continuous vertical lines mark the limits of one-third octave bands and grey discontinuous vertical ones relate the amplitudes of Hw, yy peaks and \(|\bar {F_{c}}|\) for its corresponding frequency. Top: SWL curves with studied bands highlighted; left: bands 23–25 (178–355 Hz, named A, B and C); right: bands 32–33 (1410–2240 Hz, named D and E)

Full size image

4.3 Optimization with all the geometric parameters

An optimization study considering the variation of the wheel diameter can be interesting at an industrial level under certain circumstances and provides valuable information about its influence on the wheel acoustic radiation. Therefore, for the sake of completeness, in this section, the results discussed correspond to optimization procedures where all the geometrical parameters explained in Section 3.3 are treated as design variables.

Relevant outcomes of the BFS can be found in Table 5. As expected, LA, W reductions for both methodologies are greater than those described in Section 4.2 with fixed wheel radius, with reductions of up to ΔLA, W = − 4.96 dB(A) in the case of the LA, W-min optimization and ΔLA, W = − 2.03 dB(A) in the NF-max approach. Furthermore, within this decrements just \(\sim \)0.8 dB(A) are directly attributable to the radiating area reduction, reassuring that the drop in LA, W has its origin in the modal changes and not just to purely area decrease. As shown in Fig. 10, due to the release of the constraint x1, a greater shift of the NF compared with that obtained in the outcomes of the optimization with fixed wheel radius (see Section 4.2 for details) is observed. Additionally, both Δm and ΔAm/Δσc improved, since the resulting mass is lower and the structural safety factor higher than the corresponding for the BFS with a fixed x1. Regarding the radiation emitted by the other components of the system, a decrease for the rail is observed and a slight increase for sleeper and superstructure is found, with the total radiation being reduced by ΔLA, T = − 2.05 dB(A) for the LA, W-min methodology and a more modest reduction of ΔLA, T = − 1.05 dB(A) for the NF-max one.

Table 5 Values of BFS when all x1-x4 parameters are used in the optimization. x1, x2 and x4 are expressed in m. The mass of the wheel is expressed in kg. All LA values are expressed in dB(A)
Full size table

Concerning the geometric parameters, as represented in Table 5 and Fig. 14, the patterns observed in Section 4.2 appear again: x2 and x3 are maximized and x4 tends to describe a wheel with a straight web shape, with the particularity of x1 playing a major role in both the LA, W and \(\hat {\omega }_{m}\) values. As expected, in the NF-max process, x1 has converged to the minimum value possible. This is not the case for the LA, W-min case, in which the final design presents a smaller radius than the reference wheel (x1 = 0.4222 m) but has not converged to the defined lower design boundary. Observing the SWL representations described in Fig. 15, it is possible to appreciate how, in the same manner than in Fig. 12, most of the SWL reduction contribution of the BFSs is above the 600 Hz range, with lower noise increments at the low frequency region and more significant at higher frequencies, as compared with the fixed radius case. It should be noted that the results presented in this section should be treated with caution due to possible uncertainties caused by changes in the position of the calculation points r1–r6 shown in Fig. 5. In this work and for each candidate geometry, these points are chosen with the criterion of even distribution in the web along the radial direction.

Fig. 14
figure 14

Cross sections of the BFS of each methodology for an optimization considering all geometric parameters compared with the cross section of the reference wheel (in black). a NF-max methodology and bLA, W-min methodology

Full size image
Fig. 15
figure 15

SWL of BFS wheels for an optimization considering all geometric parameters and the reference wheel (LA, W-min, NF-max, — ref. wheel)

Full size image

4.4 Response surfaces

Response surface (RS) representations, shown in Figs. 16 and 17, are generated for each methodology and for the combination of geometric parameters considered more relevant for the description of the problem. For doing so, each possible combination of pairs of the design variables conforming one of the BFS wheels is evaluated in 676 different points along the solution space, corresponding to a 26 × 26 evenly distributed sampling grid. The aims of this analysis are, firstly, studying the sensitivity of the SWL response to the design variables, and secondly, evaluating the performance of the GA and its suitability as a global optimization tool for the problem at hand, for both the LA, W-min and NF-max methodologies. For the case of the NF-max methodology, the RS generated are shown in Fig. 16a–c for the pairs of geometric parameters “x1,x3”, “x2,x4” and “x2,x3” respectively. It is immediate to see how, in this approach, the objective function presents approximately a planar behaviour and that, as expected, the maximization of NF is greater by decreasing the radius x1 and broadening of the thickness x3. Thus, Fig. 16a and c make clear how, in this methodology, the radius x1 and the web thickness factor x3 are the predominant parameters in the objective function, followed by the fillet radius x2. On the other hand, the web offset x4 effect on ObjNF is modest, as it can be appreciated on Fig. 16b. Also, in both cases, the minimum candidate in the RS fits the BFS for the respective methodology in the case of the GA optimization, and given the observed planar topology of the RS and the lack of local optima inside the design space analysed, it is clear that the NF-max methodology could be performed using local optimization algorithms, such a gradient-based optimizer. With this approach, the BFS will be probably obtained with a much lower number of objective function evaluations, that would emphasize the computational advantage of the NF-max technique.

Fig. 16
figure 16

Response surfaces for different combinations of geometric parameters for \(Obj_{NF} = \frac {1}{\hat {\omega }_{m}}\): a x1 and x3, b x2 and x4, c x3 and x2

Full size image
Fig. 17
figure 17

\(Obj_{L_{A,W}}\) response surfaces for different combination of parameters. Fixed values correspond to those of the BFS as obtained with the LA, W-min methodology with no restrictions in the wheel radius x1: a x3 and x4, b x1 and x3. Points M indicate the RS minima and are presented in Table 6

Full size image

Different outcomes are extracted from the RS generated for the LA, W-min methodology, as it is seen in Fig. 17, where the RSs together with its contour level representations are observed. Table 6 shows the minima obtained for all RS computed with the LA, W-min methodology. All minima are close to the BFS achieved through GA optimization and RSs did not result in a lower LA, W than the BFS one, reinforcing that in the case of the LA, W-min problem, a global optimization technique such as GA may be required in order to accurately find best possible points in the solution domain. The behaviour of LA, W versus geometric parameters is observed. Figure 17a shows how the offset variable x4 is one of the most relevant parameters defining a high-quality solution subspace, corresponding to magnitudes related to straight web shape. Focusing in this region, the minimum point (marked with an M) is then given by a higher web thickness factor x3 which has a visibly weaker relationship with the SWL level. A similar behaviour happens in the case of the radius x1 and more discretely the web thickness factor x3, as reflected in Fig. 17b. Here, the minima region is dominated by the radius value \(x_{1} \simeq 0.42\) m, the best possible point (marked with an M) occurring at the intersection of this value with the highest allowed possible thickness. Similar phenomena are observed for the fillet radius in the “x1,x2” and “x2,x4” RS, which are not illustrated here for the sake of brevity. Finally, it is important to note that the response surface from Fig. 17 suggests that relatively small changes in the web offset x4 or the wheel radius x1 can lead to significant noise radiation variations. From a production perspective, such parameter sensitivity may be important due the variability inherent to manufacturing tolerances, or wheel tyre wear.

Table 6 Geometric parameters together with its corresponding LA value of each minimum in the RSs with the LA-min objective function
Full size table

5 Conclusions

A procedure for the geometric optimization of the railway wheel cross section has been presented by means of a GA-based optimizer with the aim of reducing acoustic radiation. For this purpose, two different methodologies are presented: the NF-max methodology, which is based on the maximization of the wheel natural frequencies, and the LA, W-min methodology, whose objective function is directly minimizing the SWL of the wheel. In addition, response surfaces for each combination of geometrical parameters are obtained with the purpose of evaluating the suitability of the GA as optimization technique and to acquire knowledge of the problem sensitivity to the selected design domain and both objective functions.

The results obtained for both optimization approaches reflect significant noise decrease in the acoustic radiation, with reductions of up to 5 dB(A) in the case of the LA, W-min methodology. Moreover, if the whole railway system with all the components is considered, the total sound power radiation is also mitigated with the resulting wheel designs.

The underlying physical mechanism for the changes in SWL between wheel candidates is identified and explained through the shift of modeshapes along frequency spectrum and their relocation into frequencies with a weaker amplitude content of the contact force. Regarding the evolution of geometric parameters, in both approaches, the final wheel designs presented higher thickness and fillet radius together with more straight web shapes. When considered as an additional design variable, the wheel diameter evolves towards a smaller value in the LA, W-min approach and towards the lower design bound in the case of the NF-max methodology, observations which are consistent with the response surfaces obtained. It has also been shown that the differences in LA, W-min between wheel designs have physical causes that cannot be explained just with pure geometrical changes such as area reduction. The NF-max methodology is seen as a computationally inexpensive and straightforward technique to obtain optimized designs which are geometrically similar to those corresponding to a procedure requiring the SWL computation. Besides, as suggested by the response surfaces obtained, the NF-max objective function is suitable for an efficient gradient-based optimization algorithm instead of a GA, which usually requires a higher number of candidate evaluations.

Additional research is needed in order to take into account more accurately the effects of wheel geometry modifications in the rest of the components involved in the railway system (rail, sleeper, bogie frame and car body), in addition to including their vibro-acoustic models inside the optimization loop, either as constraints or as additional components to optimize.