Topology optimization of dissipative metamaterials at finite strains based on nonlinear homogenization

Abstract

This study presents a novel computational framework for designing optimal dissipative (damping) metamaterials under time-dependent loading conditions at finite deformations. In this framework, finite strain computational homogenization is integrated with a density-based multimaterial topology optimization. In addition, a thermodynamically consistent finite strain viscoelasticity model is incorporated together with an analytical path-dependent sensitivity analysis. Optimization formulations with and without stiffness and mass constraints are considered, and various new damping metamaterial designs are obtained that combine soft viscoelastic and stiff hyperelastic material phases. Multiscale stability analysis using the Bloch wave analysis and rank-1 convexity checks is also carried out to investigate stability of the optimized designs. Stability analyses demonstrate that the inclusion of voids or soft material phases can make a metamaterial more prone to lose micro and macro-stability. Furthermore, the concept of tunable metamaterials is explored wherein metamaterial’s response is steered towards a stable deformation path by tailoring the design with a preselected micro buckling mode.

Appendices

Appendix A:: Finite strain viscoelasticity model implementation

In this appendix, numerical implementation of the finite strain viscoelastic model is presented. In the context of strain-driven finite element analysis, given data at an integration point: F_k and $\boldsymbol {b}_{k}^{e}$ at previous step k, and F at current step k + 1, the goal is to find the unknown variables: P, b^e and the consistent tangent moduli at the current step k + 1. Note that the subscript k + 1 for the current step, the element number, and integration point number are removed for clarity. In addition to standard tensor notations, the following nonstandard tensor notations are used:

$$ \begin{array}{@{}rcl@{}} (\boldsymbol{A}\boxdot\boldsymbol{B})_{ijkl}&\triangleq& A_{il}B_{jk}\\ (\boldsymbol{A}\odot\boldsymbol{B})_{ijkl}&\triangleq& A_{ik}B_{lj}\\ (\boldsymbol{A}\boxtimes\boldsymbol{B})_{ijkl}&\triangleq& A_{ik}B_{jl}\\ (\boldsymbol{\mathcal{A}}\circledcirc\boldsymbol{B})_{ijk}&\triangleq&\boldsymbol{\mathcal{A}}_{imk}B_{mj}\\ (\mathbb{A}\boxplus\boldsymbol{B})_{ijkl}&\triangleq&\mathbb{A}_{imkl}B_{mj} \end{array} $$

(A.1)

where A and B are any 2nd-order tensors and $\boldsymbol {\mathcal {A}}$ and $\mathbb {A}$ are any 3rd- and 4th-order tensors, respectively.

The viscoelastic model consists of equilibrium and non-equilibrium parts. The equilibrium part is handled in the same way as the hyperelastic model. For the non-equilibrium part, the material interpolation cannot be applied outside the material subroutine since the internal variable b^e is not known and has to be solved from a set of nonlinear constitutive equations where interpolated material parameters are used. In the following derivations, the material parameters κ, μ_q, and η_d are interpolated based on the material interpolation given in Section 4.3.

1.1 A.1 Integration of rate equations

The internal variable given in (35) is integrated using the exponential map integrator (Weber and Anand 1990). With ${\mathcal{L}}_{v}[\boldsymbol {b}^{e}]=\boldsymbol {F}.\dot {\overline {{\boldsymbol {C}^{v}}^{-1}}}.\boldsymbol {F}^{T}$ where C^v = F^vT.F^v, (35) can be written as

$$ \dot{\overline{{\boldsymbol{C}^{v}}^{-1}}}=-2\boldsymbol{F}^{-1}.(\mathbb{D}:\boldsymbol{\tau}^{neq}).\boldsymbol{F}.{\boldsymbol{C}^{v}}^{-1} $$

(A.2)

Using the backward exponential integrator, (A.2) is integrated as

$$ {\boldsymbol{C}^{v}}^{-1}=\exp[-2\boldsymbol{F}^{-1}.(\mathbb{D}:\boldsymbol{\tau}^{neq}).\boldsymbol{F}{\Delta} t].{\boldsymbol{C}_{k}^{v}}^{-1} $$

(A.3)

where the subscript k denotes the term evaluated at the last time step t_k, with the time interval Δt = t_k+ 1 − t_k. Noticing that $\exp [\boldsymbol {Y}^{-1}.\boldsymbol {Z}.\boldsymbol {Y}]=\boldsymbol {Y}^{-1}.\exp [\boldsymbol {Z}].\boldsymbol {Y}$ for any 2nd-order tensor Y and Z (Y is invertible) and the relation $\boldsymbol {b}^{e}=\boldsymbol {F}.{\boldsymbol {C}^{v}}^{-1}.\boldsymbol {F}^{T}$, (A.3) can be simplified to

$$ \boldsymbol{b}^{e}=\exp[-2{\Delta} t\boldsymbol{A}].{\boldsymbol{b}^{e}}^{tr} \quad\text{with}\quad \boldsymbol{A}=\mathbb{D}:\boldsymbol{\tau}^{neq} $$

(A.4)

with ${\boldsymbol {b}^{e}}^{tr}={\boldsymbol {F}^{e}}^{tr}.{\boldsymbol {F}^{e}}^{{tr}^{T}}$ where ${\boldsymbol {F}^{e}}^{tr}\triangleq \boldsymbol {F}_{\delta }.\boldsymbol {F}_{k}^{e}$ and $\boldsymbol {F}_{\delta }=\boldsymbol {F}.\boldsymbol {F}_{k}^{-1}$. Due to the isotropy, the non-equilibrium stress τ^neq and the tensor b^e are coaxial, which results in the coaxiality of tensor b^etr with τ^neq and b^e. As a result, it is possible to express the evolution rule in the principal space. Denote the elastic principal stretch at the current step as ${\lambda _{a}^{e}}$, while ${{\lambda _{a}^{e}}}^{tr}$ (a = 1, 2, 3) for the trial step, which are the square-root of the eigenvalues of tensors b^e and b^etr, respectively. The non-equilibrium principal stresses are denoted by $\tau _{a}^{neq}$, which are the eigenvalues of the tensor τ^neq. Employing logarithmic strain, where ${\varepsilon _{a}^{e}}{\triangleq \ln \lambda _{a}^{e}}$ and ${{\varepsilon _{a}^{e}}}^{tr}\triangleq {{\ln \lambda _{a}^{e}}}^{tr}$, (A.4) can be expressed in the principal space as

$$ {\varepsilon_{a}^{e}} - {{\varepsilon_{a}^{e}}}^{tr} + \frac{\Delta t}{2\eta_{d}}\left( \tau_{a}^{neq}-p^{neq}\right)=0 ,\quad a=1,2,3 $$

(A.5)

where $p^{neq}=(\tau _{1}^{neq}+\tau _{2}^{neq}+\tau _{3}^{neq})/3$ represents the pressure which equals $\frac {1}{3}\text {tr}\left (\tau ^{neq}\right )$.

1.2 A.2 Stress tensor and consistent tangent moduli

For the non-equilibrium part, since the elastic Finger tensor b^e is not known, the non-equilibrium Kirchhoff stress τ^neq and b^e have to be calculated by using Eq. (33)₃ and (A.5). This set of nonlinear equations are solved using Newton-Raphson (NR) method. Due to the coaxiality of b^e and τ^neq, (33)₃ can be expressed in the principal space as

$$ \tau_{a}^{neq}={\lambda_{a}^{e}}\frac{\partial\psi^{neq}}{{\partial\lambda_{a}^{e}}} ,\quad a=1,2,3 $$

(A.6)

with the principal space spanned by $\boldsymbol {G}_{a}^{e}$ which are the same as ${\boldsymbol {G}_{a}^{e}}^{tr}$ that span the principal space of b^etr (see (A.4)). Combining (A.5) and (A.6), the unknown variables $\tau _{a}^{neq}$ and ${\varepsilon _{a}^{e}}$ are solved using the Newton-Raphson method. Taking $\tau _{a}^{neq}$ as implicit functions of ${\varepsilon _{a}^{e}}$ determined by (A.6), the unknown variables are reduced to ${\varepsilon _{a}^{e}}$ and the set of nonlinear equations to be solved becomes

$$ \boldsymbol{R}_{\varepsilon^{e}} = \left[\begin{array}{lll} {\varepsilon_{1}^{e}} \\ {\varepsilon_{2}^{e}} \\ {\varepsilon_{3}^{e}} \end{array}\right] - \left[\begin{array}{lll} {{\varepsilon_{1}^{e}}}^{tr} \\ {{\varepsilon_{2}^{e}}}^{tr} \\ {{\varepsilon_{3}^{e}}}^{tr} \end{array}\right]\! +\frac{\Delta t}{2\eta_{d}}\left[\begin{array}{lll} \frac{2}{3} & -\frac{1}{3} & -\frac{1}{3} \\ -\frac{1}{3} & \frac{2}{3} & -\frac{1}{3} \\ -\frac{1}{3} & -\frac{1}{3} & \frac{2}{3} \end{array}\right] \!\left[\begin{array}{lll} \tau_{1}^{neq} \\ \tau_{2}^{neq} \\ \tau_{3}^{neq} \end{array}\right] = \boldsymbol{0} $$

(A.7)

with the Jacobian matrix calculated, by employing (A.6), as

$$ \begin{array}{@{}rcl@{}} &&\frac{d\boldsymbol{R}_{\varepsilon^{e}}}{d\boldsymbol{\varepsilon}^{e}}=\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]\\ &&\qquad\qquad+\frac{\Delta t}{2\eta_{d}}\left[\begin{array}{llll} \frac{2}{3} & -\frac{1}{3} & -\frac{1}{3} \\ -\frac{1}{3} & \frac{2}{3} & -\frac{1}{3} \\ -\frac{1}{3} & -\frac{1}{3} & \frac{2}{3} \end{array}\right] \left[\begin{array}{llll} \frac{d\tau_{1}^{neq}}{d{\varepsilon_{1}^{e}}} & \frac{d\tau_{1}^{neq}}{d{\varepsilon_{2}^{e}}} & \frac{d\tau_{1}^{neq}}{d{\varepsilon_{3}^{e}}} \\ \frac{d\tau_{2}^{neq}}{d{\varepsilon_{1}^{e}}} & \frac{d\tau_{2}^{neq}}{d{\varepsilon_{2}^{e}}} & \frac{d\tau_{2}^{neq}}{d{\varepsilon_{3}^{e}}} \\ \frac{d\tau_{3}^{neq}}{d{\varepsilon_{1}^{e}}} & \frac{d\tau_{3}^{neq}}{d{\varepsilon_{2}^{e}}} & \frac{d\tau_{3}^{neq}}{d{\varepsilon_{3}^{e}}} \end{array}\right] \\ &&\frac{d\tau_{a}^{neq}}{d{\varepsilon_{b}^{e}}}=\kappa(2J^{e}-1)J^{e}+\sum\limits_{q=1}^{N}\frac{1}{9}\mu_{q}\alpha_{q}\left[\left( \hat{\lambda}_{1}^{e^{\alpha_{p}}}+\hat{\lambda}_{2}^{e^{\alpha_{p}}}+\hat{\lambda}_{3}^{e^{\alpha_{p}}}\right)\right.\\ &&\left.\qquad\qquad -3\left( \hat{\lambda}_{a}^{e^{\alpha_{p}}}+\hat{\lambda}_{b}^{e^{\alpha_{p}}}-3\hat{\lambda}_{a}^{e^{\alpha_{p}}}\delta_{ab}\right)\right] \end{array} $$

(A.8)

where κ, μ_q, and α_q (q = 1,..., N) are parameters related to the non-equilibrium strain energy. Tangent modulus for the non-equilibrium part is obtained as

$$ \begin{array}{@{}rcl@{}} &&\mathbb{A}_{ijkl}^{neq}=JF_{jm}^{-1}\mathbbm{a}_{imkn}^{neq}F_{ln}^{-1} \quad\text{with}\\ &&J\mathbbm{a}^{neq}=\frac{\partial\boldsymbol{\tau}^{neq}}{\partial{\boldsymbol{b}^{e}}^{tr}}:\left( \boldsymbol{I}\odot{\boldsymbol{b}^{e}}^{tr}\right)-\boldsymbol{\tau}^{neq}\boxdot\boldsymbol{I} \end{array} $$

(A.9)

where the derivative ∂τ^neq/∂b^etr is computed using chain rule

$$ \frac{\partial\boldsymbol{\tau}^{neq}}{\partial{\boldsymbol{b}^{e}}^{tr}}=\frac{\partial\boldsymbol{\tau}^{neq}}{\partial{\boldsymbol{\varepsilon}^{e}}^{tr}}:\frac{\partial{\boldsymbol{\varepsilon}^{e}}^{tr}}{\partial{\boldsymbol{b}^{e}}^{tr}} $$

(A.10)

in which ${\boldsymbol {\varepsilon }^{e}}^{tr}={\sum }_{a=1}^{3} {{\varepsilon _{a}^{e}}}^{tr}\boldsymbol {G}_{a}^{e}$ and the term ∂τ^neq/∂ε^etr can be derived from the (A.6) and (A.7) following the procedure given in de Souza Neto et al. (2011). The term ∂ε^etr/∂b^etr is computed in the same way, since ε^etr and b^etr are coaxial.

Appendix B:: Explicit derivatives required for the adjoint sensitivity analysis

For the objective and constraint functions, beside the energy dissipation ($f_{0}=-\overline {W}_{d}$) which depends on the solution and auxiliary variables, all the other constraints, e.g., material volume constraint and initial stiffness constraint, are only functions of the density field and their sensitivities are not path-dependent, and thus easy to compute. This appendix gives the derivatives that are used in the path-dependent sensitivity calculation of f₀. For illustration purposes, the material interpolation scheme assuming void phase for Material-0 (Section 4.3.1) is considered in the sensitivity derivation in this appendix. In the following derivations, the tensor form and matrix-vector form are both utilized for notational simplicity and the appropriate form should be clear from the context. Moreover, to simplify the derivation process, the following functions are defined

$$ \begin{array}{@{}rcl@{}} &&g_{1}(\rho_{1})=1-\rho_{1}^{p_{e}} \\ &&g_{2}(\rho_{1},\rho_{2})={\rho_{2}^{p}}\zeta^{\kappa}(\rho_{1}) \\ &&g_{3}(\rho_{1},\rho_{2})={\rho_{2}^{p}}\zeta^{\mu}(\rho_{1}) \\ &&g_{4}(\rho_{1},\rho_{2})=(1-\rho_{2})^{p}\zeta^{\kappa}(\rho_{1}) \\ &&g_{5}(\rho_{1},\rho_{2})=(1-\rho_{2})^{p}\zeta^{\mu}(\rho_{1}) \\ &&g_{6}(\rho_{1},\rho_{2})=[\epsilon+(1-\epsilon)(1-\rho_{2})^{p}]\zeta^{\kappa}(\rho_{1}) \\ &&g_{7}(\rho_{1},\rho_{2})=[\epsilon+(1-\epsilon)(1-\rho_{2})^{p}]\zeta^{\mu}(\rho_{1}) \end{array} $$

(B.1)

where the functions ζ^κ(ρ₁) and ζ^μ(ρ₁) are evaluated using the associated material parameters, e.g., g₂(ρ₁, ρ₂) and g₃(ρ₁, ρ₂) are evaluated using Material-1 parameters, g₄(ρ₁, ρ₂) and g₅(ρ₁, ρ₂) are using equilibrium part of the viscoelastic material (Material-2), while g₆(ρ₁, ρ₂) and g₇(ρ₁, ρ₂) are based on non-equilibrium part of the viscoelastic material.

1.1 B.1 Derivatives of f₀

After time and spatial domains discretization, the homogenized energy dissipation defined in (39) can be approximated by

$$ f_{0}=-\overline{W}_{d}\approx-\frac{1}{V}\sum\limits_{k=1}^{n}\sum\limits_{e=1}^{n_{ele}}\sum\limits_{s=1}^{n_{ipt}}\boldsymbol{\tau}_{e_{s}}^{neq}:\mathbb{D}:\boldsymbol{\tau}_{e_{s}}^{neq}{\Delta} t_{k} w_{e_{s}} $$

(B.2)

where $\mathbb {D}$ depends on the density variables ${\rho _{1}^{e}}$ and ${\rho _{2}^{e}}$; $\boldsymbol {\tau }_{e_{s}}^{neq}$ is the Kirchhoff stress of the non-equilibrium viscoelastic phase at s th integration point in e th element; and Δt_k = t_k − t_k− 1 is the time interval between step (k − 1) and step k. This leads to

$$ \frac{\partial f_{0}}{\partial\hat{\boldsymbol{u}}^{k}}=\boldsymbol{0} ,\quad k=1,2,...,n $$

(B.3)

The derivatives ∂f₀/∂ρ₁ and ∂f₀/∂ρ₂ are arranged as

$$ \begin{array}{@{}rcl@{}} &&\frac{\partial f_{0}}{\partial\boldsymbol{\rho}_{1}}=\left[\begin{array}{llll} \frac{\partial f_{0}}{{\partial\rho_{1}^{1}}} & \frac{\partial f_{0}}{{\partial\rho_{1}^{2}}} & ... & \frac{\partial f_{0}}{\partial\rho_{1}^{n_{ele}}} \end{array}\right] \quad\text{and}\\ &&\frac{\partial f_{0}}{\partial\boldsymbol{\rho}_{2}}=\left[\begin{array}{llll} \frac{\partial f_{0}}{{\partial\rho_{2}^{1}}} & \frac{\partial f_{0}}{{\partial\rho_{2}^{2}}} & ... & \frac{\partial f_{0}}{\partial\rho_{2}^{n_{ele}}} \end{array}\right] \end{array} $$

(B.4)

with their components computed based on chain rule as

$$ \begin{array}{@{}rcl@{}} \frac{\partial f_{0}}{{\partial\rho_{A}^{e}}}&=&-\frac{1}{V}\sum\limits_{k=1}^{n}\sum\limits_{s=1}^{n_{ipt}}\left( \boldsymbol{\tau}_{e_{s}}^{neq}:\frac{\partial\mathbb{D}}{{\partial\rho_{A}^{e}}}:\boldsymbol{\tau}_{e_{s}}^{neq}\right.\\ &&\left.+ 2\frac{\partial\boldsymbol{\tau}_{e_{s}}^{neq}}{{\partial\rho_{A}^{e}}}:\mathbb{D}:\boldsymbol{\tau}_{e_{s}}^{neq}\right){\Delta} t_{k} w_{e_{s}} ,\quad A\in \{1,2\} \end{array} $$

(B.5)

$$ \text{with}\quad \frac{\partial\mathbb{D}}{{\partial\rho_{A}^{e}}}=-\frac{\tau\mu_{0}^{neq}}{2{\eta_{d}^{2}}}\frac{\partial g_{7}}{{\partial\rho_{A}^{e}}}\mathbb{P}_{dev}^{s} $$

(B.6)

$$ \text{and}\quad \frac{\partial\boldsymbol{\tau}_{e_{s}}^{neq}}{{\partial\rho_{A}^{e}}}=\frac{\partial g_{6}}{{\partial\rho_{A}^{e}}}\left[2\frac{\partial\hat{\psi}^{neq}}{\partial\boldsymbol{b}^{e}}.\boldsymbol{b}^{e}\right]+\frac{\partial g_{7}}{{\partial\rho_{A}^{e}}}\left[2\frac{\partial\tilde{\psi}^{neq}}{\partial\boldsymbol{b}^{e}}.\boldsymbol{b}^{e}\right] $$

(B.7)

where $\mu _{0}^{neq}$ is the initial shear modulus of the non-equilibrium viscoelastic solid phase, η_d is the interpolated value, and $\hat {\psi }^{neq}$ and $\tilde {\psi }^{neq}$ are the volumetric and isochoric non-equilibrium viscoelastic strain energy of solid phase.

The derivative $\partial f_{0}/\partial \boldsymbol {v}^{k}$ is arranged as

$$ \begin{array}{@{}rcl@{}} &&\frac{\partial f_{0}}{\partial\boldsymbol{v}^{k}}=\left[\begin{array}{llll} \frac{\partial f_{0}}{\partial\boldsymbol{v}_{1}^{k}} & \frac{\partial f_{0}}{\partial\boldsymbol{v}_{2}^{k}} & ... & \frac{\partial f_{0}}{\partial\boldsymbol{v}_{n_{ele}}^{k}} \end{array}\right] \quad\text{with}\\ &&\frac{\partial f_{0}}{\partial\boldsymbol{v}_{e}^{k}}=\left[\begin{array}{llll} \frac{\partial f_{0}}{\partial\boldsymbol{v}_{e_{1}}^{k}} & \frac{\partial f_{0}}{\partial\boldsymbol{v}_{e_{2}}^{k}} & \frac{\partial f_{0}}{\partial\boldsymbol{v}_{e_{3}}^{k}} & \frac{\partial f_{0}}{\partial\boldsymbol{v}_{e_{4}}^{k}} \end{array}\right] \end{array} $$

(B.8)

$$ \text{where}\quad \frac{\partial f_{0}}{\partial\boldsymbol{v}_{e_{s}}^{k}}=-\frac{1}{V}2\boldsymbol{\tau}_{e_{s}}^{neq}:\mathbb{D}:\frac{\partial\boldsymbol{\tau}_{e_{s}}^{neq}}{\partial\boldsymbol{b}^{e}}{\Delta} t_{k} w_{e_{s}} $$

(B.9)

where element number and integration point indices on elastic Finger tensor b^e are avoided with the understanding that the derivative $\partial \boldsymbol {\tau }_{e_{s}}^{neq}/\partial \boldsymbol {b}^{e}$ is evaluated at the s th integration point inside e th element.

1.2 B.2 Derivatives of R^k

Due to the linear energy interpolation (Section 4.4) and F-bar formulation (Section 4.5), the 1st PK stress P is computed as

$$ \boldsymbol{P}=r^{-1/2}\boldsymbol{P}^{b}\quad\text{with}\quad \boldsymbol{P}^{b}=\boldsymbol{P}_{0}^{b}+\boldsymbol{P}_{1}^{b}+\left( \boldsymbol{P}_{2}^{b,eq}+\boldsymbol{P}_{2}^{b,neq}\right) $$

(B.10)

where r = r(ρ₁, u) is a function of ρ₁ and u, and $\boldsymbol {P}_{0}^{b}$, $\boldsymbol {P}_{1}^{b}$, $\boldsymbol {P}_{2}^{b,eq}$, and $\boldsymbol {P}_{2}^{b,neq}$ are 1st PK stresses contributed from different material phases, where the superscript “b” is used to denote that they are evaluated based on F^b. Based on this, it is straightforward that

$$ \begin{array}{@{}rcl@{}} &&\frac{\partial r}{\partial\rho_{1}}=\frac{\partial r}{\partial\boldsymbol{F}}:\frac{\partial\boldsymbol{F}}{\partial\rho_{1}}+\frac{\partial r}{\partial\boldsymbol{F}_{0}}:\frac{\partial\boldsymbol{F}_{0}}{\partial\rho_{1}}\quad\text{with}\\ &&\frac{\partial r}{\partial\boldsymbol{F}}=-r\boldsymbol{F}^{-T}\quad\text{and}\quad \frac{\partial r}{\partial\boldsymbol{F}_{0}}=r\boldsymbol{F}_{0}^{-T} \quad\text{and}\\ &&\frac{\partial\boldsymbol{F}}{\partial\rho_{1}}=\frac{\partial\gamma}{\partial\rho_{1}}\boldsymbol{\nabla}_{\boldsymbol{X}}\boldsymbol{u}\quad\text{and}\quad \frac{\partial\boldsymbol{F}_{0}}{\partial\rho_{1}}=\frac{\partial\gamma}{\partial\rho_{1}}\boldsymbol{\nabla}_{\boldsymbol{X}}^{0}\boldsymbol{u} \end{array} $$

(B.11)

where $\boldsymbol {\nabla }_{\boldsymbol {X}}^{0}$ denotes the gradient operator evaluated at the centroid of the element. Also,

$$ \begin{array}{@{}rcl@{}} &\frac{\partial r}{\partial\boldsymbol{u}}=\frac{\partial r}{\partial\boldsymbol{F}}:\frac{\partial\boldsymbol{F}}{\partial\boldsymbol{u}}+\frac{\partial r}{\partial\boldsymbol{F}_{0}}:\frac{\partial\boldsymbol{F}_{0}}{\partial\boldsymbol{u}} \quad\text{with}\\ &\frac{\partial\boldsymbol{F}}{\partial\boldsymbol{u}}=\gamma\boldsymbol{B} \quad\text{and}\quad \frac{\partial\boldsymbol{F}_{0}}{\partial\boldsymbol{u}}=\gamma\boldsymbol{B}_{0} \end{array} $$

(B.12)

where B and B₀ are the shape functions derivative matrices evaluated at the integration point and the centroid, respectively. Besides, due to the dependence of F^b on ρ₁ and u, the following derivatives are obtained

$$ \begin{array}{@{}rcl@{}} &\frac{\partial\boldsymbol{F}^{b}}{\partial\rho_{1}}=\frac{1}{2}r^{-1/2}\frac{\partial r}{\partial\rho_{1}}\boldsymbol{F}+r^{1/2}\frac{\partial\boldsymbol{F}}{\partial\rho_{1}} \quad\text{and}\\ &\frac{\partial\boldsymbol{F}^{b}}{\partial\boldsymbol{u}}=\frac{1}{2}r^{-1/2}\boldsymbol{F}\otimes\frac{\partial r}{\partial\boldsymbol{u}}+r^{1/2}\frac{\partial\boldsymbol{F}}{\partial\boldsymbol{u}} \end{array} $$

(B.13)

1.2.1 B.2.1 Derivatives of $\partial \boldsymbol {R}^{k}/\partial \boldsymbol {\rho }_{1}$ and $\partial \boldsymbol {R}^{k}/\partial \boldsymbol {\rho }_{2}$

The explicit dependence of R^k on ρ₁ comes from the linear energy interpolation parameter γ(ρ₁) as well as the interpolated constitutive model parameters. Thus, the derivative $\partial \boldsymbol {R}^{k}/\partial \boldsymbol {\rho }_{1}$ is computed as

$$ \begin{array}{@{}rcl@{}} &&\frac{\partial\boldsymbol{R}^{k}}{\partial\boldsymbol{\rho}_{1}}=\left[\begin{array}{llll} \frac{\partial\boldsymbol{F}_{int}^{k}}{\partial\boldsymbol{\rho}_{1}} \\ \boldsymbol{0} \\ \boldsymbol{0} \end{array}\right] \quad\text{with} \quad \frac{\partial\boldsymbol{F}_{int}^{k}}{\partial\boldsymbol{\rho}_{1}}=\overset{n_{ele}}{\underset{e=1}{\mathcal{A}}}\frac{\partial\boldsymbol{F}_{int,e}^{k}}{\partial\boldsymbol{\rho}_{1}} \quad\text{with} \\ &&\frac{\partial\boldsymbol{F}_{int,e}^{k}}{\partial\boldsymbol{\rho}_{1}}=\left[\begin{array}{lll} \frac{\partial\boldsymbol{F}_{int,e}^{k}}{{\partial\rho_{1}^{1}}} & ... & \frac{\partial\boldsymbol{F}_{int,e}^{k}}{\partial\rho_{1}^{n_{ele}}} \end{array}\right] \quad\text{where} \\ &&\frac{\partial\boldsymbol{F}_{int,e}^{k}}{{\partial\rho_{1}^{j}}}=\boldsymbol{0} \quad\text{if } j\neq e \quad \text{and} \\ &&\frac{\partial\boldsymbol{F}_{int,e}^{k}}{{\partial\rho_{1}^{e}}}=\sum\limits_{s=1}^{n_{ipt}}\boldsymbol{B}_{e_{s}}^{T}\left( \frac{\partial\gamma}{{\partial\rho_{1}^{e}}}\boldsymbol{P}_{e_{s}}^{k}+\gamma\frac{\partial\boldsymbol{P}_{e_{s}}^{k}}{{\partial\rho_{1}^{e}}}\right)w_{e_{s}} \\ &&+\sum\limits_{s=1}^{n_{ipt}}\boldsymbol{B}_{L,e_{s}}^{T}\left[-2\gamma\frac{\partial\gamma}{{\partial\rho_{1}^{e}}}(\mathbb{C}:\boldsymbol{\varepsilon}_{e_{s}})+(1-\gamma^{2})\left( \frac{\partial\mathbb{C}}{{\partial\rho_{1}^{e}}}:\boldsymbol{\varepsilon}_{e_{s}}\right)\right]w_{e_{s}} \\ &&\text{with} \\ &&\frac{\partial\boldsymbol{P}}{\partial\rho_{1}}=-\frac{1}{2}r^{-\frac{3}{2}}\frac{\partial r}{\partial\rho_{1}}\boldsymbol{P}^{b}+r^{-\frac{1}{2}}\left( \frac{\partial\boldsymbol{P}^{b}}{\partial\rho_{1}}\bigg|_{\boldsymbol{F}^{b} \text{fixed}}+\frac{\partial\boldsymbol{P}^{b}}{\partial\boldsymbol{F}^{b}}:\frac{\partial\boldsymbol{F}^{b}}{\partial\rho_{1}}\right) \end{array} $$

(B.14)

$$ \text{where}\quad \frac{\partial\boldsymbol{P}^{b}}{\partial\boldsymbol{F}^{b}}=\mathbb{A}_{0}^{b}+\mathbb{A}_{1}^{b}+\mathbb{A}_{2}^{b,eq}-\boldsymbol{P}_{2}^{b,neq}\boxdot{\boldsymbol{F}^{b}}^{-1} $$

(B.15)

in which $\mathbb {A}_{0}^{b}$, $\mathbb {A}_{1}^{b}$, and $\mathbb {A}_{2}^{b,eq}$ are the tangent moduli evaluated from each constitutive model with material interpolation, i.e., $\mathbb {A}_{0}^{b}\triangleq \partial \boldsymbol {P}_{0}^{b}/\partial \boldsymbol {F}^{b}$, $\mathbb {A}_{1}^{b}\triangleq \partial \boldsymbol {P}_{1}^{b}/\partial \boldsymbol {F}^{b}$ and $\mathbb {A}_{2}^{b,eq}\triangleq \partial \boldsymbol {P}_{2}^{b,eq}/\partial \boldsymbol {F}^{b}$; $\frac {\partial \boldsymbol {P}^{b}}{\partial \rho _{1}}\big |_{\boldsymbol {F}^{b} \text {fixed}}$ is computed by

$$ \begin{array}{@{}rcl@{}} \frac{\partial\boldsymbol{P}^{b}}{\partial\rho_{1}}\bigg|_{\boldsymbol{F}^{b} \text{fixed}}&=&\frac{\partial\boldsymbol{P}_{0}^{b}}{\partial\rho_{1}}\bigg|_{\boldsymbol{F}^{b} \text{fixed}}+\frac{\partial\boldsymbol{P}_{1}^{b}}{\partial\rho_{1}}\bigg|_{\boldsymbol{F}^{b} \text{fixed}} \\ &&+\left( \frac{\partial\boldsymbol{P}_{2}^{b,eq}}{\partial\rho_{1}}\bigg|_{\boldsymbol{F}^{b} \text{fixed}}+\frac{\partial\boldsymbol{P}_{2}^{b,neq}}{\partial\rho_{1}}\bigg|_{\boldsymbol{F}^{b} \text{fixed}}\right) \end{array} $$

(B.16)

where

$$ \begin{array}{@{}rcl@{}} &&\frac{\partial\boldsymbol{P}_{0}^{b}}{\partial\rho_{1}}\bigg|_{\boldsymbol{F}^{b} \text{fixed}}=\frac{\partial g_{1}}{\partial\rho_{1}}\left( \hat{\boldsymbol{P}}_{0,s}^{b}+\tilde{\boldsymbol{P}}_{0,s}^{b}\right) \\ &&\frac{\partial\boldsymbol{P}_{1}^{b}}{\partial\rho_{1}}\bigg|_{\boldsymbol{F}^{b} \text{fixed}}=\frac{\partial g_{2}}{\partial\rho_{1}}\hat{\boldsymbol{P}}_{1,s}^{b}+\frac{\partial g_{3}}{\partial\rho_{1}}\tilde{\boldsymbol{P}}_{1,s}^{b}\\ &&\frac{\partial\boldsymbol{P}_{2}^{b,eq}}{\partial\rho_{1}}\bigg|_{\boldsymbol{F}^{b} \text{fixed}}=\frac{\partial g_{4}}{\partial\rho_{1}}\hat{\boldsymbol{P}}_{2,s}^{b,eq}+\frac{\partial g_{5}}{\partial\rho_{1}}\tilde{\boldsymbol{P}}_{2,s}^{b,eq} \\ &&\frac{\partial\boldsymbol{P}_{2}^{b,neq}}{\partial\rho_{1}}\bigg|_{\boldsymbol{F}^{b} \text{fixed}}=\frac{\partial g_{6}}{\partial\rho_{1}}\hat{\boldsymbol{P}}_{2,s}^{b,neq}+\frac{\partial g_{7}}{\partial\rho_{1}}\tilde{\boldsymbol{P}}_{2,s}^{b,neq} \end{array} $$

(B.17)

where “s” in the subscript denotes that the term is evaluated with the non-interpolated solid material parameters. Again, the upper hat denotes the volumetric part while upper tilde denotes the isochoric part, e.g., $\hat {\boldsymbol {P}}_{2,s}^{b,eq}=\partial \hat {\psi }_{2}^{eq}/\partial \boldsymbol {F}^{b}$, where $\hat {\psi }_{2}^{eq}$ is evaluated with solid phase parameters. It should be noted that in sensitivity analysis the calculation of $\hat {\boldsymbol {P}}_{2,s}^{b,neq}$ and $\tilde {\boldsymbol {P}}_{2,s}^{b,neq}$ are based on $\hat {\psi }_{2}^{neq}(\boldsymbol {b}^{e})$ and $\tilde {\psi }_{2}^{neq}(\boldsymbol {b}^{e})$ where solid material phase parameters are used, however, the computation of b^e is based on the interpolated material parameters. Since b^e is chosen as independent variable, its dependence on ρ₁ and ρ₂ fields is not explicitly accounted. On the other hand, the dependence of R^k on ρ₂ comes from the constitutive model parameters. As a result, the derivative $\partial \boldsymbol {R}^{k}/\partial \boldsymbol {\rho }_{2}$ is computed as

$$ \begin{array}{@{}rcl@{}} &&\frac{\partial\boldsymbol{R}^{k}}{\partial\boldsymbol{\rho}_{2}}=\left[\begin{array}{lll} \frac{\partial\boldsymbol{F}_{int}^{k}}{\partial\boldsymbol{\rho}_{2}} \\ \boldsymbol{0} \\ \boldsymbol{0} \end{array}\right] \quad \text{with}\quad \frac{\partial\boldsymbol{F}_{int}^{k}}{\partial\boldsymbol{\rho}_{2}}=\overset{n_{ele}}{\underset{e=1}{\mathcal{A}}}\frac{\partial\boldsymbol{F}_{int,e}^{k}}{\partial\boldsymbol{\rho}_{2}} \\ &&\text{with} \quad \frac{\partial\boldsymbol{F}_{int,e}^{k}}{\partial\boldsymbol{\rho}_{2}}=\left[\begin{array}{lll} \frac{\partial\boldsymbol{F}_{int,e}^{k}}{{\partial\rho_{2}^{1}}} & ... & \frac{\partial\boldsymbol{F}_{int,e}^{k}}{\partial\rho_{2}^{n_{ele}}} \end{array}\right] \\ &&\text{where} \quad \frac{\partial\boldsymbol{F}_{int,e}^{k}}{{\partial\rho_{2}^{j}}}=\boldsymbol{0}\quad \text{if }j\neq e \quad \text{and} \\ &&\frac{\partial\boldsymbol{F}_{int,e}^{k}}{{\partial\rho_{2}^{e}}}=\sum\limits_{s=1}^{n_{ipt}}\gamma\boldsymbol{B}_{e_{s}}^{T}\frac{\partial\boldsymbol{P}_{e_{s}}^{k}}{{\partial\rho_{2}^{e}}}w_{e_{s}} \quad\text{with}\quad \frac{\partial\boldsymbol{P}}{\partial\rho_{2}}=r^{-\frac{1}{2}}\frac{\partial\boldsymbol{P}^{b}}{\partial\rho_{2}} \\ &&\text{where}\quad \frac{\partial\boldsymbol{P}^{b}}{\partial\rho_{2}}=\frac{\partial\boldsymbol{P}_{1}^{b}}{\partial\rho_{2}}+\left( \frac{\partial\boldsymbol{P}_{2}^{b,eq}}{\partial\rho_{2}}+\frac{\partial\boldsymbol{P}_{2}^{b,neq}}{\partial\rho_{2}}\right) \\ &&\text{with} \\ &&\frac{\partial\boldsymbol{P}_{1}^{b}}{\partial\rho_{2}}=\frac{\partial g_{2}}{\partial\rho_{2}}\hat{\boldsymbol{P}}_{1,s}^{b}+\frac{\partial g_{3}}{\partial\rho_{2}}\tilde{\boldsymbol{P}}_{1,s}^{b}\\ &&\frac{\partial\boldsymbol{P}_{2}^{b,eq}}{\partial\rho_{2}}=\frac{\partial g_{4}}{\partial\rho_{2}}\hat{\boldsymbol{P}}_{2,s}^{b,eq}+\frac{\partial g_{5}}{\partial\rho_{2}}\tilde{\boldsymbol{P}}_{2,s}^{b,eq} \\ &&\frac{\partial\boldsymbol{P}_{2}^{b,neq}}{\partial\rho_{2}}=\frac{\partial g_{6}}{\partial\rho_{2}}\hat{\boldsymbol{P}}_{2,s}^{b,neq}+\frac{\partial g_{7}}{\partial\rho_{2}}\tilde{\boldsymbol{P}}_{2,s}^{b,neq} \end{array} $$

(B.18)

1.2.2 B.2.2 Derivatives of $\partial \boldsymbol {R}^{k}/\partial \hat {\boldsymbol {u}}^{k}$ and $\partial \boldsymbol {R}^{k}/\partial \hat {\boldsymbol {u}}^{k-1}$

The derivative $\partial \boldsymbol {R}^{k}/\partial \hat {\boldsymbol {u}}^{k}$ is derived as

$$ \begin{array}{@{}rcl@{}} &&\frac{\partial\boldsymbol{R}^{k}}{\partial\hat{\boldsymbol{u}}^{k}}=\left[\begin{array}{lll} \frac{\partial\boldsymbol{F}_{int}^{k}}{\partial\boldsymbol{u}^{k}} & -\boldsymbol{M}_{1}^{T} & -\boldsymbol{M}_{2}^{T} \\ -\boldsymbol{M}_{1} & \boldsymbol{0} & \boldsymbol{0} \\ -\boldsymbol{M}_{2} & \boldsymbol{0} & \boldsymbol{0} \end{array}\right] \\ &&\text{with}\quad \frac{\partial\boldsymbol{F}_{int}^{k}}{\partial\boldsymbol{u}^{k}}=\overset{n_{ele}}{\underset{e=1}{\mathcal{A}}}\frac{\partial\boldsymbol{F}_{int,e}^{k}}{\partial\boldsymbol{u}_{e}^{k}} \\ &&\text{with}\\ &&\frac{\partial\boldsymbol{F}_{int,e}^{k}}{\partial\boldsymbol{u}_{e}^{k}}=\sum\limits_{s=1}^{n_{ipt}}\gamma\boldsymbol{B}_{e_{s}}^{T} \left( r^{-\frac{1}{2}}\frac{\partial\boldsymbol{P}^{b}}{\partial\boldsymbol{F}^{b}}:\frac{\partial\boldsymbol{F}^{b}}{\partial\boldsymbol{u}}-\frac{1}{2}r^{-\frac{3}{2}}\boldsymbol{P}^{b}\otimes\frac{\partial r}{\partial\boldsymbol{u}}\right)w_{e_{s}} \\ &&\qquad\qquad + \sum\limits_{s=1}^{n_{ipt}}(1-\gamma^{2})\boldsymbol{B}_{L,e_{s}}^{T}[\mathbb{C}]\boldsymbol{B}_{L,e_{s}}w_{e_{s}} \end{array} $$

(B.19)

where the term ∂P^b/∂F^b is calculated in (B.15). Also, R^k does not depend on $\hat {\boldsymbol {u}}^{k-1}$ explicitly and

$$ \frac{\partial\boldsymbol{R}^{k}}{\partial\hat{\boldsymbol{u}}^{k-1}}=\boldsymbol{0} $$

(B.20)

1.2.3 B.2.3 Derivatives of ∂R^k/∂v^k and ∂R^k/∂v^k− 1

Since in the free energy only $\psi _{2}^{neq}(\boldsymbol {b}^{e})$ depends on the auxiliary variable (v ≡b^e), the derivative ∂R^k/∂v^k can be derived as

$$ \begin{array}{@{}rcl@{}} &&\frac{\partial\boldsymbol{R}^{k}}{\partial\boldsymbol{v}^{k}}=\left[\begin{array}{cc} \frac{\partial\boldsymbol{F}_{int}^{k}}{\partial\boldsymbol{v}^{k}} \\ \boldsymbol{0} \\ \boldsymbol{0} \end{array}\right] \quad\text{with}\quad \frac{\partial\boldsymbol{F}_{int}^{k}}{\partial\boldsymbol{v}^{k}}=\overset{n_{ele}}{\underset{e=1}{\mathcal{A}}}\frac{\partial\boldsymbol{F}_{int,e}^{k}}{\partial\boldsymbol{v}^{k}} \\ &&\text{with} \quad \frac{\partial\boldsymbol{F}_{int,e}^{k}}{\partial\boldsymbol{v}^{k}}=\left[\begin{array}{l} \frac{\partial\boldsymbol{F}_{int,e}^{k}}{\partial\boldsymbol{v}_{1}^{k}} ... \frac{\partial\boldsymbol{F}_{int,e}^{k}}{\partial\boldsymbol{v}_{n_{ele}}^{k}} \end{array}\right] \\ &&\text{where} \quad \frac{\partial\boldsymbol{F}_{int,e}^{k}}{\partial\boldsymbol{v}_{j}^{k}}=\boldsymbol{0} \quad \text{if } j\neq e \quad \text{and} \\ &&\frac{\partial\boldsymbol{F}_{int,e}^{k}}{\partial\boldsymbol{v}_{e}^{k}}=\left[\begin{array}{llll} \frac{\partial\boldsymbol{F}_{int,e}^{k}}{\partial\boldsymbol{v}_{e_{1}}^{k}} & \frac{\partial\boldsymbol{F}_{int,e}^{k}}{\partial\boldsymbol{v}_{e_{2}}^{k}} & \frac{\partial\boldsymbol{F}_{int,e}^{k}}{\partial\boldsymbol{v}_{e_{3}}^{k}} & \frac{\partial\boldsymbol{F}_{int,e}^{k}}{\partial\boldsymbol{v}_{e_{4}}^{k}} \end{array}\right] \\ &&\text{with} \quad \frac{\partial\boldsymbol{F}_{int,e}^{k}}{\partial\boldsymbol{v}_{e_{s}}^{k}}=\gamma\boldsymbol{B}_{e_{s}}^{T}\frac{\partial\boldsymbol{P}_{e_{s}}^{k}}{\partial\boldsymbol{v}_{e_{s}}^{k}}w_{e_{s}} \\ &&\text{where}\quad \frac{\partial\boldsymbol{P}_{e_{s}}^{k}}{\partial\boldsymbol{v}_{e_{s}}^{k}}=r^{-1/2}\left[\frac{\partial\boldsymbol{\tau}^{neq}}{\partial\boldsymbol{b}^{e}}\boxplus{\boldsymbol{F}^{b}}^{-T}\right] \end{array} $$

(B.21)

Without dependence of R^k on v^k− 1

$$ \frac{\partial\boldsymbol{R}^{k}}{\partial\boldsymbol{v}^{k-1}}=\boldsymbol{0} $$

(B.22)

1.3 B.3 Derivatives of H^k

1.3.1 B.3.1 Derivatives of $\partial \boldsymbol {H}^{k}/\partial \boldsymbol {\rho }_{1}$ and $\partial \boldsymbol {H}^{k}/\partial \boldsymbol {\rho }_{2}$

The derivatives $\partial \boldsymbol {H}^{k}/\partial \boldsymbol {\rho }_{1}$ and $\partial \boldsymbol {H}^{k}/\partial \boldsymbol {\rho }_{2}$ are obtained as

$$ \begin{array}{@{}rcl@{}} &&\frac{\partial\boldsymbol{H}^{k}}{\partial\boldsymbol{\rho}_{A}}=\left[\begin{array}{lll} \frac{\partial\boldsymbol{H}_{1}^{k}}{{\partial\rho_{A}^{1}}} & \boldsymbol{0} & \boldsymbol{0} \\ \boldsymbol{0} & {\ddots} & \boldsymbol{0}\\ \boldsymbol{0} & \boldsymbol{0} & \frac{\partial\boldsymbol{H}_{n_{ele}}^{k}}{\partial\rho_{A}^{n_{ele}}} \end{array}\right] \quad\text{with} \\ &&\frac{\partial\boldsymbol{H}_{e}^{k}}{{\partial\rho_{A}^{e}}}=\left[\begin{array}{l} \frac{\partial\boldsymbol{H}_{e_{1}}^{k}}{{\partial\rho_{A}^{e}}} \\ \frac{\partial\boldsymbol{H}_{e_{2}}^{k}}{{\partial\rho_{A}^{e}}} \\ \frac{\partial\boldsymbol{H}_{e_{3}}^{k}}{{\partial\rho_{A}^{e}}} \\ \frac{\partial\boldsymbol{H}_{e_{4}}^{k}}{{\partial\rho_{A}^{e}}} \end{array}\right] , \quad A\in\{1,2\} \\ &&\text{with} \\ &&\frac{\partial\boldsymbol{H}_{e_{s}}^{k}}{{\partial\rho_{1}^{e}}}=-\left( \frac{\partial{\boldsymbol{b}^{e}}^{tr}}{\partial\boldsymbol{F}_{k-1}^{b}}:\frac{\partial\boldsymbol{F}_{k-1}^{b}}{{\partial\rho_{1}^{e}}}+\frac{\partial{\boldsymbol{b}^{e}}^{tr}}{\partial\boldsymbol{F}^{b}}:\frac{\partial\boldsymbol{F}^{b}}{{\partial\rho_{1}^{e}}}\right)\\ &&\qquad .\exp[-2{\Delta} t_{k}\boldsymbol{A}]-{\boldsymbol{b}^{e}}^{tr}.\frac{\partial}{{\partial\rho_{1}^{e}}}(\exp[-2{\Delta} t_{k}\boldsymbol{A}]) \\ &&\text{and}\quad \frac{\partial\boldsymbol{H}_{e_{s}}^{k}}{{\partial\rho_{2}^{e}}}=-{\boldsymbol{b}^{e}}^{tr}.\frac{\partial}{{\partial\rho_{2}^{e}}}(\exp[-2{\Delta} t_{k}\boldsymbol{A}]) \end{array} $$

(B.23)

where

$$ \begin{array}{@{}rcl@{}} \frac{\partial}{{\partial\rho_{A}^{e}}}(\exp[-2{\Delta} t_{k}\boldsymbol{A}])=\sum\limits_{a=1}^{3} &e^{-\frac{\Delta t_{k}}{\eta_{d}}\tilde{\tau}_{a}^{neq}}\frac{\Delta t_{k}}{\eta_{d}}\left( \frac{\tilde{\tau}_{a}^{neq}}{\eta_{d}}\frac{\partial\eta_{d}}{{\partial\rho_{A}^{e}}}\right.\\ &\left.-\frac{\partial\tilde{\tau}_{a}^{neq}}{{\partial\rho_{A}^{e}}}\right)\boldsymbol{G}_{a}^{e} ,\quad A\in \{1,2\} \end{array} $$

(B.24)

and

$$ \begin{array}{@{}rcl@{}} &&\frac{\partial{\boldsymbol{b}^{e}}^{tr}}{\partial\boldsymbol{F}^{b}}=\boldsymbol{I}\odot\left( \boldsymbol{F}_{k-1}^{b^{-1}}.\boldsymbol{b}_{k-1}^{e}.\boldsymbol{F}_{\delta}^{b^{T}}\right)+\left( \boldsymbol{F}_{\delta}^{b}.\boldsymbol{b}_{k-1}^{e}.{\boldsymbol{F}_{k-1}^{b^{-T}}}\right)\boxdot\boldsymbol{I} \\ &&\frac{\partial{\boldsymbol{b}^{e}}^{tr}}{\partial\boldsymbol{F}_{k-1}^{b}}=-\boldsymbol{F}_{\delta}^{b}\odot\left( \boldsymbol{F}_{k-1}^{b^{-1}}.\boldsymbol{b}_{k-1}^{e}.\boldsymbol{F}_{\delta}^{b^{T}}\right)-\left( \boldsymbol{F}_{\delta}^{b}.\boldsymbol{b}_{k-1}^{e}.{\boldsymbol{F}_{k-1}^{b^{-T}}}\right)\boxdot\boldsymbol{F}_{\delta}^{b} \end{array} $$

(B.25)

in which $\tilde {\tau }_{a}^{neq}=\tau _{a}^{neq}-p^{neq}$ is the isochoric part of the principal non-equilibrium Kirchhoff stress and the relationship ${\boldsymbol {b}^{e}}^{tr}=\boldsymbol {F}_{\delta }^{b}.\boldsymbol {b}_{k-1}^{e}.\boldsymbol {F}_{\delta }^{b^{T}}$ with $\boldsymbol {F}_{\delta }^{b}\triangleq \boldsymbol {F}^{b}.\boldsymbol {F}_{k-1}^{b^{-1}}$ is used in the derivation (where F^b is at step k), and the derivative $\partial \tilde {\tau }_{a}^{neq}/{\partial \rho _{A}^{e}}$ is calculated by

$$ \frac{\partial\tilde{\tau}_{a}^{neq}}{{\partial\rho_{A}^{e}}}=\frac{\partial g_{7}}{{\partial\rho_{A}^{e}}}\tilde{\tau}_{a,s}^{neq} $$

(B.26)

where the subscript “s” in $\tilde {\tau }_{a,s}^{neq}$ means that it is computed from the solid phase.

1.3.2 B.3.2 Derivatives of $\partial \boldsymbol {H}^{k}/\partial \hat {\boldsymbol {u}}^{k}$ and $\partial \boldsymbol {H}^{k}/\partial \hat {\boldsymbol {u}}^{k-1}$

The derivative $\partial \boldsymbol {H}^{k}/\partial \hat {\boldsymbol {u}}^{k}$ is obtained as

$$ \begin{array}{@{}rcl@{}} &&\frac{\partial\boldsymbol{H}^{k}}{\partial\hat{\boldsymbol{u}}^{k}}=\left[\begin{array}{lll} \frac{\partial\boldsymbol{H}^{k}}{\partial\boldsymbol{u}^{k}} & \boldsymbol{0} & \boldsymbol{0} \end{array}\right] \quad\text{with} \quad \frac{\partial\boldsymbol{H}^{k}}{\partial\boldsymbol{u}^{k}}=\overset{n_{ele}}{\underset{e=1}{\mathcal{A}}}\frac{\partial\boldsymbol{H}^{k}}{\partial\boldsymbol{u}_{e}^{k}}\\ &&\text{where}\\ &&\frac{\partial\boldsymbol{H}^{k}}{\partial\boldsymbol{u}_{e}^{k}}=\left[\begin{array}{ll} \frac{\partial\boldsymbol{H}_{1}^{k}}{\partial\boldsymbol{u}_{e}^{k}} \\ {\vdots} \\ \frac{\partial\boldsymbol{H}_{n_{ele}}^{k}}{\partial\boldsymbol{u}_{e}^{k}} \end{array}\right] \quad \text{with}\quad \frac{\partial\boldsymbol{H}_{j}^{k}}{\partial\boldsymbol{u}_{e}^{k}}=\boldsymbol{0}\quad \text{if } j\neq e \quad \text{and}\\ &&\frac{\partial\boldsymbol{H}_{e}^{k}}{\partial\boldsymbol{u}_{e}^{k}}=\left[\begin{array}{llll} \frac{\partial\boldsymbol{H}_{e_{1}}^{k}}{\partial\boldsymbol{u}_{e}^{k}} \\ \frac{\partial\boldsymbol{H}_{e_{2}}^{k}}{\partial\boldsymbol{u}_{e}^{k}} \\ \frac{\partial\boldsymbol{H}_{e_{3}}^{k}}{\partial\boldsymbol{u}_{e}^{k}} \\ \frac{\partial\boldsymbol{H}_{e_{4}}^{k}}{\partial\boldsymbol{u}_{e}^{k}} \end{array}\right] \quad\text{with}\\ &&\frac{\partial\boldsymbol{H}_{e_{s}}^{k}}{\partial\boldsymbol{u}_{e}^{k}}=-\left( \frac{\partial{\boldsymbol{b}^{e}}^{tr}}{\partial\boldsymbol{F}^{b}}:\frac{\partial\boldsymbol{F}^{b}}{\partial\boldsymbol{u}}\right)\circledcirc\exp[-2{\Delta} t_{k}\boldsymbol{A}] \end{array} $$

(B.27)

Similarly, the derivative $\partial \boldsymbol {H}^{k}/\partial \hat {\boldsymbol {u}}^{k-1}$ is obtained in the same way but with

$$ \frac{\partial\boldsymbol{H}_{e_{s}}^{k}}{\partial\boldsymbol{u}_{e}^{k-1}}=-\left( \frac{\partial{\boldsymbol{b}^{e}}^{tr}}{\partial\boldsymbol{F}_{k-1}^{b}}:\frac{\partial\boldsymbol{F}_{k-1}^{b}}{\partial\boldsymbol{u}^{k-1}}\right)\circledcirc\exp[-2{\Delta} t_{k}\boldsymbol{A}] $$

(B.28)

1.3.3 B.3.3 Derivatives of ∂H^k/∂v^k and ∂H^k/∂v^k− 1

The derivative ∂H^k/∂v^k is obtained as

$$ \begin{array}{@{}rcl@{}} &\frac{\partial\boldsymbol{H}^{k}}{\partial\boldsymbol{v}^{k}}=\left[\begin{array}{lll} \frac{\partial\boldsymbol{H}_{1}^{k}}{\partial\boldsymbol{v}_{1}^{k}} & \boldsymbol{0} & \boldsymbol{0} \\ \boldsymbol{0} & {\ddots} & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{0} & \frac{\partial\boldsymbol{H}_{n_{ele}}^{k}}{\partial\boldsymbol{v}_{n_{ele}}^{k}} \end{array}\right] \quad\text{with} \\ &\frac{\partial\boldsymbol{H}_{e}^{k}}{\partial\boldsymbol{v}_{e}^{k}}=\left[\begin{array}{llll} \frac{\partial\boldsymbol{H}_{e_{1}}^{k}}{\partial\boldsymbol{v}_{e_{1}}^{k}} & \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} \\ \boldsymbol{0} & \frac{\partial\boldsymbol{H}_{e_{2}}^{k}}{\partial\boldsymbol{v}_{e_{2}}^{k}} & \boldsymbol{0} & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{0} & \frac{\partial\boldsymbol{H}_{e_{3}}^{k}}{\partial\boldsymbol{v}_{e_{3}}^{k}} & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} & \frac{\partial\boldsymbol{H}_{e_{4}}^{k}}{\partial\boldsymbol{v}_{e_{4}}^{k}} \end{array}\right] \end{array} $$

(B.29)

$$ \frac{\partial\boldsymbol{H}_{e_{s}}^{k}}{\partial\boldsymbol{v}_{e_{s}}^{k}}=\mathbb{I}_{4}^{s}-{\boldsymbol{b}^{e}}^{tr}.\frac{\partial}{\partial\boldsymbol{b}^{e}}(\exp[-2{\Delta} t_{k}\boldsymbol{A}]) $$

(B.30)

$$ \frac{\partial}{\partial\boldsymbol{b}^{e}}(\exp[-2{\Delta} t_{k}\boldsymbol{A}])=\frac{\partial}{\partial\boldsymbol{\tau}^{neq}}(\exp[-2{\Delta} t_{k}\boldsymbol{A}]):\frac{\partial\boldsymbol{\tau}^{neq}}{\partial\boldsymbol{b}^{e}} $$

(B.31)

where $\mathbb {I}_{4}^{s}$ is the symmetric identity 4th-order tensor, i.e., $\mathbb {I}_{4}^{s}\triangleq \frac {1}{2}(\boldsymbol {I}\boxtimes \boldsymbol {I}+\boldsymbol {I}\boxdot \boldsymbol {I})$, $\boldsymbol {I}\rightarrow$ second-order identity tensor and the derivatives $\partial (\exp [-2 {\Delta } t_{k}\boldsymbol {A}])/\partial \boldsymbol {\tau }^{neq}$ and ∂τ^neq/∂b^e are computed in the principal space. Finally, the derivative ∂H^k/∂v^k− 1 is formulated in the same way as ∂H^k/∂v^k, but with

$$ \begin{array}{@{}rcl@{}} &&\frac{\partial\boldsymbol{H}_{e_{s}}^{k}}{\partial\boldsymbol{v}_{e_{s}}^{k-1}}=-\frac{\partial{\boldsymbol{b}^{e}}^{tr}}{\partial\boldsymbol{b}_{k-1}^{e}}\boxplus\exp[-2{\Delta} t_{k}\boldsymbol{A}] \quad\text{where} \\ && \frac{\partial{\boldsymbol{b}^{e}}^{tr}}{\partial\boldsymbol{b}_{k-1}^{e}}=\frac{1}{2}(\boldsymbol{F}_{\delta}^{b}\boxtimes\boldsymbol{F}_{\delta}^{b}+\boldsymbol{F}_{\delta}^{b}\boxdot\boldsymbol{F}_{\delta}^{b}) \end{array} $$

(B.32)

Appendix C: Verifications of the path-dependent sensitivity analysis

In this appendix, the path-dependent sensitivity calculation given in Section 5 and Appendix B is verified for two types of material interpolations as given in Section 4.3 for different candidates chosen for material-0. The first verification, referred to as verification-1, considers the material interpolation given in Section 4.3.1 with void phase chosen as material-0. The second verification, referred to as verification-2, considers the material interpolation in Section 4.3.2 with a soft hyperelastic phase chosen as material-0.

1.1 C.1 Sensitivity verification-1: Void for material-0

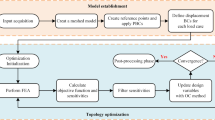
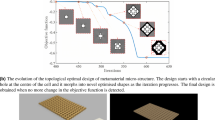
For verification-1, a parallelogram-shaped RUC with a random design shown in Fig. 15a is used. The density vectors ρ₁ and ρ₂ are plotted in Fig. 15c. The macroscopic deformation loading considers (68) to (70) with 𝜃 = 0^∘, Λ = 1.4, f = 0.009s^− 1, and t ∈ [0, 1/f]. The sensitivity comparison between the proposed adjoint method and the central difference method (with perturbation ${\Delta }\rho _{1}={\Delta }\rho _{2}={10}^{-6}$) is shown in Fig. 16 where good matches can be observed with relative error around 10^− 6 to 10^− 8. Here, the relative error is computed as the absolute value of the ratio of the difference between the central difference results and the adjoint results to the central difference results.

Fig. 15

Designs for sensitivity verifications

Fig. 16

Sensitivity comparison between the adjoint method and the central difference method for verification-1

Fig. 17

Sensitivity comparison between the adjoint method and the central difference method for verification-2

1.2 C.2 Sensitivity verification-2: Soft hyperelastic phase for material-0

For verification-2, a hexagon-shaped RUC with prescribed design shown in Fig. 15b is used. The design is with the same density vectors ρ₁ and ρ₂ shown in Fig. 15c. The macroscopic deformation loading considers (68) to (70) with 𝜃 = 45^∘, Λ = 1.4, f = 0.009s^− 1 and t ∈ [0, 1/f]. The sensitivity comparison between the proposed adjoint method and the central difference method (with perturbation ${\Delta }\rho _{1}={\Delta }\rho _{2}={10}^{-6}$) is shown in Fig. 17 where again good matches can be observed with relative error around 10^− 6 to 10^− 8.