Probabilistic optimisation of mono-stringer composite stiffened panels in post-buckling regime

Abstract

In this paper, a multi-objective probabilistic design optimisation approach is presented for reliability and robustness analysis of composite structures and demonstrated on a mono-omega-stringer stiffened panel. The proposed approach utilises a global surrogate model of the composite structure while accounting for uncertainties in material properties as well as geometry. Unlike the multi-level optimisation approach which freezes some parameters at each level, the proposed approach allows for all parameters to change at the same time and hence ensures global optimum solutions in the given parameter design space (for both probabilistic and deterministic optimisations) within a certain degree of accuracy. The proposed approach is used in this study to conduct extensive multi-objective probabilistic and deterministic optimisations (without considering safety factors) on a mono-stringer stiffened panel. In particular, a global surrogate model is developed utilising the computational power of a high-performance computing facility. The inputs of the surrogate model are the omega-stringer geometry and the mechanical properties of the composite material, while the outputs are the fundamental linear buckling load (LBL) and the nonlinear post-buckling strength (NPS). LBL and NPS are obtained via detailed parametric finite element models of the mono-stringer stiffened panel; in the nonlinear model, the interface between the skin and the omega-stringer is modelled via cohesive elements to allow for debonding in the post-buckled regime. Extensive multi-objective optimisations are conducted on the surrogate model using deterministic and probabilistic approaches to examine the omega-stringer geometric parameters mostly affecting the system robustness and reliability. The differences between deterministic and probabilistic designs are highlighted as well.

1 Introduction

Carbon fibre-reinforced composites are widely used in aircraft structures. The recent advancements in composites allowed the industry to increase their usage of composite materials dramatically. To put it into numbers, the latest models by Boeing and Airbus are made of 50 and 53% composites, respectively. These percentages will grow in the future to even further reduce the mass of the aircraft while achieving higher strengths and increased lifespan. One of the key elements of an aircraft is the composite stiffened panel, in which the skin is reinforced via adding a stringer for superior load carrying in both tension and compression. The main concern in the design of a stiffened panel, for sections of an aircraft under compression, is maximising the compressive load carrying due to the buckling phenomenon (Hao et al. 2017). For the case of omega-stringer stiffened panels, the initial buckling starts in the skin (Kassapoglou 2013; Wang and Abdalla 2015), here referred to as the fundamental linear buckling load (LBL); however, it is known that beyond the first linear buckling, a stiffened panel could carry loads of several times the magnitude of the fundamental LBL before failure, here referred to as the nonlinear post-buckling strength (NPS). Hence, designing a panel which will always operate below the fundamental LBL is very conservative; given the extra strength of the panel in the post-buckling regime, much lighter designs can be achieved by allowing the panel to operate in the post-buckling regime. This has motivated a large amount of research on stiffened panel optimisation in the post-buckling regime. In what follows, a concise review of the vast literature on optimisation of composite structures is given; more detailed reviews can be found in surveys conducted by, for instance, Venkataraman and Haftka (1999), Ghiasi et al. (2009) Ghiasi et al. (2010) and Nikbakt et al. (2018).

The traditional approach of optimisation, also known as deterministic optimisation (DO), does not account for any uncertainties in the system. Modern optimisation techniques, also known as probabilistic optimisation (PO), on the other hand, account for uncertainties (Salas and Venkataraman 2008) that could affect the design objectives, such as uncertainties associated with mechanical properties or the geometry. Two well-stablished PO techniques are robust-design optimisation (RDO) and reliability-based design optimisation (RBDO) (Chen and Qiu 2018; das Neves Carneiro and Antonio 2018; Fang et al. 2018; Hu and Duan 2018; Kaveh et al. 2018; López et al. 2017; Montoya et al. 2015; Sohouli et al. 2018; Strömberg 2017). RDO focuses on minimising the sensitivity of the objective function to random changes in the uncertain variables in the system, while RBDO aims at achieving a certain confidence in reliability of the product under a prescribed probabilistic constraint. In what follows, a brief literature review is conducted on different optimisation techniques.

One of the methods of optimising stiffened panels is the finite strip method (FSM) originally developed by Wittrick (1968) and Cheung (1968), in which the stiffened panel is divided into a finite number of strips and the motions of the strips are approximated via trigonometric functions. Further research was conducted using FSM technique for instance by Bushnell (1987), Butler and Williams (1993) and Zabinsky (1998). Homogenisation-based methods have also been used for optimisation of stiffened panels (Wang and Abdalla 2016; Wang et al. 2017; 2018; 2019). For instance, Wang et al. (2018) conducted a sensitivity analysis for optimisation of non-uniform curved stiffened composite panels in the framework of homogenisation-based local/global analysis.

The finite element (FE) technique is another method for modelling and analysis of stiffened panels which is superior to FSM. However, accurate FE models, which account for geometric nonlinearities, progressive failure and interfacial debonding, are usually very time consuming. Conducting a multi-objective optimisation (Coello 2000; Marler and Arora 2004; Zitzler et al. 2000) of stiffened panel using FE models could become very time consuming as massive computational power is required to search the multi-dimensional design space while accounting for different sources of nonlinearities. To address this problem, a multi-level approach has been suggested by Sobieszczanski-Sobieski et al. (1987) in which the large optimisation problem is divided into levels of substructures. A two-level optimisation procedure for a composite wing was developed by Liu et al. (2000), who constructed response surface for the optimal buckling load at the lower level and employed it later for global optimisation. Herencia et al. (2008a) proposed a two-level approach for layup optimisation of composite stiffened panels. A multi-level approach was developed by Wind et al. (2008), who conducted local and global optimisation on a multi-component structure. Further studies were conducted by Herencia et al. (2008b) who proposed a two-step method for optimisation of anisotropic composite stiffened panels. Bacarreza et al. (2015) employed a multi-level approach to conduct robust-design optimisation on composite stiffened panels in post-buckling regime. Although multi-level approaches reduce the computational costs, they do not guarantee a global optimum solution as in each level there is only a selection of system parameters which act as optimisation inputs while the rest are kept fixed.

Another technique for reducing the computational costs is to use a surrogate model (Albanesi et al. 2018; Marhadi and Venkataraman 2008) to approximate the response of the system. Lamberti et al. (2003) investigated the use of approximate models for conducting global optimisation on stiffened panels and concluded that it allows a greater exploration of the global design space compared to the case of utilising local optimisation together with complicated models. Having developed a surrogate model, different algorithms can be utilised to perform deterministic or probabilistic optimisation. Venkataraman and Salas (2007) proposed an approach for studying the mechanics influencing progressive failure predictability and developing surrogate models for deterministic optimisation in order to maximise performance. Barkanov et al. (2014) conducted linear buckling optimisation analysis on composite lateral wing upper covers utilising the response surface method together with optimal Latin hypercube sampling. In the second part of the study (Barkanov et al. 2016), the optimum designs based on linear buckling analysis were verified through a nonlinear buckling analysis and re-optimised if necessary; they utilised the response surface technique for surrogate modelling and optimisation purposes. Other studies have been performed on stiffened panel deterministic optimisation using surrogate modelling, for instance, by Bisagni and Lanzi (2002), Lanzi and Giavotto (2006), Irisarri et al. (2011) and Marín et al. (2012). López et al. (2017) conducted deterministic and reliability-based design optimisations of composite stiffened panels in post-buckling regime; they conducted a decoupled RBDO which separates the reliability analysis from the deterministic optimisation. Further RBDO studies of stiffened panel have been conducted by, for instance, Qu and Haftka (2003), who conducted RBDO and computed the reliability constraints employing Monte Carlo sampling and a design response surface, and Díaz et al. (2016), who performed a comparison of stochastic expansions and moment-based methods for the reliability analysis while using genetic and gradient-based techniques for deterministic optimisation.

The present study first proposes a highly reliable multi-objective probabilistic design optimisation approach through development of a global surrogate model and then applies that approach to a stiffened panel. More specifically, the proposed approach is detailed in Section 2. Then in Sections 3, 4 and 5, the approach is demonstrated for a mono-omega-stringer stiffened panel. The main advantage of the proposed approach over multi-level optimisation approaches is that it allows for all parameters to change simultaneously and hence ensures more general (near-global) probabilistic and deterministic optimum solutions. It is worth noting that in this study, a safety factor is not considered for either probabilistic or deterministic optimisations since the goal here is to differentiate between the underlying mechanism of these optimisation approaches, which comes before application of any safety factors.

2 Global multi-objective probabilistic design optimisation approach

The FE method has proven to be the most reliable technique for analysis of aircraft structures. The increased accuracy offered by FE techniques comes at the price of increased computational cost, which depending on the size and complexity of the structure could vary between hours to weeks of run time. Hence, conducting even deterministic optimisation on aircraft structures could be a computationally challenging task with months of run time. Now in the context of probabilistic optimisation which requires a large number of objective function calls (in the order of millions), it becomes impossible to use the original FE model as the objective function. In such cases, it is inevitable to use a surrogate model as an explicit approximation of the original FE model. Surrogate models have been used extensively for optimisation purposes in different fields. In the case of aircraft structures, surrogate models are usually used with very limited number of inputs and outputs in multi-level approaches to reduce computational costs; however, since some parameters are kept fixed at each level, the multi-level approaches do not guarantee global optimum result. In this study, a new surrogate model-based probabilistic optimisation approach is presented which is more efficient and more accurate than the multi-level approaches since it allows for all parameters to change simultaneously. The steps of this approach are explained for a general case in the following.

2.1 Developing a parametric FE model

The first step is developing a parametric FE model with a specific number of inputs and outputs. Although in general there is no specific limit on the number of inputs and outputs of the surrogate model of a structure, the proposed approach focuses on the main contributing input parameters of the structure under consideration to reduce the computational costs and to increase accuracy. The mechanical properties of the composite structure (E₁₁, E₂₂ = E₃₃, G₂₃ and G₁₂ = G₁₃) should always be considered as inputs since there are always uncertainties associated with their value and they could significantly affect the desired output. Apart from these four inputs, the geometric parameters which mostly affect the desired output should be considered as well. The number of geometric inputs could vary depending on the structure under consideration. After determining the desired inputs, detailed parametric FE models should be developed which calculate the outputs for a given set of inputs.

2.2 Creating matrix of design samples

Design-of-experiments methods are commonly utilised to determine the spatial distribution of samples in the design space. The main goal of design-of-experiments is to maximise the amount of information obtained from a limited number of sample points (Koziel et al. 2011). More specifically, design-of-experiments will provide a matrix of design samples which best represents the whole design space. In the proposed approach, the preferred method to create the matrix of design samples is the optimal Latin hypercube sampling technique (Park 1994). There is no general formula for the number of samples based on the number of inputs and outputs, as it depends on the sensitivity of the outputs to variations of the inputs and many other factors. The proposed approach suggests a sample size of at least 10 times the number of inputs; however, increasing the number of samples will reduce the error later on when constructing the surrogate model. After creating a matrix of design samples, the parametric FE models of the structure should be used to calculate the desired outputs for each sample in the design space. This step is the most computationally expensive part of the simulation. Parallelising simulation of the samples could decrease the total run time significantly.

2.3 Surrogate model development

Different software packages and codes are available for surrogate model development. In the present approach, the Surrogate Modelling (SUMO) toolbox (Gorissen et al. 2010) is suggested for this purpose due to its comprehensive library of algorithms. The SUMO toolbox is capable of generating surrogate models based on various algorithms and functions such as kriging, artificial neural network (ANN), radial basis functions, extreme machine learning and genetic algorithm, just to name a few. Hence, it provides a platform to generate and test various surrogate models for the system under consideration. Additionally, it offers different measures for error analysis such as cross-validation and reference data comparison. Having developed the matrix of design samples including inputs and outputs within a specific range of parameters, various surrogate models offered by the SUMO toolbox can be tested to find the one which offers the most accuracy. The accuracy of a surrogate model can be examined via two different measures, i.e. cross-validation and direct comparison to a unique data set (Gorissen et al. 2010; Rikards et al. 2006). In a situation where the desired accuracy is not met, further design samples should be created and computed using the FE models to increase the size of the matrix of the design samples. This should be repeated until the desired accuracy is met.

2.4 Global multi-objective optimisation

Having developed the surrogate model of the system, the final step is to conduct multi-objective probabilistic and deterministic optimisations on the surrogate model. Genetic algorithms are best suited for multi-objective optimisations. The main advantage of the proposed approach is that it offers a direct comparison between probabilistic and deterministic optimisation results. Deterministic optimisation, robust-design optimisation and reliability-based design optimisation are conducted on the developed surrogate model.

A general robust-design optimisation problem can be mathematically expressed as:

$$ {\displaystyle \begin{array}{l}\min \kern0.36em \left\{\mu \left(F\left(\mathbf{d},\mathbf{x}\right)\right),\sigma \left(F\left(\mathbf{d},\mathbf{x}\right)\right)\right\}\\ {}\mathrm{subject}\ \mathrm{to}:\kern0.75em {g}_m\left(\mathbf{d}\right)\le 0,\operatorname{}\operatorname{}m=1,2,...,M,\end{array}} $$

(1)

in which F stands for the objective function, d and x represent the design and random variables, μ and σ show the mean value and the standard deviation and g_m denotes the mth constraint. It should be noted that in an RDO, randomness could be associated with either design variables or other system variables. For an aircraft structure, uncertainties could be associated with mechanical properties, i.e. E₁₁, E₂₂ = E₃₃, G₂₃ and G₁₂ = G₁₃, and/or geometric parameters. Again, the global surrogate model of the structure allows for accounting for uncertainties in any of the inputs.

In a reliability-based design optimisation, on the other hand, the uncertainties are usually associated with mechanical properties. The RBDO process ensures that the final design meets a certain probabilistic constraint up to a prescribed reliability level β_t. In general, an RBDO problem can be formulated as

$$ {\displaystyle \begin{array}{l}\min \kern0.36em F\left(\mathbf{d}\right)\operatorname{}\kern1.56em \\ {}\mathrm{subject}\ \mathrm{to}:\kern0.75em {g}_m\left(\mathbf{d}\right)\le 0,\operatorname{}\operatorname{}m=1,2,...,M,\\ {}\kern5.36em P\left[{G}_n\left(\mathbf{d},\mathbf{x}\right)\le 0\right]-{P}_{\mathrm{f},n}\le 0,\operatorname{}\operatorname{}n=1,2,...,N,\end{array}} $$

(2)

where d and x are the design and random variables, respectively, and F is the objective function. g_m denotes mth deterministic constraint, while G_n stands for the nth probabilistic one. P[] represents the probability of the constraint being met, with P_f being the allowable probability of failure. For the case when the random variables are characterised by a normal distribution, P_f is related to the prescribed reliability level β_t via P_f = Φ(−β_t) in which Φ is the cumulative distribution function of the standard normal distribution (Enevoldsen and Sørensen 1994).

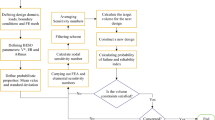
Different steps of the general approach detailed in this section are shown in Fig. 1. In what follows, the approach proposed in this section is demonstrated in detail on a mono-stringer stiffened panel.

Fig. 1

Flowchart of the proposed approach

3 Demonstration of the proposed optimisation approach on a mono-stringer stiffened panel

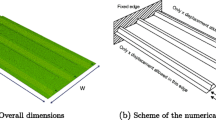
Consider a mono-stringer stiffened panel of length L and width W, as shown in Fig. 2 a. The omega-stringer geometry is detailed in Fig. 2 b, with X₁, X₂, H and θ being the foot, flange, height and angle, respectively. The mono-stringer is clamped at both ends, with the right-hand end being free to move in the longitudinal direction (shown by z in sub-figure a). Furthermore, there are no constraints on the two longitudinal edges of the skin. In this section, the approach proposed in Section 2 is implemented for this structure. In particular, the surrogate model of the structure will be developed in this section. The optimisation results will be discussed in separate sections.

Fig. 2

a Schematic representation of the mono-stringer stiffened panel. b The geometric parameters of the stringer

3.1 Parametric FE model development

The inputs of interest are the omega-stringer geometry, i.e. X₁, X₂, H and θ, as well as the mechanical properties, i.e. E₁₁, E₂₂ = E₃₃, G₂₃ and G₁₂ = G₁₃. The desired outputs are linear buckling load as well as the nonlinear post-buckling strength. In this section, two parametric FE models of the mono-stringer stiffened panel are developed in Abaqus as detailed below.

3.1.1 Linear FE model

The first parametric FE model developed in this section is a linear eigen-buckling analysis model in order to obtain the fundamental linear buckling load. An axial load is applied to the movable end of the mono-stringer and an eigen-buckling analysis is conducted to obtain the fundamental linear buckling load of the stiffened panel. Conducting a mesh convergence analysis for the linear buckling load shows that a global mesh size of 2 mm yields reliable results. The model takes 8 inputs as described before and calculates the fundamental linear buckling load.

3.1.2 Nonlinear FE model

A nonlinear parametric FE model is developed in this section in order to obtain the nonlinear post-buckling strength of the composite stiffened panel. This model is much more complex compared to the first model and accounts for geometric nonlinearities and progressive failure and additionally allows for interfacial debonding via use of cohesive elements. It is known that in the post-buckling regime, the buckled shape of the skin changes continuously due to increased compressive load. Additionally, sudden changes in the modes of buckling, known as mode-switch, occurs in the post-buckling regime which cannot be properly captured via use of quasi-static FE techniques. To this end, the nonlinear explicit dynamic FE analysis is employed in this study for analysing the nonlinear post-buckling characteristics.

Modelling the cohesive elements and correct selection of properties for modelling a traction-separation response is a challenging task. The main reason is that for typical epoxy resin matrix-based carbon fibre-reinforced composites, the length of the cohesive zone is less than 1 mm. An accurate representation of the traction in the tip of the crack and propagation of delamination requires at least three elements in the cohesive zone. Such small mesh requirement demands significant computational costs for structural analysis, such as the case of the mono-stringer stiffened panel of the present study. To address this challenge, the procedure introduced by Turon et al. (2007) is employed in this study, in which the cohesive zone length is artificially increased via decreasing the interfacial strengths; this procedure is briefly explained in the following.

In order to model the cohesive elements based on a mixed-mode fracture bilinear traction-separation, the following properties are required: the critical fracture energies G_IC, G_IIC and G_IIIC; the penalty stiffnesses K₁, K₂ and K₃; and the interfacial strengths τ⁰, ${\mu}_1^0$ and${\mu}_2^0$. In this study, it is assumed that penalty stiffnesses are the same (K₁ = K₂ = K₃ = K); furthermore, ${\mu}_1^0$ = ${\mu}_2^0$ = μ⁰ and G_IIC = G_IIIC. The penalty stiffness value should be large enough so that it has a negligible influence on the effective elastic properties of the composite. To this end, the penalty stiffness is defined as

$$ K=\alpha \frac{E_3}{t}, $$

(3)

where E₃ is the material’s transverse Young’s modulus, t is the thickness of the adjacent sublaminate and α is a coefficient much larger than 1. Turon et al. (2007) suggest a value more than 50; in the present study, α = 100 is used.

The cohesive zone lengths for modes I and II can be approximated as (Turon et al. 2007)

$$ {\displaystyle \begin{array}{l}{l}_{\mathrm{cz}}^{\left(\mathrm{I}\right)}=M{E}_2\frac{G_{\mathrm{IC}}}{{\left({\tau}^0\right)}^2},\\ {}{l}_{\mathrm{cz}}^{\left(\mathrm{I}\mathrm{I}\right)}=M{E}_2\frac{G_{\mathrm{IIC}}}{{\left({\mu}^0\right)}^2},\end{array}} $$

(4)

where M is a parameter characterised by the employed cohesive zone model; in the present study, Hillerborg’s model (Hillerborg et al. 1976) is utilised in which M = 1.

Denoting the length of the cohesive element by l_ce and assuming N_ce as the number of elements in the cohesive zone, the cohesive zone lengths in (4) can be replaced by N_cel_ce. Under the assumption of linear elastic fracture mechanics, the effect of the interfacial strengths can be neglected. Hence, based on (4), the length of the cohesive zone can be artificially increased via decreasing the interfacial strengths. As a result, the modified interfacial strengths (τ_m and μ_m) can be obtained as

$$ {\tau}_m=\sqrt{\frac{M{E}_2{G}_{\mathrm{IC}}}{N_{\mathrm{ce}}{l}_{\mathrm{ce}}}},\operatorname{}\operatorname{}{\mu}_m=\sqrt{\frac{M{E}_2{G}_{\mathrm{IIC}}}{N_{\mathrm{ce}}{l}_{\mathrm{ce}}}}. $$

(5)

The final values for interracial strengths that ensure N_ce number of elements of size l_ce span the cohesive zone are

$$ {\tau}_f=\mathit{\operatorname{Min}}\left\{{\tau}_m,{\tau}^0\right\},\operatorname{}\operatorname{}{\mu}_f=\mathit{\operatorname{Min}}\left\{{\mu}_m,{\mu}^0\right\}. $$

(6)

In the present study, N_ce = 3 and l_ce = 1.0 mm are selected. Furthermore, a global mesh size of 2.0 mm is used for both the skin and the stringer. Such selection of mesh size ensures converged and reliable predictions and practical simulation run time.

The properties of the composite and interface materials used in the present study are given in Table 1. The damage initiation is defined based on Hashin criteria (Hashin 1980; Hashin and Rotem 1973); additionally, the damage propagation is governed by the amount of energy dissipated through progressive damage (Lapczyk and Hurtado 2007).

Table 1 Material properties

The results of the nonlinear FE simulation for a mono-stringer of X₁ = 35.74 mm, X₂ = 30.0 mm, H = 25.0 mm and θ = 55.0° are shown in Fig. 3. In particular, the load–displacement curve of the mono-stringer under compressive load is shown in sub-figure a. As seen, the skin buckling (i.e. linear buckling) occurs in the vicinity of 0.5 mm shortening, while the failure occurs at around 2.2 mm shortening (i.e. point A). The mode of failure is skin-stringer debonding; the out-of-plane displacement (i.e. buckling amplitude) of the skin and stringer at points A, B and C are shown in sub-figures b–d, respectively. In this study, the nonlinear post-buckling strength, denoted as NPS, refers to the maximum load the mono-stringer stiffened panel carries before failure, i.e. the load corresponding to point A.

Fig. 3

a Load–displacement curve of the mono-stringer stiffened panel under compressive load. b–d Out-of-plane displacement of the skin and stringer corresponding to points A, B and C of sub-figure a, respectively

The nonlinear parametric FE model developed in this sub-section takes 8 inputs as described previously and calculates the nonlinear post-buckling strength.

3.2 Creating matrix of design samples

In this section, the optimal Latin hypercube sampling method is employed to create the matrix of design samples. In particular, 260 sample points are created for the 8 inputs considered with the range of the inputs given in Table 2. As mentioned in Section 2, the size of the cohesive element is set to 1 mm in this study. To ensure that this size remains fixed for all computer experiments, the foot size of the omega-stringer in the sampling matrix is rounded to the nearest integer. Furthermore, an additional 15-sample test matrix is generated as well via the optimal Latin hypercube sampling for the sole purpose of error analysis.

Table 2 Fixed and variable parameters

While the simulations run quite fast for the linear model, the nonlinear model simulation run time (utilising 20 CPU-cores) varies between 16 and 20 h per each sample, depending on the total number of cohesive elements. This means an average total run time of 4680 h (195 days!) to run all 260 samples. To be able to finish the design of experiments in a reasonable amount of time, the computational power of a high-performance computing (HPC) facility is utilised. In particular, each sample is run on one node consisting of 20 CPU-cores and 128 GB memory, and multiple samples are run at the same time. A 10× speed up is achieved using the HPC facility and the simulations are finished within almost 20 days. Having developed a 260 × 10 design matrix, as well as a 15 × 10 reference design matrix for error analysis, different surrogate models are generated and tested, as explained in the following, to obtain a reliable explicit approximation of the nonlinear and linear FE models. It is important to note that the mode of failure in all the cases examined in this section is skin-stringer debonding which initiates irreversible damage in the structure. In other words, if the skin-stringer debonding is not considered, the stiffened panel could withstand much larger loads; therefore, the skin-stringer debonding is the failure bottleneck for the case of mono-omega-stringer stiffened panel examined in this study. As a result, the nonlinear post-buckling strength (NPS) considered in this study is in fact the maximum load-carrying capacity without permanent damage.

3.3 Surrogate model development

In this section, a global surrogate model is developed in which the omega-stringer geometry (X₁, X₂, H and θ) and the mechanical properties of the composite structure (E₁₁, E₂₂ = E₃₃, G₂₃ and G₁₂ = G₁₃) are considered as inputs. The fundamental linear buckling load and the nonlinear post-buckling strengths are considered as outputs. Hence, a surrogate model with 8 inputs and 2 outputs is developed in this section using the 260 × 10 design matrix developed in the previous section. The mono-stringer length and width as well as the skin and omega-stringer thickness and layup are kept fixed in this study so as not to further increase the computational costs. In this study, the SUMO toolbox (Gorissen et al. 2010) is utilised to develop a surrogate model. As mentioned before, the SUMO toolbox includes various algorithms and functions such as kriging, ANN, radial basis functions, extreme machine learning and genetic algorithm. Hence, various algorithms can be tested to find one which best suits the present problem. Two measures for error analysis are considered: cross-validation and the 15-sample reference data set that was developed in Section 3.2. Even though the number of samples is fixed, the SUMO toolbox uses an optimisation algorithm and generates iterations of surrogate models until a best model is found. After testing various model building algorithms, it is found that the artificial neural network and kriging models give the best results for the mono-stringer stiffened panel under consideration. It is found that the surrogate model error can be further decreased by mixing the two models, with the coefficient for each model being determined via another optimisation algorithm. The final version of the mixed ANN–kriging surrogate model predicts the nonlinear post-buckling strength with less than 1.5% error and the fundamental linear buckling load with less than 0.5% error for the assumed range of inputs. This surrogate model will be used in the following sections as an explicit approximation of the linear buckling load and nonlinear post-buckling strength of the mono-stringer stiffened panel to conduct extensive multi-objective deterministic and probabilistic optimisations.

4 Multi-objective deterministic optimisation

This section conducts a multi-objective deterministic optimisation (MODO) on the surrogate model developed in the previous section; as mentioned before, a safety factor is not considered for either deterministic or probabilistic optimisations. In the present study, the Pareto envelope-based selection algorithm II (PESA-II) is utilised to conduct multi-objective optimisation (Corne et al. 2001; Corne et al. 2000). PESA-II is a multi-objective evolutionary optimisation algorithm which utilises the genetic algorithm approach along with a selection based on the Pareto envelope. Furthermore, it utilises an archive to store the approximate Pareto solutions. Parents and mutants are the chosen from this archive, based on the grids which themselves are generated based on the distribution of the archive members.

The optimisation algorithm aims at minimising the mass of the stringer and maximising both the fundamental linear buckling load and the nonlinear post-buckling strength. The multi-objective optimisation is conducted by giving a specific weight to each of the objectives and then adding/subtracting them such that they reduce into one objective; more details on the weight of the objectives are given in the discussions for each case. Since the aim of this section is to conduct deterministic optimisation, only the geometric parameters of the stringers are treated as variables in the optimisation loop. In other words, the mechanical properties are kept fixed while conducting the optimisation. The goal here is to identify the major differences between the stringer geometries optimised for maximum linear buckling load and those optimised for maximum nonlinear post-buckling strength. It should be noted that since in this study only the geometry of the stringer (and not the skin) is varied in the optimisation loop, the reported mass is that of the stringer only. The skin mass is a constant of 529.9 g throughout this study.

The results of the 3-objective PESA-II-based optimisation is shown in Fig. 4 through three sub-figures. For the sake of clarity, a 2-dimensional (2D) graph with two vertical axes is used to show the results of the 3-objective optimisation. The horizontal axis shows the mass of the stringer, while the vertical axes illustrate the LBL and NPS objectives. A portion of the solutions obtained by the optimisation algorithm are plotted, with blue dots representing NPS and orange dots showing LBL. For the 2D diagram shown in Fig. 4, the squares and circles show the Pareto envelope for the NPS and LBL, respectively. Depending on the weight given to the LBL and NPS objectives in the optimisation algorithm, different Pareto fronts are obtained. Three Pareto envelopes are examined here and shown through sub-figures a–c showing the designs with (a) maximum nonlinear post-buckling strength, (b) maximum linear buckling load, and (c) maximum LBL and NPS. Figure 4a and b clearly show the competing nature of all objectives and specifically the competing objectives of maximising both LBL and NPS against minimising the mass. It is seen in sub-figure a that when a large weight is given NPS objective, the obtained optimised designs do not show an even near-optimum LBL. On the other hand, in sub-figure b, when a large weight is given to LBL, the reported optimised designs do not display near-optimum NPS. This is due the competing nature of these objectives where fully maximising one results in non-optimum value for the other one.

Fig. 4

Deterministic multi-objective optimisation results of the mono-stringer stiffened panel: a a large weight given to NPS objective; b a large weight given to LBL objective; c similar weights to both NPS and LBL objectives. For each case, squares and circles show the Pareto fronts of NPS and LBL, respectively

To examine the optimised omega-stringer geometries in more detail, Tables 3 and 4 are constructed showing the selection of points on the Pareto fronts corresponding to Fig. 4b and a, respectively. More specifically, Table 3 shows the omega-stringer designs optimised for maximum linear buckling load and minimum mass.

Table 3 Detailed optimisation results for case b of the system of Fig. 4, i.e. stringer designs optimised for maximum LBL

Table 4 Detailed optimisation results for case a of the system of Fig. 4, i.e. stringer designs optimised for maximum NPS

It is interesting to note that the first parameter that is changed by the optimiser as the stringer mass is increased from 280 g is the flange. Additionally, it is seen that optimised designs for this case are associated with minimum height and angle and maximum flange size. Table 4 corresponds to Fig. 4a, i.e. showing the stringer designs optimised for maximum nonlinear post-buckling strength and minimum mass. As seen in this table, optimised designs for NPS are associated with maximised flange size, similar to optimised designs for LBL; however, unlike the LBL optimised results, the optimised designs for maximum NPS tend to have near maximum values for height and angle parameters. Tables 3 and 4 clearly highlight the differences in designs of minimum-mass mono-stringer stiffened panels optimised for maximum LBL versus those optimised for maximum NPS.

Figure 5 shows the geometries of mono-stringer designs optimised for (a) maximum NPS, corresponding to a stringer design of X₁ = 27.51 mm, X₂ = 30.0 mm, H = 35.0 mm and θ = 64.57°, and (b) maximum LBL, corresponding to a stringer design of X₁ = 35.74 mm, X₂ = 30.0 mm, H = 25.0 mm and θ = 55.0°. The figure clearly shows the differences between the height and angle of the two stringer designs.

Fig. 5

Mono-stringer stiffened panel geometries optimised for minimum mass and a maximum nonlinear post-buckling strength and b maximum linear buckling load. The mass of the stringer for both cases is around 344.5 g

5 Multi-objective probabilistic optimisation

In this section, multi-objective probabilistic optimisations (MOPO) are conducted on the surrogate model developed in Section 3, while considering only the nonlinear post-buckling strength as an output of the surrogate model. RDO as well as RBDO is conducted. In particular, RDO is performed while considering the uncertainties in the stringer mechanical properties as well as its geometric parameters. RBDO, on the other hand, is carried out while accounting only for uncertainties associated with mechanical properties. PESA-II multi-objective evolutionary optimisation algorithm is utilised for all the cases in this section.

5.1 Robust-design optimisation

In this section, two different RDOs are performed: one assuming uncertainties in mechanical properties, i.e. E₁₁, E₂₂ = E₃₃, G₂₃ and G₁₂ = G₁₃, and the other considering uncertainties in stringer geometry, i.e. X₁, X₂, H and θ.

5.1.1 RDO with uncertainties in mechanical properties

The RDO conducted in this section assumes that the mechanical properties have a random normal distribution with 5% coefficient of variation (Akula 2014; Yang et al. 2013) and the mean values as given in Table 1. A direct Monte Carlo sampling approach is employed to conduct a robustness analysis within the optimisation loop. To ensure the accuracy of the Monte Carlo approach, a random normal distribution consisting of 10⁵ samples is considered for each of the mechanical properties, as shown in Fig. 6.

Fig. 6

a–d Random normal distributions of the mechanical properties of the mono-stringer stiffened panel considering a coefficient of variation of 5% and 10⁵ samples

More specifically, each time the objective function is called by the optimiser, a Monte Carlo loop consisting of 10⁵ runs is performed and the mean value and standard deviation of the output, i.e. NPS, are passed to the optimiser. The optimiser objectives are minimising mass, maximising NPS mean value and minimising the standard deviation of NPS. Given that there are three objectives to be optimised, a population size of 100 is selected with a maximum of 100 iterations to ensure that all optimised solutions in the design space are found. This results in 10⁴ runs in the optimisation loop and a total of 10⁹ runs in the Monte Carlo-nested optimisation algorithm. This large number of runs requires the surrogate model to be optimised for very fast run time. It is worth noting that even a surrogate model run time of 1 ms results in 278 h (11 days!) total run time for the RDO to be completed. In this study, a 20× speed up is achieved via developing a vectorised surrogate model as well as taking advantage of parallel computing.

In order to better highlight the differences between robust and deterministic designs of the mono-stringer panel, three cases are considered and the corresponding optimisation results are plotted in Fig. 7 through sub-figures a–c. As mentioned before, the first, second and third objectives are minimising mass, maximising NPS mean value and minimising NPS standard deviation. For the first case, shown in sub-figure a, a large weight is given to the second optimisation objective, i.e. NPS mean value. This will result in stringer designs which are very similar to those obtained via deterministic optimisation; the purpose of this figure is to examine the robustness of deterministic designs in the presence of uncertainties in mechanical properties. The next two cases correspond respectively to RDOs with weights 5 (RDO-1) and 10 (RDO-2) given to the NPS standard deviation and weight 1 given to the other two objectives. The results of RDO-1 and RDO-2 are plotted in sub-figures b and c, respectively. Figure 7 clearly shows the trend that reduced NPS standard deviation comes at the price of a reduction in NPS mean value. However, comparing sub-figures a and b shows that the RDO-1 approach manages to reduce the NPS standard deviation significantly without reducing the NPS mean value by much. The reduction in the NPS mean value is more for the case RDO-2 in order to achieve narrower NPS distributions, i.e. smaller NPS standard deviations.

Fig. 7

Multi-objective robust-design optimisation results of the mono-stringer stiffened panel: a a large weight given to NPS mean value objective; b, c increased weights of NPS standard deviation objective. For each case, squares and circles show the Pareto fronts of NPS mean value and standard deviation, respectively

In order to be able to compare the stringer geometries corresponding to each case, Table 5 is constructed, listing a summary of the Pareto fronts of cases RDO-1 and RDO-2, corresponding to Fig. 7b and c, respectively. It should be noted that the stringer geometries corresponding to case 1, i.e. Fig. 7a, are almost identical to those of the deterministic optimisation given in Table 4. Comparing the results of RDO-1 to those of DO shows that for stringer masses larger than 319 g, the optimised stringer geometries based on RDO-1 have maximum possible angle (65°), while those based on DO have angles varying from 63° to 65°. A comparison of RDO-2 results with the other cases reveals that the optimised geometries based on RDO-2 have very different angles and heights compared to RDO-1 and DO results. In particular, for a large spectrum of mass, the angle and height vary in the vicinity of 58° and 26 mm, as opposed to 63–65° and 35 mm of the other two cases. For stringer masses more than 390 g, both RDOs result in the same stringer geometries while DO results in stringer geometries with reduced angle and flange size. In order to better illustrate the differences between robust and deterministic designs, the mono-stringer designs obtained based on the two approaches are plotted in Fig. 8 for a stringer of mass 399 g. The deterministic design corresponds to a stringer of X₁ = 41.04 mm, X₂ = 25.03 mm, H = 35.0 mm and θ = 59.39°, while the robust one corresponds to a stringer of X₁ = 40.53 mm, X₂ = 30.0 mm, H = 35.0 mm and θ = 65.0°. It is clearly seen in the figure that the robust design has a larger angle as well as a larger flange. The probability density function (PSD) plots of the two designs are depicted in Fig. 9, showing that the robust design has a slightly smaller NPS mean value, accompanied by a narrower distribution.

Table 5 Detailed optimisation results for cases a and b of the system of Fig. 7, denoted by RDO-1 and RDO-2, respectively

Fig. 8

Mono-stringer stiffened panel geometry optimised for maximum nonlinear post-buckling strength based on: a deterministic optimisation and b robust-design optimisation (uncertainties in mechanical properties). The mass of the stringer for both cases is around 399 g

Fig. 9

Probability density function plot of NPS distribution for the deterministic and robust mono-stringer designs given in Fig. 6

5.1.2 RDO with uncertainties in stringer geometry

The RDO conducted in this section aims at minimising mass and NPS standard deviation and maximising NPS mean value while considering uncertainties in the stringer geometry. The geometric inputs are assumed to have a truncated random normal distribution with 0.1% coefficient of variation; the mean values are determined by the optimiser each time the objective function is called. Similar to the previous case, a direct Monte Carlo sampling approach is implemented in the objective function to conduct a robustness analysis within the optimisation loop. A truncated random normal distribution consisting of 10⁵ samples is considered for each geometric input with manufacturing tolerances of ± 0.1 mm for X₁, X₂ and H and ± 0.2^° for θ. An example of the truncated random normal distribution for each of the inputs is shown in Fig. 10, for a stringer with mean geometric inputs of X₁ = 35.0 mm, X₂ = 28.0 mm, H = 30.0 mm and θ = 60.0°. Similar to the previous case, PESA-II optimisation algorithm is used with a population size of 100 and a maximum of 100 iterations.

Fig. 10

a–d Examples of truncated random normal distributions of the stringer geometric parameters considering a coefficient of variation of 0.1% and manufacturing tolerances of ± 0.1 mm for flange, foot and height and ± 0.2^° for angle

The results of the RDO with uncertainties in geometric parameters are plotted in Fig. 11. Sub-figure a corresponds to an RDO with a large weight given to the NPS mean value objective, while for the case in sub-figure b, a large weight is given to NPS standard deviation objective. As explained before, when a large weight is given to NPS mean value, the optimisation results become very similar to deterministic optimisation with only two objectives of minimising mass and maximising NPS.

Fig. 11

Multi-objective robust-design optimisation results of the mono-stringer stiffened panel: a a large weight given to NPS mean value objective; b a large weight given to NPS standard deviation objective. For each case, squares and circles show the Pareto fronts of NPS mean value and standard deviation, respectively

The goal of constructing Fig. 11a is to measure the robustness of the stringer designs with maximum possible NPS mean value, while Fig. 11b demonstrates the amount of reduction in NPS mean value as a result of minimising the NPS standard deviation. As seen in Fig. 11b, for a large portion of the mass spectrum, the NPS mean value does not change much compared to Fig. 11a while NPS standard deviation is minimised. To show the changes in stringer geometry corresponding to Fig. 11b, Table 6 is constructed showing the optimisation inputs and outputs for a wide range of stringer masses. Comparing these optimised designs to those of the deterministic optimisation shows that the stringer angle and foot have been changed slightly to accommodate more robust designs.

Table 6 Detailed optimisation results for case b of the system of Fig. 11

A comparison between the deterministic (X₁ = 26.0 mm, X₂ = 30.0 mm, H = 31.91 mm and θ = 63.0°) and robust (X₁ = 28.83 mm, X₂ = 29.82 mm, H = 28.06 mm and θ = 58.33°) designs is shown in Fig. 12 for a stringer of mass 325 g; the PDF plots of the NPS for the two designs are shown in Fig. 13. Another comparison between NPS distribution of deterministic and robust stringer designs of mass 378.7 g is shown in Fig. 14, with the robust stringer design being of X₁ = 35.46 mm, X₂ = 28.85 mm, H = 35.0 mm and θ = 62.48° and the deterministic one being of X₁ = 35.45 mm, X₂ = 30.0 mm, H = 35.0 mm and θ = 64.17°.

Fig. 12

Mono-stringer stiffened panel geometry optimised for maximum nonlinear post-buckling strength based on: a deterministic optimisation and b robust-design optimisation (geometric uncertainties). The mass of the stringer for both cases is around 325 g

Fig. 13

Probability density function plot of NPS distribution for the robust and deterministic mono-stringer designs given in Fig. 10

Fig. 14

Probability density function plot of NPS distribution for the robust and deterministic mono-stringer designs; mass of the stringer for both cases is around 378.7 g

5.2 Reliability-based design optimisation

In this section, a reliability-based design optimisation is conducted by considering uncertainties in the mechanical properties, i.e. E₁₁, E₂₂ = E₃₃, G₂₃ and G₁₂ = G₁₃. The RBDO process ensures that the final design meets a certain probabilistic constraint up to a prescribed reliability level β_t as explained in Section 2.4. The RBDO is performed by including a reliability analysis within the optimisation loop. More specifically, a reliability analysis algorithm based on the first-order reliability method (FORM) is formulated within the objective function to calculate the reliable NPS based on a prescribed reliability index β_t. The reliability analysis is solved through use of a hybrid mean value (HMV) method (Youn et al. 2003).

The reliability analysis technique employed in this study is validated using direct Monte Carlo sampling, which is commonly used as benchmark for validation purposes. Although direct Monte Carlo sampling is the most accurate method for reliability analysis, it becomes very time consuming for large reliability indices. The comparison is conducted for a stringer of X₁ = 35.0 mm, X₂ = 25.0 mm, H = 30.0 mm and θ = 60.0°, for reliability indices 3 and 4. For each reliability index, the corresponding NPS is obtained via the reliability analysis technique employed in this study (HMV) and direct Monte Carlo sampling. Three Monte Carlo sampling cases are considered with 10⁵, 10⁶ and 10⁷ samples, to ensure converged result. Due to the stochastic nature of the Monte Carlo simulations, for each case, the average of 5 different runs is reported as the final probabilistic NPS. The results of the comparison are shown in Table 7. As seen, for both β_t = 3.0 and 4.0, the results of the reliability analysis technique employed in this study are very close to those obtained via the direct Monte Carlo sampling technique verifying the accuracy of the employed method.

Table 7 Comparison of the reliability analysis results obtained via the method employed in this study (HMV) and those obtained using direct Monte Carlo sampling

The PESA-II optimisation algorithm is employed with a population size of 300 and a maximum of 100 iterations. The goal of an RBDO is to maximise/minimise an objective while meeting a certain probabilistic constraint up to a prescribed reliability level. In this study, the ultimate nonlinear post-buckling strength, denoted as NPS, is considered in both the objective function and in the probabilistic constraint. In other words, the optimiser aims at maximizing the NPS while ensuring that the reliability is larger than the prescribed value.

Since that the mass of the stringer is an optimisation objective as well, selecting a specific value for the NPS to measure the reliability from does not serve the purpose, as the maximum NPS is varying with mass. Instead, three objectives are considered and optimised, i.e. the mass of the stringer, to be minimised; deterministic NPS, to be maximised; and the NPS with the prescribed reliability of β_t, to be maximised. Hence, for a given reliability index, the optimisation algorithm finds the minimum-mass designs which are optimised for not only the maximum deterministic NPS, but also the maximum reliable NPS. The results of this multi-objective probabilistic optimisation are shown in Fig. 15 through sub-figures a and b. Sub-figure a corresponds to an optimisation with a large weight given to the deterministic NPS objective, while sub-figure b shows the results for a case with a large weight given to reliable NPS. The optimisation is conducted assuming a reliability index of β_t = 5. As seen in Fig. 15a, the designs optimised for maximum deterministic NPS are not necessarily the most reliable designs especially when the mass is larger than 390 g. Figure 15b shows that the optimum designs having maximum NPS up to the desired reliability level of β_t = 5.0 can be achieved without reducing the maximum deterministic NPS significantly. The detailed optimisation results for case b of Fig. 15 are listed in Table 8.

Fig. 15

Multi-objective reliability-based design optimisation results of the mono-stringer stiffened panel: a a large weight given to deterministic NPS objective; b a large weight given to NPS with reliability of β_t = 5.0. For each case, squares and circles show the Pareto fronts of deterministic and reliable NPS, respectively

Table 8 Detailed optimisation results for case b of the system of Fig. 15

The PDF plots of the NPS distribution associated with deterministic and reliable stringer designs of masses 368.5 and 391.5 g are depicted in Fig. 16 using 10⁶ points with the solid and dashed vertical lines showing the NPS with a reliability of β_t = 5.0 for reliable and deterministic designs, respectively. As seen, the reliable designs for both cases have slightly smaller NPS mean value, but visibly larger NPS with desired reliability level of β_t = 5.0.

Fig. 16

Probability density function plot of NPS distribution for the reliable and deterministic stringer designs of masses a 368.5 g and b 391.5 g. The solid and dashed vertical lines show the NPS with a reliability of β_t = 5.0 for reliable and deterministic designs, respectively

6 Conclusions

In this study, a multi-objective design optimisation approach is presented for probabilistic analysis of composite structures. The approach is demonstrated on a mono-stringer stiffened panel for robust and reliability-based design optimisations. In particular, an accurate and comprehensive surrogate model is developed with the stringer geometry and the composite material mechanical properties as the inputs and the fundamental linear buckling load and the nonlinear post-buckling strength as the outputs. Multi-objective probabilistic and deterministic optimisations are performed on the surrogate model. Different probabilistic optimisation methods, i.e. robust-design optimisation and reliability-based design optimisation, are utilised.

The results of the initial deterministic optimisation showed that optimised designs for maximum LBL are achieved by minimising the height and angle and maximising the flange of the stringer. The optimised designs for maximum NPS, on the other hand, are associated with maximised height and angle as well as maximised flange size.

Robust-design optimisations were conducted by considering uncertainties in mechanical properties and geometric parameters. It was shown that for both cases, compared to deterministic designs, robust designs tend to have slightly smaller NPS mean value and smaller NPS standard deviation. In other words, the RDO finds designs which are less sensitive to variations in mechanical properties and geometric parameters but at the cost of slightly reduced NPS mean value compared to the deterministic designs. Furthermore, RDO designs vary significantly depending on the weights given to the mean and standard deviation objectives.

Finally, reliability-based design optimisation results showed that more reliable designs can be achieved by slightly modifying the stringer angle and height. More specifically, it was shown that the reliable designs offer larger NPS (in the order of several KNs) with a reliability of β_t while not reducing the NPS mean value much (1 KN or less).