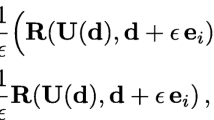Skip to main content
SpringerLink
Log in

Adjoint sensitivity analysis and optimization of transient problems using the mixed Lagrangian formalism as a time integration scheme

  • Research Paper
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

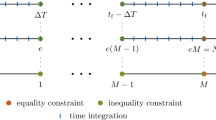
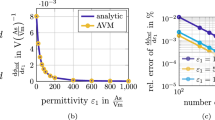
In optimization of transient problems, a robust, stable, and efficient numerical scheme for time integration is of much importance. Recently, the mixed Lagrangian formalism (MLF) has been proposed for the time integration of transient problems. MLF leads to an optimization problem for the computation of the state variables in each time step. It has shown a robust behavior, even in the presence of sharp gradients of the state variables in time. It has also been applied to a large variety of transient problems, including structural dynamics, multi-physics, and coupled problems, where it has shown its stability, robustness, and computational efficiency. Albeit the clear advantages of MLF, due to its nature, sensitivity analysis for responses of interest is challenging. However, adopting MLF within a first-order optimization framework while efficiently deriving its sensitivities will result in an efficient computational framework for the optimization of transient problems, while avoiding convergence issues in the time integration. This is done here by first reformulating the time integration scheme so as to enable working with more convenient functions. Then, for the sake of sensitivity analysis only, KKT conditions are formulated to replace the optimization problem of MLF in each time step. Finally, the sensitivity analysis is performed based on these KKT conditions. The sensitivity analysis is utilized here for the optimization of the dynamic response of a structure with tension-only yielding elements using viscous dampers.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Alberdi R, Zhang G, Li L, Khandelwal K (2018) A unified framework for nonlinear pathdependent sensitivity analysis in topology optimization. Int J Numer Methods Eng 115.1:1–56

    Google Scholar 

  • Andreassen E, Jensen JS (2014) Topology optimization of periodic microstructures for enhanced dynamic properties of viscoelastic composite materials. Struct Multidiscip Optim 49.5:695–705

    MathSciNet  Google Scholar 

  • Andreasen CS, Sigmund O (2013) Topology optimization of fluid–structure–interaction problems in poroelasticity. Comput Methods Appl Mech Eng 258:55–62

    MathSciNet  MATH  Google Scholar 

  • Apostolakis G, Dargush G (2011) Mixed Lagrangian formulation for linear thermoelastic response of structures. J Eng Mech 138.5:508–518

    Google Scholar 

  • Apostolakis G, Dargush G (2013) Variational methods in irreversible thermoelasticity: theoretical developments and minimum principles for the discrete form. Acta Mech 224.9:2065–2088

    MathSciNet  MATH  Google Scholar 

  • Behrou R, Guest JK (2017) Topology optimization for transient response of structures subjected to dynamic loads. In: 18th AIAA/ISSMO multidisciplinary analysis and optimization conference, pp 3657

  • Bogomolny M, Amir O (2012) Conceptual design of reinforced concrete structures using topology optimization with elastoplastic material modeling. Int J Numer Methods Eng 90.13:1578–1597

    MATH  Google Scholar 

  • Dahl J, Jensen JS, Sigmund O (2008) Topology optimization for transient wave propagation problems in one dimension. Struct Multidiscip Optim 36.6:585–595

    MathSciNet  MATH  Google Scholar 

  • Daniel Y, Lavan O (2014) Gradient based optimal seismic retrofitting of 3D irregular buildings using multiple tuned mass dampers. Comput Struct 139:84–97

    Google Scholar 

  • Deaton JD, Grandhi RV (2014) A survey of structural and multidisciplinary continuum topology optimization: post 2000. Struct Multidiscip Optim 49.1:1–38

    MathSciNet  Google Scholar 

  • Deng Y, Liu Z, Zhang P, Liu Y, Wu Y (2011) Topology optimization of unsteady incompressible Navier–Stokes flows. J Comput Phys 230.17:6688–6708

    MathSciNet  MATH  Google Scholar 

  • Domschke P, Geißler B, Kolb O, Lang J, Martin A, Morsi A (2011) Combination of nonlinear and linear optimization of transient gas networks. INFORMS J Comput 23.4:605–617

    MathSciNet  MATH  Google Scholar 

  • Fritzen F, Xia L, Leuschner M, Breitkopf P (2016) Topology optimization of multiscale elastoviscoplastic structures. Int J Numer Methods Eng 106.6:430–453

    MathSciNet  MATH  Google Scholar 

  • Gunzburger MD (1999) Sensitivities, adjoints and flow optimization. Int J Numer Methods Fluids 31.1:53–78

    MathSciNet  MATH  Google Scholar 

  • Ivarsson N, Wallin M, Tortorelli D (2018) Topology optimization of finite strain viscoplastic systems under transient loads. Int J Numer Methods Eng 114.13:1351–1367

    MathSciNet  Google Scholar 

  • James KA, Waisman H (2015) Topology optimization of structures under variable loading using a damage superposition approach. Int J Numer Methods Eng 101.5:375–406

    MathSciNet  MATH  Google Scholar 

  • Jensen HA (2005) Design and sensitivity analysis of dynamical systems subjected to stochastic loading. Comput Struct 83.14:1062–1075

    Google Scholar 

  • Jensen JS, Sigmund O (2011) Topology optimization for nano–photonics. Laser Photon Rev 5.2:308–321

    Google Scholar 

  • Jensen JS, Nakshatrala PB, Tortorelli D (2014) On the consistency of adjoint sensitivity analysis for structural optimization of linear dynamic problems. Struct Multidiscip Optim 49.5:831–837

    MathSciNet  Google Scholar 

  • Kang B-S, Park G-J, Arora JS (2006) A review of optimization of structures subjected to transient loads. Struct Multidiscip Optim 31.2:81–95

    MathSciNet  MATH  Google Scholar 

  • Kato J, Hoshiba H, Takase S, Terada K, Kyoya T (2015) Analytical sensitivity in topology optimization for elastoplastic composites. Struct Multidiscip Optim 52.3:507–526

    MathSciNet  Google Scholar 

  • Lavan O (2010) Dynamic analysis of gap closing and contact in the mixed Lagrangian framework: toward progressive collapse prediction. J Eng Mech 136.8:979–986

    Google Scholar 

  • Lavan O (2015) Optimal design of viscous dampers and their supporting members for the seismic retrofitting of 3D irregular frame structures. J Struct Eng 141.11:04015026

    Google Scholar 

  • Lavan O, Dargush G (2009) Multi–objective evolutionary seismic design with passive energy dissipation systems. J Earthquake Eng 13.6:758–790

    Google Scholar 

  • Lavan O, Levy R (2005) Optimal design of supplemental viscous dampers for irregular shear–frames in the presence of yielding. Earthquake Eng Struct Dyn 34.8:889–907

    Google Scholar 

  • Lavan O, Levy R (2006) Optimal peripheral drift control of 3D irregular framed structures using supplemental viscous dampers. J Earthquake Eng 10.06:903–923

    Google Scholar 

  • Lavan O, Levy R (2009) Simple iterative use of Lyapunov’s solution for the linear optimal seismic design of passive devices in framed buildings. J Earthquake Eng 13.5:650–666

    Google Scholar 

  • Lavan O, Sivaselvan M, Reinhorn A, Dargush G (2009) Progressive collapse analysis through strength degradation and fracture in the mixed Lagrangian formulation. Earthquake Eng Struct Dyn 38.13:1483–1504

    Google Scholar 

  • Levy R, Lavan O (2006) Fully stressed design of passive controllers in framed structures for seismic loadings. Struct Multidiscip Optim 32.6:485–498

    Google Scholar 

  • Li L, Khandelwal K (2017) Design of fracture resistant energy absorbing structures using elastoplastic topology optimization. Struct Multidiscip Optim 56.6:1447–1475

    MathSciNet  Google Scholar 

  • Li Y, Saitou K, Kikuchi N (2004) Topology optimization of thermally actuated compliant mechanisms considering time–transient effect. Finite Elem Anal Des 40.11:1317–1331

    Google Scholar 

  • Li L, Zhang G, Khandelwal K (2017) Topology optimization of energy absorbing structures with maximum damage constraint. Int J Numer Methods Eng 112.7:737–775

    MathSciNet  Google Scholar 

  • Li L, Zhang G, Khandelwal K (2018) Failure resistant topology optimization of structures using nonlocal elastoplastic-damage model. Struct Multidiscip Optim 58:1589–1618

    MathSciNet  Google Scholar 

  • Madah H, Amir O (2017) Truss optimization with buckling considerations using geometrically nonlinear beam modeling. Comput Struct 192:233–247

    Google Scholar 

  • Matzen R, Jensen JS, Sigmund O (2010) Topology optimization for transient response of photonic crystal structures. JOSA B 27.10:2040–2050

    Google Scholar 

  • Michaleris P, Tortorelli D, Vidal CA (1994) Tangent operators and design sensitivity formulations for transient non-linear coupled problems with applications to elastoplasticity. Int J Numer Methods Eng 37.14:2471–2499

    MATH  Google Scholar 

  • Michaleris P, Tortorelli D, Vidal CA (1995) Analysis and optimization of weakly coupled thermoelastoplastic systems with applications to weldment design. Int J Numer Methods Eng 38.8:1259–1285

    MATH  Google Scholar 

  • Min S, Kikuchi N, Park Y, Kim S, Chang S (1999) Optimal topology design of structures under dynamic loads. Struct Optim 17.2–3:208–218

    Google Scholar 

  • Nakshatrala P, Tortorelli D (2015) Topology optimization for effective energy propagation in rate independent elastoplastic material systems. Comput Methods Appl Mech Eng 295:305–326

    MathSciNet  MATH  Google Scholar 

  • Noël L., Duysinx P, Maute K (2017) Level set topology optimization considering damage. Struct Multidiscip Optim 56.4:737–753

    MathSciNet  Google Scholar 

  • Park J-H, Kim J, Min K-W (2004) Optimal design of added viscoelastic dampers and supporting braces. Earthquake Eng Struct Dyn 33.4:465–484

    Google Scholar 

  • Pedersen NL (2000) Maximization of eigenvalues using topology optimization. Struct Multidiscip Optim 20.1:2–11

    Google Scholar 

  • Pedersen CB (2004) Crashworthiness design of transient frame structures using topology optimization. Comput Methods Appl Mech Eng 193.6-8:653–678

    MATH  Google Scholar 

  • Poldneff MJ, Arora JS (1996) Design sensitivity analysis in dynamic thermoviscoelasticity with implicit integration. Int J Solids Struct 33.4:577–594

    MATH  Google Scholar 

  • Pollini N, Lavan O, Amir O (2018a) Adjoint sensitivity analysis and optimization of hysteretic dynamic systems with nonlinear viscous dampers. Struct Multidiscip Optim 57.6:2273–2289

    MathSciNet  Google Scholar 

  • Pollini N, Lavan O, Amir O (2018b) Optimization based minimum–cost seismic retrofitting of hysteretic frames with nonlinear fluid viscous dampers. Earthquake Eng Struct Dyn

  • Rozvany GI (2009) A critical review of established methods of structural topology optimization. Struct Multidiscip Optim 37.3:217–237

    MathSciNet  MATH  Google Scholar 

  • Salas R, Ramírez F, Montealegre–Rubio W, Silva E, Reddy J (2018) A topology optimization formulation for transient design of multi–entry laminated piezocomposite energy harvesting devices coupled with electrical circuit. Int J Numer Methods Eng 113.8:1370–1410

    MathSciNet  Google Scholar 

  • Sigmund O (2011) On the usefulness of non–gradient approaches in topology optimization. Struct Multidiscip Optim 43.5:589–596

    MathSciNet  MATH  Google Scholar 

  • Sigmund O (2014) Topology optimization: state of the art and future perspectives. In: The 2014–15 Newmark Distinguished Lecture, at the University of Illinois at Urbana–Champaign https://www.youtube.com/watch?v=sXXA4t9ZQ04

  • Sigmund O, Maute K (2013) Topology optimization approaches. Struct Multidiscip Optim 48.6:1031–1055

    MathSciNet  Google Scholar 

  • Sivaselvan M, Reinhorn A (2006) Lagrangian approach to structural collapse simulation. J Eng Mech 132.8:795–805

    Google Scholar 

  • Sivaselvan M, Lavan O, Dargush G, Kurino H, Hyodo Y, Fukuda R, Sato K, Apostolakis G, Reinhorn A (2009) Numerical collapse simulation of large–scale structural systems using an optimization–based algorithm. Earthquake Eng Struct Dyn 38.5:655–677

    Google Scholar 

  • Song J, Shanghvi J, Michaleris P (2004) Sensitivity analysis and optimization of thermo–elastoplastic processes with applications to welding side heater design. Comput Methods Appl Mech Eng 193.42-44:4541– 4566

    MATH  Google Scholar 

  • Steinbach MC (2007) On PDE solution in transient optimization of gas networks. J Comput Appl Math 203.2:345–361

    MathSciNet  MATH  Google Scholar 

  • Tcherniak D (2002) Topology optimization of resonating structures using SIMP method. Int J Numer Methods Eng 54.11:1605– 1622

    MATH  Google Scholar 

  • Tortorelli D, Haber RB, Lu SC (1989) Design sensitivity analysis for nonlinear thermal systems. Comput Methods Appl Mech Eng 77.1–2:61–77

    MathSciNet  MATH  Google Scholar 

  • Tortorelli D, Haber RB, Lu SC-Y (1991) Adjoint sensitivity analysis for nonlinear dynamic thermoelastic systems. AIAA J 29.2:253–263

    Google Scholar 

  • Tubul D, Lavan O (2011) Implementation of fracture mechanics concepts in dynamic progressive collapse prediction using an optimization based algorithm. In: COMPDYN 2011 – 3rd int. Conf. in computational methods in structural dynamics and earthquake engineering paper # 145

  • Van Keulen F, Haftka R, Kim N (2005) Review of options for structural design sensitivity analysis. Part 1 Linear systems. Comput Methods Appl Mech Eng 194.30-33:3213–3243

    MATH  Google Scholar 

  • Venanzi I, Materazzi A (2007) Multi–objective optimization of wind–excited structures. Eng Struct 29.6:983–990

    Google Scholar 

  • Venini P (2016) Dynamic compliance optimization: time vs frequency domain strategies. Comput Struct 177:12–22

    Google Scholar 

  • Wallin M, Jönsson V, Wingren E (2016) Topology optimization based on finite strain plasticity. Struct Multidiscip Optim 54.4:783– 793

    MathSciNet  Google Scholar 

  • Xia L, Da D, Yvonnet J (2018) Topology optimization for maximizing the fracture resistance of quasi–brittle composites. Comput Methods Appl Mech Eng 332:234–254

    MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Technion - Israel Institute of Technology, Haifa, Israel

    Oren Lavan

Authors
  1. Oren Lavan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Oren Lavan.

Ethics declarations

Conflict of interest

The author declares no conflict of interest.

Additional information

Responsible Editor: Junji Kato

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lavan, O. Adjoint sensitivity analysis and optimization of transient problems using the mixed Lagrangian formalism as a time integration scheme. Struct Multidisc Optim 61, 619–634 (2020). https://doi.org/10.1007/s00158-019-02383-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-019-02383-8

Keywords

Search

Navigation