Novel fuzzy possibilistic safety degree measure model

Abstract

The output of structure under fuzzy uncertainty can be classified into three cases, i.e., safety-failure case corresponding to that failure and safety both can occur in different membership levels, absolute failure case corresponding to that only failure can occur, and absolute safety case corresponding to that only safety can occur in any membership level. The existing fuzzy possibilistic safety degree measure models can only distinguish the structural safety degree in the safety-failure case but play no role in the absolute failure case and absolute safety case. Aiming at addressing this issue, a novel fuzzy possibilistic safety degree measure model is proposed. Before establishing the new fuzzy possibilistic safety degree measure model, a new value-interval ranking technique is first constructed. Then, the new safety possibility and failure possibility are estimated by synthesizing the information in the entire uncertain space based on the proposed value-interval ranking technique. The new fuzzy possibilistic safety degree measure model can distinguish the structural safety degree in all the three cases, and the results coincide with the human’s intuitive cognition. Several examples involving an engineering application with the finite element model are introduced to show the effectiveness of the established fuzzy possibilistic safety degree measure model.

The demonstration for the equivalency of \( {\pi}_f^{\mathrm{orig}} \) and πf

Based on the definition of the failure possibility π_f in (1), it can be written as follows:

$$ {\pi}_f=\sup \left\{\lambda |{\underset{\_}{G}}_{F\lambda}\le 0\right\} $$

(54)

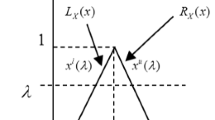
For demonstrating the equivalency of ${\pi}_f^{\mathrm{orig}}$ and π_f, three cases are considered, i.e., case 1 for 0 < π_f < 1, case two for π_f = 0, and case 3 for π_f = 1. For case 1 where 0 < π_f < 1, it is supposed that the failure possibility equals to λ^∗(0 < λ^∗ < 1), i.e., π_f = λ^∗, and it is shown in Fig. 16.

Fig. 16

The failure possibility π_f for case 1

From Fig. 16, one can see that the failure possibility π_f equals to the membership level λ^∗ which satisfies ${\underset{\_}{G}}_{F{\lambda}^{\ast }}=0$. Therefore, (3) can be further written as follows:

$$ {h}_f^{\mathrm{orig}}\left(\lambda \right)=\Big\{{\displaystyle \begin{array}{l}1\kern1.12em \lambda \le {\lambda}^{\ast}\\ {}0\kern1em \lambda >{\lambda}^{\ast}\end{array}} $$

(55)

Thus, the original-fuzzy failure possibility ${\pi}_f^{\mathrm{orig}}$ shown in (5) can be estimated by:

$$ {\pi}_f^{\mathrm{orig}}={\int}_0^1{h}_f^{\mathrm{orig}}\left(\lambda \right)\mathrm{d}\lambda ={\int}_0^{\lambda^{\ast }}1\mathrm{d}\lambda +{\int}_{\lambda^{\ast}}^10\mathrm{d}\lambda ={\lambda}^{\ast }={\pi}_f $$

(56)

For case 2 where π_f = 0, the failure possibility π_f is shown in Fig. 17.

Fig. 17

The failure possibility π_f for case 2

In this case, (3) can be further written as follows:

$$ {h}_f^{\mathrm{orig}}\left(\lambda \right)=0\kern1em 0\le \lambda \le 1 $$

(57)

The original-fuzzy failure possibility ${\pi}_f^{\mathrm{orig}}$ shown in (5) can be estimated by:

$$ {\pi}_f^{\mathrm{orig}}={\int}_0^1{h}_f^{\mathrm{orig}}\left(\lambda \right)\mathrm{d}\lambda ={\int}_0^10\mathrm{d}\lambda =0={\pi}_f $$

(58)

For case 3 where π_f = 1, the failure possibility π_f is shown in Fig. 18.

Fig. 18

The failure possibility π_f for case 3

In this case, (3) is further expressed as follows:

$$ {h}_f^{\mathrm{orig}}\left(\lambda \right)=1\kern1em 0\le \lambda \le 1 $$

(59)

Thus, the original-fuzzy failure possibility ${\pi}_f^{\mathrm{orig}}$ shown in (5) is estimated by:

$$ {\pi}_f^{\mathrm{orig}}={\int}_0^1{h}_f^{\mathrm{orig}}\left(\lambda \right)\mathrm{d}\lambda ={\int}_0^11\mathrm{d}\lambda =1={\pi}_f $$

(60)

Therefore, the failure possibility π_f defined in (Cremona and Gao 1997) is equivalent to the original-fuzzy failure possibility ${\pi}_f^{\mathrm{orig}}$ defined in (5).