Abstract
This paper presents the formulation of a new methodology to design adaptive structures. This design method synthesises structural configurations that are optimum hybrids between a passive and an active structure. An optimisation scheme searches for an optimal material distribution and actuation layout to minimise the structure whole-life energy which consists of an embodied part in the material and an operational part for structural adaptation. Instead of using more material to cope with the effect of loads, here, strategically located active elements redirect the internal load path to homogenise the stresses and change the shape of the structure to keep deflections within required limits. To ensure the embodied energy saved this way is not used up to by actuation, the adaptive solution is designed to cope with ordinary loading events using only passive load-bearing capacity whilst relying on active control to deal with larger events that have a smaller probability of occurrence. The design methodology has been implemented for statically determinate and indeterminate reticular structures. However, the formulation is general and could be implemented to other structural types. Numerical simulations on a truss system case study confirm that substantial savings up to 50% of the whole-life energy can be achieved by the adaptive solution compared to a passive solution designed using state of the art optimisation methods.
Similar content being viewed by others
1 Introduction
1.1 Motivation
The construction industry is the major consumer of mined raw materials (Straube 2006) contributing to more than a third of the global energy demand (European Environment Agency 2010). Most of the environmental impact of structures are embodied into load-bearing systems (Kaethner and Burridge 2012; Sartori and Hestnes 2007). For these reasons, it has become important to minimise environmental and energetic impacts of infrastructures, including buildings.
Civil structures are usually designed to meet strength and deformation requirements for statistically calculated load cases. The design is governed by meeting safety and serviceability criteria to withstand rare events such as unusual crowd loading and strong winds. Most structures are thus over-designed for most of their service life. Structural adaptation provides an alternative because a structure can be designed to operate with a better material utilisation if it can counteract actively rare loading events. Structural adaptation is here understood as a controlled shape change and redirection of the internal load-path. To achieve this, adaptive structures are integrated with sensors (e.g. strain, vision), actuators (e.g. hydraulics, solid-state) and control intelligence.
In civil engineering, active control has focussed mostly on the control of vibrations for building or bridges to improve on safety and serviceability during exceptionally high loads (Soong 1988). Due to concerns related to the lack of long-term reliability of control electronics combined with long service lives of buildings and long return periods for extreme loads, active structural control has been recently investigated to help satisfy serviceability requirements, such as deflection limits, rather than contributing unrealistically to improvements related to the ultimate limit state (Korkmaz 2011; Shea and Smith 1998). In this context, structural adaptation can contribute significantly to improving civil structure performance. Whilst the strength of the structure cannot be compromised, trade-offs on the stiffness can be investigated. If the structure can reduce deflections actively, its stiffness can be tuned to better utilise the material resulting in a lower embodied energy. The embodied energy is the energy required for material extraction, fabrication and construction (Hammond and Jones 2008). Such savings, however, are only possible at a cost of operational energy that is required to operate the adaptive system.
This work presents the formulation of a new computational method to synthesise structures which are minimum energy design. The main design criterion is minimisation of the whole-life energy which is understood as the sum of the energy embodied in the material and the operational energy for structural adaptation. Structural adaptation is employed to counteract the effects of large loading events via controlled shape changes and redirection of the internal load-path so that the design will not be governed by peak demands that occur rarely. The main aim is to show that through adaptation, civil structures can be designed for minimum whole-life energy reducing environmental impacts significantly more than when employing traditional passive design methods and technologies.
1.2 Previous work
1.2.1 Adaptation in structural applications
Active brace systems have been tested using hydraulic actuators fitted as cross-bracing elements in the structure to control its deflections (Abdel-Rohman and Leipholz 1983; Reinhorn et al. 1993; Bani-Hani and Ghaboussi 1998). Displacement control in cable-stayed bridges can be obtained via control forces provided by the stay cables working as active tendons (Rodellar et al. 2002; Xu et al. 2003). Active cable-tendons have been used to change the amount of pre-stress in reinforced concrete beams and in steel trusses to limit displacements under loading (Schnellenbach and Steiner 2014). Integration of actuators has been shown to be an effective way to suppress vibrations via active damping in high stiffness/weight ratio truss structures (Preumont et al. 2008; Li and Huang 2013) or via shape changes to tune the natural frequency in underslung cable-stayed beam bridges subjected to pedestrian loading (Santos and Cismaşiu 2017). Actuation has been used to modify the membrane stress state in thin plates and shells when disturbances such as local loadings, cuttings or residual stress formed after formwork removal (Sobek 1987) occur. In these cases, because the load carrying capacity is reduced significantly, actuation in the form of induced strain distributions or induced displacement of the supports (actively controlled bearings) has been employed to homogenise the stress field and in so doing minimising the maximum stress governing the design (Weilandt 2007; Neuhäuser 2014).
Active structural control has also been used for shape control. Some all-weather stadia use deployable systems for expandable/retractable roofs e.g. the Singapore National Stadium (Henry et al. 2016) and the Wimbledon Centre Court (SCX 2010). Variable geometry trusses (VGT) are equipped with length changing actuators replacing some of their members in order to achieve arbitrary geometric configurations (within the deformational/rotational limits of the joints) whilst high stiffness is maintained during deployment. Applications of this concept have been suggested for space cranes, scaffolding and large structural rings for antennas (Miura and Furuya 1988; Campanile 2003; Subramaniam and Kramer 1992). Active tensegrity structures, structures whose stability depends on self-stress, have been used for deployable systems (Tibert 2002) as well as for control of displacements (Fest et al. 2003; Veuve and Smith 2015) and of the structure fundamental frequency (Santos and Micheletti 2015; Bel Hadj Ali and Smith 2010). Active compliant structures, which can be thought of as structures working as monolithic mechanisms (Hasse and Campanile 2009) have been investigated for shape control of antenna reflectors (Jenkins 2005), for shape morphing of aircraft wings to improve on manoeuvrability (Previtali and Ermanni 2012; Kota et al. 2003) as well as for the control of direct daylight in buildings (Lienhard et al. 2011).
1.2.2 Design methods for adaptive structures
When the engineering design process is framed as an optimisation problem, defining properly the relevant constraints and the utility function (Hazelrigg 1998) is a difficult task that remain a matter of debate. Most existing design strategies for adaptive structures are based on optimisation methods which aim at minimising a combination of the control energy, structural response to external loads and other cost functions including the mass of the structure (Soong and Manolis 1987; Utku 1998). In most of these design methods, the structure and the actuation system are designed as separate systems - the location of the actuators being decided a-priori (Khot 1998; Soong and Cimellaro 2009; Molter et al. 2013). However, the derivation of an optimal actuator layout is critical to minimise control effort. The actuator layout optimisation is usually of combinatorial nature because it involves placing a certain number of actuators within a set of available sites. Most of the existing methods rely on heuristics or stochastic routines (Lu et al. 1992; Adam and Smith 2008; Rhode-Barbarigos et al. 2012). Methods based on formal analysis have been used to solve this problem in more insightful ways including efficient enumerations and continuous relaxations (Ziegler 2005; Nyashin et al. 2005; Campbell and Crawley 1997; Sepulveda and Schmit 1991). However, the solution of the actuator-placement problem remains a very challenging task due to limits to computational resources.
As already recognised by some (Utku 1998; Wada et al. 1990; Connor 2002), novel structural configurations can be generated via an integrated design approach where the actuation system is designed as an integral part of the structural system. Most methods for synthesis of integrated structural and control design focus on vibration suppression (Onoda and Haftka 1987; Hiramoto and Grigoriadis 2005; Haftka 1990; Dhingra and Lee 1995; Skelton et al. 1992). Within the context of compliant structures (i.e. joint-less mechanisms) relevant previous work proposed methods for synthesis of structures with selective compliance (Hasse and Campanile 2009). Structures with selective compliance are designed to be stiff against the external loads and flexible relative to the intended deformation pattern for shape control. Simultaneous synthesis of the structural and actuator/sensor layout for compliant systems have been proposed by some (Lu and Kota 2003; Trease and Kota 2009).
The potential for using adaptation to save material mass for civil structures has been investigated by a few. For example, in (Cha et al. 1988; Cimellaro et al. 2008), it was shown that simultaneous optimisation of structure-control parameters can lead to significant material savings. Simulation studies including a nine-story frame and a king-post bridge-beam showed that up to 45% of the mass could be saved compared to similar passive structures. Similarly in (Begg and Liu 2000; Sobek and Teuffel 2001; Teuffel 2004) it was shown that combining weight optimisation and actuator layout optimisation results in significant savings up to 70% of the mass for reticular structures under quasi-static loading subject to strict serviceability limits.
It has been shown that structural adaptation could be employed to achieve substantive material savings and thus embodied energy savings. However, whether the energy saved by using less material makes up the energy for structural control during service life is a question that has so far received little attention. Methods to minimise the control power in combination with structural optimisation have been formulated (Li et al. 2011; Smith et al. 1991; Grigoriadis et al. 1996). However, most of these formulations are impractical when applied to the design of large-scale adaptive structures of complex layout, which are usually made of many elements and degrees of freedom. In addition, in none of the published methods did the governing design criteria explicitly include the whole-life energy required during service life. This is particularly important for the design of adaptive civil structures due to their long service life. Whole-life energy minimization is an objective function (or utility function in Hazelrigg’s framework (Hazelrigg 1998)) which conveniently encapsulates material and operational energy minimisation of load-bearing systems. This explicitly address current and future challenges such as material scarcity, energy depletion and reduction of building environmental impacts. To date there is no synthesis method which employs structural adaptation in order to produce structures which are minimum energy design.
1.3 Outline
In the following sections, a new methodology is proposed that synthesises hybrid passive-adaptive structures which are minimum energy design. This method has been formulated as a dual-objective process – minimisation of the energy embodied in the material as well as the operational energy for structural adaptation. The method is presented through the example of a planar reticular structure to demonstrate the advantages it brings compared to an equivalent passive design. Section 2 states the all-in-one problem formulation and outlines a strategy to solve such problem using a nested approach. Section 3, 4 and 5 give the formulation of the three main steps in which the process is subdivided: (1) embodied energy minimisation, (2) actuator layout optimisation and (3) computation of the operational energy for force and shape control during service. Section 6 shows how to coordinate the previous steps of the design process to identify the minimum whole-life energy design.
2 Synthesis of minimum energy adaptive structures
2.1 All-in-one problem formulation
In this paper, the synthesis of adaptive reticular structures is achieved through the minimisation of the whole-life energy (Eq. 1) subject to equilibrium (Eq. 2), deflection (Eq. 3) and stress (Eq. 4) constraints:
These equations are stated here to frame the optimisation problem in its generality. A preliminary description of the notation is given here but more detail will be given throughout the paper as the methodology unfolds.
The design variables are limited to the element cross-section areas α, the optimal (or controlled) internal forces F, the actuator layout actLYT and the actuator length changes ∆L to perform force and shape control under p load cases. Note that if nodal coordinates and the structural layout are included in the design variables, the same formulation can readily be extended to shape and topology optimisation. Internal force and internal load-path have the same meaning in this paper. The actuators are thought of as replacing a certain number of elements (nACTs) of the structure. Actuator length variations generally cause internal forces and nodal displacements that are employed to counteract the effect of loading. To avoid weight penalty due to mechanisms based on moving parts and to reduce control complexity (Campanile 2003), structural adaptation will be achieved without relying on defined kinematics (e.g. pantograph mechanisms).
Note that in this formulation the dynamic response of the structure is not compensated by active means. Force and shape control is employed here to design structures with minimum energy, not for vibration suppression. In this study the objective is to achieve an optimal state which is load-case dependent. This could be thought of as a one-to-one mapping between external loads and optimal internal forces and shape. In addition, because active vibration control requires a substantial amount of energy, a hybrid system of active (shape/force control) and passive (e.g. tuned mass dampers, viscous dampers in line with actuators) would be best suited to extend this formulation to dynamics in a context where energy is a primary concern. As dynamic is not considered, seismic design in not currently part of the methodology. For the same reason, it is also assumed that fatigue is not a relevant limit state although this could be included by adding appropriate constrains.
In Eq. 1, the objective function is the sum of two terms: the first is energy embodied in the material and the second the operational energy needed for structural adaptation during service. The embodied energy is obtained by multiplying the mass of each element (αi · Li · ρi, cross-section area, length and density of the ith element respectively) by its energy intensity factor eei (MJ/kg) which is the energy per unit mass for extraction and manufacturing (Inventory of Carbon and Energy (ICE) (Hammond and Jones 2008). The operational energy is what it takes to control the internal forces from a geometrically compatible state \( {\boldsymbol{F}}_{jk}^{COMP} \)(i.e. non controlled state) to an optimal state Fjk by applying a force difference \( {\boldsymbol{\Delta F}}_{jk}={\boldsymbol{F}}_{jk}-{\boldsymbol{F}}_{jk}^{COMP} \)which requires a change of shape of the structure. To compute the operational energy, a stochastic distribution of the occurrence for each design load case j must be assumed (see Section 5). The load probability distribution is discretised in d bins each corresponding to a certain load intensity occurring for a certain number of hours Hjk. The terms ω and η are the actuator working frequency and mechanical efficiency respectively, which are assumed here to be constant for simplicity (see 5.3).
The optimal internal forces F must satisfy equilibrium (Eq. 2) and ultimate limit state constraints (Eq. 4) including admissible stress and buckling. Equilibrium equations have been augmented to account for the effect of shape change via the actuator length changes ∆L which feature as part of the external load. BRED, C and G are the equilibrium, self-stress and flexibility matrix respectively. Similarly, the left side of Eq. 3 gives the nodal displacements after the shape change caused by the actuator length changes ∆L under loading. The nodal displacements are constrained by a serviceability limit state (\( {\mathbf{u}}_{jk}^{SLS} \)). The derivation of Eqs. 3 and 4 are given in the appendix A.3.
The synthesis process stated in Eq. 1–4 is a dual-objective, mixed-integer nonlinear programming problem (MINLP). It is dual-objective because, generally, the more light-weight the structure is (small embodied energy), the higher the operational energy for control and vice versa. It is mixed-integer because some design variables are continuous (cross-section area, internal forces and control commands) whilst others are discrete (the actuator layout). The optimization of the actuator layout involves assigning a certain number of active elements to a set of available sites. For this reason, the search space grows factorially with the number of elements of the structure (see 2.2.2). In addition, the problem is generally not convex due the effect of element buckling constraints (Cheng 1995). Methods based on stochastic search or non-convex MINLPs could be employed in order to solve to optimality (Achtziger and Stolpe 2006). However, using those methods, the synthesis process stated in Eq. 1–4 is often impractical even for structures made of a small number of elements and it becomes intractable when the structure is made of many elements due to exponential complexity.
2.2 Nested approach
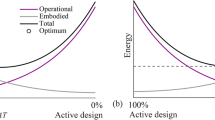
The flowchart in Fig. 1 illustrates a nested approach adopted to carry out the synthesis process stated in Eq. 1–4. The method comprises three main steps: (1) embodied energy minimisation, (2) actuator layout optimisation and (3) operational energy computation. These steps are nested within an outer optimisation process which minimises the whole-life energy. In order to coordinate embodied and operational energy optimisation an auxiliary design variable called Material Utilisation (MUT) and a state variable called Load Activation Threshold (LAT) are introduced. The MUT is a ratio of the demand over strength capacity but it is defined for the structure as a whole and can effectively be thought of as a scaling factor on the allowable stress. The MUT varies in a range of 0% < MUT ≤ 100%. The LAT is the external load causing a state of stress and displacements that violates a serviceability limit state (SLS). The LAT is in a one-to-one correspondence with the MUT: the lower the MUT, the stiffer the structure and thus the higher the activation load (LAT) which ultimately results in a lower operational energy and vice versa. For this reason, once the MUT is fixed the synthesis process stated in Eq. 1–4 simplifies into a single objective problem. Because all design variables (structural + actuator layout) are themselves function of the MUT, the objective function i.e. the whole-life energy can be thought of as a function of one main independent variable. This means that by varying the MUT one can move from least-weight structures (MUT = 100%) with small embodied but large operational energy, to stiffer structures with large embodied and smaller operational energy consumption. Figure 2 shows the notional variation of the total energy as the MUT varies. The outer optimisation process performs a search that identifies the optimal MUT corresponding to the minimum energy design. Each iteration of the outer process comprises the three main steps defined above.
2.2.1 Embodied energy minimisation
The embodied energy of the structure is minimised by computing optimal internal load paths and the corresponding material distribution. Stress constraints (ULS) are accounted for but geometric compatibility between element deformations and nodal displacements as well as SLS are ignored at this stage thus obtaining a lower bound in terms of material mass. This means that in case of power outage or actuation system failure and concurrent occurrence of a strong event, the structure might not be serviceable but load carrying capacity is not compromised (i.e. fail-safe). In other words, the structure is designed not to collapse under the worst load case even without the contribution of the active system.
This constraint could be relaxed. However, civil structures are often subjected to loads that although have a very low probability of occurrence, might be extremely damaging and therefore a fail-safe criterion for the adaptive system is often regarded as necessary in this context (Schneider and Vrouwenvelder 2017). Further consideration on fail-safe criteria for adaptive structures is given in section 7.1.
2.2.2 Actuator layout optimisation
When external loads act on the structure, the compatible forces will in general be different from the optimal forces and the resulting displacements might be beyond serviceability limits. For this reason, the second step is to design the actuation system. The actuator layout optimisation is carried out by relaxing the binary problem into a continuous linear form through sensitivity analysis (see section 4). An optimal location of the actuators must be determined to manipulate actively the flow of internal forces by changing the shape of the structure. In this way, the stress is homogenised and the displacements are reduced within required serviceability limits.
Although the embodied energy optimisation and the actuator layout optimisation are decoupled, the actuation system is an integral part of the structure. This is because the actuators, by changing the shape of the structure to meet serviceability requirements, allow it to be much leaner, with lower embodied energy. Conversely, the actuator optimal layout is very much dependent on the structure within which the actuators are to be fitted. The efficacy of an actuator to control internal forces and displacements depends on its location and the position of the nodes to be controlled. When varying the MUT, the resulting material distribution changes thus requiring a different load-path redirection and displacement compensation. For this reason, the actuator optimal layout changes for different values of the MUT.
2.2.3 Operational energy computation
The computation of the operational energy requires assuming some statistics on the frequency of occurrence of the loads. It is intuitively clear that the proposed design process will be particularly beneficial when the design is governed by large loading events that have a small probability of occurrence (storms, earthquakes, unusual crowds). For simplicity, these loads will be considered as live loads here because they are not permanent. To illustrate this, Fig. 3a shows a notional cumulative frequency of occurrence plot for a generic stochastic load.
The first step in the operational energy computation is to detect the Load Activation Threshold which is represented by a dotted line in Fig. 3a. The activation threshold demarcates two zones: on the left-hand side are the more probable low levels of load the structure will be able to withstand passively without actuation. On the right are the rarer loads with higher magnitude which the structure will only be able to resist using both passive and active load-bearing capacity. The two loading zones can also be visualised in Fig. 3b which shows the hours of occurrence of the live load whose distribution is divided in discrete steps from zero to the design load. The hours of occurrence of the loads above the activation threshold are represented by the bars in magenta colour. For all levels of loads above the activation threshold the load path is redirected and displacements are controlled by the active system via a shape change. The operational energy that it takes to perform force redirection and displacement compensation is computed thereafter. Because the actuation system is only activated when the loads reach the activation threshold, the operational energy is only consumed when necessary. The objective of the synthesis is to carefully replace passive resistance through material and form by a small amount of operational energy.
2.3 Illustrative example
In this paper, the design process is illustrated on a generic roof supporting structure described here. The structure is made of planar trusses supporting 10 m of cover each (out of plane) as shown in Fig. 4a. The trusses are simply supported. The simplicity of the case study chosen here is deliberate to illustrate effectively all the steps of the design process through a useful visual aid. However, this method has been successfully applied to other realistic spatial configurations of complex layout (Senatore et al. 2018a, b) and it has been successfully tested on a large-scale prototype adaptive structure (Senatore et al. 2018c).
It is assumed that the lateral stability of the roof system is provided separately (e.g. by some cross-bracing between trusses) and that the roof cover or the cross-bracing provide sufficient restraint against out-of-plane instability. Figure 4b shows one of the interior trusses, constrained as indicated in the diagram and subject to both permanent and live loads. All elements are assumed to have a cylindrical hollow section and to be made of structural steel (S355) with a density of 7800 kg/m3 and an energy intensity of 35 MJ/kg. To limit the complexity of the optimisation process, the wall thickness is set to 10% of the external diameter. The four load combinations considered are listed in Table 1.
The dead load on the roof panels is set to 3 kN/m2 resulting in a uniformly distributed load of 30 kN/m. There are two types of live load: a wind suction load modelled as a negative pressure on the roof panels (L1) and a lateral load L2. The load figures given in Table 1 are characteristic values typically used in the design of roof structures by practicing design engineers. For the purposes of this illustrative example the definition of “characteristic value” is the 95th percentile of the load probability distribution. Section 5.1 gives details of the load probability distribution in relation to the computation of the operational energy.
3 Embodied energy optimisation
The first stage of the design process consists in finding the member cross-section areas α that minimise the embodied energy of the structure and the set of internal forces Fjd (Eq. 5) that satisfy equilibrium constraints (Eq. 6) as well as a set of ULS inequality constraints (Eq. 7) when the structure is subjected to the design load Pjd . The subscript “j” refers to one of the “p” load cases whereas “d” refers to the bin of the load probability distribution corresponding to the design load.
In Eq. 5, αi is the cross-section area, Li the length, ρi the density and eei the material intensity factor for the ith element in the structure, which is made of n elements. Following the Simultaneous Analysis and Design approach (SAND) (Haftka 1985), the n × 1 dimension vectors α and Fjd, gathering the member cross-section areas and forces respectively, are the design variables. \( {\boldsymbol{P}}_{jd}^{RED} \) [(m − nR) × 1] is the design load reduced to the m − nR unconstrained degrees of freedom (DOFs), where m is the number of DOFs and nR the number of constrained DOFs.
Equation 6 expresses equilibrium constraints where \( {\boldsymbol{B}}^{RED} \) [(m − nR) × n] is the direction cosine matrix reduced to the unconstrained DOFs which is constant because the topology is assigned a-priori and only small-displacements are considered. However, this equality constraint is nonlinear because the self-weight of the structure changes iteratively (due to changes in α) hence so does the vector of external loads \( {\boldsymbol{P}}_{jd}^{\mathrm{RED}} \) which is the sum of live and permanent load.
Ultimate limit states are expressed by linear inequalities in Eq. 7 where σT and σC are material yield stress in tension and compression respectively which are factored by the MUT. At this stage, the MUT is constant between 0 and 100% (absolute minimum mass/embodied energy structures). Stability constraints are included in Eq. 7 where critical loads σB are computed iteratively using the Euler buckling formulation. Eq. 7 checks the design stress against the minimum between the crushing load and the buckling load. Although global stability is an important aspect in the design of slender structures (Kocvara 2002; Torii et al. 2015), it is not considered here, to limit the complexity of the formulation.
At this stage, neither geometric compatibility nor deflection constrains are included hence the internal force vector Fjd is called optimal or non-compatible. Compatibility will be enforced by the corrective actions of the actuators which redirect the compatible load-path \( {\boldsymbol{F}}_{jd}^{COMP} \) to the optimal one Fjd and at the same time change the shape of the structure to keep displacements within required serviceability limits. This initial phase of the methodology is inspired from Teuffel (Teuffel 2004) but unlike Teuffel, self-weight and local buckling constraints are considered, making the problem nonlinear.
To ensure that the cross-section areas sought and load-paths are optimum and adequate for multiple load cases, the problem requires a vector formulation. This is also useful to integrate the optimisation with the statistics of load occurrence later 5.1. Using the vector formulation, the problem stated in Eq. 5–8 is rewritten as:
where the design variable vector x concatenates the cross-section area vector α and the optimal force vector \( {\boldsymbol{F}}_d^{EXT} \) for all load cases. \( {\boldsymbol{F}}_d^{EXT} \) extends the internal force vector Fd to include the support reactions. AEQAULS and AULSb are block matrices which collate force-equilibrium balance, linear inequalities constraints (ULS) and non-linear stability inequality constraints (ULSb) for all load cases respectively. The main reason for a distinction between the ultimate limit state constraints AULS and AULSb is that the latter requires updating every iteration due to the change of the cross-section areas. However, ULS constraint equations do not double because the minimum between the admissible stress in compression and the critical load is selected. The reader is referred to appendix A.1 for a comprehensive description of the vector formulation and A.2 for a discussion on the existence and type of solutions to the problem stated in Eq. 9.
The truss is made of 26 (n) elements. There are 24 (m) DOFs of which 3 (nR) are constrained. Because there are 4 load cases, the number of design variables is 142 and that of constraints is 200 (Eq. 45). The problem is over-constrained (Eq. 46) hence members are utilised at capacity (i.e. ultimate limit state constraints are satisfied by equality) only for the worst load case (LC4). The problem was solved numerically using Sequential Quadratic Programming in Matlab. By the nature of the SQP method, sensitivities are computed numerically (Fletcher 1995). The hessian of the Lagrangian function is a positive definite quasi-Newton approximation which is calculated using Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm (Nocedal and Wright 2006). It takes 18 iterations to achieve convergence within an average time of 1500 ms using a 64-bit Intel i7 4-core processor. No parallelisation has been implemented.
The solution to Eq. 9 for the case study defined in 2.3 is shown in Fig. 5. This cross-section distribution is achieved using an MUT set to 100%. The bar chart of the cross-section areas is shown in Fig. 6. This section distribution gives a good indication of a more efficient layout for this problem. Some of the very thin elements (6,9,10,12,15) could be taken out since their contribution is negligible. Note that removing those elements makes the layout statically determinate without increasing the critical buckling length of any other member.
4 Actuator layout optimisation
The determination of the actuator layout requires a certain number of degrees of freedom nCDOFs to be controlled which is usually chosen based on the response of the structure and serviceability requirements. The minimum number of actuators nACTs to control the required displacements exactly, is equal to the sum of nCDOFs and the static indeterminacy r:
Intuitively this is the number of actuators needed to turn the structure into a controlled mechanism. In fact, one actuator can control at least one degree of freedom and for statically indeterminate structures, r (dimension of the self-stress space) extra actuators are needed to control the internal forces and enforce geometric compatibility. In case fewer actuators are fitted into the structure, displacements can still be compensated albeit only approximately.
In this nested approach, the most efficient actuator positions are those where the active elements have the largest effect towards internal load-path and displacement compensation. The problem is of combinatorial nature as it involves selecting nACTs actuators from a set of n available sites (i.e. the elements). A computation of all possible combinations is impractical even for the simple layout under consideration since it involves as many structural analyses as:
where n is the total number of elements and nACTs = 5 + 5 = 10. Instead, this problem is formulated here as a constrained least-square optimisation. The formulation of the actuator placement problem requires two prior steps: (1) computation of required load-path redirection and displacement compensation, (2) assessment of force and displacement actuation sensitivity.
4.1 Force redirection and displacement compensation
The forces \( {\boldsymbol{F}}_d^{COMP} \) are the compatible internal forces which could be computed by a standard stiffness matrix analysis of the problem. \( {\boldsymbol{F}}_d^{COMP} \) are in equilibrium with the external loads without the corrective action of the actuators. The difference between compatible and optimal forces denoted ∆Fd is:
To satisfy compatibility, this force difference must be compensated by the actuator length changes. To appreciate the effect of the load path redirection, Fig. 7 shows the optimal and compatible forces and their difference under LC4 plotted on each corresponding member of the structure. Focussing on elements 1, 9 and 12 for example, work is needed to decrease the compatible tension state via compressive forces.
The compatible displacements \( {\boldsymbol{u}}_d^{COMP} \)are those resulting from the action of the external loads without actuation. For example, Fig. 8a shows the truss deflection caused by the live load LC4.
The vertical displacement of the nodes 2 to 5 is beyond serviceability limits (span/360 = 56 mm). For this reason, the vertical degrees of freedom of those nodes are chosen to be controlled (CDOFs). The horizontal degree of freedom of node 12 is also controlled to limit the horizontal movement of the support. The controlled nodes are indicated by circles in Fig. 8b. Imposing serviceability limits on the CDOFs generates a vector of required displacements \( {\boldsymbol{u}}_d^{\mathrm{SLS}} \) and consequently a displacement compensation vector:
where ∆ud is a vector whose elements are different from zero only if the displacement of the corresponding CDOF is beyond serviceability. As for the force compensation ∆Fd, ∆ud is part of the corrective action of the actuators. Similar considerations apply for the other load cases. ∆Fd and ∆ud, are inputs to determine the optimal actuator layout.
4.2 Computation of force and displacement sensitivity matrices
The assessment of the structure actuation sensitivity is based on the computation of the force SF and displacement Su sensitivity matrices. These matrices store element forces and nodal displacements caused by a unitary length change for each element of the structure in turn. At this stage all elements are considered as actuator candidates. For illustration purposes, Fig. 9 shows the forces and displacements caused by a unit length change in element 8.
A convenient method to compute internal forces and displacements resulting from element length changes is the Integrated Force Method (IFM) (Patnaik 1973). In this section, the IFM main equations are briefly introduced to explain how to obtain the actuation sensitivity matrices. The use of the IFM to compute the effect of an element length change is described comprehensively in appendix A.3.
In statically indeterminate structures, internal stresses can be caused by geometrical imperfections (e.g. lack of fit or thermal strains) in the elements. The IFM allows an initial deformation (e.g. lack of fit) to be dealt with in a compact way and without the need to choose any specific member as redundant. In the design method presented in this paper, a deformation vector akin to a lack of fit is defined to assign the actuator length changes. In other words, the length change of an actuator is thought of as a non-elastic strain which is usually produced by thermal, plastic, creep strain or lack of fit and is referred here as eigenstrain (Ziegler 2005) (see A.3). The governing equation of the IFM is:
where BRED [(m − nR) × n] and PRED [(m − nR) × 1] are the equilibrium matrix and external load vector reduced to the unconstrained degrees of freedom; C(r × n) is a compatibility matrix whose rows are the self-stress vectors defining the null-space of BRED (see appendix A.3); G (n × n) is the local flexibility matrix (diagonal) relating the element deformation to the internal forces. Because Eq. 14 combines equilibrium and compatibility into a single matrix statement, the external load PRED must be complemented by an (r × 1) vector which in this work is defined as the eigenstrain load vector \( {\boldsymbol{P}}^{EIG} \):
where β0(n × 1) is the assigned eigenstrain, L(n × 1) is the element length vector and ° is the entry-wise product (Hadamard product). This way, the eigenstrain load vector offers a mean to set directly an eigenstrain distribution i.e. the actuator length changes ∆L(n × 1) defined as:
Solving for forces Eq. 14, the column vector \( {\boldsymbol{S}}_i^F \) of the force sensitivity matrix collating the element forces caused by a unit length change of the ith element is:
where the external load is set to a zero vector to compute only the internal forces caused by element length changes and the \( {\overset{\sim }{\boldsymbol{P}}}^{EIG} \) is obtained by setting the ith component of the eigenstrain vector β0 to 1/L but all other components to zero:
Iterating for each element the force sensitivity matrix SF(n × n) is formed. The rank of SF(n × n) is generally equal to the indeterminacy r because its columns are linear combinations of r independent self-stress vectors. Note that for the ith element to achieve an effective unitary length change it must be treated as infinitely rigid by setting its flexibility to zero (G(i,i) = 0). However, in practice, an actuator can achieve the required length change via feedback control. For statically determinate structures there is no difference between optimal and compatible forces hence the matrix C is a 0 matrix, and so is the eigenstrain load vector \( {\overset{\sim }{\boldsymbol{P}}}^{EIG} \). This means that no stress is caused by the actuator length changes i.e. SF is a 0 matrix.
The column vector \( {\boldsymbol{S}}_i^u \) collating the nodal displacements caused by a unit length change in the ith element is obtained by:
where J is the deformation coefficient matrix defined in appendix A.3. Iterating for each element the displacement sensitivity matrix Su(m × n) is formed. The rank of Su(m × n) is generally equal to (m − nR) which means there are as many independent degrees of freedom as those contained in the equilibrium matrix BRED minus those constrained at the supports.
4.3 Optimal actuator layout
To find the optimal actuator layout, the efficacy of each element to redirect the load-path and to correct displacements must be assessed. The problem is formulated as a constrained minimisation:
The objective function to minimise in Eq. 20 is the squared norm of the difference between the nodal displacements caused by the element length changes \( {\boldsymbol{\Delta L}}_d^{ALL} \) (the unknown variable vector) and the required displacement correction. The equality constraints in Eq. 20 enforce compatibility - the actuator length changes must redirect the compatible load-path to the optimal one. Eq. 20 is a constrained least square problem which can be solved in several ways (Björck 1996). A method based on generalised singular value decomposition (Van Loan 1985) was used as this produces a minimum norm solution even when the constraint matrix is rank deficient. Considering the case study defined in 2.3, the problem in Eq. 20 is solved within 3 ms on average using a 64-bit Intel i7 4-core processor.
Because the actuator positions are still unknown, \( {\boldsymbol{\Delta L}}_d^{ALL} \) is here computed considering all elements working as actuators (hence the superscript “ALL”). This will be used to evaluate the efficacy of each element to work as an actuator thus leading to the optimal actuator layout (4.3.1 and 4.3.2). Once the actuator layout is known, the actuator length changes will be computed solving an identical optimisation problem to that given in Eq. 20 but using the reduced force and displacements sensitivity matrices as described in 5.2. This way the actuator placement problem and control of forces and displacements are decoupled avoiding a mixed discrete-continuous formulation.
Note that for statically determinate structures, there is no need to redirect the load-path to enforce compatibility (4.2) and therefore the actuator length changes can be obtained directly using the pseudo-inverse of the displacement sensitivity matrix:
The problem stated in Eq. 20 or Eq. 21 can be solved exactly if the rank of Su is equal to (m − nR) and the rank of SF is equal to the degree of static indeterminacy r i.e. the number of independent equations equals the number of unknown variables n. Due to numerical issues the sensitivity matrices may not have the required rank. In this case, there can be large residuals resulting in a wrong actuator efficacy evaluation. The method given in 4.2 based on eigenstrain assignment and the IFM produces force and displacement sensitivity matrices with correct ranks.
4.3.1 Partial actuator efficacy for control of displacements
For stiffness-governed problems, displacement compensation is dominant compared to force compensation therefore the actuator efficacy is given by how effectively their length changes compensate for displacements:
The efficacy is called “partial” because it is evaluated for a single load case. The matrix Su∣CDOFs(nCDOFs × n) is obtained by extracting from Su the rows corresponding to the controlled degrees of freedom with nCDOFs being their total number. Similarly, the vector \( {\boldsymbol{\Delta u}}_{jd}^{CDOFs}\left({n}^{CDOFs}\times 1\right) \) is obtained by extracting from ∆ujd the components corresponding to the controlled degrees of freedom. The vector \( {\overset{\sim }{\boldsymbol{\Delta L}}}_{jd}^{ALL}\left(n\times 1\right) \) is obtained by extracting the block corresponding to the jth load case from \( {\boldsymbol{\Delta L}}_d^{ALL}\left[\left(n\cdotp {n}^p\right)\times 1\right] \) and setting all its components to zero except that corresponding to the length change of the ith element. The (nCDOFs × 1) vector \( {\boldsymbol{S}}^{u\mid CDOFs}\cdotp {\overset{\sim }{\boldsymbol{\Delta L}}}_{jd}^{ALL} \) contains the controlled node displacements caused by the unitary length change of the ith element. Dividing it component-wise by \( {\boldsymbol{\Delta u}}_{jd}^{CDOFs} \) evaluates the contribution of the ith element length change towards the required displacement correction of each controlled node. This result in a vector the sum of whose elements is divided by nCDOFs to give the actuator partial efficacy for the ith element. The actuator partial efficacy is constrained to be (1) non-negative and (2) smaller than unity:
If the efficacy is outside this range, it is set to 0. The 1st condition is to exclude those elements whose length changes cause a deflection which moves the controlled nodes in the opposite direction to that required. The 2nd condition is to exclude those elements whose length changes cause a deflection overshooting the required displacement correction. Collating the result for each element and for all the load cases gives the vector of partial efficacy effu(n × np).
4.3.2 Partial actuator efficacy for control of internal forces
For strength-governed problems ∆ud will in general be negligible hence displacement correction should not be needed. However, actuator work might still be needed in case ultimate limit states are exceeded. In this case, the actuator length changes ∆Ld must only redirect the load-path without changing the displacements of the controlled nodes (i.e. ∆ud ≅ 0 even after the actuator change their length). The optimal actuator positions are those where their length change is most effective to achieve the required load-path redirection ∆Fd:
Similar to 4.3.1, the (n × 1) vector \( {S}^F\cdot {\tilde{\varDelta L}}_{jd}^{ALL} \) is the change in the element axial forces caused by the length change of the ith element. Dividing it element-wise by ∆Fjd evaluates the contribution of the ith element towards the required load-path redirection. This result in a vector the sum of whose components is divided by the number of elements n to give the actuator partial efficacy for the ith element. The actuator partial efficacy is constrained to be (1) non-negative and (2) smaller than unity:
If the efficacy is outside this range is set to 0. The 1st condition is to exclude those elements whose length changes cause force variation opposite to that required (e.g. increase in tension is required but compressive forces are provided). The 2nd condition is to exclude those elements whose length changes cause force variation bigger than that required. Collating the result for each element and for all the load cases gives the vector of partial efficacy effF(n × np).
4.3.3 Global actuator efficacy
Depending on whether the problem is stiffness or strength governed the global efficacy is obtained summing the partial efficacy over all load cases:
The actuator layout is obtained by selecting the indices of those elements corresponding to the nACTs highest components in the global efficacy vector. Note that for statically determinate structures, partial and global actuator efficiency must be obtained using Eq. 22 and Eq. 26 respectively because internal forces are not changed by the actuator length changes.
Figure 10 shows the optimal actuator layout for displacement control. The nACTs = 10 actuators are integrated in the structure and mapped on the initial geometry respectively obtained using the global actuator efficacy for displacement control. Similarly, Fig. 11 show the optimal actuator layout obtained using the global actuator efficacy for force control. Generally, for indeterminate structures there is enough redundancy so that the load-path can be redirected by either actuator optimal layouts. However, when shape control is dominant, the actuator layout for displacement control must be used to achieve both displacement and load-path control.
4.4 Actuation system embodied energy
Once the actuator layout is known, the embodied energy of each actuator is added to the structure embodied energy. The actuator embodied energy increases as the actuator force capacity increases. For simplicity, it is assumed that an actuator is entirely made of steel with an energy intensity of 35 MJ/kg (Hammond and Jones 2008) and its mass is a linear function of the force capacity with a proportional constant of 0.1 kg/kN (e.g. an actuator with a push/pull load of 1000 tons weighs 1000 kg) (ENERPAC 2016).
5 Operational energy computation
The operational energy is defined here as the energy needed to operate the actuators to redirect the load-path and compensate for displacements when needed. Assuming a statistical distribution of the load occurrence, computing the operational energy involves first detecting the load threshold from which compensation of forces and displacements is needed. Then, calculating the actuator length changes to achieve the required control objectives and finally computing the work done by all the actuators throughout the service life of the structure.
5.1 Live load probability distribution and load activation threshold
To work out the load activation threshold, some assumptions about the statistics of the occurrence of the live load must be made. As noted in the introduction, one expects adaptive structures to be particularly advantageous in terms of total energy when the design is governed by large and rare loads such as storms, earthquakes, snow, and unusual crowds. Probabilistic models already exist for most of these loads. For instance, earthquakes are often modelled with a Poisson distribution and wind storms with a Weibull distribution (Flori and Delpech 2010). Should this methodology be applied in a practical case, the relevant load probability distribution should be used. For the purpose of describing the design methodology in this paper, it is more convenient to work with a generic distribution which can easily be parametrised. The effect of the assumptions made here about the probability distribution are tested systematically in (Senatore et al. 2018b) and via experimental testing on a large-scale adaptive structure prototype (Senatore et al. 2018c). A normal distribution is often used to model natural random processes. However, it is symmetric around the mean so does not provide the right bias towards the lower values of the random variable. A log-normal distribution is closely related to the normal distribution because it is a probability distribution whose logarithm has a normal distribution and it takes only positive real numbers. Therefore, the log-normal distribution is both general and simple so it will be used in the following to model the live load. For a given load case j (0 < j ≤ np) the possible values of the load ranging from 0 to the design value to Pjd are groups into nd bins and these bins are denoted Pjk (0 ≤ k ≤ nd). The probability that a load occurrence Pj falls within a bin Pjk, is pjk:
where PPDF is the probability density function; μ and σ the expected value and the standard deviation of the underlying normal distribution. For simplicity, the mean of the underlying normal distribution is set to zero. Following the limit-state design methodology, the design load Pjd is set as the characteristic value (excluding safety factors) of the load probability distribution corresponding to the 95th percentile (Nowak and Collins 2012). Once the mean and the characteristic load are set, the standard deviation is adjusted so that the design load corresponds to the 95th percentile. Assuming a 50-year service life indicated by tservice (expressed in hours), the number of hours when the load falls within the bin Pjk is obtained as:
The level of load causing the element stress to exceed ULS and/or nodal displacement to exceed SLS is defined as the load activation threshold \( {\boldsymbol{P}}_j^{\ast \ast} \). For any load of higher magnitude than the load activation threshold the active system must redirect the load-path ∆Fk and control the shape of the structure ∆uk. Considering the case study defined in 2.3, the lowest load activation threshold was found at a value of 1.45 kN/m2 for LC4 corresponding to an equivalent wind velocity of 45 m/s (category 2 hurricane of the Saffir-Simpson scale).
5.2 Load path redirection and shape control
To obtain the force difference vector (i.e. load path redirection) \( {\boldsymbol{\Delta F}}_{jk}=\left({\boldsymbol{F}}_{jk}-{\boldsymbol{F}}_{jk}^{COMP}\right) \), the optimal force vector Fjk for all the occurrences of the live load Pjk above the activation threshold \( {\boldsymbol{P}}_j^{\ast \ast } \) must be found first. The problem is similar to that described in Eq. 9 but in this case, the only unknown variables are the optimal forces \( {\boldsymbol{F}}_k^{EXT} \)(including support reactions) obtained from solving the optimisation problem:
where AEQ, AULSand AULSb are constraint matrices identical to those defined in Eq. 37, Eq. 40 and Eq. 43. However, in this case, the first column is removed because the design variable vector (in this case, \( {\boldsymbol{F}}_k^{EXT} \)) no longer contains the cross-section areas α. Fk is obtained from \( {\boldsymbol{F}}_k^{EXT} \) by removing the support reactions. If a statically determinate layout is chosen, the actuator length changes only affect the displacements but not the state of stress in the structure (small displacements assumption) hence Fk is obtained directly from equilibrium. The problem formulated in Eq. 30 was solved as was done to solve the problem formulated in Eq. 9. Considering the case study defined in 2.3, each Fk was obtained approximately in 3 iterations within 50 ms on average.
Once the optimal force vector is found, the actuator length change ∆Ljk needed to redirect the load-path (∆Fjk) and compensate for displacements \( {\boldsymbol{\Delta u}}_{jk}=\left({\boldsymbol{u}}_{jk}^{SLS}-{\boldsymbol{u}}_{jk}^{COMP}\right) \) is computed using Eq. 31:
and for statically determinate structures (see 4.2):
In these equations the sensitivity matrices Su (m × n) and SF (n × n) are reduced (hence the superscript RED) by extracting the nACTs columns corresponding to the actuator indices. In addition, Su and ∆uk must be further reduced by extracting the rows corresponding to the controlled degrees of freedom. This way the rank of the reduced matrices Su ∣ RED (nCDOFs × nACTs) and SF ∣ RED (n × nACTs) is in general equal to nCDOFs and r respectively and their sum is nACTs which is the size of the vector of the unknown variables\( {\boldsymbol{\Delta L}}_{jk}^{RED}\left({n}^{ACTs}\times 1\right) \). In this case, the problem can be solved exactly. However, there might be cases where the reduced sensitivity matrices do not have the required rank. In these cases, adding more actuators improves control accuracy. \( {\boldsymbol{\Delta L}}_{jk}^{RED} \) is obtained from ∆Ljk(n × 1) reduced to the non-zero components corresponding to the position of the actuators. Note that to account for multiple load cases Su∣RED and SF∣RED are reshaped into block matrices of dimensions [(nCDOFs · np) × (nACTs · np)] and [(n · np) × (nACTs · np)] respectively. Consequently \( {\boldsymbol{\Delta L}}_k^{RED} \) becomes a block vector of dimensions [(nACTs · np) × 1]. The least square constrained problem stated in Eq. 31 was solved in a similar way to the problem stated in Eq. 20 taking 2 ms on average to produce a solution.
The actuator length changes depend on the target shape defined by required displacements uSLS (defined in 4.1) which can be chosen in several ways. Figure 12 illustrates this. Figure 12a shows the undeformed shape under LC4 for design load P4d. Figure 12b shows the controlled shape obtained setting the displacements of all controlled nodes (indicated in Fig. 8) equal to the serviceability limit (span/360). However, this tends to create drastic curvature changes between consecutive bays. A better way is to consider the rate of change of the curvature between consecutive bays to avoid the formation of kinks as shown in Fig. 12c.
Figure 13 shows the bar chart of the actuator length changes for all load cases. Note that even when displacement compensation is substantial (e.g. 160 mm for the central nodes of the top/bottom chords under LC1 as shown in Fig. 8) the maximum actuator length change is small (below 15 mm).
To make a conservative comparison with the passive structure (see section 6.2), deflections are only considered under live load for both adaptive and passive structures. Under permanent load (LC1), the passive structure is thought of as perfectly pre-cambered whilst for the adaptive structure the actuators reduce the displacements completely thus achieving an apparent infinite stiffness. Figure 14a shows the controlled shape under LC1 whilst Fig. 14b shows the deformed shape without using actuation. In the controlled case, the top chord is kept flat whilst the central part of the bottom chord bows downward thereby locally increasing the second moment of area of the truss beam.
Because the structure takes the live load already stressed due to the initial shape change under permanent load, the compatible forces for the other load cases result from the superposition of the optimal forces under permanent load FPL and the compatible forces under live load only \( {\boldsymbol{F}}_{jd}^{COMP\_L} \). Considering LC4 for example, this means that \( {\boldsymbol{F}}_{4d}^{COMP}={\boldsymbol{F}}^{PL}+{\boldsymbol{F}}_{4d}^{COMP\_L} \).
5.3 Actuator work and operational energy
Figure 15 shows the work Wijk done by the ith actuator for the kth occurrence of the jth load case Pjk above \( {\boldsymbol{P}}_j^{\ast \ast } \). This work is represented by the hatched area; \( {F}_{ijk}^{COMP} \) is the compatible force with no active control (the actuator is locked in position) and ∆Fijk is the force needed to change length ∆Lijk. From this, it is clear that:
Because length corrections are usually small, a linear elastic force-displacement relationship is assumed for simplicity. The force \( {F}_{ijk}^{\mathrm{COMP}} \) is considered as a constant force because it is part of the total force exerted by the actuator whether it acts as an active or a passive element. The work related to this constant force is shown as the rectangular area in Fig. 15. Instead, the work related to the force correction ∆Fijk is given by the half product with the corresponding ∆Lijk.
To compute the operational energy, further assumptions are needed regarding the working frequency and mechanical efficiency of the actuators. It is assumed that the actuators always work at the first natural frequency of the structure which is likely to dominate the response of most structures excited by dynamic loads relevant to civil engineering structures. This assumption is conservative because it implies that even if the loads only vary very slowly in time, the actuators work at the 1st natural frequency of the structure. This is to obtain an upper bound of the operational energy consumption during service. In addition, it is assumed that non-active means are used to control vibrations (e.g. tuned mass dampers) if required. This is the case when vibration is caused by loads below the activation threshold (ULS and SLS respected). Whilst the active system could be used to compensate this effect, it may come at the expense of a significant additional operational energy since vibrations can occur very often.
Regarding the actuator mechanical efficiency, it is assumed that linear actuators are used with an efficiency of 80%. Assuming hydraulic actuators, mechanical efficiency is in a range 90–98% (Huber et al. 1997). The total operational energy (OpE) for the kth occurrence of the load probability distribution can be finally computed as:
where ω and η are the working frequency expressed in cycles per hours and mechanical efficiency of the actuators respectively.
Note that the energy it takes to power the control system (e.g. sensors and signal processing) is modelled here as a linear function of the number of structural elements and actuators. This assumption is based on empirical knowledge gained via experimental testing on a purpose-built large-scale adaptive truss prototype instrumented with strain gauge based sensors and fitted with mechanical linear actuators (Senatore et al. 2018c). This fixed term is part of the total operational energy but it is usually substantially lower than the energy needed by the actuators to redirect internal forces and/or to control displacements. Assuming a value of 200 W to power the control system and a total time of activation of 2.5 years (5% of the total life of the structure, which is usually the average time predicted by the simulations), the energy consumption to power the control system totals about 16 GJ which converts to 440 kg of steel (Hammond and Jones 2008). This term can be practically neglected for most cases except for very small structures for which the mass savings become comparable with the loss of energy due to the control system power requirement.
6 Total energy optimisation (TEO)
6.1 Energy savings vs MUT
The whole-life (i.e. total) energy is optimised by minimising the sum of the embodied and operational energy. The process described in sections 3, 4 and 5 is repeated iteratively within an outer loop varying the Material Utilisation factor in the range [fully passive 0 < MUT ≤ 1 fully active]. By decreasing the MUT the load path optimisation routine (section 3) returns stiffer structures and therefore a higher load activation threshold, whereas when the MUT is increased, the converse happens.
Considering the case study defined in section 2.3, Fig. 16a and b shows the load activation thresholds (dotted lines) for the adaptive solution designed with MUT = 100% and MUT = 50% respectively. As expected the load activation thresholds are higher for the case MUT = 50%. Note that for the load case LC3 (lateral load), neither force nor displacement compensation are needed and therefore the activation threshold line is not needed and it is set to zero for completeness.
A higher load activation threshold results in a lower operational energy as shown in Fig. 17a and b which compares the total energy of the adaptive structure to the embodied energy of the equivalent passive structure designed using a bespoke optimisation method outlined in Appendix A.4. This method gives results comparable with those obtained by the Modified Fully Utilised Design (Patnaik et al. 1998) and outperforms it when multiple load cases are considered.
Although the embodied energy savings are substantial (57%) when setting the MUT to 100%, the total energy savings are much lower (11%) due to a higher level of operational energy needed for structural adaptation. By contrast when setting MUT = 50% the operational energy decreases substantially but the total energy savings are low (21%) because of the extra embodied energy. Note that the embodied energy of the adaptive structure includes that of the actuators (see 4.4).
It is clear then that by varying the MUT one can move from a least-weight structure with small embodied but large operational energy, to a stiffer structure with large embodied but smaller operational energy.
6.2 Adaptive vs passive
For the truss example used in this paper, the minimum total energy configuration is found for an MUT of 76%. This means that the optimised adaptive structure is designed so that the maximum stress under the worst load combination is 76% of the yield stress. Table 2 gives energy savings and load activation thresholds. Figure 18 compares the adaptive structures obtained using MUT = 100%, MUT = 50% and the equivalent passive structure. The passive structure corresponds to MUT = 40%. Although subject to the same loads, the material distribution differs substantially between the designs.
Figure 19a shows the curves of the embodied, operational and total energy as the MUT varies. The operational energy reduces as the MUT decreases whereas the embodied energy does the opposite. Figure 19b compares the embodied energy of the equivalent passive structure and the total energy of the adaptive structure. For the optimum adaptive structure (MUT = 76%) the energy savings are 43% accounting for the embodied energy of the actuators (total mass of 255 kg) and 49% without (see 4.4). Comparing this optimum structure with the adaptive structure obtained for MUT = 100% shows that a 20% increase in embodied energy results in a 90% decrease in operational energy. By contrast, using MUT = 50% the operational energy is very low whereas the embodied energy is 50% higher that of the adaptive structure obtained with MUT = 76%.
On average, the passive structure element cross-sections areas are twice as big as those of the adaptive one as shown in Fig. 20. The biggest and smallest diameter tubes for the adaptive solution are 200 mm and 10 mm for element 3 (mid top chord) and 8 (diagonal) respectively.
Figure 21 compares the stress in the elements of the adaptive (a) and passive (b) structures. Stress homogenisation achieved by shape and force control through actuation results in most of the elements (top chord and diagonals) of the adaptive solution being utilised at 60% (average) of the capacity for LC1 (permanent load) and LC3 (wind). For the passive solution instead the average element utilisation is 30%. The maximum length changes are a 20-mm extension and a 7-mm shortening for the actuator fitted on element 12 (diagonal) under LC1 and LC4 respectively. Under live load (LC3), the highest forces in tension (489 kN) and compression (522 kN) are applied by the actuators fitted on element 26 and 7 respectively.
6.3 Design process summary and computation time
Table 3 summarises the main steps of the process providing computation times for the design of the case study truss defined in 2.3. The truss is made of 26 (n) elements. There are 24 (m) DOFs of which 3 (nR) are constrained. The controlled degrees of freedom are 5 (nCDOFs) and the number of actuators is 10 (nACTs). The design variables are α (26) + Fd (29 · 4) + Effu(26) = 168. The first nACTs components of the vector Eff is the optimal actuator layout hence it is included in the design variables. The MUT range (50% to 100%) was sampled in 50 points. Computations times are obtained running the algorithm on a 64-bit Intel i7 4-core processor. No parallelisation has been implemented. The total computational time of the synthesis process of this case study comes to less than 1.5 min which should make it very attractive to design engineers. The algorithm is given in section A.5.The data that support the findings of this study including the source code are available from the corresponding author upon reasonable request. For up to date contact information visit http://www.gennarosenatore.com.
7 Discussion
7.1 Fail-safe criteria
This paper has shown that using adaptation to counteract the effect of the external load allows large quantities of material to be saved whilst meeting safety critical requirements. The structure has been designed to cope with the worst demand in terms of ultimate limit states even without contribution of the active system. This way, in case of a power outage and concurrent occurrence of a strong event the structure load carrying capacity is not compromised.
For stiffness-governed problems, deflection limits are usually reached much earlier than any critical stress conditions hence fail-safe is satisfied. Therefore, imposing that the system can cope with extreme loading events passively should not lead to any undue conservatism. For a strength-governed problem instead, extra constrains must be added to ensure that ULS criteria are satisfied even without active control. As already discussed in section 2, this constraint could be relaxed allowing the active system to contribute to satisfying ULS attainment which would possibly lead to leaner structures. This choice depends on the reliability of the control system and a risk analysis which are implementation dependent. Both reliability and risk analyses are beyond the scope of this paper.
As described in 5.2, the actuator commands are obtained by solving a constrained least-square problem. This means that in case of failure of one or more actuators, the problem of finding control commands becomes more constrained. In other words, the structure can still be controlled albeit with less accuracy. In case of actuator failure, those that are left working will provide more output energy to reduce displacements within the required limits. Both these scenarios (i.e. power outage and actuator failure) were successfully tested on an adaptive truss prototype (Senatore et al. 2018a).
7.2 Adaptive structures value and monetary cost considerations
Whole-life energy minimization is a new design criterion introduced in this work. The traditional design goals employed, for example, life-cycle cost minimization, do not explicitly address current and future challenges such as material scarcity, energy depletion and reduction of building environmental impacts, thus hindering creative development of strategies to design structures. Whole-life energy minimization is a more appropriate objective function (or utility function (Hazelrigg 1998)) which has been chosen here since it encompasses modern design goals that include minimising material and operational energy use thus lowering environmental impact of load-bearing systems.
A monetary cost comparison was beyond the scope of this paper and it was carried out for several spatial structures of complex layout in previous work (Senatore et al. 2018a). In this study, it was shown that for stiffness-governed problems, the adaptive solution not only vastly outperforms the passive one in terms of whole-life energy savings but it becomes competitive also in terms of monetary cost. Furthermore, even in those cases when the adaptive design is more expensive as it is the case presented here, the extra cost with respect to a passive structure is not wasted but rather, it is used to reduce the environmental impact of the structure. In this regard, adaptive structures can be thought of as energy saving devices. A comparison of the cost of saving energy using structural adaptation and that of producing energy using other technologies e.g. PV, reveals that the adaptive solution is competitive and has a lower cost for slender structures or for stringent deflection limits (Senatore et al. 2018b).
The focus of this paper was to minimise the whole-life energy of the structure and thus its overall environmental impact. However, structures produced by this method can also fulfil other functions such as being extremely slender and being capable of reducing deflections completely thus achieving an effective “infinite” stiffness. ‘Infinite stiffness’ is here understood as reducing practically to zero displacements at specific points, under loading without implying the structure becomes rigid. This means that adaptive structures can meet much stricter deflection limits at the expense of a small amount of operational energy which gives several benefits including (1) buildings can be taller (Senatore et al. 2018b), roofs and bridges longer-spanning, (2) buildings can have increased floor space via reduction of structural cores, (3) people comfort and the overall structural integrity can be improved reducing deflections in real-time (Senatore et al. 2018a). Adaptive structures designed with the formulation proposed in this paper combine three performance objectives which are usually competing figures of merit: (1) the structure has a low overall environmental impact (minimum energy design); (2) the structure can be extremely slender and (3) at the same time displacements can be controlled within very tight limits (i.e. extremely stiff). Being able to combine these three objectives is unique in structural engineering.
8 Conclusions
This paper describes a methodology for the design of structures with embedded actuation. Structural adaptation is employed to counteract the effect of loads. The novelty of this work lies in the development of a methodology that produces, given any stochastic occurrence distribution of the external load, a minimum energy design. An original interpretation of the non-elastic part of the strain—e.g. eigenstrain as defined in the residual-stress literature, lies at the core of the control strategy. A computationally efficient routine based on eigenstrain assignment via the Integrated Force Method and sensitivity analysis is formulated to place the actuators in optimal positions.
Results obtained using a relatively simple case study—a 20:1 span-to-depth simply supported truss—show that when the design is governed by live loads with small probability of occurrence, such as strong wind storms, snow, earthquakes and unusual crowds, the adaptive structure vastly outperforms its equivalent passive structure in terms of whole-life energy. The ability to redirect the load-path and change the shape to control deflections using minimum operational energy lead to a light-weight structure that achieves up to 49% total energy savings compared to an equivalent passive structure designed using state of the art optimisation methods.
The assumptions taken here regarding the load probability distribution have been successfully tested via a sensitivity analysis (Senatore et al. 2018b). The results specific to the case study discussed in this paper have been generalised via the study of several spatial structures of complex layout providing both energy and monetary cost analysis (Senatore et al. 2018a). A large-scale prototype designed using the methodology formulated in this paper has been successfully tested (Senatore et al. 2018c) validating key assumptions and numerical predictions.
Although this paper focuses on reticular structures, future work could consider other structural systems. The optimisation formulation is subject to equilibrium, stress and stability constraints which can be generalised to shell, plates and solids. Force and shape control are based on the use of the Integrated Force Method which can be generalised to other structural element types as shown in (Patnaik et al. 1991).
The method proposed to solve to optimality the synthesis process stated in Eq. 1–4 (All-in-One formulation) is a nested approach. The auxiliary design variables Material Utilisation factor and state variable Load Activation Threshold coordinate embodied energy and actuator layout optimisation which are nested within an outer process minimising the whole-life energy. Because this method does not solve the All-in-One problem directly, solution optimality cannot be guaranteed. However, the substantial energy savings obtained and its scalability to structures of complex layout made of many elements (Senatore et al. 2018a) show that the proposed method has undeniable merits. Future work could look into formulating an alternative implementation based on stochastic search or mixed-integer programming to assess the quality of the solution provided by the method introduced in this paper.
The synthesis process formulated in this paper can be readily extended to shape and topology optimisation by including nodal coordinates and structural layout in the design variables. On-going work has already extended this methodology to design structures that adapt through large shape changes (via shape optimisation and geometric non-linear analysis) (Reksowardojo et al. 2017; Reksowardojo et al. 2018) as well as to include joint-stiffness control through materials with variable stiffness properties (e.g. shape memory polymers) (Senatore et al. 2017; Wang et al. 2018). Future work could investigate shape and joint-stiffness control to tune the fundamental frequencies in order to reduce the dynamic response to loading.
References
Abdel-Rohman M, Leipholz H (1983) Active control of tall buildings. J Struct Eng 109(3):628–645
Achtziger W, Stolpe M (2006) Truss topology optimization with discrete design variables—guaranteed global optimality and benchmark examples. Struct Multidiscip Optim 34(1):1–20
Adam B, Smith IFC (2008) Active tensegrity: a control framework for an adaptive civil-engineering structure. Comput Struct 86(23–24):2215–2223
Bani-Hani K, Ghaboussi J (1998) Nonlinear structural control using neural networks. J Eng Mech 124(3):319–327
Begg D, Liu X (2000) On simultaneous optimization of smart structures—part II: algorithms and examples. Comput Methods Appl Mech Eng 184:25–37
Bel Hadj Ali N, Smith IFC (2010) Dynamic behavior and vibration control of a tensegrity structure. Int J Solids Struct 47(9):1285–1296
Björck Å (1996) “Constrained least squares problems,” in numerical methods for least squares problems, Philadelphia. Society for Industrial and Applied Mathematics, pp. 181–213
Campanile L (2003) “Using compliant and active materials to adapt structural geometry—challenges and good reasons.” In 14th International Conference on Adaptive Structures and, Seoul
Campbell ME, Crawley EF (1997) “Actuator and sensor design for controlled structures”. In AIAA/ASME Structures, Structural Dynamics and Materials Conference, Kissimmee, FL, USA
Cha J, Pitarresi J, Soong T (1988) Optimal design procedures for active structures. J Struct Eng 114:2710–2723
Cheng G (1995) Some aspects of truss topology optimization. Structural Optimization 10(3–4):173–179
Cimellaro G, Soong T, Reinhorn A (2008) “Optimal integrated design of controlled structures.” In The 14th World Conference on Earthquake Engineering, Beijing.
Connor JJ (2002) Introduction to Structural Motion Control. Pearson Education, Boston
Dhingra A, Lee BH (1995) Multi-objective design of actively controlled structures using a hybrid optimization method. Int J Numer Methods Eng 38:3383–3401
ENERPAC (2016) “E328e Industrial Tools - Europe,” [Online]. Available: http://www.enerpac.com/en-us/downloads. [Accessed 12 07 2017]
European Environment Agency (2010) Material resources and waste—the European environment—state and outlook. Publications Office of the European Union, Luxembourg
Fest E, Shea K, Domer B, Smith IFC (2003) Adjustable tensegrity structures. J Struct Eng 129:515–526
Fletcher R (1995) Practical methods of optimization. Bookcraft Ltd., Bath
Flori JP, Delpech GG (2010) “Stavros Niarchos Foundation Cultural Center in Athens Part I: Climatic Analysis,” (Technical Report). Centre Scientifique et Tecnique du Batiment, Nantes
Grigoriadis K, Zhu G, Skelton R (1996) Optimal redesign of linear systems. J Dyn Syst Meas Control 118:598–605
Haftka RT (1985) Simultaneous analysis and design. AIAA J 23(7):1099–1103
R. Haftka (1990) “Integrated structure-control optimization of space structures”. In Dynamics Specialists Conference, Long Beach, CA, USA
Hammond G, Jones C (2008) Embodied energy and carbon in construction materials. Proc Inst Civ Eng Energy 161(2):87–98
Hasse A, Campanile F (2009) Design of compliant mechanisms with selective compliance. Smart Mater Struct 18(11):115016
Hazelrigg G (1998) A framework for decision-based engineering design. J Mech Des 120(120(4)):653–658
Henry A, Kam C, Smith M, Lewis C, King M, Boulter N, Hoad P, Wong R, Munro S, Ming S (2016) “Singapore sports hub: engineering the national stadium”. Struct Eng 94(9)
Hiramoto K, Grigoriadis K (2005) “Integrated design of structural and control systems with a homotopy like iterative method”. In Americal Control Conference, Portland
Huber JE, Fleck NA, Ashby MF (1997) The selection of mechanical actuators based on performance indices. Proceedings: Mathematical, Physical and Engineering Sciences 453:2185–2205
Irschik H, Ziegler F (2001) Eigenstrain without stress and static shape control of structures. AIAA J 39(10):1985–1990
Jenkins C (2005) Compliant structures in nature and engineering, 1st ed. WIT Press
Kaethner S, Burridge J (2012) Embodied CO2 of structural frames. Struct Eng 90(5):33–40
Khot N (1998) Multicriteria optimization for design of structures with active control. J Aerosp Eng 11:45–51
Kocvara M (2002) On the modelling and solving of the truss design problem with global stability constraints. Struct Multidiscip Optim 23(3):189–203
Korkmaz S (2011) A review of active structural control: challenges for engineering informatics. Comput Struct 89(23–24):2113–2132
Kota S, J H, Osborn R, Paul D, Pendleton E, Flick P, Tilmann C (2003) Design and application of compliant mechanisms for morphing aircraft structures. Proc SPIE 5054
Li W, Huang H (2013) Integrated optimization of actuator placement and vibration control for piezoelectric adaptive trusses. J Sound Vib 332:17–32
Li Q, Skelton R, Yan J (2011) “Integrating mass and control energy optimization for tensegrity structure”. In 2nd International Conference on Intelligent Control and Information Processing, Harbin, China
Lienhard J, Schleicher S, Poppinga S, Masselter T, Milwich M, Speck T, Knippers J (2011) Flectofin: a hingeless flapping mechanism inspired by nature. Bioinspiration Biomim 6:1–7
Lu KJ, Kota S (2003) Synthesis of shape morphing compliant mechanisms using a load path representation method. Smart Mater Struct 5049:337–348
Lu LY, Utku S, Wada B (1992) On the placement of active members in adaptive truss structures for vibration control. Smart Mater Struct 1:8–23
Miura K, Furuya H (1988) Adaptive structure concept for future space applications. AIAA J 26(8):995–1002
Molter A, da Silveira O, Bottega V, Fonseca J (2013) Integrated topology optimization and optimal control for vibration suppression in structural design. Struct Multidiscip Optim 47:389–297
Mura T (1991) Micromechanics of defects in solids, 2nd edn. Kluwer, Dordrecht
Neuhäuser S(2014) “Untersuchungen zur Homogenisierung von Spannungsfeldern bei adaptiven Schalentragwerken mittels Auflagerverschiebung,” (Doctoral dissertation), ILEK, University of Stuttgart, Stuttgart
Nocedal J, Wright SJ (2006) Numerical Optimization. Springer Verlag
Nowak AS, Collins KR (2012) Reliability of Structures, 2nd ed. Taylor & Francis
Nyashin Y, Lokhov V, Ziegler F (2005) Decomposition method in linear elastic problems with eigenstrain. ZAMM - Journal of Applied Mathematics and Mechanics 85(8):557–570
Onoda J, Haftka R (1987) An approach to structure/control simultaneous optimization for large flexible spacecraft. AIAA J 25(8):1133–1138
Patnaik S (1973) An integrated force method for discrete analysis. Int J Numer Methods Eng 6:237–251
Patnaik S, Hopkins D, Halford G (1991) Integrated force method versus displacement method for finite element analysis. Comput Struct 38(4):377–407
Patnaik S, Gendy A, Berke S, Hopkins D (1998) Modified fully utilized design (MFUD) method for stress and displacement constraints. Int J Numer Methods Eng 41:1171–1194
Preumont A, de Marneffe B, Deraemaeker A, Bossensb F (2008) The damping of a truss structure with a piezoelectric transducer. Comput Struct 86(3–5):227–239
Previtali F, Ermanni P (2012) Performance of a non-tapered 3D morphing wing with integrated compliant ribs. Journal of Smart Materials and Structures 21:1–12
Reinhorn AST, Riley M, C LR, Aizawa S, Higashino M (1993) Full-scale implementation of active control. II: installation and performance. J Struct Eng 119(6):1935–1960
Reissner H (1931) Eigenspannungen und Eigenspannungsquellen. Z Angew Math Mech 11(1):1–8
Reksowardojo A, Senatore G, Smith IFC (2017) “Large and reversible shape changes as a strategy for structural adaptation”. In Proceedings of the International Associtaion for Shell and Spatial Structures, Hamburg
Reksowardojo A, Senatore G, Smith IFC (2018) “Actuator layout optimization for adaptive structures performing large shape changes.” Lecture Notes in Computer Science, vol. 10864
Rhode-Barbarigos L, Schulin C, Bel Hadj Ali N, Motro R, Smith IFC (2012) Mechanism-based approach for the deployment of a tensegrity-ring module. J Struct Eng 138(4):539–548
Rodellar J, Mañosa V, Monroy C (2002) An active tendon control scheme for cable-stayed bridges with model uncertainties and seismic excitation. Struct Control Health Monit 9(1):75–94
Santos FA, Cismaşiu C (2017) Adaptive underslung beam using shape-memory alloys for frequency-tuning. J Intell Mater Syst Struct 28(10):1260–1271
Santos FRA, Micheletti A (2015) Design and experimental testing of an adaptive shape-morphing tensegrity structure, with frequency self-tuning capabilities, using shape-memory alloys. Smart Mater Struct 24:1–10
Sartori I, Hestnes AG (2007) Energy use in the life cycle of conventional and low-energy buildings: a review article. Energ Buildings 39(3):249–257
Schneider J, Vrouwenvelder T (2017) Introduction of safety and reliability of structures, 3rd edn. International Association for Bridge and Structural Engineering, Zurich
Schnellenbach MH, Steiner D (2014) Self-tuning closed-loop fuzzy logic control algorithm for adaptive prestressed structures. Struct Eng Int 24(2):163–172
SCX (2010) “Wimbledon Centre Court Retractable Roof”, [Online]. Available: http://www.scxspecialprojects.co.uk/cache/filelibrary/73/library/fileLibrary/2011/6/Wimbledon.pdf. [Accessed 15 09 2016]
Senatore G, Duffour P, Hanna S, Labbe F, Winslow P (2011) Adaptive structures for whole life energy savings. Journal of the International Association for Shell and Spatial Structures (IASS) 52(4):233–240
Senatore G, Wang Q, Bier H, Teuffel P (2017) “The use of variable stiffness joints in adaptive structures”. In Proceedings of the International Association for Shells and Spatial Structures, Hamburg
Senatore G, Duffour P, Winslow P (2018a) Energy and cost analysis of adaptive structures: case studies. J Struct Eng ASCE 144(8):04018107. https://doi.org/10.1061/(ASCE)ST.1943-541X.0002075
Senatore G, Duffour P, Winslow P (2018b) Exploring the application domain of adaptive structures. Eng Struct 167:608–628. https://doi.org/10.1016/j.engstruct.2018.03.057
Senatore G, Duffour P, Winslow P, Wise C (2018c) Shape control and whole-life energy assessment of an "infinitely stiff" prototype adaptive structure. Smart Mater Struct 27(1):015022. https://doi.org/10.1088/1361-665X/aa8cb8
Sepulveda AE, Schmit LA Jr (1991) Optimal placement of actuators and sensors in control-augmented structural optimization. Int J Numer Methods Eng 32(6):1165–1187
Shea K, Smith IFC (1998) Intelligent structures: a new direction in structural control. In: Smith IFC (ed) Artificial Intelligence in Structural Engineering. Springer, Berlin, pp 398–410
Skelton R, Hanks B, Smith M (1992) Structure redesign for improved dynamic response. J Guid Control Dyn 15(5):1271–1278
Smith MJ, Grigoriadis KM, Skelton RE (1991) “The optimal mix of passive and active control in structures.” In American Control Conference, Boston
Sobek W (1987) “Auf pneumatisch gestützten Schalungen hergestellte Betonschalen,” (Doctoral dissertation). University of Stuttgart, Stuttgart
Sobek W, Teuffel P (2001) “Adaptive systems in architecture and structural engineering.” In Proc. SPIE 4330, smart structures and materials 2001: Smart Systems for Bridges, Structures, and Highways, Newport Beach
Soong TT (1988) State of the art review: active structural control in civil engineering. Eng Struct 10:74–84
Soong T, Cimellaro G (2009) Future directions in structural control. Struct Control Health Monit 16:7–16
Soong T, Manolis G (1987) Active structures. J Struct Eng 113:2290–2302
Straube J (2006) “Green building and sustainability.” Building Science Digests, 24
Subramaniam M, Kramer SN (1992) The inverse kinematic solution of the tetrahedron based variable geometry truss manipulator. J Mech Des 114:433–437
Teuffel P (2004) “Entwerfen Adaptiver Strukturen,” (Doctoral dissertation), University of Stuttgart - ILEK, Struttgart
Tibert G (2002) “Deployable tensegrity structures for space applications,” (Doctoral dissertation), Royal Institute of Technology, Stockholm
Torii AJ, Lopez RH, Miguel LFF (2015) Modeling of global and local stability in optimization of truss-like structures using frame elements. Struct Multidiscip Optim 51:1187–1198
Trease B, Kota S (2009) Design of adaptive and controllable compliant systems with embedded actuators and sensors. J Mech Des 131(11):111001
Utku S (1998) Theory of adaptive structures: incorporating intelligence into engineered products. CRC Press LLC, Boca Raban
Van Loan C (1985) On the method of weighting for equality-constrained least-squares problems. SIAM J Numer Anal 22(5):851–864
Veuve NSS, Smith IFC (2015) Deployment of a tensegrity footbridge. J Struct Eng 141(11):1–8
Wada B, Fanson J, Crawley E (1990) Adaptive Structures. J Intell Mater Syst Struct 1(2):157–174
Wang Q, Senatore G, Kaymenaki V, Habraken A, Teuffel P (2018) “A vibration control strategy using variable stiffness joints.” In International Association for Shell and Spatial Structures (IASS), Boston
Weilandt A (2007) “Adaptivität bei Flächentragwerken,” (Doctoral dissertation), ILEK, University of Stuttgart, Stuttgart
Xu B, Wu S, Yokoyama K (2003) Neural networks for decentralized control of cable-stayed bridge. J Bridg Eng 8:229–236
Ziegler F (2005) Computational aspects of structural shape control. Comput Struct 83:1191–1204
Acknowledgements
The authors gratefully acknowledge the Engineering and Physical Sciences Research Council (EPSRC) who provided core funding for this project through UCL Doctoral Training Centre in Urban Sustainability and Resilience (Grant EP/G037698/1) as well as Expedition Engineering, the project industrial partner who provided significant additional resources. EPFL Applied Computing and Mechanics Laboratory (IMAC) is thankfully acknowledged for their support during the review process of this article.
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible Editor: Pingfeng Wang
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A. Appendix
A. Appendix
1.1 A.1 Vector Formulation
The vector formulation given here is to extend load-path and embodied energy optimisation to account for multiple load cases. The indices i, j and k refer to the ith structural element, the jth load case and kth occurrence of the live load probability distribution respectively. Note that the kth occurrence of the load distribution corresponding to the design load is denoted with the subscript d. It is convenient to concatenate cross-section area vector α and optimal force vector \( {\boldsymbol{F}}_d^{EXT} \)(including support reactions), into a single design variable vector x:
where lb and ub lower and upper bound respectively. The non-linear equality constraints (force-equilibrium balance) Eq. 6, are rewritten as:
which in compact form becomes:
where BEXT [m × (n + nR)] is the equilibrium matrix extended to include support reactions. The matrices sT and sC are defined to account for the admissible stress in tension and compression of all the elements. For example, sTis:
sC is identical but using σC as admissible stress in compression. Both the matrices sT and sC have dimensions [n × (n + nR)], the additional nR zero columns are needed to consider the support reactions. These matrices are combined to form the complete set of linear inequality constraints (ULS) given in Eq. 7 (a) for all the load cases:
or in compact form:
where I is the (n × n) identity matrix. The non-linear stability constraints (ULSb) in Eq. 7 (b) are implemented using the Euler buckling formulation which in explicit form for the ith element is:
where Ii is the smallest second moment of area of the cross section; Ei is Young’s modulus and Ki is the effective length factor. A matrix sB identical in size to sT and sC but using the term \( 1/{\sigma}_i^B \) as the diagonal component is defined to group stability constraints for all elements. Considering all the load cases:
or in compact form:
Using Eqs. 37, 40 and 43 the load path and embodied energy optimisation problem can be written as:
1.2 A.2 On the Solution of the Load Path Optimisation (LPO) Problem
The solution to the problem formulated in Eq. 44 is the global minimum weight structure in the absence of compatibility and global instability constraints. From Eq. 36 and Eq. 39 or Eq. 42 the number of optimisation constraints and variables can be stated as:
When the number of variables is larger than or equals the number of constrains:
When Eq. 46 is satisfied, each member of the structure can be utilised at capacity for all the load cases. When Eq. 46 is satisfied with a strict inequality, the problem is under-constrained (i.e. the number of variables is bigger than the number of constraints) hence there are infinitely many solutions. The minimisation of the objective function returns the solution corresponding to the minimum weight structure. When Eq. 46 is an equality, the number of variables equals the number of constraints hence the solution of the problem stated in Eq. 44 is unique. However, in most cases the problem is over-constrained hence Eq. 46 is not satisfied. This means that ultimate limit state constraints can only be satisfied by equality for the worst load case and must be satisfied by inequalities for any other load case so that members are utilised below capacity for all the load cases except the worst one.
The degree of indeterminacy r of a general pin-jointed framework can be computed as the dimension of the null-space of the extended equilibrium matrix BEXT which is equal to the number of structural elements n minus the row-space of BEXT plus the number of support reactions:
For kinematically determinate topologies, the rank of the equilibrium matrix equals the number of degrees of freedom m, hence Eq. 47 becomes the well-known Maxwell’s equation:
Using Eq. 48 with Eq. 46 and solving for r gives:
For instance, when np = 1 then the static indeterminacy r ≥ 0; np = 2, r ≥ n/2; np = 3, r ≥ 2n/3 and so on. Intuitively this means that to achieve 100% utilisation of each element for all load cases there must be enough redundancy such that the load path can be redirected. Figure 22 shows an example of a planar structural layout achieving member utilisation at capacity for two load cases.
1.3 A.3 Actuation as Eigenstrain via the Integrated Force Method (IFM)
1.3.1 A.3.1 Single Load Case
Let us consider the generic formulation first for a single load case. In contrast to displacement methods the IFM solves directly for forces. Equilibrium equations can be written in matrix form:
where F is the internal force vector, BRED is the equilibrium matrix reduced to the unconstrained degrees for freedom (no supports), PRED is the external load reduced to the unconstrained degrees of freedom. For a statically indeterminate structure, BRED is rectangular and to solve for forces, equilibrium must be supplemented with r (n − m + nR) equations of compatibility:
where β is the element total deformation vector and C(r × n) is the null space of the equilibrium matrix:
Equation 51 can be interpreted as a statement of compatibility using virtual work with the self-stress vectors as the rows of C and no external load. The total deformation of the structural members is:
where βe is the elastic deformation due to the applied loads and β0 the non-elastic part of the total strain which is referred to as eigenstrain (thermal, plastic, creep strain or lack of fit) in some of the residual-stress literature (Reissner 1931; Mura 1991; Irschik and Ziegler 2001) but in in our case it is thought of as the length change in each element as if it was an actuator. For a linear elastic material, βe is related to the length member force vector F through the local flexibility matrix G (n × n):
where L is the element length vector and the flexibility matrix G is a diagonal matrix (for truss structures) with components:
Using Eq. 53 and Eq. 54, the compatibility conditions in Eq. 51 become:
Combining equilibrium Eq. 50 and compatibility Eq. 56 into a single matrix statement:where the load vector \( {\boldsymbol{P}}^{EIG} \), here named as the eigenstrain load vector, is defined by:
The eigenstrain load vector \( {\boldsymbol{P}}^{EIG} \)(r × 1) complements the external load vector offering a way to set directly the actuator length changes ∆L(n × 1) defined as:
Rewriting Eq. 57 in compact form and solving for forces:
where S(n × n) is the governing matrix of the IFM method and P∗(n × 1) the extended external load vector. Assuming a known actuator layout, Eq. 60 returns the compatible load path FCOMP when ∆L =0 or the optimal force F when ∆L is computed via Eq. 31.
Once the force vector F is known the displacements can be obtained as:
where J is the deformation coefficient matrix composed by the first m − nR rows of [S−1]T. The ith line of Eq. 61 can be interpreted as a statement of virtual work where the vector of total deformations β ∘ L = G ·F+ ∆L is pre-multiplied by the internal force vector in equilibrium with a single unit load associated with the ith degree of freedom (with no initial deformation) which is exactly the ith column of S−1. As for the internal forces, Eq. 61 returns the compatible displacements uCOMP when ∆L =0 or the required displacements uSLS when ∆L is computed via Eq. 31.
1.3.2 A.3.2 Multiple Load Cases
Considering multiple load cases and the generic kth occurrence of the load probability distribution, the eigenstrain load vector becomes:
or in compact form:
Optimal and compatible forces are obtained as:
Similarly, for the compatible displacements (without actuation):
or in compact form:
and for the displacements compensated using actuation:
or in compact form:
1.4 A.4 Passive Structure Optimisation
To quantify the mass savings achievable through adaptation, the adaptive solution is benchmarked against an equivalent optimised passive structure. Since the structure is considered passive here, serviceability limits on displacements must be enforced during size optimisation. Using the integrated force method, the inequality constraints for serviceability are formulated as:
where J is the deformation coefficient matrix defined in Eq. 61. Strength (ULS) and stability (ULSB) inequality constraints are the same as Eq. 40 and Eq. 43 respectively. The problem is formulated as:
where AULS and AULSB are constraint matrices identical to those defined in Eq. 40 and Eq. 43 but the first column is removed because the design variable vector (in this case α) no longer includes Fd. The problem was solved as done for Eq. 44. Convergence was achieved in 30 iterations within 700 ms on average. The solution is shown in Fig. 18. The main difference with the problem in Eq. 44 is the inequality constraint in order to limit nodal displacements to stay within a required serviceability limit state and thus it offers a way to assess how force and shape control affect the synthesis process. For this reason, this method is chosen here to benchmark the performance of the adaptive structure. In addition, this method gives results comparable with those obtained by the Modified Fully Utilised Design (Patnaik et al. 1998) and outperforms it when multiple load cases are considered.
1.5 A.5 Total Energy Optimisation (TEO) Algorithm
The source code is available from the corresponding author upon reasonable request. For up to date contact information visit http://www.gennarosenatore.com
Glossary
- actLYT (n ACTs × 1)
-
actuator layout
- \( {\boldsymbol{A}}^{EQ}\left[\left(m\cdot {n}^p\right)\times \left(n+\left(n+{n}^R\right)\cdot {n}^p\right)\right] \)
-
equilibrium constraints (block matrix)
- \( {\boldsymbol{A}}^{ULS}\left[\left(2\cdot n\cdot {n}^p\right)\times \left(n+\left(n+{n}^R\right)\cdot {n}^p\right)\right] \)
-
ULS constraints (block matrix)
- \( {\boldsymbol{A}}^{ULSb}\left[\left(n\cdot {n}^p\right)\times \left(n+\left(n+{n}^R\right)\cdot {n}^p\right)\right]\operatorname{} \)
-
non-linear ULS constraints (block matrix)
- B EXT [m × (n + n R)]
-
equilibrium matrix extended to include support reactions
- B RED [(m − n R) × n]
-
equilibrium matrix reduced to the unconstrained degrees of freedom
- β[(n · n p) × 1]
-
total strain
- β e [(n · n p) × 1]
-
elastic strain
- β 0[(n · n p) × 1]
-
eigenstrain
- \( {\overset{\sim }{\boldsymbol{\beta}}}^0\left(n\times 1\right)\operatorname{} \)
-
eigenstrain unitary length change
- C [(r · n p) × (n · n p)]
-
geometric compatibility matrix
- ∆ L [(n · n p) × 1]
-
actuator length change vector
- ∆ L ALL [(n · n p) × 1]
-
actuator length change vector (nACTs = n)
- \( {\overset{\sim }{\mathbf{\Delta }\boldsymbol{L}}}^{ALL}\left[\left(n\cdotp {n}^p\right)\times 1\right]\operatorname{} \)
-
actuator length change vector for unit length change (nACTs = n)
- ∆ L RED [(n ACTs · n p) × 1]
-
actuator length change vector reduced to the number of actuators
- ∆ F [(n · n p) × 1]
-
load-path redirection (F − FCOMP)
- ∆ u [(m · n p) × 1]
-
displacement correction (uSLS − uCOMP)
- \( \boldsymbol{\varDelta} {\boldsymbol{u}}^{CDOFs}\left[\left({n}^{CDOFs}\cdot {n}^p\right)\times 1\right] \)
-
displacement correction vector reduced to the controlled degrees of freedom
- eff F(n × n p)
-
actuator partial efficacy for strength-governed design
- Eff F(n × 1)
-
actuator global efficacy for strength-governed design
- eff u(n × n p)
-
actuator partial efficacy for stiffness-governed design
- Eff u(n × 1)
-
actuator global efficacy for stiffness-governed design
- η
-
actuator mechanical efficacy
- F [(n · n p) × 1]
-
optimal (non-compatible) force vector
- F EXT [((n + n R) · n p) × 1]
-
optimal force vector extended to include support reactions
- F Cr(n × 1)
-
critical forces (Euler buckling)
- F COMP [(n · n p) × 1]
-
compatible forces
- F COMP _ L[(n · n p) × 1]
-
compatible forces caused by live load
- F PL[(n · n p) × 1]
-
optimal forces under permanent load
- G [(n · n p) × (n · n p)]
-
flexibility matrix (block matrix)
- H(n p × 1)
-
live load hours of occurrence
- J [((m − n R) · n p) × (n · n p)]
-
IFM deformation coefficient matrix (block matrix)
- K [(m · n p) × (m · n p)]
-
stiffness matrix (block matrix)
- L (n × 1)
-
structural element lengths
- LAT
-
Load Activation Threshold
- OpE
-
operational energy
- P [(m · n p) × n d]
-
live load probability distribution
- P d[(m · n p) × 1]
-
design load
- \( {\boldsymbol{P}}^{EIG} \) [(n · n p) × 1]
-
eigenstrain load
- \( {\overset{\sim }{\boldsymbol{P}}}^{EIG}\left(n\times 1\right)\operatorname{} \)
-
eigenstrain load caused by a unitary length change
- P RED[(m − n R) × 1]
-
external load vector reduced to the unconstrained degrees of freedom
- P ∗[(r · n p) × 1]
-
IFM external load
- P ∗∗[(m · n p) × 1]
-
load activation threshold
- r
-
degree of static indeterminacy
- S [(n · n p) × (n · n p)]
-
IFM governing matrix
- S F[(n · n p) × (n · n p)]
-
actuation force sensitivity matrix
- \( {\boldsymbol{S}}^{F\mid RED}\left[\left(n\cdot {n}^p\right)\times \left({n}^{ACTs}\cdot {n}^p\right)\right] \)
-
actuation force sensitivity matrix reduced to nACTs columns
- S u[(m · n p) × (n · n p)]
-
actuation displacement sensitivity
- \( {\boldsymbol{S}}^{u\mid CDOFs}\left[\left({n}^{CDOFs}\cdot {n}^p\right)\times \left(n\cdot {n}^p\right)\right] \)
-
actuation displacement sensitivity matrix reduced to CDOFs rows
- S u∣RED[(n CDOFs ⋅ n p) × (n ACTs ⋅ n p)]
-
actuation displacement sensitivity matrix reduced to CDOFs rows and nACTs columns
- s T[n × (n + n R)]
-
strength limit in tension
- s B[n × (n + n R)]
-
strength limit in buckling
- s C[n × (n + n R)]
-
strength limit in compression
- σ C
-
material strength limit in compression
- σ B(n × 1)
-
critical stress (Euler buckling)
- σ T
-
material strength limit in tension (yield point)
- t SERVICE
-
expected service life
- u COMP[(m · n p) × 1]
-
compatible nodal displacements
- u SLS[(m · n p) × 1]
-
required nodal displacements
- ω
-
actuator working frequency
- x [(n + (n + n R) · n p) × 1]
-
design variables vector (concatenates α and FEXT)
- CDOF
-
controlled degree of freedom
- d
-
design load occurrence in the load probability distribution
- DOF
-
degree of freedom
- EE
-
embodied energy (MJ)
- ee
-
material energy intensity factor (MJ/kg)
- IFM
-
Integrated Force Method
- m
-
number of degrees of freedom
- MUT
-
Material Utilisation
- n
-
number of structural elements
- n ACTS
-
number of actuators
- n CDOFs
-
number of controlled degrees of freedom
- n d
-
number of samples in the load probability distribution
- n p
-
number of load cases
- n R
-
number of constrained degrees of freedom
- α(n × 1)
-
cross-section areas
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Senatore, G., Duffour, P. & Winslow, P. Synthesis of minimum energy adaptive structures. Struct Multidisc Optim 60, 849–877 (2019). https://doi.org/10.1007/s00158-019-02224-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-019-02224-8