1 Introduction

Topology optimization concerns the optimal distribution of material within an established domain subjected to loads and boundary conditions to satisfy one or multiple functional objectives (Bensøe 1989; Bendsøe and Sigmund 2003). For structural topology optimization, these include (but are not limited to) the minimization of local stresses, compliance, or weight. More recently, attempts have been made to minimize error functionals that drive the boundaries of the structure towards attaining target deformations. Though the choice of these design objectives abound, the optimization formulation consists of a partial differential equation constraint defining the physics of the problem and typically, limited material resources—a design cost. These constitute constraints on the problem that ensure the feasibility of the optimal design.

Inspired by the pioneering work of Lakes (1987), researchers have developed frameworks for designing global auxetic phenomena (materials with negative Poisson’s ratio) (Zhu et al. 2017; Chen et al. 2018; Ha et al. 2016; Xia and Breitkopf 2015a) as well as fabrication techniques for the derived micro-structured materials (Lee et al. 2012). Such phenomena were previously limited to small deformations but recently, simple parameterization that facilitate programmable extremal properties which remain constant over large deformations have been developed (Babaee et al. 2013; Wang et al. 2014; Clausen et al. 2015). Such materials which exhibit properties that differ from the properties of the base material are called metamaterials. These materials derive their properties from their constituent micro-architecture rather than material composition and present a means to embed anisotropy as designers aim to optimize the structure for a functional objective.

A common approach to topology optimization is the Solid Isotropic Material with Penalization (SIMP) method which implements a gradient-based algorithm to determine the value of a pseudo-density function within each element of the discretized domain (Sigmund and Maute 2013). In SIMP, a penalization parameter is employed to steer optimal material layout to a binary distribution that assigns material or void to every element. This penalization, though essential to the derivation of a physical solution, results in sub-optimal layouts (Bendsøe and Sigmund 2003; Zhu et al. 2017). Despite being the most orthodox approach to topology optimization, SIMP performs poorly for multiple-load optimization problems. The final result is heavily mesh dependent and can be subject to checker-boarding (Sigmund and Maute 2013). It has been shown that some of these computational problems are abated by incoporating regularization or sensitivity filters (Sigmund and Maute 2013; Sigmund and Petersson 1998; Xia and Breitkopf 2015a), however, the necessary penalization prevents the design for tailored properties and the optimal choice of the penalization parameter is still subject to debate and is very often problem-specific.

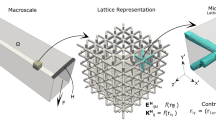
Recently, Schumacher et al. (2015) presented a robust algorithm by taking a multiscale approach to structural optimization. By discretely populating a database of microstructures with precomputed structural properties, objects were functionally designed by mapping micro-architectures to an optimization algorithm towards attaining a desired macro-scale structural behavior. This optimized tiling leveraged the precomputed library of micro-architecture families in search of best-suited neighboring cells for macro-scale structural optimization. Zhu et al. also populated a “gamut” of discrete evaluations of material properties by alternating stochastic sampling with continuous optimization and in so doing discovered families of microstructures with extremal properties (Zhu et al. 2017; Chen et al. 2018). Xia and Breitkopf solved an inverse homogenization problem by determining the best 2-D micro-architecture for a prescribed deformation, thereby populating a strain energy density property space (Xia and Breitkopf 2015b). It yielded an approximated constitutive model suitable for only compliance problems. These works aimed to develop metamaterials useful for macroscale functional grading. In this work, inspiration is taken from these recent works of Schumacher et al. (2015), Zhu et al. (2017), and Xia and Breitkopf (2015b). A pseudo density function is not employed as the control variable. Rather, a sequential multiscale approach (Engquist et al. 2005) is adopted to derive a more robust optimization algorithm by implementing a meta-model that defines mechanical properties as functions of small-scale design parameters. A lattice-based small-scale model is developed, parameterized by the normalized radii of its structural members so that it permits a microstructure’s mechanical property to be described as a function of the microscale parameters. A direct consequence of the approach is that local intermediate material property values correspond to physically derivable microstructure and material distribution can be precisely tailored for optimal structural characteristics. Herein, the development of a microscale model is described. By permuting the value of its parameters over several levels and carrying out small-scale deformation analyses as well as homogenization based on the heterogeneous multiscale method (Weinan et al. 2007), a framework is derived for populating discrete property spaces. Response models are then generated to approximate the property spaces as continuous functions. Finally, the generated response surface models are integrated into large-scale optimization algorithms to tailor mechanical properties of structures.

2 Overview

The objective of the designed framework is to enable precise functional grading of materials within structures by deploying a multiscale method over a sequence of two computational phases. The first phase constitutes the discrete evaluation of macroscale material properties in the space of small-scale parameters. The second phase constitutes using a structural optimization algorithm to achieve predefined functional objectives using the small-scale parameters of the first phase as control variables. Both scales are coupled by numerical coarsening (computational homogenization) of localized small-scale properties to derive average macroscopic properties represented by response surface models in the optimization formulations. The work by Schumacher et al., Zhu et al., and Xia et al. also feature discretely populated property spaces of micro-architectures (Schumacher et al. 2015; Zhu et al. 2017; Xia and Breitkopf 2015b). By property space, we refer to the extent covered by all achievable discrete evaluations of the material properties associated with the microscale parameterization implemented. This work differs from these recent works in two major ways: rather than optimize the topological structure of voxelized micro-cells for predefined bulk material properties and generating a library of micro-architectures for discrete tiling on the macroscale, a micro-architecture is selected of which its parameterization will ensure connectivity of adjacent microstructures and for which its geometry changes smoothly with its parameters. The property space is populated by all permutations of the microscale model parameters so that we are not limited to isotropic, orthotropic, and cubic material properties. Secondly, by generating metamodels of the discrete property spaces, a means to execute macroscale functional grading in the space of small-scale parameters is presented.

The description of the derived framework is initiated by reference to these background assumptions. Considerations have been limited to three-dimensional linear elastic theory across both scales so small deformations are assumed. The general relationship between the cauchy stress tensor, σij and strain tensor, 𝜖kl at every material point in the domain is given by

$$ \boldsymbol{\sigma}_{ij} = \boldsymbol{E}_{ijkl}\boldsymbol{\epsilon}_{kl} $$
(1)

where Eijkl = Eklij = Ejikl = Eijlk is the elasticity tensor with 21 unique components in the most general case of anisotropy for i, j, k, l = 1, 2, 3. Strain-displacement relations are given by

$$ \boldsymbol{\epsilon}_{ij} = \dfrac{1}{2}\left( \dfrac{\partial \boldsymbol{u}_{i}}{\partial \boldsymbol{x_{j}}} + \dfrac{\partial \boldsymbol{u}_{j}}{\partial \boldsymbol{x_{i}}}\right) $$
(2)

Equations (1) and (2) constitute the material law governing our problem formulations across both scales. We assume static equilibrium mechanics so that

$$ \boldsymbol{\sigma}_{ij,j} + \boldsymbol{F}_{i} = 0 $$
(3)

for relevant formulations where Fi is the sum of all external forces acting on design domain, Ω.

3 Methodology

3.1 Microscale model

On the microscale, a material property model is developed which is parameterized by the normalized radii of members of a lattice system so that the structural properties of a periodic unit cell defined at this scale is a function of the parameters of the enclosed lattice system. The lattice structure is defined within a unit cube by the normalized radii of four members connecting its corner diagonal vertices and three members connecting the face-center vertices of opposite faces. Figure 1 illustrates a typical micro-structure with its vector of normalized radii parameters, r as well as its orientation in three-dimensional space. This orientation is preserved for subsequent large scale analyses.

Fig. 1
figure 1

Microstructure parameterization

Full size image

The microscale model is initialized by defining a unit cube geometry and discretizing into structured eight-noded hexahedral elements. This regular discretization facilitates the implementation of periodic boundary conditions on opposite faces of the unit cell as described in Section 3.3. To avoid the challenges associated with remeshing complex geometries, the mesh is kept fixed for all micro-architecture simulations. Micro-architectures are defined on this mesh by assigning material properties spatially within the domain of the unit cell according to their unique vector of radii parameters.

Consider the development of a model for the micro-architecture with r = (0,0,0,0,0.2733,0,0) as shown in Fig. 2a and b. Each element in the discretization is assigned a material property, E, given as

$$ E = n_{f} E_{s} + (1-n_{f}) E_{v} $$
(4)

according to the position of its eight nodes, where Es = 209 GPa is the Young’s modulus of the base material, Ev = 10− 7 GPa is the Young’s modulus for void and nf is the fraction of the eight nodes that exist within the subdomain of the member being modelled. The subdomain of each member is defined by the radial distance about the centroidal axis of the member. Figure 2a and b demonstrate this subdomain for member 5. The perpendicular distance of each element’s node to the centroidal axis of the modelled member is evaluated as

$$ d = \dfrac{|(\mathbf{b} - \mathbf{a})\times(\mathbf{a} - \mathbf{c})|}{|\mathbf{b} - \mathbf{a}|} $$
(5)

where a and b are the position vectors of the nodes at both ends of the centroid of the modelled member and c is the position vector for the node. If the node satisfies the relation

$$ d \le r_{\gamma} \qquad \gamma = 1, 2, ..., 7 $$
(6)

in which rγ is the normalized radius of the γ-th member, then that node belongs to the subdomain which defines the γ-th member. For the micro-architecture modelled in the illustration of Fig. 2a and b for member 5, a = (0,0.5,0.5), b = (1,0.5,0.5) and r5 = 0.2733. From Fig. 2a, all nodes of element 1 satisfy (6) so that nf = 1 and E = Es. All nodes of element 4 lie outside the subdomain of member 5 so that nf = 0 and E = Ev. However, elements 2 and 3 have nf = 0.75 and 0.25 with E = 156.75 GPa and 52.25 GPa respectively. Figure 2b shows element 6 having nf = 0.5 and E = 104.5 GPa. Equation (5) is the perpendicular distance of a point c from a line ab in three-dimensional space. Given the vector of parameters, r = (r1,r2,r3,r4,r5,r6,r7), each micro-architecture is modelled by assigning material properties to the elements of the subdomains of each member following the described procedure. Elements with all nodes outside all member subdomains are modelled as voids.

Fig. 2
figure 2

Material assignment illustration

Full size image

The periodicity of unit cells on the developed model is considered by material assignment on elements with nodes that satisfy (6) in the unit cube domain for the translated centroidal axes of the diagonal members 1 to 4 in the i-th direction, where i = 1, 2, and 3 represents x, y, and z-direction respectively. The new position vector of end vertices of these diagonal centroidal axes, for translation in the i-th direction, \(\text {\textbf {a}}_{i}^{\prime }\) and \(\text {\textbf {b}}_{i}^{\prime }\) are given as

$$\begin{array}{@{}rcl@{}} \text{\textbf{a}}_{1}^{\prime} = (a_{x} \pm L_{x} \text{, }a_{y}\text{, }a_{z}) \\ \text{\textbf{a}}_{2}^{\prime} = (a_{x} \text{, }a_{y} \pm L_{y} \text{, }a_{z}) \\ \text{\textbf{a}}_{3}^{\prime} = (a_{x} \text{, }a_{y} \text{, }a_{z} \pm L_{z}) \\ \text{\textbf{b}}_{1}^{\prime} = (b_{x} \pm L_{x} \text{, }b_{y}\text{, }b_{z}) \\ \text{\textbf{b}}_{2}^{\prime} = (b_{x} \text{, }b_{y} \pm L_{y} \text{, }b_{z}) \\ \text{\textbf{b}}_{3}^{\prime} = (b_{x} \text{, }b_{y} \text{, }b_{z} \pm L_{z}) \end{array} $$
(7)

where Lx = Ly = Lz = 1 for a unit cell. Provided a sufficient scale separation exists across both scales, the implemented parameterization captures global periodicity for an infinite assembly of each micro-architecture so that structural behavior of a unit cell is fully representative of the bulk material behavior. Sufficient scale separation is an assumption of heterogeneous multiscale methods (Weinan et al. 2007) that validates the homogenization theory as implemented. The parameterization also proffers smoothly changing geometry for slowly changing lattice parameters in the large-scale optimization hence ensuring connectivity between adjacent unit cells. Its degrees of freedom can be independently perturbed to control anisotropic properties. These properties of the model have inspired the choice of the lattice system as described. Ultimately, these lattice member radii constitute a vector of design parameters that fully define the average mechanical properties of each micro-architecture derived in the large-scale optimization. Figure 3 demonstrates the concept of spatially varied micro-architectures towards meeting macroscopic functional objectives in structures. It should be noted that any unit cell parameterization that is periodic with degrees of freedom that smoothly vary its properties along with its geometry will be suitable for the derived framework. However, the microstructure parameterization implemented has been chosen because its multiple geometry-based parameters also offer full control over all components of anisotropy.

Fig. 3
figure 3

Lattice-based micro-architectures

Full size image

3.2 Micro-architecture symmetry

By perturbing each component of the vector of parameters, a means is derived to generate lattice-based microstructure of varied mechanical properties. A seven-dimensional property space is populated at discrete points by all permutations achievable by perturbing each component of the vector of parameters over seven equally spaced levels. For ease of reference, each micro-structure is identified by the level of its seven parameters. By way of illustration, the first micro-structure derived corresponds to an empty unit cell with r = (1,1,1,1,1,1,1) and the last corresponds to a fully dense unit cell with r = (7,7,7,7,7,7,7). These levels correspond directly to the radii of the lattice members. Property spaces are populated by the properties of all micro-structure between and including these extremes. Implementing a full factorial design of experiments (DOE) would require the simulation of 77 evaluation points in the property space. To reduce the number of simulations required and the consequent prohibitive computational expense, the existence of rotation and reflection symmetries is leveraged and an algorithm which sorts and classifies parent micro-architectures with their symmetry geometries is developed. All symmetry geometry properties are derivable from parent micro-architecture properties by the conventional mathematical rotation and reflection operations. These are 90∘ rotations about x-, y-, and z-axes and reflections across the y-z, x-z, and x-y planes. By applying these axes-transformation operations and all possible combinations of them to the unit cube, all unique symmetries associated with any given base micro-architecture are derived. Figure 4a presents a non-exhaustive list of symmetry geometries of a parent micro-architecture by way of illustration. By taking advantage of symmetries, simulations required were reduced by over an order of magnitude yet, the property spaces are populated by a full factorial DOE. Figure 4b presents significant reduction in simulation points associated with symmetry considerations when each lattice parameter is perturbed over n-levels. In this work, symmetry considerations reduce a full factorial 823,543 evaluation point requirement to 40,817.

Fig. 4
figure 4

Effect of symmetry considerations on number of simulations required

Full size image

3.3 Periodic boundary conditions

To determine microstructure mechanical properties, periodic boundary conditions must be prescribed to the unit cell. These are displacement constraint equations applied to boundary nodes on opposite faces of the unit cube (Xia et al. 2006). Periodic boundary conditions (PBCs) ensure that the boundaries of the unit cell do not overlap when a periodic macro-scale structure composed of the unit cells deforms. Provided the microscale model captures geometry periodicity and PBC is implemented, the structural response of a unit cell will be representative of the periodic material they form. Each lattice system enclosed by a unit cell represents a metamaterial with its own unique structural properties. If the assembly of such a micro-architecture is realizable so that micro-architectures of differing properties can be assembled with ensured connectivity, then a framework for designing structures with anisotropic properties at the material point is derived.

Suquet (1987) presented a displacement field for periodic structures given as

$$ u_{i}(x) = \bar{\epsilon}_{ik}x_{k} + u^{*}_{i}(x) $$
(8)

where \(\bar {\epsilon }_{ik}\) is the average strain vector, xk is the position vector within the unit cell, and \(u^{*}_{i}\) is a periodic function across adjacent unit cells that accounts for spatially varying material property within the cells. For homogeneous material, \(u^{*}_{i} = 0\) so that (8) becomes linear. The periodic function, \(u^{*}_{i} \), is not explicitly known but its value is equal at position xk in every unit cell to satisfy periodicity. By considering the difference of displacements at the same location within two adjacent unit cells, we eliminate \(u^{*}_{i}\) and derive the useful displacement constraint equations generally given as

$$ u^{j+}_{i} - u^{j-}_{i} = \bar{\epsilon}_{ik}{\varDelta} {x^{j}_{k}} $$
(9)

where j + and j − represent a pair of opposite faces of the cell. For unit cells, \({\varDelta } {x^{j}_{k}} = 1\). By prescribing constant average strain, \(\bar {\epsilon }_{ik}\), on a discretized unit cell in any direction-i on face-k, we derive a means to perform direct or shear deformation on the unit cell and this forms the basis for subsequent deformation analyses.

3.4 Strain deformation analyses

A unit cube was defined and its domain was discretized into \({n_{e}^{3}}\) elements using eight-noded linear bricks, where ne is the number of elements along the edge of the discretized unit cube. Following mesh studies based on the convergence of stiffness tensor components of an arbitrarily chosen micro-architecture, the mesh density was chosen so that ne = 60. Nodal material assignment was made by prescribing Young’s modulus so as to model a micro-architecture in continuum as described in Section 3.1. Regions of material were assigned material properties, Es = 209 GPa, Poisson’s ratio, ν = 0.3. Regions of void were assigned Ev = 1 × 10− 7 GPa and ν = 0.3. Periodic boundary conditions were applied as described in Section 3.3. The average properties of the micro-architectures were computed as follows.

Strain deformation analyses consisted of three direct strains and three shear strains. The unit cell was strained sequentially in the x-, y-, and z-axes as well as strained in shear across the y-z, x-z, and x-y planes. The result yielded homogenized stresses and strain fields. Volume averaging was the homogenization technique applied to evaluate effective stresses and strains and by implementing the constitutive equations in three-dimensional real space, the stiffness tensor was derived for each simulated micro-architecture. Kharevych et al. (2009) presented a detailed description of numerical coarsening (volume homogenization) as applied in this paper. The commercial finite element solver, Abaqus 6.14, was deployed for all small-scale strain deformation analyses. Abaqus is a suite of software applications for finite element analyses with modeling, visualization, and scripting features. By scripting, small-scale analyses were automated to populate the property spaces with permutations of lattice parameters, less the permutations achievable by leveraging existing symmetries.

3.5 Response surface model

By perturbing the seven components of the vector of parameters over seven equally spaced levels and each time determining the mechanical property of derived micro-architectures alongside all symmetries, an efficient method is developed to populate the property spaces. The property of each micro-architecture is fully defined by the symmetric stiffness tensor. In three-dimensional real space, the stiffness tensor consists of 21 unique terms in the most general case of anisotropy. Existing symmetries in isotropic, orthotropic and cubic microstructures result in more sparse stiffness tensors. The full factorial DOE implemented implies that property tensors were derived for all achievable permutations of the micro-scale parameters, including those for isotropic, orthotropic, and cubic micro-architectures. As a consequence, many micro-architectures possess fully anisotropic properties with fully dense property tensors so that we cover a wide range in the space of elastic material parameters. A property space was populated for each unique component of the property tensor. A full factorial DOE was evaluated for all 21 unique terms of the elasticity tensor. These discrete evaluations lie in a seven-dimensional parameter space so that each tensor component can be evaluated given the seven components of the micro-architecture vector of parameters. The mechanical property of every simulated micro-architecture (along with its symmetry geometries) is fully defined by its lattice parameters and corresponds to an evaluated point in the material parameter space of each tensor component. Figure 5 illustrates the evaluation points for some simulated micro-architectures in a hyper-plane through the E11–property space for visualization. There are 20 other such property spaces corresponding to the remaining components of the stiffness matrix and the property of each simulated micro-architecture can be referenced to a specific evaluation point in these property spaces.

Fig. 5
figure 5

Hyper-plane through seven-dimensional property space

Full size image

The objective was to formulate functional grading in the space of small-scale lattice parameters. Consequently, response surface models were generated to represent the discrete property evaluations. These metamodels are continuous functions of our small-scale model and present a means to couple both scales. The development of these metamodels consist of local approximations of discrete points in a least squares sense by a function through the minimization of an error functional,

$$D = {\varSigma}_{i}||f(\mathbf{x}_{i}) - f_{i}||^{2}$$

where f(xi) is the defined function, fi is the discrete value of the property space at valuation point xi, for i ∈ [1...N] and N = 823,543 full factorial valuation points in the property space. Details of the least square polynomial formulation is well documented in literature (Nealen 2004). Each metamodel implemented in this work belongs to the space of polynomials of the 6th degree in seven spatial dimensions with number of terms, \(k = \frac {(\alpha +\beta )!}{\alpha !\beta !}\), where α = 6 and β = 7. Polynomials of the 6th order were chosen because they generated fits with R2 > 0.95 with polynomials of higher orders resulting in overfitting. Figure 6 shows typical hyper-slices of these seven-dimensional metamodels for some components of the stiffness tensors. All metamodels for mechanical properties yielded R2 ≥ 0.9545 with off-diagonal components of the stiffness tensor giving the least accurate fits (Table 1).

Fig. 6
figure 6

Hyper-planes through typical seven-dimensional meta-models. Meta-models are 6th-order polynomial fits (mesh) to discrete property evaluations (scatter points)

Full size image
Table 1 Table of R2 values
Full size table

3.6 Large-scale optimization formulation

Equipped with metamodels that evaluate large-scale (homogenized) properties given small-scale parameters, functional grading of materials was formulated in the space of the precomputed material properties. In a classic SIMP approach, the design domain is discretized and each cell is assigned an artificial density function as a measure of local stiffness to derive the optimal distribution of material. Such optimization formulations are constrained by a partial differential equation that describes the physics of the problem as well as a limit to available material resource. Here, a pseudo-density function is not employed. Rather, the optimization problem is formulated in the space of the continuous representation of material properties enabled by the meta-models. This allows the change of local properties at the scale of the lattice micro-architectures. Upon discretizing the macroscale domain into m elements, spatially varying material property functions of the lattice parameters are defined. Optimization control variables are given as,

$$\boldsymbol{r}_{\eta\gamma} = [r_{\eta1},r_{\eta2},r_{\eta3},r_{\eta4},r_{\eta5},r_{\eta6},r_{\eta7}]$$

for η =1, 2, ...m so that there are 7m control variables. Material property is changed locally by freely perturbing the values of rηγ for γ = 1, 2, ... 7 so that each discrete cell of the large-scale problem contains a seven-dimensional material parameter. In effect, a means is devised to attain anisotropy within the domain with ensured connectivity between the micro-architectures that build up the resulting structure. Micro-architectures are not mapped directly to the solution derived by the optimization algorithm (Schumacher et al. 2015; Zhu et al. 2017). Rather, micro-architectures evolve within the cells as the distribution of each lattice parameter value is determined, a consequence of using the small-scale parameters as control variables. Provided sufficient scale separation exists between our lattice scale and the scale of the problem, the framework is capable of representing the slowly changing material properties of the large scale with slowly changing micro-architecture, representing all intermediate properties efficiently. The framework derived enables the design of tailored structural properties. The precision and process flexibility attributed to additive manufacturing implies that such optimized structures are physically derivable with minimal error between the optimized solution and physical object. The formulation for the structural optimization is written as

$$\begin{array}{@{}rcl@{}} &\text{minimize:}& \quad\textbf{J}(u(r_{\eta\gamma}), r_{\eta\gamma} ) \\ &\text{subject to:}& \quad \textbf{F}(u(r_{\eta\gamma}), r_{\eta\gamma}) = 0\\ && \quad V(r_{\eta\gamma}) \leq V_{D}\\ &&\quad r_{min} \leq r_{\eta\gamma} \leq r_{max} \end{array} $$
(10)

where J is the real-valued objective functional of choice that depends on the solution of a partial differential equation that defines the physics of the problem and the vector of lattice parameters. F = 0 stipulates that u satisfies the relevant equilibrium constraint. The cost constraint, V ≤ VD puts an upper bound on the material available to the optimal design and each control parameter, rηγ has local bound constraints. The lower bound, rmin, constitutes a manufacturing constraint on the smallest permissible thickness of the base material which exhibits the documented structural behavior. The upper bound, rmax, is determined by the highest level of perturbation of the parameters for the micro-architecture to attain a fully dense block.

To illustrate the robustness of the derived formulation, a common optimization problem in structural mechanics was attempted: compliance minimization. The optimization domain was defined and discretized, prescribing material property matrix components as spatially varying functions of the vector of lattice parameters. External forces and boundary conditions were specified. A global integral constraint, VD was defined as well as a Jacobian matrix of the sensitivity of the integral constraint with respect to the vector of control parameters. Finally, the objective functional to be minimized was defined as

$$ J = \mathbf{u}^{T} \mathbf{E}(\boldsymbol{r}_{\eta\gamma}) \mathbf{u} $$
(11)

where u is the solution to the static linear elastic equation and E(rηγ) is the local stiffness matrix in the problem domain. Sensitivities were obtained by the adjoint method using dolfin-adjoint (Farrell et al. 2013). Dolfin-adjoint is a python library in FEniCS (Alnaes et al. 2015; Logg et al. 2012), the open source finite element solver implemented for the large-scale optimization algorithms. Equation (10) is solved with the robust gradient-based numerical optimizer, Ipopt (Wächter and Biegler 2005). The large-scale optimization is terminated when an iterate satisfies the conditions of a first-order Karush-Kuhn-Tucker (KKT) point, indicating that the solution at the current point is a strict local minimizer of the constrained optimization problem.

3.7 Computational implementation

Each micro-architecture is enclosed within a three-dimensional unit cell. The microscale simulation comprises a pre-processing step which defines material assignment within the unit cell given its vector of radii parameters, a processing script which simulates six strain deformation analyses and a post-processing script which executes volume averaged homogenization and computes the stiffness tensor components of the given micro-architecture. Finally, axis transformation operations are implemented to determine the stiffness tensor components of all symmetry geometries associated with the given micro-architecture. On an Intel(R) Core(TM) i7-5600U CPU @ 2.60 GHz system with two processors, each microscale simulation takes 6 min or 28 min on a mesh density of 283 or 603 respectively. It is important to note that each simulation yields in the range of 1 to 24 unique micro-architectures, depending on the number of existing symmetries associated with the given micro-architecture. As a consequence, only 40,817 small scale simulations were run to yield a full factorial 823,543 micro-architecture property evaluation points, which corresponds to a 95% reduction in number of simulations. Each iteration of the large-scale optimization takes 3.8 mins for a 24,000 element domain on a single processor. The optimization usually converged in around 100 iterations.

4 Results and discussion

4.1 Cantilever test case

Consider the cantilever beam with geometrical dimensions L × D × W having the values shown in Fig. 7. A compliance minimization problem was set up as described in the optimization formulation of Section 3.6. The aim was to minimize the compliance/strain energy of the cantilever beam subject to a constraint on the availability of material so that VD ≤ 0.3. The cantilever beam was constrained to the linear elastic partial differential equation and loaded by a uniformly distributed force, F = 1000 N m− 2 on its top surface. Bound constraints, rmin = 0.068 and rmax = 0.38, were applied to the parameter space so that the optimization solution remained confined to the precomputed property space. Sensitivities were verified by Taylor remainder convergence tests. The optimal solution of the compliance minimization problem are displayed in Figs. 8 and 9 for the diagonal and face members respectively. The orientation of the cantilever beam corresponds to the orientation of the micro-architecture in Fig. 1. A visualization threshold, Vz, has been set at a normalized radius value of 0.25 so that the solid regions in the solutions depict rηγ ≥ 0.25. The pale blue regions depict regions where rmin < rηγ < 0.25. All other regions represent rηγ = rmin. Figure 10a shows the optimal solution for all the control variables at Vz = 0.25. The optimization convergence plot can be seen in Fig. 10b.

Fig. 7
figure 7

Compliance minimization problem definition

Full size image
Fig. 8
figure 8

Optimal distribution of diagonal lattice parameters

Full size image
Fig. 9
figure 9

Optimal distribution of face lattice parameters

Full size image
Fig. 10
figure 10

Lattice-based compliance minimization

Full size image

Figure 8a, b, c, and d show the optimal normalized radius distribution for the diagonal members at Vz = 0.25. These diagonal members dominate the cantilever beam near the root and at the top and bottom of the domain boundaries, where maximum stresses are anticipated. Away from the Dirichlet boundary condition and in the direction of the beam axis, members 5 and 6 become more dominant. Member 5 (Fig. 9a), with an orientation corresponding to the axis of the beam, develops an I-beam geometry. I-beam sections possess high second moment of area due to increased offset sectional area from the neutral axis and hence offer minimum deflections in cantilevers for given load and boundary conditions. Member 6 (Fig. 9b) provides support for the defined load and reacts to shear as illustrated by its pale blue regions. Member 7 (Fig. 9c) does not contribute significantly to maximizing the stiffness of the beam as a consequence of its orientation and is hence absent from the optimal solution at the applied visualization threshold.

Principal stress vectors (Fig. 11) show the magnitude and directions of the principal stresses associated with the load case. These load paths have been determined by determining the eigenvalues and eigenvectors of the stress tensors throughout the discretized large-scale domain. The principal stress magnitudes have been thresholded so that Vz = 2000 N m− 2 to facilitate visualization of high principal stresses. Figure 12 superimposes these principal stress flow plots with the optimal solutions obtained. The stress flow directions and magnitudes correlate with the optimization result so that the dominant regions within the control parameter space correspond with dominant principal stresses within the domain. Load paths demonstrate stress propagation from the loaded top surface to the Dirichlet boundary constraints through optimal structural layout. The added degrees of freedom associated with the multi-dimensional parameter space along with their sensitivities allows the derived algorithm to efficiently search the parameter space in search of optimality by deciding the distribution and dominance of intervening lattice members. It should be emphasized here that no penalization parameter was required to favor extreme values of the control parameters (as is the case with conventional SIMP implementation) since intermediate properties all correspond to a manufacturable physical structure. A consequence is that visualization of the optimal results can be complex and must be viewed over several thresholds to capture the properties of the radii distributions. Figure 13 shows the optimal solution for the cantilever problem above over six threshold levels. It is important to appreciate the precise functional grading capabilities afforded by the derived approach. All intermediate properties are precisely represented by the micro-architecture derived at each point in the design domain.

Fig. 11
figure 11

Maximum and minimum principal stress plots for cantilever beam, Vz = 2000 N m− 2

Full size image
Fig. 12
figure 12

Stress flow plots through dominant members at normalized radius threshold, 0.25

Full size image
Fig. 13
figure 13

Optimization result visualization thresholding

Full size image

4.2 Bench marking against SIMP

The optimization result obtained by the lattice-based (LB) approach was compared with results obtained by SIMP, for penalization parameter, p = 1 (SIMP1) and p = 3 (SIMP3), for the same load case. Figure 14 shows a plot of minimum compliance vs. design volume fraction, for all three approaches. For the same volume fraction, LB attained a stiffer solution than the classical SIMP3, with SIMP1 remaining as the theoretical best but non-physical solution. At Jc = 2.703 × 10− 3 m2/N, LB showed ≈ 22.2% reduction in mass compared to SIMP3. The implementation of the LB approach to multi-load cases promises to show proportionally improved solutions. More importantly, the LB approach can be used for precise functional grading of structural properties.

Fig. 14
figure 14

Bench marking against SIMP

Full size image

5 Conclusion

A lattice-based functional grading tool has been derived by applying multi-scale methods. A microscale model was developed and parameterized to enable discrete evaluations of macroscale properties of achievable micro-architectures. Metamodels were generated to represent the discrete property evaluations. An optimization problem was formulated in the seven-dimensional property space so that small-scale parameters were used as control variables of the macro-scale optimization problem. It is shown that the result obtained for the classical compliance problem using the derived LB approach is better than the penalized SIMP implementation: with capability for precise functional grading of structural properties as well as ensured connectivity between adjacent micro-architectures. Intermediate properties correspond to a physical structure so that the LB approach features no requirement for penalization. The method shows great promise for morphing shape-change objectives as well as multi-load compliance problems.