1 Introduction

The lateral restraint system is an indispensable part of any building. This is particularly true in a tall building structure, where the requirements for lateral strength and stiffness can govern the layout of the whole building. Consequently, the design of efficient bracing layouts to resist lateral wind loading is an area of active interest to structural engineers.

Optimization of bracing systems has often focussed on geometry or size optimization. For example, Moon et al. (2007) analysed diagrid bracing systems, using the angles between bracing members as parameters which were varied to optimize the lateral stiffness of the structure. Bobby et al. (2013) and Lee and Tovar (2014) optimized an outrigger bracing system by using binary variables to represent the existence of belt trusses; Sala and Candiani (2014) used the size optimization technique proposed by Baker (1990) to identify the optimal section sizes of a fixed topology bracing system whilst Tangaramvong and Tin-Loi (2015) used a discrete approach to optimize the bracing topology using a sparsely populated ground structure (only members connecting neighbouring nodes were considered). Others have used continuum optimization techniques (e.g. Liang et al. 2000; Allahdadian et al. 2012; Stromberg et al. 2012; Kingman et al. 2015) or genetic algorithms (e.g. Baldock 2007; Yazdi and Sulong 2011; Richardson et al. 2013). However, to date classical layout optimization methods appear not to have been used to benchmark the efficiency of commonly used bracing systems.

The mathematical basis for the problem of finding the structural layout consuming the least volume of material was developed by Michell (1904). Whilst Michell’s analytical approach provides a strong foundation for the field, it is seldom applied to practical structural design applications, partly because of the difficulty of identifying the optimal structure for specified loading and support conditions. However, the approach readily lends itself to numerical implementation, where the optimal layouts of discrete members are found from a ‘ground structure’, comprising all possible interconnections of discrete node points within a design space. Using linear programming (LP) techniques numerical layout optimization results can be found which closely approximate classical Michell forms for any given problem (Dorn et al. 1964; Hemp 1973); more recently the computational efficiency of this method was improved by Gilbert and Tyas (2003). Here, numerical layout optimization will be used as a tool to investigate optimal bracing layouts for various different scenarios.

Stromberg et al. (2012) and Liang et al. (2000) have considered the optimization of bracing systems within a beam/column frame represented by discrete beam members. Stromberg et al. (2012) optimized the bracing topology with different type connections between continuum and discrete beam elements and the effect of column stiffness on the optimal bracing layout was also considered. Liang et al. (2000) assumed that the beam/column members sized in a gravity load analysis would also be adequate for lateral load cases, and optimized the bracing topology for several bay aspect ratios. This raises the question: if the beams and columns designed for gravity loads have sufficient reserves of strength, such that they do not need to be resized to act as part of the lateral stability system, can general rules governing the optimal layout of bracing members be found? This study focuses on optimizing the layout of bracing elements within a pre-existing frame, where the members have already been designed to carry gravity loading, and are assumed to have the requisite additional reserves of strength to support lateral loads; other scenarios will be the subject of future research.

The paper is organized as follows: Section 2 outlines the assumptions made with respect to loading and pre-existing frame performance; Section 3 describes the problem types considered and the numerical layout optimization method employed to obtain initial solutions; Sections 4 and 5 consider respectively single bay and multibay / storey building types, with exact analytical solutions derived for key problem types; finally conclusions from the study are drawn and the direction of future research is outlined in Section 6.

2 Assumptions

For the design of steel framed buildings, British Standard 5950-1:2000 suggests the following load combinations:

$$ p_{1}:1.4{G}_{\text{k}}+ 1.6{Q}_{\text{k}} $$
(1.a)
$$ p_{2}: 1.0{G}_{\text{k}}+ 1.2{Q}_{\text{k}}+ 1.2{W}_{\text{k}} $$
(1.b)
$$ p_{3}: 1.0{G}_{\text{k}}+ 1.2{Q}_{\text{k}}-1.2{W}_{\text{k}} $$
(1.c)

where Gk is the characteristic permanent load, Qk is the characteristic imposed load and Wk is the characteristic wind load.

Here, for simplicity the concept of Notional Horizontal Load (NHL) (a small lateral load which is applied as part of the main gravity load case (1.a)) is ignored, and it is assumed that the bracing design is dominated by the wind load cases, (1.b) and (1.c).

From (1.a) it is clear that the maximum partial factor multipliers for gravity loads exist in load case (1.a), and that the gravity load is decreased in load cases (1.b) and (1.c). Therefore, for the purpose of the studies herein, the following assumptions have been made:

  • Assumption 1: The loads generated in the columns in load case (1.b) and (1.c) are always less than those resulting from load case (1.a).

  • Assumption 2: Vertical gravity loads are only carried by the columns in all load cases.

  • Assumption 3: The sizes of pre-existing horizontal members (i.e. floor beams and/or slabs) are dominated by the gravity load case (1.a), and the axial loads induced in them by lateral load cases (1.b) and (1.c) are small in comparison.

Assumption 1 means that the sizes of the columns are not determined by the lateral load cases, and thus that the columns may be assumed to be rigid with infinite strength when designing for lateral loads (i.e. accumulated reactions from bracing elements can be carried). Assumption 2 is widely adopted in design practice, where columns are often first designed to resist gravity loads, with the design of bracing members to resist lateral loads coming later. Together these two assumptions mean that the vertical loads in load combination (1.a) will not affect the optimal layout of the bracing system, and the wind load (i.e. 1.5Wk) is governing. Assumption 3 means that the structural members forming the floors effectively possess infinite reserves of strength, and can distribute applied lateral loads to either side of the frame. With these three assumptions, the design of a bracing system for a frame already designed to carry gravity loads is considered, where the bracing need only resist lateral loads. This effectively replicates one step in the traditional design procedure for buildings (e.g. Brown et al. 2009 suggest that the sizes of beams and columns are first determined by considering gravity loads, with the sizes of bracing members then determined by considering lateral loads). A similar approach has also been used in previous bracing topology optimization studies; for example Mijar et al. (1998), Liang et al. (2000), and Stromberg et al. (2012) take (or design) a column-beam frame capable of carrying gravity loads and then, considering only lateral loads, carry out bracing topology optimization.

3 Problem specification

3.1 Cases considered

Based on the assumptions made in Section 2, the general problem to be addressed here distils down to the simple problem shown in Fig. 1. This is a single storey frame bay subjected to a unit horizontal load P at the left top corner, with fixed pin supports at the bottom corners. For sake of simplicity the connections between members are treated as pin joints. Edge column and beam members are assumed to be pre-existing members which have infinite reserves of strength when functioning as part of a braced frame. Note that this can be viewed as removing the bending moment effect Ph from the problem and reducing it to one of finding the optimal bracing to resist the load in pure shear (e.g. see Stromberg et al. 2012). It is also worth noting that Rozvany et al. (2006) studied the effect of including fully and partially stressed pre-existing members in an optimization by fixing member cross-sectional areas. In this numerical study, in order to account for the possibility that pre-existing members can also disappear from the final structure (i.e. have zero force), pre-existing members are treated as being composed of material of infinite strength.

Fig. 1
figure 1

Bracing design case with pre-existing members around the edge of the bay, pinned supports at the bottom corners and a horizontal load at the top left corner. A ‘ground structure’ comprising interconnecting members (2 × 4 nodal division discretization shown, not including all connections for sake of clarity)

Full size image

Two load cases involving horizontal loads of equal magnitude applied in opposite directions are used to replicate real-world conditions, and to also ensure the resulting layout is symmetric. According to the superposition theory proposed by Hemp (1973), a two load case solution can be obtained by superposing the results from two design problems involving single load cases. Therefore, all design problems considered herein can be treated as single load case problems.

Three generic types of bracing systems are considered for various different aspect ratios (h : b):

  • Case 1: Tension only bracing. This is frequently employed in practice as it obviates the need to take action to ensure compression members do not buckle. Numerically, this is implemented by making the compression stress capacity of bracing members infinitesimally small.

  • Case 2: Bracing connected only at corners. Both tension and compression members are allowed to be present in the bracing system and the maximum tension stress is equal to the maximum compression stress. Numerically, bracing connected only at corners is implemented by removing the nodes along the perimeter of the design space, except at the corner points.

  • Case 3: Optimal reference bracing. Both tension and compression members can be present in the bracing system and the maximum tension stress is equal to the maximum compression stress. Connections between bracing members and the beams or columns can exist at any location. The resulting constraint-free bracing layout can be expected to be the most efficient of the three cases in terms of material consumption.

3.2 Single load case layout optimization formulation

The single load case layout optimization formulation for a two-dimensional problem can be stated as follows (after Dorn et al. 1964):

$$ \begin{array}{p{2.5cm}l} min & V=\mathbf{q}^{T}\mathbf{c}\\ subject \;to &\mathbf{B}\mathbf{q}=\mathbf{f}\\ & q^{+}_{i},q^{-}_{i}\geq 0,\; i = 1,...,m \end{array} $$
(2)

where there are m members and n nodes in the problem, and where V represents the volume of the structure, \(\mathbf {q}^{T}\,=\,\{q^{+}_{1},q^{-}_{1},q^{+}_{2},q^{-}_{2},...,q^{+}_{m},q^{-}_{m} \}\), \(\mathbf {c}^{T}\,=\,\{l_{1}/\sigma ^{+}_{1},l_{1}/\sigma ^{-}_{1},\)\(l_{1}/\sigma ^{+}_{2},l_{1}/\sigma ^{-}_{2},...,l_{1}/\sigma ^{+}_{m},l_{1}/\sigma ^{-}_{m}\}\), where and \(l_{i},q^{+}_{i},q^{-}_{i},\)\(\sigma ^{+}_{i},\sigma ^{-}_{i}\) represent, respectively, the length, tensile member force, compressive member force, tensile stress capacity and compressive stress capacity of member i. B is a 2n × 2m equilibrium matrix and \(\mathbf {f}=\{{f^{x}_{1}},{f^{y}_{1}},{f^{x}_{2}},{f^{y}_{2}},...,{f^{x}_{n}},{f^{y}_{n}}\}\), where \({f^{x}_{j}}\) and \({f^{y}_{j}}\) represent the component of load applied to node j in the x and y directions respectively. This problem is in a form suitable for solution using linear programming (LP).

The adaptive ‘member adding’ method proposed by Gilbert and Tyas (2003) is used to reduce the computational cost associated with solving problems; this involves solving a small initial problem involving sparse connectivity, and then iteratively adding further connections until a provably optimal solution is found. Additionally, to improve the quality of the optimized results, the geometry optimization rationalization procedure proposed by He and Gilbert (2015) is here used as a post-processing tool.

Finally, although formulation (2) is strictly speaking a ‘plastic’ formulation, the optimal layouts from plastic and elastic (minimum compliance) design optimization procedures are identical when only a single load case is involved.

3.3 Practical considerations

Some of the solutions generated by layout optimization are complex in form, leading to justifiable questions over their practical usefulness. However, as Cox (1965) suggested, in the field of structural design there is a need for reference solutions, against which alternatives can be judged (Cox pointed out that just as there is a limit on the theoretical thermal efficiency of a heat engine, set by the Carnot cycle, so there is a lower limit on the volume of material necessary to form a structure). Thus even a complex solution provides a useful reference against which alternative designs can be judged, where the latter may include simplified variants of the optimal reference form.

Also, many of the layouts presented in this paper contain long compression members and it might reasonably be suggested that buckling will limit the capacity of such elements in practice. However, for the purposes of this study the effect of member buckling under compressive load will be ignored. Whilst incorporating buckling may, in principle, lead to different optimal layouts, there are two reasons for this omission. Firstly, as already stated, one goal of the study is to establish definite benchmarks for optimal layout and efficiency, against which real-world designs may be judged. The significance or otherwise of buckling effects in a given scenario depends to a great extent on specific design decisions, and this emphasizes the need for benchmarks to properly assess the effects of these decisions. Secondly, previous work by two of the present authors (Tyas et al. 2005) has indicated that the reduction in the strength of real steel members due to member buckling is rarely significant when suitable member cross-sections are used. This latter study considered standard circular hollow structural steel sections, widely available in the UK, and showed that a near- linear relationship held between member cross-sectional area and the required compression capacity for a given unrestrained length. Euler buckling was significant only for very long, and/or very lightly loaded members, whereas, ‘...at most combinations of load and length, there exists a member which can effectively utilize the majority of its compressive crushing strength and minimise the effect of Euler buckling’. Also buckling can often be addressed by either selecting a suitable member cross-section in the detailed design stage, and/or by providing lateral restraint at intermediate locations (e.g. at floors), though this is likely to be more difficult in the case of small buildings, with lightly loaded members.

4 Optimized single bay bracing designs

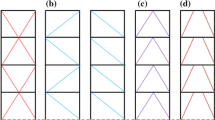
Optimized bracing layouts and associated volumes for each of the three cases described in Section 3.1 are shown for a range of aspect ratios in Fig. 2a to c. The volumes of these frames are also presented in Fig. 3. Note that although the optimized layouts were initially obtained numerically, using the approach described in Section 3, the volumes of the simple layouts (e.g. those involving diagonal bracing) can be obtained analytically via simple calculation. Also, it is shown in Sections 4.2 & 4.3 that the more complex layouts are closely related to Michell cantilevers for which known analytical solutions exist. For this reason exact analytical volumes are shown in Fig. 2.

Fig. 2
figure 2

Optimized bracing layouts for various h:b aspect ratios (4:1, 3:1, 2:1, 1:1, 1:2, 1:3 & 1:4): a Case 1 - tension only bracing; b Case 2 - bracing connected only at corners; c Case 3 - optimal reference bracing. The corresponding analytical volume is indicated below each layout, where P is the magnitude of the horizontal load applied at the top left corner of the design domain, of breadth b and height h, and σ is the limiting tensile strength. Element color key: red = tensile, blue = compressive, grey = zero force, black = pre-existing (assuming left to right loading)

Full size image
Fig. 3
figure 3

Volume comparison for the three bracing cases considered (where P is the magnitude of the horizontal load applied at the top left corner of the design domain, of breadth b and height h, and σ is the limiting tensile strength)

Full size image

4.1 Case 1: Tension only bracing

It is evident from Fig. 2a that tension only bracing leads to very simple optimized layouts. It is also evident from Fig. 3 that tension only bracing requires at least double the volume of material required by any other kind of bracing. This is because only one of the two inclined members carries a force when a horizontal load is applied. Thus, since the lateral load direction can be reversed, at least twice the volume of material must be consumed as when standard tension / compression bracing is used, assuming that the allowable stresses are equal in tension and compression. The issue of buckling must obviously be considered, but as mentioned earlier often this can be addressed by modifying the shape of the cross section and/or providing sufficient lateral restraint. The use of tension only bracing is therefore not a good choice when material savings are of paramount importance.

4.2 Case 2: Bracing connected only at corners

The optimized bracing layouts for Case 2, shown on Fig. 2b, are in most cases quite complex. It is also evident that their forms resemble Michell cantilevers. This observation gives rise to the following hypothesis:

Hypothesis 1: :

The optimized result for the case with connections only at corners is a combination of two adjacent Michell cantilevers, contained within a laterally restricted design space (so-called Michell cantilevers in a half strip).

The exact volume of a Michell cantilever in a half strip has been obtained using analytical methods by Graczykowski and Lewiński (2010). To explain the relationship between Case 2 and a Michell cantilever, first consider the influence of the infinite strength (i.e. rigid) pre-existing members. Fuchs and Moses (2000) demonstrated that a rigid member transforms any external load applied along its line of action into a ‘transmissible load’. Therefore, a horizontal load applied at the end of a pre-existing beam with infinite reserves of strength can be transmitted to any other point along the beam, as illustrated in Fig. 4. Given this, a relationship between Case 2 and a Michell cantilever problem can be established, as indicated in Fig. 5. This gives rise to the following relation:

Relation 1: :

The volume of the optimal Case 2 layout for a problem with an aspect ratio h : b, where h : b ≥ 1, is twice the volume of a Michell cantilever of aspect ratio \({h\over 2}:b\) (though the latter is subjected to a loading at the centreline).

Fig. 4
figure 4

Ability of a pre-existing beam member with infinite reserves of strength to make an external load ‘transmissible’ (i.e. each of the above cases is equivalent)

Full size image
Fig. 5
figure 5

Demonstrating the equivalence between Case 2 (bracing only connected at corners) and a Hemp-Michell cantilever: a starting problem, in this case with a frame with a 2:1 aspect ratio; b base supports replaced by reaction forces; c corner forces replaced by equivalent loads (since forces can be distributed arbitrarily along rigid members); d design domain divided along line of antisymmetry; e corner loads replaced by supports and appropriate forces added along line of division

Full size image

A similar logic can also be applied for low aspect ratio cases, leading to the following relation:

Relation 2: :

The volume of the optimal Case 2 layout for a problem with an aspect ratio h : b, where h : b ≤ 1, is \({2h}\over b\) times the volume of a Michell cantilever of aspect ratio \(h:{b\over 2}\) (though the latter is subjected to a loading at the centreline).

Therefore, using Relation 1 and 2, exact analytical solutions can be obtained for bracing problems, with numerical values for these solutions taken e.g. from Graczykowski and Lewiński (2010).

Whilst it has been demonstrated that the layouts shown in Fig. 2b are the combination of two constrained Michell cantilevers, an unconstrained Michell-Hemp cantilever (Hemp 1973) could alternatively be used. Figure 6 shows the outcome when an expanded design domain is used, in this case using a pre-existing frame with an aspect ratio of 10:1. Although unlikely to be useful in practice, it is of interest that the bracing volume is in this case reduced by 20.6%.

Fig. 6
figure 6

Optimized layout for Case 2 (connections only at corners) when the bracing elements are allowed to extend beyond the lines of the columns

Full size image

4.3 Case 3: Optimal reference bracing

In Case 3 bracing members are free to intersect pre-existing members at any location around the perimeter of the design space, as shown in Fig. 2c.

An important feature of the layouts obtained is stated in Property 1:

Property 1: :

If a pre-existing member with infinite reserves of strength actively carries load, then the optimal intersection angle between this and intersecting tension/compression member pairs will be 45∘.

This property can easily be verified with the aid of a Mohr’s circle analysis, as shown in Fig. 7. (It can also be observed that the angle between bracing members in tension and compression in the Mohr’s circle is 180∘, or 90∘ in practice, a characteristic of an optimal Michell structure.) This presupposes that tension and compression members are simultaneously intersecting a given point on the pre-existing member, or, from an optimization theory point of view that a T-region exists within the building envelope (see e.g. Rozvany et al. 1995). (Alternatively if a situation arises where there is only an intersecting tension or compression member (i.e. an R+ or R−-region) then the Mohr’s circle analysis indicates that the maximum angle of intersection is 45∘.)

Fig. 7
figure 7

Use of a Mohr’s circle analysis to demonstrate that 45∘ is the optimal intersection angle between a pre-existing beam/column and an optimal tension/compression bracing member pairs. (An optimal bracing member follows the direction of principal strain (Hemp 1973), whilst the strain in a pre-existing member is zero due to its infinite strength. Thus the subtended angle between such members will be 90∘ on the circle, or 45∘ in reality)

Full size image

For low aspect ratio cases it is evident that the optimal bracing layout resembles standard knee bracing, as shown in Fig. 8. However, some of the layouts shown in Fig. 2c are rather more complex; see the 1:3 and 1:4 aspect ratio layouts. In Table 1 the bracing volumes are compared with the volumes of standard knee bracing; this suggests that standard knee bracing is very efficient, becoming only slightly less so as the intersection angle between the bracing members and the pre-existing frame members deviates markedly from 45∘.

Fig. 8
figure 8

A standard knee bracing layout

Full size image
Table 1 Comparison between optimal reference bracing (Case 3) and standard knee bracing volumes (where P is the magnitude of the horizontal load applied at the top left corner of the design domain, of breadth b and height h, and σ is the limiting tensile strength)
Full size table

It can also be observed that the more complex layouts found for low aspect ratios have similarities with the layouts of Michell cantilevers. Thus, following a similar process to that outlined in Fig. 5, a relationship between these layouts and the corresponding Michell cantilever truss can be established, as shown on Fig. 9. This leads to the following relation:

Relation 3: :

The volume of the optimal Case 3 layout for a problem with an aspect ratio h : b, where h : b ≤ 1, is \(2h\over b\) times the volume of a Michell cantilever of aspect ratio \({b\over 2}:{2h}\) (though the latter is subjected to a loading at the centreline).

Using Relation 3, analytical solutions can be obtained for the Case 3 low aspect ratio cases, with numerical values for these solutions taken e.g. from Graczykowski and Lewiński (2010).

Fig. 9
figure 9

Demonstrating the equivalence between Case 3 (optimal reference bracing) and Hemp-Michell cantilever solutions: a starting problem, in this case using frame with 1:3 aspect ratio; b rotate the problem by 90∘ clockwise; c design domain divided into Structure I & II along the line of antisymmetry; d point loads are replaced by distributed loads (since forces can be distributed arbitrarily along rigid members); e Structure I & II are combined into a Michell cantilever

Full size image

5 Multi-storey / multi-bay buildings

Bracing members may cross several stories in multi-storey buildings (Moon et al. 2007). In such a building each floor-slab can be considered as a pre-existing member. Therefore, in this section the focus is on considering the contribution of additional intermediate beams and columns. (Also, a pin support is added to the bottom of each intermediate column.)

Firstly, it is observed that for Cases 1, 2 and 3 all layouts revert to cross bracing once intermediate beams and columns are added. Therefore, for sake of clarity, only results for a 4:1 aspect ratio structure is considered further, as shown in Fig. 10a.

Since there are intermediate connections available across the height of the multiple storey building, Case 2 & 3 become identical, with the volume of the bracing structure shown in Fig. 10a being equal to 8.00Pb/ σ in both cases. However, the volume of the Case 1 (tension only bracing) structure will still be double the volume of the corresponding Case 2 & 3 (tension / compression bracing) structures, for the reason given in Section 4.1.

It is worth noting that the cross bracing layout shown in Fig. 10a is not the only optimal solution since there are many variants of this layout that satisfy Property 1 (see Section 4.3); thus Fig. 10c shows an equivalent optimal solution. Additionally, it should be noted that although the results shown in Fig. 10 relate to the case when horizontal loads are applied only to the top of the building, due to the existence of Property 1, structures similar to Fig. 10c are found when loading is applied uniformly throughout the building height, with the density of the bracing net depending on the ground structure resolution (though with the relative sizes of the bracing members changing due to the different loading pattern involved). It can also be observed that these solutions resemble the braced tube structures that have been used in practice (e.g. see Fig. 10b & d). However, although 45∘ diagonal bracing is optimal if the assumptions stated in this paper are adopted, if bracing members are allowed to also take vertical gravity loads the optimal angle is likely to change somewhat (as is evident on Fig. 10b & d, where angles of less than 45∘ to the vertical have been adopted in practice). This suggests that there is an opportunity to develop an alternative holistic optimization approach involving multiple load cases (i.e. encompassing both gravity and lateral scenarios) for the design of new buildings, though in this case it must be borne in mind that a side effect will be a lack of clarity on what constitutes ‘bracing’, since diagonal members may be designed to be active in both gravity only and lateral load cases.

Fig. 10
figure 10

Comparison of optimal bracing layouts in multi-storey frames and sample braced tube structures constructed in practice: a the optimal layout for a 4:1 aspect ratio case with intermediate pre-existing beams and columns; b John Hancock Center in Chicago, a braced tube structure similar to (a); c an alternative optimal layout with the same volume as (a); d One Maritime Plaza in San Francisco, a braced tube structure qualitatively similar to (c). Element color key: red = tensile, blue = compressive, black = pre-existing (assuming Case 2 or 3 bracing and left to right loading). Note however that the angles in (b) and (d) differ from the 45∘ found to be optimal when bracing a pre-existing frame

Full size image

6 Conclusions

In this paper theoretically optimal layouts for bracing systems have been identified for pre-existing building frames, already designed to carry gravity loads. For sake of simplicity it has been assumed that members in such frames will have sufficient reserves of strength to accommodate the additional forces that result from lateral loads. Three different cases have been considered:

  • Case 1: Bracing systems comprising tension only members have been demonstrated to be inefficient from a theoretical standpoint. Replacing tension only bracing with tension/compression bracing will save at least 50% of the material needed if the limiting tensile and compressive material strengths are equal (i.e. assuming that buckling does not reduce the maximum compressive stress that can be sustained).

  • Case 2: When bracing is only allowed to connect at the corners of the pre-existing frame it is shown that the optimal layout takes the form of two adjacent Michell cantilevers. This allows exact reference volumes to be obtained, against which the efficiency of other bracing layouts can be judged.

  • Case 3: When bracing is allowed to connect pre-existing frame members at any location it is shown that intersecting tension/compression bracing member pairs meet each pre-existing member at 45∘ in the optimal layouts. It is also shown that traditional cross bracing and knee bracing are very efficient from a theoretical standpoint.

In the case of multi-storey frames, layouts involving diagonal cross-bracing, with braces meeting pre-existing members at 45∘, are shown to be most efficient. Also it is evident that the theoretically optimal layouts identified herein quite closely resemble those which have been employed in braced tube building frames in practice. However, the exact reference solutions derived herein are only strictly applicable when bracing a pre-existing frame; the more general holistic frame design case, where all framing elements are optimized simultaneously, under the action of multiple load cases, is the subject of future work.