Adjoint sensitivity analysis and optimization of hysteretic dynamic systems with nonlinear viscous dampers

Abstract

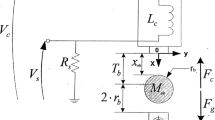
In this paper we discuss the adjoint sensitivity analysis and optimization of hysteretic systems equipped with nonlinear viscous dampers and subjected to transient excitation. The viscous dampers are modeled via the Maxwell model, considering at the same time the stiffening and the damping contribution of the dampers. The time-history analysis adopted for the evaluation of the response of the systems relies on the Newmark-β time integration scheme. In particular, the dynamic equilibrium in each time-step is achieved by means of the Newton-Raphson and the Runge-Kutta methods. The sensitivity of the system response is calculated with the adjoint variable method. In particular, the discretize-then-differentiate approach is adopted for calculating consistently the sensitivity of the system. The importance and the generality of the sensitivity analysis discussed herein is demonstrated in two numerical applications: the retrofitting of a structure subject to seismic excitation, and the design of a quarter-car suspension system. The MATLAB code for the sensitivity analysis considered in the first application is provided as “Supplementary Material”.

Appendix:: Explicit formulations of the matrices involved in the sensitivity analysis

To perform the sensitivity analysis discussed in Section 3, (27) must be solved iteratively backwards over the same time discretization adopted in the system response analysis. The matrix A _{g r,i} , and the vector b _{g r,i} have been partitioned into blocks in order to facilitate their description. More precisely, the block $\mathbf {A}^{11}_{i}$ of A _{g r,i} is also a matrix and it is presented in Table 5. The blocks $\mathbf {A}^{12}_{i}$ and $\mathbf {A}^{21}_{i}$ are the following:

$$\begin{array}{@{}rcl@{}} {\mathbf{A}}^{12}_{i} &=& \left[\begin{array}{cccccccc} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array}\right],\\ {\mathbf{A}^{21}}_{i} &=& \left[\begin{array}{ccccc} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ k_{d} & \frac{k_{d}}{2} & \frac{k_{d}}{2} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array}\right] \end{array} $$

(46)

Finally, the block $\mathbf {A}^{22}_{i}$ is defined in Table 6.

Table 6 Block $\mathbf {A}^{22}_{i}$ of the partitioned matrix A _{g r,i}

Similarly, the blocks of the vector b _{g r,i} are also vectors, and they are written as follows:

$$ \mathbf{b}^{1}_{i} \,=\, \left[\!\begin{array}{c} 0\\ 0\\ 0\\ 0\\ -\psi^{1}_{i + 1} \,+\, \mathcal{IL}\left( f_{d,i}\right)k_{d}\psi^{2}_{i + 1} \,+\, \mathcal{IL}\left( \hat{f}^{1}_{d,i}\right)k_{d}\psi^{3}_{i + 1} \ldots\\ +\mathcal{IL}\left( \hat{f}^{2}_{d,i}\right)k_{d}\psi^{4}_{i + 1} \,+\, \mathcal{IL}\left( \hat{f}^{3}_{d,i}\right)k_{d}\psi^{5}_{i + 1}\,-\,\frac{\partial h}{\partial f_{d,i}}\\ \end{array}\!\right] $$

(47)

$$ \mathbf{b}^{2}_{i} \,=\, \left[\!\begin{array}{c} 0\\ 0\\ 0\\ 0\\ -\phi^{1}_{i + 1} \,+\, \mathcal{O}\left( f_{s,i},\dot{u}_{i}\right)\phi^{2}_{i + 1} \,+\, \mathcal{O}\left( \hat{f}^{1}_{s,i},\dot{u}_{i+\frac{1}{2}}\right)\phi^{3}_{i + 1} \,+\, \ldots\\ + \mathcal{O}\left( \hat{f}^{2}_{s,i},\dot{u}_{i+\frac{1}{2}}\right)\phi^{4}_{i + 1} \,+\, \mathcal{O}\left( \hat{f}^{3}_{s,i},\dot{u}_{i + 1}\right)\phi^{5}_{i + 1} \,-\, \frac{\partial h}{\partial f_{s,i}} \end{array}\!\right] $$

(48)

$$ \mathbf{b}^{3}_{i} \,=\, \left[\!\begin{array}{c} - \mu_{i + 1}\frac{\Delta t_{i + 1}}{2} \,-\, \nu_{i + 1}\frac{\Delta t^{2}_{i + 1}}{4} \,-\, \frac{\partial h}{\partial \ddot{u}_{i}}\\ - \mu_{i + 1} \,-\, \nu_{i + 1}{\Delta} t_{i + 1} \,-\,\mathcal{Q}\left( f_{s,i},\dot{u}_{i}\right)\phi^{2}_{i + 1}\!+\ldots\\ -\frac{1}{2}\mathcal{Q}\left( \hat{f}^{1}_{s,i},\dot{u}_{i+\frac{1}{2}}\right)\phi^{3}_{i + 1}\,-\,\frac{1}{2}\mathcal{Q}\left( \hat{f}^{2}_{s,i},\dot{u}_{i+\frac{1}{2}}\right)\phi^{4}_{i + 1}\!+\ldots\\ -k_{d}\psi^{2}_{i + 1}\,-\,\frac{1}{2}k_{d}\psi^{3}_{i + 1} \,-\,\frac{1}{2}k_{d}\psi^{4}_{i + 1} \,-\, \frac{\partial h}{\partial \dot{u}_{i}}\\ - \nu_{i + 1} \,-\, \frac{\partial h}{\partial u_{i}} \end{array}\!\right] $$

(49)

where $\dot {u}_{i+\frac {1}{2}} = \frac {1}{2}\left (\dot {u}_{i + 1}+\dot {u}_{i}\right )$. We remark that Δt _i+ 1 = t _i+ 1 − t _i , and Δt _i = t _i − t _i− 1.