Skip to main content

Advertisement

SpringerLink
Log in

Configurational optimization of multi-cell topologies for multiple oblique loads

  • RESEARCH PAPER
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

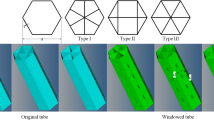
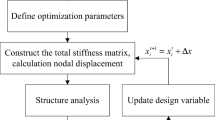
Abstract

Multi-cell thin-walled structures exhibit significant advantages in maximizing energy absorption and minimizing mass during vehicle crashes. Since the topological distribution of wall members has an appreciable effect on the crashworthiness, their design signifies an important area of research. As a major energy absorber, multi-cell tubes are more commonly encounter oblique loading in real life. Thus, this study aimed to optimize multi-cell cross-sectional configuration of tubal structures for multiple oblique loading cases. An integer coded genetic algorithm (ICGA) is introduced here to optimize topological distribution of multi-celled web members for single/multiple oblique impacting conditions. Specifically, material distribution in a form of allocating web wall thickness, starting from zero, is considered as design variables and maximization of energy absorption (EA) as the design objective under the predefined peak crushing force and structural mass constraints. The optimization allows generating uniform or non-uniform thickness distribution in different web wall configurations to maximize usage efficiency of material. Compared with the baseline structure, the optimized configurations largely improved the energy absorption in both single and multiple load cases. The examples demonstrate that the proposed ICGA-based design method not only provides a useful approach to searching for novel crashworthy structures in a systematic fashion, but also develops a series of novel multi-cell topologies for multiple oblique loading cases.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22

Similar content being viewed by others

References

  • Alavi Nia A, Parsapour M (2014) Comparative analysis of energy absorption capacity of simple and multi-cell thin-walled tubes with triangular, square, hexagonal and octagonal sections. Thin-Walled Struct 74:155–165

    Article  Google Scholar 

  • Amjady N, Shirzadi A (2009) Unit commitment using a new integer coded genetic algorithm. Eur. Trans. Electr. Power 19:1161–1176

    Article  Google Scholar 

  • Asanjarani A, Dibajian SH, Mahdian A (2017) Multi-objective crashworthiness optimization of tapered thin-walled square tubes with indentations. Thin-Walled Struct 116:26–36

    Article  Google Scholar 

  • Bandi P, Schmiedeler JP, Tovar A (2013) Design of Crashworthy Structures With Controlled Energy Absorption in the Hybrid Cellular Automaton Framework. J Mech Des 135:091002-091002-091011

    Article  Google Scholar 

  • Bendsøe MP, Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. Comput Methods Appl Mech Eng 71:197–224

    Article  MathSciNet  MATH  Google Scholar 

  • Bendsoe MP, Sigmund O (2013) Topology optimization: theory, methods, and applications, Springer Science & Business Media

  • Chapman CD, Saitou K, Jakiela MJ (1994) Genetic algorithms as an approach to configuration and topology design. J Mech Des 116:1005–1012

    Article  Google Scholar 

  • Chen S-Y, Shui X-F, Huang H (2016) Improved genetic algorithm with two-level approximation using shape sensitivities for truss layout optimization. Struct Multidiscip Optim 55:1365–1382

    Article  MathSciNet  Google Scholar 

  • Curt MC, Horvath D (2012) Future Material Opportunities and Direction for Lightweighting Automotive Body Structure, in, <http://www.nist.gov/mml/acmd/structural_materials/upload/Future-Material-Opportunities-and-Direction-for-Lighweighting-Automotive-v-Final-v2.pdf> 2012

  • Duan X, Qin X, Li F (2016) Topology optimization of Stokes flow using an implicit coupled level set method. Appl Math Model 40:5431–5441

    Article  MathSciNet  Google Scholar 

  • Duddeck F, Hunkeler S, Lozano P, Wehrle E, Zeng D (2016) Topology optimization for crashworthiness of thin-walled structures under axial impact using hybrid cellular automata. Struct Multidiscip Optim 54:415–428

    Article  Google Scholar 

  • Fang J, Gao Y, Sun G, Qiu N, Li Q (2015a) On design of multi-cell tubes under axial and oblique impact loads. Thin-Walled Struct 95:115–126

    Article  Google Scholar 

  • Fang J, Gao Y, Sun G, Zheng G, Li Q (2015b) Dynamic crashing behavior of new extrudable multi-cell tubes with a functionally graded thickness. Int J Mech Sci 103:63–73

    Article  Google Scholar 

  • Fang J, Sun G, Qiu N, Steven G, Li Q (2017a) Topology optimization of multi-cell tubes under out-of-plane crushing using a heuristic artificial bee colony (ABC) algorithm. ASME Transactions . J Mech Des 139(7):071403

  • Fang J, Sun G, Qiu N, Kim NH, Li Q (2017b) On design optimization for structural crashworthiness and its state of the art. Struct Multidiscip Optim 55:1091–1119

    Article  MathSciNet  Google Scholar 

  • Forsberg J, Nilsson L (2007) Topology optimization in crashworthiness design. Struct Multidiscip Optim 33:1–12

    Article  Google Scholar 

  • Goel MD, Matsagar VA, Gupta AK (2015) Blast resistance of stiffened sandwich panels with aluminum cenosphere syntactic foam. Int. J. Impact Eng. 77:134–146

    Article  Google Scholar 

  • Goldberg DE (1989), Genetic algorithms in search optimization and machine learning, Addison-wesley Reading Menlo Park

  • Han DC, Park SH (1999) Collapse behavior of square thin-walled columns subjected to oblique loads. Thin-Walled Struct 35:167–184

    Article  Google Scholar 

  • Huang X, Xie Y, Lu G (2007) Topology optimization of energy-absorbing structures. Int. J. Crashworthiness 12:663–675

    Article  Google Scholar 

  • Jakiela MJ, Chapman C, Duda J, Adewuya A, Saitou K (2000) Continuum structural topology design with genetic algorithms. Comput Methods Appl Mech Eng 186:339–356

    Article  MathSciNet  MATH  Google Scholar 

  • Jang HH, Lee HA, Lee JY, Park GJ (2012) Dynamic Response Topology Optimization in the Time Domain Using Equivalent Static Loads. AIAA J 50:226–234

    Article  Google Scholar 

  • Song JC, Zhao L, Liu HY (2008) Optimizing cooperative control based on genetic algorithm for electroSlag remelting process, in: 2008 I.E. Conference on Cybernetics and Intelligent Systems, 1216–1219

  • Lee H-A, Park G-J (2015) Nonlinear dynamic response topology optimization using the equivalent static loads method. Comput Methods Appl Mech Eng 283:956–970

    Article  MathSciNet  Google Scholar 

  • Li Q Li, Steven G, Xie Y (2001) Evolutionary structural optimization for connection topology design of multi-component systems. Eng Comp 18(3/4):460–479

  • Lipowski A, Lipowska D (2012) Roulette-wheel selection via stochastic acceptance. Physica A: Statistical Mechanics and its Applications 391:2193–2196

    Article  Google Scholar 

  • Mahmoodi A, Shojaeefard MH, Saeidi Googarchin H (2016) Theoretical development and numerical investigation on energy absorption behavior of tapered multi-cell tubes. Thin-Walled Struct 102:98–110

    Article  Google Scholar 

  • Marzbanrad J, Ebrahimi MR (2011) Multi-Objective Optimization of aluminum hollow tubes for vehicle crash energy absorption using a genetic algorithm and neural networks. Thin-Walled Struct 49:1605–1615

    Article  Google Scholar 

  • Mayer RR, Kikuchi N, Scott RA (1996) Application of topological optimization techniques to structueal crashworthiness. Int J Numer Methods Eng 39:1383–1403

    Article  MATH  Google Scholar 

  • Morales AK, Quezada CV (1998) A universal eclectic genetic algorithm for constrained optimization, in: Proceedings of the 6th European congress on intelligent techniques and soft computing, Citeseer, 518–522

  • Neubauer A (1997) The circular schema theorem for genetic algorithms and two-point crossover, in: Genetic Algorithms in Engineering Systems: Innovations and Applications, 1997. GALESIA 97. Second International Conference On (Conf. Publ. No. 446), IET, 209–214

  • NHTSA-US NCAP (2011) in, <http://www.safecarguide.com/exp/usncap/usncap.htm>

  • Ortmann C, Schumacher A (2013) Graph and heuristic based topology optimization of crash loaded structures. Struct Multidiscip Optim 47:839–854

    Article  MATH  Google Scholar 

  • Pedersen CBW (2003) Topology optimization for crashworthiness of frame structures. Int. J. Crashworthiness 8:29–39

    Article  Google Scholar 

  • Pedersen CBW (2004) Crashworthiness design of transient frame structures using topology optimization. Comput Methods Appl Mech Eng 193:653–678

    Article  MATH  Google Scholar 

  • Pu Y, Shi Y, Zhang T (2012) A superiority inheritance based method to search the ambiguity function main ridge slice of radar emitter signals, in: 2012 I.E. International Conference on Information Science and Technology, 806–809

  • Qi C, Yang S (2014) Crashworthiness and lightweight optimisation of thin-walled conical tubes subjectedto an oblique impact. Int. J. Crashworthiness 19:334–351

    Article  Google Scholar 

  • Qi C, Yang S, Dong F (2012) Crushing analysis and multiobjective crashworthiness optimization of tapered square tubes under oblique impact loading. Thin-Walled Struct 59:103–119

    Article  Google Scholar 

  • Qiu N, Gao Y, Fang J, Feng Z, Sun G, Li Q (2015) Crashworthiness analysis and design of multi-cell hexagonal columns under multiple loading cases. Finite Elem Anal Des 104:89–101

    Article  Google Scholar 

  • Qiu N, Gao Y, Fang J, Sun G, Kim NH (2018) Topological Design of multi-cell hexagonal tubes under axial and lateral loading cases using a modified particle swarm algorithm, Applied Mathematical Modelling 53:567–583

  • Reyes A, Langseth M, Hopperstad O (2003) Square aluminum tubes subjected to oblique loading. Int. J. Impact Eng. 28:1077–1106

    Article  Google Scholar 

  • Sigmund O (2014) A 99 line topology optimization code written in Matlab. Struct Multidiscip Optim 21:120–127

    Article  Google Scholar 

  • Song J, Guo F (2013) A comparative study on the windowed and multi-cell square tubes under axial and oblique loading. Thin-Walled Struct 66:9–14

    Article  Google Scholar 

  • Soto C (2004) Structural topology optimization for crashworthiness. Int. J. Crashworthiness 9:277–283

    Article  Google Scholar 

  • Sun G, Xu F, Li G, Li Q (2014) Crashing analysis and multiobjective optimization for thin-walled structures with functionally graded thickness. Int. J. Impact Eng. 64:62–74

    Article  Google Scholar 

  • Sun G, Pang T, Fang J, Li G, Li Q (2017) Parameterization of criss-cross configurations for multiobjective crashworthiness optimization. Int J Mech Sci 124-125:145–157

    Article  Google Scholar 

  • Tabacu S (2015) Axial crushing of circular structures with rectangular multi-cell insert. Thin-Walled Struct 95:297–309

    Article  Google Scholar 

  • Tang Z, Liu S, Zhang Z (2013) Analysis of energy absorption characteristics of cylindrical multi-cell columns. Thin-Walled Struct 62:75–84

    Article  Google Scholar 

  • Toğan V, Daloğlu AT (2008) An improved genetic algorithm with initial population strategy and self-adaptive member grouping. Comput Struct 86:1204–1218

    Article  Google Scholar 

  • Wang MY, Wang X, Guo D (2003) A level set method for structural topology optimization. Comput Methods Appl Mech Eng 192:227–246

    Article  MathSciNet  MATH  Google Scholar 

  • Woon SY, Tong L, Querin OM, Steven GP (2005) Effective optimisation of continuum topologies through a multi-GA system. Comput Methods Appl Mech Eng 194:3416–3437

    Article  MATH  Google Scholar 

  • Wu S, Zheng G, Sun G, Liu Q, Li G, Li Q (2016) On design of multi-cell thin-wall structures for crashworthiness. Int. J. Impact Eng. 88:102–117

    Article  Google Scholar 

  • Wu S, Sun G, Wu X, Li G, Li Q (2017) Crashworthiness analysis and optimization of fourier varying section tubes. Int. J. Non Linear Mech. 92:41–58

    Article  Google Scholar 

  • Xie Y, Steven GP (1993) A simple evolutionary procedure for structural optimization. Comput Struct 49:885–896

    Article  Google Scholar 

  • Yang S, Qi C (2013) Multiobjective optimization for empty and foam-filled square columns under oblique impact loading. Int. J. Impact Eng. 54:177–191

    Article  Google Scholar 

  • Yin H, Xiao Y, Wen G, Qing Q, Wu X (2015) Crushing analysis and multi-objective optimization design for bionic thin-walled structure. Mater Des 87:825–834

    Article  Google Scholar 

  • Zeng D, Duddeck F (2017) Improved hybrid cellular automata for crashworthiness optimization of thin-walled structures. Struct Multidiscip Optim 56:101–115

    Article  MathSciNet  Google Scholar 

  • Zhang X, Zhang H (2012) Numerical and theoretical studies on energy absorption of three-panel angle elements. Int. J. Impact Eng. 46:23–40

    Article  Google Scholar 

  • Zhang X, Zhang H (2014) Axial crushing of circular multi-cell columns. Int. J. Impact Eng. 65:110–125

    Article  Google Scholar 

  • Zhang X, Wen Z, Zhang H (2014) Axial crushing and optimal design of square tubes with graded thickness. Thin-Walled Struct 84:263–274

    Article  Google Scholar 

  • Zhou P, Du J, Lü Z (2017) Interval analysis based robust truss optimization with continuous and discrete variables using mix-coded genetic algorithm. Struct Multidiscip Optim 56:353–370

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work is supported by National Natural Science Foundation of China (51575172). The first author Dr. Guangyong Sun is a recipient of Australian Research Council (ARC) Discovery Early Career Researcher Award (DECRA). The third author Dr. Jianguang Fang is a recipient of University of Technology Sydney (UTS) Chancellor’s Postdoctoral Research Fellowship.

Author information

Authors and Affiliations

  1. State Key Laboratory of Advanced Design and Manufacture for Vehicle Body, Hunan University, Changsha, 410082, China

    Guangyong Sun & Tangying Liu

  2. School of Aerospace, Mechanical and Mechatronic Engineering, The University of Sydney, Sydney, NSW, 2006, Australia

    Guangyong Sun, Grant P. Steven & Qing Li

  3. Centre for Built Infrastructure Research, School of Civil and Environmental Engineering, University of Technology Sydney, Sydney, NSW, 2007, Australia

    Jianguang Fang

Authors
  1. Guangyong Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tangying Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jianguang Fang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Grant P. Steven
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Qing Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Guangyong Sun.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sun, G., Liu, T., Fang, J. et al. Configurational optimization of multi-cell topologies for multiple oblique loads. Struct Multidisc Optim 57, 469–488 (2018). https://doi.org/10.1007/s00158-017-1839-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-017-1839-5

Keywords

Search

Navigation