Abstract
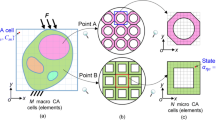
In recent years the Cellular Automata (CA) concept has been successfully applied to structural topology optimization problems. In the engineering implementation of CA, the design domain is decomposed into a lattice of cells, and a particular cell together with the cells to which it is connected forms a neighborhood. It is assumed that the interaction between cells takes place only within the neighborhood and the states of cells are updated synchronously in subsequent time steps according to some local rules.The majority of results that have been obtained so far were based on regular lattices of cells. However, a practical engineering analysis and design in many cases require using highly irregular meshes for complicated geometries and/or stress concentration regions. The aim of the present paper is to extend the concept of CA towards the implementation of unstructured grid of cells related to non-regular mesh of finite elements. Introducing an irregular lattice of cells allows to reduce the number of design variables without loosing the accuracy of results and without an excessive increase of the number of elements caused by using a fine mesh for a whole structure. The implementation of non-uniform cells of Cellular Automaton requires a reformulation of standard local rules, for which the influence of the neighborhood on the current cell is independent of sizes of the neighboring cells.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introductory remarks
For a few decades topology optimization has been one of the most important aspects of structural design. Since the early paper by Bendsoe and Kikuchi (1988), one can find in the literature numerous approaches to generating optimal topologies based both on optimality criteria and evolutionary methods. A general overview as well as a broad discussion on topology optimization concepts are provided by many survey papers, e.g. Rozvany (2008), Sigmund and Maute (2013), Deaton and Grandhi (2014). At the same time hundreds of papers present numerous solutions including classic Michell examples as well as complicated spatial engineering structures, implementing specific methods ranging from gradient-based approaches (e.g. Bendsoe, 1989) to evolutionary structural optimization (e.g. Xie and Steven, 1997), biologically inspired algorithms (e.g. Kaveh et al., 2008), material cloud method (e.g. Chang and Youn, 2006), spline-based topology optimization (e.g. Eschenauer et al., 1993) and level set method (e.g. Wang et al., 2003). Nevertheless the most robust, flexible and widely used approach for structural topology optimization is still the density method, which includes the popular solid isotropic material with the penalization (SIMP) technique.
Topology optimization is a constantly developing area, and one of the most important issues stimulating this progress nowadays is the implementation of efficient and versatile methods to the generation of optimal topologies to engineering structural elements. In recent years the Cellular Automata paradigm has been successfully applied to topology optimization problems. In the engineering implementation of Cellular Automaton the design domain is decomposed into a lattice of cells, and a particular cell together with the cells to which it is connected forms a neighborhood. It is assumed that the interaction between cells takes place only within the neighborhood, and the states of cells are updated synchronously according to some local rules.
The first application of CA to optimal structural design, and to topology optimization in particular, was proposed by Inou et al. (1994) and Inou et al. (1997). In these papers, the design domain was divided into cells, the states of which were represented by the Young moduli of the material as design variables. By applying the local CA rules iteratively, the values of the elastic moduli for all cells were updated based on the difference between the current and the target stress values. The cells with low values of elastic moduli were removed. The idea of implementing CA to optimal design was described also by Kita and Toyoda (2000), Hajela and Kim (2001), and Tatting and Gurdal (2000), where the authors proposed a new scheme for CA, in which analysis and design were performed simultaneously - a simultaneous analysis and design. This technique has been modified and extended, for example by Cortes et al. (2005), Setoodeh et al. (2006), Canyurt and Hajela (2007). For the last two decades the implementation of CA in the structural design has been intensively examined, and numerous papers related to the application of CA to the topology optimization, see e.g. Missoum et al. (2005), Abdalla et al. (2006), Hassani and Tavakkoli (2007), Penninger et al. (2009), Sanaei and Babaei (2011), Bochenek and Tajs-Zielińska (2012), Bochenek and Tajs-Zielińska (2013) or Du et al. (2013), Bochenek and Tajs-Zielińska (2015) have been published. In addition, the series of papers by Tovar and co-workers should be mentioned: Tovar et al. (2004a), Tovar et al. (2004b), Tovar et al. (2006), Penninger et al. (2011), in which a new CA technique, inspired by a process of a functional adaptation taking place in bones, has been implemented.
The majority of structural topology optimization results that have been obtained so far were based on regular lattices of cells, among which the most common choice is a rectangular grid. One can find only isolated examples of implementation of triangular or hexagonal lattices, e.g. Saxena (2009), Talischi et al. (2009), Jain and Saxena (2010), Talischi et al. (2010), Sanaei and Babaei (2011), Talischi et al. (2012), Christiansen et al. (2014), Wang et al. (2014), Jain et al. (2015). However, in many cases a practical engineering analysis and design require using highly irregular meshes for complicated geometries and/or stress concentration regions.
The aim of the present paper is to extend the concept of Cellular Automata lattice towards an irregular grid of cells related to a non-regular mesh of finite elements. The strategy which consists of resizing a traditional uniform grid of cells allows us to obtain more flexible solutions. The advantage of using a non-uniform lattice of cells is the most evident when the design domain is extremely irregular and it is even impossible to cover the design domain with uniform, e.g. rectangular cells. On the other hand, it is well known that holes and sharp edges indicate stress concentration and the regions of such intensity should be covered with a more fine mesh, which is not necessary for the structure as a whole. In other words, a non-uniform density of cells is used in order to achieve a more accurate solution without an excessive increase of the number of elements caused by using a fine mesh for the whole structure. It is worth noting that the non-uniform density of finite elements can be, but not necessarily is, directly related to the density of cells of Cellular Automaton. The implementation of non-uniform cells of Cellular Automaton requires a reformulation of standard local rules, for which the influence of the neighborhood on the current cell is independent of sizes of the neighboring cells and neglects, for example, the length of mutual boundaries. This paper proposes therefore new local update rules dedicated to implemented irregular lattices of cells. The novel concept is discussed in detail and the performance of the numerical algorithm based on the introduced idea is presented.
2 Irregular cellular automata
Most up-to-date applications of Cellular Automata in structural optimization are conventionally based on regularly spaced structured meshes. On the other hand, using irregular (unstructured) computational meshes provides more flexibility for fitting complicated geometries and allows for local mesh refinement. Some attempts to implement irregular Cellular Automata have been already reported in the literature, e.g. O’Sullivan (2001), Lin et al. (2011), but without application to topology optimization.
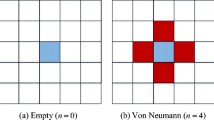
In this paper the concept of topology generator based on Cellular Automata rules is extended to unstructured meshes. Similar to regular (structured) Cellular Automata, several neighborhood schemes can be identified. The two most common ones are the von Neumann type and the Moore type. As can be seen in Fig. 1, in the case of the von Neumann configuration only three immediate neighbors are taken into account. These neighboring cells share common edges with the central cell. In the Moore type neighborhood in Fig. 2, any triangle that has common edges or common vertices with the central cell can be considered a neighbor of the central triangle. It is worth noting that this type of neighborhood involves more neighbors around the central cell and the number of neighbors can vary since it depends on a particular irregular mesh arrangement.
3 The algorithm
The performance of Cellular Automata algorithms, reported in literature, is often based on heuristic local rules. Similarly, in the present paper, the efficient heuristic algorithm, being an extension of the one introduced by Bochenek and Tajs-Zielińska (2012, 2013), has been implemented.
In this paper the structure compliance:
is minimized. In (1) u i and k i are the element displacement vector and the stiffness matrix, respectively, and M stands for the number of cells/elements.
The power law approach defining solid isotropic material with the penalization (SIMP) with design variables being the relative densities of a material has been utilized. The elastic modulus E i of each cell element is modelled as a function of relative density d i using the power law, according to (2).
In this formula, E 0 is the elastic modulus of a solid material, and the power p, usually equalling 3, penalizes intermediate densities and drives the design to a material/void structure.
The local update rule proposed by Bochenek and Tajs-Zielińska (2012, 2013) is recalled first. For each cell information is gathered from the adjacent cells forming the Moore or the von Neumann type neighborhood. Based on that, the update of the design variable d i associated with a particular cell is set up as a linear combination of design variables corrections with coefficients, values of which are influenced by the states of the neighboring cells, according to (3) and (4):
The compliance values calculated for the central cell U i and N neighboring cells U i k are compared to a selected threshold value U ∗. Based on relations (5) and (6) specially selected positive or negative coefficients \(C_{\alpha _{0}}\) for central cell and C α for the surrounding cells are transferred to the design variable update scheme (4).
The move limit m implemented in the above algorithm controls the allowable changes of the design variables values. Values of \(C_{\alpha _{0}}\) and C α are selected so as to keep \(-1 \leq \tilde {\alpha } \leq 1\).
The numerical algorithm has been built in order to implement the design rule proposed above. As for the optimization procedure, the sequential approach has been adapted meaning that for each iteration the structural analysis performed for the optimized element is followed by the local updating process. Simultaneously, a global volume constraint can be applied for a specified volume fraction V(d) = κ V 0, where V 0 stands for the design domain volume and κ is the prescribed volume fraction. The volume constraint is implemented in each iteration when local update rules have been applied to all cells. In practice, the design variables multiplier is introduced and then its value is sought for so as to fulfill the volume constraint. As a result, the generated topologies preserve a specified volume fraction of a solid material during optimization process.
In the case of irregular meshes, the novel approach is proposed. It incorporates the influence of cell sizes/areas on the update process. Assuming that the quantities A i and A i k stand for areas of central and neighboring cells, respectively, the update rule takes the following form:
where
The specified values of power α 0 and α k are transferred to the update rule (7) according to the following relations:
The form of rule (7) together with relations (9) and (10) guarantee that \(-1 \leq \tilde {\alpha } \leq 1\). Comparing (4) and (7), it is visible that in the latter case the fixed values of \(C_{\alpha _{0}}\) and C α from (4) have been replaced by quantities, the values of which depend on the sizes of the neighboring cells. The new proposal mentioned above can be therefore treated as a generalization of the original rule directed towards an irregular cell lattice.
Below, the pseudo-code of the algorithm is presented:
GET input data
SELECT reference energy value U ∗
SET initial values of design variables
SELECT neighborhood type
ASSIGN neighboring cells to each cell
SELECT move limit m
DO UNTIL stopping criteria are met
PERFORM structural analysis
IMPORT data from structural analysis
FOR all cells
CALCULATE local compliances U(d i )
END FOR
FOR all cells
UPDATE design variables d i
END FOR
IMPOSE volume constraint
END DO
DISPLAY results
4 Introductory example
The rectangular Michell-type structure shown in Fig. 3, clamped at the left edge and loaded by a vertical force applied at the bottom right corner, has been chosen as an introductory example. The irregular mesh that consists of triangular elements/cells has been applied. The denser mesh surrounds the bottom right corner of the rectangle. The two cases are considered, namely the larger and the smaller area of mesh concentration shown in Figs. 4 and 5, respectively. Since a similar number of cells has been chosen for both cases, for the latter case smaller cell sizes have been selected for the concentration region.
The results of a structural analysis performed for force P=500 N and material data E=200 GPa, ν=0.3, are as follows. For the irregular lattice of 10594 cells distributed as in Fig. 4: the maximal equivalent stress 11.8 kPa, the maximal displacement 0.24 10−6 m and the compliance 11.5 10−5 Nm have been found. In the case of the irregular lattice of 10439 cells distributed according to Fig. 5: the maximal equivalent stress 14.8 kPa, the maximal displacement 0.24 10−6 m and the compliance 11.5 10−5 Nm are obtained.
The comparison of results for the two implemented irregular meshes shows that displacements and compliances are practically the same, whereas significant difference regards the maximal stress value. Since values of stresses are influenced by the implemented mesh density in order to better describe stresses in the vicinity of the bottom right corner of the rectangle,a denser mesh should be applied in this area.
The topology optimization has been performed for the irregular mesh distributed according to Fig. 5. The obtained results are as follows: the maximal equivalent stress 14.8 kPa, the maximal displacement 0.18 10−6 m and the compliance 8.5 10−5 Nm. The distribution of equivalent stress and displacement is presented together with the final topology in Figs. 6 and 7, respectively.
The question now arises: what if a regular mesh is applied? It occurs that the regular lattice of 42230 cells has to be applied in order to get the same level of displacements, compliance and equivalent stress values. The obtained results are presented in Fig. 8: the maximal equivalent stress 14.5 kPa and in Fig. 9: the maximal displacement 0.18 10−6 m. The compliance for the final topology is 8.5 10−5 Nm.
Based on the above discussion of results, one can observe that the implementation of irregular lattice of cells can significantly reduce the number of cells/elements necessary to perform the analysis and topology optimization and at the same time retain the correct information regarding the stress and displacement distribution.
5 Generation of optimal topologies based on irregular cell lattices
Selected examples of compliance-based topologies generated using the approach presented in this article are discussed. The first example in this section is a C-shaped structure presented in Fig. 10, with an irregular lattice of cells distributed as shown in Fig. 11. The iterations history and topology evolution overview are presented in Figs. 12 and 13, respectively. The results of the structural analysis of optimized structure performed for force P=1 kN and material data E=200 GPa, ν=0.3, are as follows. For an irregular lattice of 5272 cells: the maximal equivalent stress 7.33 MPa, the maximal displacement 0.79 10−6 m and the compliance 1.56 10−3 Nm. The distributions of stresses and displacements are presented in Figs. 14 and 15, respectively. In order to reflect such stress and displacement values with a regular mesh, 20062 cells have been used. The topology optimization has been performed and the obtained results are: the maximal equivalent stress 7.52 MPa, the maximal displacement 0.76 10−6 m and the compliance 1.50 10−3 Nm. The final topology with the map of stresses and displacements is presented in Figs. 16 and 17.
The next example is the hook structure shown in Fig. 18. As with the previous case, an irregular mesh that consists of triangular elements/cells has been applied, see Fig. 19. The denser mesh surrounds the region of loading application. The iterations history and topology evolution overview are presented in Figs. 20 and 21, respectively. The results of structural analysis of optimized structure performed for force P=1 kN and material data E=200 GPa, ν=0.25, are as follows. For an irregular lattice of 6169 cells: the maximal equivalent stress 3.89 kPa, the maximal displacement 0.20 10−6 m and the compliance 1.89 10−4 Nm. The distributions of stresses and displacements are presented in Figs. 22 and 23, respectively. In order to obtain the same level of stress and displacement values with a regular mesh 27942 cells have been used. The topology optimization has been performed and the obtained results are: the maximal equivalent stress 3.87 kPa, the maximal displacement 0.19 10−6 m and the compliance 1.80 10−4 Nm. The final topology with a map of stresses and displacements is presented in Figs. 24 and 25.
Another example is a portal frame presented in Fig. 26, with an irregular lattice of cells distributed according to Fig. 27. The iterations history and topology evolution overview are presented in Figs. 28 and 29, respectively. The results of the structural analysis performed for force P=100 N and material data E=200 GPa, ν=0.25 are as follows. For the irregular lattice of 14024 cells: the maximal equivalent stress 50.46 kPa, the maximal displacement 1.70 10−6 m and the compliance 4.98 10−6 Nm. The distributions of stresses and displacements are presented in Figs. 30 and 31, respectively. In order to reflect such stress and displacement values with a regular mesh 39146 cells have been used. The topology optimization has been performed and the obtained results are: the maximal equivalent stress 50.49 kPa, the maximal displacement 1.69 10−6 m and the compliance 4.86 10−6 Nm. The final topology with a map of stresses and displacements is presented in Figs. 32 and 33. Incidentally, it can be pointed out that a similar example was discussed in James and Weisman (2014), where topology optimization of structures sustaining material damage was investigated.
The final example is the half-ring structure shown in the Fig. 34. As with the previous cases, the irregular/unstructured mesh that consists of triangular elements/cells has been applied. The denser mesh shown in Fig. 35 surrounds regions of loading application. The iterations history and topology evolution overview are presented in Figs. 36 and 37, respectively. The results of structural analysis performed for force P=1 N and material data E=1 kPa, ν=0.25, are as follows. For irregular lattice of 9522 cells: maximal equivalent stress 63.76 Pa, maximal displacement 0.10 m and compliance 7.95 10−2 Nm. The distributions of stresses and displacements are presented in Figs. 38 and 39, respectively. In order to obtain the same level of stress and displacement values with a regular mesh 33106 cells have been used. The topology optimization has been performed and the obtained results are: the maximal equivalent stress 66.34 Pa, the maximal displacement 0.10 m and the compliance 7.86 10−2 Nm. The final topology with a map of stresses and displacements is presented in Figs. 40 and 41. It is worth noting that in order to obtain comparable results more than 3 times more cells were required for a regular mesh.
The half-ring structure has also been examined in Wang et al. (2014) as an example of applying a new adaptive method of topology optimization. For 6984 elements of a regular mesh the final compliance of 7.8 10−2 Nm has been obtained there. These calculations have been, for comparison, repeated within the approach of this paper and the final compliance obtained here for a regular lattice of cells is 7.83 10−2 Nm. As to irregular lattice only 2258 elements are enough to guarantee the same compliance, maximal equivalent stress and maximal displacement for the initial structure. In what follows, the topology optimization performed for that number of elements gives resulting compliance equal to 7.86 10−2 Nm.
In the supplement to the above discussion, it is worth mentioning that for the performed numerical calculations a computational cost is generated mostly by the structural analysis. The optimization algorithm based on the proposed Cellular Automata local rules returns here almost immediate response. To be specific: for the examples discussed in this paper the total time used for calculations ranges from about 3 minutes for the C-shaped structure to 9 minutes for the half-ring structure. The desktop computer AMD Phenom II X4 955 with 3.2 GHz processors and 4 GB RAM and with Ansys 12.1 as the finite element code has been used.
The final observation is that the implementation of a dense mesh in specific structure regions does not influence generated topologies significantly. As an example, let us reconsider the C-shaped structure with a regular mesh of 20062 elements (e.g. Fig. 16). The dense mesh is now added in the regions indicated in Fig. 11 and for this irregular mesh of 20642 elements topology has been generated. The results are presented in Fig. 42. As can easily be seen, there are no significant differences in topologies obtained for regular and irregular meshes.
6 Concluding remarks
The proposal of extension of the Cellular Automata concept towards an irregular grid of cells related to non-regular mesh of finite elements has been presented. It is worth noting that an irregular mesh suited for structural analysis can be but does not have to be directly used in the optimization process. The local update rules proposed for irregular CA have been efficiently and successfully applied to the generation of minimal compliance topologies. The analysis of obtained results allows formulating some conclusions. It is not necessary to use a very fine mesh for the whole structure, therefore the number of elements and design variables can be significantly reduced. Although the number of cells is limited, because of only the local mesh refinement, the information about stresses and displacements can still be reasonable. The approach presented in this paper demonstrates a significant potential of application to problems which cannot be adequately represented by regular grids. The use of irregular meshes can be helpful while modelling a domain geometry, accurately specifying design loads or supports and computing the structure response.
References
Abdalla MM, Setoodeh S, Gurdal Z (2006) Cellular Automata paradigm for topology optimisation, Bendsoe MP et al., (eds.), IUTAM Symposium on Topological Design Optimization of Structures, Machines and Materials, Status and Perspectives, Springer
Bendsoe MP (1989) Optimal shape design as a material distribution problem. Struct Optim 1:193–202
Bendsoe MP, Kikuchi N (1988) Generating optimal topologies in optimal design using a homogenization method. Comput Methods Appl Mech Eng 71:197–224
Bochenek B, Tajs-Zielińska K (2012) Novel local rules of Cellular Automata applied to topology and size optimization. Eng Optim 44(1):23–35
Bochenek B, Tajs-Zielińska K (2013) Topology optimization with efficient rules of cellular automata. Eng Comput 30(8):1086– 1106
Bochenek B, Tajs-Zielińska K (2015) Minimal compliance topologies for maximal buckling load of columns. Struct Multidisc Optim 51:1149–1157
Canyurt OE, Haleja P (2007) A SAND approach based on cellular computation models for analysis and optimization. Eng Optim 2(1):381–396
Chang SY, Youn SK (2006) Material cloud method for topology optimization. Numer Methods Eng 65:1585–1607
Christiansen AN, Nobel-Jorgensen M, Aage N, Sigmund O, Baerentzen JA (2014) Topology optimization using an explicit interface representation. Struct Multidisc Optim 49:387–399
Cortes H, Tovar A, Munoz JD, Patel NM, Renaud JE (2005) Topology optimization of truss structures using cellular automata with accelerated simultaneous analysis and design. In: Herskovits J, Mazorche S, Canelas A (eds) Proceedings of the 6th World Congress on Structural and Multidisciplinary Optimization, ISSMO. CD-ROM, Rio de Janeiro, Brazil, p 10
Deaton JD, Grandhi RV (2014) A survey of structural and multidisciplinary continuum topology optimization: post 2000. Struct Multidisc Optim 49:1–38
Du Y, Chen D, Xiang X, Tian Q, Zhang Y (2013) Topological Design of Structures Using a Cellular Automata Method. CMES: Comput Model Eng Sci 94(1):53–75
Eschenauer HA, Kobelev VV, Schumacher A (1993) Bubble method for topology and shape optimization of structures. Struct Optim 8:42–51
Haleja P, Kim B (2001) On the use of energy minimization for CA based analysis in elasticity. Struct Multidisc Optim 23:24–33
Hassani B, Tavakkoli SM (2007) A multi-objective structural optimization using optimality criteria and cellular automata. Asian J Civil Eng (Build Hous) 8(1):77–88
Inou N, Shimotai N, Uesugi T (1994) A cellular automaton generating topological structures. Proc 2nd Eur Conf Smart Struct Mater 2361:47–50
Inou N, Uesugi T, Iwasaki A, Ujihashi S (1997) Self-organization of mechanical structure by cellular automata. In: Tong P, Zhang TY, Kim J (eds) Fracture and strength of solids, Part 2: Behaviour of materials and structure. Proceedings of the 3th International Conference, Hong Kong, pp 1115–1120
Jain C, Saxena A (2010) An Improved Material-Mask Overlay Strategy for Topology Optimization of Structures and Compliant Mechanisms. Journal of Mechanical Design 132(6):10
Jain N, Bankoti S, Saxena R (2015) Topological optimization of isotropic material using optimal criteria method. Int J Res Emerg Sci Technol 2(2):41–47
James KA, Waisman H (2014) Topology optimization of structures under variable loading using a damage superposition approach. Int J Numer Methods Eng 101(5):375–406
Kaveh A, Hassani B, Shojaee S, Tavakkoli SM (2008) Structural topology optimization using ant colony methodology. Eng Struct 30(9):2559–2565
Kita E, Toyoda T (2000) Structural design using cellular automata. Struct Multidisc Optim 19:64–73
Lin Y, Mynett AE, Li H (2011) Unstructured Cellular Automata for modelling macrophyte dynamics. J River Basin Manag 9(3-4):205–220
Missoum S, Gurdal Z, Setoodeh S (2005) Study of a new local update scheme for cellular automata in structural design. Struct Multidisc Optim 29:103–112
O’Sullivan D (2001) Exploring spatial process dynamics using irregular cellular automaton models. Geogr Anal 33(1):1–18
Penninger CL, Tovar A, Watson LT, Renaud JE (2009) KKT conditions satisfied using adaptive neighboring in hybrid cellular automata for topology optimization. In: Proceedings of the 8th World Congress on Structural and Multidisciplinary Optimization, LNEC. CD-ROM, Lisbon, Portugal, p 10
Penninger CL, Tovar A, Watson LT, Renaud JE (2011) KKT conditions satisfied using adaptive neighboring in hybrid cellular automata for topology optimization. Int J Pure Appl Math 66(3):245–262
Rozvany GIN (2008) A critical review of established methods of structural topology optimization. Struct Multidisc Optim 37:217–237
Sanaei E, Babaei M (2011) Cellular Automata in Topology Optimization of Continuum Structures. International Journal of Engineering, Science and Technology 3(4):27–41
Saxena A (2009) A Material-Mask Overlay Strategy for Continuum Topology Optimization of Compliant Mechanisms Using Honeycomb Discretization. ASME J. Mech. Des 130(8):1–9
Setoodeh S, Adams DB, Gurdal Z, Watson L (2006) Pipeline implementation of cellular automata for structural design on message-passing multiprocessors. Math Comput Model 43:966– 975
Sigmund O, Maute K (2013) Topology optimization approaches. Struct Multidisc Optim 48:1031–1055
Talischi C, Paulino GH, Le CH (2009) Honeycomb Wachspress finite elements for structural topology optimization. Struct Multidisc Optim 37(6):569–583
Talischi C, Paulino GH, Pereira A, Menezes IFM (2010) Polygonal finite elements for topology optimization: a unifying paradigm. Int J Numer Methods Eng 82(6):671–698
Talischi C, Paulino GH, Pereira A, Menezes IFM (2012) PolyTop: a Matlab implementation of a general topology optimization framework using unstructured polygonal finite element meshes. Struct Multidisc Optim 45:329–357
Tatting B, Gurdal Z (2000) Cellular automata for design of two-dimensional continuum structures, Proceedings of 8th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Long Beach, CA
Tovar A, Niebur GL, Sen M, Renaud JE (2004a) Bone structure adaptation as a cellular automaton optimization process, Proceedings of the 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Palm Springs, California
Tovar A, Patel N, Kaushik AK, Letona GA, Renaud JE (2004b), Albany, New York
Tovar A, Patel NM, Niebur GL, Sen M, Renaud JE (2006) Topology optimization using a hybrid cellular automaton method with local control rules. J Mech Des 128:1205–1216
Wang Y, Kang Z, He Q (2014) Adaptive topology optimization with independent error control for separated displacement and density fields. Comput Struct 135:50–61
Wang MY, Wang X, Guo D (2003) A level set method for structural topology optimization. Comput Methods Appl Mech Eng 192(12):227–246
Xie XM, Steven GP (1997) Evolutionary structural optimisation. Springer, Berlin
Author information
Authors and Affiliations
Corresponding author
Additional information
Full version of the paper presented at the Congress WCSMO11, Sydney 2015.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bochenek, B., Tajs-Zielińska, K. GOTICA - generation of optimal topologies by irregular cellular automata. Struct Multidisc Optim 55, 1989–2001 (2017). https://doi.org/10.1007/s00158-016-1614-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-016-1614-z