1 Introduction

The present paper refers to the three force problem in the following meaning: find the lightest plane structure of a bounded stress level capable of bearing three self-equilibrated forces acting in the plane at fixed application points. This problem belongs to the class of Michell’s (1904) problems. It involves many parameters and its general solution has not been found till now. A selected class of solutions to this problem has been discovered by H.S.Y. Chan (1966), see Rozvany (1998) for a review. The problem of transmitting an arbitrarily directed point load applied between two point supports also belongs to this class; then the points of application of the three forces (two of them being reactions) lie along one line. New and surprisingly complicated highly accurate numerical solutions to this problem have been recently reported by He and Gilbert (2015).

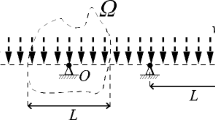
The present paper is aimed at delivering the solutions to a subclass of the three force problem posed to the present authors by George Rozvany: find the Michell truss transmitting a given horizontal force to the two point supports, one of them being a roller, see Fig. 1.

Fig. 1
figure 1

Posing George Rozvany’s problem

Full size image

The solution depends on the feasible domain Ω and the position of the point of application of the force, see Fig. 2, where the exemplary family of numerical solutions is displayed, all of them referring to the feasible domain being a square domain over the line linking the supports.

Fig. 2
figure 2

Family of numerical solutions to George Rozvany’s problem posed in Fig. 1

Full size image

This family is driven by the point load, applied at many possible places within the feasible square domain. The subdomain where the point load can be applied will be denoted by Ω P . Some of these layouts are well known from the literature, some of them have been only announced, reported without a derivation. Yet some of the layouts shown have never been reported.

For the sake of enabling a direct reference to the previous papers, especially to Sokół and Lewiński (2010), the problem will be posed as in Fig. 3; the line of supports is a vertical line, while the point load of magnitude P is applied upwards. Note that the axes x, y of the Cartesian system are different than those used in the paper cited above, which should not lead to misunderstandings. The unknown structures are trusses of finite or infinite number of members. The axial stress σ in the members is assumed to be bounded: \(\left | \sigma \right | \le \sigma _{p}\); σ p being the stress limit common for tension and compression

Fig. 3
figure 3

Scheme of notation of the problem to be solved coordinate

Full size image

George Rozvany’s problem to be discussed reads: find the least volume truss within a given feasible domain Ω which, under the condition \(\left | \sigma \right | \le \sigma _{p}\) at each member, transmits the given force P to the hinge support R and to the roller at H, see Fig. 3.

In Rozvany’s problem as originally posed the feasible domain is a square: 0≤x≤h, 0≤y≤h denoted by Ω1. In the present paper we shall discuss Rozvany’s problem in this domain or we shall extend this domain to make the problem simpler. The solution depends on the coordinates (x N, y N) of point N of the application of the force, hence it depends on two non-dimensional parameters:

$$ \xi = \frac{x_{\text{N}}}{h}, \qquad \eta = \frac{y_{\text{N}}}{h} $$
(1.1)

Two possible cases: a) ξ 2+η 2≤1, b) ξ 2+η 2≥1 will be discussed separately. The preliminary numerical results of Rozvany’s problem were reported at the CMM2011 conference (cf. Sokółand Rozvany 2011). For the special case of the point load applied at the middle point of the feasible square domain, or for ξ=1/2, η=1/2, the optimal layout as well as the numerical layout have been announced (without derivations) in Fig. 4 in Lewiński and Sokół (2014). This is probably the first Michell truss in which a curvilinear fan appears.

Fig. 4
figure 4

Geometry of the layout of possible solutions to Rozvany’s problem. Parameterization of the subsequent subdomains: RAB, NAC, ABDC, BDH

Full size image

The problem of minimizing the weight of the truss under the condition |σ|≤σ p reduces to two auxiliary mutually dual problems. The primal problem is formulated as a minimization problem of an integral of a norm of the statically admissible stress within the two-dimensional domains and along the reinforcing bars, see (2.6)–(2.7) in Graczykowski and Lewiński (2006a). This formulation will be discussed in Sec. 6. The dual problem reduces to maximizing the virtual work L(w) over the virtual displacement fields w=(u, v) being continuous and satisfying the locking-like condition pointwise in the feasible domain:

$$\boldsymbol{\varepsilon} \left(\textbf{w} (\textbf{x}) \right) \in {\mathcal{B}}, \quad \forall\ \textbf{x} = (x,\,y) \in {\Omega}. $$
(1.2)

Here \({\mathcal B}\) is the unit ball: the set of second rank tensors ε with bounded eigenvalues: |ε I|≤1, |ε II|≤1. The volume of the optimal truss is expressed by

$$\begin{array}{@{}rcl@{}} V & = & \frac{1}{\sigma_{p}} \max \left\{ L(\textbf{w})\ \left| \textbf{w}\ \text{being kinematically admissible and} \right.\right.\\ & & \left.\left.\boldsymbol{\varepsilon} (\textbf{w}(\textbf{x})) \in {\mathcal B},\ \textbf{x} \in {\Omega} \right. \right\} \end{array} $$
(1.3)

The equivalence of both the problems mentioned: primal and dual has been proved in Bouchitté et al. (2008) with using subtle tools of the variational calculus.

In Rozvany’s problem considered the condition of kinematic admissibility of a field w means its continuity in Ω, vanishing at point R of both its components and vanishing of its x-component at point H. In the present paper we shall make use of the construction of this field based on the two pointwise conditions

$$\varepsilon_{\text{I}} (\textbf{w}(\textbf{x})) = 1, \qquad \varepsilon_{\text{II}} (\textbf{w}(\textbf{x})) = - 1 $$
(1.4)

at each point x of the domain Ω m occupied by the optimal structure. The above conditions mean that the pair (ε I, ε II) lies at the vertex (1, −1) of the locking locus \({\mathcal B}\). The maximization operation in (1.3) imposes the strain field to lie as far as possible from the origin (0, 0) being the middle point of \({\mathcal B}\). In the problems in which shear deformation prevails, and Rozvany’s problem is of this type, the conditions (1.4) are satisfied in the whole material domain Ω m identically. The field w should be continuously extended beyond this region such that the condition (1.2) is fulfilled in the whole feasible domain Ω. Note, however, that such an extension is not unique. Such extensions will not be constructed in the present paper, since the question of correctness has been resolved by repeating the computation of the volumes with using the stress-based formula mentioned above. In all cases both the results occur to be the same up to arbitrary accuracy. The duality gap is thus zero, which ends the proof of the correctness of the constructions put forward.

The conditions (1.4) are highly restrictive: they determine very specific shapes of trajectories of the virtual principal strains. These trajectories will be parameterized by the curvilinear system forming Hencky nets (α, β), known from the theory of plasticity. In this paper we shall make use of the known parameterizations of these nets. However, the construction of the virtual displacement field w satisfying (1.4) for Rozvany’s problem is only partly known. We shall perform one construction of the virtual field w to make the paper complete. To this end we make use of the analytical methods by Carathéodory and Schmidt (1923), Chan (1966, 1967), Hemp (1973) and by the techniques developed in Graczykowski and Lewiński (2006a, (Graczykowski and Lewiński 2006b)b, 2007) and Sokół and Lewiński (2010).

The present paper delivers both analytical and numerical solutions to a wide subclass of Rozvany’s problem. We depict the domains of point load application for which the solutions constructed are fully complete, justified by the criterion of the duality gap being zero and confirmed numerically by the newest version of the ground structure method. It turns out that convexity is one of the properties which determines the range of applicability of the analytical layouts discussed.

To make the denotation of references to frequently cited papers as short as possible we shall adopt the following convention: Eq. (n.m) from the paper by Sokół and Lewiński (2010) will be referred to as (SL n.m). Similarly, equation Eq. (n) from the paper by Lewiński et al. (1994a) (or 1994b) will be referred to as Eq. (LZRa n) (or Eq. (LZRb n)). Moreover Eq. (GLa n.m), Eq. (GLb n.m) refer to Eq. (n.m) in Graczykowski and Lewiński (2006a, b)).

The Hencky net is formed by curvilinear parametric lines (α, β). The curvilinear coordinates of a specific point are usually denoted by (λ, μ). The virtual displacements along the (α, β) coordinate lines are denoted by (u, v). The displacements along the axes x or y are denoted by w x , w y . Points will be denoted by straight fonts, like A, B, R, N, H, while functions will be denoted by italic fonts, like F, G. In particular, Lamé coefficients are functions and will be denoted by A, B. Frequently used two-argument Chan’s functions F n , G n are defined as in Eqs (LZRa 1-2).

2 Parameterization of the feasible domain. Case of the domain Ω P being ξ 2+η 2≤1

The structure to be constructed should be supported at the fixed hinge R and should have a roller support at H, with the slide along the vertical direction. The structure should lie to the right of the line RH (the line x=0) and admit members tangential to this line. Let us note that the point N of the application of the force P lies in the quarter of the circle of origin at R and of radius h: \({\Omega }_{P} = \left \{ (x_{\text {N}},\,y_{\text {N}}) \right .|\, x_{\text {N}}^{2} + y_{\text {N}}^{2} \le h^{2},\left .\,x_{\text {N}} \ge 0 \right \}\). It turns out that a broad class of solutions is encompassed by the layout shown in Fig. 4, composed of:

a) the circular fan RAB

b) the circular fan NAC

c) the domain ABDC generated by two circular arcs

d) the domain BDH tangent to RH, called Chan’s domain

The numerical solutions will show that the solutions to George Rozvany’s problem considered assume the form of Fig. 4 if the point N lies sufficiently close to the axis x (y=0). A detailed description of this condition will be given in Section 7.

In the circular fan domains RAB and NAC the polar coordinate systems are introduced: (r, β) and (r, α) where β∈[0, 𝜃 2] and α∈[0, 𝜃 1]. In these domains the virtual displacement field w=(u, v) is constructed: u – along the radii and v – along the circles of r=const.

The parametric lines (α, β) in the domain ABDC are extensions of the radial lines running from within the fans RAB, NAC. The geometry of the parametric lines (α, β) in the domain ABDC has been for the first time mathematically described by Carathéodory and Schmidt (1923). This construction can be found in Hemp (1973), cf. Lewiński et al. (1994a). The parametric lines are defined with respect to the Cartesian system (x 0, y 0) of origin at A, see Fig. 4. These formulae are given by Eqs (SL 2.5-2.7). The Lamé coefficients in the domain ABDC at a point of coordinates (λ,μ) are denoted by A(λ, μ), B(λ, μ) and expressed by Eqs (SL 2.4). The extension of the parameterization (α, β) into the domain BDH has been elaborated by Chan (1967). We repeat here the Eqs (GLa 7.30) expressing the parameterization referred to the Cartesian coordinate system (x 0, y 0)

$$\begin{array}{@{}rcl@{}} x_{0} (\lambda,\,\mu) & = & \bar{x} (\lambda,\,\mu) \cos (\mu -\lambda ) \\ & & {}-\bar{y} (\lambda,\,\mu) \sin (\mu -\lambda) \\ y_{0} (\lambda,\,\mu) & = & \bar{x} (\lambda,\,\mu) \sin (\mu -\lambda ) \\ & & {}+ \bar{y} (\lambda,\,\mu) \cos (\mu -\lambda) \end{array} $$
(2.1)

where

$$\begin{array}{@{}rcl@{}} \bar{x} (\alpha,\,\beta) & = & r_{2} F_{2} (\beta,\,\alpha) + r_{1} F_{1} (\alpha,\,\beta) \\ & & {}-r_{2} F_{2} (\beta -\theta_{2},\,\alpha + \theta_{2}) \\ & & {}-r_{1} F_{3} (\beta -\theta_{2},\,\alpha + \theta_{2}) \\ \bar{y} (\alpha,\,\beta) & = & r_{2} F_{1} (\beta,\,\alpha) + r_{1} F_{2} (\alpha,\,\beta) \\ & & {}-r_{2} F_{1} (\beta -\theta_{2},\,\alpha + \theta_{2}) \\ & & {}-r_{1} F_{2} (\beta -\theta_{2},\,\alpha + \theta_{2}) \end{array} $$
(2.2)

These equations determine Lamé coefficients A(α, β), B(α, β), cf. Eqs (GLa 7.31)

$$\begin{array}{@{}rcl@{}} A (\alpha,\,\beta) & = & r_{2} G_{1} (\beta,\,\alpha) + r_{1}G_{0} (\alpha,\,\beta) \\ & & {}-r_{2}G_{1} (\beta -\theta_{2},\,\alpha + \theta_{2}) \\ & & {}-r_{1}G_{2} (\beta -\theta_{2},\,\alpha + \theta_{2})\\ B (\alpha,\,\beta) & = & r_{2}G_{0} (\beta,\,\alpha) + r_{1}G_{1} (\alpha,\,\beta) \\ & & {}-r_{2}G_{0} (\beta -\theta_{2},\,\alpha + \theta_{2}) \\ & & {}-r_{1}G_{1} (\beta -\theta_{2},\,\alpha + \theta_{2}) \end{array} $$
(2.3)

Let us note that the Lamé coefficient B vanishes along the line BH, since there β=α+𝜃 2 and one can easy check that B(α, α+𝜃 2)=0. Let us add that the points (x 0, y 0) lie along the line RBH if

$$x_{0} + r_{2} = y_{0} \text{cot}\,\theta_{2} $$
(2.4)

The parameters r 1, r 2, 𝜃 1, 𝜃 2 determine the position of point N by the equations

$$\begin{array}{@{}l@{}} x_{\text{N}} = r_{1}\cos \theta_{2} + r_{2}\sin \theta_{2} \\ y_{\text{N}} = -r_{1}\sin \theta_{2} + r_{2}\cos \theta_{2} \end{array} $$
(2.5)

The equilibrium condition Q h−P x N=0 yields

$$Q = \xi P $$
(2.6)

The coordinates (α, β) of point H are (𝜃 1, 𝜃 1+𝜃 2). The equations (2.1), (2.2) determine the coordinates \((x_{0}^{\text {H}},\,y_{0}^{\text {H}})\) of the point H. One can prove that the substitution λ=𝜃 1, μ=𝜃 1+𝜃 2 into these formulae results in the expressions for \(x_{0}^{\text {H}},\,y_{0}^{\text {H}}\) which satisfy (2.4) identically. This proof will be omitted. In particular we find

$$y_{0}^{\text{H}} = h\sin \theta_{2}, \quad h = M(\theta_{1},\,\theta_{1} + \theta_{2}) $$
(2.7)

where

$$\begin{array}{@{}rcl@{}} M(\alpha,\,\beta) & = & r_{1}\left[F_{1}(\alpha,\,\beta) -F_{3}(\alpha,\,\beta) \right] \\ & & {}+ r_{2} \left[F_{0}(\alpha,\,\beta) -F_{2}(\alpha,\,\beta) \right] \end{array} $$
(2.8)

By inverting (2.5) and substitution the results into (2.8) one finds a new form of the equation h=M(𝜃 1, 𝜃 1+𝜃 2) which links ξ, η, 𝜃 1, 𝜃 2

$$\begin{array}{@{}l@{}} \xi \left[ \cos \theta_{2} \left(F_{1} (\alpha,\,\beta) -F_{3}(\alpha,\,\beta) \right) \right.\\ \left.{}+ \sin \theta_{2} \left(F_{0} (\alpha,\,\beta) -F_{2}(\alpha,\,\beta) \right) \right]_{| \alpha = \theta_{1},\,\beta = \theta_{1} + \theta_{2}} + \\ {}+\eta \left[ -\sin \theta_{2} \left(F_{1} (\alpha,\,\beta) -F_{3}(\alpha,\,\beta) \right)\right. \\ \left.{}+ \cos \theta_{2} \left(F_{0}(\alpha,\,\beta) -F_{2}(\alpha,\,\beta) \right) \right]_{| \alpha = \theta_{1},\,\beta = \theta_{1} + \theta_{2}} = 1. \end{array} $$
(2.9)

3 Construction of the virtual, kinematically admissible displacement field. Case of the domain Ω P being ξ 2+η 2≤1

The point N of application of the force is assumed to lie within the quarter of the circle of the origin at R and of the radius h or ξ 2+η 2≤1. The field w=(u, v) is constructed consecutively: starting from the domains RAN, RAB, NAC, through the domain ABDC and then is found in the domain BDH by subsequent extensions of the solutions through the boundaries AB, AC, BD. The field w should vanish at point R and its horizontal component should vanish at H. To simplify the analysis we shall retain only the first condition and determine w up to an angle of rigid rotation around R. Thus the expression for the virtual work involves now two terms

$$L = Pw_{y}^{\text{N}} + Qw_{x}^{\text{H}} $$
(3.1)

and the final result is obviously independent of the angle of rigid rotation around R. Just the expression (3.1) will be used to compute the optimal volume of the structure by the formula (1.3). The operation max in (1.3) will be performed over the parameters r 1, r 2, 𝜃 1, 𝜃 2 of the design predicted in the form as in Fig. 4. These parameters are linked by the constraints determined by the position of the force and the position of the support at H.

To compute the optimal volume one should construct the fields (u, v) in the whole feasible domain and compute \(w_{y}^{\text {N}},\,w_{x}^{\text {H}}\). The fields (u, v) have already been built in the triangle RAN and in the domain RBDCNA, see Sokół and Lewiński (2010), but its extension along BDH has never been constructed. This extension will be performed in the present paper.

The displacement fields (u, v) in the domain NAC are given by Eqs (SL 2.55). The parameter ψ involved there represents an angle of rigid rotation of the whole structure around R. The value of ψ does not affect the value of the virtual work, if computed by (3.1). The value of ψ will be chosen to be equal −1, as in the papers by Chan (1966) and Sokół and Lewiński (2010). Under this choice the virtual displacements of point N, referred to the Cartesian system (x 0, y 0) read

$$w_{x_{0}}^{\text{N}} = r_{2} -r_{1}, w_{y_{0}}^{\text{N}} = r_{1} -r_{2} $$
(3.2)

Thus the virtual work (3.1) is expressed by

$$L = P\left[ (\cos \theta_{2} -\sin \theta_{2}) (r_{2} -r_{1}) -\xi v^{\text{H}} \right] $$
(3.3)

where v H is the displacement of point H measured along β coordinate line. Computation of the virtual work is thus reduced to computing v H. To this end one should construct the virtual field (u, v) first in ABDC and then in BDH. The fields (u, v) in ABDC are given by Eqs (SL 2.70, 2.72); these results correspond to ψ=−1.

To extend these fields towards the domain BDH we make use of the integral representation, see Eqs (LZRa 74-75) involving the angle of infinitesimal in-plane rotation ω

$$\begin{array}{@{}rcl@{}} v(\lambda,\,\mu) &=& \tilde{v}_{\theta} (\lambda,\,\mu) + \int\limits_{\theta}^{\mu} \left[ -\cos (\beta -\mu) \right.\\ &&\left.-\sin (\beta -\mu) \omega (\lambda,\,\beta) \right] B (\lambda,\,\beta)\, \mathrm{d}\beta \end{array} $$
(3.4)

with

$$\begin{array}{@{}rcl@{}} \tilde{v}_{\theta} (\lambda,\,u) & = & \sin (\theta -\mu)\,u(\lambda,\,\theta) + \\ & & \cos (\theta -\mu)\,v (\lambda,\,\theta) \end{array} $$
(3.5)

where 0≤𝜃≤μ. The angle of rotation of the whole structure around R is equal ψ=−1, hence ω(0, 0)=−1. We insert this value into the formula for the field ω, see Eq. (LZRa 73) to find

$$\omega (\lambda,\,\beta) = -2 (\lambda + \beta) -1 $$
(3.6)

This result will be used in (3.4). The Lamé coefficient B in the domains ABDC and BDH can be expressed as below, cf. Eq. (GLb 6.21)

$$\begin{array}{@{}l@{}} B(\lambda,\,\beta) = \left\{ \begin{array}{@{}l@{\quad}l@{}} B^{*} (\lambda,\,\beta), & 0 \le \beta \le \theta_{2} \\ B^{*} (\lambda,\,\beta) + B^{\bullet} (\lambda,\,\beta), &\theta_{2} \le \beta \le \theta_{1} + \theta_{2} \end{array} \right. \end{array} $$
(3.7)

where

$$\begin{array}{@{}rcl@{}} B^{*} (\lambda,\,\beta) & = & r_{2}G_{0} (\beta,\,\lambda) + r_{1}G_{1}(\lambda,\,\beta) \\ B^{\bullet} (\lambda,\,\beta) & = &-r_{2} G_{0} (\beta -\theta_{2},\,\lambda + \theta_{2}) \\ & & {}-r_{1} G_{1} (\beta -\theta_{2},\,\lambda + \theta_{2}) \end{array} $$
(3.8)

Note that the first of the above formula coincides with the formula for B in the domain ABDC, see Eq. (SL 2.4).

Substitution of (3.6)–(3.8) into (3.4) in case of 𝜃=𝜃 2 gives

$$v (\lambda,\,\mu) = v^{*} (\lambda,\,\mu) + v_{1} (\lambda,\,\mu) $$
(3.9)

where

$$\begin{array}{@{}rcl@{}} v^{*} (\lambda,\,\mu) & = & \tilde{v}_{0} (\lambda,\,\mu) + \int\limits_{0}^{\theta_{2}} \left[ -\cos (\beta -\mu)\right. \\ & &\left. {}-\sin (\beta -\mu) \omega (\lambda,\,\beta) \right] B^{*} (\lambda,\,\beta)\,\mathrm{d}\beta + \\ & + & \int\limits_{\theta_{2}}^{\mu} \left[ -\cos (\beta -\mu)\right. \\ & & \left.{}-\sin (\beta -\mu) \omega (\lambda,\,\beta) \right] B^{*} (\lambda,\,\beta)\, \mathrm{d}\beta \end{array} $$
(3.10)

and

$$\begin{array}{@{}rcl@{}} v_{1} (\lambda,\,\mu) & = & \int\limits_{\theta_{2}}^{\mu} \left[ -\cos (\beta -\mu)\right. \\ & & \left.{}-\sin (\beta -\mu) \omega (\lambda,\,\beta) \right] B^{\bullet} (\lambda,\,\beta)\, \mathrm{d}\beta \end{array} $$
(3.11)

Note that the expression (3.10) can be written as follows

$$\begin{array}{@{}rcl@{}} v^{*} (\lambda,\,\mu) & = & \tilde{v}_{0} (\lambda,\,\mu) + \int\limits_{0}^{\mu} \left[ -\cos (\beta -\mu)\right. \\ & & \left.{}-\sin (\beta -\mu) \omega (\lambda,\,\beta) \right] B^{*} (\lambda,\,\beta)\, \mathrm{d}\beta \end{array} $$
(3.12)

and because B ∗(λ, β) is equal to B(λ, β) determined within the domain ABDC, hence the function v ∗(λ, μ) is expressed by Eq. (SL 2.72), although now this expression applies to a different range of the arguments (λ, μ). Thus the field v ∗(λ, μ) is expressed by

$$\begin{array}{@{}rcl@{}} v^{*} (\lambda,\,\mu) & = & -2r_{1}\mu G_{1} (\lambda,\,\mu) -r_{2} (1 + 2\mu) G_{0} (\lambda,\,\mu) \\ & & {}+ (r_{2} -r_{1}) [ F_{1}(\lambda,\,\mu) + F_{2}(\lambda,\,\mu) ] \end{array} $$
(3.13)

Now, to find v 1(λ, μ), we insert (3.6) and (3.8) into (3.11) and perform integration over β. Thus we arrive at the result being a sum of four terms:

$$\begin{array}{@{}rcl@{}} v_{1} (\lambda,\,\mu) & = & r_{1} [ b_{1} (\theta_{2};\,\lambda,\,\mu) + b_{2} (\theta_{2};\,\lambda,\,\mu) ] \\ & & {}+ r_{2} [ f_{1}(\theta_{2};\,\lambda,\,\mu) + f_{2} (\theta_{2};\,\lambda,\,\mu) ] \end{array} $$
(3.14)

where

$$\begin{array}{@{}rcl@{}} f_{1} (\theta;\,\lambda,\,\mu) \!&=&\! {\int}_{\theta}^{\mu} \cos (\beta \,-\,\mu) G_{0} (\beta -\theta,\,\lambda + \theta) \, \mathrm{d}\beta \\[-1pt] f_{2} (\theta;\,\lambda,\,\mu) \!&=&\! {\int}_{\theta}^{\mu} \omega (\lambda,\,\beta) \sin (\beta \,-\,\mu) G_{0} (\beta \,-\,\theta,\,\lambda \,+\, \theta)\, \mathrm{d} \beta \\[-1pt] b_{1} (\theta;\,\lambda,\,\mu) \!&=&\! {\int}_{\theta}^{\mu} \cos (\beta \,-\,\mu) G_{1} (\beta \,-\,\theta,\,\lambda \,+\, \theta)\, \mathrm{d} \beta \\[-1pt] b_{2}(\theta;\,\lambda,\,\mu) \!&=&\! {\int}_{\theta}^{\mu} \omega (\lambda,\,\beta) \sin (\beta \,-\,\mu) G_{1} (\beta \,-\,\theta,\,\lambda + \theta)\, \mathrm{d} \beta \end{array} $$
(3.15)

and the function ω(λ, β) is given by (3.6). The above integrals can be explicitly expressed in terms of functions F n , G n . According to Eqs (LZRa 16) one finds

$$\begin{array}{@{}l@{}} f_{1}(\theta;\,\lambda,\,\mu) = F_{1} (\mu -\theta,\,\lambda + \theta) \\ b_{1}(\theta;\,\lambda,\,\mu) = F_{2} (\mu -\theta,\,\lambda + \theta) \end{array} $$
(3.16)

The remaining integrals are expressed by

$$\begin{array}{@{}rcl@{}} f_{2}(\theta;\,\lambda,\,\mu) & = & (1 + 2\lambda) F_{2} (\mu -\theta,\,\lambda + \theta) \\ & & {}+ 2g_{5} (\theta;\,\mu,\,\lambda ) \\ b_{2} (\theta;\,\lambda,\,\mu) & = & (1 + 2\lambda) F_{3} (\mu -\theta,\,\lambda + \theta) \\ & & {}+ 2g_{6} (\theta;\,\mu,\,\lambda) \end{array} $$
(3.17)

while the functions g 5, g 6 are defined by Eqs (LZRa A.11, A.12). The above results make it possible to express the function v 1(λ, μ) in terms of F n , G n functions. By substituting this result into (3.9) and using (3.13) one arrives at the final expression for the field v:

$$v (\lambda,\,\mu) = r_{1} a_{1} (\lambda,\,\mu) + r_{2} a_{2} (\lambda,\,\mu) $$
(3.18)

with

$$\begin{array}{@{}rcl@{}} a_{1}(\lambda,\,\mu) & = & -2\mu G_{1} (\lambda,\,\mu) -F_{1} (\lambda,\,\mu) \\ & - & F_{2} (\lambda,\,\mu) -3F_{2} (\mu -\theta_{2},\,\lambda + \theta_{2}) \\ & + & F_{3} (\mu -\theta_{2},\,\lambda + \theta_{2}) \\ & + & 2 (\mu -\theta_{2}) G_{1} (\mu -\theta_{2}),\,\lambda + \theta_{2}), \\ a_{2} (\lambda,\,\mu) & = & -(1 + 2\mu) G_{0} (\lambda,\,\mu) + F_{1} (\lambda,\,\mu) \\ & + & F_{2} (\lambda,\,\mu) -F_{1} (\mu -\theta_{2},\,\lambda + \theta_{2}) \\ & + & F_{2} (\mu -\theta_{2},\,\lambda + \theta_{2}) \\ & + & 2 (\mu -\theta_{2}) G_{0} (\mu -\theta_{2},\,\lambda + \theta_{2}). \end{array} $$
(3.19)

Having the fields v and B one can construct the field u by

$$u(\lambda,\,\mu) = -\frac{\partial v (\lambda,\,\mu)}{\partial \mu} -B(\lambda,\,\mu) $$
(3.20)

Let us recall the definitions of the fields

$$\begin{array}{@{}l@{}} u^{0} (\lambda,\,\mu) = u (\lambda,\,\mu) -2\lambda A(\lambda,\,\mu) \\ v^{0} (\lambda,\,\mu) = v (\lambda,\,\mu) + 2\mu B (\lambda,\,\mu) \end{array} $$
(3.21)

They satisfy the differential equations

$$\begin{array}{@{}l@{}} \frac{\partial^{2} u^{0} (\lambda,\,\mu)}{\partial \lambda\, \partial\mu} -u^{0} (\lambda,\,\mu) = 0, \\ \frac{\partial^{2} v^{0} (\lambda,\,\mu)}{\partial \lambda\, \partial \mu} -v^{0} (\lambda,\,\mu) = 0 \end{array} $$
(3.22)

In the domain BDH the field v 0(λ, μ) is given by

$$v^{0} (\lambda,\,\mu) = r_{1} {a_{1}^{0}} (\lambda,\,\mu) + r_{2} {a_{2}^{0}} (\lambda,\,\mu) $$
(3.23)
$$\begin{array}{@{}rcl@{}} {a_{1}^{0}} (\lambda,\,\mu) & = & -F_{1} (\lambda,\,\mu) -F_{2} (\lambda,\,\mu) \\ & & {}-3F_{2} (\mu -\theta_{2},\,\lambda + \theta_{2}) \\ & & {}+ F_{3} (\mu -\theta_{2},\,\lambda + \theta_{2}) \\ & & {}-2\theta_{2} G_{1} (\mu -\theta_{2},\,\lambda + \theta_{2}), \\ {a_{2}^{0}} (\lambda,\,\mu) & = & -G_{0} (\lambda,\,\mu) + F_{1} (\lambda,\,\mu) \\ & & {}+ F_{2} (\lambda,\,\mu) -F_{1} (\mu -\theta_{2},\,\lambda + \theta_{2}) \\ & & {}+ F_{2} (\mu -\theta_{2},\,\lambda + \theta_{2}) \\ & & {}-2\theta_{2} G_{0} (\mu -\theta_{2},\,\lambda + \theta_{2}) \end{array} $$
(3.24)

It is seen that the second of Eqs (3.22) is fulfilled, since the functions F n , G n satisfy the same equation, see Eq. (LZRa 5).

Let us recall that the function B(α, β) vanishes along the line BH where β=α+𝜃 2. Consequently,

$$v (\alpha,\,\alpha + \theta_{2}) = v^{0} (\alpha,\,\alpha + \theta_{2}), $$
(3.25)

which makes the computation of v H easier. We obtain

$$\begin{array}{@{}rcl@{}} -v^{\text{H}} & = & 2\theta_{2} \left(r_{1} G_{1} (\theta_{1},\,\theta_{1} + \theta_{2}) + r_{2} G_{0} (\theta_{1},\,\theta_{1} + \theta_{2}) \right) \\ & + & r_{2} \left(F_{0} (\theta_{1},\,\theta_{1} + \theta_{2}) -F_{2}(\theta_{1},\,\theta_{1} + \theta_{2}) \right) \\ & + & r_{1} \left(F_{1} (\theta_{1},\,\theta_{1} + \theta_{2}) -F_{3} (\theta_{1},\,\theta_{1} + \theta_{2}) \right) \\ & + & 4r_{1} F_{2} (\theta_{1},\,\theta_{1} + \theta_{2}) \end{array} $$
(3.26)

By using (2.7), (2.8) one can rearrange the above formula to the form

$$\begin{array}{@{}rcl@{}} -v^{\text{H}} & = & h + 2\theta_{2} (r_{1}G_{1} (\theta_{1},\,\theta_{1} + \theta_{2}) \\ & & {} +r_{2} G_{0} (\theta_{1},\,\theta_{1} + \theta_{2}) ) \\ & & {} + 4r_{1} F_{2} (\theta_{1},\,\theta_{1} + \theta_{2}) \end{array} $$
(3.27)

Note that the expression in the braces is equal to the Lamé field B in the domain ABDC, see Eq. (SL 2.4).

Thus the formulae (3.3) and (3.27) determine the virtual work L. It is expressed in terms of r 1, r 2, 𝜃 1, 𝜃 2. The optimal volume is computed by performing the maximization operation in (1.3) over admissible values of r 1, r 2, 𝜃 1, 𝜃 2. More details connected with this topic are discussed in Section 7.

4 Construction of the Hencky nets and virtual displacement fields for the special case of vanishing fan NAC (r 1=0)

The analytical construction of the Hencky nets and the fields (u, v) in domains of Fig. 4 comprise the degenerated case of the fan NAC being reduced to one point N=A=C. A formal substitution of r 1=0 into the formulae of Secs 2 and 3 gives a correct description of geometry of nets and their kinematics, see Fig. 5.

Fig. 5
figure 5

Geometry of the layout of possible solutions to Rozvany’s problem in case of r 1=0. Parameterization of the subsequent subdomains: RAB, ABD, BDH

Full size image

The parametric equations of the Hencky net in ABD are given by (2.1) in which

$$\begin{array}{@{}l@{}} \bar{x} (\alpha,\,\beta) = r_{2} F_{2} (\beta,\,\alpha), \\ \bar{y} (\alpha,\,\beta) = r_{2} F_{1} (\beta,\,\alpha) \end{array} $$
(4.1)

while in the domain BDH the Hencky net is given by (2.1) with

$$\begin{array}{@{}l@{}} {\bar{x} (\alpha,\,\beta)}/{r_{2}} = F_{2} (\beta,\,\alpha) -F_{2} (\beta -\theta_{2},\,\alpha + \theta_{2}) \\ {\bar{y} (\alpha,\,\beta)}/{r_{2}} = F_{1} (\beta,\,\alpha) -F_{1} (\beta -\theta_{2},\,\alpha + \theta_{2}) \end{array} $$
(4.2)

The Lamé coefficients A(α, β), B(α, β) in the domain ABD are

$$\begin{array}{@{}l@{}} A (\alpha,\,\beta) = r_{2} G_{1} (\beta,\,\alpha), \\ B (\alpha,\,\beta) = r_{2} G_{0} (\beta,\,\alpha) \end{array} $$
(4.3)

and in the domain BDH:

$$\begin{array}{@{}l@{}} {A (\alpha,\,\beta)}/{r_{2}} = G_{1} (\beta,\,\alpha) -G_{1} (\beta -\theta_{2},\,\alpha + \theta_{2}) \\ {B (\alpha,\,\beta)}/{r_{2}} = G_{0} (\beta,\,\alpha) -G_{0} (\beta -\theta_{2},\,\alpha + \theta_{2}) \end{array} $$
(4.4)

Moreover (cf. (2.7)–(2.8))

$$h = r_{2} \left(F_{0} (\theta_{1},\,\theta_{1} + \theta_{2}) -F_{2} (\theta_{1},\,\theta_{1} + \theta_{2}) \right) $$
(4.5)

and \(\tan \theta _{2} = \xi /\eta \). To find the fields u, v in the domains ABD, BDH it is sufficient to put r 1=0. In particular we can express the value of v at H

$$-v^{\text{H}} = h + 2\theta_{2} r_{2} G_{0} (\theta_{1},\,\theta_{1} + \theta_{2}) $$
(4.6)

The layout in the form as shown in Fig. 5 is determined by three numbers: h, x N, y N; they determine the values of r 2, 𝜃 1, 𝜃 2. The formula (4.5) is the transcendental equation to find 𝜃 1. We see that the substitution of r 2, 𝜃 1, 𝜃 2 into (4.6) determines the optimal volume by (1.3) uniquely, since maximization runs over one-parameter set.

The analysis here applies also to the peculiar case of 𝜃 1=0; then h=r 2 and v H=−(1+2𝜃 2)r 2. The optimal layout has the shape of a sector of a circular domain.

5 Construction of the Hencky nets and virtual displacement fields. Case of the domain Ω P being ξ 2+η 2≥1

Consider the case of ξ 2+η 2≥1 corresponding to the point N lying outside the circle of the origin at R and of radius h. The optimal layout is composed of a circular fan RAB and the adjacent region BAN, see Fig. 6. The geometry of Hencky net and displacement field of the region BAN are derived in Lewiński et al. (1994b, see Fig. 1) and here we recall only the final formulae transformed to the new coordinate system.

Fig. 6
figure 6

Geometry of the layout of possible solutions to Rozvany’s problem in case of ξ 2+η 2≥1. Parameterization of the subsequent subdomains: RAB, BAN

Full size image

The parameterization of the region BAN presented in Fig. 6 leads to the following relation between Cartesian and angular coordinates (cf. Eqs (LZRa 58), (LZRb 194- 195)):

$$\begin{array}{@{}rcl@{}} x(\alpha,\,\beta) & = & \cos (\alpha -\beta )\,\bar{x} (\alpha,\,\beta) -\sin (\alpha -\beta )\,\bar{y} (\alpha,\,\beta )\\ y(\alpha,\,\beta) & = & h -\sin (\alpha -\beta)\,\bar{x}(\alpha,\,\beta )\\ & & {}-\cos (\alpha -\beta)\,\bar{y}(\alpha,\,\beta) \end{array} $$
(5.1)

with Mikhlin variables \(\bar {x} (\alpha ,\,\beta )\) and \(\bar {y} (\alpha ,\,\beta )\) expressed by

$$\begin{array}{@{}l@{}} {\bar{x} (\alpha,\,\beta)}/{h} = F_{1}(\alpha,\,\beta) -F_{3}(\beta,\,\alpha) \\ {\bar{y} (\alpha,\,\beta)}/{h} = F_{2}(\beta,\,\alpha) -F_{2}(\alpha,\,\beta) \end{array} $$
(5.2)

Note that the angles α and β in BAN are restricted by α∈[0, 𝜃 1] and \(\beta \in [0,\,\min (\alpha ,\,\theta _{2})]\), and that parametric lines α are tangent to the line y=h. Moreover, the limiting angles 𝜃 1 and 𝜃 2 can be determined directly from (5.1) for a prescribed position of node N, i.e.

$$\left\{ \begin{array}{l} x_{\text{N}} = x(\theta_{1},\,\theta_{2}) = \xi h\\ y_{\text{N}} = y(\theta_{1},\,\theta_{2}) = \eta h \end{array} \right. $$
(5.3)

It should be noted here that the solution to the above transcendental system of two unknowns 𝜃 1 and 𝜃 2 is in general not unique, but the uniqueness holds for physically admissible angles 𝜃 1∈[0, π/2] and 𝜃 2∈[0, 𝜃 1].

According to the applied parameterization, see Fig. 6, displacements of a point lying in the region BAN, referred to the local curvilinear coordinate system α, β are given by (cf. Eqs (LZRb 203-204))

$$\begin{array}{@{}rcl@{}} {u(\alpha,\,\beta)}/{h} & = & G_{1}(\beta,\,\alpha) + 2(\beta - \alpha) G_{0} (\beta,\,\alpha) \\ & & {}-2F_{1}(\beta,\,\alpha) \\ {v(\alpha,\,\beta)}/{h} & = & G_{0}(\beta,\,\alpha) + 2(\alpha -\beta) G_{1}(\beta,\,\alpha) \\ & & {}+ 2F_{2}(\beta,\,\alpha) \end{array} $$
(5.4)

Consequently, the displacements of the node N referred to the global Cartesian system x, y are expressed by

$$\begin{array}{@{}l@{}} w_{x}^{\text{N}} = \cos (\theta_{1} \,-\,\theta_{2})\,u(\theta_{1},\,\theta_{2}) \,+\, \sin (\theta_{1} \,-\,\theta_{2})\,v(\theta_{1},\,\theta_{2}) \\ w_{y}^{\text{N}} = -\sin (\theta_{1} \,-\,\theta_{2})\,u(\theta_{1},\,\theta_{2}) \,+\, \cos (\theta_{1} \,-\,\theta_{2})\,v(\theta_{1},\,\theta_{2}) \end{array} $$
(5.5)

and finally, the volume of the Michell structure of the layout presented in Fig. 6 is determined by the following formula

$$V = \frac{P w_{y}^{\text{N}}}{\sigma_{p}} $$
(5.6)

Note that in the present case of ξ 2+η 2≥1 the displacement field (5.4) of the region BAN satisfies the boundary condition at point B=H, i.e. \(w_{x}^{\text {H}} =\) \(\left . u(\alpha ,\,\beta ) \right |_{\alpha = 0,\,\beta = 0} = 0\). Thus contrary to the previous sections and especially to (3.1) we do not need to include the work \(Q w_{x}^{\text {H}}\). Moreover, all formulae presented in this section cover the limiting case ξ 2+η 2=1 giving 𝜃 2=0, which means that the optimal structure reduces to a circular fan RAB.

Remark 1

The layouts of Figs. 4, 5 and 6 do not encompass the whole family of the exact solutions to Rozvany’s problem discussed. The numerical experiments reveal that if point N lies close to the line RH, then point N becomes surrounded by the fibers and the layouts become different, more complicated. The subdomain of Ω P of possible places of point N for which the layouts of Figs. 4–6 correspond to the exact solutions will be described in Section 7.

6 The optimal volume expressed by the stress fields

In Michell structures the mass is either distributed in the plane or along the lines or curves along which the reinforcing bars are placed. The tensor field N=(N i j ) represents the in-plane stress within the domains in which the mass is distributed in the plane, the eigenvalues N I, N II being called principal in-plane stresses. In the reinforcing bars lying along the curve Γ where the mass is concentrated the stress resultant is represented by the axial force F. The limit stress is σ p . The condition of constant distribution of stress in all structural members links the volume of the structure with the stress field. The aim of the present section is just to express the volume of the optimal structure in terms of the stress fields. This formula for the volume will be compared with the kinematic formula (1.3). We shall show that for the optimal structures of the shapes outlined in Figs 4, 5 both the formulae produce the same results up to arbitrarily assumed accuracy. Thus the duality gap is zero, which confirms correctness of both the approaches: kinematic and static ones.

6.1 Optimal structures in the shape of the layouts of Fig. 4

The volume of the optimal structure of the shape of Fig. 4, referring to the case of r 1≥0, is determined by two equivalent formulae: Eq. (1.3) and by

$$\begin{array}{@{}rcl@{}} V & = & \frac{1}{\sigma_{p}} \min \left\{ \underset{\Omega}{\int} \left( |N_{\text{I}}| + |N_{\text{II}}| \right)\,\mathrm{d} {\Omega} + \underset{\Gamma}{\int} |F|\,\mathrm{d} s \right.\\ & & |\ \text{over the statically admissible stress} \\ & & \left.\text{fields \textbf{N} and \textit{F}} \right\} \end{array} $$
(6.1)

cf. Eqs (GLa 2.6-7). In the class of problems discussed here the Hencky net (α, β) found in the previous sections determines the trajectories of principal stresses. Let us introduce Hemp’s fibrous stress fields

$$T_{1} = B N_{\text{I}},\,T_{2} = A N_{\text{II}} $$
(6.2)

These fields represent the in-plane forces measured per a unit angle. They satisfy the equations

$$\frac{\partial T_{1}}{\partial \alpha} -T_{2} = 0, \qquad \frac{\partial T_{2}}{\partial \beta} -T_{1} = 0 $$
(6.3)

The fibrous stress fields (6.2) and the axial force F in the reinforcing bar are linked along the edge Γ by the known equilibrium equations of plane arches.

Remark 2

As in the theory of homogenization of elastic composites the theory of Michell structures introduces the stress fields at two different observation levels: at the macrolevel (or in the domain Ω) and at the microlevel (i.e. within the representative volume element, RVE). At the microlevel the stress state is strip-wise uniaxial and the stresses in the strips are equal either to −σ p or to σ p ; the units of this stress state is Pa=N/m 2. On the other hand we deal with the non-uniformly distributed stress field N at the macrolevel (with units N/m), and, for the sake of convenience, we deal with the fibrous stress fields T 1, T 2 (or Hemp’s forces) of units N, defined by (6.2). Since the reinforcing bars inevitably occur to transmit point loads to point supports, the axial force F in these members appears (of unit N). The cross section of these bars is chosen such that the axial stress is equal to −σ p or to σ p , like in strips at the RVE level.

Note that we do not face the problem of stress concentration: the norm of the stress state within the domain Ω at the RVE level and in the reinforcing bars equals σ p . Thus the stress is not only bounded everywhere, but made uniformly distributed, like in the least compliant trusses of minimal weight.

The equilibrium problem of the structure of Fig. 4 is governed by the same equations as the Hemp’s fields and the axial force F in the cantilever discussed in Sec. 6 of the paper by Graczykowski and Lewiński (2007). On the basis of the latter results we report below all the formulae for the stress fields in the structure of Fig. 4.

The interior of the fan RAB

The radial forces read

$$\begin{array}{@{}rcl@{}} {T_{1}(\beta)_{| \text{RAB}}}/{Q} & = & G_{0} (\theta_{1} + \theta_{2} -\beta,\,\theta_{1}) \\ & & {}-G_{2} (\theta_{1},\,\theta_{1} + \theta_{2} -\beta) \end{array} $$
(6.4)

The interior of the fan NAC

The radial forces read

$$\begin{array}{@{}rcl@{}} {T_{2}(\alpha)_{|\text{NAC}}}/{Q} & = & G_{1}(\theta_{1} -\alpha,\,\theta_{1} + \theta_{2}) \\ & & {}-G_{1}(\theta_{1} + \theta_{2},\,\theta_{1} -\alpha) \end{array} $$
(6.5)

The interior of the domain ABHDC

$$\begin{array}{@{}rcl@{}} {T_{1}(\alpha,\,\beta)_{|\text{ABHDC}}}/{Q} & = & G_{0} (\theta_{1} + \theta_{2} -\beta,\,\theta_{1} -\alpha) \\ & & {}-G_{2} (\theta_{1} -\alpha,\,\theta_{1} + \theta_{2} -\beta) \\ {T_{2}(\alpha,\,\beta)_{|\text{ABHDC}}}/{Q} & = & G_{1} (\theta_{1} -\alpha,\,\theta_{1} + \theta_{2} -\beta) \\ & & {}-G_{1} (\theta_{1} + \theta_{2} -\beta,\,\theta_{1} -\alpha) \end{array} $$
(6.6)

Thus the formulae above are valid for two adjacent regions: ABDC and BDH. The line BD is a line of their continuous extension.

The edge bar HDCN

The axial force in this bar is constant and equal to F=−Q.

The edge bar BH

The force F in this bar is varying, since each line α approaches the line BH in a tangent manner giving a subsequent contribution to the value of F. The points along BH have the coordinates (λ, λ+𝜃 2), λ∈[0, 𝜃 1]. The axial force along BH equals

$$F(\lambda)_{|\text{BH}} = {\int}_{\lambda}^{\theta_{1}} T_{1} (\alpha,\,\alpha + \theta_{2})_{|\text{BH}}\, \mathrm{d}\alpha $$
(6.7)

where T 1(α, α+𝜃 2)|BH is given by (6.6) or

$$\begin{array}{@{}rcl@{}} {T_{1}(\alpha,\,\alpha + \theta_{2})_{|\text{BH}}}/{Q} & = & G_{0}(\theta_{1} -\alpha,\,\theta_{1} -\alpha) \\ & & {}-G_{2}(\theta_{1} -\alpha,\,\theta_{1} -\alpha) \end{array} $$
(6.8)

The edge bar RB

The force F in RB is constant and equals

$$F_{\text{RB}} = {\int}_{0}^{\theta_{1}} T_{1} (\alpha,\,\alpha + \theta_{2})_{|\text{BH}}\,\mathrm{d}\alpha = F(0)_{|\text{BH}} $$
(6.9)

The edges RA and NA are not reinforced by bars. The point loads at R and N are transmitted by the axial forces in bars RB and NC as well as by the radial forces in the fans RAB and NAC. Let us write down the equilibrium equations of the nodes N and R.

The equilibrium equations of the node N (along the directions x 0, y 0) read

$$\begin{array}{@{}l@{}} P\cos \theta_{2} + T_{x_{0}} -Q\sin \theta_{1} = 0 \\ P\sin \theta_{2} + T_{y_{0}} -Q\cos \theta_{1} = 0 \end{array} $$
(6.10)

where the resultants of the radial forces in the fan NAC are

$$\begin{array}{@{}l@{}} T_{x_{0}} = {\int}_{0}^{\theta_{1}} \sin\alpha\ T_{2} (\alpha)_{|\text{NAC}}\,\mathrm{d} \alpha \\ T_{y_{0}} = {\int}_{0}^{\theta_{1}} \cos \alpha\ T_{2} (\alpha)_{|\text{NAC}}\,\mathrm{d} \alpha \end{array} $$
(6.11)

Upon performing integration in (6.11) one reduces (6.10) to the formulae

$$\begin{array}{@{}l@{}} \cos \theta_{2} + \xi \left[ F_{3} (\theta_{1},\,\theta_{1} + \theta_{2}) -F_{1}(\theta_{1},\,\theta_{1} + \theta_{2}) \right] = 0 \\ \sin \theta_{2} + \xi \left[ F_{2} (\theta_{1},\,\theta_{1} + \theta_{2}) -F_{0}(\theta_{1},\,\theta_{1} + \theta_{2}) \right] = 0 \end{array} $$
(6.12)

Note that if both equations (6.12) are satisfied, then the condition (2.9) is fulfilled identically.

The equilibrium conditions of the node R, along the directions x and y, are

$$\begin{array}{@{}l@{}} {}-Q + S_{x_{0}} \sin \theta_{2} -S_{y_{0}} \cos \theta_{2} = 0 \\ F_{\text{RB}} -P + S_{x_{0}} \cos \theta_{2} + S_{y_{0}} \sin \theta_{2} = 0 \end{array} $$
(6.13)

where

$$\begin{array}{@{}l@{}} S_{x_{0}} = {\int}_{0}^{\theta_{2}} \cos \beta \,T_{1} (\beta)_{|\text{RAB}}\,\mathrm{d}\beta \\ S_{y_{0}} = {\int}_{0}^{\theta_{2}} \sin \beta \,T_{1} (\beta)_{|\text{RAB}}\, \mathrm{d}\beta \end{array} $$
(6.14)

are the resultants of the radial forces in the fans along the axes (x 0, y 0). The integrals have been found, but the final formulae are fairly complicated and will not be reported. The above formulae determine the volumes of the subsequent segments of the structure of Fig. 4.

The volume of the interior of the fan RAB

$$V_{\text{RAB}} = \frac{r_{2}}{\sigma_{p}} {\int}_{0}^{\theta_{2}} T_{1} (\beta)_{|\text{RAB}}\,\mathrm{d} \beta $$
(6.15)

The volume of the interior of the fan NAC

$$V_{\text{NAC}} = -\frac{r_{1}}{\sigma_{p}} {\int}_{0}^{\theta_{1}} T_{2} (\alpha)_{|\text{NAC}}\,\mathrm{d}\alpha $$
(6.16)

The volume of the interior of the domain ABDC

$$\begin{array}{@{}rcl@{}} V_{\text{ABDC}} & = & \frac{1}{\sigma_{p}} {\int}_{0}^{\theta_{1}}\,\mathrm{d}\alpha {\int}_{0}^{\theta_{2}} \left(T_{1}(\alpha,\,\beta) A (\alpha,\,\beta) \right.\\ & & \left.{}-T_{2}(\alpha,\,\beta) B(\alpha,\,\beta) \right)\,\mathrm{d}\beta \end{array} $$
(6.17)

where T 1, T 2, A, B refer to the domain ABDC, see Eqs (6.6) and Eq. (SL 2.4).

The volume of the interior of the domain

BDH

$$\begin{array}{@{}rcl@{}} V_{\text{BDH}} & = & \frac{1}{\sigma_{p}} {\int}_{0}^{\theta_{1}}\,\mathrm{d}\alpha {\int}_{\theta_{2}}^{\theta_{2} + \alpha} \left(T_{1}(\alpha,\,\beta) A(\alpha,\,\beta)\right. \\ & &\left. {}-T_{2}(\alpha,\,\beta) B(\alpha,\,\beta) \right)\,\mathrm{d}\beta \end{array} $$
(6.18)

where T 1, T 2 are given by (6.6) while A, B – by (2.3).

The volume of the bar NC

$$V_{\text{NC}} = \frac{r_{1}}{\sigma_{p}} Q $$
(6.19)

The volume of the bar CH

$$\begin{array}{@{}rcl@{}} V_{\text{CH}} & = & \frac{Q}{\sigma_{p}} \left({\int}_{0}^{\theta_{2}} B(\theta_{1},\,\beta)_{|\text{ABDC}}\,\mathrm{d}\beta \right. \\ & & \left. + {\int}_{\theta_{2}}^{\theta_{1}+\theta_{2}} B(\theta_{1},\,\beta)_{|\text{BDH}}\,\mathrm{d} \beta \right) \end{array} $$
(6.20)

The volume of the bar

BH

$$V_{\text{BH}} = \frac{1}{\sigma_{p}} {\int}_{0}^{\theta_{1}} F(\lambda)_{|\text{BH}} A(\lambda,\,\lambda + \theta_{2})_{|\text{BDH}}\,\mathrm{d}\lambda $$
(6.21)

The volume of the bar RB

$$V_{\text{RB}} = \frac{r_{2}}{\sigma_{p}} F_{\text{RB}} $$
(6.22)

The volume of the whole structure equals

$$\begin{array}{@{}rcl@{}} V & = & V_{\text{RAB}} + V_{\text{NAC}} + V_{\text{ABDC}} + V_{\text{BDH}} \\ & & {}+ V_{\text{NC}} + V_{\text{CH}} + V_{\text{BH}} + V_{\text{RB}} \end{array} $$
(6.23)

The volume V can be expressed in terms of P, r 1, r 2, 𝜃 1, 𝜃 2, but this formula is long and is not reported. Minimization of V over admissible parameters determines the volume of the optimal structure.

6.2 Optimal structures in the shape of the layous of Fig. 5

The optimal structure of Fig. 5 differs from the structure in Fig. 4: the fan NAC degenerates to a point A=N=C, but simultaneously a new stiffener arises: the bar RN (or RA) of finite cross section, transmitting the axial force denoted by F RN. Let us write down the equilibrium equations of the nodes: A=N=C and R.

The equations of equilibrium of the forces acting at the node N=A=C, in directions x 0, y 0, read

$$\begin{array}{@{}l@{}} P\cos \theta_{2} + U_{x_{0}} -F_{\text{RN}} -Q\sin \theta_{1} = 0 \\ P\sin \theta_{2} + U_{y_{0}} -Q\cos \theta_{1} = 0 \end{array} $$
(6.24)

where \(U_{x_{0}},\,U_{y_{0}}\) are resultants of the force T 2 along the line β in the curvilinear fan around the point A=N=C, see Fig. 5. These forces are equal to \(T_{x_{0}},\,T_{y_{0}}\) given by (6.11), where T 2(α) is given by (6.6) for β=0. The second condition of (6.24) has the form of the second condition of (6.12) while the first of (6.24) assumes the form

$$\begin{array}{@{}rcl@{}} F_{\text{RN}} & = & P\cos \theta_{2} + Q [ F_{3}(\theta_{1},\,\theta_{1} + \theta_{2}) \\ & & {}-F_{1} (\theta_{1},\,\theta_{1} + \theta_{2}) ] \end{array} $$
(6.25)

Let us write down the equilibrium conditions (along x and y) of the forces acting at the node R

$$\begin{array}{@{}l@{}} {}-Q + (F_{\text{RN}} + S_{x_{0}}) \sin \theta_{2} -S_{y_{0}} \cos \theta_{2} = 0 \\ F_{\text{RB}} -P + (F_{\text{RN}} + S_{x_{0}}) \cos \theta_{2} + S_{y_{0}} \sin \theta_{2} = 0 \end{array} $$
(6.26)

where \(S_{x_{0}},\,S_{y_{0}}\) are given by (6.14).

Thus we have all necessary formulae to determine the stress state within the structure of Fig. 5.

The volume of the bar RN equals

$$V_{\text{RN}} = \frac{r_{2}}{\sigma_{p}} |F_{\text{RN}}| $$
(6.27)

The volume of the structure of Fig. 5 equals

$$\begin{array}{@{}rcl@{}} V & = & V_{\text{RAB}} + V_{\text{ABDC}} + V_{\text{BDH}} + V_{\text{CH}} \\ & & {}+ V_{\text{BH}} + V_{\text{RB}} + V_{\text{RN}} \end{array} $$
(6.28)

and in the appropriate places one should substitute r 1=0.

The equations (6.23), (6.28) refer to the case of ξ 2+η 2≤ 1.

7 Discussion of the solutions generated by varying position of the lateral force P

The optimal layouts of Rozvany’s problem strongly depend on the position N of the force P. The domain of possible points N has been denoted by Ω P . The main division of this domain is its separation by the circle: (x N)2+(y N)2=h 2 or ξ 2+η 2=1. The case of \({\Omega }_{P}^{\text {ext}}\) given by ξ 2+η 2≥1, ξ≤1, η≤1 has been fully solved, see Sec. 5. The case of \({\Omega }_{P}^{\text {int}}\) defined by ξ 2+η 2≤1 has turned out to be much more complicated. The numerical experiments reveal that the layouts of Figs. 4 and 5 describe the exact solutions correctly, if point N lies outside the shaded region \({\Omega }_{P}^{*}\) of \({\Omega }_{P}^{\text {int}}\), see Fig. 7. The region \({\Omega }_{P}^{\text {int}} \backslash {\Omega }_{P}^{*}\) determines the scope of applicability of formulae derived in Secs 2–4 and 6. This region can then be divided into two sub-regions \({{\Omega }_{P}^{1}}\), \({{\Omega }_{P}^{0}}\) of non-vanishing (r 1>0) and vanishing (r 1=0) fan NAC. As explained before, the limiting case of ξ 2+η 2=1 refers to the layouts composed of one circular fan RAB.

Fig. 7
figure 7

Separation of the domain Ω P corresponding to different optimal layouts

Full size image

The line separating the regions \({\Omega }_{P}^{*}\) and \({{\Omega }_{P}^{0}}\) can be derived from the following observations on the basis of the numerical results (see Electronic Supplementary Material attached to this paper): a) in the whole region \({{\Omega }_{P}^{0}}\) there is r 1=0, hence \(\theta _{2} = \arctan (\xi /\eta )\) and b) on the sought line the angle 𝜃 1 approaches its limiting value 𝜃 1=π/2. Then the coordinates ξ and η of this line can be obtained from (2.9) or (4.5) giving an implicit relation

$$h_{1} (\xi,\,\eta) = 0 $$
(7.1)

where

$$\begin{array}{@{}rcl@{}} h_{1}(\xi,\,\eta) & = &1 - \sqrt{\xi^{2} + \eta^{2}} \left(F_{0}(\theta_{1},\,\theta_{1} + \theta_{2}) \right.\\ & & {}\left.\left. -F_{2}(\theta_{1},\,\theta_{1} + \theta_{2}) \right) {\vphantom{\sqrt{\xi^{2} + \eta^{2}} \left(F_{0}(\theta_{1},\,\theta_{1} + \theta_{2}) \right.}}\right|_{\theta_{1} = \pi /2 \atop \theta_{2} = \text{arctan} (\xi/\eta)} \end{array} $$
(7.2)

It turns out that the structure of Fig. 5 is always convex: the angle π/2−𝜃 1 between the axis x 0 and the tangent to the line α=𝜃 1 at A=N=C is always nonnegative, hence 𝜃 1≤π/2. Just the border line between \({\Omega }_{P}^{*}\) and \({{\Omega }_{P}^{0}}\) corresponds to the layouts for which 𝜃 1=π/2 and the line α=𝜃 1 becomes tangent to RA at A.

The line separating regions \({{\Omega }_{P}^{0}}\) and \({{\Omega }_{P}^{1}}\) is more difficult to obtain. Note that in the region \({{\Omega }_{P}^{1}}\) the Eq. (6.12) hold, which means that angles 𝜃 1 and 𝜃 2 depend only on ξ. As before on the border line there holds \(\theta _{2} = \arctan (\xi /\eta )\), thus for a fixed value of ξ∈[0, 1] one can calculate 𝜃 1 and η from (6.12) giving the line η=η(ξ). The angle 𝜃 1 is redundant here but cannot be eliminated in an algebraic way because (6.12) are transcendental and implicit equations with regard to 𝜃 1. In other words, the procedure to obtain η=η(ξ) can be performed only numerically.

For now the present authors cannot precisely determine the line separating regions \({\Omega }_{P}^{*}\) and \({{\Omega }_{P}^{1}}\) so in the Fig. 7 this line is marked ‘approximately’ by a dashed straight segment which, however, corresponds well with the line separating different layouts obtained numerically.

Let us recall that the data are: P, x N, y N, h, σ p . In case of \({\Omega }_{P} = {\Omega }_{P}^{\text { int}} \backslash {\Omega }_{P}^{*}\) the optimal solution is predicted to be of the form shown in Fig. 4. The geometry of the optimal structure can be found by solving the dual (maximization) problem (1.3) or by solving the primal (minimization) problem (6.1). It turns out that the former problem is easier. Thus the strategy is to solve the dual problem and then insert the optimal parameters into the stress-based expression (6.1), specified in the forms (6.23) or (6.28) to check whether the volumes found by the mentioned formulae coincide. Thus in the first step the optimal volume is computed by performing maximization over w in the expression (1.3) with L given by (3.3) and (3.27). The field w is parameterized by the geometric quantities r 1, r 2, 𝜃 1, 𝜃 2 linked by the three equations: (2.5) and (2.9). Thus the virtual work L becomes a function Λ(r 1, r 2, 𝜃 1, 𝜃 2) and the problem (1.3) can be reduced to

$$ \begin{array}{@{}l@{}} \text{maximize}\, \frac{1}{\sigma_{p}} {\Lambda}(\theta_{1},\,\theta_{2},\,r_{1},\,r_{2}) \\ \ \quad\mathrm{subject~to~Eqs~(2.5)~and~Eq~(2.9)}\\ \ \quad\text{and}\ \, r_{1},\,r_{2},\,\theta_{1},\,\theta_{2} \ge 0 \end{array} $$
(7.3)

and then solved numerically with using for example FindMaximum procedure available in Mathematica.

It is worth noting that the solution to (7.3) is based only on the kinematically admissible displacement field. If we take into account the equilibrium conditions of the node N (or R) we can get an additional equation which eliminates the necessity of performing the maximization procedure. In the problem investigated in the present paper the design variables r 1, r 2, 𝜃 1, 𝜃 2 can uniquely be determined from the system of the following equations: (2.5) 1,2, (2.9) and (6.12) 1.

The exact solutions described by the formulae derived in Secs 2-6 have been verified numerically using the adaptive ground structure method put forward in Gilbert and Tyas (2003), then gradually developed and improved (see Sokół 2011, 2014, and Sokół and Rozvany GIN 2015). The comparison of exact optimal volumes and layouts with the corresponding numerical results clearly indicates the correctness of the formulae derived. The series of optimal solutions parameterized by (ξ i , η j ), with ξ i =i/10, η j =j/10; i=1, 2, …, 10, j=0, 1, …, 10 were performed using the ground structures of 200×200 cells with almost 500 million potential non-overlapping bars. Exemplary solutions are shown in Fig. 8 and Table 1. It has been mentioned earlier that in the region \({{\Omega }_{P}^{1}}\) the angles 𝜃 1 and 𝜃 2 depend only on ξ and this interesting property can easily be observed in the first three rows of Table 1, where the values of 𝜃 1 and 𝜃 2 are constant. For fixed ξ and increasing η the radius r 2 increases while r 1 decreases to zero, where the domain \({{\Omega }_{P}^{0}}\) begins. For more detailed comparison of numerical and analytical results for various ξ and η the Reader is referred to the Electronic Supplementary Material attached to this paper.

Fig. 8
figure 8

Selected analytical and numerical solutions for: a ξ=0.4, η=0; b ξ=0.6, η=0.4; c ξ=0.8, η=0.6; d ξ=0.9, η=0.9 (here V a represents the value of the volume found analytically, while V n represents its numerical approximation)

Full size image
Table 1 The characteristic data of the analytical solutions for selected values of ξ and η ∗)
Full size table

The numerical solutions corresponding to the shaded domain \({\Omega }_{P}^{*}\) for selected ξ and η are presented in Fig. 9. They considerably differ from the layouts of Figs 4 and 5, since the point N is surrounded by a fibrous material domain.

Fig. 9
figure 9

Selected numerical solutions beyond the applicability range of the theoretical layouts predicted in the present paper

Full size image

Finally, the volumes of the optimal structures are checked by the stress-based formulae (6.23), (6.28),with the design parameters being maximizers of (7.3). The results thus computed compare favorably with those found by (7.3), which proves correctness of all resultsreported.

To be specific let us show for example the partial and final results concerning the layout (b) in Fig. 8, corresponding to ξ=0.6 and η=0.4. By solving the problem (7.3) we find the optimal geometrical parameters: r 1=0, r 2/h=0.7211102551, 𝜃 1=0.3534865826, 𝜃 2=0.9827937232.

The virtual work equals L=1.7021587177P h, which gives the optimal volume V=L/σ p according to the kinematic method. The optimal volume can alternatively be computed by using the formula (6.28) based on the static analysis. By using the formulae of Sec. 6.1, putting there r 1=0 and by (6.27) one computes all the components in the formula (6.28) contributing to the total volume of the structure. The volumes of the subsequent parts of the structure are:

$$\begin{array}{@{}l@{\,}c@{\,}l@{}} V_{\text{RAB}} & = & 0.5338748252 Ph/\sigma_{p}\\ V_{\text{ABDC}} & = & 0.2027894518 Ph/\sigma_{p}\\ V_{\text{BDH}} & = & 0.0316196155 Ph/\sigma_{p}\\ V_{\text{CH}} & = & 0.5338748252 Ph/\sigma_{p}\\ V_{\text{BH}} & = & 0.0287387300 Ph/\sigma_{p}\\ V_{\text{RB}} & = & 0.1561668567 Ph/\sigma_{p}\\ V_{\text{RN}} & = & 0.2150944133 Ph/\sigma_{p} \end{array} $$

Summing up these values one finds V=1.7021587177P h/σ p , exactly the same volume as that found by the kinematic formula.

Similar computations can be shown for all other optimal layouts reported in the present paper. This check is of vital importance taking into account that the formula (1.3) necessitates the construction of the virtual field w in each case in the whole feasible domain, while our constructions of the virtual field have been restricted to the domain, where the mass is present. Such extensions can be performed, but as they are non-unique they have only theoretical value.

Remark 3

Basing on the partial volumes presented above one can note that V CH=V RAB. This interesting property is not accidental and results from the relationship between integrals (6.15), (6.16) and (6.20). It can be proved that for a more general case of \(r_{1} \geqslant 0\) (i.e. for both domains \({{\Omega }_{P}^{1}}\) and \({{\Omega }_{P}^{0}}\)), the equality V CH=V RAB+V NAC holds. It means that the total volume of the infinitesimally thin fibrous bars in the fans RAB and NAC is equal to the volume of the rod CH of a finite cross section. The proof is omitted here.

8 Final remarks

The present paper shows that George Rozvany’s problem can be viewed as a problem of finding the optimum structure to turn an applied load through 90 degrees onto the roller support. The paper shows that the layouts predicted in Figs 4, 5 are correct if the point load lies in appropriate distance to the line linking the supports. For closer placement of the point load, in the domain \({\Omega }_{P}^{*}\), the optimal layouts extend those predicted; the fibers around the load application point appear to strengthen the structure. The optimal layouts become non-convex.

The solutions concerning the domain \({\Omega }_{P}^{*}\) are complicated due to the condition of the feasible domain Ω lying to the right of the line of supports. Yet if one removes this condition and allows for placing the material left to this line, then immediately the optimal solutions become clear, easier for analytical description, see Fig. 10. The analytical formulae of Secs 2–4 suffice to construct the exact solutions; they will be the subject of a separate paper.

Fig. 10
figure 10

An exemplary numerical solution for the case of the feasible domain Ω being the whole plane (here ξ=0.3 and η=0.5)

Full size image

Topology optimization methods, and Michell’s theory in particular, are helpful in designing the connection sections in thin-walled shells subjected to tangent point loads of large magnitudes, see the recent paper by Zhang et al. (2015). The aim is to transmit a given concentrated force towards the main part of the shell to make the interaction forces as uniform as possible. Let us note that the solution to the problem of Fig. 6 gives a hint of how to solve this optimal diffusion problem, since it delivers the construction of the analytical solution to the problem of equilibrating a given vertical force of magnitude P 0 by the system of n vertical forces of the vertical total resultant equal P 0, acting at points along a horizontal line in a distance from the point where the force P 0 is applied, and forming a system of forces symmetric with respect to the line along which the force P 0 is acting. The number n can be arbitrarily large. The Michell truss being solution to this problem is constructed by superimposing the optimal solutions corresponding to the triplets of forces (P i , −2P i , P i ) acting at points N′, R, N, where N′ is the image of point N by the reflection across the y 0 axis. In the problem considered, see Fig. 6, the points N and N′ lie on the x 0 axis. Consequently, the optimal structure carrying this i-th triplet of forces is constructed by the reflection of the Michell structure of Fig. 6 across the y 0 axis. Superposition of all the Michell trusses corresponding to the triplets of vertical forces (P i , −2P i , P i ) results in the optimal structure equilibrating the system of applied vertical forces of magnitude P i by one vertical force of magnitude P 0. This construction comprises the case of the force systems in which one of the forces is applied at the middle point of the interval N′N (or at B, cf Fig. 6); the only change in the layout is that one more straight bar appears linking the points B and R. The Michell solution described above has been confirmed numerically by the ground structure method, see Fig. 11 corresponding to 11 vertical forces of magnitudes: P/2, P, …, P, P/2 equilibrated by one vertical force of magnitude P 0=10P. To model a uniformly distributed load the magnitudes of the forces lying at extreme points are two times smaller than magnitudes of the other 9 forces. The optimal layout includes the Hencky nets strengthened by internal ribs linking point R with points of applications of the applied forces. Moreover, a horizontal non-prismatic bar appears to assure the equilibrium. Similar solutions for arbitrary number of vertical forces can be constructed thus approximating the solution to the Michell problem of optimal transition of a point load into a uniformly distributed load.

Fig. 11
figure 11

Michell’s problem of the transition of a vertical point load into a system of vertical forces replacing a uniformly distributed load. The numerical result found by the ground structure method with using 125 million bars

Full size image

The Michell-like solution of Fig. 11 neglects the interaction of the bars with the plate or the shell in which this structure is embedded. This interaction can be modelled by the methods used by Zhang et al. (2015) or those proposed by Zegard and Paulino (2013).

Let us note that the solution of Fig. 11 has much in common with the designs proposed in Zhang et al. (2015), assuring a uniform diffusion of concentrated forces applied along the generating lines of a thin cylindrical shell. The present authors do cherish the hope that the exact solutions to George Rozvany’s problem will be also helpful for solving the optimal force diffusion problem in the case of the load acting parallel to the edges.