Distributed material density and anisotropy for optimized eigenfrequency of 2D continua

Abstract

A practical approach to optimize a continuum/structural eigenfrequency is presented, including design of the distribution of material anisotropy. This is often termed free material optimization (FMO). An important aspect is the separation of the overall material distribution from the local design of constitutive matrices, i.e., the design of the local anisotropy. For a finite element (FE) model the amount of element material is determined by a traditional optimality criterion (OC) approach. In this respect the major value of the present formulation is the derivation of simple eigenfrequency gradients with respect to material density and from this values of the element OC. Each factor of this expression has a physical interpretation. Stated alternatively, the optimization problem of material distribution is converted into a problem of determining a design of uniform OC values. The constitutive matrices are described by non-dimensional matrices with unity norms of trace and Frobenius, and thus this part of the optimized design has no influence on the mass distribution. Gradients of eigenfrequency with respect to the components of these non-dimensional constitutive matrices are therefore simplified, and an additional optimization criterion shows that the optimized redesign of anisotropy are described directly by the element strains. The fact that all components of an optimal constitutive matrix are expressed by the components of a strain state, imply a reduced number of independent components of an optimal constitutive matrix. For 3D problems from 21 to 6 parameters, for 2D from 6 to 3 parameters, and for axisymmetric problems from 10 to 4 parameters.

Appendix A: Direction of largest longitudinal material stiffness

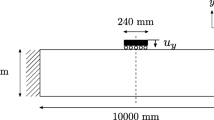
For illustration of the optimized designs the distributions of material density has been shown. However, for anisotropic material the anisotropy should also be illustrated, but without going into detail of the six components $\widetilde L_{1111}, \widetilde L_{2222}, \widetilde L_{1212}, \widetilde L_{1122}, \widetilde L_{1112}, \widetilde L_{2212}$ given in the global x, y coordinate system. It is chosen to show a plot of the directions of largest longitudinal material stiffness.

According to laminate theory $\widetilde L_{1111}$ as a function of rotation, termed f(𝜃), is given by the six components in the x,y coordinate system

$$\begin{array}{@{}rcl@{}} f(\theta) &=& (\widetilde L_{1111} + \widetilde L_{2222})/ 2 + \widetilde L_{2} \cos(2\theta) - \widetilde L_{3} (1 - \cos(4\theta)) \\ &&+ \widetilde L_{6} 2 \sin(2\theta) + \widetilde L_{7} \sin(4\theta) \end{array} $$

(25)

where the practical parameters are defined by

$$\begin{array}{@{}rcl@{}} \widetilde L_{2} & =& (\widetilde L_{1111} - \widetilde L_{2222})/ 2 \\ \widetilde L_{3} & =& (\widetilde L_{1111} + \widetilde L_{2222} - 2 (\widetilde L_{1122} + 2 \widetilde L_{1212})) / 8 \\ \widetilde L_{6} & =& (\widetilde L_{1112} + \widetilde L_{2212})/ 2 \\ \widetilde L_{7} & =& (\widetilde L_{1112} - \widetilde L_{2212})/ 2 \end{array} $$

(26)

For orthotropic materials $\widetilde L_{6} = \widetilde L_{7} = 0$ in specific directions, but for the free material subjected to multiple load cases this will not always be the case, so we need to analyze the more complicated material. More extremum solutions for f(𝜃) exist in the actual interval of 0≤𝜃<π. To locate the maximum of f(𝜃) it is therefore decided to evaluate (25) at a number of 𝜃 values (here chosen with increments Δ 𝜃=π/1800). This has been done for each elements.

1.1 A.1 Levels of anisotropy

Lines for direction of largest longitudinal material stiffness in addition to the color scale for distribution of material density give some physical information about the optimized material, but not much about the level of local anisotropy. Improved information is obtained by adding a color scale for the value of the larger longitudinal stiffness, i.e., the maximum of f(𝜃) found in determining the directions 𝜃.

The values of f _max has an upper bound of 1 and a lower bound of 1/3. This follows from the trace being 1, and thus having eigenvalues in this interval. This then also follows for the non-dimensional longitudinal stiffness. For higher values of f _max a single fiber direction is approached and for lower values of f _max an isotropic material with zero Poisson’s ratio material is approached.