1 Introduction

The level-set method was originally developed as a mathematical tool for tracking the motion of interfaces in two or three dimensions (Osher and Sethian 1988; Sethian 1999; Osher and Fedkiw 2003). The key idea is to represent interfaces using a discretized implicit function, which is then evolved under a velocity field to track interface motion. This approach naturally allows for complicated phenomena to occur, such as interface merging or splitting. Sethian and Wiegmann (2000) were first to utilise the level-set method for structural optimization, noting its natural handling of topological changes, coupled with a clear and smooth interface representation. This attractive combination has seen significant interest in level-set based structural optimization methods in recent years and they have become a viable alternative to traditional topology optimization methods based on element-wise design variables, such as the Solid Isotropic Material with Penalisation (SIMP) method (Bendsøe and Sigmund 2003) and Evolutionary Structural Optimization (ESO) methods (Huang and Xie 2010).

This introduction intends to provide a general overview of the range of approaches to level-set based optimization. For more comprehensive reviews see: van Dijk et al. (2013), Sigmund and Maute (2013), Deaton and Grandhi (2014) and the critical comparison of several level-set methods by Gain and Paulino (2013). The key common feature of all level-set methods is the representation of the boundary as the zero level-set of an implicit function. In level-set based optimization, sensitivities are then used to update the implicit function and hence optimize the position of the boundaries. The implicit boundary representation allows natural handling of topological changes, such as merging or insertion of holes. This allows for some degree of topology optimization, although special techniques are often required to create new holes during optimization (Allaire et al. 2005; Park and Youn 2008; Dunning and Kim 2013). The initial approaches to level-set based optimization used shape derivatives coupled with the original level-set method for front tracking. In this approach the implicit function is frequently re-initialized to become a signed distance function and it is updated by solving a Hamilton-Jacobi (H-J) type equation using an explicit upwind scheme (Allaire et al. 2004; Wang et al. 2003). This is sometimes called the conventional approach (Deaton and Grandhi 2014). Variations on the conventional approach include solving the H-J equation using semi-implicit additive operator splitting (Luo et al. 2008) or a semi-Lagrange approach (Xia et al. 2006). These methods can overcome the Courant–Friedrichs–Lewy (CFL) stability condition that limit the efficiency of the conventional approach. Alternative implicit functions have also been employed in level-set based optimization. Radial basis functions can be used to convert the Hamilton-Jacobi PDE into an ODE (Wang and Wang 2006a) or a simple set of algebraic equations (Luo et al. 2007). The spectral level set method represents the implicit function as coefficients of a Fourier series and the design variables are the coefficients of the basis functions (Gomes and Suleman 2006). There are also methods based on phase fields (Takezawa et al. 2010; Blank et al. 2010) where the implicit function is used to define the material phase of a point and the update is performed by solving a reaction–diffusion equation.

Practical engineering problems often involve several constraints and various approaches have been employed to handle constraints in level-set based optimization. Some approaches are limited to problems with a single constraint, such as the maximum material volume. This constraint can be added to the objective using a fixed Lagrange multiplier (Allaire et al. 2004; Wang and Wang 2006a). This is effectively a penalty method, which cannot guarantee the constraint is satisfied. An alternative is to obtain the Lagrange multiplier under the assumption that the volume remains constant during the level-set update (Wang et al. 2003). However, conserving volume or mass with the level-set method can be difficult. This method can be improved by adjusting the Lagrange multiplier to account for the current feasibility of the constraint (Wang and Wang 2006b) or by using Newton’s method to correct the Lagrange multiplier if the constraint becomes infeasible (Osher and Santosa 2001). A further approach is to explicitly compute the Lagrange multiplier each iteration, using a one-dimensional optimization technique, to ensure constraint feasibility (Wang et al. 2007; Zhu et al. 2010; Dunning and Kim 2013).

The methods discussed so far have been applied to only single constraint problems where the constraint is usually an upper limit on material volume. To handle multiple constraints, a gradient projection method has been used, where the decent direction of the objective function is projected onto the tangential space of the active constraints (Wang and Wang 2004). However, a return mapping algorithm is required to handle non-linear constraints and infeasible initial designs (Yulin and Xiaoming 2004). This algorithm modifies the velocity function by adding a linear combination of the violated constraint gradients, so that they become feasible over one or more iterations. The gradient projection method has been demonstrated for multiple volume constraints for multiple materials (Wang and Wang 2004; Yulin and Xiaoming 2004) and for a volume and input displacement constraint for compliant mechanism design (Yulin and Xiaoming 2004). Another approach to handle multiple constraints is to use the augmented Lagrange multiplier method (Luo et al. 2008, 2009). However, the choice of penalty parameters can affect the convergence and efficiency of the level-set method (Zhu et al. 2010) and it can be difficult to satisfy the constraint unless the parameter is very large (van Dijk et al. 2012).

All the constraint handling methods discussed so far are applicable to conventional level-set optimization methods. Some alternative level-set methods are formulated such that traditional optimization techniques can be applied. This is often the case when using parameterizations other than the signed distance function. For example, the Method of Moving Asymptotes (MMA) can be used when the implicit function is parameterized using compactly supported radial basis functions, which converts the H-J PDE into a set of algebraic equations (Luo et al. 2007). The level-set optimization method proposed by van Dijk et al. (2012) links implicit function values at the nodes to density values within elements using an exact Heaviside function. Gradients are first obtained at the element level and then linked to the level-set design variables using the chain rule, thus allowing multiple constraints to be handled without using penalty parameters. However, the relationship between the nodal implicit function values and element densities is non-linear, which can lead to an ill-conditioned optimization problem. The method was used to solve problems with multiple compliance constraints, although further regularization was required to remove numerical artifacts from the solutions, such as material islands. Another limitation of this approach is that it is linked to the density based material model for sensitivity analysis and is not easily applicable to other material models, such as the eXtended Finite Element Method (X-FEM) (Wei et al. 2010), superimposed moving mesh (Wang and Wang 2006b) or an adaptive moving mesh (Liu and Korvink 2008).

This paper presents a new approach for handling multiple constraints in the conventional level-set topology optimization method. The key features of the new method are discretized boundary integrals to estimate function changes and the formulation of an optimization sub-problem to attain the velocity function. This approach does not require penalty parameters to handle constraints and has the additional benefit of being able to simultaneously optimize non-level-set design variables. The simultaneous optimization of the level-set implicit function and additional design variables has received little attention in the literature. However, level-set methods that use a parameterization that allows the use of mathematical programming could potentially be extended to include other design variables (Luo et al. 2007; van Dijk et al. 2012), although this is not discussed by the authors.

The paper is organized as follows: first we review the conventional level-set method, then an approach is developed where the velocity function sub-problem is formulated as a linear program (LP), called the LP level-set method. This is further developed where the sub-problem is solved using Sequential LP, called the SLP level-set method. This is followed by numerical implementation details and a range of numerical examples is used to demonstrate the new method.

2 Level-set based optimization

This section reviews the conventional level-set method for optimization. First, the boundary of the structure is defined as the zero level set of an implicit function:

$$ \left\{\begin{array}{c}\hfill \phi (x)\ge 0,x\in \varOmega \hfill \\ {}\hfill \phi (x)=0,x\in \varGamma \hfill \\ {}\hfill \phi (x)<0,x\notin \varOmega \hfill \end{array}\right. $$
(1)

where Ω is the domain for the structure, Γ is the boundary of the structure, ϕ(x) is the implicit function and x ∈ Ω d , where Ω d is the design domain containing the structure, Ω ⊂ Ω d . This implicit description allows the boundary to break and merge naturally, allowing topological changes to occur during optimization. In the conventional approach, the implicit function is initialized as a signed distance function, where the magnitude is the distance to the boundary and the sign is defined by (1). The signed distance property promotes stability in the level-set method and it is desirable to maintain this property throughout the optimization (Allaire et al. 2004; Yulin and Xiaoming 2004).

The position, shape and topology of the structure boundary is optimized by iteratively solving the following advection equation:

$$ \frac{\partial \phi (x)}{\partial t}+\nabla \phi \left(x,t\right)\frac{dx}{dt}=0 $$
(2)

where t is a fictitious time domain. The advection equation (2) becomes a Hamilton-Jacobi type equation by considering advection velocities of the type: dx / dt = V ⋅ ∇ϕ (x) (Sethian 1999; Osher and Fedkiw 2003). The equation is then discretized and solved using an explicit forward Euler scheme, producing the following update rule for the discrete implicit function values:

$$ {\phi}_i^{k+1}={\phi}_i^k-\Delta t\left|\nabla {\phi}_i^k\right|{V}_i $$
(3)

where k is the iteration number, i is a discrete point in the design domain, Δt is the time step and V i is the velocity value at the point i. In the conventional approach to level-set based optimization, the velocity function is obtained from a shape derivative.

There are two common methods for obtaining the velocity values at the discrete points. If the design is analysed using the ersatz material method, where weak material is used to model the void, then derivative and velocity values can be computed directly at all points in the domain. This is known as the natural velocity extension method (Osher and Santosa 2001; van Dijk et al. 2013). The disadvantage of this method is that the implicit function requires frequent re-initialization to maintain the signed distance property of the implicit function, which is important for the stability of the conventional level-set method. The second approach is to compute sensitivity and velocity values only at the structural boundary and then extend velocities to discrete points in such a way that the signed distance function is preserved after solving (2) (Liu and Korvink 2008; Dunning et al. 2011). The second velocity extension approach is used during the development of the SLP level-set method, which is introduced in the next section.

3 The SLP level-set method

3.1 Preliminaries

To illustrate the new method, we use a generic optimization problem where one of the design variables is the position of a structural boundary:

$$ \begin{array}{l}\mathrm{Minimise}:f\left(\varOmega, \mathbf{x}\right)\\ {}\mathrm{Subject}\ \mathrm{t}\mathrm{o}:{h}_i\left(\varOmega, \mathbf{x}\right)={\overline{h}}_i,\kern1em i=1\cdots m\\ {}\kern4.5em {g}_i\left(\varOmega, \mathbf{x}\right)\le {\overline{g}}_i,\kern1.7em i=1+m\cdots p\end{array} $$
(4)

where f is the objective function, h i and g i are the constraint functions, m is the number of equality constraints, p is the total number of constraints and x is a vector of additional non-level-set design variables.

The level-set description of the boundary presents a large design space for the optimization problem (4), therefore gradient-based methods are usually employed to solve the problem. This requires at least the first derivatives of the objective and constraints with respect to each design variable. It is assumed that the first derivatives with respect to the non-level-set design variables, x can be obtained. The remaining variable in our problem is the position of some part of a boundary, Ω. Shape derivatives provide information about how a function changes over time with respect to a movement of the boundary and usually take the form of a boundary integral (Allaire et al. 2004):

$$ \Delta t\ \frac{\partial f\left(\varOmega, x\right)}{\partial \varOmega }=\Delta t{\displaystyle {\int}_{\varGamma}\left({s}_f \cdot V\right)}d\varGamma $$
(5)

where s f is a shape sensitivity function and V is a velocity function acting normal to the boundary. In equation (5) the shape derivative, ∂f /∂Ω, is multiplied by the time step to compute the total change in the function f after updating the implicit function using (3) with the specified time step, Δt, and velocity function, V. The shape sensitivity and velocity functions vary along the boundary and are usually assumed smooth. Therefore, the shape derivative is characterised as a boundary integral involving a velocity function. This definition can be blurred when using fictitious material models and the natural velocity extension method. In the following we assume that shape sensitivity values are only computed at points along the boundary. Details of our velocity extension approach are included in Section 4.1.

After computing the shape sensitivities, we are free to choose the velocity function and the time step. The time step in (5) can be eliminated by replacing the velocity function by a boundary movement function, z:

$$ \Delta t\frac{\partial f\left(\varOmega, x\right)}{\partial \varOmega }={\displaystyle {\int}_{\varGamma}\left({s}_f \cdot z\right)}d\varGamma, \kern0.5em z=\Delta t \cdot V $$
(6)

To evaluate the integral, the boundary is discretized. The discretization of the shape derivative for the objective function can be written as:

$$ \Delta t\frac{\partial f\left(\varOmega, x\right)}{\partial \varOmega } \approx {\displaystyle \sum_{j=1}^n\left({s}_{f,j} \cdot {z}_j \cdot {l}_j\right)}=\mathbf{c} \cdot \mathbf{z},\kern0.5em {c}_j={s}_{f,j} \cdot {l}_j $$
(7)

where l j is a discrete length of the boundary (or surface area in 3D) around a discrete point j, s f,j is a discrete value of the objective shape sensitivity, n is the number of discrete points and c is a vector of integral coefficients for the objective. The definition of c j in (7) is equivalent to using a numerical integration method that assumes piecewise constant velocity and sensitivity values. More accurate schemes can be employed and our implementation uses a piecewise linear assumption for the shape sensitivity functions (see Section 4.2). Similarly, discretizations of the constraint function shape derivatives can be written as:

$$ \Delta t\frac{\partial {h}_i\left(\varOmega, x\right)}{\partial \varOmega } \approx {\displaystyle \sum_{j=1}^n\left({s}_{i,j} \cdot {z}_j \cdot {l}_j\right)}={\mathbf{a}}_i \cdot \mathbf{z},\kern0.5em {a}_{i,j}={s}_{i,j} \cdot {l}_j $$
(8)

where s i,j is a discrete value of the shape sensitivity for constraint i and a i,j is an integral coefficient for constraint i, boundary point j.

The change in the objective and constraints are now explicit functions of the boundary move function, z, though functions (7) and (8). The key aspect of the LP and SLP level-set methods developed in this paper is that an optimization sub-problem is used to attain z to meet the constraints, whilst improving the objective.

3.2 The LP level-set method

We first introduce an approach similar to the SLP level-set method called the Linear Programming (LP) level-set method. This is used to motivate several features of the SLP level-set method.

For a problem that does not have additional non-level-set design variables, a good choice for the boundary movement function would be one that minimizes the objective shape derivative whilst meeting the constraints, or at least moving towards a feasible solution. This can be achieved by solving the following LP sub-problem:

$$ \begin{array}{l}\mathrm{Minimize}:\ \mathbf{c}\cdot \mathbf{z}\hfill \\ {}\mathrm{Subject}\ \mathrm{t}\mathrm{o}:\ {\mathbf{a}}_i \cdot \mathbf{z}={\overline{h}}_i-{h}_i,\kern1em i=1\cdots m\hfill \\ {}{\mathbf{a}}_i \cdot \mathbf{z}\le {\overline{g}}_i-{g}_i,\kern2em i=1+m\cdots p\hfill \\ {}{\mathbf{z}}_{min}\le \mathbf{z}\le {\mathbf{z}}_{max}\hfill \end{array} $$
(9)

where h i and g i are the current constraint function values and z min and z max are side constraints on the boundary movement, which are usually dictated by the CFL condition or by the limits of the design domain. The LP sub-problem is used to attain the discrete values of the boundary movement function, which is then used with the conventional level-set method to update the boundary of the structure:

$$ {\phi}_i^{k+1}={\phi}_i^k-\Delta t\left|\nabla {\phi}_i^k\right|{V}_i={\phi}_i^k-\left|\nabla {\phi}_i^k\right|{z}_i $$
(10)

Note that the boundary movement function values have to be extended to all discrete points in the domain using a velocity extension method.

For problems with non-level-set design variables, the LP sub-problem can be defined as (11) which includes the computation of the step change in x during an iteration of the main optimization loop:

$$ \begin{array}{l}\mathrm{Minimize}:\ \mathbf{c}\cdot \mathbf{z}+\nabla {f}_{\mathbf{x}}\cdot \Delta \mathbf{x}\hfill \\ {}\mathrm{Subject}\ \mathrm{t}\mathrm{o}:\ {\mathbf{a}}_i \cdot \mathbf{z}+\nabla {h}_{i,\mathbf{x}} \cdot \Delta \mathbf{x}={\overline{h}}_i-{h}_i,\kern0.5em i=1\cdots m\hfill \\ {}\kern5em {\mathbf{a}}_i \cdot \mathbf{z}+\nabla {g}_{i,\mathbf{x}} \cdot \Delta \mathbf{x}\le {\overline{g}}_i-{g}_i,\kern0.5em i=1+m\cdots p\hfill \\ {}\kern5em {\mathbf{z}}_{min}\le \mathbf{z}\le {\mathbf{z}}_{max}\hfill \\ {}\kern5em \Delta {\mathbf{x}}_{min}\le \Delta \mathbf{x}\le \Delta {\mathbf{x}}_{max}\hfill \end{array} $$
(11)
$$ \begin{array}{l}\nabla {f}_{\mathbf{x}}={\left\{\begin{array}{cccc}\hfill \partial f/\partial {x}_1\hfill & \hfill \partial f/\partial {x}_2\hfill & \hfill \cdots \hfill & \hfill \partial f/\partial {x}_n\hfill \end{array}\right\}}^T\\ {}\nabla {h}_{i,\mathbf{x}}={\left\{\begin{array}{cccc}\hfill \partial {h}_i/\partial {x}_1\hfill & \hfill \partial {h}_i/\partial {x}_2\hfill & \hfill \cdots \hfill & \hfill \partial {h}_i/\partial {x}_n\hfill \end{array}\right\}}^T\\ {}\nabla {g}_{i,\mathbf{x}}={\left\{\begin{array}{cccc}\hfill \partial {g}_i/\partial {x}_1\hfill & \hfill \partial {g}_i/\partial {x}_2\hfill & \hfill \cdots \hfill & \hfill \partial {g}_i/\partial {x}_n\hfill \end{array}\right\}}^T\end{array} $$
(12)

where Δx is a vector of step changes for the non-level-set design variables and Δx min and Δx max are the side constraints. In the main optimization loop, the update of the non-level-set variables can then be computed by:

$$ {\mathbf{x}}^{k+1}={\mathbf{x}}^k+\Delta \mathbf{x} $$
(13)

The LP level-set method can thus handle multiple constraints, beyond a simple volume limit, and also simultaneously optimize for non-level-set design variables. However, we found that the solution for z from the LP sub-problem may not be smooth along the boundary. This can be seen in an example of the compliance minimization of an aspect ratio 2 cantilever beam, subject to a 50 % volume constraint (the initial design is shown in Fig. 1a). The solution obtained using the LP level-set method, Fig. 1c is compared to the solution obtained using the Lagrange multiplier approach where a one-dimensional optimization technique is used to compute the multiplier each iteration, Fig. 1b. The solution obtained with the LP level-set method has a rough boundary, Fig. 1c compared with the Lagrange multiplier solution, Fig. 1b, although the overall topology is similar. The aim of our level-set topology optimization method is to produce smooth boundary solutions. Furthermore, the shape sensitivity function of the compliance for an optimal structure is constant on the boundary (Wang et al. 2003), which unlikely if the boundary is rough. We therefore develop the LP level-set method further to obtain a smoother boundary move function.

Fig. 1
figure 1

Cantilever example: a Initial design, loading and boundary conditions, b Solution using Lagrange multiplier method, c Solution using LP level-set method

Full size image

3.3 Development of the SLP level-set method

To obtain a smooth boundary, without using additional smoothing or regularization techniques, we require a smooth boundary move function along the structure boundary. This is achieved by constructing a boundary movement function from a linear combination of the shape sensitivities:

$$ \mathbf{z}\left(\boldsymbol{\uplambda} \right)={\lambda}_f \cdot {\mathbf{s}}_f+{\displaystyle \sum_{i=1}^p{\lambda}_i \cdot {\mathbf{s}}_i},\kern1.25em {\mathbf{z}}_{\min}\le \mathbf{z}\le {\mathbf{z}}_{\max } $$
(14)

where λ is a vector of weights for each shape sensitivity function. Now the variables in the sub-problem are the weight values, in place of the discrete values of z. This choice of the boundary move function restricts the admissible vector fields, compared with the LP level-set approach (9). However, the number of variables in the sub-problem is significantly reduced, which reduces the computational cost of the method. Also, the smoothness of the boundary move function is now dependent on the smoothness of the shape sensitivity fields.

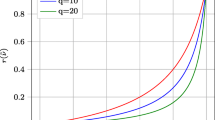
In (14) z is a linear function of λ and because the discretized shape derivatives are linear functions of z (7, 8) then we could directly solve for λ using LP. However, the side limits on z also need to be satisfied, which is not guaranteed if an LP problem is solved for λ only. To explain this further, assume we choose some admissible λ such that the upper side limits on z are just active along a portion of the boundary. Now an increase in magnitude of λ will result in a violation of the z side limits along the boundary portion. The approach developed in this work does not use z as a variable in the sub-problem and the side limits are implicitly enforced after first evaluating z for a given λ. Using this approach, the discretized shape derivatives are no longer linear functions of λ because of the second step of enforcing the side limits on z. This effect is shown in Fig. 2, where the computed value of the shape derivative for the compliance objective of the cantilever in Fig. 1a is shown against the λ value for the objective shape sensitivity. The sub-problem is solved using Sequential LP for λ. We call this the SLP level-set method.

Fig. 2
figure 2

Shape derivative of compliance with respect to the weight value λ f

Full size image

In the SLP level-set method, the objective and constraint boundary integrals are linearized about the current value of λ using a first order Taylor expansion:

$$ \Delta t\frac{\partial f\left(\varOmega \right)}{\partial \varOmega}\left({\boldsymbol{\uplambda}}^k\right) \approx \mathbf{c} \cdot \mathbf{z}\left({\boldsymbol{\uplambda}}^k\right)+\left(\boldsymbol{\uplambda} -{\boldsymbol{\uplambda}}^k\right) \cdot {\nabla}_{\lambda}\frac{\partial f\left(\varOmega \right)}{\partial \varOmega}\left({\boldsymbol{\uplambda}}^k\right) $$
(15)

where λ k is the value of λ at iteration k of the SLP sub-problem. The change in the objective function is linked to λ through the definition of the boundary movement function (14) and the discretized boundary integral (7). The following LP problem is then solved for the new value of λ:

$$ \begin{array}{l}\mathrm{Minimize}:\ \nabla {f}_{\boldsymbol{\uplambda}}\cdot {\boldsymbol{\uplambda}}^{k+1}\hfill \\ {}\mathrm{Subject}\ \mathrm{t}\mathrm{o}:\ \nabla {h}_{i,\boldsymbol{\uplambda}}^k \cdot {\boldsymbol{\uplambda}}^{k+1}={\overline{h}}_i-{h}_i+\nabla {h}_{i,\boldsymbol{\uplambda}}^k\cdot {\boldsymbol{\uplambda}}^k,\kern0.5em i=1\cdots m\hfill \\ {}\kern5em \nabla {g}_{i,\boldsymbol{\uplambda}}^k \cdot {\boldsymbol{\uplambda}}^{k+1}\le {\overline{g}}_i-{g}_i+\nabla {g}_{i,\boldsymbol{\uplambda}}^k \cdot {\boldsymbol{\uplambda}}^k,\kern0.5em i=1+m\cdots p\hfill \\ {}\kern5em {\boldsymbol{\uplambda}}_{min}\le \boldsymbol{\uplambda} \le {\boldsymbol{\uplambda}}_{max}\hfill \end{array} $$
(16)

where:

$$ \begin{array}{l}{\nabla}_{\boldsymbol{\uplambda}}={\left\{\begin{array}{cccc}\hfill \partial /\partial {\lambda}_f\hfill & \hfill \partial /\partial {\lambda}_1\hfill & \hfill \cdots \hfill & \hfill \partial /\partial {\lambda}_p\hfill \end{array}\right\}}^T\\ {}\nabla {f}_{\boldsymbol{\uplambda}}={\nabla}_{\boldsymbol{\uplambda}} \cdot \frac{\partial f\left(\varOmega \right)}{\partial \varOmega },\ \nabla {h}_{i,\boldsymbol{\uplambda}}={\nabla}_{\boldsymbol{\uplambda}} \cdot \frac{\partial {h}_i\left(\varOmega \right)}{\partial \varOmega },\ \nabla {g}_{i,\boldsymbol{\uplambda}}={\nabla}_{\boldsymbol{\uplambda}} \cdot \frac{\partial {g}_i\left(\varOmega \right)}{\partial \varOmega}\end{array} $$
(17)

A SLP method is then used to iteratively find the optimal values of λ and our implementation is detailed in Section 4.3. The LP problem in (16) is extended to include non-level-set design variables, in the same manner as the LP level-set method (11).

To solve the LP problem in (16) we require the derivatives of the objective and constraint change boundary integrals with respect to λ, (17). This is not easily obtained analytically; therefore we employ finite differences to compute the required derivatives. The finite difference method is often avoided in optimization due to the high computational cost associated with many function evaluations and many variables. However, the function evaluations here only involve computing z, for given λ using (14) and a dot product to compute the objective or constraint change boundary integral, (7, 8). Thus, the function evaluations are reasonably cheap. Also, the number of weight variables is equal to the number of constraints plus one. So, for problems with a small number of constraints, the finite difference approach does not add significant computational cost to the SLP level-set method.

3.4 Setting side limits

To solve the LP problem in (16) side limits on λ are required. The limits should be set such that any choice of λ does not activate all side constraints on the boundary move function (14). If this occurs then a small change in λ could result in no change in z, leading to zero gradients in (17).

If there are no constraints, then the side limits for λ f can be defined from the values of s f and the side constraints:

$$ {\lambda}_{f, \min }=\underset{j}{ \min}\left({\overline{z}}_j\right),\kern0.5em {\lambda}_{f, \max }=\underset{j}{ \max}\left({\overline{z}}_j\right),\kern0.5em {\overline{z}}_j=\left(\frac{z_{j, \min }}{s_{f,j}},\frac{z_{j, \max }}{s_{f,j}}\right) $$
(18)

When we introduce a constraint, setting appropriate side limits for both weight values is not straightforward, as the side limits for λ f will affect the required side limits for λ 1 and visa versa:

$$ {\lambda}_{f, \min }=\underset{j}{ \min}\left({\overline{z}}_j\right),\kern0.5em {\lambda}_{f, \max }=\underset{j}{ \max}\left({\overline{z}}_j\right),\kern0.5em {\overline{z}}_j=\left(\frac{z_{j, \min }-{\lambda}_1{s}_{1,j}}{s_{f,j}},\frac{z_{j, \max }-{\lambda}_1{s}_{1,j}}{s_{f,j}}\right) $$
(19)
$$ {\lambda}_{1, \min }=\underset{j}{ \min}\left({\overline{z}}_j\right),{\lambda}_{1, \max }=\underset{j}{ \max}\left({\overline{z}}_j\right),\kern0.5em {\overline{z}}_j=\left(\frac{z_{j, \min }-{\lambda}_f{s}_{f,j}}{s_{1,j}},\frac{z_{j, \max }-{\lambda}_f{s}_{f,j}}{s_{1,j}}\right) $$
(20)

We devise a methodology to set appropriate side limits for λ, which has been shown to work well for a wide range of problems. The first step is to reduce the problem to find the side limits of λ f only. This is achieved by assuming relationships between λ f and the λ i values. The relationships are formed using ratios of the discretized objective and constraint boundary integrals when the boundary movement vector is set to its maximum or minimum values:

$$ {r}_{i, \min }=\frac{\mathbf{c} \cdot {\mathbf{z}}_{\min }}{{\mathbf{a}}_i \cdot {\mathbf{z}}_{\min }},\kern0.5em {r}_{i, \max }=\frac{\mathbf{c} \cdot {\mathbf{z}}_{\max }}{{\mathbf{a}}_i \cdot {\mathbf{z}}_{\max }} $$
(21)

These ratios provide an estimate on the ratio of λ f to λ i when the boundary move function is set to either extreme. Whilst computing the side limits, the λ i values are assumed to equal λ f multiplied by one of the ratios defined in (21).

The next step is to compute side limits on λ f at each boundary point in a similar manner to (19) and (20) except the ratios in (21) are used to compute the extreme maximum and minimum values:

$$ \begin{array}{l}{\lambda}_{f,j, \min }= \min \left(\frac{z_{j, \min }}{s_{f,j}+{\overline{s}}_{j, \min }},\frac{z_{j, \min }}{s_{f,j}+{\overline{s}}_{j, \max }}\right)\\ {}{\lambda}_{f,j, \max }= \max \left(\frac{z_{j, \max }}{s_{f,j}+{\overline{s}}_{j, \min }},\frac{z_{j, \max }}{s_{f,j}+{\overline{s}}_{j, \max }}\right)\end{array} $$
(22)
$$ {\overline{s}}_{j, \min }={\displaystyle \sum_{i=1}^p \min \left({r}_{i, \min } \cdot {s}_{i,j},{r}_{i, \max } \cdot {s}_{i,j}\right)},\kern0.5em {\overline{s}}_{j, \max }={\displaystyle \sum_{i=1}^p \max \left({r}_{i, \min } \cdot {s}_{i,j},{r}_{i, \max } \cdot {s}_{i,j}\right)} $$
(23)

Once limits for λ f have been computed at each boundary point, the median values are used to set the side limits on λ f , where median values are used instead of extreme values to provide conservative side limits. The side limits for λ i values are then computed from the side limits on λ f and the ratios in (21):

$$ {\lambda}_{i, \min }={\overline{r}}_i{\lambda}_{f, \min },\kern0.5em {\lambda}_{f, \max }={\overline{r}}_i{\lambda}_{f, \max },\kern0.5em {\overline{r}}_i= \min \left(\left|{r}_{i, \min}\right|,\left|{r}_{i, \max}\right|\right) $$
(24)

where \( {\overline{r}}_i \) is defined to give conservative side limits for λ i .

4 Numerical implementation

4.1 Conventional level-set method

The examples in this paper use a 2D Cartesian grid to discretize the implicit function. The Cartesian grid is also used to form a FE mesh of bilinear four node plane stress elements (Cook et al. 2002).

The FE mesh remains fixed throughout the optimization. This will result in some elements being cut by the structural boundary. For this paper we use the area-fraction approach to compute the stiffness matrix of a cut element (Dunning et al. 2011), which is similar to the ersatz material approach used by Allaire et al. (2004). The idea is to weight the stiffness matrix of a cut element by the fraction of material within the element:

$$ {\mathbf{K}}_c=\left({\alpha}_c/{\alpha}_E\right){\mathbf{K}}_E $$
(25)

where K c is the approximated stiffness matrix of the cut element, K E is the stiffness matrix of the same element without a cut, whose area is α E , and α c is the area of the cut element that lies inside the structure. To compute the internal area of a cut element, α c , the implicit function is interpolated along element edges to find points where the boundary intersects an element edge. The collection of intersection points and element nodes that lie inside the structure are then used to compute the internal area, Fig. 3. Note that the SLP level-set method does not rely on a particular FE analysis approach and can be used with other analysis techniques.

Fig. 3
figure 3

Element internal area calculation from nodal implicit function values

Full size image

In the SLP level-set method, sensitivity values are only computed at the boundary, not directly at grid nodes using a natural velocity extension approach. However, it is known that the approximated stiffness used in the area-fraction fixed grid approach leads to reduced accuracy at the boundary (Jang et al. 2004; Wei et al. 2010; Dunning et al. 2011). Therefore, we use a weighted least-squares method to compute more accurate sensitivities at boundary points (Dunning et al. 2011).

The sub-problem in the SLP level-set method only computes boundary move values at the boundary. The boundary move function is the velocity function multiplied by the time step (6). Therefore, a velocity extension method can be used to extrapolate boundary move values to grid nodes. Maintaining the signed distance property of the implicit function is important for the stability of the conventional level-set method. Therefore, it is desirable to define the grid node velocities, or boundary move values, such that this property is maintained during the update. This approach reduces the frequency of re-initialization steps required for a stable algorithm. In this work, the fast marching method is used to efficiently compute a velocity extension that maintains the signed distance property (Adalsteinsson and Sethian 1999).

The narrow band method is used to improve efficiency by limiting the velocity extension to a small region around the boundary, instead of the entire domain (Sethian 1999; Wang et al. 2003). Re-initialization of the implicit function is performed using the same fast marching method employed for velocity extension. Note that re-initialization is not performed after each update, but only when the boundary is near the edge of the current narrow band, or after 20 iterations have passed since the last re-initialization.

The upwind finite difference scheme is often used to compute spatial gradients of the implicit function because of its favourable stability when solving the Hamilton-Jacobi equation (Sethian 1999). This scheme is utilized here where each gradient component is approximated using the higher order weighted essentially non-oscillatory method (Jiang and Peng 2000) that improves the stability and accuracy of the upwind scheme.

A simple termination criterion is used, where the optimization is stopped if the maximum relative change in the objective over the previous ten iterations is less than a small number:

$$ \left({f}_{max}^i-{f}_{min}^i\right)/\left({f}_{max}^i+{f}_{min}^i\right)<\gamma, i\in \left[k-9,k\right] $$
(26)

where f is the objective value, k is the iteration number and γ is a small number. The convergence criterion is only checked if the constraints are satisfied within a 1 % tolerance. The optimization algorithm is composed of the following major steps:

  1. 1.

    Compute area-fractions and boundary discretization from the current implicit function (Fig. 2).

  2. 2.

    Assemble global matrices from area-fraction weighted element matrices, (25).

  3. 3.

    Solve the primary and adjoint equations (if required).

  4. 4.

    If all constraints are satisfied, then check for convergence using (26).

  5. 5.

    For the objective and constraints: compute shape sensitivities at all discrete boundary points and gradients for any non-level-set design variables.

  6. 6.

    Compute boundary integral coefficients (Section 4.2).

  7. 7.

    Solve the SLP sub-problem for the boundary move function and non-level-set design variable step updates, (16).

  8. 8.

    Extension of the boundary move function using the fast marching method.

  9. 9.

    Spatial gradient calculation using an upwind scheme.

  10. 10.

    Update the implicit function, (10) and non-level-set design variables, 13). Return to step 1.

4.2 Boundary integral

The procedure used to compute boundary integrals is split into two stages. The first stage is to discretize the boundary. The second is the numerical integration of the shape derivative boundary integrals for the objective and constraint functions.

The boundary is discretized into linear segments, which are obtained during the computation of internal area for elements cut by the boundary, Fig. 3. This provides an explicit description of the current boundary. Shape sensitivity values are computed at all discrete boundary points. We then assume a piece-wise linear variation of the shape sensitivity function along each segment and a piece-wise constant velocity value in the neighborhood of each boundary point, Fig. 4.

Fig. 4
figure 4

Numerical integration of boundary a function

Full size image

The neighborhood that the velocity function is constant around a boundary point is weighted to obtain a more even discretization of the velocity function. The boundary integral coefficient for boundary point 3 in Fig. 4 is obtained by computing the shaded area. The required boundary segments weight values, w 23 and w 34 , are computed from the neighbouring segment lengths:

$$ {w}_{23}={l}_{34}/\left({l}_{12}+{l}_{34}\right),\ {w}_{34}={l}_{45}/\left({l}_{34}+{l}_{45}\right) $$
(27)

These weighting functions help divide the numerical integration more evenly between the boundary points. This approach is used for all examples in this paper. However, experiments with simpler numerical integration schemes have also yielded comparable results, such as using a piecewise constant assumption for the shape sensitivity functions and no weighting.

4.3 SLP filter method

A SLP filter method is used to solve the sub-problem for the boundary movement function (Fletcher et al. 1998). The idea of the filter method is to treat the non-linear constrained optimization problem as a multi-objective problem, where the second “objective” is to minimize the constraint violation. The main advantage of this approach for the SLP level-set method is that it can robustly handle the situation where an infeasible problem is posed. This is because filter method can find the solution that minimizes the constraint violation, even if the problem is infeasible. This solution is then used to define the boundary move function and non-level-set design variable updates.

The two main approaches for solving LP problems are simplex methods and interior-point methods (Rao 2009). When the number of variables in the LP problem is small (less than 10) we use the revised simplex method. For larger problems it is more efficient to use an interior point method. A primal-dual interior point method is used, following the implementation by Zhang (1996) with a start point suggested by Mehrotra (1992).

4.4 Further details of constraint handling

The sub-problem in the SLP level-set method aims to meet the constraints. However, if the current design is in the infeasible region then it may not be possible to meet the constraints during the current iteration of the level-set method. This problem is handled by setting limits for the maximum and minimum constraint changes during the current iteration. The limits are computed from the discretized boundary integrals and z side limits:

$$ \begin{array}{l}{\beta}_i=\left\{{\mathbf{a}}_i \cdot {\mathbf{z}}_{\max },\ {\mathbf{a}}_i \cdot {\mathbf{z}}_{\min },0\right\}\\ {}{h}_{i, \max }=0.2 \max \left({\beta}_i\right),\ {h}_{i, \min }=0.2 \min \left({\beta}_i\right)\\ {}{g}_{i, \max }=0.2 \max \left({\beta}_i\right),\ {g}_{i, \min }=0.2 \min \left({\beta}_i\right)\end{array} $$
(29)

where the 0.2 factor has been seen to work well for a range of problems. If the violation of an equality constraint lies outside the limits, then the constraint value in the sub-problem is changed accordingly:

$$ \begin{array}{l}\mathrm{if}\ {\overline{h}}_i-{h}_i>{h}_{i, \max}\kern0.5em \mathrm{set}:{\overline{h}}_i={h}_i+{h}_{i, \max}\\ {}\mathrm{if}\ {\overline{h}}_i-{h}_i<{h}_{i, \min}\kern0.5em \mathrm{set}:\ {\overline{h}}_i={h}_i+{h}_{i, \min}\end{array} $$
(30)

The same principle is applied to inequality constraints:

$$ \mathrm{if}\ {\overline{g}}_i+{g}_i<{g}_{i, \min}\kern0.5em \mathrm{set}:\ {\overline{g}}_i={g}_i+{g}_{i, \min } $$
(31)

This method allows the design to approach the feasible region over several iterations of the level-set method.

An active constraint method is also employed, where inequality constraints that are not active, and not close to becoming active, are not considered during the sub-problem. A constraint is removed from the sub-problem if: \( {\overline{g}}_i-{g}_i>{g}_{i, \max } \).

4.5 Numerical parameters

The numerical implementation of the SLP level-set method presented in this paper has three numerical parameters that need to be specified by a user. The first is related to the choice of side limits for λ (22–24), where the median of the values computed for each boundary point (22) is used to form the final limits. Values other than the median can be chosen, although experience has shown that the median value works well for a wide range of problems. The second parameter is the method used to compute the integral coefficients for the shape derivatives. A, weighted, piece-wise linear shape sensitivity function is used in this work, Fig. 4. However, as discussed in Section 4.2, comparable results can be obtained with simpler methods. The third parameter is the 0.2 factor used to set the constraint change targets for infeasible designs (29). Lower values tend to result in slower convergence for initially infeasible designs, whereas higher values are more likely to yield an infeasible sub-problem. In our experience a value of 0.2 was found to be a good compromise and is used consistently for all the examples in this paper and we have not yet come across a case where a different value was needed.

5 Examples

The SLP level-set method is applied to solve a range of example problems to demonstrate its effectiveness in constrained optimization and inclusion of non-level-set design variables.

5.1 Cantilever beam

The first example is a cantilever beam with aspect ratio 2, shown in Fig. 1a. The design domain is discretized using 160 × 80 unit sized elements. Material properties are Young’s modulus of 1.0 and Poisson’s ratio of 0.3. The beam is optimized for two problem formulations. First, the total compliance is minimized subject to a volume constraint set to 50 % of the design domain. Then, the final compliance value (5.94 × 103) is used as a constraint in the dual problem, where the volume is minimized, subject to an upper limit on the compliance. The resulting solutions of the two problems compare very closely, Fig. 5, and the final compliance and volume values are within the convergence tolerance.

Fig. 5
figure 5

Cantilever beam solutions: a minimization of compliance, b minimization of volume

Full size image

Non-level-set design variables are added to the compliance minimization of the cantilever beam. The structure of Fig. 1a is reinforced with bar elements that coincide with element edges in the mesh and the cross sectional areas of the bars are optimized simultaneously with the topology of the continuum. This approach can optimize for continuum and truss topology simultaneously. The design space contains purely truss type, purely continuum type structures and combinations of the two. In practice, the areas that contain just the bar elements can be considered a truss structure, the continuum areas are panel structures and the combined areas are reinforced panel structures. For this example, the mesh size is 80 × 40 and there are 6,520 non-level-set design variables. The volume constraint is replaced with an upper limit on the total mass of the structure, set to 100.0, which includes both the continuum material and bar reinforcements. The edge length, thickness and density of the 2D elements are 2.0, 0.1 and 0.1, respectively. The material properties for the bar elements are the same as the 2D elements and bar areas are limited to be between 10−6 and 0.1. The solution and convergence history for the reinforced cantilever beam are shown in Fig. 6. This example demonstrates that the SLP level-set method can effectively handle problems with many non-level-set design variables.

Fig. 6
figure 6

Cantilever with bar reinforcement: a solution, b convergence history

Full size image

5.2 Simultaneous optimization of topology and supports

Buhl (2002) introduced a method for simultaneously optimizing the topology and support boundary conditions of a structure. Designable supports are introduced by attaching springs to each degree of freedom at nodes within a support region. The spring stiffness can range from a very high value, representing an active support, to a very small value, representing an inactive support. The support springs are aggregated into one design variable per element within the support region. A power penalization method is used to force the support design variables to be either completely active or inactive. To avoid the trivial solution that all supports are active, a constraint is added to problem that limits the total cost of the supports. Buhl (2002) demonstrated the effectiveness of this approach using the SIMP method for the topology optimization. In this paper the support optimization approach is combined with the SLP level-set, where the support design variables are introduced as non-level-set design variables.

The simultaneous optimization of topology and supports using the SLP level-set method is demonstrated by minimizing the compliance of a bridge structure, taken from Buhl (2002), Fig. 7a. The design domain is 1.0 × 0.5 and discretized using 200 × 100 elements. A uniformly distributed load is applied along the top edge and the supports at the top left are right corners are fixed and not subject to optimization. The top two rows of elements are fixed to remain part of the structure. The red region in Fig. 7a indicates the support design region subject to optimization. The problem has two constraints, an upper limit on material volume, set to 20 % of the design domain, and an upper limit on the total support cost, set to 20 % of the maximum possible cost, where the cost of a support design variable varies linearly from one, if it is active, to zero, if it is inactive. The solution obtained using the SLP level-set method is shown in Fig. 7b, which agrees favourably to the solution obtained when SIMP was used to optimize the topology (Buhl 2002).

Fig. 7
figure 7

Bridge topology and support optimization: a initial design, boundary conditions and support region (shown in red), b solution (active supports shown using hatching)

Full size image

5.3 Natural frequency problems

This example is taken from Shu et al. (2011). The initial design and boundary conditions are shown in Fig. 8. The design domain is 2 × 1 m and discretized using 100 × 50 elements. The material properties are Young’s modulus of 200 GPa, Poisson’s ratio of 0.3 and density of 7,800 kg/m3. The thickness of the structure is 0.01 m. Consistent element mass matrices are used. The area in the central grey square has a density of 1.56 × 106 kg/m3 and is not subject to optimization. To prevent spurious modes occurring in the void region, elements completely outside the structure are given a stiffness of 0.2 GPa and density of 7.8 × 10−2 kg/m3. In this example the eigenvalues remain simple (multiplicity of one) throughout the optimization, therefore special methods for handling repeated eigenvalues are not required.

Fig. 8
figure 8

Natural frequency example: initial design and boundary conditions

Full size image

The example in Fig. 8 is first optimized to maximise the first natural frequency, ω 1 , subject to a volume constraint, set to 40 % of the design domain. The solution is shown in Fig. 9a and the convergence history, including the second natural frequency, ω 2 , is shown in Fig. 9b. The convergence history shows that the first and second natural frequencies almost coalesce at iteration 28 and the final frequency ratio is only: ω 2 / ω 1  = 1.04.

Fig. 9
figure 9

Maximize 1st natural frequency: a solution, b convergence history

Full size image

The maximization of first natural frequency problem is solved with an additional constraint that the second natural frequency must be at least 1.2 × ω 1 . This type of constraint can be used to prevent mode switching during the optimization (Odaka and Furuya 2005). Also, a design problem may require a specific frequency gap (Osher and Santosa 2001). The solution of the problem with a frequency ratio constraint is shown in Fig. 10a and convergence history in Fig. 10b. The solution meets both constraints and the first natural frequency is within 0.1 % of the value obtained in the original problem. The topology of the solutions is the same, although there are differences in the shape, shown in Fig. 11.

Fig. 10
figure 10

Natural frequency ratio constraint problem: a solution, b convergence history

Full size image
Fig. 11
figure 11

Natural frequency example, comparison of solutions

Full size image

5.4 Compliant mechanism design

The SLP level-set method is now used to design a crushing compliant mechanism, taken from Sigmund (1997). The objective is to maximize the mechanical advantage, defined as the ratio of the crushing force, F out , applied to a rigid work piece to the input force, F in , subject to upper limits on the displacement at the input force location and the total volume. The initial design, loading and boundary conditions are shown in Fig. 12, where the circle represents the rigid work piece and the grey area is not subject to optimization. Symmetry is used and only the top half of the mechanism is modelled. The design domain is discretized using 200 × 66 elements. The Young’s modulus is 3 GPa, Poission’s ratio is 0.4 and the thickness is 10 mm. The input force is 50 N and the input displacement constraint is 0.1 mm. The volume constraint is 33 % of the design domain.

Fig. 12
figure 12

Crushing mechanism: initial design and boundary conditions. Only top half is shown here due to symmetry

Full size image

The solution of for the mechanism problem is shown in Fig. 13, which has a similar topology to the solution obtained by Sigmund (1997) using the SIMP method. The constraints are satisfied at the optimum and the final mechanical advantage is 1.0.

Fig. 13
figure 13

Crushing mechanism solution

Full size image

6 Conclusions

A new method is developed to handle multiple constraints and simultaneously optimize for non-level-set design variables when using the conventional level-set topology optimization method. The key components of the new approach are discretized boundary integrals to estimate function changes and a sub-problem to compute the velocity function and step changes for the non-level-set design variables. The sub-problem is solved using SLP, thus the new method is termed the SLP level-set method.

The velocity function is defined as a linear combination of the shape sensitivity functions for the objective and constraints. This approach produces a smooth velocity function from sensitivity functions and further regularization of the velocity function is not required. The velocity function attained from the sub-problem is extended to grid nodes using the fast marching method. This approach helps maintain the signed distance property of the implicit function during the level-set update, which promotes stability and requires only occasional re-initialization. A further advantage of the SLP level-set method is that it does not rely on a particular FEA approach. The method is demonstrated to successfully optimize a wide range of optimization problems with multiple constraints and non-level-set design variables.