Analysis and design of acoustic transition sections for impedance matching and mode conversion

Abstract

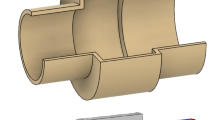
This work considers the problem of designing passive transition sections to provide impedance matching and mode conversion for acoustic wave propagation. The base configuration consists of two waveguides connected by a transition section. The objective is to find a placement of material inside this section to make it function as an impedance matcher or a mode converter with minimal losses. A finite element approximation of the Helmholtz equation in a truncated domain together with Dirichlet-to-Neumann type non-reflecting boundary conditions models the wave propagation. Material distribution techniques solve the resulting topology optimization problem and the resulting interfacial devices show good transmission properties.

Appendices

Appendix A: Dirichlet-to-Neumann map

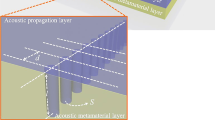
To derive the non-reflecting boundary conditions at the truncated waveguides, we consider the setup in a semi-discrete manner as illustrated in Fig. 14. That is, we will treat the problem continuously in the lengthwise direction and discretely in the radial direction. In this derivation, we consider a pipe extending infinitely to the left and assume that we have a discrete piecewise bi-quadratic representation p _h of the complex amplitude in the domain S marked grey on the right side. (In the numerical experiments, we have a piecewise bi-quadratic approximation p _h of the complex amplitude function p in Ω). Without loss of generality and to simplify notation, it is henceforth assumed that Γ consists of points x = (z,r) with z = 0.

Fig. 14

The boundary Γ (dashed line) separates the computational region S (grey) to the right and the semi-discretized infinite pipe to the left. The dash-dotted line is a symmetry line

We first consider a discrete version of the one-dimensional eigenproblem in the radial direction,

$$ \frac{\partial}{\partial r}\left( r \frac{\partial f}{\partial r} \right) = \lambda r f, $$

(23)

to find eigenvalues λ _m and eigenfunctions f _m . Let $V_{\Gamma }^{h}$ denote the space of all functions being quadratic on each edge of Γ and let M be the dimension of this space. Letting f denote the coefficient vector of f on Γ, the discrete eigenproblem can be written as

$$ \upgamma\mathbf{K} \mathbf{f} = \lambda \upgamma\mathbf{M} \mathbf{f}, $$

(24)

where γ M and γ K are the mass and stiffness matrices corresponding to problem (23). (Note that, γ can be viewed as a discrete trace operator; for the problem we are interested in, γ M ^L and γ K ^L are sub-matrices of M ^L and K ^L, respectively, corresponding to the unknowns on Γ ^L. The boundary matrices M ^L and K ^L are defined in (10)). Eigenproblem (24) above has eigenvalues λ _m and eigenvectors f _m , m=0,1,…,M. The eigenvalues are sorted so that λ _i >λ _j whenever i>j and that the eigenvectors f _m are real and scaled so that

$$ \mathbf{f}_{m}^{\mathsf{T}\!} \upgamma\mathbf{M}\mathbf{f}_{n} = \left\{\begin{aligned} 1 & \text{if}~m=n, \\ 0 & \text{whenever}~ m\neq n. \end{aligned}\right. $$

(25)

Let f _m (r) denote the function in $V^{h}_{\Gamma }$, that has nodal values given by f _m . On Γ, the complex amplitude function p _h can be written as

$$ p_{h}(0,r) = \sum\limits_{m=0}^{M} G_{m}(p_h) f_{m}(r), $$

(26)

where $G_{m}(p_h)= \mathbf {f}_{m}^{\mathsf {T}\!} \upgamma \mathbf {M} \upgamma \textbf {p}$ in which γ p denotes coefficient vector of p _h | _Γ . The solution of the semi-discretized wave propagation problem in the semi-infinite waveguide can be found using separation of variables and is formally written as

$$ p_{h}(z,r) = \sum\limits_{m=0}^{M} f_{m}(r) \left( A_{m} \mathrm{e}^{-\mathrm{i} k_{m} z} + B_{m} \mathrm{e}^{\mathrm{i} k_{m} z} \right), $$

(27)

where A _m and B _m are complex constants determining the amplitudes of the right and left going waves of mode m, respectively, and $k_{m}^{2} = k^{2} - \lambda _{m}$ is the reduced wave-number for this mode. The smallest eigenvalue for problem (24) is zero and corresponds to a constant vector (the plane wave mode), hence we have that k ₀=k. Evaluating the above expression (27) at z=0 and comparing it with expression (26) implies that G _m (p _h )=A _m +B _m . Hence, we define the semi-discrete Dirichlet-to-Neumann type operator on Γ by

$$ \text{DtN}^{\mathrm{h}}(p_h) = -\mathrm{i} \sum\limits_{m=0}^{M} f_{m}(r) k_{m} G_{m}(p_h). $$

(28)

By subtracting the above operator acting on the complex amplitude function p _h at Γ from the normal derivative of p _h , it follows that

$$\begin{array}{rcl} \frac{\partial p_{h}}{\partial n} &-& \text{DtN}^{\mathrm{h}}(p_h) = \mathrm{i} \sum\limits_{m=0}^{M} f_{m}(r) k_{m} \left( A_{m} - B_{m} \right)\notag\\ & +& \mathrm{i} \sum\limits_{m=0}^{M} f_{m}(r) k_{m} G_{m}(p_h) = 2 \mathrm{i} \sum\limits_{m=0}^{M} f_{m}(r) k_{m} A_m. \end{array} $$

(29)

Thus, by using a boundary condition of the type above, it is possible to set the constants A _m determining the complex amplitudes of the incoming waves while perfectly absorbing all outgoing waves. If there is no incoming wave, the operator DtN indeed produces the Neumann data given the Dirichlet data on boundary Γ. The above boundary condition is thus numerically exact in the discrete case, that is, it perfectly absorbs all outgoing waves (the M outgoing wave modes) while specifying the amplitudes of the M incoming wave modes over Γ.

Now, consider the integrals over Γ ^L and Γ ^R in problem (8) and let $\mathbf {f}_{m}^{\mathrm {L}}$ be the mth eigenvector of problem (24) with γ M and γ K replaced by γ M ^L and γ K ^L respectively; and let $\mathbf {f}_{m}^{\mathrm {L}}$ be scaled to satisfy expression (25) with γ M replaced by γ M ^L. Define $\mathbf {w}_{m}^{\mathrm {L}}$ as the coefficient vector of $w^{h}_{m}\in V^{h}$ so that $\upgamma \mathbf {w}_{m}^{\mathrm {L}} = \mathbf {f}_{m}^{\mathrm {L}}$ and all other components of $\mathbf {w}_{m}^{\mathrm {L}}$ is zero. In matrix notation, the boundary integral over Γ ^L in the left hand side of problem (8) can be written

$$\begin{array}{rcl} \int_{\Gamma^{\mathrm{L}}} \varphi_{i} \text{DtN}^{\mathrm{h}}(p_h) = \mathbf{e}_{i}^{\mathsf{T}\!} \mathbf{M}^{\mathrm{L}} \mathbf{DtN}(p_h) \notag\\ &&\qquad = \mathbf{e}_{i}^{\mathsf{T}\!} \mathbf{M}^{\mathrm{L}} \mathrm{i} \sum\limits_{m=0}^{M} k_{m} \mathbf{w}_{m} \left( \mathbf{M}^{\mathrm{L}}\mathbf{w}_{m} \right)^{\mathsf{T}\!} \mathbf{p} \notag\\ &&\qquad = \sum\limits_{j=1}^{N} p_{j} \mathbf{e}_{i}^{\mathsf{T}\!} \underbrace{\left( \mathrm{i} \sum\limits_{m=0}^{M} k_{m} \mathbf{M}^{\mathrm{L}} \mathbf{w}_{m} \left( \mathbf{M}^{\mathrm{L}}\mathbf{w}_{m} \right)^{\mathsf{T}\!} \right)}_{\mathbf{B^{\mathrm{L}}}} \mathbf{e}_j. \end{array} $$

(30)

By letting B ^R denote a similar matrix corresponding to the integral over Γ ^R, the discretized variational problem (8) can be written in matrix form as

$$ \left( \mathbf{K}(\alpha_h) - k^{2} \mathbf{M}(\alpha_h) - \mathbf{B}^{\mathrm{L}} - \mathbf{B}^{\mathrm{R}} \right) \mathbf{p} = 2\mathrm{i} k \mathbf{M}^{\mathrm{L}} \mathbf{w}_{0}^{\mathrm{L}}. $$

(31)

Appendix B: Conservation

The derivation below shows that the numerical treatment of the problem is mimetic in that it guarantees conservation of the power in the discrete case.

Before turning to the discrete case, let us first look at sound power of a traveling wave in a cylindrical waveguide in the continuous case. The sound power of this wave is given by the integral of intensity (the product of pressure and velocity) with respect to area. Here, we are studying time harmonic wave propagation in cylindrical symmetry and the sound power for the traveling wave is given by

$$ W = \pi \text{Re} \left\{ \int_{\Gamma} r p\overline{u} \mathrm{d}{\Gamma} \right\}, $$

(32)

where the complex valued functions p and u correspond to pressure and velocity, respectively. By using separation of variables and the relation between pressure and velocity, the functions p and u can be expanded as

$$\begin{array}{@{}rcl@{}} p &=& \sum\limits_{m=0}^{\infty} A_{m} f_{m}(r) e^{-\mathrm{i} k_{m} z}\quad\quad\quad\mathrm{ and } \notag\\ u &=& \sum\limits_{m=0}^{\infty} \frac{A_{m} f_{m}(r) k_me^{-\mathrm{i} k_{m} z}}{\rho c k}, \end{array} $$

(33)

where k _m are the reduced wave numbers and the eigenfunctions satisfy a continuous version of (25), that is, they are scaled so that

$$ \int_{\Gamma} r f_{m}(r) \overline{{f}_{n}(r)} \mathrm{d}{\Gamma} = \left\{\begin{aligned} 1 & \text{if}~m=n, \\ 0 & \text{whenever}~m\neq n. \end{aligned}\right. $$

(34)

By inserting expansions (33) for p and u into the expression for sound power (32) and by using the orthonormality of the eigenmodes (34), we get

$$\begin{array}{rcl} W &=& \pi \text{Re} \int_{\Gamma} r p\overline{u} \mathrm{d}{\Gamma} = \pi \text{Re} \left\{ \sum_{m=0}^{\infty} \sum_{n=0}^{\infty} A_{m} \overline{A_{n}}\right. \notag\\ &&\qquad\quad\left.\frac{\overline{k_{n}}}{\rho c k}e^{-\mathrm{i} k_{m} z}\overline{e^{-\mathrm{i} k_{n} z}} \int_{\Gamma} r f_{m}(r) \overline{f_{n}(r)} \mathrm{d}{\Gamma} \right\}\notag\\ &=&\frac{\pi}{\rho c} \text{Re} \left\{ \sum_{m=0}^{\infty} |A_m|^{2} \frac{\overline{k_{m}}}{k} \right\} = \frac{\pi}{\rho c}\sum_{m=0}^{M_{p}}\frac{k_{m}}{k} |A_m|^{2}, \end{array} $$

(35)

where

$$ M_{p} = \max_{m\in \mathbb{N}} m \quad \text{subject to}\,\, k_{m} \in \mathbb{R} $$

(36)

corresponds to the highest possible propagating mode (having a real reduced wave number) in the waveguide. Next, by defining the normalized sound power $W^{\text {norm}} = \frac {\rho c}{\pi } W$ and letting

$$ P_m=\frac{k_{m}} {k} |A_m|^2 $$

(37)

represent the normalized power of the mth mode wave, we get that the normalized sound power for this traveling wave is given

$$ W^{\text{norm}} = \frac{\rho c}{\pi} W = \frac{\rho c}{\pi}\frac{\pi}{\rho c} \sum\limits_{m=0}^{M_{p}}\frac{k_{m}}{k} |A_m|^{2} = \sum\limits_{m=0}^{M_{p}} P_m. $$

(38)

For the problem studied in this article, the wave propagation in the left waveguide consists of the input wave traveling towards the transition section and the reflected waves, traveling to the left, while the wave propagation in the right waveguide consists of the transmitted waves traveling to the right. Since we have no losses, we have that

$$ W_{\text{refl}}^{\text{norm}} + W_{\text{trans}}^{\text{norm}} = W_{\text{in}}^{\text{norm}}, $$

(39)

where $W_{\text {refl}}^{\text {norm}}$, $W_{\text {trans}}^{\text {norm}}$, and $W_{\text {in}}^{\text {norm}}$ are the normalized power of the reflected wave, the transmitted wave, and the input wave respectively. Boundary conditions (4c) and (4d) ensures that input is planar wave in the left waveguide and specifies the amplitude such that $W_{\text {in}}^{\text {norm}}=1$ and the power balance (39) can be written as

$$ W_{\text{refl}}^{\text{norm}} + W_{\text{trans}}^{\text{norm}} = 1. $$

(40)

It is perhaps interesting to note that for the chosen input wave, $W_{\text {refl}}^{\text {norm}}$ is the fraction of input power that gets reflected back to the left waveguide, a fraction commonly referred to as the power reflection coefficient. Similarly, $W_{\text {trans}}^{\text {norm}}$ is the fraction of input power that gets transmitted to the right waveguide, that is, the power transmission coefficient.

Now, let us turn to the discrete case. The numerical treatment is designed so that it guarantees conservation of power, as shown below. First, making the particular choice $q_h=\overline {p_{h}}$ in expression (8) yields

$$\begin{array}{rcl} \int_{\Omega} \alpha r \nabla \overline{p_{h}} \cdot \nabla p_{h} - k^{2} \int_{\Omega} \alpha r \overline{p_{h}} p_h -\int_{\Gamma^{\mathrm{L}}} r \overline{p_{h}} \text{DtN}^{\mathrm{h}}(p_h) \notag\\ &&\qquad - \int_{\Gamma^{\mathrm{R}}} r \overline{p_{h}} \text{DtN}^{\mathrm{h}}(p_h) = 2 \mathrm{i} k \int_{\Gamma^{\mathrm{L}}} r \overline{p_{h}} f_{0}^{\mathrm{L}}. \end{array} $$

(41)

The integrands in the domain integrals above are real. By taking the imaginary part of the previous expression and rearrangeing the terms, we obtain

$$\begin{array}{rcl} 0 = \text{Im} &&\left\{ \int_{\Gamma^{\mathrm{R}}} r \overline{p_{h}} \text{DtN}^{\mathrm{h}}(p_h)\right. \notag\\ &&\left. + \int_{\Gamma^{\mathrm{L}}} r \overline{p_{h}} \left( 2 \mathrm{i} k f_{0}^{\mathrm{L}} + \text{DtN}^{\mathrm{h}}(p_h) \right)\right\}. \end{array} $$

(42)

Recall from Appendix A that, in a semi-infinite waveguide and under the assumption that we have discretized the radial direction, the wave propagation can be written as in expression (27) and the DtN^h operator is defined in expression (28). Let $A_{m}^{\mathrm {L}}$ and $A_{m}^{\mathrm {R}}$ denote the complex constants determining the amplitudes of the incoming (that is moving toward the transition section) waves of mode m at Γ ^L, and Γ ^R, respectively. Similarly, let $B_{m}^{\mathrm {L}}$ and $B_{m}^{\mathrm {R}}$ denote the complex constants determining the amplitudes of the outgoing waves of mode m at Γ ^L, and Γ ^R, respectively.

By the boundary conditions on Γ ^L and Γ ^R, we know that $A_{0}^{\mathrm {L}}=1$, $A_{m}^{\mathrm {L}}=0$ for all m>0, and $A_{m}^{\mathrm {R}}=0$ for all m. The constants $B_{m}^{\mathrm {L}}$ and $B_{m}^{\mathrm {R}}$ are in the discrete case given by

$$\begin{array}{@{}rcl@{}} B_{m}^{\mathrm{L}} &=& \left( \mathbf{w}_{m}^{\mathrm{L}}\right)^{\mathsf{T}\!}\mathbf{M}^{\mathrm{L}} \mathbf{p} - A_{m}^{\mathrm{L}} \quad \mathrm{ and } \notag\\ B_{m}^{\mathrm{R}} &=& \left( \mathbf{w}_{m}^{\mathrm{R}}\right)^{\mathsf{T}\!}\mathbf{M}^{\mathrm{R}} \mathbf{p} - A_{m}^{\mathrm{R}}, \end{array} $$

(43)

respectively. Here, the notation follows the same style as in Appendix A with the addition of the exponents L and R clarifying whether the object belongs to the left or right waveguide, respectively.

Inserting the series expansions for the complex amplitude function on Γ ^R into the second integral in expression (42) and expanding the Dirichlet-to-Neumann operator yields

$$\begin{array}{rcl} \int_{\Gamma^{\mathrm{R}}} r \overline{p_{h}} \text{DtN}^{\mathrm{h}}(p_h) \notag \\&&\qquad = \int_{\Gamma^{\mathrm{R}}} \left( \sum_{m=0}^{M^{\mathrm{R}}} f_{m}^{\mathrm{R}}(r) \overline{B_{m}^{\mathrm{R}}} \right) r \left( -\mathrm{i} \sum_{n=0}^{M^{\mathrm{R}}} k_{n}^{\mathrm{R}} f_{n}^{\mathrm{R}}(r) B_{n}^{\mathrm{R}} \right) \notag\\ &&\qquad = - \mathrm{i} \sum_{m=0}^{M^{\mathrm{R}}}\sum_{n=0}^{M^{\mathrm{R}}} k_{n}^{\mathrm{R}}\overline{B_{m}^{\mathrm{R}}}B_{n}^{\mathrm{R}} \int_{\Gamma^{\mathrm{R}}} f_{m}^{\mathrm{R}}(r) r f_{n}^{\mathrm{R}}(r), \end{array} $$

(44)

where M ^R denotes the number of nodes on Γ ^R, $f_{m}^{\mathrm {R}}$ is a piecewise quadratic function on Γ ^R whose nodal values given by $\mathbf {f}_{m}^{\mathrm {R}}$ (the mth eigenvector of problem (24) with γ M and γ K replaced by γ M ^R and γ K ^R respectively), and $k_{m}^{\mathrm {R}}$ is the reduced wave number for the mth mode in the right waveguide. By expression (25), the integral above vanishes whenever m≠n and equals 1 for m=n, thus the above expression simplifies to

$$ \int_{\Gamma^{\mathrm{R}}} r \overline{p_{h}} \text{DtN}^{\mathrm{h}}(p_h) = - \mathrm{i} \sum_{m=0}^{M^{\mathrm{R}}} k_{m}^{\mathrm{R}} |B_{m}^{\mathrm{R}}|^2. $$

(45)

Similarly, inserting the expansions for the complex amplitude function on Γ ^L into the first integral in expression (42) yields

$$\begin{array}{rcl} &&\int_{\Gamma^{\mathrm{L}}} r \overline{p_{h}} \left( 2 \mathrm{i} k f_{0}^{\mathrm{L}} + \text{DtN}^{\mathrm{h}}(p_h) \right) \notag\\ &&\qquad = \mathrm{i} k - \mathrm{i} k B_{0}^{\mathrm{L}} + \mathrm{i} k \overline{B_{0}^{\mathrm{L}}} - \sum_{m=0}^{M^{\mathrm{L}}} \mathrm{i} k_{m}^{\mathrm{L}} |B_{m}^{\mathrm{L}}|^2. \end{array} $$

(46)

Inserting (45) and (46) into (42) yields

$$\begin{array}{@{}rcl@{}} 0 &=&\text{Im} \left\{ \mathrm{i} k + 2 k \text{Im} \left\{ B_{0}^{\mathrm{L}} \right\} - \mathrm{i} \sum\limits_{m=0}^{M^{\mathrm{L}}} k_{m}^{\mathrm{L}} |B_{m}^{\mathrm{L}}|^2 - \mathrm{i} \sum\limits_{m=0}^{M^{\mathrm{R}}} k_{m}^{\mathrm{R}} |B_{m}^{\mathrm{R}}|^{2} \right\} \notag \\ &=& k - \sum\limits_{m=0}^{M_{\mathrm{p}}^{\mathrm{L}}} k_{m}^{\mathrm{L}} |B_{m}^{\mathrm{L}}|^{2} - \sum\limits_{m=0}^{M_{\mathrm{p}}^{\mathrm{R}}} k_{m}^{\mathrm{R}} |B_{m}^{\mathrm{R}}|^{2}, \end{array} $$

(47)

where

$$\begin{array}{@{}rcl@{}} M_{p}^{\mathrm{L}} &=& \max\limits_{m\in \{1,2,\ldots,M^{\mathrm{L}} \}} m \quad \mathrm{subject~to}~k_{m}^{\mathrm{L}} \in \mathbb{R} \quad \text{and} \notag\\ M_{p}^{\mathrm{R}} &=& \max\limits_{m\in \{1,2,\ldots,M^{\mathrm{R}} \}} m \quad \mathrm{subject~to}~k_{m}^{\mathrm{L}} \in \mathbb{R} \end{array} $$

(48)

correspond to the highest possible propagating mode (having a real reduced wave number) in the left and right waveguide, respectively. Rearranging the terms and dividing by k, the previous expression reduces to

$$ \sum\limits_{m=0}^{M_{\mathrm{p}}^{\mathrm{L}}} \frac{k_{m}^{\mathrm{L}}}{k} |B_{m}^{\mathrm{L}}|^{2} + \sum\limits_{m=0}^{M_{\mathrm{p}}^{\mathrm{R}}} \frac{k_{m}^{\mathrm{R}}}{k} |B_{m}^{\mathrm{R}}|^{2} = 1, $$

(49)

that is, the sum of the outgoing modes square-absolute-amplitudes scaled by their (relative) propagation speed is constant, independent of the material distribution in the transition section. Thus the discrete version of the problem perfectly conserves power. Similarly as in the continuous case above, we let

$$ P_{m}^{\mathrm{L}}=k_{m}^{\mathrm{L}}|B_{m}^{\mathrm{L}}|^2/k, \quad m= 0,\ldots,M_{\mathrm{p}}^{\mathrm{L}} $$

(50)

and

$$ P_{m}^{\mathrm{R}}=k_{m}^{\mathrm{R}}|B_{m}^{\mathrm{R}}|^2/k, \quad m= 0,\ldots,M_{\mathrm{p}}^{\mathrm{R}} $$

(51)

represent the normalized sound power of the mth mode outgoing wave in the left and right waveguides, respectively. (The sound power of the mth mode outgoing wave in the left and right waveguides is given by $\frac {\pi }{\rho c}P_{m}^{\mathrm {L}}$ and $\frac {\pi }{\rho c}P_{m}^{\mathrm {R}}$, respectively). Inserting expressions (50) and (51) into expression (49) yields

$$ \sum\limits_{m=0}^{M_{\mathrm{p}}^{\mathrm{L}}} P_{m}^{\mathrm{L}} + \sum\limits_{m=0}^{M_{\mathrm{p}}^{\mathrm{R}}} P_{m}^{\mathrm{R}} = 1. $$

(52)

that is, the same power balance (40) as in the continuous case.

Appendix C: Sensitivity analysis

The method of moving asymptotes requires gradients of each component of the objective function. Below follows a short derivation on how to get the gradient of $B_{n}^{\mathrm {R}}$, that is complex amplitude of the nth outgoing wave mode in the right waveguide. Fix α _h and let δ α _h be an arbitrary design variation. Linearizing problem (11), taking into account that K and M are linear in α, yields

$$\begin{array}{rcl} \left( \mathbf{K}(\delta \alpha_h) - k^{2} \mathbf{M}(\delta \alpha_h) \right) \mathbf{p} \notag\\&&\qquad+ \left( \mathbf{K}(\alpha_h) - k^{2} \mathbf{M}(\alpha_h) - \mathbf{B}^{\mathrm{L}} - \mathbf{B}^{\mathrm{R}} \right) \delta \mathbf{p} = 0, \end{array} $$

(53)

where δ p is the first variation of p. In matrix form, $B_{n}^{\mathrm {R}}$ can be computed as $B_{n}^{\mathrm {R}} = \left ( \mathbf {w}_{n}^{\mathrm {R}}\right )^{\mathsf {T}\!}\mathbf {M}^{\mathrm {R}} \mathbf {p} - A_{n}^{\mathrm {R}}$ and $A_{n}^{\mathrm {R}}$ is zero by the boundary condition on Γ ^R. Differentiating this expression for $B_{n}^{\mathrm {R}}$ gives

$$ \delta B_{n}^{\mathrm{R}} = \left( \mathbf{w}_{n}^{\mathrm{R}}\right)^{\mathsf{T}\!} \mathbf{M}^{\mathrm{R}} \delta \mathbf{p}. $$

(54)

Letting $\mathbf {z}_{n}^{R}$ be the solution of problem (11) with right-hand side replaced by $\mathbf {M}^{\mathrm {R}}\mathbf {w}_{n}^{\mathrm {R}}$, multiplying the linearized state problem (53) with $(\mathbf {z}_{n}^R)^{T}$ and using that the state matrix is symmetric, it follows that

$$\begin{array}{rcl} 0 &=& (\mathbf{z}_{n}^R)^{T} \left( \mathbf{K}(\delta \alpha_h) - k^{2} \mathbf{M}(\delta \alpha_h) \right) \mathbf{p} \notag\\ &&\qquad + (\mathbf{z}_{n}^R)^{T} \left( \mathbf{K}(\alpha_h) - k^{2} \mathbf{M}(\alpha_h) - \mathbf{B}^{\mathrm{L}} - \mathbf{B}^{\mathrm{R}} \right) \delta \mathbf{p} \notag\\ &=& (\mathbf{z}_{n}^R)^{T} \left( \mathbf{K}(\delta \alpha_h) - k^{2} \mathbf{M}(\delta \alpha_h) \right) \mathbf{p} + \left( \mathbf{w}_{n}^{\mathrm{R}}\right)^{\mathsf{T}\!} \mathbf{M}^{\mathrm{R}} \delta \mathbf{p}. \end{array} $$

(55)

From the two above expression, we identify the partial derivatives of $B_{n}^{\mathrm {R}}$ with respect to the pixel value α _E in element E as

$$ \frac{\partial B_{n}^{\mathrm{R}}}{\partial \alpha_{E}} = (\mathbf{z}_{n}^R)_{E}^{T} \left( \mathbf{K}_{E} - k^{2} \mathbf{M}_{E} \right) \mathbf{p}_{E}, $$

(56)

where p _E and $(\mathbf {z}_{n}^R)_{E}$ are vectors containing the components of p and $\mathbf {z}_{n}^{R}$ corresponding to nodes in element E while M _E and K _E are the element mass and stiffness matrices for element E.