Maxwell’s reciprocal diagrams and discrete Michell frames

Abstract

This paper unites two major legacies of James Clerk Maxwell’s ground-breaking paper, “On Reciprocal Figures, Frames, and Diagrams of Forces” (Maxwell, Philos Mag 26:250-261, 1864; Edinb Roy Soc Proc 7:160–208, 1870): (i) the fundamental theorem used by Michell (Philos Mag 8(47):589–597, 1904) to derive trusses of least weight and (ii) reciprocal frames. This paper presents some remarkable relationships between discrete Michell frames and their corresponding reciprocal force polygons using Graphic Statics. Several examples are given to illustrate the notions of duality and self-reciprocity in these diagrams, with particular emphasis placed on discrete optimal benchmark structures. For a given connectivity of nodes, Graphic Statics provides all of the information needed to determine the total load path of the structure in the form and force diagrams. Because the form and force diagrams are reciprocal, in the course of finding one minimum load path structure, a second minimum load path structure is also found. These observations between the corresponding form and force diagrams are generalized for discrete cantilever Michell frames, and several comments on the extensions of this work are included.

1 Introduction

“Maxwell” is the first word in A. G. M. Michell’s seminal paper “The Limits of Economy of Material in Frame-structures” (Michell 1904). Michell is referring to James Clerk Maxwell’s paper “On Reciprocal Figures, Frames, and Diagrams of Forces” (Maxwell 1870). The first equation in Michell’s paper (stating that the difference between the total tension load paths and the total compression load paths is equal to a constant is inferred from Maxwell’s paper, which is also cited as the origin of reciprocal diagrams and Graphics Statics.

It should be noted that terminology has changed over the 150 years of work which form the basis of this paper. The terms “frames”, “structures”, and “trusses” are used interchangeably within this paper and denote what are currently known as trusses.

Maxwell starts with concepts from W. J. Macquorn Rankine’s paper, “Principle of the Equilibrium of Polyhedral Frames,” (Rankine 1864) and extends the work to show how certain trusses have reciprocal diagrams which represent the forces in the trusses. This approach had a major impact on the field of structural engineering.

Maxwell’s work was interpreted and expanded by many others including Jenkin (1869), Culmann (1864), Cremona (1890), Wolfe (1921), and others as noted in Kurrer (2008). It is of interest that Maxwell and Cremona considered two-dimensional form diagrams (trusses) and their two-dimensional reciprocal force diagrams as the projection of three-dimensional polyhedra (one polyhedron for members and one polyhedron for forces). Maxwell used a paraboloid of revolution reciprocal mapping which resulted in reciprocal lines that were perpendicular to each other in projection, while Cremona used a hyperboloid reciprocal mapping which resulted in reciprocal lines being parallel to one another. The parallel mapping of reciprocal lines has generally been used in practice.

Although Graphic Statics was a leading method of analyzing trusses in the late 19th and early 20th centuries, it is not commonly employed in the 21st century. Historically, graphical solutions for truss systems, cables and arches have been used for a variety of design problems. Graphical calculation methods were a common method to calculate the equilibrium of structures since the fundamental work by Culmann (1864) for the engineers of the late 19th century and early 20th century. Unfortunately, graphical methods progressively lost popularity with the development of other mathematical approaches. Examples of structures designed using graphical methods include the work of the brilliant structural designer Maillart (Zastavni 2008, 2010).

This paper will bring together these two threads of Maxwell’s paper and show that some discrete Michell trusses (frames) have a very remarkable relationship to the reciprocal force polygons as determined by Graphic Statics. The remainder of this paper is organized as follows: Section 2 provides a review of graphical methods and the notation used throughout this paper. Next, relationships between paired optimal frames, with emphasis placed on their corresponding reciprocal diagrams, are described in Section 3. Section 4 introduces the notion of self-reciprocity in Graphic Statics with several examples to illustrate the key concepts. Generalized observations on discrete cantilever Michell frames are provided in Section 5 followed by some concluding remarks and extensions of this work.

2 Graphic statics

Graphical methods have been used for centuries to analyze and design a variety of structures. In this section, we give a brief historical review of such methods and introduce the methodology and notation used throughout this work.

2.1 A history of graphical methods

The origin of Graphic Statics can be traced back to the writings of Simon Stevin (1586), in which a parallelogram rule using force vectors and polygons was first used to analyze forces in a structure. Later, Pierre Varignon (1687, 1725) demonstrated the law of force polygon and introduced the use of funicular polygons, but graphical (equilibrium) analysis using vectorized diagrams was not formalized until Culmann wrote his Die graphische Statik (Culmann 1864; Block et al. 2006).

It was Maxwell, however, who first introduced the notion of structural reciprocity to solve structural frames (Maxwell 1864, 1870). In these papers, Maxwell describes how one could find forces in structural frames: a reciprocal diagram can be generated by drawing lines perpendicular to the lines of action of the structural members, such that all members connected at a single node create a polygon. The resulting diagrams were considered reciprocal, as Maxwell defined, “two figures are reciprocal when the properties of the first relative to the second are the same as those of the second relative to the first”. The resulting lengths of the lines in the new diagram are proportional to the forces in the original member diagram. This concept is described in more detail in Section 3. Also, in this work, Professor Rankine was acknowledged for being the first one to apply the most general statement of graphical methods at the time.

Luigi Cremona (1890) further refined the method by introducing a different node to polygon mapping technique, in which the lines in the force diagram were parallel to the lines of action of the structural members. These diagrams were easier to read than those of Maxwell, which were rotated 90°. The Graphic Statics method introduced by Cremona became so popular that nowadays, the graphical method of solving structural trusses is often called the Cremona method.

Other contributors to the graphical methods include Levy, who used them to calculate trusses and masonry arch bridges in Levy (1888); Poleni; Lame and Clapeyron; Poncelet; Rankine; Bow; Mohr, and Ritter. For more information, the interested reader can refer to the work of Wolfe (1921), which explains how to solve various structural problems using Graphic Statics. The book by Zalewski and Allen (1998) also presents step-by-step instructions for construction of the form and force diagrams, which we discuss briefly in the next section. Furthermore, we note that similarly to the methodology presented next to find minimal load path structures, Graphic Statics has also been applied in Chapter 14 of the book by Zalewski and Allen (1998) for form finding of trusses by graphically solving for the nodal locations that give desired relative member forces.

More recently, Graphic Statics have been used in Block et al. (2006) and Block and Ochsendorf (2007) for the understanding of arch behavior, which is particularly useful in compression shell design. In this work, a methodology for generating compression-only vaulted surfaces and networks based on thrust line analysis and graphical methods is discussed. A complete review of this methodology, Thrust Network Analysis (TNA) and its applications, with emphasis on analysis of complex masonry vaults, can be found in Block (2009).

2.2 Methodology and notation of Graphic Statics

Graphic Statics is a graphical method of solving for the forces in structural frames using two reciprocal diagrams, and can be created using simple drafting tools. As noted in the Maxwell quote above, each of the reciprocal diagrams can be mapped into the other using the same procedure. Each of the reciprocal diagrams in Graphic Statics consists of a set of points, or nodes, straight lines interconnecting all the nodes, and polygons defined by those lines. These polygons can be closed (i.e. defined by areas with closed loops of finite lines) or open (i.e. defined by chains of finite lines between two nodes with external loads).

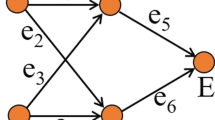
The lines in the first diagram, called the form diagram, represent structural members, or rather lines of action of the structural members (see Fig. 1a). The lines in the second diagram, known as the force diagram, represent forces carried by the members from the form diagram (see Fig. 1b). In this figure, dashed line vectors are used to represent these external forces both in the form and force diagrams. For every line of action in the form diagram, there is a reciprocal line in the force diagram. That reciprocal line is drawn parallel to the original line and its length is proportional to the force in the original member. The reciprocity of the two diagrams is as follows: Each polygon in the form diagram maps to a node in the force diagram, each node in the form diagram maps to a polygon in the force diagram and each line in the form diagram maps to a parallel line in the force diagram.

Fig. 1

Graphic Statics diagrams: a form diagram, b force diagram

For simplicity, the notation used in the following diagrams is a version of Bow’s notation, also known as interval notation (Bow 1873). For the form diagram, the capital letters, A, B, C,..., are sequentially placed clockwise in the intervals between external forces (open polygons) and numbers, 1, 2, 3,..., are placed in the internal spaces (closed polygons) between members. Each line in the form diagram is bordered by two polygons. Thus, a member may be called using the corresponding letter or number of the adjacent polygons, e.g. A-1 or 2-3, and a joint called with a series of letters and numbers, e.g. A-B-3-2-1-A. Similarly, the external forces are called using the adjacent open polygons, for example $F_{AB}$. The open polygons denoted by capital letters in the form diagram correspond to points (nodes) on the load line of the force diagram, denoted by the lowercase letters, a, b, c,.... The numbers denoting the closed polygons in the form diagram also have corresponding nodes in the force diagram.

This graphical methodology allows the user to determine the axial force in a truss member by measuring the length of the reciprocal line in the force diagram. The relative scale of the force diagram is set by drawing the load line representing the external forces to a scale. For example, the force in member A-1 in Fig. 1a is proportional to the length of the line between points a and 1 in Fig. 1b. Similarly, the force in the member between polygons 2 and 3 is proportional to the length of the line between points 2 and 3 of the force diagram. The remaining forces in the other members can be computed likewise. Thus, the forces acting on a node in the form diagram correspond to a polygon in the force diagram, where each force is an edge of the polygon. For example, at node A-B-3-2-1-A, the polygon of forces is given by points a-b-3-2-1-a. Reading clockwise around joint A-B-3-2-1-A in the form diagram, we can determine if members A-1 and 2-3 are in tension or compression. If read from 1 to a on polygon a-b-3-2-1-a, we move from the left to the right, towards the joint A-B-3-2-1-A of the form diagram. Thus, member A-1 is in compression. Moving from 3 to 2 on the force polygon goes from the upper left to the lower right, or away from the joint in the form diagram, so member 3-2 is in tension.

3 Paired optimal trusses

As shown in Stromberg et al. (2012), the minimal volume problem for a given set of balanced forces and nodal connectivity can be written as follows:

$$ \min_{\mathbf{x}}V=\min_{\mathbf{x}}\frac{1}{\sigma}\sum|P|\cdot L $$

(1)

where x is a vector of design variables containing the nodal coordinates of the unloaded nodes, σ is a constant that represents the allowable stress, L represents the lengths of the members and P the internal forces of the members. We note that if the structure is optimal, the assumption of constant stress is valid. The quantity, $\sum |P|\cdot L$, represents the total load path of the structure; therefore, minimizing the total load path of a structure corresponds directly to minimizing its volume, or weight. For a given connectivity of nodes, Graphic Statics has all of the information needed to determine this quantity: The form diagram gives the length, L, of each member and the force diagram gives the force, P, in each member.

A minimal load path structure can be found by changing the design variables, or in this case, the nodal locations in the force diagram subject to the rules of reciprocal diagrams such that $\sum |P|\cdot L$ is minimized. In Graphic Statics, the form diagram and the force diagram are, as Maxwell noted, reciprocal. This leads to the remarkable observation that the force diagram could also represent the geometry of another optimal truss with its own external loads. In the course of finding one minimum load path structure, a second minimum load path structure is also found. In addition, the forces in the second minimum load path structure are represented by the length of the lines in the original structure. These two trusses are both discrete optimal trusses for their external loads in the sense that they are solutions to (1).

In Figs. 2 and 3, the structures (form diagrams) given on the left are both different discrete optimal structures (Hemp 1973; Mazurek et al. 2011). The supposition that the force diagram in Fig. 2 is also the geometry of a second discrete optimal truss with its own loading is explored in Fig. 3. The geometry of the truss in Fig. 3 (the form diagram) is taken from the force diagram for Fig. 2.

Fig. 2

Example illustrating the duality of optimal trusses: a form diagram, b force diagram

Fig. 3

Example illustrating the duality of optimal trusses in Fig. 2: a form diagram, b force diagram

Now that two optimal truss geometries have been found, the remaining task is to find the external loads that correspond to a truss represented by the geometry of the force diagram. The external forces for this second truss are found by closing the “open” polygons of the original form diagram in a continuous manner. The vector formed by closing an open polygon in the original form diagram is the external force that would be applied to the node in the force diagram that corresponds to the original open polygon. Closing the open polygons provides the proper external forces for the dual structure because it closes the force polygon at the node which corresponds to the open polygon in the original form diagram.

It is clear that the form and force reciprocal diagrams in Figs. 2 and 3 are interchangeable. In order to make the relationships more clear, Bow’s notation in Fig. 3 is reversed.

For the problem in (1), the lengths are taken from the truss on the left and the internal forces from the truss on the right, though the reverse (i.e. internal forces from the left diagram, lengths from the right diagram) would result in the same optimal solution. The advantage to using Graphic Statics for this class of optimal problems is that it provides all of the information about the loads and the pathsin a graphical manner.

Another example of paired or dual discrete trusses is given in Fig. 4, where the discrete truss on the left (form diagram) is the minimum load path structure for a given set of forces and nodal connectivity (Prager 1970). The reciprocal force diagram in the middle not only represents the forces of truss but also the geometry of another optimal truss, where the external forces for this optimal structure can also be found by closing the open polygons in the form diagram. For example, the external force applied at node a in Fig. 4b is given by closing the “open” polygon, A, or drawing a line from joint A-3-C-A to joint A-B-1-A. Figure 4c shows the dual truss with the external loads given by closing all of the polygons in (a).

Fig. 4

Example illustrating the duality of optimal trusses: a form diagram, b force diagram, c dual truss

The Appendix has a chart showing some dual discrete trusses along with the Bow notation. This chart graphically shows both the geometry and the forces for each pair of optimal trusses.

4 Self-reciprocal discrete Michell frames

For some cases of paired trusses, it can be shown that the geometry of the reciprocal force diagram is the exact same as the member diagram; it can be said that these types of structures are self-reciprocal. An example of a self-reciprocal structure is the optimal discrete Michell truss taken from Chan (1960) and Mazurek et al. (2011) shown in Fig. 5. This self-reciprocity can be observed for an unbounded cantilever with an equal number of members at each support when there is a single applied load acting parallel to a line drawn through the supports and the reactions intersect the tip of the cantilever. Figure 6 shows another example of a self-reciprocal frame for the three-point problem. We note here that the notion of self-reciprocity can also apply for non-symmetric structures. The reasons for this remarkable self-reciprocity for certain discrete Michell Frames is explained in Section 5.

Fig. 5

The solution to the discrete Michell cantilever (Chan 1960; Mazurek et al. 2011) is self-reciprocal: a form diagram, b force diagram. The geometries of the form and force diagrams are the same

Fig. 6

The solution to this three-point discrete frame is also self-reciprocal: a form diagram, b force diagram

Even though the form and force diagrams of self-reciprocal discrete Michell Frames are the same, the mapping between reciprocal lines is complex. For example, the forces in the outside chords of the Michell cantilever in Fig. 5 are proportional to the lengths of the lines in the fans at the supports. It is noteworthy that self-reciprocal Michell Frames provide both the geometry and the forces in one diagram if one knows how to “read” the structure. As more and more members are added to the discrete trusses, the solution approaches the continuum solutions of Michell, Chan, and others.

5 Generalized observations on discrete cantilever Michell frames

Discrete optimal trusses for 3-point or 3-force problems have been obtained in Mazurek et al. (2011) and Mazurek (2012). The 3-point problem can be described by finding the optimal (minimum load path) structure for two points of support and a single point load. The 3-force problem is when the optimal structure is found for three loaded points (the three point loads must be in equilibrium). It has been shown in Mazurek et al. (2011) and Mazurek (2012) that the geometry of the optimal discrete trusses is fairly regular regardless of the number of elements utilized in the solutions. The optimal truss geometry can also be defined using only two parameters (i.e. angles $\gamma$ and one of $\psi _{\alpha }$ or $\psi _{\beta }$) for a 3-point problem (see Fig. 7a) or three parameters (i.e. angles $\gamma$, one of $\psi _{\alpha }$ or $\psi _{\beta }$ and one of $\lambda _{\alpha }$ or $\lambda _{\beta }$) for the 3-force problem (see Fig. 7b).

The configuration of the members at every node of these trusses is exactly the same and, therefore, they can be constructed through a process of repetition. Even though in the examples shown, the externally loaded or constrained nodes for 3-point and 3-force problems are in the same locations and the tip load is applied in the same magnitude and direction for both problems, the optimal trusses have different geometries (see Fig. 7). This is because in the 3-point problem, the directions of the reactions are not prescribed, and they vary depending on the structure, whereas in the 3-force problem, all of the forces are given. Since the 3-point problem has one less parameter constrained (the direction of the reactions), the volume of the truss is always smaller or equal to the one obtained for the 3-force problem.

Fig. 7

Discrete optimal trusses for the a 3-point problem and b 3-force problem with a 3 × 3 discretization

In the creation of reciprocal diagrams for a 3-point or 3-force optimal truss (Fig. 8), certain geometrical similarities with its original form diagram can be observed. We note that these geometric rules may not hold if additional constraints are incorporated into the optimization problem, such as a bound on the feasible design space. For unconstrained 3-point or 3-force problems, from the geometrical dependencies of the lines, it can be concluded that, except for the following three differences, the geometry of the force diagram is the same as the corresponding form diagram:

• The numbers of elements $n_{\alpha }$ and $n_{\beta }$ at the nodes of reacting forces are reversed in the force diagram.

• The left and right turn angles $\psi _{\alpha }$ and $\psi _{\beta }$ are swapped.

• Angles $\lambda _{\alpha }$ and $\lambda _{\beta }$ are replaced with $\chi _{\alpha }$ and $\chi _{\beta }$, respectively.

With the differences listed above, a certain family of discrete optimal structures can be described where force diagrams are directly proportional to their form diagrams. Namely, if we select a discrete optimal truss with $n_{\alpha }=n_{\beta }$ for a problem that produces $\lambda _{\alpha }=\chi _{\alpha }\iff \lambda _{\beta }=\chi _{\beta }\Rightarrow \psi _{\alpha }=\psi _{\beta }=90^{\circ }$, the force diagram will be self-reciprocal. Also, because $\psi _{\alpha }=\psi _{\beta }$ and $\lambda _{\alpha }=\chi _{\alpha }$, the acting force is parallel to the line between nodes of the reacting forces. From the direct proportionality, it can be shown that the lines of reaction forces in these trusses intersect at the tip node of the truss, as the reaction at the $\alpha$-support (node A-3-6-C-A) can be expressed by vector ca in the force diagram and the reaction at the $\beta$-support (node C-8-7-B-C) by vector bc (see Fig. 9).

Fig. 8

Duality in optimal trusses for the generalized 3-force problem

Fig. 9

Dual optimal trusses for the 3-force problem with $n_{\alpha }=n_{\beta }$, $\lambda _{\alpha }=\chi _{\alpha }$, $\lambda _{\beta }=\chi _{\beta }$, and $\psi _{\alpha }=\psi _{\beta }=90^{\circ }$ produces a force diagram directly proportional to its form diagram

Even more interesting is the observation that if we select a discrete optimal truss with $\lambda _{\beta }=\chi _{\alpha }$ and $\lambda _{\alpha }=\chi _{\beta }$, the geometry of the force diagram will be proportional to a mirror of the form diagram (see Fig. 10). From Mazurek et al. (2011) we also know that the criterion $\lambda _{\beta }=\chi _{\alpha }$ defines solutions where the acting forces are located along their line of action producing structures of least volume. It is quite remarkable that the two diagrams come together so nicely for these optimal trusses. Thus, the ratio of the force in member 2-4 to the length of member B-3 is the same as the force applied at B-1-A-B to the distance between C-A-2-4-C and C-5-B-C. The same ratio exists between the force in member C-5 and the length of member A-1, and so on.

Fig. 10

Dual optimal trusses for the 3-force problem with $\lambda _{\beta }=\chi _{\alpha }$ and $\lambda _{\alpha }=\chi _{\beta }$; the force diagram is a mirror reciprocal of the form diagram

6 Concluding remarks

Maxwell’s work on structural reciprocity and load paths in 1864 and 1870 launched two trajectories in the theory and design of trusses that this paper attempts to reconnect. The first trajectory was that of reciprocal diagrams and Graphic Statics. This aspect was quickly embraced and enlarged by Culmann, Cremona and others and widely used by engineers as a practical method of designing and analyzing trusses. Michell, in his landmark paper Michell (1904), starts with another aspect of Maxwell’s 1870 paper and develops optimal frames of minimal total load path. The total load path of a structure is the result of Graphic Statics with one diagram representing the paths (lines of action) and the reciprocal diagram representing the forces (loads). This paper connects these two legacies of Maxwell through the application of Graphic Statics to discrete optimal trusses. It results in some observations worth noting:

• The reciprocal diagrams of Graphic Statics provide the information needed to determine the total load path of a structure. This provides an avenue for determining minimum load path structures for a given connectivity by varying the geometry of the force diagram subject to the restrictions of reciprocal diagrams. A subsequent paper by the authors will explore this subject in more detail.

• The force diagram that corresponds to the form diagram of an optimal discrete truss represents the geometry of another optimal truss with possibly different external loads. This leads to recognition that optimal trusses are the dual of other optimal trusses, so once dual trusses are properly paired, one can determine the forces in the members of one truss by observing the lengths of reciprocal members in the other truss. A table of some dual trusses is provided (see Appendix).

• Certain discrete Michell Frames are self-reciprocal. This means that by observing the geometry of certain Michell Frames one can also determine the forces in the members if one knows how to “read” the structure.

• A general overview of discrete optimal trusses and their duals is provided for the 3-point and 3-force problems.

As an extension of this work, the design of optimal bridges and cable systems using Graphic Statics and Rankine’s Theorem are currently under investigation by the authors.

Appendix

The following table presents a summary of the reciprocal relationships between the form and force diagrams of several optimal structures.

	Form diagram	Force diagram	Dual truss
I.
II.
III.
IV.
V.
VI.
VII.
VIII.

1. I. Classical discrete Michell solution for the centrally-loaded beam (Michell 1904; Hemp 1973; Mazurek et al. 2011)
2. II. Two discrete Michell solutions for semi-infinite space (Michell 1904; Hemp 1973)
3. III. Self-reciprocal cantilever with two points of support (Chan 1960; Mazurek et al. 2011)
4. IV. Optimal shear bracing solution (Hemp 1973; Stromberg et al. 2012). Note: Overlaying lines have been merged
5. V. Two dual minimal weight trusses given in Prager (1970)
6. VI. Discrete Michell cantilever truss with a circular support (Michell 1904)
7. VII. Discrete self-reciprocal Michell cantilever ($n_{\alpha }=n_{\beta }$, $\lambda _{\alpha }=\chi _{\alpha }$, $\lambda _{\beta }=\chi _{\beta }$, $\psi _{\alpha }=\psi _{\beta }=90^{\circ }$)
8. VIII. Discrete mirror-reciprocal Michell cantilever ($\lambda _{\beta }=\chi _{\alpha }$, $\lambda _{\alpha }=\chi _{\beta }$)