On minimum compliance problems of thin elastic plates of varying thickness

Abstract

The paper deals with two minimum compliance problems of variable thickness plates subject to an in-plane loading or to a transverse loading. The first of this problem (called also the variable thickness sheet problem) is reduced to the locking material problem in its stress-based setting, thus interrelating the stress-based formulation by Allaire (2002) with the kinematic formulation of Golay and Seppecher (Eur J Mech A Solids 20:631–644, 2001). The second problem concerning the Kirchhoff plates of varying thickness is reduced to a non-convex problem in which the integrand of the minimized functional is the square root of the norm of the density energy expressed in terms of the bending moments. This proves that the problem cannot be interpreted as a problem of equilibrium of a locking material. Both formulations discussed need the numerical treatment in which stresses (bending moments) are the main unknowns.

1 Introduction

The problem of optimum design of the thickness h of a linearly elastic anisotropic plate loaded in-plane to minimize its compliance is well posed, provided that the thickness variation is subjected to the conditions: $h \ge h_{\textrm min} >$ 0, as proved in Cea and Malanowski (1970), see also Litvinov and Panteleev (1980), Bendsøe (1995, Sec. 1.5.1) and Petersson (1999). This optimization problem is equivalent to the problem of the optimal transversely homogeneous distribution of one material within a plate loaded in-plane in its convexified version, see Sec. 5.2.5 in Allaire (2002). By virtue of this analogy one can note that the question of correctness of the formulation of the minimum compliance problem of plates (loaded in plane) of varying thickness with the condition $h_{\textrm min} >$ 0 can be concluded from the Th. 5.2.8 in Allaire (2002). The main aim of the present paper is the discussion of the problem of optimal distribution of the plate thickness under the condition $h_{\textrm min}$ $=$ 0. To be specific let us set the problem:

Find optimal distribution of the thickness $h$ of a plate made of an elastic material of the in-plane (reduced) moduli $C_{ijkl}$ subject to the in-plane loading and fixed on a part $\Gamma _{2}$ of the contour of $\Omega$, to minimize the compliance of the plate under the condition of the plate volume being given. The in-plane stiffnesses $A_{ijkl}=h(x)C_{ijkl}$ are involved in the formulation; they are referred to a Cartesian frame ($x_{1}$, $x_{2})$, $x=\left ( {x_1 ,x_2} \right )\in \Omega .$

The problem thus formulated can be reduced to the following minimization problem

$$ Z=\inf \left\{ {\int\limits_{\Omega} {\left\| {{\boldsymbol\tau} } \right\|_c \;dx} \;\left| {{{\boldsymbol\tau} }\in \Sigma \left( \Omega \right)} \right.} \right\} $$

(1.1)

where $\Sigma (\Omega )$ is the set of statically admissible stress fields $\boldsymbol \tau = (\tau _{\mathit {ij}})$ referred to the plane domain $\Omega$ and $\| \cdot \|_{c}$ is a norm given by the formula

$$ \left\| {{\boldsymbol\tau} } \right\|_c =\sqrt {{{\boldsymbol\tau} }\cdot \left( {{\textbf{c}}\;{{\boldsymbol\tau} }} \right)} $$

(1.2)

where c $=$ C $^{-1}$ and the dot means the scalar product. The formulation (1.1) can be read off from the result (5.51, 5.52) in Allaire (2002). The result (1.1) is not identical to the result referred to, since in the present paper the merit function is the compliance while in the book by Allaire (2002) the merit function is the weighted sum of the compliance and the volume, see (5.49), see also the discussion of the formulations (4.6), (4.7) ibidem. In the present paper it is proved that the solution $\boldsymbol \tau$ $=$ $\boldsymbol \tau$* (provided it exists) to the problem (1.1) determines directly the thickness $h^{\ast }$ of the optimal plate.

The assumption $h_{\textrm min}$ $=$ 0 is essential, since it makes it possible to determine the sub-domains of the design domain where $h^{\ast }$ $=$ 0, or the appearance of openings as well as the unnecessary segments close to the edges. The solution $\boldsymbol \tau$* to the problem (1.1) can vanish on a sub-domain $\Omega _{0}$ of $\Omega$. There the thickness $h^{\ast }$ of the optimal plate vanishes. Thus the solution of the problem (1.1) cuts off the part of the plate which is unnecessary. In this manner specific mathematical difficulties are circumvented, linked with admitting very small values for $h_{\textrm min}$ in the original setting of the optimization problem discussed.

The problem (1.1) has a mathematical structure similar to the stress-based formulation of the Michell truss problem, as set in Strang and Kohn (1983) inspired by Rozvany (1976):

$$ Z_M =\inf \left\{ {\int\limits_{\Omega} {\left\| {{{\boldsymbol\tau} }\left( x \right)} \right\|_M dx} \left| {\;{{\boldsymbol\tau} }\in \Sigma \left( \Omega \right)} \right.} \right\} $$

(1.3)

where

$$ \left\| {{\boldsymbol\tau} } \right\|_M =\left| {\tau_I} \right|+\left| {\tau _{II}} \right| $$

(1.4)

$\tau$ $_{I} \ge$ $\tau$ $_{II}$ being the principal values of $\boldsymbol \tau$. The problem (1.3) is more difficult than (1.1) due to the integrand (1.4) being non-smooth, yet the common feature of both the problems (1.1) and (1.3) is the linear growth of the integrands. Similarity between (1.1) and (1.3) suggests similar mathematical forms of the dual settings. In the paper by Strang and Kohn (1983) the problem dual to (1.3) has been derived; it reads

$$ Z_M =\sup \left\{ {f\left( {\textbf{v}} \right)\left| {\;{\textbf{v}}\in V,\quad {{\boldsymbol\varepsilon} }\left( {{\textbf{v}}\left( x \right)} \right)\in B_M \;\textrm{a.e. in } \Omega} \right.} \right\} $$

(1.5)

where v $=$ (${\textit v}_{1}$, ${\textit v}_{2})$ is the displacement vector in the plane $\Omega$, the strain $\varepsilon$(v) $=$ ($\varepsilon _{ij}$(v)) is defined by components 2$\varepsilon _{ij}=\partial {\textit v}_{i}$/ $\partial x_{j}+\partial$ ${\textit v}_{j}$/ $\partial x_{i}$ and

$$ B_M =\left\{ {{{\boldsymbol\varepsilon} }\in E_s^2 \left| {\;\left| {\varepsilon_I} \right|\le 1\;,\;\left| {\varepsilon_{II}} \right|\le 1} \right.} \right\} $$

(1.6)

is a ball in $E_{S}^{2}$, $E_{S}^{2}$ being the set of 2nd order tensors in the 2D case considered. Moreover, f (v) represents the virtual work of the loading, while V is the set of kinematically admissible displacements referred to the plane domain $\Omega$. The set $B_{M}$ is called a locking locus, as in the theory of the materials with locking, see Demengel and Suquet (1986). Note that 0 lies in this set and this set is both convex, closed and bounded.

Proceeding similarly as in Strang and Kohn (1983) one can work the passage from the formulation (1.1) to the dual formulation. It reads

$$ Z=\max \left\{ {f\left( {\textbf{v}} \right)\left| {{\textbf{v}}\in V,\;{{\boldsymbol\varepsilon} }\left( {{\textbf{v}}\left( x \right)} \right)\in B_C ,\;\textrm{ a.e.}\;\textrm{ } x\in \Omega} \right.} \right\} $$

(1.7)

where

$$ B_C =\left\{ {{{\boldsymbol\varepsilon} }\in E_S^2 \left| {\quad \left\| {{\boldsymbol\varepsilon} } \right\|_C \le 1} \right.} \right\} $$

(1.8)

and

$$ \left\| {{\boldsymbol\varepsilon} } \right\|_C =\sqrt {{{\boldsymbol\varepsilon} }\cdot \left( {{\textbf{C}}\;{{\boldsymbol\varepsilon} }} \right)} $$

(1.9)

The norms $\vert \vert$ $\cdot$ $\vert \vert _{c}$ and $\vert \vert$ $\cdot$ $\vert \vert _{C}$ are mutually dual.

The formulation (1.7) is known, it was for the first time derived in Golay and Seppecher (2001), directly from the displacement-based setting. The primal formulation (1.1) has not been reported there.

In the present paper it is shown that the problem (1.1) can be the point of departure for the numerical approach developed in Czarnecki and Lewiński (2012) to solve the free material design problem of planar elasticity. Due to some mathematical similarities, this numerical approach, with slight adjustment, applies here. The stress fields $\tau$ are interpolated by polynomials over the polygons forming the mesh—see Czarnecki and Lewiński (2012).

The very idea of using a stress-based numerical scheme to solve the minimum compliance problem is not new, see the paper by Allaire and Kohn (1992), where the Airy stress function method had been used to set the numerical method based on the FE approach. The novelty of the present paper is that the subject of the numerical analysis is the problem (1.1) in which the thickness h is absent, hence it does not need to be bounded from below, while in the shape optimization algorithm proposed by Allaire and Kohn (1992) the volume fraction had to be bounded by a small value to assure the numerical stability. A price to pay is to deal with a non typical problem (1.1) in which the functional involves an integrand of linear growth. Thus this problem should be numerically solved in its original setting, by appropriate interpolating the statically admissible stress fields and by performing the minimization over the stress representations. The numerical approach does not lead to a set of linear equations with a non-singular square matrix, which is typical while using the finite element method. In particular, no stiffness matrices occur. The method proposed exceeds the FEM framework: we have to develop a new numerical method in which only the meshing of the domain is a step common with any FE approaches. The algorithm put forward has been by no means supported by the experience we have from solving problems of solid body mechanics.

If the plate is transversely loaded, its bending stiffnesses equal ($h^{3}(x)$/12)$C_{ijkl}$, while the isoperimetric condition has the same form as in the in-plane loaded case. The problem of the compliance minimization of the plate in bending of thickness $h \ge h_{\textrm min} >$ 0 is badly posed, which had been the subject of discussions in the numerous papers starting from Kozłowski and Mróz (1970), Cheng and Olhoff (1981), Rozvany (1989), Lur’e and Cherkaev (1986), (cf. the papers published in the volume: Cherkaev and Kohn (1997)), Krog and Olhoff (1997), Bendsøe (1995), Cherkaev (2000) and Lewiński and Telega (2000, Sec. 27). In the paper by Muñoz and Pedregal (2007) a review of the relaxation methods of this problem can be found; the aim of the relaxation is to make the problem well posed, without losing its original setting.

In the present paper an emphasis is put on the stress based formulation (the bending moments play the role of stresses) in which $h_{\textrm min}$ $=$ 0. It occurs that the integrand of the minimized functional is non-convex: it is expressed by the square root of the norm of the bending moment tensor. This form of the functional explains clearly why both analytical and numerical attempts to solve the minimum compliance problem of the plate in bending in its original (unrelaxed) formulation have to fail to succeed. The numerical results, as mesh dependent, have to behave at random.

Thus the stress-based formulations of the minimum compliance problems of thin plates (both: loaded in—plane or loaded out of plane), admitting $h_{\textrm min}$ $=$ 0, disclose explicitly whether the problems are well posed.

The thin plate problems discussed have much in common with the formulations used in the penalized density methods, like SIMP, concerning the generalized shape design in elasticity. The last section of this paper provides a stress-based formulation of SIMP thus paving the way for the new numerical algorithms of shape optimization. The discussion shows a close link between SIMP for the case of $p = 3$ and of the Kirchhoff plate optimization.

The usual summation convention for the indices: i, j, k, l $=$ 1, 2 is adopted. The scalar product of ${{\boldsymbol \sigma } },{{\boldsymbol \tau } }\in E_S^2$ is defined by ${{\boldsymbol \sigma } }\cdot {{\boldsymbol \tau } }=\sum \limits _{i,j=1}^2 {\sigma _{ij} \;\tau _{ij}}$. It determines the Euclidean norm $\left \| {{\boldsymbol \sigma } } \right \|=\sqrt {{{\boldsymbol \sigma } }\cdot {{\boldsymbol \sigma } }}$ for ${{\boldsymbol \sigma } }\in E_S^2$. If C $=$ ($C_{ijkl})$ is a Hooke tensor, then $\left ( {{\textbf {C}}\;{{\boldsymbol \sigma } }} \right )_{ij} =\sum \limits _{k,l=1}^2 {C_{ijkl} \;\sigma _{kl}}$. For the plane stress case and isotropy the norm (1.9) is expressed by

$$ \begin{array}{@{}l} \,\left\| {{\boldsymbol\varepsilon} } \right\|_C =\sqrt {\frac{E}{1-\nu^2}\left[ {\left( {\varepsilon_{11}} \right)^2+2\nu \varepsilon_{11} \varepsilon _{22} +\left( {\varepsilon_{22}} \right)^2+2(1-\nu )\left( {\varepsilon _{12}} \right)^2} \right]} \end{array} $$

(1.10)

or

$$ \|\boldsymbol{\varepsilon}\|_{C} = \sqrt{\frac{E}{1-{\textit v}^{2}} \left((\varepsilon_{I})^{2} + 2{\textit v}\varepsilon_{I}\varepsilon_{II} + (\varepsilon_{II})^{2}\right) } $$

(1.11)

$\varepsilon _{\mathit {I}}$, $\varepsilon _{\mathit {II}}$ being the principal strains; E, $\nu$ are the Young modulus and Poisson’s ratio. Lastly, let us define the mean value of a function f defined on $\Omega$ by

$$ \left\langle f \right\rangle =\frac{1}{\left| \Omega \right|}\int\limits_{\Omega} {f\left( x \right)} \;dx. $$

(1.12)

2 The stress based formulation of the minimum compliance problem of plates of varying thickness. The in-plane problem

2.1 Arbitrary variation of the plate thickness

We refer here to the optimum design problem of plates subjected the an in-plane loading, sketched in the Introduction. Let $L\left ( {\Omega ,E_S^2} \right )$ be the space of tensor fields $\boldsymbol \tau$ $=$ ($\tau$ $_{ij})$ of appropriate regularity to satisfy the local equilibrium equations. We demand that ${{\boldsymbol \tau } }\in L^2\left ( {\Omega ,E_S^2} \right )$ and $\text {div}\;{{\boldsymbol \tau } }\in L^2\left ( {\Omega , R^2} \right )$, see Duvaut and Lions (1976). Let $\Sigma (\Omega )$ be a subset of $L\left ( {\Omega ,E_S^2} \right )$ of trial tensor fields $\boldsymbol \tau$ satisfying the variational equilibrium condition:

$$ \forall {\textbf{v}}\in V\quad \int\limits_{\Omega} {{{\boldsymbol\tau} }\cdot {{\boldsymbol\varepsilon} }\left( {\textbf{v}} \right)} \;dx=f\left( {\textrm {\textbf v}} \right). $$

(2.1)

A field $\boldsymbol \tau$ $\in$ $\Sigma (\Omega )$ is said to be statically admissible. Note that 0, the zero element in $L\left ( {\Omega ,E_S^2} \right )$ does not belong to the set $\Sigma (\Omega )$.

The components $A_{ijkl}$ of tensor A represent the in-plane stiffnesses of the plate.

We know that among all $\boldsymbol \tau$ $\in$ $\Sigma (\Omega )$ one can find one field $\boldsymbol \sigma$ such that

$$ \exists {\textbf{u}}\in V\quad {{\boldsymbol\sigma} }={\textbf{A}}\;{{\boldsymbol\varepsilon} }\left( {\textbf{u}} \right). $$

(2.2)

The regularity assumptions in V are specified in Duvaut and Lions (1976), see also Nečas and Hlavaček (1981). Tensor A is positive definite, hence the functional over ${{\boldsymbol \tau } }\in L^2\left ( {\Omega ,E_S^2} \right )$ given by

$$ \left\| {{\boldsymbol\tau} } \right\|_{L^2\left( {\Omega ,E_S^2} \right)} =\sqrt {\int\limits_{\Omega} {{{\boldsymbol\tau} }\cdot \left( {{\textrm {\textbf A}}^{-1}\;{{\boldsymbol\tau} }} \right)dx}} $$

(2.3)

has properties of a norm.

The compliance $\Upsilon$ can be either defined by $\Upsilon$ $=$ f (u) or by

$$ \Upsilon =\min\limits_{{{\boldsymbol\tau} }\in \Sigma \left( \Omega \right)} \left( {\left\| {{\boldsymbol\tau} } \right\|_{L^2\left( {\Omega ,E_S^2} \right)}} \right)^2 $$

(2.4)

since the minimizer of the latter problem is just $\boldsymbol \tau$ $=$ $\boldsymbol \sigma$. The equality (2.4) is the Castigliano theorem, see Duvaut and Lions (1976) and Nečas and Hlavaček (1981).

As indicated in the Introduction we assume that the plate is made of a homogeneous material whose reduced moduli (for the generalized plane stress case) form a tensor $C_{ijkl}$, all the components being constant with respect to x $\in$ $\Omega$. The in-plane stiffness tensor A depends linearly on h, or A($x)=h(x)$ C, x $\in$ $\Omega$.

Let us re-write the expression for the compliance disclosing its dependence on the design variable $h(x)$

$$ \Upsilon =\min \left\{ {\int\limits_{\Omega} {\frac{1}{h\left( x \right)}{{\boldsymbol\tau} }\left( x \right)\cdot \left( {{\textbf{c}}\;{{\boldsymbol\tau} }\left( x \right)} \right)dx} \left| {{{\boldsymbol\tau} }\in \Sigma \left( \Omega \right)} \right.} \right\} $$

(2.5)

where c $=$ C $^{-1}$. Our aim is to choose $h(x)$ such that $\Upsilon$ attains minimum over all plates of given volume

$$ \int\limits_{\Omega} {h\left( x \right)dx} =V_0 . $$

(2.6)

The optimum design problem to be discussed reads

$$\begin{array}{lll} J&{}={}&\inf \left\{ \int\limits_{\Omega} {\frac{1}{h\left( x \right)}{{\boldsymbol\tau} }\left( x \right)\cdot \left( {{\textbf{c}}\;{{\boldsymbol\tau} }\left( x \right)} \right)dx} \left|{} \;1/h\in L^1\left( {\Omega ,R^+} \right),\right.\right.\,\,\,\,\,\,\,\,\,\\&&\qquad\left.\left.{{\boldsymbol\tau} }\in \Sigma \left( \Omega \right),\;\int\limits_{\Omega} {h\left( x \right)dx=V_0} \right. \right\}. \end{array} $$

(2.7)

Let

$$ F\left( x \right)={{\boldsymbol\tau} }\left( x \right)\cdot \left( {{\textrm {\textbf c}}\;{{\boldsymbol\tau} }\left( x \right)} \right). $$

(2.8)

Note that the problem

$$\begin{array}{lll} \Upsilon &=&\inf \left\{ \int\limits_{\Omega} {\frac{F\left( x \right)} {h\left( x \right)}dx} \left| \;1/h\in L^1\left( {\Omega ,R^+} \right),\right.\right.\\&&\qquad \left.\left. \int\limits_{\Omega} {h\left( x \right)dx=V_0} \right. \right\} \end{array} $$

(2.9)

is explicitly solvable, cf. Appendix. According to (A.4) for p $=$ 1 the minimizer $h^{\ast }$ equals

$$ h^{\ast} \left( x \right)=V_0 \frac{\sqrt {F\left( x \right)}} {\int\limits_{\Omega} {\sqrt {F\left( x \right)} \;dx}} $$

(2.10)

while, by (A.5) for p $=$ 1

$$ \Upsilon =\frac{1}{V_0} \left( {\int\limits_{\Omega} {\sqrt {F\left( x \right)} \;dx}} \right)^2. $$

(2.11)

The optimum design problem (2.7) is thus reduced to

$$ J=\inf \left\{ {\frac{1}{V_0} \left( {\int\limits_{\Omega} {\sqrt {{{\boldsymbol\tau} }\left( x \right)\cdot \left( {{\textbf{c}}\;{{\boldsymbol\tau} }\left( x \right)} \right)} dx}} \right)^2\left| {{{\boldsymbol\tau} }\in \Sigma \left( \Omega \right)} \right.} \right\}, $$

(2.12)

which can be re-written as below

$$ J=\frac{Z^2}{V_0} , $$

(2.13)

where

$$ Z=\inf \left\{ {\int\limits_{\Omega} {\left\| {{\boldsymbol\tau} } \right\|_c \;dx} \;\left| {{{\boldsymbol\tau} }\in \Sigma \left( \Omega \right)} \right.} \right\} $$

(2.14)

and $\left \| \cdot \right \|_c$ is defined by (1.2). The result (2.13, 2.14) is compatible with the result (5.51, 5.52) in Allaire (2002) concerning the convexified formulation of the layout problem of one material within $\Omega$. The integrand in (2.14) is convex, but of linear growth. However, we cannot expect that the infimum in (2.14) will lie within $\Sigma (\Omega )$. Therefore, to make this problem well posed it should be relaxed by admitting the solutions to lie in the space of measures, cf. the results by Demengel and Suquet (1986) on a related problems of the bodies with locking, and the recent book by Plotnikov and Sokołowski (2012) concerning the compressible Navier–Stokes fluids.

If $\boldsymbol \tau$ $=$ $\boldsymbol \tau$* is the argument of infimum of (2.14), then the optimal thickness is given by (2.10) or

$$ h^{\ast} \left( x \right)=V_0 \frac{\left\| {{{\boldsymbol\tau} }^{\ast} \left( x \right)} \right\|_c} {\int\limits_{\Omega} {\left\| {{{\boldsymbol\tau} }^{\ast} \left( x \right)} \right\|_c \;dx}} . $$

(2.15)

For the plane stress case and isotropy the norm (1.2) is expressed by

$$ \begin{array}{@{}l} \left\| {{\boldsymbol\tau} } \right\|_c =\sqrt {\frac{1}{E}\left[ {\left( {\tau _{11}} \right)^2-2\nu \tau_{11} \tau_{22} +\left( {\tau_{22}} \right)^2+2(1+\nu )\left( {\tau_{12}} \right)^2} \right]} \end{array} $$

(2.16)

or

$$ \left\| {{\boldsymbol\tau} } \right\|_c =\sqrt {\frac{1}{E}\left( {\left( {\tau _I} \right)^2-2\nu \tau_I \tau_{\mathit{II}} +(\tau_{\mathit{II}} )^2} \right)} $$

(2.17)

where $\tau$ $_{I}$, $\tau$ $_{II}$ are principal stresses.

The regularity assumptions concerning the trial stress fields in (2.14) do not hinder the solution of (2.14) from vanishing on a subdomain of $\Omega$. If this happens, $h^{*}$ would vanish on this subdomain, which violates the initial assumptions on h, see (2.7). In fact, these assumptions were too strong. It is sufficient to require in (2.7) that

$$ j(x)=\frac{{\boldsymbol\tau} \left( x \right)\cdot \left( {{{{\textbf c}\boldsymbol\tau}}\left( x \right)} \right)}{h\left( x \right)} $$

(2.18)

is integrable. If $\tau$ $^{\ast }$, $h^{\ast }$ are chosen as above, $j=j^{\ast }$ and

$$ j^{\ast} (x)=a\left\| {{{\boldsymbol\tau} }^{\ast} \left( x \right)} \right\|_c ,\quad a=\frac{1}{V_0} \int\limits_{\Omega} \left\| {{{\boldsymbol\tau} }^{\ast} \left( x \right)} \right\|_c dx $$

(2.19)

and we see that $j^{\ast }$ is integrable, even if (2.18) is an undetermined quantity 0/0. Thus the formulation (2.13)–(2.16) is a natural extension of (2.7), as admitting vanishing of h on some subdomains of $\Omega$. By solving (2.13)–(2.16) we circumvent all difficulties in detecting places where the material is unnecessary. Instead of detecting these places e.g. by the topological derivative method, see Sokołowski and Żochowski (1999), Lewiński and Sokołowski (2003) we search the subdomains, where $\boldsymbol \tau {^{\ast }} =$ 0.

2.2 Bounded variation of the plate thickness

Assume now that the plate thickness assumes the values between $h_{\textrm max}$ and $h_{\textrm min} >$ 0. Instead of discussing the problem

$$\begin{array}{lll} &&{} \inf \left\{\vphantom{\int\limits_{\Omega} {h\left( x \right)dx} =V_0} \Upsilon \left| \;1/h\in L^1\left( {\Omega ,R^+} \right),\quad h_{\min} <h\left( x \right)<h_{\max} \right.\right.\\ &&\quad\left.\left.\textrm{a.e. in } \Omega ,\quad \int\limits_{\Omega} {h\left( x \right)dx} =V_0 \right. \right\} \end{array} $$

(2.20)

where $\Upsilon$ is the compliance given by (2.5), we follow Allaire (2002) and discuss the problem of minimizing a weighted sum of the compliance and the plate volume

$$\begin{array}{lll} J_1 &=&\inf \left\{ \Upsilon +\lambda \int\limits_{\Omega} {h\left( x \right)dx} \left| \;1/h\in L^1\left( {\Omega ,R^+} \right),\right.\right.\\ &&\;\;\quad\left.\left. h_{\min} <h\left( x \right)<h_{\max} \quad \textrm{a.e. in}~ \Omega \right. \vphantom{\Upsilon +\lambda \int\limits_{\Omega} {h\left( x \right)dx} \left| \;1/h\in L^1\left( {\Omega ,R^+} \right),\right.}\right\} \end{array} $$

(2.21)

with $\lambda$ being a multiplier.

For a fixed value of $\lambda$ for the solution to the problem (2.21) one can recover the value of the plate volume $V_{0}$. Then, for this value $V_{0}$ the solution to (2.21) coincides with the solution to the initial problem (2.20), see comments on p. 263 in Allaire (2002), which apply here, although the problems (2.20), (2.21) and the problems (4.6), (4.7) in Allaire (2002) are different.

Let us substitute (2.5) into (2.21) and perform minimization over h analytically. The optimum design problem (2.21) reduces to:

$$ J_1 =\inf \left\{ {\int\limits_{\Omega} {W_{\lambda} \left( {{\boldsymbol\tau} } \right)dx\left| {\;{{\boldsymbol\tau} }\in \Sigma \left( \Omega \right)} \right.}} \right\} $$

(2.22)

with

$$ W_{\lambda} \left( {{\boldsymbol\tau} } \right)=\left\{ {{\begin{array}{lll} \frac{1}{h_{\min} } \left\| {{\boldsymbol\tau} } \right\|_c^2 +\lambda h_{\min} &\text{if} &\left\| {{\boldsymbol\tau} } \right\|_c \le \sqrt \lambda \;h_{\min} \\[2em] {2\sqrt \lambda \left\| {\boldsymbol\tau}\right\|_c} &\text{if} &\sqrt \lambda \;h_{\min} \le \left\| {{\boldsymbol\tau} } \right\|_c \\[1em] &&\quad\le \sqrt \lambda \;h_{\max} \\ \frac{1}{h_{\max} } \left\| {{\boldsymbol\tau} } \right\|_c^2 +\lambda h_{\max} &\text{if} &\left\|{{\boldsymbol\tau} } \right\|_c \ge \sqrt \lambda \;h_{\max} \\ \end{array}} } \right.$$

(2.23)

where $\left \| {{\boldsymbol \tau } } \right \|_c$ is defined by (1.2). The problem (2.22) can be interpreted as an equilibrium problem of a non-linear elastic body of complementary energy given by (2.23). The potential $W_{\lambda }$ is smooth and convex. Assume that ${{\boldsymbol \tau } }={{\boldsymbol \tau } }_{\lambda }^{\ast }$ is the solution to problem (2.22). Having found ${{\boldsymbol \tau } }_{\lambda }^{\ast }$ one can determine the optimal thickness by

$$ h_{\lambda}^{\ast} \left( x \right)=\left\{ {{\begin{array}{@{}l@{\quad}l@{\quad}l} h_{\min} &\text{if} & \left\| {{{\boldsymbol\tau} }_{\lambda}^{\ast} \left( x \right)} \right\|_c \le \sqrt \lambda \;h_{\min} \\[1.5em] {{\frac{1}{\sqrt \lambda} \left\| {{\boldsymbol\tau}_{\lambda}^{\ast} \left( x \right)} \right\|_c}} &\text{if} & \sqrt\lambda \;h_{\min} \le \left\| {{{\boldsymbol\tau} }_{\lambda}^{\ast} \left( x \right)} \right\|_c \\[1em] &&\quad\le \sqrt \lambda \;h_{\max} \\ h_{\max} &\text{if}& \left\| {{{\boldsymbol\tau} }_{\lambda}^{\ast} \left( x \right)} \right\|_c \ge \sqrt \lambda \;h_{\max} \\ \end{array}} } \right.$$

(2.24)

Assume that the whole optimal solution is characterized by

$$ \sqrt \lambda \;h_{\min} \le \left\| {{{\boldsymbol\tau} }_{\lambda}^{\ast} \left( x \right)} \right\|_c \le \sqrt \lambda \;h_{\max} $$

(2.25)

Then the isoperimetric condition (2.6) implies

$$ \frac{1}{\sqrt \lambda} \int\limits_{\Omega} {\left\| {{{\boldsymbol\tau} }_{\lambda}^{\ast} \left( x \right)} \right\|_c dx} =V_0 $$

(2.26)

which leads to $h^{\ast }$ given by the formula (2.15) found previously.

Let us note that $W_{\lambda }$ given by (2.23) can be put in the form

$$\begin{array}{lll} &W_{\lambda} \left( {{\boldsymbol\tau} } \right)\\ &\;\;\;=2\sqrt \lambda \left\| {{\boldsymbol\tau} } \right\|_c \\ &\;\;\;\quad+\left\{ {{\begin{array}{@{}c@{\quad}l@{\quad}l} \left( {\frac{\left\| {{\boldsymbol\tau} } \right\|_c} {\sqrt {h_{\min} }} -\sqrt \lambda \sqrt {h_{\min} } } \right)^2&\text{if}&\left\| {{\boldsymbol\tau} } \right\|_c \le \sqrt \lambda \;h_{\min} \\[1.5em] &\text{if} & \sqrt \lambda \;h_{\min} \le \left\| {{\boldsymbol\tau} } \right\|_c \\[1em] &&\quad \le \sqrt \lambda \;h_{\max} \\[1.5em] \left( {\frac{\left\| {{\boldsymbol\tau} } \right\|_c} {\sqrt {h_{\max} }} -\sqrt \lambda \sqrt {h_{\max} } } \right)^2 & \text{if} & \left\| {{\boldsymbol\tau} } \right\|_c \ge \sqrt \lambda \;h_{\max} \\ \end{array}} } \right.\,\,\,, \end{array}$$

(2.27)

which shows that the plot of $W_{\lambda }$ lies over the plot of $2\sqrt \lambda \left \| {{\boldsymbol \tau } } \right \|_c$.

3 The in-plane problem. Passage to the kinematic formulation of the variable thickness problem

This section reveals essential differences between the kinematic formulations of the variable thickness problems for two cases: (a) of arbitrary variation of the thickness (case of $h >$ 0) and (b) of bounded variation of the thickness (case of 0 $< h_{\textrm min} < h < h_{\textrm max})$.

3.1 The case of h $>$ 0

Let us reveal the condition (2.1) in (2.14)

$$ Z=\inf\limits_{{{\boldsymbol\tau} }\in L\left( {\Omega ,E_s^2} \right)} \sup\limits_{{\textbf{v}}\in V} \left\{ {\int\limits_{\Omega} {\left\| {{\boldsymbol\tau} } \right\|_c \;dx} {}+{}f\left( {\textbf{v}} \right){}-{}\int\limits_{\Omega} {{{\boldsymbol\tau} }\cdot {{\boldsymbol\varepsilon} }\left( {\textbf{v}} \right)\;dx}}{} \right\}. $$

(3.1)

The components of the virtual field v play now the role of Lagrangian multipliers. By using the arguments of Strang and Kohn (1983) the operations inf and sup can be interchanged thus leading to

$$ Z=\sup\limits_{{\textbf{v}}\in V} \left[ {f\left( {\textbf{v}} \right)+R\left( {{{\boldsymbol\varepsilon} }\left( {\textbf{v}} \right)} \right)} \right] $$

(3.2)

with

$$ R\left( {{\boldsymbol\varepsilon} } \right)=\inf\limits_{{{\boldsymbol\tau} }\in L\left( {\Omega ,E_s^2} \right)} \int\limits_{\Omega} {\left( {\left\| {{\boldsymbol\tau} } \right\|_c -{{\boldsymbol\tau} }\cdot {{\boldsymbol\varepsilon} }} \right)\;dx} . $$

(3.3)

Let us introduce the norm dual to (1.2)

$$ \left\| {{\boldsymbol\varepsilon} } \right\|^{\ast} =\sup\limits_{{{\boldsymbol\tau} }\in E_s^2} \frac{\left| {{{\boldsymbol\tau} }\cdot {{\boldsymbol\varepsilon} }} \right|}{\left\| {{\boldsymbol\tau} } \right\|_c} . $$

(3.4)

It is not difficult to prove that

$$ \left\| {{\boldsymbol\varepsilon} } \right\|^{\ast} =\left\| {{\boldsymbol\varepsilon} } \right\|_C \;,\;{\textbf{C}}={\textbf{c}}^{-1} $$

(3.5)

where $\left \| {{\boldsymbol \varepsilon } } \right \|_C$ is defined by (1.9). The solution of (3.3) can now be written with using the norm (3.4)

$$ R\left( {{\boldsymbol\varepsilon} } \right)=\left\{ {{\begin{array}{@{}l@{\quad}c} {0}& \;\;\text{if}~{\left\| {{\boldsymbol\varepsilon} } \right\|_C \le 1} \\[1em] {-\infty} &\text{otherwise}\\ \end{array}} } \right. $$

(3.6)

which simplifies (3.2) to the form

$$ Z=\sup \left\{ {f\left( {\textbf{v}} \right)\left| {{\textbf{v}}\in V,\;{{\boldsymbol\varepsilon} }\left( {{\textbf{v}}\left( x \right)} \right)\in B_C \;\textrm{ a.e. in } \Omega } \right.} \right\} $$

(3.7)

with $B_{C}$ defined by (1.8). Note that the above, both simple and specific reformulation of the problem (3.1) is a consequence of the integrand in (2.14) being of linear growth. The subtle problem of attainability of the supremum in (3.7) lies outside the scope of the present paper.

The results (2.13) and (3.7) are in full agreement with the formulation (2.1) in Golay and Seppecher (2001).

The formulation (2.14) is superior to (3.7) because of two reasons

• the local conditions: $\varepsilon$(v(x)) $\in$ $B_{c}$ for a.e. x $\in$ $\Omega$ are difficult to implement into a numerical algorithm;

• there is no direct link between the maximizer of (3.7) and the optimal $h^{\ast }$. On the other hand, having the minimizer of (2.14) we obtain $h^{\ast }$ directly by (2.15).

3.2 The case of 0 $<$ h $_{\textrm min} \le$ h $\le$ h $_{\textrm max}$

In this section we consider the optimum design problem in which the thickness is bounded from both sides, the lower bound $h_{\textrm min}$ being strictly positive. We show that the kinematic formulation of this problem, dual to (2.22), can be constructed, yet it does not reduce to a locking problem, but to an equilibrium problem of an effective body of non-smooth elastic potential.

To find the problem dual to (2.22) we substitute (2.1) into (2.22) to obtain

$$ J_1 =\inf\limits_{{{\boldsymbol\tau} }\in L\left( {\Omega ,E_S^2} \right)} \sup\limits_{{\textbf{v}}\in V} {}\left\{ {\int\limits_{\Omega} {W_{\lambda} \left( {{\boldsymbol\tau} } \right)dx} {}+{}f\left( {\textbf{v}} \right){}-{}\int\limits_{\Omega} {{{\boldsymbol\tau} }\cdot {{\boldsymbol\varepsilon} }\left( {\textbf{v}} \right)dx}}{}\right\} $$

(3.8)

Since inf and sup operations can be interchanged, one can rearrange (3.8) to the form

$$ J_1 =\sup\limits_{{\textbf{v}}\in V} \left\{ {f\left( {\textbf{v}} \right)-\int\limits_{\Omega} {W_{\lambda}^{\ast} \left( {{{\boldsymbol\varepsilon} }\left( {{\textbf{v}}\left( x \right)} \right)} \right)dx}} \right\} $$

(3.9)

where

$$ W_{\lambda}^{\ast} \left( {{\boldsymbol\varepsilon} } \right)=\sup\limits_{{{\boldsymbol\tau} }\in E_S^2} \left( {{{\boldsymbol\tau} }\cdot {{\boldsymbol\varepsilon} }-W_{\lambda} \left( {{\boldsymbol\tau} } \right)} \right) $$

(3.10)

is the potential dual to $W_{\lambda }$. By virtue of the formula (2.27) the sup operation in (3.10) can be performed analytically. The final result reads

$$ W_{\lambda}^{\ast} \left( {{\boldsymbol\varepsilon} } \right)=\left\{ {{\begin{array}{@{}l} {\frac{1}{4}h_{\min} \left\| {{\boldsymbol\varepsilon} } \right\|_C^2 -\lambda h_{\min} \;\;\;\textrm{ if } \;\;\;\left\| {{\boldsymbol\varepsilon} } \right\|_C \le 2\sqrt \lambda} \hfill \\[1.5em] {\frac{1}{4}h_{\max} \left\| {{\boldsymbol\varepsilon} } \right\|_C^2 -\lambda h_{\max} \;\;\;\textrm{ if } \;\;\;\left\| {{\boldsymbol\varepsilon} } \right\|_C \ge 2\sqrt \lambda} \hfill \\ \end{array}} } \right. $$

(3.11)

The potential $W_{\lambda }^{\ast } \left ( {{\boldsymbol \varepsilon } } \right )$ is continuous but not smooth. Consequently, the displacement-based formulation (3.9) involves the effective constitutive equations having a jump for $\left \| {{\boldsymbol \varepsilon } } \right \|_C =2\sqrt \lambda$.

Let us note that the sliding regime in (2.23) reduces to a point in the expression (3.11). One can conjecture that this non-smoothness will cause difficulties in developing efficient numerical schemes for solving (3.9), (3.11).

4 Numerical algorithm for (2.14). Case studies

To solve the problem (2.14) numerically we use the program developed recently, see Czarnecki and Lewiński (2012), aimed at solving selected problems of the free material design in case of a single load condition. Thus the description of the numerical method is omitted. We note only that the statically admissible trial stress fields are interpolated with using the singular value decomposition (SVD) method. These representations involve free parameters which are determined by minimization of the functional in (2.14), using the available optimizers for the unconstrained problems. Having found the minimizer of (2.14) we compute the optimal thickness by (2.15).

Example 1

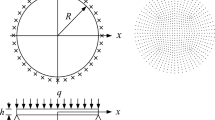
The example concerns a rectangular plate of length $L_{x}= 4.0$ and height $L_{y}= 2.0$. The finite element mesh is defined by $n_{x} \times n_{y}= 40 \times 20 = 800$ quadrilateral modules (see Fig. 1). The total number of nodes $N= (n_{x} + 1)(n_{y} + 1) = 861$, which gives the total number of the columns and rows in the static matrix B equal to $n=3N = 2583$ and $M = 2N = 1722$, respectively (n and M are also equal to the total number of the unknown nodal, stress parameters and total number of the degrees of freedom, respectively).

Fig. 1

The body $\Omega$—rectangular plate $L_{x} \times L_{y}$, boundary conditions, and loading P defined by weight function traction

The cantilever plate is fully clamped at left edge and subject to a vertical load at the right edge (tangent to the vertical edge), see Fig. 1. The traction T is modeled by the weight function (see Fig. 1)

$$ \forall y\in \left[ {0,L_y} \right]\quad T=T\left( y \right)=T_{\max} \;e^{-\left( {\frac{y-y_0} {{\textit w}}} \right)^2} $$

(4.1)

where $T_{\textrm max} = 0.376$, $y_{0} = 1.0$, $\textit {w} = 0.15$. The vertical resultant of the traction loading equals $P = 1$ (emulation of the unit force). The optimal distribution of the thickness computed by (2.16) is shown in Fig. 2 for two various values of the Poisson ratio $\nu = 0.0$, $\nu = 0.3$, using the scatter plot and contours graphic output in Voxler Graphical System. Number of iterations of the numerical optimization algorithm was 50. Violet and red color in rainbow scale denotes the minimal (numerically equal to 0) and maximal optimal thickness of the plate, respectively.

Fig. 2

Distribution of the optimal $h^{\ast } (x)$ for various values of the Poisson ratio $\nu$ (denoted as nu) and for the maximal volume $V_{0}$ $=$ 1 (denoted as V)

Because the problems (2.14) and (3.7) are similar to the Michell’s primal (1.3) and dual (1.5) formulations, the optimal numerical layouts of the cantilever problem above compare well with the well-known solutions to the Michell truss problem, see Graczykowski and Lewiński (2010). Note that neither an upper bound nor a lower bound on the unknown thickness have been imposed, since the formulation (1.1) does not involve the thickness. The optimal thickness vanishes on the domains where the solution to this problem is equal to zero, which can happen on some parts of the plate domain, not only on some lines or at some points.

Example 2

Consider now a simpler problem in which the plate is subject to a self-equilibrated load, see Fig. 3. The support conditions are formally added. The unknown is the plate thickness $h(x)$ which corresponds to the minimal value of the plate compliance, under the condition concerning the volume of the plate, (2.6). The statically admissible stress fields $\boldsymbol \tau$ $=$ ($\tau$ $_{ij})$ in $\Omega$ satisfy the local equilibrium equation: div $\boldsymbol \tau$ $=$ 0 within $\Omega$ and the static boundary conditions:

$$\begin{array}{rll} \tau_{ij} n_{j} &=& 0\;\textrm{on the edges}\left| {x_1} \right|=c+\frac{b}{2},\quad \left| {x_2} \right|\le \frac{a}{2} \\ \tau_{ij} n_{j} &=& 0\;\textrm{on the edges}\left| {x_1} \right|\le c+\frac{b}{2},\quad \left| {x_2} \right|=\frac{a}{2} \\ \tau_{2j} n_{j} &=& \left\{ {{\begin{array}{*{20}c} 0 &\quad\; {\textrm{if } x_1 \in \left( {-c-\frac{b}{2},-\frac{b}{2}} \right),} & {\left| {x_2} \right|=\frac{a}{2}} \\ {\pm q} & {\textrm{if } x_1 \in \left( {-\frac{b}{2}, \frac{b}{2}} \right),} & {x_2 =\pm \frac{a}{2}} \\ 0 & {\textrm{ if } x_1 \in \left( {\frac{b}{2},c+\frac{b}{2}} \right),} & {\left| {x_2} \right|=\frac{a}{2}} \\ \end{array}} } \right. \end{array} $$

where n $=$ ($n_{1}$, $n_{2})$ is the unit vector outward normal to the contour of $\Omega$.

Fig. 3

Self-equilibrated plate

We divide the plate domain into three sub-domains

$$\begin{array}{lll} \Omega_1 &=\left\{ {\left( {x_1 ,x_2} \right)\left| {-c-b/2\le x_1 \le -b/2,\left| {x_2} \right|} \right.\le a/2} \right\} \\ \Omega_2 &=\left\{ {\left( {x_1 ,x_2} \right)\left| {-b/2\le x_1 \le b/2,\left| {x_2} \right|} \right.\le a/2} \right\} \\ \Omega_3 &=\left\{ {\left( {x_1 ,x_2} \right)\left| {b/2\le x_1 \le b/2+c,\left| {x_2} \right|} \right.\le a/2} \right\} \end{array} $$

The optimal problem considered is formulated in two manners: as a static (primal) problem (2.14) and as the kinematic problem, dual to (2.14). We shall solve both the problems analytically.

We shall start from the kinematic method, or from the problem (3.7). We take the trial field v of components

$$ {\textit v}_1 =-\frac{k}{\sqrt E} x_1, \,\,\, {\textit v}_2 =\frac{1}{\sqrt E} x_2 $$

(4.2)

in the whole domain $\Omega$. This field can be complemented by a rigid body motion to fulfil the kinematic boundary conditions of Fig. 3. The constant k is chosen such that the trial strain lies on the boundary of the locking locus (1.8). According to (1.10) we compute

$$ \left\| {{\boldsymbol\varepsilon} } \right\|_C =\sqrt {\frac{k^2-2\nu k+1}{1-\nu^2}} $$

(4.3)

The assumption k $=$ $\nu$ gives $\left \| {{\boldsymbol \varepsilon } } \right \|_C =1$. Now we compute the virtual work of the load q on the displacements

$$ {\textit v}_2 \left( {x_1 ,-a/2} \right)=\frac{-a}{2\sqrt E}, \,\,\,\, {\textit v}_2 \left( {x_1 ,a/2} \right)=\frac{a}{2\sqrt E} $$

(4.4)

and find $Z = f$(v) by (3.7)

$$ f({\textbf{{\textit v}}})=[-q{\textit v}_2 \left( {x_1 ,-a/2} \right)+q{\textit v}_2 \left( {x_1 ,a/2} \right)]b=\frac{qab}{\sqrt E} $$

(4.5)

Consider now the static problem (2.14). We assume the trial stress field in the form

$$ \begin{array}{lll} \tau_{11} &=\tau_{12} =0 ~~ {\text{in}} ~~ \Omega \\ \tau_{22} &=\left\{ {{\begin{array}{*{20}c} 0 & {\text{in}} & {\Omega_{\textrm{1}}} \\ q & {\text{in}} & {\Omega_{\textrm{2}}} \\ 0 & {\text{in}} & {\Omega_{\textrm{3}}} \\ \end{array}} } \right. \end{array} $$

(4.6)

The trial field assumed this way is of class $\Sigma (\Omega )$. We compute the norm of the trial stress field by (2.16)

$$ \left\| {{\boldsymbol\tau} } \right\|_c^ =\left\{ {{\,\begin{array}{*{20}c} {0\textrm{ in } \Omega_{\textrm{1}} \textrm{ } } \hfill \\ {q\textrm{ /}\sqrt E \textrm{ in } \Omega_{\textrm{2}} \textrm{ } } \hfill \\ {0\textrm{ in } \Omega_{\textrm{3}} \textrm{ } } \hfill \\ \end{array}} } \right.\textrm{ } $$

(4.7)

Thus, by (2.14) we compute

$$ Z=\frac{qab}{\sqrt E} $$

(4.8)

which coincides with (4.5). Since the upper bound given by the static method and the lower bound provided by the kinematic method coincide, both the problems have been correctly solved and by (2.15) determine the same distribution of the optimal thickness:

$$ h^{\ast} =\left\{ {{\begin{array}{*{20}c} {0\textrm{ in } \Omega_{\textrm{1}} \textrm{ } } \hfill \\ {V_0 \textrm{ } /ab\textrm{ in } \Omega_{\textrm{2}} \textrm{ } } \hfill \\ {0\textrm{ in } \Omega_{\textrm{3}} \textrm{ } } \hfill \\ \end{array}} } \right.\textrm{ } $$

(4.9)

This shows that the optimal plate occupies only the middle sub-domain of the design domain, since the optimal thickness is zero in the left and right sub-domains.

The numerical test was performed for the following rectangular plate (see Figs. 3, 4 and 5):

$$\begin{array}{rll} L_x \times L_y &=&3.0\times 1.0,\;V_0 =3.0,\;a=1.0,\;b=1.0, \\ E&=&1.0,\;\nu =0.0,\;q=-1.0 \end{array}$$

The mesh is defined by 60 $\times$ 20 $=$ 1200 4-node, quadrilateral, isoparametric sub-domains with bilinear shape functions interpolating stress fields.

Fig. 4

Numerical solution of the example 3: optimal thickness $h^{\ast }$

Fig. 5

Numerical solution of the example 3: minimizer $\tau$*, where the components $\tau$ $_{11}^{\ast }$, $\tau$ $_{12}^{\ast }$, $\tau$ $_{22}^{\ast }$ are denoted as $\tau$ $^{\ast }$11, $\tau$ $^{\ast }$12, $\tau$ $^{\ast }$22 , respectively

Exact solution: $h^{\ast } =3.0,\;\;\;Z^{\ast } =1.0$, $J^{\ast } =\frac {\left ( {Z^{\ast }} \right )^2}{V_0} \approx 0.333$, of the thickness constant in $\Omega _{\textrm {2}}$. Numerical solution: maximal thickness $h^{\ast } \approx 2.75$, $Z^{\ast } \approx \textrm {1.148}$, $J^{\ast } =\frac {\left ( {Z^{\ast }} \right )^2}{V_0} \approx \textrm {0.439}$.

The example above has been exactly solved analytically, hence can be treated as a benchmark. The abrupt change of the optimal thickness could not be exactly approximated, since the trial stress fields in problem (2.14) have been interpolated continuously in the whole domain.

Example 3

Consider now a plate subject to a self-equilibrated system of three forces, see Fig. 6. The structure under consideration is not supported at any node, because the system of the three forces is self-equilibrated. The unknown is the plate thickness $h(x)$ which corresponds to the minimal value of the plate compliance, under the condition concerning the volume of the plate, (2.6). The three concentrated forces are emulated by the four tractions $T_{i}(i$ $=$ 1, 2, 3, 4) modeled by the four weight functions (4.1), see Fig. 7 (see also example shown in Fig. 13, page 845 in Sokół and Lewiński (2010))

$$\begin{array}{rll} \forall x_2 \in \left[ {0,L_y} \right]\;\;\;T_1 \left( {x_2} \right)&=T_1^{\max} \;e^{-\left( {\frac{x_2 -h}{{\textit w}}} \right)^2}, \\ T_2 \left( {x_2} \right)&=-T_2^{\max} \;e^{-\left( {\frac{x_2 -L_y} {{\textit w}}} \right)^2}, \\ T_3 \left( {x_2} \right)&=-T_3^{\max} \;e^{-\left( {\frac{x_2 -h}{{\textit w}}} \right)^2} \\ \forall x_1 \in \left[ {0,L_x} \right]\;\;\;T_4 \left( {x_1} \right)&=T_4^{\max} \;e^{-\left( {\frac{x_1} {{\textit w}}} \right)^2}. \end{array}$$

The values of the $T_{i}^{\textrm max}(i$ $=$ 1, 2, 3, 4) are such that the absolute values of the four integrals $int T_{i}(s)$ ds(i $=$ 1, 2, 3, 4) are equal exactly P. The loading assumed in Fig. 7 is self-equilibrated.

Fig. 6

Self-equilibrated plate—three force member

Fig. 7

The self-equilibrated plate subject to the tractions $T_{1}$, $T_{2}$, $T_{3}$, $T_{4}$ emulating the three force system shown in Fig. 6

The numerical test was performed for the following data:

$$\begin{array}{rll} L_x \times L_y &= 1.0\times 1.5,\;V_0 =0.15,\;h=0.5, \\ E&=1.0,\;P=1.0,\;{\textit w}=0.15 \\ T_1^{\max} &= T_3^{\max} \cong \textrm{3.76}\;\textrm{,}\;T_2^{\max} =T_4^{\max} \cong \textrm{7.52} \end{array}$$

Three different values of the Poisson ratio are tested: $\nu$ $=$ 0.5, 0.0, $-$0.5. These choices are admissible in the 2D elasticity where the condition of the energy density being positive is satisfied if the effective Poisson ratio runs between $-$1 and 1.

The mesh is defined by 30 $\times$ 45 $=$ 1350 4-node, quadrilateral, isoparametric sub-domains with bilinear shape functions interpolating stress fields.

The layouts of Fig. 8 are similar to the Michell’s solution shown in Fig. 9. Similar three forces problems were the subject of numerical analysis in Golay and Seppecher (2001) based on the FEM approximation of problem (3.7). The results in Fig. 3 of the above paper are similar in nature to those of Fig. 8.

Fig. 8

Distribution of the optimal $h^{\ast } (x)$ for various values of the Poisson ratio $\nu$ (denoted as nu) in the Example 4

Fig. 9

The shape of the optimal Michell’s layout for the problem in Fig. 6 found in Sokół and Lewiński (2010, Fig. 13)

5 On optimal design of thin Kirchhoff plates of varying thickness

Consider the problem of compliance minimization of a transversely symmetric Kirchhoff plate of thickness $h(x)$. The tensor of bending stiffnesses depends on the thickness by: ${\textbf {D}}=\frac {h^3}{12}{\textbf {C}}$, where C has the same meaning as before. We assume that the loading is applied transversely to the plate. Assume the plate is supported in a manner admissible within the theory of Kirchhoff. Let V be the space of virtual appropriately regular deflections v which satisfy the kinematic boundary conditions. The changes of curvature are described by ${{\boldsymbol \kappa } }\left ( {\textit v} \right )=\left ( {\kappa _{ij} \left ( {\textit v} \right )} \right ),\;\kappa _{ij} \left ( {\textit v} \right )=-\frac {\partial ^2{\textit v}}{\partial x_i \partial x_j}$. Let $f({\textit v})$ represent now the virtual work of the transverse loading. The bending moment tensors K $=$ ($K_{ij})$ of $L^2\left ( {\Omega ,E_s^2} \right )$ class are said to be statically admissible if they satisfy the equilibrium equation:

$$ \forall {\textit v}\in V\quad \int\limits_{\Omega} {{\textbf{K}}\cdot {{\boldsymbol\kappa} }\left( {\textit v} \right)\;dx} =f\left( {\textit v} \right). $$

(5.1)

The set of such bending moments, satisfying additionally the condition $K_{ij,ij} \in L^2\left ( \Omega \right )$, is denoted by $\Sigma ^{\prime } (\Omega )$. One can show only one field M $\in \Sigma ^{\prime } (\Omega )$ such that

$$ {\textbf{M}}={\textbf{D}}\;{{\boldsymbol\kappa} }\left( {\textit w} \right). $$

(5.2)

with ${\textit w}$ being kinematically admissible or ${\textit w} \in V$. Let $L'\left ( {\Omega ,E_s^2} \right )$ be the space of fields K $=$ ($K_{ij})$ in $\Omega$ such that $K_{ij,ij}$ $\in$ $L^{2}(\Omega )$. Let us introduce a norm in $L^2 \left ( {\Omega ,E_s^2} \right )$

$$ \left\| {\textbf{K}} \right\|_{L^2\left( {\Omega ,E_s^2} \right)} =\sqrt {\int\limits_{\Omega} {{\textbf{K}}\left( x \right)\cdot \left( {{\textrm {\textbf D}}^{-1}\;{\textbf{K}}\left( x \right)} \right)} \;dx} . $$

(5.3)

The compliance $\Upsilon$ of the plate in bending is equal to $f({\textit w})$ or, by Castigliano theorem,

$$ \Upsilon =\min\limits_{{\textbf{K}}\in \Sigma '\left( \Omega \right)} \left( {\left\| {\textbf{K}} \right\|_{L^2\left( {\Omega ,E_s^2} \right)}} \right)^2. $$

(5.4)

The minimizer of this problem is equal to M, or is equal to the bending moment tensor being the solution of the plate equilibrium problem. Let us re-write (5.4) by disclosing the dependence of D on h

$$ \Upsilon =\inf \left\{ {\int\limits_{\Omega} {\frac{1}{h^3\left( x \right)}{\textbf{K}}\left( x \right)\cdot \left( {{\textbf{c}}\;{\textrm {\textbf K}}\left( x \right)} \right)} \;dx\left| {{\textbf{K}}\in \Sigma '\left( \Omega \right)} \right.} \right\} $$

(5.5)

or

$$ \Upsilon =\inf \left\{ {\int\limits_{\Omega} {\frac{1}{h^3(x)}\left\| {{\textbf{K}}(x)} \right\|_c^2 dx\left| {\;{\textbf{K}}\in \Sigma^{\prime}\left( \Omega \right)} \right.}} \right\} $$

(5.6)

where the norm $\left \| \cdot \right \|_c$ is defined by (1.2). We consider plates of fixed volume, see (2.6) and set only the condition $h >$ 0 or $h_{\textrm min}$ $=$ 0, $h_{\textrm max}=\infty$. Assume additionally that $h^{-3}\in L^1\left ( {\Omega ,R^+} \right )$. The subject of the study is the optimum design problem

$$\begin{array}{lll} J&=&\inf \left\{ \int\limits_{\Omega} {\frac{\left( {\left\| {{\textrm {\textbf K}}\left( x \right)} \right\|_c} \right)^2}{h^3\left( x \right)}} \;dx\left| \;{\textbf{K}}\in \Sigma '\left( \Omega \right), \right.\right.\\ &&\quad\left. \left.\int\limits_{\Omega} {h\left( x \right)\;dx} =V_0 ,\;h^{-3}\in L^1\left( {\Omega ,R^+} \right) \right. \right\}. \end{array} $$

(5.7)

Then we can apply the results of the Appendix for p $=$ 3. We obtain

$$ J=\frac{\left( {Z_3} \right)^4}{V_0^3}, $$

(5.8)

$$ Z_3 =\inf \left\{ {\int\limits_{\Omega} {\sqrt {\left\| {{\textbf{K}}\left( x \right)} \right\|_c} \,dx} \left| {\;{\textbf{K}}\in \Sigma '\left( \Omega \right)} \right.} \right\}. $$

(5.9)

Assume that K $^{\ast }$ solves the above problem. Then the optimal h is given by

$$ h^{\ast} \left( x \right)=V_0 \frac{\sqrt {\left\| {{\textbf{K}}^{\ast} \left( x \right)} \right\|_c} } {\int\limits_{\Omega} {\sqrt {\left\| {{\textrm {\textbf K}}^{\ast} \left( x \right)} \right\|_c} \;dx}} \quad $$

(5.10)

a.e. in $\Omega$.

The integrand of (5.9) is not convex and is not of linear growth. Consequently the problem dual to (5.9) does not reduce to a locking material problem, like (3.7).

Problem (5.7) can be viewed as problem of mixing infinite number of materials, as discussed in Lur’e and Cherkaev (1986).

Remark 5.1

By analogy to Section 2.2 one can consider the optimum design problem (5.7) with additional restrictions: 0 $< h_{\textrm min} \le h(x) \le h_{\textrm max}$, on the plate thickness distribution. One can construct the counterpart of (2.22), (2.23), which will not be put here. This problem is not well posed. The hitherto known results on the relaxation of this problem are discussed in the review paper by Muñoz and Pedregal (2007).

6 On the penalized density methods in shape optimization

The previous results concerning the plate optimization clear up the behaviour of numerical schemes based on the penalized density method, like SIMP, see Bendsøe (1989), Zhou and Rozvany (1991), Bendsøe and Sigmund (1999), Azegami et al. (2011).

Assume that a thin domain of a shape of plate of unit thickness, of a middle plane $\Omega$ (i.e. of cylindrical shape) is to be filled up with a homogeneous elastic material of volume $V_{0}$. Thus $V_0 \le \left | \Omega \right |$. The material is characterized by the moduli $C_{ijkl}$ as before. To omit the subtle problem of considering holes we introduce an effective material of moduli $E_{ijkl}(x)$ expressed by a mass density $\rho$($x)$ such that

$$ E_{ijkl} \left( x \right)=\rho^p\left( x \right)\;C_{ijkl} ,0\le \rho \left( x \right)\le 1 $$

(6.1)

where $p >$ 0 and

$$ \int\limits_{\Omega} {\rho \left( x \right)} =V_0 . $$

(6.2)

Note that $\rho$ $=$ 1 corresponds to E $=$ C. Consider the problem

$$\begin{array}{lll} J_{\lambda} &=\inf \left\{ \int\limits_{\Omega} {\rho^{-p}\left( x \right)\;{{\boldsymbol\tau} }\left( x \right)\cdot \left( {{\textbf{c}}\;{{\boldsymbol\tau} }\left( x \right)} \right)\;dx} \right.\\ &\quad\quad\quad\left.+\, \lambda \int\limits_{\Omega}\, {\rho \left( x \right)\;dx} \left| \rho^{-p}\in L^1\left( {\Omega ,R^+} \right),\;{{\boldsymbol\tau} }\,\in\, \Sigma \left( \Omega \right), \right.\right.\\ &\quad\quad\quad\left.\left.0\le \rho \left( x \right)\le 1\textrm{ for a.e. } x\,\in\, \Omega \right. \vphantom{\int\limits_{\Omega} {\rho^{-p}\left( x \right)\;{{\boldsymbol\tau} }\left( x \right)\cdot \left( {{\textbf{c}}\;{{\boldsymbol\tau} }\left( x \right)} \right)\;dx}}\right\} \end{array} $$

(6.3)

The minimization over $\rho$ can be performed analytically. The problem (6.3) reduces to

$$ J_{\lambda} =\inf \left\{ {\int\limits_{\Omega} {W_{\lambda ,p} \left( {{\boldsymbol\tau} } \right)dx\left| {\;{{\boldsymbol\tau} }\in \Sigma \left( \Omega \right)} \right.}} \right\} $$

(6.4)

where

$$ W_{\lambda ,p} \left( {{\boldsymbol\tau} } \right)={\textit w}_{\lambda ,p} \left( {\left\| {{\boldsymbol\tau} } \right\|_c} \right) $$

(6.5)

while

$$ {\textit w}_{\lambda ,p} \left( x \right)=\left\{ {{\begin{array}{*{20}c} {\lambda^{\frac{-p}{p+1}}\left( {p^{\frac{1}{p+1}}+p^{\frac{p}{p+1}}} \right)\left| x \right|^{\frac{2}{p+1}}\qquad\textrm{ if } \qquad\left| x \right|\le \sqrt {\frac{\lambda} {p}}} \hfill \\ {x^2+\lambda \qquad\textrm{ if } \qquad\left| x \right|\ge \sqrt {\frac{\lambda} {p}}} \hfill \\ \end{array}} } \right. $$

(6.6)

Let us look at the family of functions: ${\textit w}_{\lambda ,p}(x)$ for p $=$ 1, 3, 6, 16, 44 and for a fixed value $\lambda$ $=$ 1, see Fig. 10.

Fig. 10

Diagrams of ${\textit w}_{\lambda ,p}(x)$ for selected values of p; $\lambda$ $=$ 1

We note that the function ${\textit w}_{\lambda ,1}(x)$ is convex while all other functions ${\textit w}_{\lambda ,p}(x)$, $p >$ 1 are non-convex and non-differentiable at x $=$ 0. We conclude that the SIMP method leads to badly posed problems for p $>$ 1.

The formulation (6.4) for p $=$ 1 is similar to the variable thickness problem (2.22) for $h_{\textrm min}$ $=$ 0, $h_{\textrm max}$ $=$ 1. The problem (6.3) for p $=$ 3 is similar to the variable thickness problem of the Kirchhoff plate, with no bounds on $h(x)$, see (5.7). The latter similarity suggests that the relaxation methods developed for (5.7) should be applicable to make (6.3) well posed. Other way is to apply the numerical method which directly approximates the relaxation by homogenization formulation, developed recently by Dzierżanowski (2012).

7 Final remarks

The optimum design problem (2.7) of a plate of varying thickness subject to the in-plane loading has been reduced to the problem (2.14) with the integrand of linear growth. For some load cases one can expect that $\tau$* $=$ 0 in a subdomain. Consequently the thickness vanishes there, which goes beyond the assumptions in (2.7), but is compatible with the kinematic formulation (3.7).

The paper discloses that the problem of design of the thickness of a Kirchhoff plate reduces to (5.9). The integrand is there non-convex. Similarly, the problem (6.4) with $p =$ 3, corresponding to the SIMP problem, involves a non-convex integrand. The present paper discloses once again, from a new perspective, why both problems are badly posed and special techniques should be applied to correct them and to develop appropriate numerical schemes.

Appendix

Let $\Omega$ be a plane domain. Let $F\in L^{\frac {1}{p+1}}\left ( {\Omega ,R^+} \right )$. For $p \ge$ 1 we define the functional

$$ T_p \left( u \right)=\int\limits_{\Omega} {u^{-p}\left( x \right)\;F\left( x \right)\;dx} $$

(A.1)

such that $u^{-p} \in L^{1}(\Omega$, $R^{+})$ with respect to the Radon measure of density F.

Consider the problem

$$ U_p \,=\, \min \left\{ {T_p \left( u \right)\left| {u^{-p}\in L^1\left( {\Omega ,R^+} \right),\;\int\limits_{\Omega} {u\;dx} =V_0} \right.} \right\}\\ $$

(A.2)

for given $V_{0}$. Its solution reads

$$ U_p =T_p \left( {u^{\ast}} \right) $$

(A.3)

$$ u^{\ast} \left( x \right)=V_0 \frac{F^{\frac{1}{p+1}}\left( x \right)}{\int\limits_{\Omega} {F^{\frac{1}{p+1}}\left( x \right)\;dx}} $$

(A.4)

and

$$ T_p \left( {u^{\ast}} \right)=\frac{1}{V_0^p}\left[ {\int\limits_{\Omega} {F^{\frac{1}{p+1}}\left( x \right)\;dx}} \right]^{p+1}. $$

(A.5)

Let us sketch the derivation of (A.3–A.5). Introduce the Lagrangian

$$ L=\int\limits_{\Omega} {u^{-p}\left( x \right)\;F\left( x \right)} \;dx+\lambda \left( {\int\limits_{\Omega} {u\left( x \right)} \;dx-V_0} \right). $$

(A.6)

The condition $\delta$L $=$ 0 with respect to $\delta$u gives

$$ p\cdot u^{-\left( {p+1} \right)}\left( x \right)=\frac{\lambda} {F\left( x \right)} $$

(A.7)

hence

$$ u\left( x \right)=\left( {\frac{p}{\lambda} } \right)^{\frac{1}{p+1}}F^{\frac{1}{p+1}}\left( x \right). $$

(A.8)

We fulfill the isoperimetric condition in (A.2) and arrive at

$$ \left( {\frac{p}{\lambda} } \right)^{\frac{1}{p+1}}=V_0 \left( {\int\limits_{\Omega} {F^{\frac{1}{p+1}}\left( x \right)\;dx}} \right)^{-1}. $$

(A.9)

Substituting (A.9) into (A.8) we obtain (A.4). This is the minimizer, since the integrand of (A.1) is convex with respect to u for $p \ge$ 1. Substitution of (A.4) into (A.1) gives (A.5).