Abstract
The present paper studies multi-objective design of lightweight thermoelastic structure composed of homogeneous porous material. The concurrent optimization model is applied to design the topologies of light weight structures and of the material microstructure. The multi-objective optimization formulation attempts to find minimum structural compliance under only mechanical loads and minimum thermal expansion of the surfaces we are interested in under only thermo loads. The proposed optimization model is applied to a sandwich elliptically curved shell structure, an axisymmetric structure and a 3D structure. The advantage of the concurrent optimization model to single scale topology optimization model in improving the multi-objective performances of the thermoelastic structures is investigated. The influences of available material volume fraction and weighting coefficients are also discussed. Numerical examples demonstrate that the porous material is conducive to enhance the multi-objective performance of the thermoelastic structures in some cases, especially when lightweight structure is emphasized. An “optimal” material volume fraction is observed in some numerical examples.







Similar content being viewed by others
References
Allaire G, Jouve F, Toader AM (2002) A level-set method for shape optimization. C R Math 334(12):1125–1130
Ambrosio L, Buttazzo G (1993) An optimal-design problem with perimeter penalization. Calc Var Partial Differ Equ 1(1):55–69
Amir O, Sigmund O (2007) On reducing computational effort in topology optimization: how far can we go? Struct Multidisc Optim 44(1):25–29
Bendsøe MP (1989) Optimal shape design as a material distribution problem. Struct Multidisc Optim 1(4):193–202
Bendsøe MP, Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. Comput Methods Appl Mech Eng 71(2):197–224
Bendsøe MP, Sigmund O (1999) Material interpolation schemes in topology optimization. Arch Appl Mech 69(9–10):635–654
Bendsøe MP, Sigmund O (2003) Topology optimization: theory methods and applications. Springer, Berlin
Bensoussan A, Lions JL, Papanicolaou G (1978) Asymptotic analysis for periodic structures. North-Holland, Amsterdam
Bourdin B (2001) Filters in topology optimization. Int J Numer Methods Eng 50(9):2143–2158
Cheng G, Olhoff N (1981) An investigation concerning optimal design of solid elastic plates. Int J Solids Struct 17(3):305–323
Coelho PG, Fernandes PR, Guedes JM, Rodrigues HC (2008) A hierarchical model for concurrent material and topology optimisation of three-dimensional structures. Struct Multidisc Optim 35(2):107–115
Colombo P (2006) Conventional and novel processing methods for cellular ceramics. Philos Trans R Soc A 364(1838):109–124
Gao T, Zhang WH (2010) Topology optimization involving thermo-elastic stress loads. Struct Multidisc Optim 42(5):725–738
Guedes JM, Lubrano E, Rodrigues HC, Turteltaub S (2006) Hierarchical optimization of material and structure for thermal transient problems. In: Iutam symposium on topological design optimization of structures, machines and materials: status and perspectives, vol 137, pp 527–536
Guest JK (2009) Imposing maximum length scale in topology optimization. Struct Multidisc Optim 37(5):463–473
Guest JK, Prevost JH (2006) Optimizing multifunctional materials: design of microstructures for maximized stiffness and fluid permeability. Int J Solids Struct 43:7028–7047
Guest JK, Prevost JH, Belytschko T (2004) Achieving minimum length scale in topology optimization using nodal design variables and projection functions. Int J Numer Methods Eng 61(2):238–254
Hashin Z (1983) Analysis of composite materials—a survey. J Appl Mech 50:481–505
Kruijf Nd, Zhou SW, Li Q, Mai YW (2007) Topological design of structures and composite materials with multiobjectives. Int J Solids Struct 44(22–23):7092–7109
Liu S, Cheng G (1995) Homogenization-based method for predicting thermal expansion coefficients of composite materials. J Dalian Univ Technol 35(5):451–457
Liu ST, Cheng GD, Gu Y, Zheng XG (2002) Mapping method for sensitivity analysis of composite material property. Struct Multidisc Optim 24(3):212–217
Liu T, Deng ZC, Lu TJ (2006) Design optimization of truss-cored sandwiches with homogenization. Int J Solids Struct 43(25–26):7891–7918
Liu L, Yan J, Cheng GD (2008) Optimum structure with homogeneous optimum truss-like material. Comput Struct 86(13–14):1417–1425
Niu B, Yan J, Cheng GD (2009) Optimum structure with homogeneous optimum cellular material for maximum fundamental frequency. Struct Multidisc Optim 39(2):115–132
Patzak B, Bittnar Z (2001) Design of object oriented finite element code. Adv Eng Softw 32(10–11):759–767
Pedersen P, Pedersen NL (2010) Strength optimized designs of thermoelastic structures. Struct Multidisc Optim 42(5):681–691
Petersson J, Sigmund O (1998) Slope constrained topology optimization. Int J Numer Methods Eng 41(8):1417–1434
Rodrigues H, Fernandes P (1995) A material based model for topology optimization of thermoelastic structures. Int J Numer Methods Eng 38(12):1951–1965
Rodrigues H, Guedes JM, Bendsoe MP (2002) Hierarchical optimization of material and structure. Struct Multidisc Optim 24(1):1–10
Rozvany GIN, Zhou M, Birker T (1992) Generalized shape optimization without homogenization. Struct Optim 4(3–4):250–252
Sigmund O (1994a) Design of material structures using topology optimization. Technical University of Denmark, Denmark
Sigmund O (1994b) Materials with prescribed constitutive parameters: an inverse homogenization problem. Int J Solids Struct 31:2313–2329
Sigmund O (2007) Morphology-based black and white filters for topology optimization. Struct Multidisc Optim 33(4–5):401–424
Sigmund O, Petersson J (1998) Numerical instabilities in topology optimization: a survey on procedures dealing with checkerboards, mesh-dependencies and local minima. Struct Optim 16(1):68–75
Sigmund O, Torquato S (1997) Design of materials with extreme thermal expansion using a three-phase topology optimization method. J Mech Phys Solids 45(6):1037–1067
Studart AR, Gonzenbach UT, Tervoort E, Gauckler LJ (2006) Processing routes to macroporous ceramics: a review. J Am Ceram Soc 89(6):1771–1789
Svanberg K (2002) A class of globally convergent optimization methods based on conservative convex separable approximations. Siam J Optim 12(2):555–573
Taylor CM, Smith CW, Miller W, Evans KE (2011) The effects of hierarchy on the in-plane elastic properties of honeycombs. Int J Solids Struct 48:1330–1339
Terada K, Kikuchi N (2001) A class of general algorithms for multi-scale analyses of heterogeneous media. Comput Methods Appl Mech Eng 190(40–41):5427–5464
Wang MY, Wang SY (2005) Bilateral filtering for structural topology optimization. Int J Numer Methods Eng 63(13):1911–1938
Wang MY, Wang XM, Guo DM (2003) A level set method for structural topology optimization. Comput Methods Appl M 192(1–2):227–246
Wang B, Yan J, Cheng GD (2011) Optimal structure design with low thermal directional expansion and high stiffness. Eng Optim 43(6):581–595
Wen ZH, Han YS, Liang L, Li JB (2008) Preparation of porous ceramics with controllable pore sizes in an easy and low-cost way. Mater Charact 59(9):1335–1338
Xia Q, Wang MY (2008) Topology optimization of thermoelastic structures using level set method. Comput Mech 42(6):837–857
Xie YM, Steven GP (1993) A simple evolutionary procedure for structural optimization. Comput Struct 49(5):885–896
Xie YM, Zuo ZH, Huang XD, Rong JH (2012) Convergence of topological patterns of optimal periodic structures under multiple scales. Struct Multidisc Optim 46(1):41–50
Xu SL, Cai YW, Cheng GD (2010) Volume preserving nonlinear density filter based on heaviside functions. Struct Multidisc Optim 41(4):495–505
Yan J, Cheng GD, Liu L (2008) A uniform optimum material based model for concurrent optimization of thermoelastic structures and materials. Int J Simul Multidisc Des Optim 2:259–266
Yang J, Yu J, Huang Y (2011) Recent developments in gelcasting of ceramics. J Eur Ceram Soc 31(14):2569–2591
Zhang WH, Sun SP (2006) Scale-related topology optimization of cellular materials and structures. Int J Numer Methods Eng 68(9):993–1011
Zhou M, Shyy YK, Thomas HL (2001) Checkerboard and minimum member size control in topology optimization. Struct Multidisc Optim 21(2):152–158
Acknowledgements
The financial support for this research was provided by the Program (90816025, 10902018) of NSFC, the National Basic Research Program of China (2011CB610304, 2010CB832703), the Major National Science and Technology Project (2011ZX02403-002) and the Science Research Foundation of Dalian University of Technology (DUT11LK05). These supports are gratefully appreciated.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work has been presented on 6th China-Japan-Korea Joint Symposium on Optimization of Structural and Mechanical Systems, Kyoto, June 22–25, 2010, Japan.
Appendices
Appendix A: Theoretical proof
Proposition
For porous material composed of one solid phase and one void phase, its effective thermal expansion coefficient tensor \(\alpha_{\it ij}^H \) equals to that \(\alpha_{\it ij}\) of the solid phase, i.e.
Proof
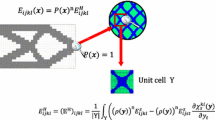
Let \(E_{\it ijkl}\) and \(E_{\it ijkl}^H \) represent elastic modulus tensor of the solid phase and effective elastic modulus tensor of the porous material respectively. The thermo stress tensor is defined as
And the effective thermo stress tensor is defined as
By virtue of homogenization theory, \(E_{\it ijkl}^H \) and \(\beta_{\it ij}^H \) can be obtained respectively as (Sigmund and Torquato 1997; Rodrigues and Fernandes 1995)
Where Y identifies the design domain of the unit cell occupied with material, and periodic displacements \(X^{\it ij}\) are solutions to the equilibrium equations in the unit cell.
Substitute (41) into (43), we can have
Since \(E_{\it ijpm}=E_{\it pmij}\), (42) can be stated as
As \(E_{\it ijkl}^H =E_{\it klij}^H \), (45) can be written as
Change index k with i, and l with j, (46) can be stated as
As \(E_{\it klij}=E_{\it ijkl}\), from (47), we can have
Substitute (48) into (44), we can have
Since (49) equals to (41), we can have
Define the compliance tensor \(C_{\it ijkl}^H \) as the inverse of \(E_{\it ijkl}^H \), and multiply it to the left side of (50), we can obtain the following statement and complete our proof.
It should be mentioned, if the material is composed of three or more phases (at least two solid phases and one void phase), \(\alpha _{\it kl}\) could not be extracted from (44) and thus (51) could not be obtained. □
Appendix B: Plane truss example
The stiffness matrix of a plane truss element in local coordinate is
Where E e , A e and L e are respectively the elastic modulus, sectional area and length of the truss element. The element stiffness matrix in global coordinate is
Where T e denotes the transformation matrix, and is expressed as
Where θ is the angle between the direction of the truss element and the positive direction of X coordinate axis.
The element nodal load by temperature load in local coordinate is
Where γ is the thermal expansion coefficient of the material and ΔT e is the temperature variation of the truss member. The element nodal load by temperature load in global coordinate is
Now, let’s consider our plane truss example in Fig. 7. We fix A 1 and find an optimum A 2 (0 ≤ A 2 ≤ 2A 1) which minimizes obj. And we set the initial value of A 2 to A 1/2. Since the structure has only one degree of nodal freedom, after simple derivation, we can easily obtain the structural stiffness matrix, the nodal load by thermal load and mechanical load as
Solving equation KU M = F M, we can obtain U M and then
Solving equation KU \(^\mathit{Tem}\) = F \(^\mathit{Tem}\), we can obtain U \(^\mathit{Tem}\) and then
Since A 1 is fixed and 0 ≤ A 2 ≤ 2A 1, to minimize f c , A 2 should satisfy A 2 = 2 A 1. And to minimize f u , A 2 should satisfy A 2 = A 1. Therefore, to minimize obj (ω ∈ [0, 1]), the optimum A 2 ∈ (A 1, 2A 1). This means A 2 is not “the larger the better” in the sense of minimizing the multi-objective performance of the thermoelastic truss structure.
Rights and permissions
About this article
Cite this article
Deng, J., Yan, J. & Cheng, G. Multi-objective concurrent topology optimization of thermoelastic structures composed of homogeneous porous material. Struct Multidisc Optim 47, 583–597 (2013). https://doi.org/10.1007/s00158-012-0849-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-012-0849-6