Skip to main content
SpringerLink
Log in

Phase-field based topology optimization with polygonal elements: a finite volume approach for the evolution equation

  • Research Paper
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

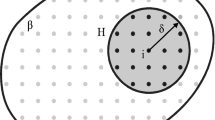
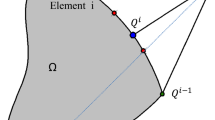
Uniform grids have been the common choice of domain discretization in the topology optimization literature. Over-constraining geometrical features of such spatial discretizations can result in mesh-dependent, sub-optimal designs. Thus, in the current work, we employ unstructured polygonal meshes constructed using Voronoi tessellations to conduct structural topology optimization. We utilize the phase-field method, derived from phase transition phenomenon, which makes use of the Allen-Cahn differential equation and sensitivity analysis to update the evolving structural topology. The solution of the Allen-Cahn evolution equation is accomplished by means of a centroidal Voronoi tessellation (CVT) based finite volume approach. The unstructured polygonal meshes not only remove mesh bias but also provide greater flexibility in discretizing complicated (e.g. non-Cartesian) domains. The features of the current approach are demonstrated using various numerical examples for compliance minimization and compliant mechanism problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

References

  • Allaire G, Jouve F (2004) Structural optimization using sensitivity analysis and a level-set method. J Comput Phys 194:363–393

    Article  MathSciNet  MATH  Google Scholar 

  • Allen SM, Cahn JW (1979) A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall 27:1085–1095

    Article  Google Scholar 

  • Aranson IS, Kalatsky VA, Vinokur VM (2000) Continuum field description of crack propagation. Phys Rev Lett 85(1):118–121

    Article  Google Scholar 

  • Bendsøe MP (1989) Optimal shape design as a material distribution problem. Struct Optim 1:193–202

    Article  Google Scholar 

  • Bendsøe MP, Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. Comput Methods Appl Mech Eng 71(2):197–224

    Article  Google Scholar 

  • Bendsøe MP, Sigmund O (1999) Material interpolation schemes in topology optimization. Arch Appl Mech 69(9–10):635–654

    Google Scholar 

  • Bendsøe MP, Sigmund O (2003) Topology optimization—theory, methods and applications. Springer, New York

    Google Scholar 

  • Bolander JE, Saito S (1998) Fracture analysis using spring networks with random geometry. Eng Fract Mech 61:569–591

    Article  Google Scholar 

  • Bourdin B (2001) Filters in topology optimization. Int J Numer Methods Eng 50(8):2143–2158

    Article  MathSciNet  MATH  Google Scholar 

  • Bourdin B, Chambolle A (2003) Design-dependent loads in topology optimization. ESAIM—Control Optim Calc Var 9:19–48

    Article  MathSciNet  MATH  Google Scholar 

  • Burger M, Stainko R (2006) Phase-field relaxation of topology optimization with local stress constraints. SIAM J Control Optim 45(4):1447–1466

    Article  MathSciNet  MATH  Google Scholar 

  • Caginalp G (1986) An analysis of a phase field model of a free boundary. Arch Ration Mech Anal 92(3):205–245

    Article  MathSciNet  MATH  Google Scholar 

  • Cahn JW, Hillard JE (1958) Free energy of a nonuniform system. I. Interfacial energy. J Chem Phys 28:258–267

    Article  Google Scholar 

  • Céa J, Garreau S, Guillaume P, Masmoudi M (2000) The shape and topological optimizations connection. Comput Methods Appl Mech Eng 188(4):713–726

    Article  MATH  Google Scholar 

  • Courant R, Friedrichs KO, Lewy H (1928) Über die partiellen Differenzengleichungen der mathematischen Physik. Math Ann 100(1):32–74

    Article  MathSciNet  MATH  Google Scholar 

  • Cuthill E, McKee J (1969) Reducing the bandwidth of sparse symmetric matrices. In: Proceedings of the 24th national conference. ACM Press, New York, pp 157–172

    Chapter  Google Scholar 

  • Diaz AR, Sigmund O (1995) Checkerboard patterns in layout optimization. Struct Multidisc Optim 10(1):40–45

    Google Scholar 

  • Eschenauer H, Schumacher A (1994) Bubble method for topology and shape optimization of structures. Struct Optim 8(1):42–51

    Article  Google Scholar 

  • Feng X, Wu H (2008) A posteriori error estimates for finite element approximations of the Cahn–Hilliard equation and the Hele–Shaw flow. J Comput Math 26(6):767–796

    MathSciNet  MATH  Google Scholar 

  • Ghosh S (2011) Micromechanical analysis and multi-scale modelling using the Voronoi cell finite element method. CRC Press, Boca Raton, FL

    Book  Google Scholar 

  • Ghosh S, Mukhopadhyay SN (1991) A two-dimensional automatic mesh generator for finite element analysis for random composites. Comput Struct 41(2):245–256

    Article  MATH  Google Scholar 

  • Guest JK, Prevost JH, Belytschko T (2004) Achieving minimum length scale in topology optimization using nodal design variables and projection functions. Int J Numer Methods Eng 61(2):238–254

    Article  MathSciNet  MATH  Google Scholar 

  • Kobayashi R (1993) Modeling and numerical simulations of dendritic crystal growth. Phys D: Nonlin Phenom 63(3–4):410–423

    Article  MATH  Google Scholar 

  • Lloyd S (1982) Least squares quantization in PCM. IEEE Trans Inf Theory 28(2):129–137

    Article  MathSciNet  MATH  Google Scholar 

  • March R (1992) Visual reconstructions with discontinuities using variational methods. Image Vis Comput 10:30–38

    Article  Google Scholar 

  • Martin S, Kaufmann P, Botsch M, Wicke M, Gross M (2008) Polyhedral finite elements using harmonic basis functions. Comput Graph Forum 27(5):1521–1529

    Article  Google Scholar 

  • Nguyen TH, Paulino GH, Song J, Le CH (2010) A computational paradigm for multiresolution topology optimization (MTOP). Struct Multidisc Optim 41(4):525–539

    Article  MathSciNet  Google Scholar 

  • Nguyen TH, Song J, Paulino GH (2011) Single-loop system reliability-based topology optimization considering statistical dependence between limit-states. Struct Multidiscipl Optim 44(5):593–611

    Article  MathSciNet  Google Scholar 

  • Osher S, Fedkiw R (2003) Level set methods and dynamic implicit surfaces. Springer, New York

    MATH  Google Scholar 

  • Osher S, Sethian JA (1988) Front propagating with curvature-dependent speed: algorithms based on Hamilton–Jacobi formulations. J Comput P 79:12–49

    Article  MathSciNet  MATH  Google Scholar 

  • Paulino GH, Menezes IFM, Gattass M, Mukherjee S (1994a) Node and element resequencing using the Laplacian of a finite element graph. Part I: General concepts and algorithm. Int J Numer Methods Eng 37(9):1994

    Google Scholar 

  • Paulino GH, Menezes IFM, Gattass M, Mukherjee S (1994b) Node and element resequencing using the Laplacian of a finite element graph. Part II: Implementation and numerical results. Int J Numer Methods Eng 37(9):1531–1555

    Article  Google Scholar 

  • Pendry PD, Schurig D, Smith DR (2006) Controlling electromagnetic fields. Science 312:1780–1782

    Article  MathSciNet  MATH  Google Scholar 

  • Pingen G, Waidmann M, Evgrafov A, Maute K (2010) A parametric level-set approach for topology optimization of flow domains. Struct Multidisc Optim 41(1):117–131

    Article  MathSciNet  Google Scholar 

  • Rozvany GIN, Querin OM, Gaspar Z, Pomezanski V (2003) Weight-increasing effect of topology simplification. Struct Multidisc Optim 25(5–6):459–465

    Article  Google Scholar 

  • Rozvany GIN, Zhou M, Birker T (1992) Generalized shape optimization without homogenization. Struct Multidisc Optim 4(3–4):250–252

    Google Scholar 

  • Sethian JA (1999) Level-set methods and fast marching methods: evolving interfaces in computational geometry, fluid mechanics, computer vision and materials science. Cambridge University Press, Cambridge, UK

    MATH  Google Scholar 

  • Sigmund O, Peterson J (1998) Numerical instabilities in topology optimization: a survey on procedures dealing with checkerboards, mesh-dependencies and local minima. Struct Optim 16(1):68–75

    Article  Google Scholar 

  • Sokolowski J, Zochowski A (1999) On the topological derivatives in shape optimization. SIAM J Control Optim 37:1251–1272

    Article  MathSciNet  MATH  Google Scholar 

  • Sukumar N, Tabarraei A (2004) Conforming polygonal finite elements. Int J Numer methods Eng 61(12):2045–2066

    Article  MathSciNet  MATH  Google Scholar 

  • Sun Y, Beckermann C (2007) Sharp interface tracking using the phase-field equation. J Comput Phys 220(2):626–653

    Article  MathSciNet  MATH  Google Scholar 

  • Sutradhar A, Paulino GH, Miller MJ, Nguyen TH (2010) Topology optimization for designing patient-specific large craniofacial segmental bone replacements. Proc Natl Acad Sci 107(30):13222–13227

    Article  Google Scholar 

  • Suzuki K, Kikuchi N (1991) A homogenization method for shape and topology optimization. Comput Methods Appl Mech Eng 93(3):291–318

    Article  MATH  Google Scholar 

  • Takezawa A, Nishiwaki S, Kitamura M (2010) Shape and topology optimization based on the phase field method and sensitivity analysis. J Comput Phys 229:2697–2718

    Article  MathSciNet  MATH  Google Scholar 

  • Talischi C, Paulino GH, Pereira A, Menezes IFM (2010) Polygonal finite elements for topology optimization: A unifying paradigm. Int J Numer Methods Eng 82:671–698

    MATH  Google Scholar 

  • Talischi C, Paulino GH, Pereira A, Menezes IFM (2011) PolyMesher: A general-purpose mesh generator for polygonal elements written in MATLAB. Struct Multidisc Optim 45(3):309–328

    Article  MathSciNet  Google Scholar 

  • Vasconcellos JFV, Maliska CR (2004) A finite-volume method based on Voronoi discretization for fluid flow problems. Numer Heat Transf B 45:319–342

    Article  Google Scholar 

  • Wallin M, Ristinmaa M, Askfelt H (2012) Optimal topologies derived from a phase-field method. Struct Multidisc Optim 45(2):171–183

    Article  MathSciNet  Google Scholar 

  • Wang MY, Wang X, Guo D (2003) A level-set method for structural topology optimization. Comput Methods Appl Mech Eng 192:227–246

    Article  MATH  Google Scholar 

  • Wang MY, Zhou S (2004a) Phase field: A variational method for structural topology optimization. Comput Model Eng Sci 6(6):547–566

    MathSciNet  MATH  Google Scholar 

  • Wang MY, Zhou S (2004b) Synthesis of shape and topology of multi-material structures with a phase-field method. J Comput-Aided Mater Des 11:117–138

    Article  Google Scholar 

  • Warren JA, Kobayashi R, Lobkovsky AE, Carter WC (2003) Extending phase field models of solidification to polycrystalline materials. Acta Mater 51(20):6035–6058

    Article  Google Scholar 

  • Wicke M, Botsch M, Gross M (2007) A finite element method on convex polyhedra. Comput Graph Forum 26(3):355–364

    Article  Google Scholar 

  • Yip M, Mohle J, Bolander JE (2005) Automated modeling of three-dimensional structural components using irregular lattices. Comput-Aided Civil Infrastruct Eng 20(6):393–407

    Article  Google Scholar 

  • Zhou S, Wang MY (2007) Multimaterial structural topology optimization with generalized Cahn-Hilliard model of multiphase transitions. Struct Multidiscipl Optim 33:89–111

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil and Environmental Engineering, University of Illinois at Urbana-Champaign, 205 N. Mathews Ave., Urbana, IL, 61801, USA

    Arun L. Gain & Glaucio H. Paulino

Authors
  1. Arun L. Gain
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Glaucio H. Paulino
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Glaucio H. Paulino.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Gain, A.L., Paulino, G.H. Phase-field based topology optimization with polygonal elements: a finite volume approach for the evolution equation. Struct Multidisc Optim 46, 327–342 (2012). https://doi.org/10.1007/s00158-012-0781-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-012-0781-9

Keywords

Search

Navigation