Skip to main content
SpringerLink
Log in

Novel insights for multi-objective optimisation in engineering using Normal Boundary Intersection and (Enhanced) Normalised Normal Constraint

  • Research Paper
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

Normal Boundary Intersection (NBI) and (Enhanced) Normalised Normal Constraint (E)NNC are attractive and popular approaches to generate an approximation of the Pareto set in nonlinear multi-objective optimisation problems. All three methods are based on similar ideas, but do not always yield identical results, which may confuse practitioners. Hence, the current paper provides theoretical insights in the conditions under which identical results are obtained. Typically, NBI and ENNC are able to generate the same candidate Pareto points, if all additional inequalities in the ENNC subproblem are active. In general, NBI and NNC do not return the same points when three or more objectives are considered. Equivalence relations between the resulting lagrange multipliers for the additional NBI and ENNC (in)equality constraints have been derived. Moreover, the obtained relations have lead to novel criteria for detecting non-Pareto optimal points that in adverse situations maybe generated by these methods. The major advantage is that the removal criteria do not rely on a time-consuming pairwise comparison but only need matrix multiplications. A Matlab implementation has been added for completeness. The insights are illustrated for a general nonlinear bi-objective and three-objective optimisation problem, and a dynamic three-objective tubular reactor optimisation problem from chemical engineering. Finally, practical guidelines are added.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  • Das I, Dennis J (1997) A closer look at drawbacks of minimizing weighted sums of objectives for Paretoset generation in multicriteria optimization problems. Struct Optim 14:63–69

    Article  Google Scholar 

  • Das I, Dennis J (1998) Normal-boundary intersection: a new method for generating the Pareto surface in nonlinear multicriteria optimization problems. SIAM J Optim 8:631–657

    Article  MathSciNet  MATH  Google Scholar 

  • Houska B, Ferreau H, Diehl M (2011) ACADO Toolkit—an open-source framework for automatic control and dynamic optimization. Optim Control Appl Methods 32:298–312

    Article  MathSciNet  MATH  Google Scholar 

  • Kim I, de Weck O (2005) Adaptive weighted-sum method for bi-objective optimization: Pareto front generation. Struct Multidisc Optim 29:149–158

    Article  Google Scholar 

  • Logist F, Smets I, Van Impe J (2008) Derivation of generic optimal reference temperature profiles for steady-state exothermic jacketed tubular reactors. J Process Control 18:92–104

    Article  Google Scholar 

  • Logist F, Houska B, Diehl M, Van Impe J (2010a) Fast pareto set generation for nonlinear optimal control problems with multiple objectives. Struct Multidisc Optim 42:591–603

    Article  Google Scholar 

  • Logist F, Sager S, Kirches C, Van Impe J (2010b) Efficient multiple objective optimal control of dynamic systems with integer controls. J Process Control 20:810–822

    Article  Google Scholar 

  • Marler R, Arora J (2004) Survey of multi-objective optimization methods for engineering. Struct Multidisc Optim 26:369–395

    Article  MathSciNet  Google Scholar 

  • Messac A, Mattson C (2004) Normal constraint method with guarantee of even representation of complete Pareto frontier. AIAA J 42:2101–2111

    Article  Google Scholar 

  • Messac A, Ismail-Yahaya A, Mattson C (2003) The normalized normal constraint method for generating the Pareto frontier. Struct Multidisc Optim 25:86–98

    Article  MathSciNet  Google Scholar 

  • Miettinen K (1999) Nonlinear multiobjective optimization. Kluwer Academic Publishers, Boston

    MATH  Google Scholar 

  • Sanchis J, Martinez M, Blasco X, Salcedo J (2008) A new perspective on multiobjective optimization by enhanced normalized normal constraint method. Struct Multidisc Optim 36:537–546

    Article  Google Scholar 

Download references

Acknowledgments

Work supported in part by Projects OT/10/035, OPTEC (Center-of-Excellence Optimization in Engineering) PFV/10/002 and SCORES4CHEM KP/09/005 of the Katholieke Universiteit Leuven, and by the Belgian Program on Interuniversity Poles of Attraction, initiated by the Belgian Federal Science Policy Office. J.F. Van Impe holds the chair Safety Engineering sponsored by the Belgian chemistry and life sciences federation essenscia.

Author information

Authors and Affiliations

  1. Chemical and Biochemical Process Technology and Control (BioTeC) & Optimization in Engineering Center (OPTEC), Department of Chemical Engineering, K.U. Leuven, W. de Croylaan 46, 3001, Leuven, Belgium

    Filip Logist & Jan Van Impe

Authors
  1. Filip Logist
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jan Van Impe
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jan Van Impe.

Electronic Supplementary Material

Below is the link to the electronic supplementary material.

(M File 1.61 KB)

(M File 1.48 KB)

Appendix

Appendix

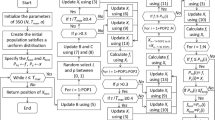
The matlab code for both removal criteria is depicted in Figs. 15 and 16. The corresponding matlab m-files are available as Supplementary Material to this article.

Fig. 15
figure 15

Matlab code for removal of candidate points generated by ENNC

Full size image
Fig. 16
figure 16

Matlab code for removal of candidate points generated by NBI

Full size image

Rights and permissions

Reprints and permissions

About this article

Cite this article

Logist, F., Van Impe, J. Novel insights for multi-objective optimisation in engineering using Normal Boundary Intersection and (Enhanced) Normalised Normal Constraint. Struct Multidisc Optim 45, 417–431 (2012). https://doi.org/10.1007/s00158-011-0698-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-011-0698-8

Keywords

Search

Navigation