Abstract
An algebraic proof is presented for the finite strong standard completeness of the Involutive Uninorm Logic with Fixed Point (\({{\mathbf {IUL}}^{fp}}\)). It may provide a first step towards settling the standard completeness problem for the Involutive Uninorm Logic (\({\mathbf {IUL}}\), posed in G. Metcalfe, F. Montagna. (J Symb Log 72:834–864, 2007)) in an algebraic manner. The result is proved via an embedding theorem which is based on the structural description of the class of odd involutive FL\(_e\)-chains which have finitely many positive idempotent elements.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Mathematical fuzzy logics have been introduced in [8], and the topic is a rapidly growing field ever since ([1, 4, 6]). Substructural fuzzy logics were introduced in [15] as substructural logics that are standard complete, that is, complete with respect to standard algebras which are the algebras where the real unit interval [0, 1] is their lattice reduct, and standard completeness for several substructural logics, all are stronger than the there-introduced Uninorm Logic (\(\mathbf {UL}\)), has been proven, too, with the notable exception of the Involutive Uninorm Logic (\(\mathbf {IUL}\)). Its standard completeness has remained an open problem, which has stood against the attempts using the widely used embedding method of [13] or the density elimination technique of [15]. It is fair to mention, however, that there is already a claimed proof for the standard completeness of \(\mathbf {IUL}\) in [18], but the presented proof-theoretic proof via density elimination is very hard to read and even harder to check, and as a consequence, as of today, the result is not generally recognizedFootnote 1.
An algebraic semantics for \(\mathbf {IUL}\) is the variety of bounded involutive FL\(_e\)-chains. The structure of involutive FL\(_e\)-chains is quite rich; even the integral algebras thereof (the class of IMTL-chains) is a class containing, e.g., the connected rotations [12] of all MTL-chains without zero divisors. This richness renders their algebraic description a very hard task. Therefore, as a first step toward this goal, we focus on odd involutive FL\(_e\)-chains, which is a subclass of involutive FL\(_e\)-chains. Bounded odd involutive FL\(_e\)-chains constitute the algebraic semantics for the Involutive Uninorm Logic with Fixed Point (\(\mathbf {IUL}^{fp}\)) [14]. Prominent examples of odd involutive FL\(_e\)-algebras are lattice-ordered abelian groups and odd Sugihara monoids. The former constitutes an algebraic semantics for Abelian Logic [3, 16, 17] while the latter constitutes an algebraic semantics for \(\mathbf {IUML}^*\), which is a logic at the intersection of relevance logic and many-valued logic [7].
As defined in [15] substructural fuzzy logics are based on a countable propositional language with formulas built inductively as usual from a set of propositional variables, binary connectives \(\odot \) \(\rightarrow \), \(\wedge \), \(\vee \), and constants \(\bot \), \(\top \), \({\mathbf {f}}\), \({\mathbf {t}}\), with defined connectives:
\({\mathbf {MAILL}}\) consists of the following axioms and rules:
-
1.
\(A\rightarrow A\)
-
2.
\((A\rightarrow B)\rightarrow ((B\rightarrow C)\rightarrow (A\rightarrow C))\)
-
3.
\((A\rightarrow (B\rightarrow C))\rightarrow (B\rightarrow (A\rightarrow C))\)
-
4.
\((A\odot (B\rightarrow C))\leftrightarrow (A\rightarrow (B\rightarrow C))\)
-
5.
\((A\wedge B)\rightarrow A\)
-
6.
\((A\wedge B)\rightarrow B\)
-
7.
\(((A\rightarrow B)\wedge (A\rightarrow C))\rightarrow (A\rightarrow (B\wedge C))\)
-
8.
\(A\rightarrow (A\vee B)\)
-
9.
\(B\rightarrow (A\vee B)\)
-
10.
\(((A\rightarrow C)\wedge (B\rightarrow C))\rightarrow ((A\vee B)\rightarrow C)\)
-
11.
\(A\leftrightarrow ({\mathbf {t}}\rightarrow A)\)
-
12.
\(\bot \rightarrow A\)
-
13.
\(A\rightarrow \top \)
$$\begin{aligned} \begin{array}{rc} &{} A \ \ \ A\rightarrow B \\ &{} B \end{array}(mp)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \begin{array}{rc} &{} A \ \ \ B \\ &{} A\wedge B \end{array}(adj) \end{aligned}$$
Further substructural fuzzy logics are defined by extending \(\mathbf {MAILL}\). In particular, Uninorm Logic (\(\mathbf {UL}\)) is the schematic extension of \(\mathbf {UL}\) by the axiom \(((A\rightarrow B)\wedge {\mathbf {t}})\vee ((B\rightarrow A)\wedge {\mathbf {t}})\), Involutive Uninorm Logic (\(\mathbf {IUL}\)) is the schematic extension of \(\mathbf {UL}\) by the axiom \(\lnot \lnot A\rightarrow A\), and Involutive Uninorm Logic with Fixed Point ([14], \(\mathbf {IUL}^{fp}\)) is the schematic extension of \(\mathbf {IUL}\) by the axiom \({\mathbf {t}}\leftrightarrow {\mathbf {f}}\).
In order to make a possible first step toward settling the standard completeness problem for \(\mathbf {IUL}\) in an algebraic manner, in this paper we prove the finite strong standard completeness of \(\mathbf {IUL}^{fp}\), a somewhat simpler logic than \(\mathbf {IUL}\). The key ingredient in our proof is constructing an embedding, based on a representation theorem of the class of odd involutive FL\(_e\)-chains which possess only finitely many positive idempotent elements, by means of totally ordered abelian groups and a modified version of the lexicographic product construction [9, 11].
As said, standard algebras for a mathematical fuzzy logic L are the ones from the corresponding variety which universe is the real unit interval [0, 1]. A mathematical fuzzy logic L enjoys finite strong standard completeness if the following conditions are equivalent for each formula \(\varphi \) and finite theory T:
-
1.
\(T\vDash _L \varphi \),
-
2.
for each standard L-algebra \({\mathbf {A}}\) and each \({\mathbf {A}}\)-model e of T, e is an \({\mathbf {A}}\)-model of \(\varphi \).
There are other alternatives for defining standard completeness of L. The same definition as above but without confining to finite theories yields the definition of strong standard completeness, whereas by setting \(T=\emptyset \) we obtain the definition of (weak) standard completeness. A possible way of proving finite strong standard completeness is to embed finitely generated L-chains into standard L-chains, since this way one proves that any formula of L which can be falsified in a totally ordered model of finitely many L-formulas (which is always a finitely generated L-chain) can also be falsified in a standard L-algebra. Knowing the facts that \(\mathrm{IUL}^{fp}\)-chains constitute an algebraic semantics of \(\mathbf {IUL}^{fp}\), and that \(\mathrm{IUL}^{fp}\)-chains are exactly non-trivial bounded odd involutive FL\(_e\)-chains, we shall prove that any non-trivial finitely generated bounded odd involutive FL\(_e\)-chain embeds into an odd involutive FL\(_e\)-chain over the real unit interval [0, 1] such that its top element is mapped into 1 and its bottom element is mapped into 0.
2 Preliminaries
We start with the necessary definitions. Commutative residuated lattices are the f-free reducts of FL\(_e\)-algebras. An FL\(_e\)-algebra is a structure  such that \(( X, \wedge ,\vee )\) is a lattice,
such that \(( X, \wedge ,\vee )\) is a lattice,  is a commutative, residuated monoid, and f is an arbitrary constant. Being residuated means that there exists a binary operation
is a commutative, residuated monoid, and f is an arbitrary constant. Being residuated means that there exists a binary operation  , called the residual operation of
, called the residual operation of  , such that
, such that  if and only if
if and only if  . This equivalence is called adjointness condition, (
. This equivalence is called adjointness condition, ( ) is called an adjoint pair. Equivalently, for any x, z, the set
) is called an adjoint pair. Equivalently, for any x, z, the set  has its greatest element, and
has its greatest element, and  , the residuum of x and z, is defined as this element:
, the residuum of x and z, is defined as this element:  ; this is called the residuation condition. One defines
; this is called the residuation condition. One defines  and calls an FL\(_e\)-algebra involutive if \({({x}{^\prime })}{^\prime }=x\) holds. In every involutive FL\(_e\)-algebra
and calls an FL\(_e\)-algebra involutive if \({({x}{^\prime })}{^\prime }=x\) holds. In every involutive FL\(_e\)-algebra  holds, hence for every term there exists an equivalent term which contains (besides \(\wedge \) and \(\vee \)) only the product and the residual complement operations but not the residual operation. An involutive FL\(_e\)-algebra is called odd if \(t=f\) holds. As shown in [11], the
holds, hence for every term there exists an equivalent term which contains (besides \(\wedge \) and \(\vee \)) only the product and the residual complement operations but not the residual operation. An involutive FL\(_e\)-algebra is called odd if \(t=f\) holds. As shown in [11], the  -reduct of an odd involutive FL\(_e\)-algebra is a lattice-ordered abelian group if and only if it has a single idempotent element, and it is if and only if
-reduct of an odd involutive FL\(_e\)-algebra is a lattice-ordered abelian group if and only if it has a single idempotent element, and it is if and only if  is cancellative. Therefore, one can loosely speak about subgroups of odd involutive FL\(_e\)-algebras by meaning a cancellative subalgebras. A totally ordered algebra is called discretely ordered if every element has its lower and upper cover. A totally ordered abelian group is called discrete if its unit element has an upper cover. Discrete totally ordered abelian groups are discretely ordered. Algebras will be denoted by bold capital letters, their underlying sets by the same regular letter. The lexicographic product of two totally ordered sets \({\mathbf {A}}=(A,\le _1)\) and \({\mathbf {B}}=(B,\le _2)\) is a totally order set \({\mathbf {A}}\overset{\rightarrow }{\times }{\mathbf {B}}=(A\times B,\le )\), where \(A\times B\) is the Cartesian product of A and B, and \(\le \) is defined by \(\langle a_1,b_1 \rangle \le \langle a_2,b_2 \rangle \) if and only if \(a_1<_1 a_2\) or \(a_1=a_2\) and \(b_1\le _2 b_2\). We shall view such a lexicographic product as an enlargement: each element of A is replaced by a whole copy of B. The lexicographic product \({\mathbf {A}}\overset{\rightarrow }{\times }{\mathbf {B}}\) of two FL\(_e\)-chains \({\mathbf {A}}\) and \({\mathbf {B}}\) is an FL\(_e\)-chain over the lexicographic product of their respective universes such that all operations are defined coordinatewise.
is cancellative. Therefore, one can loosely speak about subgroups of odd involutive FL\(_e\)-algebras by meaning a cancellative subalgebras. A totally ordered algebra is called discretely ordered if every element has its lower and upper cover. A totally ordered abelian group is called discrete if its unit element has an upper cover. Discrete totally ordered abelian groups are discretely ordered. Algebras will be denoted by bold capital letters, their underlying sets by the same regular letter. The lexicographic product of two totally ordered sets \({\mathbf {A}}=(A,\le _1)\) and \({\mathbf {B}}=(B,\le _2)\) is a totally order set \({\mathbf {A}}\overset{\rightarrow }{\times }{\mathbf {B}}=(A\times B,\le )\), where \(A\times B\) is the Cartesian product of A and B, and \(\le \) is defined by \(\langle a_1,b_1 \rangle \le \langle a_2,b_2 \rangle \) if and only if \(a_1<_1 a_2\) or \(a_1=a_2\) and \(b_1\le _2 b_2\). We shall view such a lexicographic product as an enlargement: each element of A is replaced by a whole copy of B. The lexicographic product \({\mathbf {A}}\overset{\rightarrow }{\times }{\mathbf {B}}\) of two FL\(_e\)-chains \({\mathbf {A}}\) and \({\mathbf {B}}\) is an FL\(_e\)-chain over the lexicographic product of their respective universes such that all operations are defined coordinatewise.
For an FL\(_e\)-algebra  , denote
, denote  for \(x\in X\) and let
for \(x\in X\) and let  . If \({\mathbf {X}}\) is odd then there is a cancellative subalgebra \({\mathbf {X}}_\mathbf {gr}\) of \({\mathbf {X}}\) over \(X_{gr}\), call it the group part of \({\mathbf {X}}\).
. If \({\mathbf {X}}\) is odd then there is a cancellative subalgebra \({\mathbf {X}}_\mathbf {gr}\) of \({\mathbf {X}}\) over \(X_{gr}\), call it the group part of \({\mathbf {X}}\).
Lemma 1
[11] Let  be an involutive FL\(_e\)-algebra. The following statements hold true.
be an involutive FL\(_e\)-algebra. The following statements hold true.
-
1.
\(Range(\tau )=\{ \tau (x): x\in X \}\) is equal to the set of positive idempotent elements of X.
-
2.
If \({\mathbf {X}}\) is totally ordered and odd and A is an \({\mathbf {X}}\)-term which contains only the operations
 ,
,  and \({^\prime }\) then for any evaluation e of the variables of A into X, \(\tau (e(A))\) equals the maximum of the \(\tau \)-values of the variables and constants of A under e. Stated it in another way, for \(x,y\in X\), \(\tau ({x}{^\prime })=\tau (x)\),
and \({^\prime }\) then for any evaluation e of the variables of A into X, \(\tau (e(A))\) equals the maximum of the \(\tau \)-values of the variables and constants of A under e. Stated it in another way, for \(x,y\in X\), \(\tau ({x}{^\prime })=\tau (x)\),  ,
,  .
.
\(\square \)
The main theorem which we shall rely on in proving the main result of the present paper is Theorem 1 below. It says that every odd involutive FL\(_e\)-chain \({\mathbf {X}}\), which has only \(n\ge 1\) positive idempotent elements can be built by starting with a totally ordered abelian group, and iteratively enlarging it in some way by other totally ordered abelian groups. Each such enlargement increases the number of positive idempotent elements of the enlarged algebra by the number of positive idempotent elements of the algebra we enlarge with. Since the totally ordered abelian group we start with has a single idempotent element (its unit element), and likewise each algebra we enlarge with does, after \(n-1\) enlargement we obtain \({\mathbf {X}}\). Odd involutive FL\(_e\)-chains (even with only finitely many positive idempotent elements) are rather complex mathematical objects, and this renders the description of their algebraic structure a hard task of [9, 11]. The price to pay for describing such complex structures by such simple ones as totally ordered abelian groups is that the way of enlargements is quite involved (including several parameterers), and this makes up for a correspondingly involved notation, too. These enlargements are described in Definition 1
Definition 1
[9, 11] (Partial lex and sublex products) Let  and
and  be odd involutive FL\(_e\)-chains with residual complement operations
be odd involutive FL\(_e\)-chains with residual complement operations  and
and  , respectively.
, respectively.
-
A.
Add a new element \(\top \) to G as a top element and annihilator (for \(\star \)), then add a new element \(\bot \) to \(G\cup \{\top \}\) as a bottom element and annihilator. Let
$$\begin{aligned} {{\mathbf {Z}}}\le {\mathbf {Y}}_\mathbf {gr} \text{ and } {\mathbf {H}}\le {\mathbf {Z}}\overset{\rightarrow }{\times }{\mathbf {G}}. \end{aligned}$$(1)Let
 (2)
(2)where
 (3)
(3)-
\(\le \) is the restriction of the lexicographical order of \(\le _Y\) and \(\le _{G\cup \{\top ,\bot \}}\) to the respective universes,
-
 is defined coordinatewise,
is defined coordinatewise,  is (provisionally) the residual operation of
is (provisionally) the residual operation of 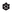 , and the residual complement operation \({^\prime }\) is given by
, and the residual complement operation \({^\prime }\) is given by  (4)
(4)Call
 the type I partial lexicographic extension (lex extension, for short) of \({\mathbf {Y}}\) by \({\mathbf {Z}}\overset{\rightarrow }{\times }{\mathbf {G}}\), and
the type I partial lexicographic extension (lex extension, for short) of \({\mathbf {Y}}\) by \({\mathbf {Z}}\overset{\rightarrow }{\times }{\mathbf {G}}\), and 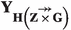 the type I partial sublex extension of \({\mathbf {Y}}\) by \({\mathbf {H}}\) (where \({\mathbf {H}}\) is in \({\mathbf {Z}}\overset{\rightarrow }{\times }{\mathbf {G}}\)). In the notations
the type I partial sublex extension of \({\mathbf {Y}}\) by \({\mathbf {H}}\) (where \({\mathbf {H}}\) is in \({\mathbf {Z}}\overset{\rightarrow }{\times }{\mathbf {G}}\)). In the notations  and
and  the arrow above the \(\times \) symbol refers to the lexicographic nature of the extension, and the two extra small lines attached to the arrow reminds that in this version two extra elements (\(\top \) and \(\bot \)) are used (compare it with the following construction below).
the arrow above the \(\times \) symbol refers to the lexicographic nature of the extension, and the two extra small lines attached to the arrow reminds that in this version two extra elements (\(\top \) and \(\bot \)) are used (compare it with the following construction below).
-
-
B.
For a totally ordered set \((Y, \le _Y)\) for \(x\in Y\) let \(x_\downarrow =z\) if there exists \(z\in Y\) such that x covers z, and let \(x_\downarrow =x\) otherwise; define \(x_\uparrow \) dually. With this notation, Y is discretely ordered iff for \(x\in Y\), \(x\notin \{ x_\uparrow ,x_\downarrow \}\). We say for \(Z\subseteq Y\) that Z is discretely embedded into Y if for \(x\in Z\) it holds true that \(x\notin \{ x_\uparrow ,x_\downarrow \}\subseteq Z\). We shall also use the term discretely embedded for algebras if it holds true for their totally ordered set reducts. Assume that
$$\begin{aligned} \begin{array}{c} {\mathbf {Y}}_\mathbf {gr} \text{ is } \text{ discretely } \text{ embedded } \text{ into } {\mathbf {Y}} \\ \text{ and } {\mathbf {H}}\le {\mathbf {Y}}_\mathbf {gr}\overset{\rightarrow }{\times }{\mathbf {G}}, \end{array} \end{aligned}$$(5)Add a new element \(\top \) to G as a top element and annihilator. Let
 (6)
(6)where
 (7)
(7)-
\(\le \) is the restriction of the lexicographical order of \(\le _Y\) and \(\le _{ G\cup \{\top \}}\) to the respective universes,
-
 is defined coordinatewise,
is defined coordinatewise,  is (provisionally) the residual operation of
is (provisionally) the residual operation of 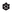 , and the residual complement operation \({^\prime }\) is given by
, and the residual complement operation \({^\prime }\) is given by  (8)
(8)
Call
 the type II partial lex extension of \({\mathbf {Y}}\) by \({\mathbf {Y}}_{gr}\overset{\rightarrow }{\times }{\mathbf {G}}\), and call
the type II partial lex extension of \({\mathbf {Y}}\) by \({\mathbf {Y}}_{gr}\overset{\rightarrow }{\times }{\mathbf {G}}\), and call  the type II partial sublex extension of \({\mathbf {Y}}\) by \({\mathbf {H}}\) (where \({\mathbf {H}}\) is in \({\mathbf {Y}}_{gr}\overset{\rightarrow }{\times }{\mathbf {G}}\)). In the notations
the type II partial sublex extension of \({\mathbf {Y}}\) by \({\mathbf {H}}\) (where \({\mathbf {H}}\) is in \({\mathbf {Y}}_{gr}\overset{\rightarrow }{\times }{\mathbf {G}}\)). In the notations  and
and 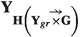 the arrow above the \(\times \) symbol refers to the lexicographic nature of the extension, and the single extra small line attached to the arrow reminds that in this version only one extra element (\(\top \)) is used.
the arrow above the \(\times \) symbol refers to the lexicographic nature of the extension, and the single extra small line attached to the arrow reminds that in this version only one extra element (\(\top \)) is used. -
Remark 1
If the required condition of Definition 1 holds, namely, the conditions in (1) in case of a type I extension, or the conditions in (5) in case of a type II extension, then the respective algebra in (2) or in (6) is said to exist or said to be well-defined.
Remark 2
The interested reader can find detailed, enlightening motivation for these constructions in [11, Sect. 3] along with related 3D plots of the graphs of the example operations.
Lemma 2
[9, 11] Type I and II partial lex and sublex products, as defined in Definition 1, are odd involutive FL\(_e\)-algebras such that

\(\square \)
Remark 3
A type I partial lex product is a particular, simpler instance of a type I partial sublex product, and a type II partial lex product is a particular, simpler instance of a type II partial sublex product, where \(H=Z\times G\) and \(H = Y_{gr}\times G\), respectively.
Remark 4
About the two simpler notions: think of  such that \({\mathbf {Z}}\) (which is in the group part of \({\mathbf {Y}}\)) is enlarged by \({\mathbf {G}}\) in a type I manner (as described in the first row of (3)), and think of
such that \({\mathbf {Z}}\) (which is in the group part of \({\mathbf {Y}}\)) is enlarged by \({\mathbf {G}}\) in a type I manner (as described in the first row of (3)), and think of  such that \({\mathbf {Y}}_{gr}\) (the group part of \({\mathbf {Y}}\)) is enlarged by \({\mathbf {G}}\) in a type II manner (as described in the first row of (7)).
such that \({\mathbf {Y}}_{gr}\) (the group part of \({\mathbf {Y}}\)) is enlarged by \({\mathbf {G}}\) in a type II manner (as described in the first row of (7)).
Remark 5
Since \({\mathbf {Z}}\) is a subgroup and since the monoidal operation is defined coordinatewise, the group part of  is \({\mathbf {Z}}\overset{\rightarrow }{\times }{\mathbf {G}}_{\mathbf {gr}}\), the group part of
is \({\mathbf {Z}}\overset{\rightarrow }{\times }{\mathbf {G}}_{\mathbf {gr}}\), the group part of  is \({\mathbf {Y}}_{\mathbf {gr}}\overset{\rightarrow }{\times }{\mathbf {G}}_{\mathbf {gr}}\), and the group part of both
is \({\mathbf {Y}}_{\mathbf {gr}}\overset{\rightarrow }{\times }{\mathbf {G}}_{\mathbf {gr}}\), and the group part of both  and
and  is \({\mathbf {H}}\).
is \({\mathbf {H}}\).
As said, the main theorem which we shall rely on in proving the main result of the present paper is Theorem 1. It asserts that up to isomorphism, every odd involutive FL\(_e\)-chain which has only finitely many positive idempotent elements can be built by starting with a totally ordered abelian group and iteratively enlarging it by other totally ordered abelian groups until we obtain the given algebra. In more technical terms, every odd involutive FL\(_e\)-chain which has only finitely many positive idempotent elements can be built by iterating finitely many times the type I and type II partial sublex product constructions using only totally ordered abelian groups, as building blocks. We shall also refer to this fact that every odd involutive FL\(_e\)-chain which has only finitely many positive idempotent elements has a partial sublex product group representation.
Theorem 1
([9, 11]) If \({\mathbf {Y}}\) is an odd involutive FL\(_e\)-chain, which has only \(n\in {\mathbb {N}}\), \(n\ge 1\) positive idempotent elements then it has a partial sublex product group representation, that is, there exist a totally ordered abelian group \({\mathbf {H}}_1\) and for \(i=2,\ldots ,n\), totally ordered abelian groups \({\mathbf {H}}_i\), \({\mathbf {G}}_i\), \({\mathbf {Z}}_{i-1}\) along with \(\iota _i\in \{I,II\}\) such that \( {\mathbf {Y}}\cong {\mathbf {Y}}_n, \) where for \(i\in \{2,\ldots ,n\}\),

\(\square \)
Notice that Theorem 1 claims isomorphism between \({\mathbf {Y}}\) and \({\mathbf {Y}}_n\) hence \({\mathbf {Y}}_n\) and consequently for \(i=n-1,\ldots , 2\), the \({\mathbf {Y}}_i\)’s are claimed implicitly to exist (to be well defined). By Definition 1, since \(({\mathbf {Y}}_i)_{\mathbf {gr}}={\mathbf {H}}_i\) holds for \(i\in \{1,\ldots ,n\}\) (by assumption if \(i=1\), and by Remark 5 if \(i\in \{2,\ldots ,n\}\)) therefore, it is necessarily that
Let \({\mathbf {Y}}\) be a non-trivial finitely generated bounded odd involutive FL\(_e\)-chain. Roughly, our plan is first to show that \({\mathbf {Y}}\) has a partial sublex product group representation, and then to take guidance from the way \({\mathbf {Y}}\) is built iteratively from totally ordered abelian groups in constructing the embedding of \({\mathbf {Y}}\) into \({\mathbf {X}}^*\), which is an odd involutive FL\(_e\)-chain over the unit interval, in a step-by-step iterative fashion, and guided by the iterative steps of the group representation of \({\mathbf {Y}}\). Meanwhile we want the universes of the intermediately constructed \({\mathbf {X}}^*_i\)’s to stay as close to the topological structure of the unit interval as possible, to achieve in the end the universe of \({\mathbf {X}}^*_n={\mathbf {X}}^*\) be order isomorphic to the unit interval. For this, we shall need and make use of the characterization in Lemma 3; note that the open unit interval and \({\mathbb {R}}\) are order isomorphic. A totally ordered set \((X,\le )\) is called Dedekind complete if every non-empty subset of X bounded from above has a supremum.
Lemma 3
([2, Theorem 2.29]) A totally ordered set \((K,\le )\) is order isomorphic to \({\mathbb {R}}\) if and only if \((K,\le )\) possesses the following four properties: \((K,\le )\) has no least neither greatest element, \((K,\le )\) is densely ordered, there exists a countable dense subset of \((K,\le )\), and \((K,\le )\) is Dedekind complete.
3 The proof of finite strong standard completeness
To ensure that Theorem 1 will be applicable to our problem, first we show that
Proposition 1
Every finitely generated odd involutive FL\(_e\)-chain has only finitely many positive idempotent elements.
Proof
Since the order is total, \(\tau (x\wedge y),\tau (x\vee y)\in \{\tau (x), \tau (y)\}\) holds. Therefore, using claim 2 in Lemma 1, an easy induction on the recursive structure of the term that generates a given element x of the algebra shows that the \(\tau \)-value of x coincides with the \(\tau \)-value of one of its generators or constants. Therefore, since the algebra is finitely generated, all elements of the algebra share only the (finitely many) \(\tau \)-values of the finitely many generators. Claim 1 in Lemma 1 concludes the proof. \(\square \)
Group representations are not unique, and hence even in a group representation of a finitely generated algebra the algebras which are employed in the iterative process in (9) (the \({\mathbf {G}}_i\)’s, the \({\mathbf {Z}}_i\)’s, the \({\mathbf {H}}_i\)’s, and the \({\mathbf {Y}}_i\)’s) are not necessarily finitely generated. More precisely they always are with the exception of the \({\mathbf {G}}_i\)’s. Our next aim is to achieve, by modifying the \({\mathbf {G}}_i\)’s in (11), that all the algebras are finitely generated in some group representation of \({\mathbf {Y}}\). Later we shall make use of this property of the \({\mathbf {G}}^\prime _i\)’s (the modified groups which we shall iteratively extend with) and the enlarged parts (the \({\mathbf {Z}}_i\)’s). This will make it possible, e.g., to embed the \({\mathbf {G}}_i\)’s into appropriate odd involutive FL\(_e\)-algebras over the unit interval, a key intermediate step of our construction later in (21). Our aim will be achieved in Proposition 2 by defining a unique (or canonical) group representation for every odd involutive FL\(_e\)-chain.
Proposition 2
If \({\mathbf {Y}}\) is a finitely generated odd involutive FL\(_e\)-chain then there exists a group representation of \({\mathbf {Y}}\) in which all the employed algebras are finitely generated.
Proof
Let \({\mathbf {Y}}\) be an odd involutive FL\(_e\)-chain which has finitely many positive idempotent elements, and let a representation of \({\mathbf {Y}}\) by partial sublex products be given, according to Theorem 1, see it in (9). We modify the enlarging groups, and leave all the other algebras which are employed in (9) unchanged: for \(i\in \{2,\ldots ,n\}\) let
Trivially, for \(i\in \{2,\ldots ,n\}\), \({\mathbf {G}}^\prime _i\le {\mathbf {G}}_i\) and

since the condition in (10) (the one with the \({\mathbf {G}}_i\)’s) holds and hence it trivially holds with the modified \({\mathbf {G}}_i\)’s, too, that is,
and for all \(i\in \{2,\ldots ,n\}\), the universe of  and the universe of
and the universe of  (and hence all their operations, too) is equal to the universe of
(and hence all their operations, too) is equal to the universe of  and the universe of
and the universe of  , respectively.
, respectively.
We shall prove that all algebras used in the group representation of \({\mathbf {Y}}\) in (12) are finitely generated. The statement is obvious if \(n=1\), since then the only algebra in the group representation of \({\mathbf {Y}}\) is \({\mathbf {Y}}\). Therefore, we may assume \(n\ge 2\). Since \(n\ge 2\),

holds, and hence
holds, see (3) and (7). Therefore,
If finitely many elements \((a_1,b_1)\), \(\ldots \) \((a_k,b_k)\) generate \({\mathbf {Y}}_n\), and in particular, generate the element \((a,\bot )\) if \(\iota _n=I\) (resp. \((a,\top )\) if \(\iota _n=II\)) in \(Y_{n-1}\times \{\bot \}\) (resp. in \(Y_{n-1}\times \{\top \}\)) then \((a_1,\bot )\), \(\ldots \) \((a_k,\bot )\) together with \((t_{Y_{n-1}},\bot )\) (resp. \((a_1,\top )\), \(\ldots \) \((a_k,\top )\) together with \((t_{Y_{n-1}},\top )\)) can generate the same element: use the equivalent term which contains only  and \({^\prime }\), replace each generator and constant \((a_i,b_i)\) in it by \((a_i,\bot )\) (resp. \((a_i,\top )\)), and apply a multiplication by \((t_{Y_{n-1}},\bot )\) (resp. \((t_{Y_{n-1}},\top )\)) in the end. Since the multiplication is defined coordinatewise, and since at the residual complement operation the first coordinate of the result depends only on the first coordinate of the argument (see (4) and (8)), and since \(\bot \) (resp. \(\top \)) is an annihilator in the second coordinate, such a generation process trivially results in \((a,\bot )\) (resp. \((a,\top )\)). Therefore, \({\mathbf {Y}}_{n-1}\) is finitely generated. Summing up, if \({\mathbf {Y}}={\mathbf {Y}}_n\) is finitely generated then so is \({\mathbf {Y}}_{n-1}\). This way an easy downward induction shows that \( {\mathbf {Y}}_i \) is finitely generated for \(i=n,n-1,\ldots ,1\). In particular, \({\mathbf {H}}_1={\mathbf {Y}}_1\) is finitely generated, too. Trivially, if an element is invertible then its inverse is its residual complement, hence its residual complement is invertible, too. Also trivially, the product of two elements cannot be invertible if at least one of them is noninvertible. Therefore, if an element in \(({\mathbf {Y}}_i)_\mathbf {gr}\), that is, an invertible element is generated, then all the generator elements employed in the generating term (the equivalent one which does not contain the residual operation) must be invertible, too. Hence it follows that for \(i\in \{2,\ldots ,n\}\), \({\mathbf {H}}_i=({\mathbf {Y}}_i)_\mathbf {gr}\) is finitely generated. It is well-known that subgroups of finitely generated abelian groups are themselves finitely generated [5, page 80]. Hence \({\mathbf {Z}}_i\) \(i\in \{1,\ldots ,n-1\}\) is finitely generated, too, since by assumption, \({\mathbf {Z}}_{i-1}\le {\mathbf {H}}_{i-1}\) holds for \(i\in \{2,\ldots ,n\}\). Trivially, for \(i\in \{2,\ldots ,n\}\), \({\mathbf {G}}^\prime _i\) is a homomorphic image of \({\mathbf {H}}_i\), see (11). Therefore, \({\mathbf {G}}^\prime _i\) is finitely generated, too, since being finitely generated inherits to homomorphic images. \(\square \)
and \({^\prime }\), replace each generator and constant \((a_i,b_i)\) in it by \((a_i,\bot )\) (resp. \((a_i,\top )\)), and apply a multiplication by \((t_{Y_{n-1}},\bot )\) (resp. \((t_{Y_{n-1}},\top )\)) in the end. Since the multiplication is defined coordinatewise, and since at the residual complement operation the first coordinate of the result depends only on the first coordinate of the argument (see (4) and (8)), and since \(\bot \) (resp. \(\top \)) is an annihilator in the second coordinate, such a generation process trivially results in \((a,\bot )\) (resp. \((a,\top )\)). Therefore, \({\mathbf {Y}}_{n-1}\) is finitely generated. Summing up, if \({\mathbf {Y}}={\mathbf {Y}}_n\) is finitely generated then so is \({\mathbf {Y}}_{n-1}\). This way an easy downward induction shows that \( {\mathbf {Y}}_i \) is finitely generated for \(i=n,n-1,\ldots ,1\). In particular, \({\mathbf {H}}_1={\mathbf {Y}}_1\) is finitely generated, too. Trivially, if an element is invertible then its inverse is its residual complement, hence its residual complement is invertible, too. Also trivially, the product of two elements cannot be invertible if at least one of them is noninvertible. Therefore, if an element in \(({\mathbf {Y}}_i)_\mathbf {gr}\), that is, an invertible element is generated, then all the generator elements employed in the generating term (the equivalent one which does not contain the residual operation) must be invertible, too. Hence it follows that for \(i\in \{2,\ldots ,n\}\), \({\mathbf {H}}_i=({\mathbf {Y}}_i)_\mathbf {gr}\) is finitely generated. It is well-known that subgroups of finitely generated abelian groups are themselves finitely generated [5, page 80]. Hence \({\mathbf {Z}}_i\) \(i\in \{1,\ldots ,n-1\}\) is finitely generated, too, since by assumption, \({\mathbf {Z}}_{i-1}\le {\mathbf {H}}_{i-1}\) holds for \(i\in \{2,\ldots ,n\}\). Trivially, for \(i\in \{2,\ldots ,n\}\), \({\mathbf {G}}^\prime _i\) is a homomorphic image of \({\mathbf {H}}_i\), see (11). Therefore, \({\mathbf {G}}^\prime _i\) is finitely generated, too, since being finitely generated inherits to homomorphic images. \(\square \)
Our next aim is to make things simpler. The next proposition states that every finitely generated odd involutive FL\(_e\)-chain embeds into an odd involutive FL\(_e\)-chain, which has a group representation as in Proposition 2 with the additional specificity that instead of the partial sublex product construction, only the simpler partial lex product construction is used in the iterative steps.
Proposition 3
Any finitely generated odd involutive FL\(_e\)-chain \({\mathbf {Y}}\) is embeddable into a finitely generated odd involutive FL\(_e\)-chain \({\mathbf {X}}\) which has a partial lex product representation in which all the algebras are finitely generated.
Proof
Let \({\mathbf {Y}}\) be a finitely generated odd involutive FL\(_e\)-chain. Then \({\mathbf {Y}}\) has a partial sublex product representation by Proposition 2, see it in (12), such that all the algebras employed are finitely generated. Also (13) holds. Let

Clearly, all the algebras employed in (14) are finitely generated because they are all inherited from (12).
To see that the \({\mathbf {X}}_i\)’s are well-defined, we need to verify that
The first one is immediate since \( {\mathbf {Z}}_1 \overset{(13)}{\le } {\mathbf {H}}_1 = ({\mathbf {H}}_1)_{\mathbf {gr}} \overset{(14)}{=} ({\mathbf {X}}_1)_{\mathbf {gr}} \) and for \(i\in \{3,\ldots ,n\}\) \(({\mathbf {X}}_{i-1})_{\mathbf {gr}}={\mathbf {Z}}_{i-2}\overset{\rightarrow }{\times }{\mathbf {G}}^\prime _{i-1}\) holds by (14) and Remark 5, yielding \( {\mathbf {Z}}_{i-1} \overset{(13)}{\le } {\mathbf {H}}_{i-1} \overset{(13)}{\le } {\mathbf {Z}}_{i-2}\overset{\rightarrow }{\times }{\mathbf {G}}^\prime _{i-1} = ({\mathbf {X}}_{i-1})_{\mathbf {gr}} \).
As for the second row of (15), if \(\iota _2=II\) then \( ({\mathbf {X}}_1)_{\mathbf {gr}} = {\mathbf {H}}_1 \) is discretely embedded into \({\mathbf {Y}}_1\) by (13), and \({\mathbf {Y}}_1={\mathbf {X}}_1\) by the construction. Let \(\iota _i=II\) for some \(i\in \{3,\ldots ,n\}\). Then, since \(i\ge 3\),
holds by Remark 5. Now, \({\mathbf {G}}^\prime _{i-1}\) is a finitely generated totally ordered abelian group by Proposition 2, and such groups are known to be either trivial, or discrete and hence discretely ordered. First we prove that for \(i\in \{3,\ldots ,n\}\), \({\mathbf {G}}^\prime _{i-1}\) cannot be trivial. Since \(\iota _i=II\), by (13) it holds that \(H_{i-1}\) is discretely embedded into

see Definition 1. However, it cannot be that case if \({\mathbf {G}}^\prime _{i-1}\) is trivial, since then the cover of \((a,1)\in H_{i-1}\)Footnote 2 in \(Y_{i-1}\) would be \((a,\top )\), and \((a,\top )\) is not an element of \(H_{i-1}\) since \((a,\top )\) is not invertible. This contradiction shows that for \(i\in \{3,\ldots ,n\}\), \({\mathbf {G}}^\prime _{i-1}\) is discretely ordered. We claim that \({X_{i-1}}_{gr}\) is discretely embedded into \(X_{i-1}\). Since \(i\ge 3\),

For any element (a, g) in \({X_{i-1}}_{gr}\) its second coordinate g is an element of \(G^\prime _{i-1}\) by (16), and since \(G^\prime _{i-1}\) is discretely ordered, the upper neighbor s of g exists in \(G^\prime _{i-1}\), hence (a, s), which is the upper cover of (a, g) in \(X_{i-1}\) by (18), is in \({X_{i-1}}_{gr}\), too. An analogous argument works for the lower cover of (a, g). The proof of the second row of (15) is concluded.
We claim that for \(i\in \{1,\ldots ,n\}\), \({\mathbf {Y}}_i \le {\mathbf {X}}_i\) holds. Indeed, the claim being straightforward for \(i=1\), assume \({\mathbf {Y}}_{i-1} \le {\mathbf {X}}_{i-1}\) for some \(i\in \{2,\ldots ,n\}\). It follows that

compare the respective rows of (17) and (18). Therefore,

In particular, we have confirmed \({\mathbf {Y}}\cong {\mathbf {Y}}_n\le {\mathbf {X}}_n={\mathbf {X}}\). \(\square \)
Thanks to Proposition 3, in the rest of the paper it will be sufficient to work with partial lex products only. For this simpler construction a simpler notation will come handy in formulating the following three lemmas. Henceforth we shall denote  by
by  , and
, and  by
by  . The first two assert associativity-like properties for partial lex product extensions. First we recall from [10] that two (and thus also finitely many) consecutive type II partial lex extensions can be replaced by a single type II partial lex extension, see Lemma 4, and that a type I partial lex extension followed by a type II partial lex extension can be replaced by a single type I partial lex extension, see Lemma 5.
. The first two assert associativity-like properties for partial lex product extensions. First we recall from [10] that two (and thus also finitely many) consecutive type II partial lex extensions can be replaced by a single type II partial lex extension, see Lemma 4, and that a type I partial lex extension followed by a type II partial lex extension can be replaced by a single type I partial lex extension, see Lemma 5.
Lemma 4
([10, Lemma 1]) For any odd involutive FL\(_e\)-algebras \({\mathbf {A}}\), \({\mathbf {B}}\), \({\mathbf {C}}\), it holds true that

that is, if the algebra on one side is well-defined then the algebra on the other side is well-defined, too, and the two algebras are isomorphic. \(\square \)
Lemma 5
([10, Lemma 2]) For any odd involutive FL\(_e\)-algebras \({\mathbf {A}}\), \({\mathbf {Z}}\), \({\mathbf {L}}\), \({\mathbf {B}}\) it holds true that

that is, if the algebra on one side is well-defined then the algebra on the other side is well-defined, too, and the two algebras are isomorphic. \(\square \)
The last lemma here is about the preservation of the ‘order isomorphic to \({\mathbb {R}}\)’ property.
Lemma 6
([10, Lemma 4]) Let \({\mathbf {A}}\) and \({\mathbf {D}}\) be odd involutive FL\(_e\)-chains which are order isomorphic to \({\mathbb {R}}\), \({\mathbf {Z}}\le {\mathbf {A}}_\mathbf {gr}\), \({\mathbf {Z}}\) is countable. Then  is order isomorphic to \({\mathbb {R}}\). \(\square \)
is order isomorphic to \({\mathbb {R}}\). \(\square \)
It is well-known that among all totally ordered abelian groups up to isomorphism only the subgroups of \({\mathbb {R}}\) (\({\mathbb {R}}\), \({\mathbb {Q}}\), \({\mathbb {Z}}\), and \(\mathbbm {1}\))Footnote 3 can be embedded qua totally ordered abelian groups into \({\mathbb {R}}\). However, since all totally ordered abelian groups are particular instances of odd involutive FL\(_e\)-chains, we have to be able to embed all finitely generated totally ordered abelian groups into \({\mathbb {R}}\). Surprisingly, it is possible qua odd involutive FL\(_e\)-algebras, and it is because we are not confined to use the usual addition of the real numbers. To this end in (21), we define three series of odd involutive FL\(_e\)-chains and first state some basic properties of them.
Definition 2
For \(j\in {\mathbb {N}}\), \(j\ge 1\), let

We shall denote the universes of \({\mathbb {Z}}_j\), \({\mathbb {Q}}_j\), and \({\mathbb {R}}_j\) by \({\mathbb {Z}}_j\), \({\mathbb {Q}}_j\), and \({\mathbb {R}}_j\), respectively, and for \(j\ge 2\) we denote the new top element to be added here (according to Definition 1/B) to \({\mathbb {Z}}_j\) (or \({\mathbb {Q}}_j\) or \({\mathbb {R}}_j\)) by \(\underbrace{\top \times \ldots \times \top }_j\).Footnote 4
Proposition 4
The following statements hold true.
-
(a)
For \(j\ge 2\), \({\mathbb {Z}}_j=\{ (x_1,\ldots ,x_j)\in {\mathbb {Z}}\times \underbrace{({\mathbb {Z}}\cup \{\top \})\times \ldots \times ({\mathbb {Z}}\cup \{\top \})}_{j-1} \ |\) if \(x_i=\top \) for some
\(i\in \{2,\ldots ,j\}\) then for all \(i\le l\le j\), \(x_l=\top \}\),
\({\mathbb {Q}}_j=\{ (x_1,\ldots ,x_j)\in {\mathbb {Z}}\times \underbrace{({\mathbb {Z}}\cup \{\top \})\times \ldots \times ({\mathbb {Z}}\cup \{\top \})}_{j-2}\times ({\mathbb {Q}}\cup \{\top \}) \ |\) if \(x_i=\top \) for some
\(i\in \{2,\ldots ,j\}\) then for all \(i\le l\le j\), \(x_l=\top \}\),
\({\mathbb {R}}_j=\{ (x_1,\ldots ,x_j)\in {\mathbb {Z}}\times \underbrace{({\mathbb {Z}}\cup \{\top \})\times \ldots \times ({\mathbb {Z}}\cup \{\top \})}_{j-2}\times ({\mathbb {R}}\cup \{\top \}) \ |\) if \(x_i=\top \) for some
\(i\in \{2,\ldots ,j\}\) then for all \(i\le l\le j\), \(x_l=\top \}\).
-
(b)
For \(j\ge 1\), \(({\mathbb {Z}}_j)_\mathbf {gr}=\underbrace{{\mathbb {Z}}\overset{\rightarrow }{\times }\ldots \overset{\rightarrow }{\times }{\mathbb {Z}}}_{j}\), \(({\mathbb {Q}}_j)_\mathbf {gr}=\underbrace{{\mathbb {Z}}\overset{\rightarrow }{\times }\ldots \overset{\rightarrow }{\times }{\mathbb {Z}}}_{j-1}\overset{\rightarrow }{\times }{\mathbb {Q}}\), \(({\mathbb {R}}_j)_\mathbf {gr}=\underbrace{{\mathbb {Z}}\overset{\rightarrow }{\times }\ldots \overset{\rightarrow }{\times }{\mathbb {Z}}}_{j-1}\overset{\rightarrow }{\times }{\mathbb {R}}\).
-
(c)
For \(j\in {\mathbb {N}}\), \(({\mathbb {Z}}_j)_\mathbf {gr}\) is discretely embedded into \({\mathbb {Z}}_j\), and for any \(x\in {\mathbb {Z}}_j{\setminus } ({\mathbb {Z}}_j)_\mathbf {gr}\) and \(x\ne y\in {\mathbb {Z}}_j\), there exists \(z\in ({\mathbb {Z}}_j)_\mathbf {gr}\) such that z is strictly in between x and y.
-
(d)
For \(j\in {\mathbb {N}}\), \({\mathbb {Z}}_j\) and \({\mathbb {Q}}_j\) are countable.
-
(e)
For \(j\in {\mathbb {N}}\), \({\mathbb {Z}}_j\), \({\mathbb {Q}}_j\), and \({\mathbb {R}}_j\) have no least neither greatest element.
-
(f)
For \(j,k\ge 1\),
 and
and  .
. -
(g)
For \(j\in {\mathbb {N}}\), \({\mathbb {Z}}_j\) and \({\mathbb {R}}_j\) are Dedekind complete.
-
(h)
For \(j\in {\mathbb {N}}\), \({\mathbb {R}}_j\) is order isomorphic to \({\mathbb {R}}\).
Proof
-
(a)
We shall present the proof only for, e.g., \({\mathbb {R}}_j\) since the proof is analogous for \({\mathbb {Q}}_j\) and \({\mathbb {Z}}_j\). \({\mathbb {R}}_2\) is equal to \({\mathbb {Z}}\times ({\mathbb {R}} \cup \{\top \})\) by the first row of (7), hence the statement holds for \(j=2\). Let \(j\ge 3\) and assume that the statement holds for \(j-1\). By the first row of (7) we obtain \({\mathbb {R}}_j= {\mathbb {Z}}\times ({\mathbb {R}}_{j-1})\cup ({\mathbb {Z}}\times \{\ \underbrace{\top \times \ldots \times \top }_{j-1} \}) \), which is clearly equal, using the induction hypothesis, to the set stated in (a).
-
(b)
is obvious for \(j=1\), and follows from (a) for \(j\ge 2\) since \(\top \) is an annihilating element in the respective coordinate(s), and hence an element with a \(\top \) coordinate it is never invertible.
-
(c)
is obvious for \(j=0,1\), and it follows in a straightforward manner for \(j\ge 2\) from (a) and (b) using that \({\mathbb {Z}}\) is unbounded.
-
(d)
readily follows from (a) since \({\mathbb {Z}}\) and \({\mathbb {Q}}\) are countable.
-
(e)
readily follows from (a) since \({\mathbb {Z}}\) is unbounded.
-
(f)
readily follows from Lemma 4.
-
(g)
Dedekind completeness easily follows from (a), too: The statement clearly holds for \(j=0,1\) since \({\mathbb {Z}}\) and \({\mathbb {R}}\) are Dedekind complete. Let \(j\ge 2\) and assume that the statement holds for \(j-1\), that is, \({\mathbb {Z}}_{j-1}\) and \({\mathbb {R}}_{j-1}\) are Dedekind complete. Let a subset X of \({\mathbb {R}}_j\) (the proof for \({\mathbb {Z}}_j\) is analogous) with an upper bound \(m=(m_1,m_2)\) be given where \(m_1\in {\mathbb {Z}}\). Since the ordering on \({\mathbb {R}}_j\) is lexicographical, \(m_1\) must be an upper bound of \(X_1=\{x_1\in {\mathbb {Z}} : (x_1,x_2)\in X\}\), ensuring the existence of the supremum \(z_1\) of \(X_1\) since \({\mathbb {Z}}\) is Dedekind complete. In fact then \(z_1\) is the greatest element of \(X_1\) since if a subset of \({\mathbb {Z}}\) has a supremum then its supremum is necessarily its greatest element. If \((z_1, \top ,\ldots ,\top )\) is an element of X then it is clearly the maximal element of X and we are done. If not then, referring to (a), for every \((z_1,x_2)\in X\), the first coordinate of \(x_2\) must be in \({\mathbb {Z}}\), and hence \(x_2\in {\mathbb {R}}_{j-1}\). Therefore, the set \(X_2=\{ x_2\in {\mathbb {R}}_{j-1} : (z_1,x_2)\in X\}\) is nonempty. If the first coordinates of the elements of \(X_2\) are unbounded from above then \((z_1, \top ,\ldots ,\top )\) is clearly the maximal element of X and we are done, whereas if the first coordinates of the elements of \(X_2\) are bounded from above, say by a, then \((a, \underbrace{\top ,\ldots ,\top }_{j-2})\in {\mathbb {R}}_{j-1}\) is an upper bound of \(X_2\). Then, by the induction hypothesis, there exists a supremum \(z_2\) of \(X_2\) in \({\mathbb {R}}_{j-1}\), and hence \((z_1,z_2)\) is clearly the supremum of X, so the proof of (g) is concluded.
-
(h)
Finally, to prove (h), because of Lemma 3, in addition to (e) and (g) we only need to prove that \({\mathbb {R}}_j\) is densely ordered, and that \({\mathbb {Q}}_j\) is a dense subset of \({\mathbb {R}}_j\); both are obvious from (a). \(\square \)
Remark 6
If \({\mathbb {G}}\) is a finitely generated totally ordered abelian group then \({\mathbb {G}}\) embeds (qua an ordered abelian group) into \({\mathbb {Z}}^n:={\mathbb {Z}}\overset{\rightarrow }{\times }\ldots \overset{\rightarrow }{\times }{\mathbb {Z}}\) (n-times) for some positive integer n. Indeed, since the divisible closure of \({\mathbb {G}}\) is a finite dimensional rational vector space, \({\mathbb {G}}\) has only a finite number (say n) of convex subgroups. Therefore, by Hahn’s Theorem, \({\mathbb {G}}\) can be embedded (qua an ordered abelian group) into \({\mathbb {R}}^n:={\mathbb {R}}\overset{\rightarrow }{\times }\ldots \overset{\rightarrow }{\times }{\mathbb {R}}\) (n-times). Since \({\mathbb {G}}\) is finitely generated, so is every (group-)homomorphic image of \({\mathbb {G}}\). Therefore each canonical projection (to the \(i^{th}\) coordinate, \(i=1,\ldots ,n\)) of \({\mathbb {G}}\), is a finitely generated subgroup of \({\mathbb {R}}\), and hence it is either trivial (in which case that index could have been omitted from the Hahn-product \({\mathbb {R}}^n\)) or it is isomorphic to \({\mathbb {Z}}\). Clearly, \({\mathbb {G}}\) is a subalgebra of the lexicographic product of its canonical projections, and so \({\mathbb {G}}\) embeds into \({\mathbb {Z}}^n\), as stated.
We are ready to prove the main result of the paper.
Theorem 2
\(\mathbf {IUL}^{fp}\) enjoys finite strong standard completeness.
Proof
Let \({\mathbf {Y}}_1\) be a non-trivial finitely generated bounded odd involutive FL\(_e\)-chain. Hence it has at least three elements. Our plan is to embed \({\mathbf {Y}}_1\), guided by its group representation, into an odd involutive FL\(_e\)-chain over [0, 1]. As shown in [11, Proposition 5.3.], odd involutive FL\(_e\)-chains are diagonally strictly increasing, that is, \(x_1<x\) and \(y_1<y\) imply  . Therefore the \(\top \) and the \(\bot \) of \({\mathbf {Y}}_1\) cannot arise as products of other elements (ones in between \(\bot \) and \(\top \)). The corresponding statement is obvious for the minimum, the maximum, and the residual complement operations, and hence also for the residual operation due to
. Therefore the \(\top \) and the \(\bot \) of \({\mathbf {Y}}_1\) cannot arise as products of other elements (ones in between \(\bot \) and \(\top \)). The corresponding statement is obvious for the minimum, the maximum, and the residual complement operations, and hence also for the residual operation due to  . Therefore, there is a subalgebra \({\mathbf {Y}}\) over the universe of \({\mathbf {Y}}_1\) deprived its top and bottom elements. Since in every bounded odd involutive FL\(_e\)-algebra its bottom element is the zero element, and its top element acts like a zero element for all elements except the bottom one, it follows that also \({\mathbf {Y}}\) is a finitely generated (not necessarily bounded) odd involutive FL\(_e\)-chain. We shall embed \({\mathbf {Y}}\), guided by its group representation, into an odd involutive FL\(_e\)-chain \({\mathbf {X}}^*\) over a universe which is order isomorphic to \({\mathbb {R}}\). Then, using the order isomorphism together with an order isomorphism between \({\mathbb {R}}\) and ]0, 1[, we can carry over the structure of \({\mathbf {X}}^*\) into ]0, 1[, and finally we can add a top and a bottom element (as in item A in Definition 1) to get an odd involutive FL\(_e\)-chain over [0, 1], in which \({\mathbf {Y}}_1\) embeds.Footnote 5
. Therefore, there is a subalgebra \({\mathbf {Y}}\) over the universe of \({\mathbf {Y}}_1\) deprived its top and bottom elements. Since in every bounded odd involutive FL\(_e\)-algebra its bottom element is the zero element, and its top element acts like a zero element for all elements except the bottom one, it follows that also \({\mathbf {Y}}\) is a finitely generated (not necessarily bounded) odd involutive FL\(_e\)-chain. We shall embed \({\mathbf {Y}}\), guided by its group representation, into an odd involutive FL\(_e\)-chain \({\mathbf {X}}^*\) over a universe which is order isomorphic to \({\mathbb {R}}\). Then, using the order isomorphism together with an order isomorphism between \({\mathbb {R}}\) and ]0, 1[, we can carry over the structure of \({\mathbf {X}}^*\) into ]0, 1[, and finally we can add a top and a bottom element (as in item A in Definition 1) to get an odd involutive FL\(_e\)-chain over [0, 1], in which \({\mathbf {Y}}_1\) embeds.Footnote 5
Since \({\mathbf {Y}}\) is finitely generated, by Proposition 3, \({\mathbf {Y}}\) embeds into an odd involutive FL\(_e\)-chain \({\mathbf {X}}\) which has a partial lex product representation in which all the employed algebras are finitely generated, see it in (14). In particular,
and all groups \({\mathbf {H}}_1\), \({\mathbf {G}}^\prime _i\) \((i=2,\ldots ,n)\) are finitely generated. By Remark 6, \( {\mathbf {H}}_1 \hookrightarrow {\mathbb {Z}}^{k_1} \) holds for some positive integer \(k_1\), and for \(i\in \{2,\ldots ,n\}\), \( {\mathbf {G}}^\prime _i \hookrightarrow {\mathbb {Z}}^{k_i} \) holds for some positive integer \(k_i\). So \({\mathbf {H}}_1\) and the \({\mathbf {G}}^\prime _i\)’s are countable, and unless equal to the one-element group, they are discretely ordered. The embedding naturally extends to an embedding between the induced odd involutive FL\(_e\)-chains. Referring to claims (b) and (a) in Proposition 4, for \(i\in \{2,\ldots , n\}\), qua odd involutive FL\(_e\)-chains,
Now, we are ready to define the embedding of
We shall inherit the types of the extensions (the \(\iota \) values) and the enlarged parts (the \({\mathbf {Z}}_i\)’s) from the representation of \({\mathbf {X}}\) in (14), meanwhile we enlarge the other algebras corresponding to each iterative step in a subtle way: the definition of \({\mathbf {X}}^*_i\) will depend not only on \(\iota _i\) but also on \(\iota _{i+1}\); \(\iota _i\) will determine the type of the extension and \(\iota _{i+1}\) will determine the enlarging algebraFootnote 6. Formally, for \(i\in \{1,\ldots ,n\}\) let

and let \({\mathbf {X}}^*={\mathbf {X}}^*_n\). We shall prove by induction that for \(1\le i\le n\), \({\mathbf {X}}^*_i\) is well-defined, \({\mathbf {X}}_i\) embeds into \({\mathbf {X}}^*_i\), and \({\mathbf {X}}^*_n\) is order isomorphic to \({\mathbb {R}}\), thus concluding the proof of the theorem.
The statement holds if \(n=1\): \({\mathbf {X}}_1\overset{(14)}{=}{\mathbf {H}}_1\overset{(21)}{\hookrightarrow }{\mathbb {R}}_{k_1}\overset{(22)}{=}{\mathbf {X}}^*_1\), and \({\mathbb {R}}_{k_1}\) is order isomorphic to \({\mathbb {R}}\) by claim (h) in Proposition 4. Hence in the sequel we assume \(n>1\).
Claim 1
First we claim that for \(i\in \{1,\ldots ,n\}\), \({\mathbf {X}}^*_i\) is well-defined and \({\mathbf {X}}_i\) embeds into \({\mathbf {X}}_i^*\).
-
(i)
The statement holds for \(i=1\): \({\mathbf {X}}_1\overset{(14)}{=}{\mathbf {H}}_1\) embeds into \({\mathbf {X}}^*_1\) by (21) since \({\mathbf {X}}^*_1\) is equal to either \({\mathbb {Z}}_{k_1}\) or \({\mathbb {R}}_{k_1}\) by (22). Induction hypothesis: assume that for some \(i\in \{2,\ldots ,n\}\), \({\mathbf {X}}^*_{i-1}\) exists and \({\mathbf {X}}_{i-1}\) embeds into \({\mathbf {X}}_{i-1}^*\).
-
Assume \(\iota _i=I\). To see that \({\mathbf {X}}_i^*\) is well-defined, we need to verify that \({\mathbf {Z}}_{i-1}\) is a subalgebra of the group part of \({\mathbf {X}}^*_{i-1}\), see the third and fifth rows of (22). It readily follows since \({\mathbf {Z}}_{i-1}\) is a subalgebra of the group part of \({\mathbf {X}}_{i-1}\) by (14), and \({\mathbf {X}}_{i-1}\) embeds into \({\mathbf {X}}^*_{i-1}\) by the induction hypothesis (hence the group part of \({\mathbf {X}}_{i-1}\) clearly embeds into the group part of \({\mathbf {X}}^*_{i-1}\) since \({\mathbf {X}}_{i-1}\) and \({\mathbf {X}}^*_{i-1}\) share the same unit element and therefore the invertible elements in \(X_{i-1}\) are also invertible in \(X^*_{i-1}\)).
Next we show that \({\mathbf {X}}_i\) embeds into \({\mathbf {X}}^*_i\). Since \(i\ne 1\), by (14) and (22)

Here, in each row the algebra on the left is embeddable into the algebra on the right. Indeed, by the first row of (3), the universes of
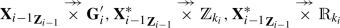
are
$$\begin{aligned} \begin{array}{c} (Z_{i-1}\times G^\prime _i)\cup (Z_{i-1}\times \{\top \}) \cup \left( X_{i-1}\times \{\bot \}\right) , \\ (Z_{i-1}\times {\mathbb {Z}}_{k_i})\cup (Z_{i-1}\times \{\top \}) \cup \left( X^*_{i-1}\times \{\bot \}\right) , \\ (Z_{i-1}\times {\mathbb {R}}_{k_i})\cup (Z_{i-1}\times \{\top \}) \cup \left( X^*_{i-1}\times \{\bot \}\right) , \end{array} \end{aligned}$$respectively, and \({\mathbf {X}}_{i-1}\) embeds into \({\mathbf {X}}^*_{i-1}\) by the induction hypothesis and \({\mathbf {G}}^\prime _i\) embeds into \({\mathbb {Z}}_{k_i}\) and into \({\mathbb {R}}_{k_i}\) by (21). Therefore, \(X_i\hookrightarrow X^*_i\) holds, and the coordinatewise definition of the multiplication and the residual complement operation in Definition 1 shows that all the operations of \({\mathbf {X}}^*_i\) are extensions of the corresponding operations of \({\mathbf {X}}_i\). As noted before, the unit element of \({\mathbf {X}}^*_i\) is the same as the unit element of \({\mathbf {X}}_i\).
-
Assume \(\iota _i=II\). To see that \({\mathbf {X}}_i^*\) is well-defined, we need to verify that \((X_{i-1}^*)_{gr}\) is discretely embedded into \(X_{i-1}^*\), see the forth and sixth rows of (22).
If \(i=2<n\) then \({\mathbf {X}}_1^*={\mathbb {Z}}_{k_1}\) by the second row of (22), and \(({\mathbb {Z}}_{k_1})_{gr}\) is discretely embedded into \({\mathbb {Z}}_{k_1}\) by claim (c) of Proposition 4. If, for \(i\in \{3,\ldots ,n\}\), \(\iota _i=II\) then by (22), \({\mathbf {X}}_{i-1}^*\) is equal to either
 (if \(\iota _{i-1}=I\), see the third row) and then
(if \(\iota _{i-1}=I\), see the third row) and then 
or
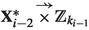 (if \(\iota _{i-1}=II\), see the forth row) and then
(if \(\iota _{i-1}=II\), see the forth row) and then 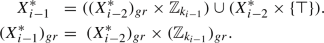
In both cases \((X_{i-1}^*)_{gr}\) is clearly discretely embedded into \(X_{i-1}^*\) since \(({\mathbb {Z}}_{k_{i-1}})_{gr}\) is discretely embedded into \({\mathbb {Z}}_{k_{i-1}}\) by item (c) in Proposition 4.
-
Next we show that \({\mathbf {X}}_i\) embeds into \({\mathbf {X}}^*_i\). Since \(i\ne 1\), by (14) and (22)

Here, in each row the algebra on the left is embeddable into the algebra on the right. Indeed, by the first row of (7), the universes of

are
respectively, and \({\mathbf {X}}_{i-1}\) embeds into \({\mathbf {X}}^*_{i-1}\) by the induction hypothesis and \({\mathbf {G}}^\prime _i\) embeds into \({\mathbb {Z}}_{k_i}\) and into \({\mathbb {R}}_{k_i}\) by (21). Therefore, \(X_i\hookrightarrow X^*_i\) holds, and the coordinatewise definition of the multiplication and the residual complement operation in Definition 1 shows that all the operations of \({\mathbf {X}}^*_i\) are extensions of the corresponding operations of \({\mathbf {X}}_i\). As noted before, the unit element of \({\mathbf {X}}^*_i\) is the same as the unit element of \({\mathbf {X}}_i\).
Claim 2
Finally, we prove that \({\mathbf {X}}^*_n\) is order isomorphic to \({\mathbb {R}}\). Let
Since \(n\in M\), to conclude, it suffices to prove that for \(m\in M\), \({\mathbf {X}}_m^*\) is order-isomorphic to \({\mathbb {R}}\). We proceed by induction.
Let m be the least element of M. If \(m=1\) then either \(n\ge 2\) and \(\iota _2=I\) or \(m=n=1\). In both cases, \({\mathbf {X}}^*_1={\mathbb {R}}_{k_1}\) by the first row of (22), and \({\mathbb {R}}_{k_1}\) is order isomorphic to \({\mathbb {R}}\) by claim (h) in Proposition 4. If \(m>1\) then for all \(1<i\le m\) it holds true that \(\iota _i=II\), and either \(m<n\) and \(\iota _{m+1}=I\) or \(m=n\). In both cases  holds using the second row, then iteratively the forth row, and finally the last row of (22). Now,
holds using the second row, then iteratively the forth row, and finally the last row of (22). Now,  by Lemma 4 and claim (f) in Proposition 4, and hence \({\mathbf {X}}^*_m\) is order isomorphic to \({\mathbb {R}}\) by claim (h) in Proposition 4, as stated.
by Lemma 4 and claim (f) in Proposition 4, and hence \({\mathbf {X}}^*_m\) is order isomorphic to \({\mathbb {R}}\) by claim (h) in Proposition 4, as stated.
Induction hypothesis: Assume that for \(m\in M{\setminus }\{n\}\), \({\mathbf {X}}_m^*\) is order-isomorphic to \({\mathbf {R}}\), and let \(r=\min \{ i\in M \ | \ i>m\}\) be the next element of M (it exists since \(m\ne n\)). Then \(r\ge 2\).
-
If \(r=m+1\) then either \(\iota _{r+1}=I\) or \(r=n\), and since \(m\in M{\setminus }\{n\}\), \(\iota _{m+1}=\iota _r=I\) holds. Hence the fifth row of (22) applies yielding
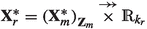 . Here, \({\mathbf {X}}_m^*\) and \({\mathbb {R}}_{k_r}\) are order isomorphic to \({\mathbb {R}}\) by the induction hypothesis and by claim (h) in Proposition 4, respectively, and \({\mathbf {Z}}_m\) is countable by (20). Therefore, Lemma 6 can be applied, which yields that \({\mathbf {X}}_r^*\) is order isomorphic to \({\mathbb {R}}\).
. Here, \({\mathbf {X}}_m^*\) and \({\mathbb {R}}_{k_r}\) are order isomorphic to \({\mathbb {R}}\) by the induction hypothesis and by claim (h) in Proposition 4, respectively, and \({\mathbf {Z}}_m\) is countable by (20). Therefore, Lemma 6 can be applied, which yields that \({\mathbf {X}}_r^*\) is order isomorphic to \({\mathbb {R}}\). -
If \(r>m+1\) then \(\iota _m=I\) and for all \(m<i\le r\) it holds true that \(\iota _i=II\), and either \(r<n\) and \(\iota _{r+1}=I\) or \(r=n\). In both cases, using the third row, then (iteratively if \(r>m+2\)) the forth row, and finally the last row of (22),

holds. By applying Lemmas 4 and 5 consecutively, it is isomorphic to

which is isomorphic to

by claim (f) in Proposition 4. Here, \({\mathbf {X}}_m^*\) and \({\mathbb {R}}_{k_{m+1}+\ldots +k_r}\) are order isomorphic to \({\mathbb {R}}\) by the induction hypothesis and by claim (h) in Proposition 4, respectively, and \({\mathbf {Z}}_m\) is countable by (20). Therefore, Lemma 6 can be applied, which yields that \({\mathbf {X}}_r^*\) is order isomorphic to \({\mathbb {R}}\). \(\square \)
4 Conclusion
Substructural logics without the weakening rule are far less understood than substructural logics with it. In this paper a first example of a standard completeness proof of such a logic (\({\mathbf {IUL}^{fp}}\)) is presented. The proof is algebraic and is based on a construction of an embedding which, in turn, is based on the algebraic description of the related variety in [9, 11].
Notes
See the remark of the author himself in [18, second section in page 43].
Here \(a\in Z_{i-2}\) and 1 denotes the single element of \({\mathbf {G}}^\prime _{i-1}\), c.f. the first line of (13).
By abuse of notation, in the sequel we will use the symbols \({\mathbb {R}}\), \({\mathbb {Q}}\), \({\mathbb {Z}}\) for the totally ordered abelian groups, for the induced odd FL\(_e\)-algebras, for their universes, and also for the respective totally ordered sets.
According to Definition 1/B the added new top element is denoted by \(\top \). Strictly speaking here we consider an isomorphic structure when adding \(\underbrace{\top \times \ldots \times \top }_j\) to be that new top element. We do so in order to keep the “ length” of all elements inside a given algebra \({\mathbb {Z}}_j\), \({\mathbb {Q}}_j\) or \({\mathbb {R}}_j\) the same.
We shall work with \({\mathbf {Y}}\) rather than with \({\mathbf {Y}}_1\) because we do not want to bother with the embedding of the top and bottom elements throughout each step of the proof.
Intuitively, this is because if the coming extension is type II then we need to ensure that the group part of the algebra to be extended is discretely embedded in the algebra, whereas if the coming extension is not type II then we do not have such confinements, and hence in the preceeding extension we want to get as close to the topological structure of \({\mathbb {R}}\) as possible.
References
Běhounek, L., Cintula, P., Hájek, P.: Introduction to Mathematical Fuzzy Logic. In P. Cintula, P. Hájek, C. Noguera, editors, Handbook of Mathematical Fuzzy Logic - Volume 1, volume 37 of Studies in Logic, Mathematical Logic and Foundations, pp. 1–101, College Publication, (2011)
Bukovský, L.: The Structure of the Real Line, p. 452. Springer Science & Business Media, Berlin (2011)
Casari, E.: Comparative logics and Abelian \(\ell \)-groups. In: Ferro, R., et al. (eds.) Logic Colloquium 88, pp. 161–190. North Holland, Amsterdam (1989)
Cintula, P., Hájek, P., Noguera, C., (eds.): Handbook of Mathematical Fuzzy Logic I-III, pp. 1356, College Publications, London (2011)
Fuchs, L.: Infinite Abelian Groups, Volume 1, Volume 36-I, Academic Press, pp. 290 (1970)
Gabbay, D., Metcalfe, G., Olivetti, N.: Proof Theory for Fuzzy Logics, p. 276. Springer, Netherlands (2008)
Galatos, N., Raftery, J.G.: A category equivalence for odd Sugihara monoids and its applications. J. Pure Appl. Algebra 216, 2177–2192 (2012)
Hájek, P.: Metamathematics of Fuzzy Logic. Kluwer Academic Publishers, Dordrecht (1998)
Jenei, S.: Correction to: The Hahn embedding theorem for a class of residuated semigroups. Stud. Logica. 109, 887–901 (2021) [Stud. Logica. 110, 923–924 (2022)]
Jenei, S.: Group-like Uninorms. Int. J. Comput. Intelligence Syst. 13(1), 954–965 (2020)
Jenei, S.: The Hahn embedding theorem for a class of residuated semigroups. Stud. Logica. 108, 1161–1206 (2020)
Jenei, S.: On the structure of rotation-invariant semigroups. Arch. Math. Logic 42, 489–514 (2003)
Jenei, S., Montagna, F.: A proof of standard completeness of Esteva and Godo’s logic MTL. Stud. Logica. 70, 184–192 (2002)
Metcalfe, G.: Proof Theory for Propositional Fuzzy Logics. PhD thesis, King’s College London (2003)
Metcalfe, G., Montagna, F.: Substructural fuzzy logics. J. Symb. Log. 72, 834–864 (2007)
Meyer, R.K., Slaney, J.K.: Abelian logic (from A to Z). In: Routley, R., et al. (eds.) Paraconsistent Logic: Essays on the Inconsistent, pp. 245–288. Philosophia, Munich (1989)
Paoli, F., Spinks, M., Veroff, R.: Abelian Logic and the Logics of Pointed Lattice-Ordered Varieties. Log. Univers. 2(2), 209–233 (2008)
Wang, S.M.: A Proof of the Standard Completeness for the Involutive Uninorm Logic. Symmetry 11(4), 445 (2019)
Funding
Open access funding provided by University of Pécs.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The present scientific contribution was supported by the GINOP 2.3.2-15-2016-00022 grant and the Higher Education Institutional Excellence Programme 20765-3/2018/FEKUTSTRAT of the Ministry of Human Capacities in Hungary.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jenei, S. Involutive Uninorm Logic with Fixed Point enjoys finite strong standard completeness. Arch. Math. Logic 62, 67–86 (2023). https://doi.org/10.1007/s00153-022-00839-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00153-022-00839-1





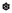 ,
,  and
and  ,
,  .
.

 is defined coordinatewise,
is defined coordinatewise,  is (provisionally) the residual operation of
is (provisionally) the residual operation of 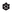 , and the residual complement operation
, and the residual complement operation 
 the type I partial lexicographic extension (lex extension, for short) of
the type I partial lexicographic extension (lex extension, for short) of 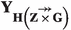 the type I partial sublex extension of
the type I partial sublex extension of  and
and  the arrow above the
the arrow above the 

 is defined coordinatewise,
is defined coordinatewise,  is (provisionally) the residual operation of
is (provisionally) the residual operation of 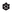 , and the residual complement operation
, and the residual complement operation 
 the type II partial lex extension of
the type II partial lex extension of  the type II partial sublex extension of
the type II partial sublex extension of  and
and 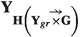 the arrow above the
the arrow above the  and
and  .
.
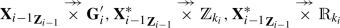
 (if
(if 
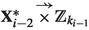 (if
(if 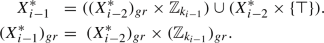
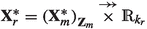 . Here,
. Here, 

