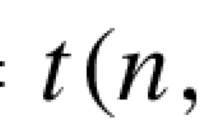Abstract
In this note we show that proof-theoretic uniform boundedness or bounded collection principles which allow one to formalize certain instances of countable Heine–Borel compactness in proofs using abstract metric structures must be carefully distinguished from an unrestricted use of countable Heine–Borel compactness.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In [11] we introduced formal theories of classical analysis (formulated in the language of functionals of finite types) augmented with abstract metric and normed structures X giving rise to systems \(\mathcal{{A}}^{\omega }[X,d], \mathcal{{A}}^{\omega }[X,d,W]\) and \(\mathcal{{A}}^{\omega }[X,\Vert \cdot \Vert ,C], \mathcal{{A}}^{\omega }[X,\langle \cdot ,\cdot \rangle ,C]\) treating abstract bounded metric spaces (X, d) or bounded W-hyperbolic spaces (X, d, W) or bounded convex subsets \(C\subseteq X\) of normed linear or inner product spaces \((X,\Vert \cdot \Vert ).\) These structures are added as a kind of atoms using a new base type X for objects in X rather than stipulating X to be separable and explicitly represented as the completion of a countable structure. This lack of any separability assumptions makes it possible to extract uniform bounds which only depend on a bound on the metric rather than requiring any compactness assumption. In [7], this approach is extended to unbounded metric structures and unbounded convex subsets of normed spaces using an extension of the Howard-Bezem concept of majorizability. General logical bound extraction metatheorems for such systems based on a monotone functional interpretation have been developed for abstract classes of structures and applied extensively during the past 15 years to obtain numerous new explicit rates of asymptotic regularity, metastability and other effective bounds from proofs in nonlinear analysis, ergodic theory, metric fixed point theory and continuous optimization (see [13] for a book treatment and—for a more recent survey—[15]). In [1, 2], these techniques have subsequently also been adapted to the so-called bounded functional interpretation (first introduced without the structures X in [5]) and applied to specific proofs for the first time in the recent paper [4].
The aforementioned logical uniform bound extraction theorems roughly speaking allow for the extraction of effective uniform bounds from proofs of \(\forall {\underline{x}}\exists n\in {{\mathbb {N}}}\,A_{\exists }\)-sentences which only depend via majorants on the (universally quantified) parameters \({\underline{x}}.\) Here \(A_{\exists }\) is a purely existential formula where the existence quantifiers may range over objects of modestly restricted types including \({{\mathbb {N}}}\) and X. For parameters from bounded metric structures the bounds only depend on some bound on the metric.
While these results take the form of rules one may ask whether the corresponding version formulating them as implicative ‘nonstandard’ axioms is consistent and permitted to be utilized in formalizing proofs while the extracted bounds are true in all structures considered (which certainly is not the case for these new axioms themselves). This has in fact been achieved first in [12], where a so-called uniform boundedness principle \(\exists \)-UB\(^X\) is studied for bounded metric structures X. A special form of this principle asserts
where \(A_{\exists }(x,n)\) is a purely existential formula (here the existence quantifiers may even range over objects of arbitrary types) which may contain also parameters other than x, n.
In [12] it is shown that the use of \(\exists \)-UB\(^X\) in proofs of a large class of \(\forall \exists \)-theorems is tame in the sense that it does not add to the complexity of extractable uniform bounds which can be verified to be true in all bounded metric structures axiomatized in the respective theory.
In the context of bounded functional interpretation such uniform boundedness principles have been studied in rather general form under the name of bounded collection bC\(^{\omega ,X}_{bd}\) in [1]. Engrácia [1] shows results on bC\(^{\omega ,X}_{bd}\) similar to ours for \(\exists \)-UB\(^X\) by a proof-theoretic conservation result combined with semantical considerations to obtain again the truth in all structures at hand.
While [12] (see also [13]) gives a number of general applications of the use of \((*),\) the first actual application in a concrete ‘proof mining’ context has recently been made in [4]. Here the authors show that certain uses of weak sequential compactness can be replaced by \((*)\) explaining in terms of uniform boundedness why the unwinding of a proof using weak sequential compactness (in the context of Hilbert spaces) in [14] was possible using only primitive recursive functionals without having to resort to Spector’s schema of bar recursion (needed to interpret weak sequential compactness).
In the applications known so far, the required logical form of \(A_{\exists }\) to be purely existential is a consequence of the fact that this formula describes an open (in the strong topology) subset. Based on this heuristic, \((*)\) is called in [4] a (countable) ‘Heine–Borel covering principle’ which-formally—can be stated as
where \(x\in \Omega _n\) is a formula (with x, n among its free variables) of the formal system at hand (in [4], CHBC is not discussed as a formal principle but merely as an informal way of thinking about bounded collection and uniform boundedness since an instance of CHBC indeed becomes a consequence of the former principles if the open sets can be represented in the syntactic form required which is the case in the situation studied in [4]).
In this paper we show that despite of this useful heuristic, the uniform bounded principle \(\exists \)-UB\(^X\) needs to be strictly distinguished from general countable Heine–Borel compactness as it can be shown to not imply the latter for certain definable (in the respective system) sequences of (even provably) open subsets \(\Omega _n.\) The issue here is that \(x\in \Omega _n\) in general cannot be written as a formula having the required logic form (e.g. being purely existential in the case of \(\exists \)-UB\(^X\)). In fact, we establish this by showing that the respective instance of CHBC does indeed prove \(\forall \exists \)-theorems of the form permitted in the aforementioned \(\exists \)-UB\(^X\)-elimination theorems which are not true in general in the class of metric structures considered (not even in general bounded closed and convex subsets of \(l_2\)). So these uniform bound extraction theorems which hold for \(\exists \)-UB\(^X\) are false if \(\exists \)-UB\(^X\) is replaced by CHBC and \(\exists \)-UB\(^X\) is rather to be considered as a logical compactness principle (than as a principle stating some form of compactness of X).
In [4], X is a bounded closed convex subset of a Hilbert space as this is the context of the particular application studied. In our paper we choose the setting of bounded W-hyperbolic spaces (which are metric generalizations of bounded convex subsets of normed linear spaces) as this makes the principles particularly easy to state since we do not have to axiomatize the ambient unbounded normed space (which, nevertheless, is not a problem and has been done already in [11]). Our actual counterexample, however, is indeed a bounded convex subset of a normed space which can also be adapted to get a counterexample in the Hilbert space case.
2 Main result
We work in the framework of so-called (W-)hyperbolic spaces which are a metric generalization of convex subsets of normed linear spaces:
Definition 1
([11]) (X, d, W) is called a hyperbolic space if (X, d) is a metric space and \(W:X\times X\times [0,1]\rightarrow X\) a function satisfying
-
(i)
\(\forall x,y,z\in X\forall \lambda \in [0,1] \big ( d(z,W(x,y,\lambda ))\le (1-\lambda )d(z,x)+\lambda d(z,y)\big ),\)
-
(ii)
\(\forall x,y\in X\forall \lambda _1,\lambda _2\in [0,1] \big ( d(W(x,y,\lambda _1),W(x,y,\lambda _2))=|\lambda _1-\lambda _2|\cdot d(x,y)\big ),\)
-
(iii)
\(\forall x,y\in X \forall \lambda \in [0,1]\big ( W(x,y,\lambda )=W(y,x,1-\lambda )\big ),\)
-
(iv)
\(\forall x,y,z,w\in X,\lambda \in [0,1] \big ( d(W(x,z,\lambda ),W(y,w,\lambda )) \le (1-\lambda )d(x,y)+\lambda d(z,w)\big ).\)
For a discussion of this notion and its relation to various other related notions in the literature, see [11].
\(W(x,y,\lambda )\) should be viewed of as a generalized concept of a convex combination and we use the notation \((1-\lambda )x\oplus \lambda y\) to denote \(W(x,y,\lambda ).\)
As a special case of [12](Theorem 3.5.2) (see also [13](Theorem 17.101) we have
Theorem 2
([12]) Let
be a sentence of \(\mathcal{L}(\mathcal{{A}}^{\omega }[X,d,W]),\) where \(A_{\exists }\) is an \(\exists \)-formula. From a proof
one can extract a (bar-recursively) computable functional \(\Phi :{{\mathbb {N}}}^{{{\mathbb {N}}}} \times {{\mathbb {N}}}^2\rightarrow {{\mathbb {N}}}\) such that
holds in any b-bounded hyperbolic space (X, d, W).
Let (X, d, W) be a bounded (W-)hyperbolic space and \(T:X\rightarrow X\) be a nonexpansive mapping. For \(x_0\in X\) we define the Krasnoselski iteration of T with starting point \(x_0\) by
As has been shown in [8] (generalizing a result from [9] from the linear to the geodesic setting) one has (as a special case of a much more general result) asymptotic regularity in the sense that \(\lim \limits _{n\rightarrow \infty } d(x_n,Tx_n)=0.\)
Using a logic-based approach (‘proof mining’) and the fact that this convergence proof can be formalized in \(\mathcal{{A}}^{\omega }[X,d,W],\) an explicit rate of convergence \(\Phi (k,b)\) (depending only on the error \(2^{-k}\) and a bound \(b\ge diam(X)\)) has been extracted from the convergence proof in [17]. In this note we only need that
The sequence \((x_n)\) is easily shown to be Féjer monotone w.r.t. the fixed point set F(T) of T, i.e.
We can now prove our main result:
Theorem 3
\(\mathcal{{A}}^{\omega }[X,d,W]+\)CHBC proves a sentence A of the form considered in Theorem 2 such that A does not hold in general in bounded hyperbolic spaces (not even bounded closed convex subsets of a Hilbert space).
Proof
Trivially one has (taking \(p:=x)\)
and so by (classical) logic
If T is nonexpansive then (provably in \(\mathcal{{A}}^{\omega }[X,d,W]\)) for all k, n
is an open set: let \(x\in U_{n}.\)
Case 1: for some \(p\in F(T)\) one has that \(d(p,x)<2^{-k}.\) Let \(\varepsilon >0\) be so small that \(d(p,x)+\varepsilon <2^{-k}\). Then each y in the open ball \(B_{\varepsilon }(x)\) with center x and radius \(\varepsilon \) satisfies
and so belongs to \(U_{n}.\)
Case 2: not Case 1. Then \(d(x,Tx)> 2^{-n}.\) Let \(\varepsilon >0\) be so small that \(d(x,Tx)-2\varepsilon >2^{-n}.\) If \(y\in B_{\varepsilon }(x),\) then \(d(y,Ty)>d(x,Tx)-2\varepsilon >2^{-n}\) and so \(y\in U_{n}.\)
So in either case we found an \(\varepsilon \)-ball around \(x\in U_{n}\) which belongs to \(U_{n}.\)
By CHBC we can now infer (using the monotonicity of the formula in n)
Here ‘n.e.’ abbreviates ‘nonexpansive’. Now we can reason as in the proof of Theorem 4.1 in [18] to show that \((x_n)\) (for any \(x_0\in X\)) is a Cauchy sequence: let \(k\in {{\mathbb {N}}}.\) By (1) above let \(N\in {{\mathbb {N}}}\) be so large that \(d(x_N,Tx_N)\le 2^{-n_k}.\) Then there exists a \(p\in F(T)\) with \(d(p,x_N)< 2^{-k}\) and so by (2)
Thus
In particular, we can prove the metastable version (see [19]) of the Cauchy property (which—noneffectively—implies back the Cauchy property)
Modulo prenexing ‘\(\left( T\ \text{ n.e. } \, \rightarrow \exists n\in {{\mathbb {N}}}\, (d(x_n, x_{n+g(n)})<2^{-k})\right) \)’ (since ‘\(T\ \text{ n.e }\)’ is a \(\forall \)-formula) this sentence has the logical form of a sentence A as stated in the theorem but in general it fails to hold in bounded hyperbolic spaces (even in bounded closed convex subsets of \(l_2\)) as we show now: first take X to be the bounded, closed and convex subset
\(c_0\) (of all sequences in \({{\mathbb {R}}}\) which converge to 0 with the sup-norm) and take as T one of the well-known fixed point-free nonexpansive selfmappings \(:B^+_{c_0}\rightarrow B^+_{c_0},\) e.g. take \(T(x_n):=(1,x_1,x_2,\ldots )\) (see [10], Example 2.1 on p.36.).
Clearly, \(B^+_{c_0}\) is a complete hyperbolic space (X, d, W) with d induced by the norm and \(W(x,y,\lambda ):=(1-\lambda )x+\lambda y.\) If A would hold in this structure, then \((x_n)\) defined in terms of such a T would be Cauchy and hence convergent. By the continuity of T and (1) the limit had to be a fixed point of T, contradiction. To get a counterexample in the Hilbert space case, we can use a construction from [6] who produce a bounded closed and convex subset \(C\subset l_2\) and a nonexpansive selfmapping \(T:C\rightarrow C\) and a point \(x_0\in C\) such that the Krasnoselski iteration \((x_n)\) of T starting with \(x_0\) does not converge strongly (although here, by the Browder-Göhde-Kirk fixed point theorem, T clearly does have a fixed point). \(\square \)
Corollary 4
Theorem 2 does not hold if \(\exists \)-UB\(^X\) is replaced by CHBC. In particular, \(\mathcal{{A}}^{\omega }[X,d,W]+\exists \)-UB\(^X\) does not prove CHBC.
Remark 5
Theorem 2 also holds if one adds new constants \(c^{\rho }\) (of suitably restricted type \(\rho \) which includes the type X(X)) to the language together with universal axioms (again with some type restrictions) implying that c is majorized by some closed term of \(\mathcal{L}(\mathcal{{A}}^{\omega })\cup \{ b^0_X\},\) where \(b_X\) is the constant used to express the boundedness of X. This e.g. applies to adding a constant \(T^{X(X)}\) to the language together with the axiom stating that T is nonexpansive. In this theory (with e.g. fixing \(x_0\) as \(0_X\)), it is then provable that \(U_{n}\) is open for all n (and k). So even for provably open sequences of open sets which are explicitly definable in the language of our theory, CHBC in general cannot be inferred from \(\exists \)-UB\(^X.\)
Instead of using \(\mathcal{{A}}^{\omega }[X,d,W]\) one can also use the framework \(\mathcal{{A}}^{\omega }[X,\langle \cdot ,\cdot \rangle ,C]\) from [11] which axiomatizes C as a bounded convex subset of an abstract inner product space X and formulate (the required special form of) \(\exists \)-UB\(^{X}\) as
Theorem 2 can easily adapted to this context in which one can prove a-fortiori that \(\Vert x_n-Tx_n\Vert \rightarrow 0\) for Krasnoselski iterations of nonexpansive mappings \(T:C\rightarrow C.\) Since the counterexample at the end of the proof of Theorem 3 lives in the context of bounded convex subsets of the Hilbert space \(l_2\) it follows as in the previous Corollary that:
Corollary 6
\(\mathcal{{A}}^{\omega }[X,\langle \cdot ,\cdot \rangle ,C]+\exists \)-UB\(^X\) does not prove CHBC.
Let us discuss the counterexample constructed in the proof of Theorem 3 a bit further. What
expresses is that T is metrically regular w.r.t. F(T) in the sense of [18], where any function \(\Phi (k)\) providing \(n_k\) as a function of k is called a ‘modulus of regularity’ of T w.r.t. F(T) (in [18] we use for convenience the more common \(\varepsilon /\delta \)-formulation of this fact). Our argument based on countable Heine–Borel compactness given above is used in [18] to show the (noneffective) existence of a modulus of regularity whenever X is (boundedly) compact. In [16], we analyzed the situation from the perspective of both reverse mathematics and computability theory and showed that if X is represented as a complete totally bounded space then arithmetical comprehension (ACA\(_0\)) is sufficient and necessary to prove the existence of \(\Phi \) while the version \((+)\) without the existence of a modulus function can be proved by (and is equivalent to) the weak König’s lemma WKL. However, in our formal systems X is treated as an abstract space and not represented as a completion of a countable (pseudo-)metric space and although CHBC is known to imply full Heine–Borel compactness of metric spaces and hence total boundedness this is not a fact we can already use when formalizing CHBC. This is why—in order to bring
into the syntactic form required in \(\exists \)-UB\(^X\)—we would have to add e.g. a comprehension functional \(\Phi :X\times {{\mathbb {N}}}\rightarrow {{\mathbb {N}}}\) in \(x\in X\) such that
With the inessential change of using ‘\(\le \)’ instead of ‘<’, we could use \(\exists \)-UB\(^{X}\) to rewrite ‘\(\exists p\in F(T)\,(d(p,x)\le 2^{-k})\)’ equivalently as ‘\(\forall m\in {{\mathbb {N}}}\,\exists p\in X\,\left( d(p,x)\le 2^{-k} \wedge d(p,Tp)\le 2^{-m}\right) \)’. Alternatively, a more local comprehension functional \(\Phi :X\rightarrow {{\mathbb {N}}}\)
would also be sufficient. In either case, one would need a comprehension over points x or p in X using a formula which contains a universal quantifier over natural numbers (hidden in \(p\in F(T)\) resp. present as \(\forall m\in {{\mathbb {N}}}\)) which is not available in our formal system. In the situation studied in [16] we could, relying on the representation of X being totally bounded, replace the dependence on x by that of indices \(\in {{\mathbb {N}}}\) of suitable elements from an \(\varepsilon \)-net to make the comprehension a comprehension over numbers (which—by subsequent arguments—is even an arithmetical comprehension over natural numbers).
The results in this note carry over mutatis mutandis to the bounded collection principle bC\(^{\omega ,X}_{bd}\) from [1, 2] showing that this principle does not imply CHBC over the framework PA\(^{\omega ,X}_{\unlhd }\) used in the bounded functional interpretation.
Final comment: as a reaction to our note, Fernando Ferreira communicated to us a different example showing that in formal systems of infinite dimensional Hilbert spaces, CHBC actually can be shown to be inconsistent [3].
References
Engrácia, P.: Proof-theoretical studies on the bounded functional interpretation. PhD Thesis, Universidade de Lisboa (2009)
Engrácia, P., Ferreira, F.: Bounded functional interpretation with an abstract type. In: Rezus, A. (ed.) Contemporary Logic and Computing. Landscapes in Logic, vol. 1, pp. 87–112. College Publications, New York (2020)
Ferreira, F.: Personal communication (June 8 2020)
Ferreira, F., Leuştean, L., Pinto, P.: On the removal of weak compactness arguments in proof mining. Adv. Math. 354, 106728 (2019). pp. 55
Ferreira, F., Oliva, P.: Bounded functional interpretation. Ann. Pure Appl. Logic 135, 73–112 (2005)
Genel, A., Lindenstrauss, J.: An example concerning fixed points. Israel J. Math. 22, 81–86 (1975)
Gerhardy, P., Kohlenbach, U.: General logical metatheorems for functional analysis. Trans. Am. Math. Soc. 360, 2615–2660 (2008)
Goebel, K., Kirk, W.A.: Iteration processes for nonexpansive mappings. In: Singh, S.P., Thomeier, S., Watson, B. (eds.) Topological Methods in Nonlinear Functional Analysis. Contemporary Mathematics, vol. 21, pp. 115–123. AMS, New York (1983)
Ishikawa, S.: Fixed points and iterations of a nonexpansive mapping in a Banach space. Proc. Am. Math. Soc. 59, 65–71 (1976)
Kirk, W.A., Sims, B. (eds.): Handbook of Metric Fixed Point Theory, p. xi+703. Kluwer Academic Publishers, Dordrecht (2001)
Kohlenbach, U.: Some logical metatheorems with applications in functional analysis. Trans. Am. Math. Soc. 357(1), 89–128 (2005)
Kohlenbach, U.: A logical uniform boundedness principle for abstract metric and hyperbolic spaces. Electronic Notes in Theoretical Computer Science (Proceedings of WoLLIC 2006) 165, 81–93 (2006)
Kohlenbach, U.: Applied Proof Theory: Proof Interpretations and Their Use in Mathematics. Springer Monographs in Mathematics. Springer, New York (2008)
Kohlenbach, U.: On quantitative versions of theorems due to F. E. Browder and R. Wittmann. Adv. Math. 226, 2764–2795 (2011)
Kohlenbach, U.: Recent progress in proof mining in nonlinear analysis. IFCoLog J. Logics Appl. 10, 3357–3406 (2017)
Kohlenbach, U.: On the reverse mathematics and Weihrauch complexity of moduli of regularity and uniqueness. Computability 8, 377–387 (2019)
Kohlenbach, U., Leuştean, L.: Mann iterates of directionally nonexpansive mappings in hyperbolic spaces. Abstr. Appl. Anal. 2003(8), 449–477 (2003)
Kohlenbach, U., López-Acedo, G., Nicolae, A.: Moduli of regularity and rates of convergence for Fejér monotone sequences. Israel J. Math. 232, 261–297 (2019)
Tao, T.: Soft analysis, hard analysis, and the finite convergence principle. Essay posted May 23, 2007. In: Tao, T. (ed.) Structure and Randomness: Pages from Year One of a Mathematical Blog, p. 298. AMS (2008)
Acknowledgements
The author has been supported by the German Science Foundation (DFG Project KO 1737/6-1).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kohlenbach, U. Proof-theoretic uniform boundedness and bounded collection principles and countable Heine–Borel compactness. Arch. Math. Logic 60, 995–1003 (2021). https://doi.org/10.1007/s00153-021-00771-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00153-021-00771-w
Keywords
- Uniform boundedness principle
- Bounded collection principle
- Monotone functional interpretation
- Bounded functional interpretation
- Proof mining