Old-age support policy and fertility with strategic bequest motives

Abstract

This paper presents an analysis of the effects of public old-age support on individuals’ fertility decisions and on the long-term equilibrium in an overlapping generation economy with strategic bequest motives. Parents must pay their adult children at least the reservation wage to receive informal old-age support from them (individual rationality constraint). Formal old-age support is financed through wage taxes on children. The increased present value of formal old-age support tends to increase old-age utility, thereby decreasing the family support demand and decreasing savings for the old age. The increased wage tax reduces the opportunity cost of child-rearing time, thereby increasing the fertility rate. The effects of increased formal old-age support on per-worker capital and labor are indeterminate, as is the effect on the long-term lifetime utility of individuals. A strategic bequest motive might engender a higher fertility rate than that of the social optimum.

1 Introduction

Most developed economies have a population exhibiting extended longevity and declining fertility, or postponement of births, during past decades (Pestieau and Ponthiere 2016). Longer life expectancy increases the likelihood of long-term care needs of individuals and of entire countries (Mayhew 2011). Because the health conditions of individuals during old age vary to a great degree among individuals, some countries have public long-term care support systems designed to supplement or substitute for informal support, such as the systems of Japan, Germany, Korea, Luxembourg, Austria, Canada, the UK, and the US.¹ The increased elderly care time, both formally and informally, might affect the time allocation of people of the working generation, especially their child-rearing time and thereby fertility. Analyzing that relation is the aim of this paper.

Figure 1 presents the total fertility rate, the respective fertility rates of mothers aged 15–29 and of 30–45, and the university entrance rate of women in Japan after 1980. Often, women care for elderly family members in economically developed countries (e.g., Pestieau and Sato 2008). The university entrance rate of women, which is shown on the right-hand axis, increased considerably after about 1990. The fertility rate of mothers aged 30–49 also increased, especially greatly after introduction of the Long-term Care Insurance system, which was launched by the Japanese government in 2000 and which was revised considerably in 2005. That system is a mandatory insurance system, in which all residents 40 years old and older in Japan must enroll and pay a premium. Women who were about 20 years old in 1990 had become older than 40–45 by the late 2010s. Yamashita and Soma (2020) report, based on a 2012–2018 sample survey of parents who have children of university student age and younger, that about 30% of Japanese people have experienced caring for both parents and children. Suh (2016) also finds for 2012 that about half of people of ages 47–59 cared for parents aged 65 and older and simultaneously for children under age 18 or provided financial support to children older than 18 in the US (see also Carney 2023). Figure 1 shows that mothers who received greater bequests of university tuition fees apparently reared more children after introduction of the Long-term Care Insurance system. Because education investment is apparently the most important intergenerational (inter vivos) transfer, both increases in formal long-term care provision and increases in bequests occur simultaneously.² Therefore, they are apparently positively related.³ Klimaviciute et al. (2017) describe that transfers can be compensated at a much later date in different ways in exchange models.⁴ This paper presents an analysis of whether the strategic bequest motive hypothesis can explain this relationship between formal old-age support and fertility.

Fig. 1

Total fertility rate, fertility rates of mothers aged 15–29 and 30–45 and the female university entrance rate (fuer) in Japan. Sources: Ministry of Education, Culture, Sports, Science and Technology of Japan (2022); National Institute of Population and Social Security Research (2023)

This paper presents analyses of the effects of public old-age support on fertility rates by incorporating endogenous fertility decisions of individuals into an overlapping generations model and by incorporating the strategic bequest motives of individuals.⁵ Working generations choose the allocation of time endowment among market labor, child rearing, and family old-age support for elderly parents. They also choose bequests in exchange for old-age support from their children during old age. Few reported studies have described the effects of formal old-age support on fertility using such a dynamic model based on strategic bequest motives.

As population aging progresses in countries, numerous theoretical studies of effects of elderly long-term care on family labor supply decisions have come to be presented (Pestieau and Sato 2008; Cremer and Roeder 2013; Ponthiere 2014; Cremer et al. 2017; Yakita 2020a). Many empirical analyses of family caregiving effects on the market labor supply of family members have also been presented (van Houtven et al. 2013; Skira 2015). A vast literature related to Japan has presented analyses of Japanese Long-term Care Insurance system effects on the market labor supply of families (Tamiya et al. 2011; Sugawara and Nakamura 2014; Yamada and Shimizutani 2015; Fu et al. 2017; Niimi 2017; Oshio and Usui 2017). Most such studies specifically examine the female labor supply because long-term care is often provided by women. The results are mixed. Nevertheless, not one of these theoretical and empirical studies considers endogenous fertility decisions of families simultaneously.

Since the work reported by Becker, e.g., Becker and Barro (1988), many reports have described analyses of fertility decisions (e.g., Galor and Weil 1996; Yakita 2001, 2018; de la Croix and Doepke 2003; Apps and Rees 2004). Nevertheless, few reports describe long-term care effects on the fertility decisions which families make.

Yakita (2023a) presents an analysis of public long-term care effects on the fertility rate in an overlapping generations model in which children are altruistic toward their parents. He demonstrates that, depending on the cost-efficiency of public care provision, increases in public long-term care provision might not raise the fertility rate. By contrast, this study examines such issues, assuming strategic bequest motives of individuals.⁶ Although family old-age support based on (forced) altruism requires children to bear the opportunity costs of support time for parents, strategic bequest motive-derived old-age support requires that children have no costs because the old-age support time is compensated by bequests (i.e., individual rationality constraint). Therefore, the effects of formal old-age support policy on family old-age support and fertility decisions of individuals differ from those in an altruistic bequest motive model.

As described herein, the author also considers broader old-age support services such as inclusion of chore assistance, rather than narrowly defined long-term care services such as activities of daily living (ADL) and instrumental activities of daily living (IADL) services.⁷ In Japan, for example, the ratio of individuals in need of long-term care among people aged 75 and older is 32.1%; the ratio of those aged 85 and older is 60.6% (Ministry of Health, Labour and Welfare of Japan 2020). The life expectancy at birth was 81.47 years for men and 87.57 years for women in Japan in 2021 (Ministry of Health, Labour and Welfare of Japan 2021). Therefore, one might infer that most elderly people are supported by family members or by public programs, even if they do not even need narrowly defined long-term care services such as IADL services.⁸ To simplify the arguments, I assume for these analyses that all elderly people receive old-age support both informally from family members and formally from governments. Herein, I consider only old-age support in kind.⁹

The main result is that an increase in the wage tax rate for formal old-age support provision raises the fertility rate when the individual rationality constraint is binding. Increased formal support tends to substitute family old-age support for the old-age consumption from the old-age utility maximization. The worker’s time freed from family support provision is at least partly allocated to child rearing, although the market labor supply of workers might not be increased. Because the increased old-age support, financed by taxes paid by workers, increases the old-age utility in a relative sense, savings of workers might become smaller. The effect of a tax increase on per-worker capital stock is also indeterminate. Consequently, public old-age support would not necessarily improve the steady-state lifetime utility of individuals. Finally, by defining the lifetime utility of an individual as the social objective function, I can infer that intergenerational exchanges based on strategic bequest motives might engender an excessively higher fertility rate compared to the social optimum.

The remainder of this paper is presented as described hereinafter. The next section introduces an overlapping generations model with strategic bequest motives of individuals.¹⁰ Section 3 presents an examination of the model dynamics. Section 4 presents comparative static results with respect to old-age support provision. Section 5 gives a comparison of the results with the social optimum. The objective of a social planner is to maximize the individual lifetime utility in steady states. The last section concludes the paper.

2 Model

A discrete-time overlapping generations model is considered for the analyses. The model assumes unisex individuals. Individuals are homogeneous and live for three periods: childhood, a working period, and old-age retirement period. The lifetime is certain. The length of each period is normalized to unity. An individual is fed by a parent during childhood. The individual then supplies labor to the labor market, consumes some of the wage income, and rears children during the second working period. The working individual also provides family old-age support for the parent in exchange for bequests, i.e., with strategic bequest motives.¹¹ Governments provide formal old-age support, produced using labor, with financing secured through wage taxes.¹² Non-health consumption goods are produced under Cobb–Douglas technology using capital and labor.

2.1 Individuals

While consuming part of the sum of personal wage income and a bequest from a parent, the individual saves the remainder for old-age retirement in the second period. During the second period, he also provides parental care for his children and old-age care for his parent simultaneously, i.e., a sandwich caregiver. He consumes a part of the fruits of savings and makes bequests to his children in exchange for old-age support from them during the third period. The lifetime optimization problem of an individual can be split into two stages: The first is maximization of utility during the old-age period; the second is the maximization of lifetime utility in the second working period. After first considering the choice of a strategic bequest in the third period of an individual’s life, this report presents consideration of the choice of consumption-savings plan in the second period in turn.

An old-age individual in period $t+1$ allocates the fruit of the individual’s lifecycle savings between old-age non-health consumption and bequests to maximize old-age utility. The old-age utility function is assumed as ${u}_{2t+1}={c}_{2t+1}^{1-\gamma }{({n}_{t}{z}_{t+1}+\varepsilon {\Lambda }_{t+1}^{G})}^{\gamma }$, where ${c}_{2t+1}$ represents non-health consumption during the old-age period, ${n}_{t}$ stands for the number of that person’s children, ${z}_{t+1}$ denotes old-age support per child for a parent, and $\varepsilon {\Lambda }_{t+1}^{G}$ denotes public old-age support provided by government. I assume here that because old-age support is labor-time intensive, old-age support is produced using labor-time input. A linear production technology is assumed for both formal and informal old-age support: One unit of labor-time produces one unit of family old-age support, whereas one unit of labor-time is transformed to $\varepsilon$ units of formal old-age support. Letting ${\Lambda }_{t+1}^{G}$ be the labor-time employed by the government, then the provision level of formal old-age support is $\varepsilon {\Lambda }_{t+1}^{G}$. In this sense, parameter $\varepsilon >0$ represents the degree of cost-efficiency of formal old-age support time relative to family support.¹³

As described herein, I assume that parents know that the labor-time employed depends positively on the population size of the children’s generation: If the population size of the children’s generation is small, then the employment size will be small. For analytical simplicity, I assume here that individuals perceive that the formal old-age support level per parent is proportional to the number of children, i.e., ${\Lambda }_{t+1}^{G}={n}_{t}{z}_{t+1}^{G}$. Therefore, it follows that ${u}_{2t+1}={c}_{2t+1}^{1-\gamma }{[{n}_{t}({z}_{t+1}+\varepsilon {z}_{t+1}^{G})]}^{\gamma }$.¹⁴

A parent must pay at least the reservation wage of the child to receive informal old-age support. This requirement is called the individual rationality constraint. Letting ${b}_{t+1}$ be the bequest per child, then the constraint can be written as

$${b}_{t+1}\ge (1-\tau ){w}_{t+1}{z}_{t+1}$$

(1)

where $\tau \in (\mathrm{0,1})$ denotes the wage tax rate and where ${w}_{t+1}$ denotes the wage rate for period $t+1$. No child provides family old-age support unless that child receives a bequest greater than or equal to the opportunity cost of support provision. The opportunity cost of old-age support time is the after-tax wage rate. The coefficient of ${z}_{t+1}$ in constraint (1), $(1-\tau ){w}_{t+1}$, corresponds to the equilibrium price of the private market of old-age support in a model of exchange motives for caring (Klimaviciute et al. 2017). In equilibrium, ${b}_{t+1}$ is the amount paid for ${z}_{t+1}$. Therefore, the parent must pay ${n}_{t}{b}_{t+1}$ to receive family old-age support ${n}_{t}{z}_{t+1}$. The total old-age support, formal and informal, per child is expressed as ${z}_{t+1}+\varepsilon {z}_{t+1}^{G}$ in terms of family support.

Letting ${I}_{t+1}$ be the fruit of the child’s lifecycle savings from the working period, the budget constraint in the old-age retirement period is given as¹⁵

$${I}_{t+1}={c}_{2t+1}+{n}_{t}{b}_{t+1}$$

(2)

The optimization problem of the old-age individual is to choose non-health consumption ${c}_{2t+1}$ and bequests to children ${n}_{t}{b}_{t+1}$ for old-age support (demand) ${n}_{t}{z}_{t+1}$ to maximize the old-age utility for a given level of formal old-age support $\varepsilon {\Lambda }_{t+1}^{G}$. Because of maximization by the individual, it is natural to consider equality for the individual rationality constraint (1) (Laitner and Ohlson 2001). Therefore, the choice of family support demand ${z}_{t+1}$ can be regarded as the choice of bequests to children ${b}_{t+1}$. Inserting the equal constraint into the budget constraint yields

$${I}_{t+1}={c}_{2t+1}+{n}_{t}(1-\tau ){w}_{t+1}{z}_{t+1}$$

(3)

The first-order conditions for old-age utility maximization are

$$(1-\gamma ){c}_{2t+1}^{-\gamma }{n}_{t}^{\gamma }{({z}_{t+1}+\varepsilon {z}_{t+1}^{G})}^{\gamma }-\mu =0$$

(4a)

and

$$\gamma {c}_{2t+1}^{1-\gamma }{n}_{t}^{\gamma }{({z}_{t+1}+\varepsilon {z}_{t+1}^{G})}^{\gamma -1}-\mu {n}_{t}(1-\tau ){w}_{t+1}=0$$

(4b)

Variable $\mu$ is the Lagrange multiplier attached to constraint (3). From (4a) and (4b), I obtain

$${c}_{2t+1}=\frac{1-\gamma }{\gamma }{n}_{t}(1-\tau ){w}_{t+1}({z}_{t+1}+\varepsilon {z}_{t+1}^{G})$$

(5)

Inserting ${c}_{2t+1}$ from (5) into budget constraint (3) gives

$${z}_{t+1}+\varepsilon {z}_{t+1}^{G}=\gamma [{I}_{t+1}+{n}_{t}(1-\tau ){w}_{t+1}\varepsilon {z}_{t+1}^{G}]/[{n}_{t}(1-\tau ){w}_{t+1}]$$

(6)

From (5) and (6), the indirect old-age utility ${u}_{t2+1}^{*}$ is obtainable as

$$\begin{array}{c}{u}_{2t+1}^{*}={(\frac{1-\gamma }{\gamma })}^{1-\gamma }{[{n}_{t}(1-\tau ){w}_{t+1}]}^{1-\gamma }{({z}_{t+1}+\varepsilon {z}_{t+1}^{G})}^{1-\gamma }{n}_{t}^{\gamma }{({z}_{t+1}+\varepsilon {z}_{t+1}^{G})}^{\gamma }\\ ={Q}_{t+1}[{I}_{t+1}+{n}_{t}(1-\tau ){w}_{t+1}\varepsilon {z}_{t+1}^{G}]\end{array}$$

(7)

where ${Q}_{t+1}={(1-\gamma )}^{1-\gamma }{\gamma }^{\gamma }{[(1-\tau ){w}_{t+1}]}^{-\gamma }$. Because the individual rationality constraint is satisfied with equality, each child provides old-age support ${z}_{t+1}$ to a parent in exchange for bequest ${b}_{t+1}$. Income ${I}_{t+1}$ and the number of children ${n}_{t}$ are already determined during the prior period. Public old-age support ${z}_{t+1}^{G}$ and tax rate $\tau$ are government-determined. Market prices (i.e., wage rate ${w}_{t+1}$ and interest rate ${r}_{t+1}$) are given for individuals.

Next, I consider the optimization of working individuals. Each individual chooses the time allocation among market labor supply, child rearing time, and family old-age support time. Each individual also allocates the sum of wage income and bequest received between non-health consumption during the working period and lifecycle savings. Market labor ${m}_{t}$ comprises the labor of people employed in non-health consumption goods production and of people employed in the public old-age support provision sector. For convenience, the former is designated as ${l}_{t}$ and the latter as ${z}_{t}^{G}$. I assume that labor in the public sector is compensated using the same wage rate ${w}_{t}$ as in the non-health consumption goods production sector during period $t$ because a cost-minimizing government must pay the same wage rate to employ labor in the public support provision sector. Therefore, workers are indifferent between employment in the non-health consumption goods sector and in the formal old-age support provision sector. Assuming that the child-rearing time per child is constant at $\phi >0$, then the time constraint of a working individual is written as

$${m}_{t}+{z}_{t}+\phi {n}_{t}=1$$

(8)

where ${m}_{t}={l}_{t}+{z}_{t}^{G}$ is the market labor supply and where ${z}_{t}+\phi {n}_{t}$ is the labor supply for family production of family old-age support and childcare.

The budget constraint of a working individual in period $t$ is given as

$${b}_{t}+(1-\tau ){w}_{t}({l}_{t}+{z}_{t}^{G})={c}_{1t}+\frac{{I}_{t+1}}{1+{r}_{t+1}}$$

(9)

Therein, ${c}_{1t}$ denotes non-health consumption during the working period. Because the individual rationality constraint is satisfied with equality for each generation, it is the case that ${b}_{t}=(1-\tau ){w}_{t}{z}_{t}$. Therefore, budget constraint (9) can be rewritten as

$$(1-\tau ){w}_{t}(1-\phi {n}_{t})={c}_{1t}+\frac{{I}_{t+1}}{1+{r}_{t+1}}$$

(10)

The lifetime utility function is assumed as $\widetilde{U}={\text{ln}}{c}_{1t}+\sigma {\text{ln}}{n}_{t}+\beta {\text{ln}}{u}_{2t+1}^{*}$. From (7) and because ${Q}_{t+1}$ is given for the individual, the objective function of the utility maximizing individual can be expressed as

$$U={\text{ln}}{c}_{1t}+\sigma {\text{ln}}{n}_{t}+\beta {\text{ln}}[{I}_{t+1}+{n}_{t}(1-\tau ){w}_{t+1}\varepsilon {z}_{t+1}^{G}]$$

(11)

The optimization problem of the individual is to choose non-health consumption ${c}_{1t}$, the number of children ${n}_{t}$, and lifecycle savings ${I}_{t+1}/(1+{r}_{t+1})\equiv {s}_{t}$ to maximize lifetime utility (11). The first-order conditions for lifetime utility maximization are

$$\frac{1}{{c}_{1t}}-{\lambda }_{t}=0$$

(12)

$$\frac{\beta }{{I}_{t+1}+{n}_{t}(1-\tau ){w}_{t+1}\varepsilon {z}_{t+1}^{G}}-\frac{{\lambda }_{t}}{1+{r}_{t+1}}=0$$

(13)

and

$$\frac{\sigma }{{n}_{t}}+\frac{\beta (1-\tau ){w}_{t+1}\varepsilon {z}_{t+1}^{G}}{{I}_{t+1}+{n}_{t}(1-\tau ){w}_{t+1}\varepsilon {z}_{t+1}^{G}}-{\lambda }_{t}(1-\tau ){w}_{t}\phi =0$$

(14)

Variable ${\lambda }_{t}$ is the Lagrange multiplier attached to constraint (10). Conditions (12) and (13) provide the optimal intertemporal allocation between the working-period consumption and the retired-period consumption, including old-age support services. The first term on the right-hand side of (14) represents the marginal utility of having an extra child. The second term is the marginal utility of old-age support from the child net of bequest (costs) given to the individual. The third term stands for the opportunity cost of child rearing time in terms of utility. The wage tax rate lowers the cost of having children.

From (12) and (13), I obtain

$${c}_{1t}=\frac{{I}_{t+1}+{n}_{t}(1-\tau ){w}_{t+1}\varepsilon {z}_{t+1}^{G}}{\beta (1+{r}_{t+1})}$$

(15)

Using (10) and (15) and defining ${G}_{t+1}=\frac{{n}_{t}(1-\tau ){w}_{t+1}\varepsilon {z}_{t+1}^{G}}{1+{r}_{t+1}}$ then gives

$${c}_{1t}=\frac{1}{1+\beta }[(1-\tau ){w}_{t}(1-\phi {n}_{t})+{G}_{t+1}]$$

(16)

Herein, ${G}_{t+1}$ is the discounted present value of public old-age support in terms of family old-age support. Using the definition of lifecycle savings, I obtain

$${s}_{t}=\frac{1}{1+\beta }[\beta (1-\tau ){w}_{t}(1-\phi {n}_{t})-{G}_{t+1}]$$

(17)

I also have

$${n}_{t}=\frac{1}{\phi }[\frac{\sigma }{1+\beta +\sigma }+\frac{{G}_{t+1}}{(1-\tau ){w}_{t}}]$$

(18)

A greater discounted present value of public old-age support leads to a greater number of children. It is noteworthy that Eqs. (15)–(18) present implicit solutions for non-health consumption, savings, and the number of children. Consumption during the working period increases with the present value of public old-age support. Lifecycle savings decrease with the present value of old-age support. In addition, the number of children increases with the present value of old-age support.

2.2 Government

Governments provide public old-age support to old-age individuals while employing labor from the labor market. A government must pay its employees the market wage rate to employ them.¹⁶ The government old-age support provision is financed by a wage income tax, with government balancing the budget in each period. I assume that this government only expends tax revenues for old-age support. By maintaining a balanced budget, the government budget constraint is given as

$$\tau {w}_{t}({l}_{t}+{z}_{t}^{G}){N}_{t}={w}_{t}{z}_{t}^{G}{N}_{t}$$

(19)

Therein, variable ${N}_{t}$ stands for the number of workers in period $t$. The left-hand side represents the tax revenues. The right-hand side is the labor cost of public old-age support provision.¹⁷ For a given tax rate $\tau$ and market wage rate ${w}_{t}$, an employment level ${z}_{t}^{G}$ is chosen by this government to satisfy the budget constraint (19). From (19), it follows that $\tau {w}_{t}{l}_{t}=(1-\tau ){w}_{t}{z}_{t}^{G}$ in per-worker terms.

2.3 Non-health consumption goods production

The production function of non-health consumption goods is assumed as

$${Y}_{t}={K}_{t}^{\alpha }{L}_{t}^{1-\alpha }\left(0<\alpha <1\right)$$

(20)

In that equation, ${Y}_{t}$ is the aggregate output. In addition, ${K}_{t}$ and ${L}_{t}$ represent the aggregate capital and labor in period $t$. The production function can be rewritten as ${y}_{t}={k}_{t}^{\alpha }{l}_{t}^{1-\alpha }$ in per-worker terms, where ${y}_{t}={Y}_{t}/{N}_{t}$, ${k}_{t}={K}_{t}/{N}_{t}$, and ${l}_{t}={L}_{t}/{N}_{t}$. Assuming perfectly competitive factor markets, I have

$${w}_{t}=(1-\alpha ){k}_{t}^{\alpha }{l}_{t}^{-\alpha }=(1-\alpha ){y}_{t}/{l}_{t}$$

(21)

$$1+{r}_{t}=\alpha {k}_{t}^{\alpha -1}{l}_{t}^{1-\alpha }=\alpha {y}_{t}/{k}_{t}$$

(22)

The marginal productivity of each factor is equal to the factor price.

2.4 Capital market

The capital market clearing condition is given as

$${K}_{t+1}={s}_{t}{N}_{t}\,\mathrm{ or},\text{in per-worker terms}, {n}_{t}{k}_{t+1}={s}_{t}$$

(23)

I assume that capital stock depreciates after one-period use, where one period lasts about 30 years.

3 Dynamics and long-term equilibrium

This section studies the dynamics of the economy. First, I consider the temporary equilibrium. Then, I examine the system dynamics.

3.1 Temporary equilibrium

I first analyze a temporary equilibrium in a period, period $t$. From the government budget constraint and from the definition of ${G}_{t+1}$, I have ${G}_{t+1}=\varepsilon \theta {n}_{t}{k}_{t+1}$, where $\theta =[(1-\alpha )/\alpha ]\tau$ is the wage tax burden relative to capital income (hereinafter, the tax parameter). Using (17) and (23), I obtain ${n}_{t}{k}_{t+1}=\varepsilon \theta \beta (1-\tau ){w}_{t}(1-\phi {n}_{t})/(1+\beta +\varepsilon \theta )$. Therefore,

$${G}_{t+1}=\frac{\varepsilon \theta \beta (1-\tau ){w}_{t}(1-\phi {n}_{t})}{1+\beta +\varepsilon \theta }$$

(24)

From (12), (16), and (24), the following is obtained:

$$\frac{1}{{\lambda }_{t}}=\frac{1+\varepsilon \theta }{1+\beta +\varepsilon \theta }(1-\tau ){w}_{t}(1-\phi {n}_{t})$$

(25)

Inserting ${G}_{t+1}$ from (24) and $1/{\lambda }_{t}$ from (25) into condition ${\lambda }_{t}{G}_{t+1}+\sigma ={\lambda }_{t}(1-\tau ){w}_{t}\phi {n}_{t}$, which is obtained from (13) and (14), one can obtain

$$(1-\phi {n}_{t})[\varepsilon \theta \beta +\sigma (1+\varepsilon \theta )]=(1+\beta +\varepsilon \theta )\phi {n}_{t}$$

(26)

Therefore, the fertility rate in period $t$ is given as

$${n}_{t}=\frac{\sigma (1+\varepsilon \theta )+\varepsilon \theta \beta }{\phi (1+\varepsilon \theta )(1+\beta +\sigma )}$$

(27)

The right-hand side of (27) is independent of the period. The fertility rate in each period is constant, i.e., ${n}_{t}=n$ for all $t$, when the wage tax rate $\tau$ and $\theta$ are kept constant. It is noteworthy that even when parents are non-altruistic toward their children, i.e., $\sigma =0$, parents want to have children merely for exchange motives.¹⁸

From (6), (23), and definition ${s}_{t}\equiv {I}_{t+1}/(1+{r}_{t+1})$, one obtains

$$(1-\tau ){w}_{t+1}[{z}_{t+1}+\varepsilon {z}_{t+1}^{G}(1-\gamma )]=\gamma (1+{r}_{t+1}){k}_{t+1}$$

(28)

From (21), (22), and from the government budget constraint (19), it follows that

$${z}_{t+1}=\{[\gamma -(1-\gamma )\varepsilon \theta ]/\theta \}{z}_{t+1}^{G}$$

(29)

The government budget constraint (19) is rewritten from (21) and (22) as

$${l}_{t+1}=\frac{1-\alpha (1+\theta )}{\alpha \theta }{z}_{t+1}^{G}$$

(30)

where $1-\alpha (1+\theta )>0$. Inserting these into the time constraint, one obtains

$$[\frac{1-\alpha (1+\theta )}{\alpha \theta }+\frac{\gamma -(1-\gamma )\varepsilon \theta +\theta }{\theta }]{z}_{t+1}^{G}=1-\phi n$$

from which one has

$${z}_{t+1}^{G}=\frac{\alpha \theta }{1-\alpha (1-\gamma )(1+\varepsilon \theta )}\frac{1+\beta +\varepsilon \theta }{(1+\varepsilon \theta )(1+\beta +\sigma )}$$

(31)

From the time constraint (8), one obtains

$${z}_{t}=\frac{\alpha [\gamma -(1-\gamma )\varepsilon \theta ]}{1-\alpha (1-\gamma )(1+\varepsilon \theta )}\frac{1+\beta +\varepsilon \theta }{(1+\varepsilon \theta )(1+\beta +\sigma )}$$

(32)

The right-hand sides of (30), (31), and (32) are independent of the period. Therefore, for a given tax rate, not only public old-age support, but also the labor employment in non-health consumption goods sector, and family old-age support time are constant through all periods, i.e., ${z}_{t}^{G}={z}^{G}$, ${l}_{t}=l$, and ${z}_{t}=z$ for all $t$. For family and public old-age support to be positive, it must be the case that $\gamma -\varepsilon \theta (1-\gamma )>0$. The condition is assumed to be satisfied for the analyses described in this paper.¹⁹

3.2 Dynamics of the economy

From (17), (23), and ${G}_{t+1}=\varepsilon \theta {n}_{t}{k}_{t+1}$, the rule of motion of capital per worker is given by

$${k}_{t+1}=\frac{\beta (1-\tau )(1-\phi n)(1-\alpha ){l}^{-\alpha }}{(1+\beta +\varepsilon \theta )n}{k}_{t}^{\alpha }$$

(33)

Because the coefficient of ${k}_{t}^{\alpha }$ is positively constant and because $0<\alpha <1$, the amount of capital per worker exhibits stable dynamics. In addition, the long-term equilibrium steady state is unique. From (33), the long-term steady state capital per worker is

$$k={[\frac{\beta (1-\tau )(1-\phi n)(1-\alpha ){l}^{-\alpha }}{(1+\beta +\varepsilon \theta )n}]}^{1/(1-\alpha )}$$

(34)

where $\tau =[\alpha /(1-\alpha )]\theta$.

4 Effects of public old-age support policy

This section presents analyses of the effects of public old-age support policy changes on the steady state. The next subsection presents analyses of the effects. SubSect. 4.2 provides a numerical example.

4.1 Policy effects

The effect of the wage tax on the fertility rate is ascertained by differentiating (27) with respect to tax parameter $\theta$ as

$$\frac{dn}{d\theta }=\frac{1}{\phi (1+\beta +\sigma )}\frac{\varepsilon \beta }{{(1+\varepsilon \theta )}^{2}}>0$$

(35)

Therefore, I come to the following proposition.

Proposition 1

I assume that individuals have strategic bequest motives and that the individual rationality constraint is binding. Increases in the tax for public old-age support always raise the fertility rate.

This result is consistent with others reported in the literature. Among others, Yakita (2018) shows that increases in the female wage rate lower child-rearing time and increase the market labor supply.²⁰

Next, I present analyses of policy effects on the time allocation of working individuals. The effect on public old-age support is demonstrated by differentiating (31) with respect to $\theta$ as

$$\frac{d{z}^{G}}{d\theta }=\frac{1}{(1+\varepsilon \theta )(1+\beta +\sigma )}[\frac{\alpha [1-\alpha (1-\gamma )](1+\beta +\varepsilon \theta )}{{[1-\alpha (1-\gamma )(1+\varepsilon \theta )]}^{2}}-\frac{\varepsilon \beta }{1+\varepsilon \theta }]$$

(36)

Although the first term in brackets on the right-hand side is positive, the second term is negative from (35). Therefore, the sign of the effect is not determined a priori. However, one can reasonably consider that an increase in the tax rate will increase public old-age support. Otherwise, there will be no government incentive to introduce the tax for old-age support provision. Therefore, I assume that the sign of (36) is positive in the following. When the discount factor is sufficiently small, the assumption is likely satisfied.

The policy effect on family old-age support is derived from (32) as

$$\begin{array}{c}\frac{dz}{d\theta }=\frac{1}{[1-\alpha (1-\gamma )(1+\varepsilon \theta )](1+\varepsilon \theta )(1+\beta +\sigma )}[\frac{\alpha (\alpha -1)\varepsilon (1-\gamma )(1+\beta +\varepsilon \theta )}{1-\alpha (1-\gamma )(1+\varepsilon \theta )}\\ -\frac{\varepsilon \beta \alpha [\gamma -(1-\gamma )\varepsilon \theta ]\phi }{1+\varepsilon \theta }]<0\end{array}$$

(37)

Increases in the tax rate decrease family old-age support. However, summing up the comparative static analyses presented above and from the individual time constraint, the net policy effects on the market labor supply $l$ and $l+{z}^{G}$ are indeterminate. This result contrasts against those obtained with a fixed fertility rate. For instance, decreases in the after-tax wage rate decrease the market labor supply of families, thereby increasing family long-term care, as reported by Yakita (2020a), who assumes children’s altruism toward elderly parents. Therefore, the following proposition can be adopted.

Proposition 2

Effects of old-age support tax changes on the total old-age support, family and public, and the market labor supply are indeterminate a priori.

Finally, the policy effects on per-worker capital stock in the non-health consumption production are ambiguous, depending on the effect on the labor in the consumption goods sector. A higher fertility rate works to lower per-worker capital. Therefore, I have the following proposition:

Proposition 3

An increase in the tax rate does not always lower the steady-state level of per-worker capital stock indeterminately.

These results described above can be interpreted as follows. I assume that a rise in the wage tax rate always increases formal old-age support. For an individual to retain the optimal allocation (5), the increased formal old-age support tends to increase old-age non-health consumption and tends to decrease family old-age support $z$ (see (6)).²¹ Nevertheless, the increased formal old-age support raises old-age utility ${u}_{2}^{*}$, which will induce workers to decrease lifecycle savings $s$ (see (7), (11), and (17)). The increased present value of formal old-age support induces individuals to increase the number of children, i.e., the fertility rate $n$, ceteris paribus (see (18)). Because the after-tax wage rate is the opportunity cost of child-rearing time, the lowered after-tax wage rate also contributes to the increase of the fertility rate (see (14)).

The worker’s time which is freed from family support provision is at least partly allocated to child rearing, although the market labor supply of workers ${l}_{t}+{z}^{G}$ might not be increased. The increased number of children in turn works to decrease family old-age support per child (see (5)). It also might work to decrease the savings of workers. The increased formal old-age support provision requires the use of labor time ${z}^{G}$. Together with the increased child-rearing time, the labor employed in consumption goods sector $l$ might become less. Both the higher fertility rate and the smaller labor supply in the consumption goods sector render the tax effect on the per-worker capital stock $k$ ambiguous. Therefore, the effect of the increased formal old-age support on lifetime utility $\widetilde{U}$ is ambiguous.

To clarify the contributions of my work to the literature, two remarks are noteworthy at this stage of argument. First, time constraint (8) can be rewritten as $1-\phi n=l+z+{z}^{G}$. From (29) and (30), the shares of the right-hand side are, respectively, $1-\alpha (1+\theta )$, $\alpha [\gamma -(1-\gamma )\varepsilon \theta ]$, and $\alpha \theta$. If the left-hand side $1-\phi n$ remains constant, then the increased tax rate increases ${z}^{G}$ and decreases $l$ and $z$. Nevertheless, because the higher fertility rate decreases the left-hand side in this paper, the effects of the tax hike on $l$ and $z$ become indeterminate.²² This result contrasts to that reported by Miyazawa (2010), who assumes an exogenous fertility rate.

Second, the result of the positive fertility effect of formal old-age support is independent of whether public old-age support is cost-efficient relative to family support, i.e., whether $\varepsilon \ge 1$ or $\varepsilon <1$. This finding contrasts against the result reported by Yakita (2023a), which was reached under the assumption of altruistic elderly care supply for parents. Yakita (2023a) demonstrates that an expansion of public long-term care lowers fertility when public long-term care provision is less cost-efficient than family care is. The negative fertility effect can be true even when public long-term care is more cost-efficient.²³ In Yakita (2023a), unlike the analyses presented herein, the exogenously given minimum long-term care must be provided by family and the government. Therefore, the cost of inefficiency must be borne by workers. In the present model with strategic bequest motives, the cost of providing family old-age support is compensated with strategic bequests. In addition, the total old-age support level is chosen in intergenerational exchanges irrespective of the cost-efficiency of formal old-age support provision.

4.2 Numerical example

This subsection presents numerical results obtained by assuming model parameters to examine the effects of policy changes qualitatively.

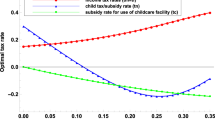
According to de la Croix and Doepke (2003), the utility weight of children is set as $\sigma =0.271$. In addition, the discount factors are $\beta ={0.99}^{120}=0.299$, for which it is assumed that one period lasts 30 years.²⁴ The income share of capital is assumed to be $\alpha =0.3$, as usual in the macroeconomics literature. The scale parameter for non-health consumption goods is set to unity for this example. Although the burden rate for social security varies from country to country, I set $\tau =0.10$ as a benchmark rate because, for example, the social security benefits–GDP ratio was 23.6%, approximately half of which was of pension benefits in Japan in 2019 (Ministry of Health, Labour and Welfare of Japan 2023).²⁵ In this case, $\theta =0.23$. The contribution ratio of old-age support to the old-age utility is assumed to be $\gamma =0.864$. Liu et al. (2023) show that an increase in Long-term Care Insurance (LTCI) increases non-health consumption by 0.157%. The elasticity of substitution between non-health consumption and old-age support might be nearly zero (e.g., ADL), whereas the demand for old-age support depends on its price (Sano et al. 2022).²⁶ The magnitude of the marginal effect approximates an elasticity. The cost-efficiency of public old-age support is set as $\varepsilon =0.5$. Yakita (2023a) calculates it from empirical works elucidating the Japanese long-term care industry, such as work reported by Aya (2014).²⁷ Per-child rearing time is assumed variously in the literature. I set the variable $\phi =0.19$. This value is approximately equal to 0.15, as assumed by de la Croix and Doepke (2003). The parameter set engenders the equilibrium fertility rate of about unity. Using these parameters, I calculate the steady state values of endogenous variables of the model. For comparative statics, I consider variations of $\tau$ by 0.01 from the benchmark case. Table 1 presents the results.

Table 1 Simulation results

As shown in Proposition 1, a tax increase for old-age support increases the fertility rate. In addition, capital stock per worker and family support decrease. With the assumed parameters, the tax rise increases public old-age support, as expected by the policymaker. Market labor $l+{z}^{G}$ decreases along with the tax rise. Although old-age non-health consumption decreases, total old-age support $z+\varepsilon {z}^{G}$ increases. Consequently, the net effect on the old-age utility ${u}_{2}^{*}$ is positive. Nevertheless, the negative effect on the working-period non-health consumption through the negative income effect overwhelms the positive effect on fertility, consequently lowering lifetime utility $\widetilde{U}$.,²⁸²⁹

5 Discussion: social optimum

As described earlier, it was demonstrated that tax increases to fund public old-age support always increase the fertility rate, although tax increases lower the per-worker capital stock. This section presents evaluation of the policy of public old-age support by comparing the decentralized long-term equilibrium under a public old-age support policy with the social optimum. In doing so, the role of strategic bequest motives in the dynamic allocation might be clarified.

The long-term equilibrium is achieved as a steady state. Therefore, the social optimum is regarded as the steady state which maximizes the lifetime utility of an individual by controlling the resource allocation centrally. The total old-age support per worker is designated as $Z$.

The social optimization problem of the social planner can be formalized as

$${\underset{c_{1}, c_{2}, n, Z, k, l}{Max}}\,\, {\widetilde{U}}={\text{ln}}{c}_{1}+\sigma {\text{ln}}n+\beta (1-\gamma ){\text{ln}}{c}_{2}+\beta \gamma {\text{ln}}{(nZ)}$$

$$\mathrm{subject\, to}\, {k}^{\alpha }{l}^{1-\alpha }-{c}_{1}-\frac{{c}_{2}}{n}-nk=0$$

(38)

and

$$1-l-Z-\phi n=0$$

(39)

Constraint (38) is the resource constraint. In addition, (39) is the time constraint per individual. Derivation of the solution is set aside for presentation in the Appendix. From the first-order conditions for maximization, the optimal resource allocations are obtained as

$$\frac{{c}_{1}}{y}=\frac{1-\alpha }{1+\beta (1-\gamma )}$$

(40a)

$$\frac{{c}_{2}/n}{y}=\frac{(1-\alpha )\beta (1-\gamma )}{1+\beta (1-\gamma )}$$

(40b)

and

$$\frac{nk}{y}=\alpha$$

(40c)

From (40c), I can immediately obtain $\alpha y/k[=\alpha {k}^{\alpha -1}{l}^{1-\alpha }]=n$. This is the Golden Rule condition for capital accumulation.

Using (40a)–(40c), I obtain the following socially optimum constant allocation rules:

$${n}_{so}=\frac{(1-\alpha )(\sigma +\beta )-\alpha [1+\beta (1-\gamma )]}{\phi \{(1-\alpha )(1+\sigma +2\beta )-\alpha [1+\beta (1-\gamma )]\}}$$

(41)

$${l}_{so}=\frac{(1-\alpha )[1+\beta (1-\gamma )]}{(1-\alpha )(1+\sigma +2\beta )-\alpha [1+\beta (1-\gamma )]}$$

(42)

and

$${Z}_{so}=\frac{\beta \gamma (1-\alpha )}{(1-\alpha )(1+\sigma +2\beta )-\alpha [1+\beta (1-\gamma )]}$$

(43)

Subscript $so$ designates the optimal value of variables in the Golden Rule optimum. For these values to be non-negative, the denominators on the right-hand sides of these equations must be positive. I assume that these conditions are satisfied. For expositional purposes, I also assume that the social optimum fertility rate is positive, i.e., ${n}_{so}>0$.³⁰ Assuming a non-negative fertility rate, I have ${l}_{so}>0$ and ${Z}_{so}>0$.

After comparing these optimum solutions with those obtained under decentralization with public old-age support policy, one can infer the following: First, the tax rate which achieves the optimum fertility rate is obtainable from (27) and (41), i.e., $\tau =[\alpha /(1-\alpha )]\theta$ satisfying the following condition.

$$\theta \varepsilon =\frac{(1+\beta )\{\beta (1-\alpha )-\alpha [1+\beta (1-\gamma )]\}}{(1-\alpha )\beta (\sigma +\beta )+\alpha [1+\beta (1-\gamma )]}$$

(44)

Two remarks must be made: First, tax rate $\theta$ is inversely proportional to the relative cost-efficiency of public old-age support $\varepsilon$. When the public support efficiency is higher, the tax rate is lower by comparison.³¹ Nevertheless, the possibility cannot be ruled out that the decentralized fertility rate with zero wage tax, i.e., with no old-age support policy, can be higher than the social optimum fertility rate. To illustrate this point, I set $\tau =0$ in (27). Then, the decentralized fertility rate without policies is

$${n}_{ss\left|\tau =0\right.}=\frac{\sigma }{\phi (1+\beta +\sigma )}$$

(45)

From (41) and (45), the difference between two rates ${n}_{so}-{n}_{ss\left|\tau =0\right.}$ can be demonstrated as

$${n}_{so}-{n}_{ss\left|\tau =0\right.}=\frac{(1+\beta )\{(1-\alpha )\beta -\alpha [1+\beta (1-\gamma )]\}}{\phi \{(1-\alpha )(1+\sigma +2\beta )-\alpha [1+\beta (1-\gamma )]\}(1+\beta +\sigma )}$$

(46)

The sign of expression (46) cannot be ascertained a priori. If it is negative, i.e., if ${n}_{so}-{n}_{ss\left|\tau =0\right.}<0$, then the public old-age support provision fails to achieve the optimum fertility rate because an increase in $\tau$ always raises the fertility rate, as condition (35) shows.³²

Second, even if a wage tax $\tau$ achieves the optimum fertility rate, the tax rate might not achieve the overall resource allocation efficiency.³³ The tax rate equalizing ${l}_{ss}$ in (31) with ${l}_{so}$ in (42) might not equalize ${n}_{so}$ with ${n}_{ss}$.

With the parameters assumed in the preceding section, the social optimum fertility rate is ${n}_{so}=0.460$. The optimum level of lifetime utility is ${\widetilde{U}}_{so}=-1.085$, whereas ${k}_{so}=0.397$, ${l}_{so}=0.731$, and ${Z}_{so}=0.182$. The utility of individuals during the third period is ${u}_{2}=0.060$. Although the social optimum rate is too low to maintain the population size in the steady state, some strategic bequest motives are observed as reported for Japan by Horioka et al. (2018). Therefore, when individuals have strategic bequest motives, the equilibrium fertility rate would be higher than the social optimum, even without public old-age support. This finding implies that if government aims to maintain, or even increase, the population size, then the optimal policy would be to provide sufficient public old-age support, consequently lowering the lifetime utility, in the decentralized system with strategic bequest motives.³⁴

Summing up the arguments presented above, I obtain the following proposition.

Proposition 4

Presuming that individuals have strategic bequest motives, then an old-age support policy alone might not lead the decentralized long-term equilibrium to the social optimum.

In the model, there are two potential sources of inefficiency: finite lifetimes and strategic behaviors. Nevertheless, the numerical example implies that strategic bequest motives might engender a high fertility rate compared to the optimum.³⁵ For this study, only old-age support financed by wage taxes is considered. Dynamic efficiency in the sense of a golden rule might require multiple policy measures.

6 Concluding remarks

For a dynamic general equilibrium model in which old-age support is provided by children to parents based on strategic bequest motives, an analysis of the fertility decisions of individuals is presented. The formal old-age support provision increases the fertility rate but engenders ambiguous effects on the lifetime utility of individuals a priori. Nevertheless, the numerical example illustrates that a tax increase lowers per-worker labor and per-worker capital stock in the non-health consumption sector. It also decreases non-health consumptions during the working period and during the old age period. Although old-age utility increases, the lifetime utility decreases in spite of the increased number of children.

After comparing the decentralized long-term equilibrium with the golden rule social optimum, one can infer that public old-age support provision might not be socially desirable under strategic bequest behaviors of individuals. Even when no public old-age support is provided, strategic bequest motives of individuals might engender a fertility rate that is higher than the social optimum rate.

Additional avenues for future research directions can be inferred. First, as Horioka et al. (2018; 2021) demonstrate, individuals might have both altruistic and strategic bequest motives simultaneously. The analyses can be extended to such a case. Although the effect of public old-age support on fertility is independent of the cost-efficiency of public support in this study, Yakita (2023a) demonstrates that public long-term care provision lowers fertility if the public provision is inefficient. Second, these analyses have not considered any child policy. If old-age support affects child policy, then that influence must be considered in a model simultaneously. Third, whether an old individual becomes dependent and the degree to which dependency exists can be expected to vary among individuals. Such uncertainty must be considered. Many works such as those reported by Pestieau and Sato (2008) and by Cremer and Roeder (2013) introduce such uncertainty. Fourth, these analyses assume only child-rearing time costs. This assumption simplifies the analyses together with Cobb–Douglas utility functions. The goods costs of rearing and educating children might be considerably large. Incorporation of these costs makes the fertility decisions dependent on the relative magnitudes of the wage rate and the goods price (Becker and Barro 1988).

Finally, and more importantly, I have assumed that steady-state old-age support, family plus public, is determined as an interior solution. However, given the level of public support, individuals might want to make the level of family support negative. In other words, the public old-age support is perceived as too great relative to old-age non-health consumption. If the level of public support is merely equal to the necessary level for old-age individuals to subsist, then the chosen fertility rate might be a corner solution to their utility maximization. In this case, the negative income effect of tax increases becomes strong for individuals, consequently affecting the fertility rate negatively. Therefore, under such circumstances, together with positive effects of the opportunity cost change, the net effect of a tax increase on the fertility rate might be indeterminate a priori. This possibility presents an interesting avenue for future research in this area.