1 Introduction

Some occupations exert a higher toll on human health than others. In this paper, we investigate in a unified framework how job characteristics affect health and aging before and after retirement. The related literature (discussed below) usually addresses these problems separately: it investigates the effects of occupation or the effects of retirement and focuses on the state of health. Here, we focus on the process of physiological aging, i.e., the deterioration of health with chronological age, before and after retirement.

Our holistic approach to the aging process of elderly individuals makes it possible to test predictions of health economic theories on the development of health over the human life cycle and how aging is shaped by occupational health burdens. Specifically, we investigate predictions of the health capital model (Grossman 1972) and the health deficit model (Dalgaard and Strulik 2014). The health capital model assumes that individuals accumulate a health capital stock that is subject to (perhaps age-dependent) depreciation. It predicts that the health of healthy persons (endowed with much health capital) deteriorates faster than that of less healthy persons of the same age because in every time increment healthy persons lose more health capital due to depreciation. The health deficit model, in contrast, considers human aging as a self-productive process of health deficit accumulation, which means that existing health deficits are conducive to the development of more health deficits during the next time increment. The health deficit model predicts that unhealthy persons age faster in physiological terms than healthy persons of the same chronological age.

The effects of occupation on the process of aging have been studied by Case and Deaton (2005). We follow their approach by assuming that the health burden from occupation may exert a level effect or a rate effect on health. A level effect means that taking up a burdensome occupation reduces the state of health. A rate effect means that working in a burdensome occupation increases the speed at which health deteriorates with chronological age. Likewise, we conceptualize retirement as the removal of occupation-specific level or rate effects. The removal of an occupation-specific level effect means a “spontaneous” change in the state of health at or shortly after retirement. The removal of an occupation-specific rate effect means that retirement changes the speed at which health deteriorates.

The health capital model predicts that the health status of workers converges before retirement if occupation exerts a level effect on health (Case and Deaton 2005) and that the health status of workers from different occupations always converges after retirement. The health deficit model, in contrast, predicts that health status of workers diverges before retirement, irrespective of whether occupation exerts a level or rate effects on health. The health status of workers from different occupations is predicted to diverge further after retirement, unless retirement leads to the full recovery of the occupation-specific loss of health. We develop these predictions in more detail in Section 2.

Identifying processes of converging or diverging health status is important beyond the assessment of health economic theories. It is relevant for policy makers designing social insurance systems. For example, the level of accumulated health deficits is strongly associated with mortality (e.g., Mitnitski et al. 2002; Hosseini et al. 2022; Dalgaard et al. 2022). Designing fair pension policies (where lifelong contributions match expected benefits) is less challenging if occupation-specific health differences depreciate after retirement, rather than if they continue to widen (Grossmann et al. 2002).

In order to measure biological aging and how it is affected by occupation and retirement, we follow an established method in gerontology (Mitnitski et al. 2001; Searle et al. 2008) and construct a frailty index (health deficit index). The index counts the number of health deficits that a person has at a given age relative to the number of potential health deficits. Health deficits include serious disabilities as well as mild illnesses that relate to the aging process. We then use information on retirement to construct a dummy variable that indicates whether an individual is retired. For this purpose, we employ the Survey of Health, Aging, and Retirement in Europe (SHARE) which contains health-related information, as well as retirement and the life-history of individuals.

We use the log of the frailty index as the dependent variable and age and retirement as the explanatory variables. In order to assess occupation-specific health effects that operate independently of the personal characteristics of workers, we exploit the panel dimension of the data and control for individual fixed effects. In order to account for the potential endogeneity of retirement we instrument it with two dummy variables that indicate whether an individual has reached the early or normal statutory retirement ages, in a similar vein to Mazzona and Peracchi (2012; 2017). We first split the sample according to educational level, with 11 years of schooling as the threshold. We next consider the last job as reported in the SHARE dataset and, following Mazzona and Peracchi (2017), we classify jobs as being demanding or not in three different ways: overall job burden; physical job burden; and psychosocial burden. Finally, we classify occupations into white and blue collar jobs.

We find that individuals in low-status occupations display more health deficits at any age before and after retirement. This difference is observed for low vs. high education individuals, individuals in blue vs. white collar occupations, individuals in occupations of high vs. low physical burden, and for individuals in occupations of high vs. low psychosocial burden. We also find that retirement leads to a reduction of health deficits, which is statistically significant and large for individuals from low-status occupations and small and frequently insignificant for individuals from high-status occupations. The only “anomaly” is that we also observe large health benefits from retirement for women in white collar occupations. Most importantly, we find that individuals in low-status occupations develop new health deficits faster before and after retirement. In other words, we find evidence for diverging aging processes across occupational groups.

Our study is inspired by the work of Case and Deaton (2005) who also emphasize the dynamic process of aging but focus mainly on the working life. Using self-reported health from the National Health Interview Surveys (NHIS), they observe a health-cost especially of low-paid or manual work such that workers in these occupations have both lower health status and more rapidly deteriorating health. The authors conclude that the observation of a widening occupational health gap as workers become older is hard to reconcile with Grossman’s (1972) health capital model. In their cross-sectional study, Case and Deaton control for a wide array of potentially confounding variables and argue that they provide “prima facie evidence for the existence of occupational specific health effects that operate, at least in part, independently of the personal characteristics of the workers” (p. 199). We try to improve on this state of affairs by using panel data and controlling for individual fixed effects, i.e., we investigate the individual aging process of workers in specific occupational groups and control for unobserved heterogeneity at the individual level. We also refine the health metric by replacing the crude measure of self-reported health with the gerontologically founded frailty index.

Our study is also related to the influential work of Michael Marmot (and coauthors). Initially based on longitudinal studies of British civil servants and then extended in other directions, Marmot argues that occupational status is mainly associated with health status because of occupational stress, social position, and sense of being in control of one’s life (e.g., Marmot et al. 1991, 1997; Marmot 2005). We contribute to this line of research by investigating the impact of psychosocial job burden on health deficit accumulation and by showing that it is as large, if not larger, than the impact of physical job burden.

More recent work by Fletcher et al. (2011) constructs measures of physical demands and environmental stress of job characteristics for a sample of US households and finds negative effects on self-reported health for individuals working in jobs with high physical demands or harsh conditions, in particular for women and older workers. Gueorguieva et al. (2009) investigate self-rated health for a sample of older workers from seven waves of the Health and Retirement Survey (HRS) and find health effects of occupation on the level of health but not on the speed of aging. Kelly et al. (2014) investigate occupational effects on health behavior and find that blue collar work early in life is associated with increased probabilities of obesity and smoking, and decreased physical activity later in life. Ravesteijn et al. (2018) investigate health satisfaction in a panel of German workers. Controlling for selection by lagged health, they find level and rate effects on health of blue collar work, as well as of physical strain and low job control. Morefield et al. (2012) investigate health transitions and observe that workers in physically more demanding jobs are more likely to transit from good to bad health but do not have different probabilities of health improvements.

In the rich literature on the effects of retirement on health, many but not all studies suggest that retirement improves health. Coe and Zamarro (2011) are perhaps the first who exploit statutory retirement age as an instrument for retirement. Using data for a sample of countries from the first wave of SHARE, they find a large positive impact of retirement on self-reported health as well as on an index of objective health measures. They also find, surprisingly, that age has only a small effect on health and no evidence for a non-linear age-health relationship. A limitation of the cross-sectional study is certainly that it cannot consider the aging process of individuals and that it cannot control for individual heterogeneity by including individual fixed effects. Behncke (2012) uses data for England and a propensity score matching methodology and finds that retirement significantly increases the risk of suffering from chronic conditions such as cardiovascular diseases and cancer. Insler (2014) uses panel data from the HRS and self-reported predictions of working past ages 62 and 65 as instruments. He observes a large positive impact of retirement on individual health measured by a health index comprising objective and subjective health indicators. Eibich (2015) uses a regression discontinuity design and financial incentives in the German pension system and finds that retirement improves subjective health status at the individual level, which is particularly strong for low-skilled individuals. The study also suggests several channels of health behavior by showing that retirement leads to less smoking, more sleep and physical activity. Finally, evidence for Scandinavian countries is provided by Grotting and Lillebo (2020), who show that retirement benefits a composite physical health score of individuals in Norway (especially those with low socioeconomic status); and by Hagen (2018), who finds no evidence of retirement affecting mortality in Sweden.

Mazzonna and Peracchi (2017) consider the first two waves of SHARE data and merge individuals’ last occupation with indices of overall, physical and psychosocial job burden from Kroll (2011), i.e., the indices that we will also employ in our study. In first-difference regressions and instrumenting by statutory retirement age, the study finds a positive effect of retirement on a health index of male workers in physically demanding jobs but no such effect for women or individuals in jobs with low or median physical burden. Gorry et al. (2018) use panel data from the Health and Retirement Study, instrument several measures of social security by eligibility, and find that retirement improves self-reported health but not the number of diagnosed health conditions. Leimer (2017) uses fives waves of the SHARE data, instruments by statutory retirement age, and finds a positive impact of retirement on self-assessed health as well as on other health indicators. Workers in blue collar or in physically demanding jobs, however, are not found to benefit more from retirement in terms of self-assessed health (albeit in terms of mobility limitations and grip strength).

A comprehensive review of the literature on the health effects of retirement, provided by Garrouste and Perdrix (2022), concludes a consensus view that retirement leads to better self-reported health while results for effects on physical health and mortality are mixed and frequently insignificant (the meta-analytical study by Filomena and Picchio (2022) and the unified analysis of Nishimura et al. (2018) arrive at similar conclusions). Given that individuals correctly perceive that their health improved through retirement, the question arises why these improvements are not picked up by indicators of physical health and mortality. One explanation is that these indicators are too coarse. Our approach using a long-term longitudinal approach and the multi-dimensional frailty index resolves these problems. The high dimensionality of the index makes it possible to measure effects on mild health deficits and physical limitations that go unnoticed in studies that focus on one- or low-dimensional health indicators. Initially mild improvements are amplified (due to the self-productivity of health deficits) and measured as a slowdown in the development of further health deficits. These effects may remain unnoticed in studies focusing on a narrow time window around the age of retirement. Suppose an individual suffers from work-related back pain that goes away after retirement. This induces the individual to exercise more after retirement and to develop other chronic and eventual lethal diseases later in life. Such life cycle trajectories are estimated in our study using the frailty index and a long-term longitudinal approach.

The remainder of the paper is organized as follows. In the next section we provide the theoretical background for the discussion of occupational effects on aging before and after retirement. In Sections 3 we describe the data used and the empirical strategy. In Sections 4 we present and discuss the results. Section 5 concludes the paper.

2 Aging before and after retirement: theory

2.1 Two models of health over the life cycle

In order to derive testable hypotheses from a theoretical background, we consider stylized versions of the health capital model (Grossman 1972) and the health deficit model (Dalgaard and Strulik 2014). To generate a comparable situation, we impose a ceteris paribus assumption and consider two individuals of the same age and state of health at the time of entry into the workforce. In both types of health models it is usually assumed that the evolution of health depends also on health behavior (health investments, consumption of unhealthy goods etc.). These features are omitted here to isolate the direct health effects of occupation in bare-bones versions of the models, in which the state of health depends only on age, work status, and the physical or mental burden of the job.

The health capital model conceptualizes aging as loss of health capital, which depreciates at a certain rate (\(\delta \)) as individuals grow older such that \(H(t+1)=(1-\delta (t)) H(t)\), in which H(t) is the health capital stock at age t. The depreciation rate \(\delta (t)\) may be constant or increasing in age.

The health deficit model captures a stylized fact from gerontology, namely that individuals accumulate health deficits as they grow older: \(D(t+1)=(1+\mu ) D(t)\), in which D(t) are health deficits at age t, and \(\mu \) is the rate of aging. This formulation implies that health deficits are self-productive: individuals with many deficits develop new deficits more quickly.

The self-productive nature of health deficit accumulation has been established in the gerontological literature (e.g., Mitnitski et al. 2006) and, more recently, also in economics (Hosseini et al. 2022). Expressed in continuous time, health deficits are accumulated as \(\textrm{d} D / \textrm{d} t = \mu D\). The solution of the differential equation implies that health deficits grow exponentially, i.e., at constant rate with age, \(D(t)=\exp (\mu t) \bar{D}\), with initial deficits \(\bar{D}\). The gerontological literature has provided ample evidence for exponential accumulation of deficits at a rate between 2 and 5% per year (e.g., Mitnitski et al. 2002; Mitnitski and Rockwood 2016; Abeliansky and Strulik 2018a, b; Abeliansky et al. 2020). The self-productivity of health deficits has a micro-foundation in theoretical biology, based on reliability theory (Gavrilov and Gavrilova 1991) and network models of human aging (e.g., Rutenberg et al. 2018).Footnote 1

2.2 Occupation and health capital

As explained in the Introduction, we follow Case and Deaton (2005) and explore two alternative ways how occupation may affect health: level effects and rate effects. Consider first the case of a level effect. Then, the health capital model implies that health differences across occupations are largest for young workers. This feature has first been emphasized by Muurinen and Le Grand (1985) with respect to social classes. Intuitively, the argument is that the component of health decline that reflects biological aging (rather than occupational effects) is small for young workers and large for old workers (Case and Deaton 2005). Formally, consider two individuals who enter the workforce at age t with health capital \(\bar{H}\). Worker A experiences no health damage from work, while worker B suffers from the health burden \(b>0\) of the occupation. As a level effect, job burden reduces health capital by factor \((1-b)\). Suppose, for simplicity, that \(\delta \) is constant. The difference of health capital stocks at age T is then given by \(H_A(T)-H_B(T)=(1-\delta )^{T-t}\bar{H} -(1-\delta )^{T-t} \bar{H}(1-b)= (1-\delta )^{T-t} b \bar{H}\). The model predicts convergence of health status: the difference of health status is initially largest and then depreciates as both individuals grow older and suffer from “normal” aging. If health depreciation were age-dependent, the depreciation effect of a level effect would be smaller at young ages and even greater at old ages. Convergence would be faster than for an age-independent depreciation rate.

If occupation exerts a rate effect, the health capital model provides ambiguous predictions for aging before retirement. To see this, assume the simplest case of a constant rate of health capital depreciation. Consider two individuals, A and B, which share the same age and initial health status and assume that depreciation of health is larger for individual B. Then, the difference between the individual’s health capital stock is \(\bar{H} \left[ (1-\delta _A)^t - (1-\delta _B)^t \right] \), which assumes a maximum at age \(t=t^*\),

$$\begin{aligned} t^*=\left( {1-\delta _B \over 1-\delta _A } \right) / \log \left( { 1-\delta _A \over 1-\delta _B } \right) . \end{aligned}$$

The state of health of workers diverges before age \(t^*\) and converges after age \(t^*\). Allowing for age-dependent depreciation rates preserves the ambiguity.

We conceptualize retirement as the elimination of work-related health consequences. Retirement has potentially many other health relevant aspects (increasing leisure, loss of social contacts etc.). These aspects, however, do not dependent systematically on occupational health burden and are thus not in the focus of our study. Consider two workers A and B who retire at the same age R. Regardless of whether work exerted a level or rate effect on health, the worker who experienced the greater occupational health burden, say, B, thus retires with a smaller stock of health capital. After retirement, the self-depleting feature of health capital depreciation implies that the health differences between retirees disappear. Specifically, the difference of health capital is \(H_A(T)-H_B(T)=(1-\delta )^{T-R} H_A(R) -(1-\delta )^{T-R} H_B(R)= (1-\delta )^{T-R} (H_A(R)-H_B(R))\). The health difference is largest at retirement age and depreciates away as individuals grow older. The health capital model predicts convergence of the state of health after retirement. This conclusion is independent from whether depreciation is age-dependent or not.

2.3 Occupation and health deficits

The health deficit model, generally predicts that occupational health differences become larger as workers grow older. Consider two workers of the same age, A and B, with health deficits \(\bar{D}\) before entry into the workforce and a level effect on health deficits of size b only for worker B. Health deficits of worker B are thus shifted upwards by factor b and given by \(\bar{D} (1+b)\). The difference in health deficits at age T is then computed as \(D_B(T)-D_A(T)= (1+\mu )^{T-t} \bar{D}(1+b)-(1+\mu )^{T-t} \bar{D} = (1+\mu )^{T-t} b\bar{D}\), i.e., the model predicts divergence: occupational health differences increase with the age of workers.

Next, assume that the health burden from occupation increases the natural rate of aging, which is \(\mu \) without burden (individual A) and \(\mu +\mu _b\) with burden (individual B). The health gap between the two individuals is obtained as \(\bar{D} (1+\mu )^t \left[ (1+\mu _b/(1+\mu ))^t-1 \right] \). It grows with increasing age of the individuals.

After retirement, individuals accumulate new health deficits at the same rate. Since individual B experienced harsher work conditions, he enters retirement with more health deficits and the difference in health deficits at age \(T>R\) is obtained as \(D_B(T)-D_A(T)=(1+\mu )^{T-R} (D_B(R)-D_A(R))\). It becomes larger with increasing age of the individuals. Thus, the health deficit model predicts divergence of occupational health differences before and after retirement.

2.4 Identification of level and rate effects and occupational health differences

Our study focuses on level and rate effects in context of the health deficit model. Although we do not explicitly test the health capital model, inferences about the health capital model are feasible if there is a negative association between health capital and health deficits. This seems to be a rather mild assumption. In contrast to health deficits, there exists no standardized metric for health capital but empirical attempts to measure health capital are frequently based on the absence of health deficits (e.g., Wagstaff 1993) or on self-evaluated health (e.g., Grossman 2000). In the latter case, we need to assume that individuals with fewer health deficits evaluate their health better, which seems to be plausible. Under these restrictions, empirical support of the health deficit model in terms of divergence of health deficits before or after retirement implies a refutation of the health capital model. This is so because, in the terminology of Dragone and Vanin (2022), the process of human aging can only be either self-depleting or self-productive, but not both at the same time.

We compare workers from two different occupational groups, A and B.Footnote 2 Consider first a level effect of occupation that is potentially (partially) resolved with retirement. Recall that the continuous accumulation of health deficits is represented as exponential increase of health deficits with age, \(D_j(t) = \bar{D}_j \textrm{e}^{\mu _j t} \textrm{e}^{ \mathbbm {1}_{[t\ge R]} \beta _j}\), with \(j=A,B\). Notice that the rate of aging \(\mu \) is allowed to differ between occupations. The level effect assumption is represented by the feature that the rate of aging does not change with retirement. The size of the level effect at retirement is obtained by \(\mathbbm {1}_{[j=R]} \beta _j \), in which \(\mathbbm {1}_{[j=R]}\) is an indicator function that attains a value of one for retired individuals and \(\beta _j\) is an occupation-specific coefficient. Taking logs, we have

$$\begin{aligned} \log D_j(t)=\alpha _j + \mathbbm {1}_{[t\ge R]} \beta _j + \mu _j t , \end{aligned}$$
(1)

in which \(\alpha _j \equiv \log \bar{D}_j\). Occupational health differences are measured by \(\alpha _A - \alpha _B\) and the occupation-specific effect of retirement is \(\beta _A - \beta _B\). Suppose \(\alpha _B > \alpha _A\). Then the state of health of workers from the two groups diverges if \(D_B(t)-D_A(t)\) increases with age.

A straightforward way to introduce rate effects of retirement is to move the retirement-indicator from the level to the rate:

$$\begin{aligned} \log D_j(t)=\alpha _j + \mu _j t + \mathbbm {1}_{[t\ge R]} \omega _j t, \end{aligned}$$
(2)

in which \(\omega _j\) measures the occupation-specific change in the rate of aging after retirement. If there are occupation-specific rate effects of retirement, we expect \(\omega _B < \omega _A\) for \(\alpha _B > \alpha _A\), i.e., the rate of aging slows down by more after retirement for workers from burdensome occupations. This rate effect specification implies that there is also a level effect of retirement. To see this, note that at the moment before retirement, denoted \(R^{(-)}\), a worker has \(D_j=\bar{D}_j \textrm{e}^{\mu _j R^{(-)}}\) deficits whereas at the moment after retirement, denoted \(R^{(+)}\), the worker has \(D_j=\bar{D}_j \textrm{e}^{(\mu _+\omega _j) R^{(+)}}\) deficits, implying a jump of deficits at retirement by factor \(\textrm{e}^{\omega _j}\). Thus, any rate effect is associated with a level effect of a certain size.

The co-occurrence of level and rate effects is intuitive and plausible. For example, retirement may “spontaneously” resolve back pain, which induces behavior (more exercise, less drug consumption) that slows down aging, i.e., it postpones the development of other health deficits. On the other hand, retirement may not be associated with a health shock and only entail gradual adjustments of health. Formally, such an outcome would be predicted by the health capital model and the health deficit model under the assumption that retirement does not exert a shock on health. To allow for this case, we set up a third specification, in which we additionally impose that both occupation and retirement have (if at all) only rate effects. These assumptions are represented by a two-step setup:

$$\begin{aligned} \log D_j(t)= & {} \alpha + \mu _j t \qquad \text{ for } t < R, \end{aligned}$$
(3a)
$$\begin{aligned} \log D_j(t)= & {} \log [D_j(R)] + \omega _j (t-R) \qquad \text {for}\,\, t \ge R, \end{aligned}$$
(3b)

in which the constant in the second equation is the predicted log of health deficits at the transition into retirement obtained from the first equation. Occupational rate effects on health during the work life exist if \(\mu _A \not = \mu _B\). They imply divergence of health across occupational groups. Occupational health effects are resolved with retirement if \(\omega _A=\omega _B\). A common rate of aging after retirement, however, does still imply divergence because the health gap that prevailed at retirement is amplified as the retirees grow older (due to the non-linear, exponential age-deficit association). In general, inspection of coefficients for the level and/or rate effects in specifications (1) to (3b) is insufficient to infer divergence or convergence of health deficits. For that, we need to compare the implied life cycle health trajectories.

3 Empirical method and data

3.1 Data

In order to study aging before and after retirement, we use the Survey of Health, Aging, and Retirement in Europe (SHARE dataset release 7.0.0) and the Job Episodes Panel (release 7.0.0),Footnote 3 We use five waves from SHARE that provide health-related information (wave 1, 2, 4, 5 and 6); for methodological details, see Börsch-Supan et al. (2013); Brugiavini et al. (2019). Wave 1 took place in the year 2004, wave 2 in 2006/7, wave 4 in 2011 (in 2012 for Germany), wave 5 in 2013, and wave 6 in 2015.Footnote 4 We considered adults aged 50 and above in 10 countries that participated in the survey: Austria, Belgium, Switzerland, Germany, Denmark, Spain, France, Italy, Netherlands and Sweden. We focused on these countries because their relevant statutory retirement ages do not depend on individual characteristics (other than age) as in other countries like, for example, the Czech Republic where the number of children is also decisive for the statutory retirement age. We also omit Israel and Greece because they participated in the survey less often than the other countries. We only used observations of individuals aged 85 and below because several very old people show “super healthy” characteristics (likely because of selection effects).

For each observation of each surveyed individual we constructed a frailty index following Mitnitski et al. (2002) and Searle et al. (2008). We took into consideration 38 symptoms, signs, and disease classifications, which can be found in Table A.1 in the Appendix. We followed Mitnitski et al. (2002) and coded multilevel deficits using a mapping to the Likert scale within the interval 0–1. Details on the construction of each variable are available in Table A.2 in the Appendix. We then obtained the frailty index as an individual’s ratio of deficits. If information on specific deficits was not there for an individual, we instead calculated the index based on the information which was available about potential deficits (i.e., if data was not available for x potential health deficits, the observed health deficits were divided by \(38-x\)). From the surveyed people, we retained only those with information on at least 30 health deficits for at least 2 waves and also removed individuals younger than 50 since this was not the targeted population of the survey (and this group very likely represented partners of the actual targeted people). We further removed a few individuals with a frailty index of zero (1.3% of the sample) because we use the logarithm of health deficits. We arrived at a sample of 83,659 observations, which corresponds to 28,664 individuals.Footnote 5

We first split the sample by educational level. We took 11 years of schooling as the threshold for high- and low-educational levels since this was the mean value of years of education (across countries and waves). Next we split the sample according to the level of job burden (high/low) that each individual had in their last job. Each person was asked in wave 1 which was their last job, and the answer was coded following the ISCO-88 classification. Since this information is only available for wave 1, the sample for this analysis only includes individuals that were present in wave 1 (and onwards). The ISCO-88 code on the last job is used to match it with the classification from Kroll (2011). Kroll (2011) classified the jobs according to their overall intensity, which is comprised of physical and mental strain, and assigned a value from 1 to 10 to each job in the ISCO-88 classification. Mazzonna and Peracchi (2017, p.135), drawing from the classification of Kroll (2011), define a physical burdensome job as one with high environmental pollution and ergonomic stress and a psychosocially burdensome job as one with high level of “mental stress, social stress, and temporal loads”. We follow Mazzona and Peracchi (2017) and use the interval [1,5] to classify occupations of “low burden” and occupations with an index above 5 as “high burden”. Finally, we also use the reported last job with its ISCO-88 classification and assign it the category of “blue collar” or “white collar” using the classification of Eurofund (2020).Footnote 6

We recorded individuals as “retired” when they replied “retired” to the question “In general, how would you describe your current situation?”. Following the literature, we omitted those individuals who answered “permanently sick or disabled” since this group could benefit from early retirement benefits due to disability and because their aging process could be different. Moreover, we erased those individuals who refused to provide an answer. We also complimented the retirement information with that of the Job Episode Panel, provided by SHARE in another dataset. Facing the problems of endogeneity of retirement and of reverse causality, we use an instrumental variable approach. We take the “normal” and “early” statutory retirement ages as external instruments, since the statutory age is not chosen individually. The SHARE dataset provides the “normal” statutory retirement age for most individuals but the “early” statutory retirement age is reported only for a severely reduced group of individuals. Because relying on the “early” information from SHARE would reduce our sample size considerably, we have complemented it with information on early retirement provided in Leimer (2017) (for a more detailed description of statutory retirement ages refer to Appendix B). In the robustness analysis we only kept individuals who are retired, employed or unemployed (in a similar vein to Heller-Sahlgren 2017), which reduces our sample by about a quarter of the observations. We perform this exercise to observe whether retirement has a particular effect on those who are in the job market (either working or actively looking for work).

Table 1 Summary statistics
Full size table

Table 1 shows the summary statistics of the samples used for the educational split, job intensity splits as well as for the collar split. Females have, on average, more health deficits than men. This observation is line with Abeliansky and Strulik (2018a, 2018b, 2019, 2020). We also observe that individuals with higher educational levels have, on average, fewer deficits (as previously shown by Harttgen et al. 2013). The mean age of females and males is similar; while individuals are, on average, 3 to 4 years younger in the high education group. In line with this observation, the percentage of observations of retired individuals is somewhat lower among the highly educated. As expected, the mean early statutory retirement age is lower than the statutory retirement age. With respect to the sample splits according to job burden, we observe that within burden-classes men are, on average, about 1.5 years older than women. Across burden classes there are only small age differences. Men and women in high-burden occupations display on average more health deficits. This difference is most pronounced for men in occupations of high physical burden who display about 20% more health deficits than their counterparts in low-burden occupations. Occupational differences are greatest across collar groups. Men and women in blue collar occupations display on average almost 30% more health deficits than their counterparts in white collar occupations.

3.2 Model specification

As our baseline specification, we focus on level effects and estimate equation (1) separately for two occupational groups (A and B) with the following regression:

$$\begin{aligned} \log D_{iw} = \mu \cdot age_{iw} + \alpha \cdot retirement_{iw} + \lambda _i + \epsilon _{iw}, \end{aligned}$$
(4)

where D is the frailty index, i represents the individual, w the wave, age represents the age at the interview, retirement is a dummy variable that takes the value of one if the individual is retired, \(\lambda _i\) are individual fixed effects and \(\epsilon \) is the error term. Standard errors are clustered at the year-of-birth level.Footnote 7

We estimate (4) separately for men and women since previous studies have shown that males and females accumulate health deficits at different rates and levels (e.g., Mitnitski et al. 2002; Abeliansky and Strulik 2018a, b, 2019). Furthermore, gender and gender-specific aging affects selection into occupations and the retirement decision (Strulik 2022). In instrumental variable (IV) regressions for (4) we control for the potential endogeneity of individual retirement status by instrumenting it with the statutory retirement age. To that end, we construct a dummy variable RetAge that takes the value of one if the person is not younger than the statutory retirement age, zero otherwise; and a dummy variable EarlyRetAge that takes the value of one if the person is not younger than the statutory early retirement age and zero otherwise. The effect of retirement on aging investigated in this study is the average effect of retirement on aging for those led to retire by reaching the (early/standard) statutory retirement threshold (i.e., local average treatment effect, LATE). The group of compliers includes individuals who are forced into retirement by their working contracts and those who choose to retire.Footnote 8

Alternatively, we consider that occupational factors affect the rate of aging when working. Again, given the potential threats to endogeneity we use an instrumental variable approach. Based on (2), we estimate the following econometric model:

$$\begin{aligned} \ln D_{iw} = \mu \cdot age_{iw} + \omega \cdot age_{iw} \cdot retirement_{iw} + \lambda _i + \epsilon _{iw}. \end{aligned}$$
(5)

Finally, we impose the assumption that retirement has no level effects and estimate the only-rate-effects model. In order to obtain the occupation-specific level of health deficits at the transition to retirement, we need to abandon individual fixed effects and individual ages of retirement. This approach is thus only informative about aging at the group level and less immune against time-invariant omitted variables than specifications (4) and (5). Specifically we estimate equations (3) jointly for two groups of occupation (A and B) as:

$$\begin{aligned} \log D_{iw}= & {} \alpha + \mu _A \cdot age_{iw} + \gamma \cdot D_{B} \cdot age_{iw} + \epsilon _{iw}, \qquad \text{ for } age_{iw} < R, \end{aligned}$$
(6a)
$$\begin{aligned} \log D_{iw}= & {} \beta _A \cdot (1-D_{B}) + \delta \cdot D_{B} + \omega _A \cdot age_{iw} + \omega _B \cdot D_{B} \cdot age_{iw}\nonumber \\{} & {} + \epsilon _{iw}, \text {for}\,\, age_{ij} \ge R, \end{aligned}$$
(6b)

in which \(R=65\), \(D_B\) is a dummy variable that equals one if the individual belongs to group B and is zero otherwise, and \(\beta _A\) is the predicted frailty index of group A, at the transition to retirement (at age 64), obtained from the estimates of (6a). Equation (6b) is estimated constraining \(\beta _A\) to the value of the deficit level of group A at age 64, and \(\delta \) to the difference in deficits at age 64 (in log terms) between group A and B. Due to the requirement to constrain the coefficients to estimate equation (6b), we can only use Ordinary Least Squares for the estimations.

Our estimates could suffer from a “healthy worker effect” having survived the last job. While we are unable to deal directly with this issue, we show that there is no difference in attrition by death regarding those with low- and high-burden jobs.Footnote 9

4 Results: health and aging before and after retirement

4.1 Level effects of retirement

Table 2 shows the results of estimating equation (4) for men and women, according to their educational level. On average, individuals develop about 2% more health deficits from one birthday to the next. We see that elderly women start from a higher level of initial health deficits than men (larger constant) and that men, as they age, accumulate health deficits at a greater speed than women, in line with the previous literature (i.e., Mitnitski et al. 2002; Abeliansky and Strulik 2018a). Columns (1), (4), (7) and (10) show the baseline results when the retirement dummy is not included. We see that within-gender groups, individuals with low education age faster. While this result is known in principle from the literature (e.g., Harttgen et al. 2013), we here show that it holds true when controlling for time-invariant individual characteristics by including individual fixed effects in the regression.

In columns (2), (5), (8), and (11) we include the retirement dummy in the fixed effects regressions. We observe a statistically significant effect of retirement only for women with low education and for men with high education. The results, however, are likely driven by endogeneity-bias. This view is confirmed when we consider the results from IV regressions in columns (3), (6), (9), and (12). The first stage results are shown in Table F.1 in the Appendix. The instruments are sufficiently strong in predicting retirement according to the Kleibergen Paap Wald F-statistic (above the threshold of 10) and in most of the cases the Hansen statistic fails to reject the null hypothesis that the over-identifying restrictions are valid. We now observe that retirement has a significant effect on health deficits. For all four gender-occupation groups, the entry into retirement shifts the age-deficit trajectory downwards. Among women, the point estimate is only marginally higher (in absolute value) for women with low education. Among men, we observe that men with low education age more rapidly and benefit more from retirement than those with high education.

Table 2 Health deficits and retirement — education split
Full size table

As a further robustness check, we verify that similar conclusions are obtained when we use the 45-item frailty index from Börsch-Supan et al. (2021) (see Appendix Table D.1) and when we remove 3 dimensions (selected randomly) from the index in two exercises (see Appendix Tables I.2 and I.3).Footnote 10 Moreover, similar conclusions arise when we restrict the age of the individuals from 55 to 75 years of age (see Table I.1 in the Appendix).

Another concern might be that job burden influences the likelihood of attrition by death. In order to assess whether the education/job characteristic of the worker affects the probability of being in the sample in the next wave (i.e., if a person will be in the next wave since they have not passed away) we estimate a “Mundlak regression” (correlated random effects estimator) where we have as the dependent variable of a random effects regression whether the person is present in the next wave or not because he or she has passed away. As independent variables we include the type of education/job the person has, the age (which is a predictor of death), the mean age (as required by the Mundlak methodology), country and wave dummies, and a year of birth trend. The benefit of using this methodology is that we are able to simulate a fixed effects regression, while controlling for unobserved heterogeneity for the time changing variables. Table E.1 (also in the Appendix) shows that neither education nor other occupational group assignments influence the probability that a person will be present in the next wave (the only exception here is for females performing jobs with low physical burden).

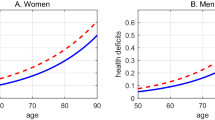
The precise effects of education on health deficit accumulation before and after retirement are difficult to assess from the estimated coefficients. In particular, the issue of convergence or divergence motivated in the theory section is hard to resolve by inspection of Table 2. To simplify inferences, we thus use the point estimates from the IV regressions for a graphical representation of biological aging of men and women distinguished by educational class. These results are shown in Fig. 1. We took the gender-specific average retirement age as the shift point. Women are represented in panel A and men are represented in panel B of Fig. 1. Health deficits by age are represented by blue (solid) lines for individuals with high education and by red (dashed) lines for individuals with low education.

Fig. 1
figure 1

Health deficits by age: high vs. low education. Predictions for estimates from IV-regression, columns (3), (6), (9), and (12) from Table 2. Retirement at the average gender-specific retirement age. Blue (solid) lines: high education; red (dashed) lines: low education

Full size image

The results from Fig. 1 show that individuals with low education have at any age accumulated more health deficits and that the distance between health deficits by skill-group gets larger with increasing age, before and after retirement. Thus health deficits diverge, as predicted by the health deficit model (and in disagreement with the health capital model). Divergence after retirement follows from the feature that health deficit accumulation is a self-productive process (cf. theory section) together with the result that the age coefficient is larger for low-educated individuals at all ages.

While it is reasonable that part of the effect of education on aging works through occupation, it is well known that education affects health also through other pathways than occupation (e.g., Grossman 2006; Strulik 2018; Galama and Van Kippersluis 2019). With our next sample split we thus focus on the physical and psychosocial burden of occupation, classified to be either high or low, as explained in Section 3. By including individual fixed effects in the regression, we control for education as a selection device since it can be reasonably argued that education is finished at the age of 50 (the youngest age in our sample). A shortcoming of these regressions is that the job burden refers to the current job or the last job that retired individuals had. If individuals, as they age, move from health-demanding occupations to less health-demanding occupations, we do not capture the job burden of the whole work-life correctly and the regressions tend to overestimate the health toll of low-burden jobs, i.e., to underestimate the occupational differences of aging and retirement.

Table 3 shows the results for the aggregate job burden split as well as separated by physical burden and psychosocial burden. Focusing on the IV regressions, we observe a statistically significant impact of retirement only for men and women in high-burden occupations. For both men and women the age coefficient is similar across burden levels but the constant is significantly larger in high-burden occupations. Retirement causes a particularly large reduction of health deficits for men in high-burden occupations, regardless of the dimension of burden.

Table 3 Health deficits and retirement — job burden splits
Full size table

Finally, Table 4 shows the results using a different categorization: whether the last job was classified either as “white collar” or “blue” collar. In the case of men, we observe the familiar pattern: the health of men with blue collar jobs benefits more from retirement. For women, we observe a new and perhaps surprising pattern: women in white collar jobs benefit more in terms of health deficit reduction from retirement than those in blue collar jobs. The point estimates, however, are quite close and the occupational differences in the benefit from retirement are no longer statistically significant when we remove home-makers and individuals having reported “other” as their last occupation (Table G.5 in the Appendix).

Table 4 Health deficits and retirement — white/blue collar split
Full size table

The first stages of the instrumental variable regressions are reported in Appendix F. In Appendix Tables G.1–G.5, we replicate the above regressions for a reduced sample in which we kept only individuals who are employed, unemployed, or retired. The estimated coefficients are of similar size and significance as in the benchmark regressions. As another robustness test, we merged the burden indicator at the two-digit ISCO-level. The benefit of this approach is that we gain in sample size, but given the high aggregation level we lose the difference between the general burden index and the physical burden index. Overall, the aging pattern for high-burden individuals remains the same in terms of statistical significance and similar in size (see Tables H.1 and H.2 in the Appendix). A robust result of all performed tests is that individuals who are or were in high-burden occupations benefit from retirement in terms of health deficit reduction. In some specifications also individuals with low burden benefit from retirement.

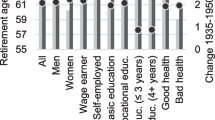
Due to the interaction of the age coefficient, the constant, and the retirement coefficient it is not always easily inferred from the estimated numbers whether the difference of health deficits between occupational groups increases or declines with advancing age, i.e., whether the results reject the health capital model or the health deficit model. In order to assess this issue in a convenient and condensed way we used the point estimates of the IV regressions from Tables 2, 3, and 4 and the average gender-specific retirement age and computed the predicted health deficits by age for the average individual from the occupational groups. We then computed the predicted difference of health deficits between occupational groups. Results are shown in Fig. 2. A downward shift of the curve indicates that individuals from low-status group benefit more in terms of health from retirement than individuals from high-status groups. A curve remaining in the positive quadrant indicates non-convergence. An upward sloping curve indicates divergence of health deficits between low- and high-status groups.

Panels A and B show results for the educational split, which is just another representation of the information shown in Fig. 1. For example, the line in Panel A shows the difference between the blue and red line of Panel A in Fig. 1. We observe that health differences between educational groups increase with increasing age for men and women before and after retirement while retirement as such reduces educational differences. The interpretation is that retirement leads to a reduction of acute job-related health deficits (e.g., acute back pain) but does not level all job-related health deficits. Some job-related deficits remain (e.g., chronic back pain) and are conducive to the development of further health deficits in retirement, as predicted by gerontological models (Gavrilov and Gavrilova 1991; Mitnitski et al. 2006; Rutenberg et al. 2018) and the health deficit model in economics (Dalgaard and Strulik 2014).

Fig. 2
figure 2

Health deficits difference by age: low- vs. high-status groups. Health differences by age between occupational groups. A, B Low vs. high education. C, D High vs. low physical job burden. E, F High vs. low psychosocial job burden. G, H Blue vs. white collar occupation. Predictions for estimates from IV-regression, columns (3), (6), (9), and (12) from Tables 2, 3, and 4. Retirement at the average gender- and occupation-specific retirement age

Full size image

Panels C-D show results for the sample split by physical job burden. The occupational difference of health deficits is particularly large and steeply increasing with age during working age. Retirement is associated with a large reduction in health deficits, which are however not fully equalized across occupational groups. After retirement, health deficits diverge again albeit at a slower pace than during working age. Panels E-F show results for the sample split according to psychosocial job burden. While health deficits diverge before retirement for both genders, health differences for men are basically flat after retirement. For women, we observe again divergence. Finally, panels G-H show results for groups identified by collar color. For men, we observe that health deficits of blue collar workers rise at a higher rate before and after retirement. The health difference between blue and white collar women stays basically constant before retirement and increases after retirement. Interestingly, we observe that the health of white collar women benefits more from retirement, i.e., we observe a rare case where retirement increases health deficits between low- and high-status workers.

With respect to health economic theory, we conclude that we almost always observe divergence of health status between groups of low and high education, blue and white collar color, and high and low physical or psychosocial job burden. We never observe convergence of health deficits with increasing age. The results contradict the predictions of the health capital model and are supportive of the predictions of the health deficit model. Divergence is explained by the self-productivity of health deficits: many existing health deficits are conducive to the faster development of new deficits. Retirement leads to a significantly greater reduction of health deficits for workers from the low-status groups. However, average health deficits of the low-status groups are still higher after retirement, which means that the self-productivity-driven divergence of health deficits is also observed after retirement. An exception is the group of men with high psychosocial job burden. Here, retirement apparently removes all job-related health deficits such that the occupational health gap disappears after retirement.

4.2 Rate effects of retirement

We next turn to the analysis of rate effects of retirement by estimating specification (5). Results are summarized in Table 5 (and the first stage results are shown in Tables F.4–F.6 in the Appendix). Focusing on the IV regressions, we observe the following regularities. Men and women with low education, or in blue collar work, or in occupations with high physical or psychosocial burden age faster when working (larger age coefficient) and the pace of aging slows down by more in retirement (the negative coefficient for age-retirement interaction is larger in absolute terms). Individuals in high-burden occupations always benefit significantly from retirement in terms of a reduction of the rate at which health deficits accumulate; while in most cases, individuals with low job burden do not significantly benefits from retirement. The exception from theses regularities is, again, the case of white collar women who benefit strongly from retirement and more so than their bluecollar counterparts.

Table 5 Rate effects of retirement
Full size table

We use these results to take up again the question of convergence/divergence. Since the rate of aging declines by more after retirement for individuals in high-burden occupations and for low-skilled/blue collar workers, there is, in principle, potential for convergence of health deficits across occupations after retirement. A necessary, not sufficient condition for convergence is that the rate of aging gets smaller after retirement, i.e., the sum of age coefficient plus age-retirement coefficient is smaller for individuals in high-burden occupations after retirement. The condition is not sufficient because initial values matter as well. In order to clarify the convergence question, we visually inspect the aging patterns predicted by the point estimates from the IV regressions in Table 5.

Fig. 3
figure 3

Rate effects of retirement. Predictions for estimates from IV-regression, columns (3), (6), (9), and (12) from Table 5. Retirement at the average statutory retirement age from Table 1. Blue (solid) lines: A high education; B low physical burden; C white collar. Red (dashed) lines: A low education; B high physical burden; C blue collar

Full size image

Results are shown in Fig. 3. As explained in the theory section, the age-retirement interaction also causes a drop of health deficits at entry into retirement. It turns out that this drop is of similar magnitude as the one predicted by the level-model. In fact, aging before and after retirement is predicted to be strikingly similar in the rate-model and in the level-model. For men, the divergence of health deficits with age across occupational groups is clearly discernible. For women, divergence is much smaller and can be identified only by computing analytically the occupational difference of health deficits. From age 60 to 90, the deficits difference between women in occupations of high vs. low physical burden increases from 1.5 to 1.9% and the deficits difference between blue and white collar women increases from 2.9 to 3.7%.

Finally, we proceed to estimate equations (6a) and (6b). Ideally, we would like to continue using fixed effects with an instrumental variable approach, but we are unable to do so since the restriction imposed on the coefficients in the constrained regression is not computationally feasible with fixed effects. The results are available in the Appendix in Tables J.1–J.5. In columns (2) and (4) of these tables the constants are constrained to the (log) deficit level at age 65 and thus they exhibit no standard error. We observe systematically that high occupational status groups age significantly slower before retirement. The point estimates suggest that high-status groups develop new health deficits at a rate that is 0.3 to 0.4 percentage points lower than low-status groups. An exception are men with high vs. low psychosocial job burden, for which there is no aging differential observed before retirement.

After retirement there are mostly no significant occupational differences in the rate of aging. An exception are women in occupations with low physical or psychosocial job burden, who are found to age faster after retirement and men in white collar occupations who continue to age slower after retirement. An equal rate of aging after retirement, however, still implies divergence after retirement when the low-status groups enter retirement with more health deficits. This shown in Appendix Fig. A.1 which shows the predicted aging based on the point estimates of Tables J.1–J.5.

Overall, the results of estimating equations (6a) and (6b) provide some reinforcing evidence that low-status occupational groups age faster before retirement and at similar rates as high-status groups after retirement. These estimates, however, should be taken with caution — individual fixed effects are not taken into account and, in particular in the before-retirement stage, the age range (50 to 64 years of age) is short and the sample size is small. We therefore prefer the rate-cum-level regressions from Table 5 to the rate-only regressions from Tables J.1–J.5.

With respect to health economic theory, we conclude that we almost always observe divergence of health status between groups of low and high education, blue and white collar color, and high and low physical or psychosocial job burden. The rate-cum-level results suggest that workers from low-status groups (low education, high job burden, blue collar) benefit greatly from retirement, both immediately and in the long-run through slower aging, but that this relief is insufficient to compensate for the faster deterioration of health during working life, implying that the occupational health gap continues to widen after retirement.

5 Conclusion

In this study we provide evidence for occupational health effects before and after retirement using the frailty index, an encompassing measure of health and aging developed in gerontology, and panel data for 10 European countries. We find that, controlling for individual fixed effects, individuals with low education, in blue collar jobs, and in physically or psychosocially demanding occupations develop new health deficits faster than individuals in the corresponding higher status groups. We instrument for retirement by statutory retirement ages and find that retirement provides a strong relief from health deficit accumulation for individuals in low-status occupations but does not lead to a complete reset of health deficits to the corresponding level in high-status occupations. Consequently, individuals in low-status occupations develop health deficits faster before and after retirement. Public policy should take these features into consideration and adjust statutory retirement according to the health burden of occupations. This conclusion becomes particulary compelling when one considers that health deficits are a strong predictor of mortality (e.g., Mitnitski et al. 2002; Dalgaar et al. 2022), implying that members of groups with low status will experience a shorter life span in retirement if the retirement age is not adjusted by the health burden of the occupations (Grossmann et al. 2002).

Overall, we observe a widening occupational health gradient not only during the work-life but also in retirement, which is particularly large for men. Diverging states of health refute the predictions of the convergence-generating health capital model. They are supportive of the self-productive nature of health deficit accumulation according to the health deficit model.