Abstract
A small but increasing body of literature finds that parents invest in their children unequally. However, the evidence is contradictory, and providing convincing causal evidence of the effect of child ability on parental investment in a low-income context is challenging. This paper examines how parents respond to the differing abilities of primary school-aged Ethiopian siblings, using rainfall shocks during the critical developmental period between pregnancy and the first 3 years of a child’s life to isolate exogenous variations in child ability within the household, observed at a later stage than birth. The results show that on average parents attempt to compensate disadvantaged children through increased cognitive investment. The effect is significant, but small in magnitude: parents provide about 3.9% of a standard deviation more in educational fees to the lower-ability child in the observed pair. We provide suggestive evidence that families with educated mothers, smaller household size and higher wealth compensate with greater cognitive resources for a lower-ability child.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A large body of evidence has developed during the past three decades showing that in utero and early life conditions have a significant impact on children’s early life ability, subsequent development and therefore on outcomes in adulthood (surveyed by Currie and Almond (2011) and Almond et al. (2018)). Most of these studies are reduced-form estimates of the total effect of an early life shock or adverse event on final adult health. However, ability in early life impacts later human capital not only through the biological channel (Heckman 2007) but also through the channel of parental involvement—in theory, parents can either reinforce or compensate for revealed early ability. It is then an empirical question whether parental actions amplify or mute the ultimate effect of early life shocks and circumstances on adult human capital outcomes.
Our paper contributes to this latter research question, which is of direct policy relevance. The current literature comprises a body of empirical evidence that appears somewhat contradictory, containing studies that document both compensatory and reinforcing parental behaviour. Attempting to clearly identify such effects given the econometric concerns is extremely difficult, and could be one reason for the apparently conflicting results. Alternatively, there may be important differences across country contexts (either cultural or economic) that lead to such different conclusions.
Our contribution extends the existing literature in three specific ways. First, we examine the response of parents to differences in child cognitive ability in early childhood in a low-income country, using a measure of ability rather than a proxy like birth weight or height. We are aware of only two previous studies that have analysed parental responses to observed cognitive ability beyond birth. Frijters et al. (2013) find that parents reinforce cognitive resources in response to differences in cognitive ability in the USA. Ayalew (2005) also finds reinforcing effects, but these results are based on estimates from only one village in Ethiopia.Footnote 1
Second, we use both sibling fixed-effects and a plausibly exogenous source instrument (rainfall in early life) for variation in cognitive ability to more convincingly identify parental responses, rather than relying on within-twin estimation, since twins are not the ideal group on which to study such effects (Bhalotra and Clarke 2018). Other instruments have been utilised in the literature. Frijters et al. (2013) use handedness as an instrument of a child’s ability, the validity of which has been contested (Grätz and Torche 2016). Leight (2017) uses grain yields as a plausible instrument for differences in ability proxied by height-for-age. There is an extremely careful literature that has analysed whether parents compensate or reinforce specific (plausibly exogenous) policies and events experienced in childhood (Halla et al. 2014; Adhvaryu and Nyshadham 2016), which is highly informative, but may only be generalisable to larger policy shocks, whereas our use of variation in rainfall could be seen as ‘normal’ shocks to childhood experienced by children in low-income countries (Maccini and Yang 2009).
Third, we descriptively examine heterogeneity in parental responses across socio-economic status, in a low-income setting. Such heterogeneity has been examined, but only in country contexts that are more developed than Ethiopia (Cabrera-Hernandez 2016; Hsin 2012; Grätz and Torche 2016; Restrepo 2016). To preview our results, we find that on average, parents provide more cognitive investment to the lower-ability child to reduce intrahousehold inequality. The compensatory parental responses appear to be concentrated in relatively higher-SES families. Specifically, we find suggestive evidence that families with educated mothers, smaller household size and higher wealth compensate through a higher level of cognitive investment when there are differences in ability, while families with non-educated mothers, larger size and lower wealth exhibit only small and modest compensatory behaviours.
The paper proceeds as follows. In the next section, we briefly review the relevant literature, and in subsequent sections then present our data, including the cognitive ability measures, followed by our econometric approach, our results and robustness checks and a concluding discussion.
2 Literature review
There are two competing theories on the direction of parental responses to observed ability in their children, both originating from theoretical models which are by now more than 40 years old. Becker and Tomes (1976) predict that parents reinforce differences in child ability by investing more in the high-ability child, under the assumption that marginal return to investment is higher when the ability of the child is higher. In this case, parents’ concern is for efficiency more than equity. On the contrary, Behrman et al. (1982) suggest that parents will compensate for ability differences to achieve equality among children when parents’ inequality aversion preferences outweigh efficiency concerns.
In response, a burgeoning empirical literature has examined the effect of child endowments on parental responses. However, the results of this literature are mixed, indicating overall either that there is no clear direction of parental response on child endowment, or that the response depends heavily on context. Some studies have found evidence of reinforcing parental responses (Aizer and Cunha 2012; Adhvaryu and Nyshadham 2016; Behrman et al. 1994; Datar et al. 2010; Frijters et al. 2013; Grätz and Torche 2016; Hsin 2012; Rosales-Rueda 2014); some have found compensating parental responses (Behrman et al. 1982; Bharadwaj et al. 2018; Cabrera-Hernandez 2016; Del Bono et al. 2012; Frijters et al. 2009; Griliches 1979; Halla et al. 2014; Leight 2017); some have found mixed responses (Ayalew 2005; Hsin 2012; Restrepo 2016; Yi et al. 2015); some have found no effect at all (Abufhele et al. 2017; Almond and Currie 2011).
Many of the recent empirical studies have relied heavily on the variation in birth weight to answer the question of parental responses, using a sibling fixed-effects (FE) model (Abufhele et al. 2017; Bharadwaj et al. 2018; Del Bono et al. 2012; Cabrera-Hernandez 2016; Datar et al. 2010; Hsin 2012; Restrepo 2016; Rosales-Rueda 2014). However, some studies argue that birth weight might be associated with prenatal endogenous input, and hence exploit a source of exogenous variation in the endowment at birth. Halla et al. (2014) study the effect of an exogenous shock on the Austrian 1986 cohort, who experienced a prenatal exposure to radioactive fallout from the Chernobyl accident. The shock decreases the birth weight, live births and Apgar score; and increases premature births and days for maternity leave. They find robust empirical evidence that parents compensate the children for experiencing input shocks. Adhvaryu and Nyshadham (2016) exploit variation in a plausible random in utero exposure to an iodine supplementation programme in Tanzania, and show that parents choose reinforcing investment in higher-ability children. Using Norwegian administrative data, Nicoletti et al. (2018) find that mothers compensate for low child birth weight by reducing maternal labour supply 2 years after birth. They instrument child birth weight by father’s health endowment at birth, which arguably only brings variation in birth weight of child through genetic transmission without a direct impact on the mother’s postnatal investments when conditioning on parental human capital and prenatal investments.
Meanwhile, other studies tackle this problem by using within-twins differences as a exogenous source of variation in endowment since prenatal parental investment is impossible to vary (Abufhele et al. 2017; Bharadwaj et al. 2018; Yi et al. 2015; Grätz and Torche 2016). For example, Abufhele et al. (2017) find that parents are neutral to the difference in birth weight of twins in Chile and support the existing evidence that parents do not invest differentially between twins. Using the same data, Bharadwaj et al. (2018) find similar results that parents do not invest differentially within twins, while, using a sample of parents with singleton siblings, compensatory behaviour is found. As Almond and Mazumder (2013) noted, the reason could be that it might be especially costly for parents to implement differential treatment between twins.
Important concerns about using twins as an instrument have been raised. Using individual data in 72 countries, Bhalotra and Clarke (2018) find that the distribution of twins is not random in the population and that indicators of the mother’s health and health-related behaviours and exposures are systematically positively associated with the probability of a twin birth. Certainly, twins are not a large proportion of the population, and may be seen more as a special case.
We build on two recent studies that examine the effect of child endowment on parental investment and, rather than relying on twins data, use instrumental variables to alleviate concerns of endogeneity bias resulting from both unobserved household heterogeneity and child-specific heterogeneity. Using sibling differences in handedness as an instrument for cognitive ability differences, Frijters et al. (2013) find reinforcing behaviours of parents who are more likely to allocate more cognitive resources on an advantaged child in the USA. Grätz and Torche (2016), however, argue that handedness might vary over time so that it might not be an adequate instrument for child’s early ability. Using the same technique but using variation in grain yields during the early life period of siblings as an instrument for physical health, Leight (2017) shows that Chinese parents invest more cognitive resources in the less-healthy child (as proxied by height-for-age) in Gansu province.
We combine a sibling-difference approach with instrumental variables, using the quasi-exogenous rainfall shocks occurring during the critical developmental period of a child as an instrument for differences in child ability between siblings.Footnote 2 As studies find that rainfall shocks have a substantial impact on child development in agricultural contexts (see Almond et al. (2018) for a review), we exploit differences between siblings by looking at rainfall shocks from in utero during the first 3 years of their lifeFootnote 3 as a source of exogenous variation in nutritional inputs during the critical development period experienced by the siblings.Footnote 4Glewwe et al. (2001) note that a suitable instrument to capture within-sibling differences should be “(i) of sufficient magnitude and persistence to affect a child’s stature; (ii) sufficiently variable across households; and (iii) sufficiently transitory not to affect the sibling’s stature” (p. 350). We provide robustness checks in this paper to argue that rainfall shock timing does indeed provide a plausible source of exogenous variation.
To our knowledge, there are two other studies examining the pattern of parental investment in the context of Ethiopia. Ayalew (2005) examines catch-up growth of children in the dimensions of health and cognitive ability, using the first three rounds of the Ethiopia Rural Household Survey from 1994–1995. He finds compensating behaviour in health but reinforcing behaviour in cognitive skills. Arguably, the results for cognitive skills are less persuasive, since they use information on only one village in the survey.Footnote 5 Second, using the Young Lives Older Cohort data and relying on ordinary least squares (OLS) and fixed-effects (FE) estimations for identification, Dendir (2014) finds reinforcing behaviours, proxying parental investment with enrolment and child time allocation and measuring ability using raw Peabody Picture Vocabulary Test (PPVT) scoresFootnote 6. Although the fixed-effects estimation successfully deals with the endogeneity issue caused by unobserved household characteristics, there is a potential high degree of correlation between child ability and unobserved child heterogeneity, such as parental preferences over one particular child, which is an individual effect. Dendir (2014) measured PPVT scores at adolescence (ages 12 and 15), which increases the probability that this measure of ability is contaminated by unobserved child characteristics and consequently biases the results, and therefore exogenous variation in cognitive ability is necessary for more plausible estimation.
While most of the existing literature reveals how parents respond to the difference in health within siblings, to the best of our knowledge, only the two studies discussed above (Ayalew 2005; Frijters et al. 2013) have examined differences in cognitive ability, and both have limitations. As it is of interest to show the specific parental response to one dimension of human capital, one would ideally like to disentangle the effect of investment in that particular dimension of human capital. However, constrained by data, only a few empirical studies have specific measures of investment in different dimensions, while most of the existing studies use a general measure of parental investment, such as time spent with the child. Yi et al. (2015)’s theory predicts that given the same early health shock, parents respond differently along different dimensions of human capital. The data they use contain detailed information on investment in family health and education. Yi et al. (2015) find mixed results: while parents compensate for the harmful effect of an early health shock by devoting more health resources to the worse-health child, they reinforce in the domain of cognition by allocating fewer educational resources to the disadvantaged child. Restrepo (2016) and Rosales-Rueda (2014) use the same dataset from the USA, the National Longitudinal Survey of Youth-Children 1979 (NLSY-C79), which gives information on inputs of time and goods in either cognitive or socio-emotional development. They suggest that parents tend to simultaneously reinforce the effect of low birth weight by providing less cognitive stimulation and emotional support to the low-birth-weight child. In our study, we measure direct cognitive investment using total expenditure on educational fees at the individual child level.
Most existing research attempts to examine parental responses to child endowments on average. Some sociological studies emphasise that in theory, socio-economic heterogeneity should be taken into account, specifically, the degree and direction of parental responses might vary by family socio-economic status (SES) (Lareau 2011; Lynch and Brooks 2013). Some consider that lower-class parents have difficulty in affording costly and risky investment in disadvantaged children, and would be more likely to reinforce differences in ability. Higher-class parents tend to be averse to inequity so may compensate for a low ability outcome (Conley 2008). On the contrary, others suggest that high-SES families may reinforce gaps in child ability by providing more educational investment to the advantaged child, while offering direct transfers, such as gifts or bequests, to the disadvantaged child (Becker and Tomes 1976; Becker 1991).
To date, only a small number of empirical studies have looked at variation in parental responses by SES, though these are all in a developed country context. Grätz and Torche (2016) find out that advantaged parents allocate more cognitive stimulation to higher-ability children, while disadvantaged parents behave indifferently to ability gaps. Yet, Halla et al. (2014) show that families with low socio-economic status chose to give birth to fewer children when their children experienced the Chernobyl accident; similarly, families with high socio-economic status compensate their low-endowed children by supplying less maternal labour (and investing more in childcare). Hsin (2012) uses maternal educational level to measure family socio-economic status. On average, no compensating or reinforcing investment is found for low-birth-weight outcomes. However, low-educated mothers prefer reinforcing investment by spending more time with heavier-birth-weight children at 6 years old, while high-educated mothers compensate low-birth-weight children by spending more time with them. Restrepo (2016) finds reinforcing behaviour on average, with low-SES families reinforcing the differences in birth weight with a greater amount of investment compared with high-SES families. None of these studies provide evidence in the context of developing countries, except Cabrera-Hernandez (2016) who finds that high-educated mothers in Mexico compensate for the low-birth-weight outcome by offering more school expenditure to the disadvantaged child.
3 Data and measures
Young Lives is an international longitudinal study of 12,000 children growing up in four developing countries (Ethiopia, India, Peru and Vietnam) over 15 years (Barnett et al. 2012), examining the causes and consequences of childhood poverty. The main cohort (2000 children in each country) were born within 12 months of each other in 2001. An older cohort (1000 children in each country) born 7 years earlier is used as a comparison group. This paper uses data from four rounds of the Ethiopia survey, focusing on the Younger Cohort (YC) and their siblings. Round 1 was conducted in 2002 (when YC index children were, on average, 1 year old), round 2 in 2006 (approximately age 5), round 3 in 2009 (approximately age 8) and round 4 in 2013 (approximately age 12). In rounds 3 and 4, one sibling, closest in age to the YC index child (either younger or older), was interviewed. This brings variation in that YC index children could be either born earlier or later in our analysis.Footnote 7
To reduce heterogeneity in child activities and parental investment, we confine the sample of YC index childrenFootnote 8 and their siblings to be aged from 7 to 14 in round 4, being old enough to enter primary school and young enough to stay in the primary school in Ethiopia. The sample is reduced to 701 sibling pairs (1402 observations) in the sibling-difference specification, born from 1998 to 2006.
3.1 Rainfall
We use monthly rainfall data at the community level additionally provided to us by Young Lives, which we merge with the survey data using birth year, birth month and birthplace (from round 1 and round 2 survey), in order to generate instrumental variables at the child-specific level. Annual rainfall is measured for each child from the 12 months prior to the birth month, so that the rainfall shock varies monthly and yearly. We use standardised annual rainfall from in utero, the first, second and third years of the child’s life in the birthplace of the child as instrumental variable, following the literature arguing that this is the critical developmental period (Almond et al. 2018). During this period, adequate rainfall contributes to improved income for the household and therefore translates into a positive nutritional input for child ability (Maccini and Yang 2009). The mean and standard deviation are calculated at the birth community level using rainfall from 1985 to 2008. In the context of Ethiopia, an extremely drought-prone agricultural country, we hypothesise that the more rainfall during the critical development period, the higher the child’s ability (Dercon and Porter 2014).
Since the sibling pairs in our sample are mainly born in the same community, the variation in the child-specific instrument variable relies on the time dimension, namely the birth month and birth year.Footnote 9 As the sibling pairs in the sample are born between 1998 and 2006, we check the distribution of annual rainfall in each community during the period from 1998 to 2008 (i.e. the second of year of life for a child born in 2006). Figure 1 shows that rainfall in most of the communities is volatile, characterised by two severe droughts in 1999 and 2002 in Ethiopia. As 90% of the sibling pairs in our sample are born at least 2 years apart, the correlation of the rainfall instrumenting for each child ability is arguably weak.Footnote 10 Furthermore, we carry out a series of t tests to examine the difference in rainfall that sibling pairs experience in their early life respectively and find that the annual rainfall during the critical developmental period between index child and the sibling is statistically different. Specifically, the index child is reported to be exposed to a statistically lower level of rainfall as they are mostly born during 2001 and 2002, when drought hit Ethiopia.
3.2 PPVT scores as a measure of cognitive ability
To analyse the effect of children’s cognitive ability on within-household allocation of cognitive resources, our main independent variable of interest is the child’s cognitive ability in 2009 (round 3). The Peabody Picture Vocabulary Test (PPVT) is a receptive vocabulary test designed by Dunn and Dunn (1997), a consistent test measuring cognition ability for both index children and siblings in Young Lives. Therefore, we measure the child’s cognitive ability using this metric.Footnote 11 The PPVT is a widely used test to measure verbal ability and general cognitive development (see Crookston et al. (2013); Paxson and Schady (2007)), and the PPVT test score is positively correlated with other common measures of intelligence such as the Wechsler and McCarthy Scales (Campbell 1998). Given that round 3 is the first round that has information on siblings, our analysis only uses the latter two available rounds of the Young Lives data.
Given the difficulty of comparing raw PPVT scores across different rounds of data collection as children age, we employ item response theory (IRT) to standardise cognitive measures by language, following Leon and Singh (2017).Footnote 12 Figure 2 showsFootnote 13 that the IRT PPVT scores increase along with age, yet the means of IRT PPVT scores vary by language, consistent with findings of Leon and Singh (2017) (Tigrigna is the highest, followed by Amarigna and Oramifa). To ease the interpretation of subsequent estimation results, and given that is is not advisable to compare across languages (Cueto and Leon 2012), the IRT scores have been standardised by language as our measure of cognitive ability, with a mean of 0 and a standard deviation of 1.
3.3 Total educational fees as a measure of cognitive resources
Our dependent variable is the allocation of parental cognitive resources, measured by the total educational fees paid in 2013 (round 4) per child. As Fig. 3 shows, an advantage of our panel data is that it leaves a longer period of time (4 years between round 3 and round 4) to measure potential parental responses after children are assessed by PPVT in round 3, while prior research mostly relies on the parental involvement measured quite soon after child ability is observed. The total educational fees are the sum of school fees and private tuition fees, serving as a direct measurement of cognitive investment.
To alleviate the concern that public educational investment and private tuition investment are substitute goods, we use Pearson’s correlationFootnote 14 to test the strength and direction of the association between these two continuous variables. While the Pearson correlation coefficient between the school fees and tuition fees, r = 0.732 at 95% confidence level, suggests that in the pooled sample higher school fees are related to higher tuition fees, the correlation coefficient estimating the association between school fees and tuition fees within-family (r = − 0.020) is statistically non-significant at 95% confidence level. This lack of correlation leads us to use total educational fees as the dependent variable of our main analysis.Footnote 15
Figure 4 shows how total educational fees are reported. In the pooled sample, shown by the left-hand chart, 76% of parents report zero total educational fees in Ethiopia, while 24% report non-zero educational fees.Footnote 16 Looking at the allocation between siblings, indicated by the right-hand chart, 16% of parents differentiate their financial educational resources among their children, while 13% of parents allocate financial resources to child education and adopt no differentiating strategy in investing their children. Our interest is to find out whether the parental investing strategy of those who invest financial resources in their children is responsive to the difference in cognitive ability.
School fees and private tuition fees as a proxy of cognitive resources are specifically documented in parents’ answers to the questions such as ‘how much you spend on school (private tuition) fees per year?’. For the sake of interpretation, we standardise the total educational fees for the analysis.
To understand whether parents report a higher level of investment for the index children, we perform a t test on the total educational fees between index children and their siblings. The t statistics (= 0.132) shows that the difference in investment between two children is not statistically different, suggesting that parents do not deliberately report a higher investment for the index children.
Figure 5 shows the raw correlation between mean cognitive ability and mean cognitive resources for each 5 percentile for the included sample. Despite the flat relationship on the left tail of the distribution, the aggregate correlation between ability and parental investment is positive in the cross-section OLS estimation. Our interest is to find out whether this plausible positive relationship continues to hold when we apply our empirical methods accounting for child observable and unobservable factors.
Therefore, we include a series of child observable characteristics as confounding factors. First, to alleviate the concern that the cognitive investments are age-related, we control for several age-related factors in the regression analysis. We make use of age in months, together with square and cube of age in months and dummies of birth year. Then, since evidence suggests that children born earlier receive the greater investment (Price 2008; Buckles and Kolka 2014), we control for birth order. Other child-level differences which might contribute to investment variation are also controlled for in the regression analysis. Specifically, maternal age at birth, height-for-age Z-score (HAZ) in round 3, birthplace, birth quarter and type of siblings (e.g. born as an older brother with a younger sister, or born as an older sister with a younger brother) are taken into account.Footnote 17 See Table 1 for summary statistics.
3.4 Socio-economic status
To understand whether educational investment varies by socio-economic status (SES), we carry out several exploratory t tests and find that families investing in education are indeed the high-SES families. The families who make positive investments in child education are significantly richer (t = − 12.253), with a significantly better educated mother (t = − 9.749) and smaller size (t = − 3.991). In order to further investigate whether these better-off families who invest in education differentiate their investment based on the ability gap between their children, we stratify our analysis on parental responses. Specifically, we employ several household characteristics (maternal education, family wealth and household size) as indicators of family SES, while we dichotomise each indicator generating a high-SES group and a low-SES group following Grätz and Torche (2016). With regard to maternal education, in fact, half of the mothers in our sample are not educated at all, so that we distinguish between families with an educated mother or a non-educated mother. In the case of family wealth and household size, we dichotomise them using the median of wealth index and size of the family.Footnote 18
Figure 6 shows the intrahousehold difference in total educational fees by SES. The distributions of within-sibling difference in educational fees are similar across three indicators. In general, the high-SES families have bigger differences in allocating educational resources among their offspring. The mean of the difference in total educational fees in low-SES families is small but non-zero.
4 Econometric strategy
To identify the causal effect of cognitive ability on parental investment, the analysis is based on an IV-FE model, targeting three main endogeneity threats. First, this approach relates within-sibling pair differences in ability in 2009 (round 3) with within-sibling pair differences in parental cognitive investment 4 years later in 2013 (round 4) to address the threat of reverse causality. Second, the sibling fixed-effects (FE) models control for unobserved heterogeneity at the household level, following most existing empirical works. Third, we use instrumental variables to isolate the exogenous variation in child ability, addressing endogeneity resulting from unobserved child heterogeneity.
The sibling fixed-effects structural model can be written as follows:
where ΔIh is the difference in cognitive investment between siblings in family h in round 4 (i.e. total educational fees), ΔCAh is the difference in ability between siblings in round 3, ΔXh is a vector of differences in other characteristics between siblings (e.g. child’s age, maternal age at birth, height-for-age in round 3, birthplace, birth quarter, birth year, birth order, type of sibling pairs—gender of older and younger child) and Δ𝜖h is the difference of the idiosyncratic error term between siblings. In this estimation, time-invariant household observable characteristics and household unobservable confounding factors are purged from the specification, but unobserved child heterogeneity, such as personality, remains.
As noted above, we overcome endogeneity bias resulting from unobserved child heterogeneity, with an instrumental variables (IV) estimation procedure. The first-stage equation is:
where ΔRh is the difference in rainfall shock from in utero to the first 3 years of a child’s life between siblings as a source of exogenous variation in nutritional inputs experienced by the siblings, and Δμh is a random error term in the first stage.
The IV approach is also helpful in the sense of overcoming attenuation bias related to measurement error in cognitive ability. Even if we consider the PPVT test score a good proxy for ability observed by parents, there is still likely to be measurement error in the test, and in its relation to parental perception of ability. For example, parents may have some other perception of their children’s cognitive ability than the PPVT score. This potential problem of measurement error can be solved by our IV approach if it is classical. Indeed, in a sibling FE model, attenuation bias caused by measurement error is augmented if one’s analysis moves from a cross-sectional setting to a FE setting (Bound and Solon 1999).
The sibling FE model coupled with the IV strategy helps us interpret β as the Local Average Treatment Effect of change in parental cognitive investment caused by the variation in child cognitive ability, which is driven by the exogenous variation in rainfall during the critical developmental period of the two children. We note that the monotonicity assumption applies to LATE estimates (Angrist and Pischke 2008), that for an change in rainfall, there should be a monotonic increase in ‘treatment’ intensity. If β > 0, parental investment increases with relative ability. Parents reinforce the differences in ability by allocating more resources to the high-ability child. If β < 0, it means parents compensate for the difference in ability, allocating more resources to the low-ability child.
Under the assumption of higher marginal returns to investment in higher-ability children, the case of β > 0 also implies that parents are concerned more with the efficiency of investment and try to maximise their children’s total future wealth. The case of β < 0, on the other hand, implies that when equity outweighs efficiency, parents forgo maximising returns from educational investment, trying to achieve higher equity among children. Del Bono et al. (2012) note also that there may also be a ‘pure endowment effect’, whereby if marginal utility of parents with respect to any individual child’s ability is positive but decreasing (i.e. the second derivative of the utility function is negative), then higher endowment of that child effectively increases family resources, but these can only be released by decreasing investment in that child. This effect is then expected to operate in the same direction as the equity effect.
We report two types of standard errors: one robust to general heteroskadasticity and the other one robust to within community dependence.Footnote 19
5 Results
In order to test the relationship between cognitive ability and deployed cognitive resources, we regress parental cognitive resource allocation in primary school on cognitive ability observed one period earlier. In all of the estimation results, total educational fees paid for each child is the proxy for cognitive resources, while PPVT scores are the proxy for cognitive ability.
For each specification, we use the sample of children who have a surveyed sibling and the information for both siblings is available. Furthermore, we have restricted the sibling-pairs to be of primary school age and use the same language in PPVT test. A set of child-level covariates is included in all models, such as age in months, maternal age at birth, height-for-age in round 3, birthplace, birth quarter, birth order, type of sibling pairs and birth year.
5.1 Preliminary results
Table 2 presents the preliminary results from the OLS models and FE model. The inconsistency of the estimates from these models is evident, the magnitudes and signs of which are not stable as we add additional controls, suggesting severe endogeneity of the variable of interest. For example, the cross-sectional OLS estimate reported in column 1, when only child-level controls are included in the model, suggests a positive relationship between ability and total educational fees. However, when we include household-level traits, maternal educational background and regional fixed–effects in the model, the point estimate decreases from 0.133 to 0.059.
However, the OLS estimate is still likely to be biased due to unobserved characteristics within the family, such as genetically innate ability, parental preferences for child quality and budget constraints. Hence, we exploit the sibling FE model, using a similar strategy to Bharadwaj et al. (2018), Datar et al. (2010) and Hsin (2012) studying parental responses to birth weight, controlling for unobserved household-level characteristics. In column 5 of Table 2, the FE estimate suggests a negative association between ability and investment, although it is not statistically significant. Aside from this, endogeneity bias might still persist since the cognitive ability is postnatal and time-varying, which allows after-birth ability to embody a significant component of prior parental investment.
To address the bias, we isolate the exogenous variation in cognitive ability using quasi-exogenous variation in rainfall during the critical developmental period. Thus, we apply instrumental variable methods to the sibling fixed-effects approach (IV-FE), a similar approach to Frijters et al. (2013) and Leight (2017), who use the same strategy but different instruments to ours.
5.2 Main results
5.2.1 IV-FE models: first-stage results and diagnostics
Before presenting our main IV-FE results, we discuss the first-stage results, as well as the underidentification and weak identification tests in Table 3. Specifically, in the first-stage estimations, endogenous cognitive ability is regressed on the exogenous regressors and excluded instruments (i.e. the rainfall during critical developmental period). We find that children who experienced relatively good rainfall aged 0–24 months have significantly higher test scores than their siblings in their early childhood; rainfall during infancy is relevant to cognitive ability as proxied by receptive vocabulary.
Shown in columns 1 to 4 in Table 3, we regress ability in childhood on annual rainfall from in utero to the first 3 years of child life respectively. We find that annual rainfall during 0 to 12 months of life and 13 to 24 months of life is significant. Therefore, we construct an IV using the average rainfall during 0 to 24 months of life and report the result in column 5. The estimate is positive and statistically significant, with a t statistic of 5.70, suggesting that an increase of one standard deviation in rainfall during the first 2 years of life is correlated with an increase of 15.6% of one standard deviation in cognitive ability in early childhood. In column 6, when we include both the rainfall during the first year and the second year of life as IVs into the IV-FE model, both of the estimates are positive and statistically significant.
With regard to the underidentification tests,Footnote 20 the p values for the specifications 2, 3, 5 and 6 all reject the hypothesis that the IV models are underidentified respectively, though not specifications 1 and 4, suggesting that the IV models are likely to be underidentified using either rainfall in utero (column 1) or rainfall in the third year of life (column 4) as the excluded instrument variable. Therefore, in the following, we focus on four IV-FE models: three of them are single IV models using rainfall from 0 to 12 months, rainfall from 13 to 24 months and average rainfall from 0 to 24 months; the last one is a two-IV model using both rainfall from 0 to 12 months and from 13 to 24 months.
We further examine the validity of the IVs by conducting a battery of weak identification tests. Noting that the traditional Cragg-Donald weak instrument test applies to the case of i.i.d. data only, we report a robust weak instrument test by Olea and Pflueger (2013) which gives valid test statistics Montiel–Plueger (M-P) effective F statistics and Montiel-Plueger critical values in the existence of heteroskedasticity at 95% confidence level.Footnote 21 Although the robust M-P F statistics in the specifications 2 and 3, which are 25.582 and 24.716, satisfy the ‘rule of thumb’ recommended by Staiger et al. (1997), when comparing them with the robust critical values given by M-P test, we notice that these statistics are slightly higher than the M-P critical value for a maximum IV bias of 10%, suggesting that there is a 5% chance that the bias in the IV estimator is 10% of the worst case possible.
When we use average rainfall between the age of 0 to 24 months as the excluded instrument, the robust weak instrument test suggests that this IV is reasonably ‘strong’. In column 5 in Table 3, the robust M-P F statistic is 32.539, which is sufficiently above the robust M-P critical value for a maximum IV bias of 10%. Additionally, the combined sets of instruments in column 6 are also ‘stronger’ than the ones in columns 2 and 3, as its M-P F statistic is 17.169 which is higher than the critical value for a maximum IV bias of 5%.
To conclude, the single instrument of average rainfall at the age from 0 to 24 months and combined set of instruments of rainfall at the age from 0 to 24 months are respectively relevant, implying the second-stage inferences will be valid and point estimates are only likely to include a relative bias lower than 10% at a 95% confidence level. These results could also serve as a supplement to the studies investigating whether some periods during the critical developmental period are more important. We find that children are particularly vulnerable at the age of 0 to 24 months in developing cognitive ability in Ethiopia, which is consistent with the findings of Maccini and Yang (2009), though Dercon and Porter (2014) find children exposed to famine at the age of 12 to 36 months are shorter than their peers in Ethiopia. In Table 9, we show IV redundancy test of a specified IV, which supports the hypothesis that rainfall at the age from 0 to 24 months are not redundant.
5.2.2 IV-FE models: second-stage results
Our main estimation results are presented in Table 4, where the second-stage estimations using four IV models selected from above are presented. Across the four IV-FE models, the point estimatesFootnote 22 are significantly negative, suggesting a compensating behaviour when parents observe their child to be underdeveloped. Particularly, remembering that the preferred IVs used in specifications 5 and 6 in Table 3, whose corresponding results are shown in columns 3 and 4 in Table 4, are relatively more relevant, the point estimates of these two specifications are very close (− 0.038 and − 0.039). It suggests that an increase in cognitive ability of one standard deviation decreases cognitive resources by 3.8–3.9% of a standard deviation.Footnote 23
The confidence intervals given by a set of weak identification testsFootnote 24 are negative. Specifically, the Anderson–Rubin (AR) test gives negative confidence sets of estimated β that is robust to potential bias introduced by weak instruments gives negative confidence intervals at a 90% confidence level. In the two-IV model, besides the AR test, the Moreira CLR test, K test and K-J test are available. The K-J test is more efficient than the AR test, and Moreira CLR test and K test obtain more power than AR test when the model is overidentified. Compared with K test, K-J test and Moreira CLR test do not suffer from spurious power losses (Finlay et al. 2016). While all of the AR, Moreira CLR, K and K-J tests give negative confidence sets, the latter three are almost identical, between [− 0.067,− 0.023] at a 90% confidence level. The J test rejection probability is low everywhere except for very high values of β, suggesting that the instruments are exogenous.
To allay the concern of our proposed IV being possibly not perfectly exogenous, we further exploit a newly developed estimator by Conley et al. (2012), which identifies a threshold for the plausible estimate even if the IV is imperfect, i.e. the excluded instrument is directly correlated with the dependent variable.Footnote 25 Specifically, one might worry that rainfall in infancy might have a direct impact on contemporaneous parental investment, despite our argument that the impact on household income is only contemporaneous and short-lived (Glewwe et al. 2001); another concern might be that early life rainfall would affect early life parental responses, which are auto-correlated with contemporary parental responses—our outcome variable. We argue that if such auto-correlation exists, the direction will be positive, if parental investment strategy is consistent over time. In particular, we assume that parents would not switch from reinforcement in early life to compensation in later life. Therefore, if early compensation effort exists, the difference of parental investment would be negatively correlated with the difference of rainfall in early life. To generate a robust estimate under this prior (Conley et al. 2012), we allow departures from the assumption of strict exogeneity of rainfall so that rainfall could have a non-zero and direct impact on parental investment, whose size is in the interval of [−δ,δ].Footnote 26 They relax this restriction so that γ is not necessarily zero, but in the bounds of [−δ,δ], allowing us to see whether this direct effect is large enough to render the IV estimate insignificant. As shown in Fig. 8, we identify the lower bound of the direct effect which would render the second-stage estimate of the interest parameter insignificant at a 10% confidence level. The results show that if the lower bound is greater than − 0.003, the second-stage estimate would be significant. As the overall reduced-form effect of rainfall on parental response is − 0.0059, we are confident that the lower bound of the model still is significant, given that the direct effect would have to be greater than 51% of the overall effect to render the IV point estimate insignificant.Footnote 27
To further allay the concern of rainfall having a long-term effect on consumption, in the robustness check shown in row 11 of Table 6, we also provide results on whether the idiosyncratic rainfall during the period when children are aged between 0 and 2 years old has a direct impact on consumption in the future at household level, and this is not significant.
Another related threat to the exclusion restriction would arise if rainfall in one sibling’s infancy affects the other’s ability (earlier or later than the critical periods in question). Therefore, we regress ability on rainfall exposure of both own and sibling rainfall shock in infancy, while replacing the household fixed effects by county fixed effects since estimating coefficients on own and sibling rainfall exposure would not be possible in a family fixed-effects model. Shown in Table 8, the estimates of rainfall during infancy of the sibling are insignificant and the magnitude is as small as a tenth of the one of our interest variable (in absolute value). The coefficient of a child’s ‘own’ rainfall during the first 2 years of life remains significant and large in magnitude after including the sibling’s rainfall.
Finally, we consider that parents’ education decision may be influenced not only by cognitive development but also by the child’s health. To address this concern, we add current health to the vector of controls. Removing HAZ does not change our results, as shown in row 10 of Table 6. We also considered health as an alternative main variable of interest, given that early rainfall may also affect health, and nutrition can be proxied by height-for-age. We therefore reran our main model with HAZ in 2009 as the proxy for child ‘ability’. Rainfall was a weak instrument for HAZ, and the second-stage results were insignificant.Footnote 28 This echoes the health literature which shows that children may recover from early height deficits by mid-childhood, but cognitive ability in mid-childhood is still highly correlated with early nutrition (Casale and Desmond 2016).
We compare our results with others using the IV-FE approach to examine parental responses. We noted some limitations of Frijters et al. (2013) handedness instrument earlier. In addition, the traditional Cragg–Donald F statistic of 12.32 under the assumption of an i.i.d. error only satisfies the ‘rule of thumb’ marginally, and arguably fails to provide strong evidence that handedness is a valid instrument to identify child’s ability. On the contrary, Leight (2017)’s grain yield instrument is robust to the existence of weak instrument using the p value from an AR test.
More generally, our finding of a strong negative relationship between cognitive ability and cognitive resources is consistent with a number of studies finding that parents prefer inequality aversion (Behrman 1988; Bharadwaj et al. 2018; Rosenzweig and Wolpin 1988; Del Bono et al. 2012; Frijters et al. 2009; Halla et al. 2014; Leight 2017; Yi et al. 2015).
5.3 Heterogeneity of parental responses to children’s early ability
After studying the parental response at an aggregate level, we now explore heterogeneities in responses by stratifying the sample by maternal education, household size and wealth. Splitting the sample according to endogeneous characteristics is not an ideal solution; however, we follow the existing literature on this topic for more developed countries than Ethiopia (Cabrera-Hernandez 2016; Hsin 2012; Grätz and Torche 2016; Restrepo 2016), given that the heterogeneous characteristics we are interested in are fixed at the household level, so these cannot be interacted in the IV model; we interpret our results here with some caution.
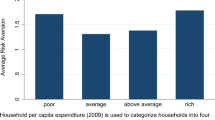
Table 5 suggests that the association between early ability and later cognitive resources does vary by family socio-economic standing (models 2–7). Specifically, the point estimates show high-SES parents provide more cognitive stimulation to their low-ability child, whereas low-SES parents compensate less cognitive investment in ability between their children. This heterogeneous variation in parental responses across SES is consistent using three indicators of socio-economic standing (maternal education, household size and family wealth). We should emphasise that the Young Lives sample is already a ‘pro-poor’ sample from communities that are relatively poor, in a country that is poor by global standards (Outes-Leon and Sanchez 2008).
Table 5 shows that among better-off parents (educated mothers, small household or high family wealth), a one standard deviation increase in ability leads to 5.3 to 6.3% of a standard deviation decrease in total educational fees, while worse-off parents only compensate 2.1 to 2.7% of a standard deviation more educational investment to the low-ability child. Given the size of the standard errors, there is some overlap in the 95% confidence intervals for the point estimates, which means we cannot conclude definitively that they are significantly different, but given the fairly small sample sizes, we do consider the evidence as strongly suggestive. In comparison, using a sibling FE model, Hsin (2012) and Restrepo (2016) suggest a compensating effect among high-educated mothers by providing more time and more cognitive and emotional stimulations to the low-birth-weight children in the USA. The result is also consistent with Cabrera-Hernandez (2016) which uses a sibling FE model and finds out higher-educated mothers compensate expenditure in school for the low-birth-weight outcome in Mexico. However, Grätz and Torche (2016) use a twin FE model and find that advantaged families provide more cognitive stimulation to higher-ability children, and lower-class parents do not respond to ability differences in the USA.
An unanswered question based on the existing findings is that whether the heterogeneous result by maternal education is caused by the difference in wealth, in differential preferences for compensation or ability to observe a difference in the cognitive outcomes of the siblings. Figure 7 shows that on average, mothers with education are generally better off in terms of wealth, implying that educated mothers might have a higher capacity to compensate disadvantaged children, simply because they have sufficient financial resources.
5.4 Robustness checks
We now present some additional robustness tests. First, we restrict the sibling pairs to have an age gap larger than 2 years, i.e. the older sibling should be born at least 3 years earlier than the younger one, in order to avoid a direct relationship between the rainfall shock experienced by one and outcome of the other. For example, one could argue that if one child is born 1 year after the older sibling, the rainfall experienced by the older one in the second year of life would be the rainfall the next child experiences in the first year of life; also, when the newborn child is exposed to an adverse shock at birth, the parent might reallocate the resources immediately among the children, which would directly influence the nutritional input of the older child in the second year of life. The restricted sample has 844 observations. In row 1 of Table 6, the first-stage coefficient of rainfall in the first 2 years of life equals 0.187 (t = 5.67), which is only slightly larger than the one of full sample presented in Table 3. The full diagnostics of the first stage using restricted sample are shown in Table 10, which are consistent with the results of the full sample. The second-stage estimate equals − 0.036(z = − 2.57), very close to the one in full sample which equals − 0.038. To conclude, it is consistent with the previous result that parents compensate disadvantaged children by offering higher educational resources to them. This can also serve as a suggestive evidence that there is not much difference in the compensation effect when siblings are further separated in age.
In row 2, we re-estimate our model without the covariates (i.e. maternal age, birth order, birth year, birth quarter, HAZ, birthplace and the type of sibling), only controlling for age. The IV-FE estimate equals − 0.045 (z = − 2.81). This result provides extra support for our assumption that rainfall is exogenously determined because it shows that our estimate is not conditional on the set of control variable included in the model.
In row 3, we show results using only the private tuition fees as the dependent variable and find consistent results, which are higher in magnitude. When parents observe an increase of one standard deviation in ability, they reduce private tuition fees by 9.9% of a standard deviation. Next, we investigate whether the likelihood to take private tuition is contingent upon cognitive ability, using a dummy variable of taking private tuition as the dependent variable. Shown in row 4, the result suggests a compensating behaviour of parents: the probability of offering private tuition to a child will increase by 30.8% if the child is underdeveloped by one standard deviation in cognitive ability.
We also exploit child time use as a potential measure for educational investment. Firstly, we study parental responses using study hours. Row 5 shows that the coefficient is negative and significant, with the estimate equal to − 0.542 (z = − 2.16), suggesting a child’s study hours will increase by 54.2% of a standard deviation if the child’s ability is one standard deviation lower. In row 6, we examine parental responses in respect to child hours spent in caring, doing chores and tasks and working, and find the coefficient being a positive and significant, with the estimate equals 0.425 (z = 1.68), suggesting a child might spend more time in care, chores, tasks and work by 42.5% of standard deviation when the child’s ability is higher by one standard deviation. This implies consistent compensating parental responses in terms of child time use.
We restrict the sample to siblings born in the same place and find no change in the coefficient, with the estimate equals to − 0.038 (z= − 2.92), as shown in row 7. In row 8, when the sample is restricted to children younger than 8 (i.e. the index child is paired with a young sibling), the coefficient does not change much, with the estimate equal to − 0.040 (z=− 3.08). In row 9, the compensating effect is consistent using a sub-sample of siblings both enrolled in school, as the estimate equals to − 0.038 (z= − 2.92). In row 10, we drop the control of HAZ in the specification, and it does not change the result; the estimate is − 0.039 (z= − 3.00).
In row 11, we regress the household consumer durables index in round 4 on rainfall in early life and find no significant effect (t= 0.56), implying that rainfall shocks in early life do not have a persistent impact on consumption patterns of the household in the later life of children. This supports our assumption that rainfall in early life does not affect parental investment in later life through a direct mechanism.
Finally, we checked the difference in increment of outcomes of the two siblings between round 5 (2016) and round 4 (2013), to examine whether the investment differential did close the gap in ability. In a difference-in-difference specification, we found the coefficient on investment was negative and statistically insignificant, with a p value of 0.24. So, at least in the 3-year period, attempts to compensate were largely unsuccessful which may be (i) due to the relatively small magnitude of the difference in investments (3.9% of a standard deviation at the mean), or (ii) because the low level of early ability constrains the return to later investment, consistent with Heckman’s (2007) hypothesis of dynamic complementarities in the human capital production function.
6 Conclusion
We find that for a sample of poor Ethiopian households, on average, parental investment compensates weakly for a low-ability outcome. We use an instrumental variable approach combined with panel data and a sibling fixed-effects model to provide robust evidence. This is of policy relevance since the results suggest that the detrimental effects of early life shocks might be mediated or muted by parental responses and hence the biological effects of early nutritional shocks might be larger than policymakers observe. In addition, it complements the literature on reduced-form estimates of the total effect of an early life shock or adverse event on final adult health in Ethiopia (e.g. Dercon and Porter (2014)).
This finding is in line with results from some previous studies reporting compensating parental behaviour (Behrman 1988; Bharadwaj et al. 2018; Rosenzweig and Wolpin 1988; Del Bono et al. 2012; Frijters et al. 2009; Halla et al. 2014; Leight 2017; Yi et al. 2015). It is also consistent with the intrafamily resource allocation model introduced by Behrman et al. (1982), suggesting parents favour equity over efficiency.
However, we have indicative evidence that this effect varies across family SES. Relatively advantaged parents provide more cognitive investment to lower-ability children, and lower-class families exhibit only small and modest compensatory behaviours. The finding is consistent across all measures of parental socio-economic advantage (maternal education, household wealth and household size), though the 95% confidence intervals for the estimates overlap. Consistent with prior findings, mothers with higher education compensate for lower-endowed children (Cabrera-Hernandez 2016; Hsin 2012; Restrepo 2016).
Our results therefore complement the literature which studies whether the effect of shocks to early ability can be eliminated or mitigated through investments, which themselves depend on family socio-economic status. Most studies have found that compared with the low-ability children born in higher-class families, the low-ability child born in lower-class families have worse outcomes in adulthood. One hypothesis in the literature is that parental involvement plays a role in reinforcing the poor ability outcome. Specifically, higher-class parents compensate for the differences in ability, or at least are not reinforcing the differences. Our results support the hypothesis that parental investment varies by family SES, even in a context of low-income by international standards. What is difficult, given the high correlation between SES as measured by wealth and by parental education, is to differentiate whether high-SES parents are more able to observe the difference in ability or more able to compensate for the difference, or both of these. More work on this issue is needed where suitable data can be collected.
Notes
Other results on health in the study are based on a much larger sample.
Rainfall information is external data matched with location by the Young Lives survey since the residence of interviewees is confidential.
Hill and Porter (2017) find that droughts cause a reduction in consumption of households in both rural and urban areas in Ethiopia.
The outcome measure used is Ravens’s Progressive Matrices scores, which did not work successfully in the Ethiopian context during Young Lives (Cueto and Leon 2012) as children were unable to understand the task.
We discuss a better measure of ability and parental investment in Section 3.
There are 610 YC index children older than their surveyed siblings, and 91 who are younger. The average age difference in month is 27 months. See Table 1 for details.
In the following, we will describe YC index children as “index children” for simplicity.
Three per cent of the sample were born in different communities due to migration: we include these and controls for community fixed effects. The results are robust excluding this 3%, shown in Table 6 row 7.
We acknowledge that as a cohort study, half of the index children in our sample are born within 12 months of one another, and therefore if any policy or other shock which is correlated with rainfall happened during the birth period, then results may be influenced by such an unobserved cohort effect. However, examining the community data files from the Young Lives survey we did not find any such event.
In the Young Lives study, there are two other cognitive tests, the Early Grade Reading Assessment (EGRA) and a maths test. However, they are only available for index children, not for siblings.
Scatterplots and locally smoothed regression lines using the ‘lowess’ command in STATA 13.
We use Stata command pwcorr to carry out Pearson’s correlation test.
We provide analysis using private tuition fees as the dependent variable in the robustness check. See Table 6.
Our sample also includes those who are at school age but not enrolled currently (121 children). We assign zero educational fees to them. The high percentage of zero educational fees is also due to the abolition of school fees in public schools for grades 1 to 10 in Ethiopia in 1994. However, hidden costs remain (Oumer 2009). UNICEF (2009) find that there were still payments in various forms in government schools after the policy of abolishing school fees. According to the Policy and Human Resource Development (PHRD) study, on average, a government school was levying about Birr 10 to 15 per year per student.
There are eight factor variables to denote the type of siblings: born as an older brother with a younger sister, born as younger sister with a older brother, born as an older sister with a younger brother, born as a younger brother with a older sister, born as an older brother with a younger brother, born as younger brother with a older brother, born as an older sister with a younger sister, born as a younger sister with a older sister. When we use our fixed-effects strategy, many are dropped due to their multicollinear relationship when the information of index children is deducted by their siblings’. Note that we only include time-varying household characteristics due to our sibling difference specification.
The wealth index is the average of housing quality index, consumer durable index and housing service quality index.
There are 46 clusters in the sample.
The underidentification test is an LM version of the Kleibergen and Paap (2006), which allows for non-i.i.d. errors.
We use weakivtest programmed in Stata by Pflueger and Wang (2015). The Montiel–Plueger effective F statistics are very close to the built-in Kleibergen-Paap rk Wald F statistics in the programme xtivreg2 written by Schaffer et al. (2015). However, the robust critical values of the latter are not provided. Thus, we use the Montiel–Plueger critical values as thresholds in order to report the bias.
The IV-FE point estimates are given by xtivreg2 programmed by Schaffer et al. (2015).
The mean of the total educational fees is 123.23 Birr.
The AR, Moreira CLR, K, J and K-J confidence intervals are given by weakiv, programmed by Finlay et al. (2016).
We use plausexog programmed in Stata by Clarke et al. (2017), using the union of confidence interval approach for estimation of bounds.
Following Conley et al. (2012)’s ‘plausible exogeneity’ test, we propose a model derived from (1), ΔIh = βΔCAh + γΔRh + ΔXhΛ + Δ𝜖h, where difference in rainfall has a non-zero impact on parental responses. In the conventional IV approach, γ is set to be zero. Conley et al. (2012) note that in theory if we know γ we could subtract it from both sides of the equation and continue with a consistent IV estimate.
The overall reduced-form is estimated using the model ΔIh = γΔRh + ΔXhΛ + Δ𝜖h.
See Table 11 for full results.
References
Abufhele A, Behrman J, Bravo D (2017) Parental preferences and allocations of investments in children’s learning and health within families. Soc Sci Med 194:76–86
Adhvaryu A, Nyshadham A (2016) Endowments at birth and parents’ investments in children. Econ J 126(593):781–820
Aizer A, Cunha F (2012) The production of human capital: endowments, investments and fertility. Technical report, National Bureau of Economic Research
Almond D, Currie J (2011) Killing me softly: the fetal origins hypothesis. J Econ Perspect 25(3):153–172
Almond D, Currie J, Duque V (2018) Childhood circumstances and adult outcomes: act II. J Econ Lit 56(4):1360–1446
Almond D, Mazumder B (2013) Fetal origins and parental responses. Annual Review of Economics 5(1):37–56
Angrist JD, Pischke J-S (2008) Mostly harmless econometrics: an empiricist’s companion. Princeton University Press, Princeton
Ayalew T (2005) Parental preference, heterogeneity, and human capital inequality. Econ Dev Cult Chang 53(2):381–407
Barnett I, Ariana P, Petrou S, Penny ME, Duc LT, Galab S, Woldehanna T, Escobal JA, Plugge E, Boyden J (2012) Cohort profile: the Young Lives study. Int J Epidemiol 42(3):701–708
Becker GS (1991) A treatise on the family. Harvard University Press, Cambridge
Becker GS, Tomes N (1976) Child endowments and the quantity and quality of children. J Polit Econ 84(4, Part 2):S143–S162
Behrman J (1988) Nutrition, health, birth order and seasonality: intrahousehold allocation among children in rural India. J Dev Econ 28(1):43–62
Behrman J, Pollak RA, Taubman P (1982) Parental preferences and provision for progeny. J Polit Econ 90(1):52–73
Behrman J, Rosenzweig MR, Taubman P (1994) Endowments and the allocation of schooling in the family and in the marriage market: the twins experiment. J Polit Econ 102(6):1131–1174
Bhalotra SR, Clarke D (2018) The twin instrument: fertility and human capital investment. The twin instrument: fertility and human capital investment. IZA Institute of Labor Economics Discussion Paper 11878
Bharadwaj P, Eberhard J, Neilson C (2018) Health at birth, parental investments, and academic outcomes. J Labour Econ 36(2)
Bound J, Solon G (1999) Double trouble: on the value of twins-based estimation of the return to schooling. Econ Educ Rev 18(2):169–182
Buckles K, Kolka S (2014) Prenatal investments, breastfeeding, and birth order. Soc Sci Med 118:66–70
Cabrera-Hernandez F (2016) The accident of birth: effects of birthweight on educational attainment and parents’ compensations among siblings. Center for Economic Research and Teaching (CIDE)
Campbell J (1998) Book review: Peabody picture vocabulary test. J Psychoeduc Assess 16(4):334–338
Casale D, Desmond C (2016) Recovery from stunting and cognitive outcomes in young children: evidence from the South African birth to twenty cohort study. J Dev Orig Health Dis 7(2):163–171
Clarke D, et al. (2017) Plausexog: Stata Module to implement Conley et al’s plausibly exogenous bounds. Statistical Software Components
Conley D (2008) Bringing sibling differences in: Enlarging our understanding of the transmission of advantage in families. Social class: how does it work? pp 179–200
Conley TG, Hansen CB, Rossi PE (2012) Plausibly exogenous. Rev Econ Stat 94(1):260–272
Crookston BT, Schott W, Cueto S, Dearden KA, Engle P, Georgiadis A, Lundeen EA, Penny ME, Stein AD, Behrman J (2013) Postinfancy growth, schooling, and cognitive achievement: Young Lives. Am J Clin Nutr 98(6):1555–1563
Cueto S, Leon J (2012) Psychometric characteristics of cognitive development and achievement instruments in round 3 of Young Lives, Technical Report 15, Young Lives
Currie J, Almond D (2011) Human capital development before age five. In: Handbook of labor economics, vol 4. Elsevier, pp 1315–1486
Datar A, Kilburn MR, Loughran DS (2010) Health endowments and parental investments in infancy and early childhood. Demography 47(6):145–162
Del Bono E, Ermisch J, Francesconi M (2012) Intrafamily resource allocations: a dynamic structural model of birth weight. J Labor Econ 30(3):657–706
Dendir S (2014) Children’s cognitive ability, schooling and work: evidence from Ethiopia. Int J Educ Dev 38:22–36
Dercon S, Porter C (2014) Live aid revisited: long-term impacts of the 1984 Ethiopian famine on children. J Eur Econ Assoc 12(4):927–948
Doyle O, Harmon CP, Heckman JJ, Tremblay RE (2009) Investing in early human development: timing and economic efficiency. Econ Hum Biol 7(1):1–6
Dunn LM, Dunn LM (1997) PPVT-III: Peabody picture vocabulary test. American Guidance Service
Finlay K, Magnusson L, Schaffer ME, et al. (2016) Weakiv: Stata module to perform weak-instrument-robust tests and confidence intervals for instrumental-variable (IV) estimation of linear, probit and tobit models. Statistical software components
Frijters P, Johnston DW, Shah M, Shields MA (2009) To work or not to work? Child development and maternal labor supply. Am Econ J Appl Econ 1 (3):97–110
Frijters P, Johnston DW, Shah M, Shields MA (2013) Intrahousehold resource allocation: do parents reduce or reinforce child ability gaps? Demography 50 (6):2187–2208
Glewwe P, Jacoby HG, King EM (2001) Early childhood nutrition and academic achievement: a longitudinal analysis. J Public Econ 81(3):345–368
Grätz M, Torche F (2016) Compensation or reinforcement? The stratification of parental responses to children’s early ability. Demography 53(6):1883–1904
Griliches Z (1979) Sibling models and data in economics: beginnings of a survey. J Polit Econ 87(5, Part 2): S37–S64
Halla M, Zweimüller M, et al. (2014) Parental response to early human capital shocks: evidence from the Chernobyl Accident, Technical report, The Austrian Center for Labor Economics and the Analysis of the Welfare State. Johannes Kepler University Linz, Austria
Heckman JJ (2007) The economics, technology, and neuroscience of human capability formation. Proc Natl Acad Sci USA, 13250–13255
Hill RV, Porter C (2017) Vulnerability to drought and food price shocks: evidence from Ethiopia. World Dev 96:65–77
Hsin A (2012) Is biology destiny? Birth weight and differential parental treatment. Demography 49(4):1385–1405
Kleibergen F, Paap R (2006) Generalized reduced rank tests using the singular value decomposition. J Econ 133(1):97–126
Lareau A (2011) Unequal childhoods: class, race, and family life, University of California Press, Berkeley
Leight J (2017) Sibling rivalry: endowment and intrahousehold allocation in Gansu Province, China. Econ Dev Cult Chang 456–493
Leon J, Singh A (2017) Equating test scores for receptive vocabulary across rounds and cohorts in Ethiopia, India and Vietnam, Technical report, Young Lives
Lynch JL, Brooks R (2013) Low birth weight and parental investment: do parents favor the fittest child? J Marriage Fam 75(3):533–543
Maccini S, Yang D (2009) Under the weather: health, schooling, and economic consequences of early-life rainfall. Am Econ Rev 99(3):1006–1026
Nicoletti C, Salvanese K, Tominey E (2018) Response of parental investments to child’s health endowment at birth. Health Economics (Contributions to Economic Analysis, Vol. 294), Emerald Publishing Limited, pp. 175--199. https://doi.org/10.1108/S0573-855520180000294009
Olea JLM, Pflueger C (2013) A robust test for weak instruments’. J Bus Econ Stat 31(3):358–369
Oumer J (2009) The challenges of free primary education in Ethiopia, UNESCO. International Institute for Educational Planning
Outes-Leon I, Sanchez A (2008) An assessment of the Young Lives sampling approach in Ethiopia, Technical Report 1, Young Lives
Paxson C, Schady N (2007) Cognitive development among young children in Ecuador the roles of wealth, health, and parenting. J Hum Resour 42(1):49–84
Pflueger C, Wang S (2015) A robust test for weak instruments in Stata. Stata J 15(1):216–225
Price J (2008) Parent-child quality time: does birth order matter? J Hum Resour 43(1):240–265
Restrepo BJ (2016) Parental investment responses to a low birth weight outcome: who compensates and who reinforces? J Popul Econ 29(4):969–989
Rosales-Rueda MF (2014) Family investment responses to childhood health conditions: intrafamily allocation of resources. J Health Econ 37:41–57
Rosenzweig MR, Wolpin KI (1988) Heterogeneity, intrafamily distribution, and child health. J Hum Resour, 437–461
Schaffer ME, et al. (2015) Xtivreg2: Stata Module to perform extended IV/2SLS, GMM and AC/HAC, LIML and k-class regression for panel data models. Statistical Software Components
Staiger D, Stock JH, et al. (1997) Instrumental variables regression with weak instruments. Econometrica 65(3):557–586
UNICEF (2009) Abolishing school fees in Africa lessons from Ethiopia, Ghana, Kenya, Malawi, and Mozambique
Victora CG, de Onis M, Hallal PC, Blössner M, Shrimpton R (2010) Worldwide timing of growth faltering: revisiting implications for interventions. Pediatrics pp peds–2009
Yi J, Heckman JJ, Zhang J, Conti G (2015) Early health shocks, intra-household resource allocation and child outcomes. Econ J 125(588):F347–F371
Acknowledgement
The authors would like to thank the anonymous referees for helpful comments and suggestions. Their views are not necessarily those of Young Lives, the University of Oxford, DFID or other funders. Thanks to Liang Bai, Amalavoyal Chari, Marta Favara, Kalle Hirvonen, Pascal Jaupart, Tatiana Kornienko, Jessica Leight, Patricia Espinoza Revollo, and Mark Schaffer for helpful suggestions, and to seminar and conference participants in Young Lives, Jun 2017; SGPE conference, Jan 2018; CSAE conference, Mar 2018; University of Sussex, Mar 2018; UNICEF Ethiopia, Apr 2018; SEHO conference, May 2018; SMYE, May 2018 and ESPE, June 2018.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Responsible editor: Junsen Zhang
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Disclaimer
The views expressed here are those of the author(s). All errors and omissions are our own.
The data are from Young Lives, a 15-year study of the changing nature of childhood poverty in Ethiopia, India, Peru and Vietnam (www.younglives.org.uk). Young Lives was core funded by UK aid from the Department for International Development (DFID) from 2001–2018.
Appendices
Appendix A: Tables
Appendix B: Graphs
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Fan, W., Porter, C. Reinforcement or compensation? Parental responses to children’s revealed human capital levels. J Popul Econ 33, 233–270 (2020). https://doi.org/10.1007/s00148-019-00752-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00148-019-00752-7