Abstract
Forward secrecy is considered an essential design goal of modern key establishment (KE) protocols, such as TLS 1.3, for example. Furthermore, efficiency considerations such as zero round-trip time (0-RTT), where a client is able to send cryptographically protected payload data along with the very first KE message, are motivated by the practical demand for secure low-latency communication. For a long time, it was unclear whether protocols that simultaneously achieve 0-RTT and full forward secrecy exist. Only recently, the first forward-secret 0-RTT protocol was described by Günther et al. (Eurocrypt, 2017). It is based on puncturable encryption. Forward secrecy is achieved by “puncturing” the secret key after each decryption operation, such that a given ciphertext can only be decrypted once (cf. also Green and Miers, S&P 2015). Unfortunately, their scheme is completely impractical, since one puncturing operation takes between 30 s and several minutes for reasonable security and deployment parameters, such that this solution is only a first feasibility result, but not efficient enough to be deployed in practice. In this paper, we introduce a new primitive that we term Bloom filter encryption (BFE), which is derived from the probabilistic Bloom filter data structure. We describe different constructions of BFE schemes and show how these yield new puncturable encryption mechanisms with extremely efficient puncturing. Most importantly, a puncturing operation only involves a small number of very efficient computations, plus the deletion of certain parts of the secret key, which outperforms previous constructions by orders of magnitude. This gives rise to the first forward-secret 0-RTT protocols that are efficient enough to be deployed in practice. We believe that BFE will find applications beyond forward-secret 0-RTT protocols.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
One central ingredient to secure today’s Internet is key exchange (KE) protocols with the most prominent and widely deployed instantiations thereof in the transport layer security (TLS) protocol [45]. Using a KE protocol, two parties (e.g., a server and a client) are able to establish a shared secret (session key) which afterward can be used to cryptographically protect data to be exchanged between those parties. The process of arriving at a shared secret requires the exchange of messages between client and server, which adds latency overhead to the protocol. The time required to establish a key is usually measured in round-trip times (RTTs). A novel design goal, which was introduced by Google’s QUIC protocol [47] and is also adopted in TLS version 1.3 [45], aims at developing zero round-trip time (0-RTT) protocols with strong security guarantees. So far, quite some effort was made in the cryptographic literature, e.g., [35, 49], and, indeed, 0-RTT protocols are probably going to be used heavily in the future Internet as TLS version 1.3 adoption is growing rapidly. Besides TLS 1.3, Google’s QUIC protocol is used on Google webservers and within the Chrome and Opera browsers to support 0-RTT. Unfortunately, none of the above mentioned protocols are enjoying 0-RTT and full forward secrecy at the same time. Only recently, Günther, Hale, Jager, and Lauer (GHJL henceforth) [33] made progress and proposed the first 0-RTT key exchange protocol with full forward secrecy for all transmitted payload messages. However, although their 0-RTT protocol offers the desired features, their construction is not yet practical.
In more detail, GHJL’s forward-secret 0-RTT key-exchange solution is based on puncturable encryption (PE), which they showed can be constructed in a black-box way from any selectively secure hierarchical identity-based encryption (HIBE) scheme. Loosely speaking, PE is a public-key encryption primitive which provides a \(\mathsf Puncture\) algorithm that, given a secret key and a ciphertext, produces an updated secret key that is able to decrypt all ciphertexts except the one it has been punctured on. PE has been introduced by Green and Miers [31] (GM henceforth) who provide an instantiation relying on a binary-tree encryption (BTE) scheme—or selectively secure HIBE—together with a key-policy attribute-based encryption (KP-ABE) [30] scheme for non-monotonic (NM) formulas with specific properties. In particular, the KP-ABE needs to provide a non-standard property to enhance existing secret keys with additional NOT gates, which is satisfied by the NM KP-ABE in [44]. Since then, PE has proved to be a valuable tool to construct public-key watermarking schemes [20], forward-secret proxy re-encryption [24],Footnote 1 or to achieve chosen-ciphertext security for fully homomorphic encryption [17]. However, the mentioned PE instantiations from [17, 20] are based on indistinguishability obfuscation and, thus, do not yield practical schemes at all.
When looking at the two most efficient PE schemes available, i.e., GM and GHJL, they still come with severe drawbacks. In particular, puncturing in GHJL is highly inefficient and takes several seconds to minutes on decent hardware for reasonable deployment parameters. In the GM scheme, puncturing is more efficient, but the cost of decryption is very significant and increases with the number of puncturings. More precisely, cost of decryption requires a number of pairing evaluations that depends on the number of puncturings, and can be in the order of \(2^{10}\) to \(2^{20}\) for realistic deployment parameters. These issues make both of them especially unsuitable for the application in forward-secret 0-RTT key exchange in a practical setting.
Contributions In this paper, we introduce Bloom filter encryption (BFE), which can be considered as a variant of PE [17, 20, 31, 33]. The main difference to other existing PE constructions is that in case of BFE, we tolerate a non-negligible correctness error.Footnote 2 This allows us to construct PE with highly efficient puncturing and in particular where puncturing only requires a few very efficient operations, i.e., to delete parts of the secret key, but no further expensive cryptographic operations. Altogether, this makes BFE a very suitable building block to construct practical forward-secret 0-RTT key exchange. In more detail, our contributions are as follows:
-
We formalize the notion of BFE by presenting a suitable security model. The intuition behind BFE is to provide highly efficient decryption and puncturing. Interestingly, puncturing mainly consists of deleting parts of the secret key. This approach is in contrast to existing puncturable encryption schemes, where puncturing and/or decryption is a very expensive operation.
-
We propose efficient constructions of BFE. First, we present a direct construction which uses ideas from the Boneh–Franklin identity-based encryption (IBE) scheme [12]. This construction allows us to achieve constant size public keys. Second, we present a black-box construction from a ciphertext-policy attribute-based encryption (CP-ABE) scheme that only needs to be small-universe (i.e., bounded) and to support threshold policies, which allows us to achieve constant size ciphertexts. Third, we describe a generic construction from identity-based broadcast encryption (IBBE), which is efficiently instantiable with the IBBE scheme by Delerablée [22]. This construction allows us to simultaneously achieve compact public keys and constant size ciphertexts. Finally, we propose time-based BFE (TB-BFE), an enhancement of BFE which additionally provides forward secrecy and thus prevents message suppression attacks, and provide a generic construction of TB-BFE from selectively secure HIBEs.
-
We adapt the Fujisaki–Okamoto (FO) transformation [25] to obtain CCA security in the random oracle model (ROM) to the BFE setting. This is technically non-trivial, and therefore we consider it as another interesting aspect of this work. In particular, the original FO transformation [25] works only for schemes with perfect correctness. Recently, Hofheinz et al. [37] have described a variant which works also for schemes with negligible correctness error. We formalize additional properties that are required to apply the FO transform, and show that our CPA-secure constructions satisfy them. This serves as a template that allows an easy application of the FO transform in a black-box manner to BFE schemes. Moreover, we also discuss how to achieve CCA security in the standard model.
-
We provide a construction of a forward-secret 0-RTT key exchange protocol (in the sense of GHJL) from TB-BFE. Furthermore, we give a detailed comparison of (TB-)BFE with other PE schemes and discuss the efficiency in the context of the proposed application to forward-secret 0-RTT key exchange. In particular, our construction of forward-secret 0-RTT key-exchange from TB-BFE has none of the drawbacks mentioned in Introduction (at the cost of a somewhat larger secret key, that, however, shrinks with the number of puncturings). Consequently, our forward-secret 0-RTT key exchange can be seen as a significant step forward to construct very practical forward-secret 0-RTT key exchange protocols.
On tolerating a non-negligible correctness error for 0-RTT The huge efficiency gain of our construction stems partially from the relaxation of allowing a non-negligible correctness error, which, in turn, stems from the potentially non-negligible false-positive probability of a Bloom filter. While this is unusual for classical public-key encryption schemes, we consider it as a reasonable approach to accept a small, but non-negligible correctness error for the 0-RTT mode of a key exchange protocol, in exchange for the huge efficiency gain.
For example, a 1/10000 chance that the key establishment fails allows to use 0-RTT in 9999 out of 10,000 cases on average, which is a significant practical efficiency improvement. Furthermore, the communicating parties can implement a fallback mechanism which immediately continues with running a standard 1-RTT key exchange protocol with perfect correctness, if the 0-RTT exchange fails. Thus, the resulting protocol can have the same worst-case efficiency as a 1-RTT protocol, while most of the time 0-RTT is already sufficient to establish a key and full forward secrecy is always achieved.
Compared to other practical 0-RTT solutions, note that both TLS 1.3 [45] and QUIC [47] have similar fallback mechanisms. Furthermore, to achieve at least a very weak form of forward secrecy, they define so called tickets [45] or server configuration (SCFG) messages [47], which expire after a certain time. Forward secrecy is only achieved after the ticket/SCFG message has expired and the associated secrets have been erased. Therefore, the lifetime should be kept short. If a client connects to a server after the ticket/SCFG message has expired, then the fallback mechanism is invoked and a full 1-RTT handshake is performed. In particular for settings where a client connects only occasionally to a server, and for reasonably chosen parameters and a moderate life time of the ticket/SCFG message, which at least guarantees some weak form of forward secrecy, this requires a full handshake more often than with our approach.
Finally, note that puncturable encryption with perfect (or negligible) correctness error inherently seems to require secret keys whose size at least grows linearly with the number of puncturings. This is because any such scheme inherently must (implicitly or explicitly) encode information about the list of punctured ciphertexts into the secret key, which lower-bounds the size of the secret key [41]. By tolerating a non-negligible correctness error, we are also able to restrict the growth of the secret key to a limit which seems tolerable in practice.
Remark on forward secrecy and time-based constructions In the literature, time-based puncturable encryption schemes are often termed puncturable forward-secure encryption schemes [31, 33], which may seem confusing as the puncturable encryption schemes already provide mechanisms to achieve forward secrecy. The motivation for why time-based constructions was initially introduced is along the same lines and goes back to Green and Miers [31]. They described a message suppression attack against the forward secrecy of puncturable encryption. An adversary that suppresses message delivery can break forward secrecy of the primitive by compromising the receiving party’s secret at a later point in time, and retroactively decrypting all suppressed messages.
Hence, Green and Miers proposed to construct a time-based construction where the attack is only feasible until both parties move to the next time slot, achieving a form of delayed forward secrecy. As the time-based constructions were inspired by forward-secure encryption, the qualifier “forward-secure” was added to the primitive’s name. For a detailed discussion on the meaning of forward secrecy in non-interactive settings such as 0-RTT, we refer to a recent work by Gellert and Boyd [14].
We believe a distinction between time-based and non-time-based constructions is meaningful. It makes explicit that the non-time-based constructions puncture out ciphertexts, in order to remove decryption capability for this ciphertext. In contrast, time-based constructions additionally allow to puncture time slots, which removes decryption capability for all possible ciphertexts from previous time slots. For our constructions, this also makes it possible to keep the size of secret keys smaller, as we explain in Sect. 4.
Differences to the conference version [23] In contrast to the conference version [23], this extended version contains some additions and updates. First, we chose to present all constructions explicitly as Bloom filter key encapsulation mechanisms (BFKEMs) instead of referring to them as Bloom filter encryption (cf. Sect. 2 for a discussion). Second, we provide an additional generic construction of a \(\mathsf {BFKEM}\)from identity-based broadcast encryption (IBBE) in Sect. 3.4. Furthermore, we have corrected some ambiguities and minor issues within the definitional framework. Third, we provide a more elaborate discussion on the choice of parameters to provide more insights and decision support for the practical application of our proposals.
Follow-up work After the conference version of this paper, there was some follow-up work which we want to mention for completeness. Aviram et al. [3] study practical forward secrecy for 0-RTT in TLS 1.3 and in particular the session resumption feature of TLS 1.3. Lauer et al. [40] introduce a single-pass circuit construction protocol with forward secrecy for Tor, called Tor 0-RTT (T0RTT), which they construct from BFE. Dallmeier et al. [21] use BFE to implement the first fully forward-secret 0-RTT key exchange in Google’s QUIC protocol and analyze its performance. Finally, there is follow-up work on puncturable encryption from Sun et al. [46] providing further constructions with negligible correctness error and different trade-offs.
Outline The remainder of this paper is organized as follows. In Sect. 2, we introduce the concept of Bloom filter encryption including a discussion on how to choose suitable Bloom filter parameters for our schemes. In Sect. 3, we present three constructions of Bloom filter encryption alongside with a modified Fujisaki–Okamoto transformation to achieve CCA security for our schemes. In Sect. 4, we formally define time-based Bloom filter encryption and present a generic construction based on hierarchical identity-based encryption. Section 5 explains that our time-based construction can be used to construct forward-secret 0-RTT key exchange. In Sect. 6, we compare computational efficiency and parameter size of our constructions with existing constructions in literature. Section 7 concludes the results of our work.
2 Bloom Filter Encryption
Notation Let \(\lambda \in \mathbb {N}\) be the security parameter. For a finite set \(\mathcal {S}\), we denote by  the process of sampling s uniformly from \(\mathcal {S}\). For an algorithm A, let
the process of sampling s uniformly from \(\mathcal {S}\). For an algorithm A, let  be the process of running A on input \((\lambda ,x)\) with access to uniformly random coins and assigning the result to y. (We may omit to mention the \(\lambda \)-input explicitly and assume that all algorithms take \(\lambda \)as input.) To make the random coins r explicit, we write \(A(\lambda ,x;r)\). We say an algorithm A is probabilistic polynomial time (PPT) if the running time of A is polynomial in \(\lambda \). A function f is negligible if its absolute value is smaller than the inverse of any polynomial (i.e., if \(\forall ~c~\exists ~k_0~\forall ~\lambda \ge k_0:|f(\lambda )|<1/ \lambda ^c\)). Furthermore, for \(n\in \mathbb {N}\), let \([n]:=\{1,\ldots ,n\}\) and let \(\mathsf {BilGen}\) be an algorithm that, on input a security parameter \(1^\lambda \), outputs
be the process of running A on input \((\lambda ,x)\) with access to uniformly random coins and assigning the result to y. (We may omit to mention the \(\lambda \)-input explicitly and assume that all algorithms take \(\lambda \)as input.) To make the random coins r explicit, we write \(A(\lambda ,x;r)\). We say an algorithm A is probabilistic polynomial time (PPT) if the running time of A is polynomial in \(\lambda \). A function f is negligible if its absolute value is smaller than the inverse of any polynomial (i.e., if \(\forall ~c~\exists ~k_0~\forall ~\lambda \ge k_0:|f(\lambda )|<1/ \lambda ^c\)). Furthermore, for \(n\in \mathbb {N}\), let \([n]:=\{1,\ldots ,n\}\) and let \(\mathsf {BilGen}\) be an algorithm that, on input a security parameter \(1^\lambda \), outputs  , where \(\mathbb {G}_1\), \(\mathbb {G}_2\), \(\mathbb {G}_T\) are groups of prime order q with bilinear map \(e : \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\) and generators \(g_i \in \mathbb {G}_i\) for \(i \in \{1,2\}\). Finally, we will use square brackets to access the individual bits of bitstrings, i.e., T[i] denotes the i-th bit of a bitstring \(T = \{0,1\}^m\), for \(m\in \mathbb {N}\).
, where \(\mathbb {G}_1\), \(\mathbb {G}_2\), \(\mathbb {G}_T\) are groups of prime order q with bilinear map \(e : \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\) and generators \(g_i \in \mathbb {G}_i\) for \(i \in \{1,2\}\). Finally, we will use square brackets to access the individual bits of bitstrings, i.e., T[i] denotes the i-th bit of a bitstring \(T = \{0,1\}^m\), for \(m\in \mathbb {N}\).
Bloom Filter Encryption The key idea behind Bloom filter encryption (BFE) is that the key pair of such a scheme is associated with a Bloom filter (BF) [10], a probabilistic data structure for the approximate set membership problem with a non-negligible false-positive probability in answering membership queries. A BF initially represents a bit array of m bits, all set to 0. Insertion takes an element and inputs it to k different hash functions each mapping the element to one of the m array positions, which are then set to 1. When querying the BF on an element, it is considered to be in the BF if all positions obtained by evaluating the hash evaluations are set to 1. The initial secret key \(\mathsf {sk} \) output by the key generation algorithm of a BFE scheme corresponds to an empty BF. Encryption takes a message M and the public key \(\mathsf {pk} \), samples a random element s (acting as a tag for the ciphertext) corresponding to the universe \(\mathcal {U}\) of the BF and encrypts a message using \(\mathsf {pk} \) with respect to the k positions set in the BF by s. A ciphertext is then basically identified by s and decryption works as long as at least one index pointed to by s in the BF is still set to 0. Puncturing the secret key with respect to a ciphertext (i.e., the tag s of the ciphertext) corresponds to inserting s in the BF (i.e., updating the corresponding indices to 1 and deleting the corresponding parts of the secret key). This basically means updating \(\mathsf {sk} \) such that it no longer can decrypt any position indexed by s.
A note on modeling BFE For 0-RTT key establishment, our prime application in this paper, we do not need a full-blown encryption scheme, but only a key-encapsulation mechanisms (KEM) to transport a symmetric encryption key. Consequently, we chose to focus on what we call Bloom filter key encapsulation mechanisms (BFKEMs). We stress that defining BFKEM instead of BFE does not represent any limitation, as any KEM can generically be converted into a secure full-blown encryption scheme [25]. Conversely, any secure encryption scheme trivially yields a secure KEM. For the reasons mentioned before we, henceforth, may thus use the terms BFE and BFKEM interchangeably. Nonetheless, for completeness, we give stand-alone definitions of BFE tolerating a non-negligible correctness error in “Appendix A.”
2.1 Formal Definition of Bloom Filters
A Bloom filter (BF) [10] is a probabilistic data structure for the approximate set membership problem. It allows a succinct representation T of a set \(\mathcal {S}\) of elements from a large universe \(\mathcal {U}\). For elements \(s\in \mathcal {S}\) a query to the BF always answers 1 (“yes”), i.e., its false-negative probability is 0. Ideally, a BF would always return 0 (“no”) for elements \(s \not \in \mathcal {S}\), but the succinctness of the BF comes at the cost that for any query to \(s \not \in \mathcal {S}\) the answer can be 1, too, but only with small probability (called the false-positive probability).
We will only be interested in the original construction of Bloom filters [10] and omit a general abstract definition. Instead, we describe the construction from [10] directly. For a general definition, we refer to [43].
Definition 1
(Bloom Filter) A Bloom filter \(\mathsf {B}\) for set \(\mathcal {U}\) consists of algorithms \(\mathsf {B}= ({\mathsf{BFGen}}, {\mathsf{BFUpdate}}, {\mathsf{BFCheck}})\), which are defined as follows.
- \({\mathsf{BFGen}}(m,k)\)::
-
This algorithm takes as input two integers \(m,k \in \mathbb {N}\). It first samples k universal hash functions \(H_1, \ldots , H_k\), where \(H_j : \mathcal {U}\rightarrow [m]\), defines \(H := (H_j)_{j \in [k]}\) and \(T := 0^m\), and outputs (H, T).
- \({\mathsf{BFUpdate}}(H,T,u)\)::
-
Given \(H = (H_j)_{j \in [k]}\), \(T \in \{0,1\}^m\), and \(u\in \mathcal {U}\), this algorithm defines the updated state \(T'\) by first assigning \(T' := T\). Then, it sets \(T'[H_j(u)] := 1\) for all \(j \in [k]\), and finally returns \(T'\).
- \({\mathsf{BFCheck}}(H,T,u)\)::
-
Given \(H = (H_j)_{j \in [k]}\), \(T \in \{0,1\}^m\), and \(u\in {\mathcal {U}}\), this algorithm returns a bit \(b := \bigwedge _{j\in [k]} T[H_j(u)]\).
2.1.1 Relevant Properties of Bloom Filters
Let us summarize the properties of Bloom filters relevant to our work.
- Perfect completeness.:
-
A Bloom filter always “recognizes” elements that have been added with probability 1. More precisely, let \({\mathcal {S}} = (s_1, \ldots , s_n) \in {\mathcal {U}}^n\) be any vector of n elements of \({\mathcal {U}}\). Let
 and define $$\begin{aligned} T_i = {\mathsf{BFUpdate}}(H,T_{i-1},s_i) \text { for } i \in [n]. \end{aligned}$$
and define $$\begin{aligned} T_i = {\mathsf{BFUpdate}}(H,T_{i-1},s_i) \text { for } i \in [n]. \end{aligned}$$Then, for all \(s^* \in {\mathcal {S}}\) and all
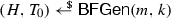 with \(m, k \in \mathbb {N}\), it holds that $$\begin{aligned} \mathsf {Pr}\left[ {\mathsf{BFCheck}}(H,T_n,s^*) = 1 \right] = 1, \end{aligned}$$
with \(m, k \in \mathbb {N}\), it holds that $$\begin{aligned} \mathsf {Pr}\left[ {\mathsf{BFCheck}}(H,T_n,s^*) = 1 \right] = 1, \end{aligned}$$where the probability is taken over the random coins of \({\mathsf{BFGen}}\).
- Compact representation of \(\mathcal {S}\):
-
Independent of the size of the set \({\mathcal {S}} \subset {\mathcal {U}}\) and the representation of individual elements of \({\mathcal {U}}\), the size of representation T is a constant number of m bits. A larger size of \({\mathcal {S}}\) increases only the false-positive probability, as discussed below, but not the size of the representation.
- Bounded false-positive probability:
-
The probability that an element which has not yet been added to the Bloom filter is erroneously “recognized” as being contained in the filter can be made arbitrarily small, by choosing m and k adequately, given (an upper bound on) the size of \({\mathcal {S}}\).
More precisely, let \({\mathcal {S}} = (s_1, \ldots , s_n) \in {\mathcal {U}}^n\) be any vector of n elements of \({\mathcal {U}}\). Then, for any \(s^* \in {\mathcal {U}} \setminus {\mathcal {S}}\), the false positive probability \(\mu \) is bounded by
$$\begin{aligned} \mu := \mathsf {Pr}\left[ {\mathsf{BFCheck}}(H,T_n,s^*) = 1 \right] \le \left( 1-e^{- \frac{(n+1/2)k}{m-1}}\right) ^k, \end{aligned}$$where
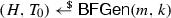 , \(T_i = {\mathsf{BFUpdate}}(H,T_{i-1},s_i) \text { for } i \in [n]\), and the probability is taken over the random coins of \({\mathsf{BFGen}}\). See Goel and Gupta [29] for a proof of this bound.
, \(T_i = {\mathsf{BFUpdate}}(H,T_{i-1},s_i) \text { for } i \in [n]\), and the probability is taken over the random coins of \({\mathsf{BFGen}}\). See Goel and Gupta [29] for a proof of this bound.
Discussion on the choice of parameters In order to provide a first intuition on the concrete selection of Bloom filter parameters and their impact on the size of ciphertexts, public and secret keys for BFE, we subsequently give some examples.
Suppose we are given an upper bound n on the number of elements inserted into the Bloom filter, and an upper bound p on the false positive probability for this number of elements that we can tolerate. Our goal is to determine the size m of the Bloom filter and the number k of hash functions to achieve a false positive probability of \(\mu \le p\) with respect to n. As already mentioned above, Goel and Gupta [29] proved that the false positive probability \(\mu \) of a Bloom filter is strictly bounded by
Hence, if we set
then due to our choice of k we obtain
and therefore
Furthermore, due to the choice of m in (1), we obtain a bound on k as
which yields the desired bound \(\mu \le 2^{-k} \le p\) on the false positive probability of the Bloom filter.
Table 1 lists m and k for different values of p and n. In order to give an intuition of the impact of different choices of p and n, Table 1 also lists the size of ciphertexts, secret and public keys, when the BFE construction in Sect. 3.1 is instantiated for these parameters using the pairing-friendly BLS12-381 curve, which provides a security level of about “120-bit.”
Here, we need to emphasize that initially the secret key (representing the empty BF) has its maximum size, but every puncturing (i.e., addition of an element to the BF), reduces the size of the secret key. Moreover, we stress that the false-positive probability represents an upper bound as it assumes that all n elements are added to the BF. The false positive probability before n insertions, as a function of the number of inserted elements and for given parameters m and k, is discussed below. Finally, we note that when we use our time-based BFE approach (TB-BFE) from Sect. 4, we can even reduce the secret key size by reducing the maximum number of puncturings at the cost of switching the time intervals more frequently.
False-positive probability p before n insertions So far we have argued that we can bound the probability of an non-inserted element being recognized by a BF after n elements have been added to the BF. However, we stress that this probability is far lower if only a fraction of the n elements have been added. We can illustrate this by computing the false-positive probability of an element after only \(\alpha < n\) insertions.
Lemma 1
Let \((H, T_\alpha )\) be a Bloom filter where \(\alpha \) random elements have been added. The false-positive probability of a random element \(u \in \mathcal {U}\) being recognized by the Bloom filter is
We prove the above lemma in “Appendix B.”
To give some intuition how the false-positive probability evolves over time, we plot the above function for \(n = 2^{20}\) and \(k \in \{8, 11, 17, 21\}\) in Fig. 1. Furthermore, we provide plots for \(n \in \{2^{16}, 2^{24}, 2^{30}\}\) in “Appendix C.” It is clearly visible that the false-positive probability is overwhelmingly low if only a fraction of the n elements have been added to the Bloom filter.
A remark on Bloom filters in adversarial environments For our bounds of the correctness error in the \(\mathsf {BFKEM}\), we assume that the puncturing inserts random elements (ciphertexts) into the BF. Now, an adversary could more efficiently exhaust a BF by a clever choice of the ciphertexts and thus violating our bounds. This would essentially represent a denial-of-service (DoS) attack on the scheme. We, however, stress that this class of attacks is hard to prevent in our application in general and thus we do not consider this as an attack vector. Nevertheless, one approach to counter such types of attacks on BFs is the concept of adversarial resilient Bloom-filters introduced by Naor and Yogev in [43]. However, the efficient approach to construct such BFs in [43] requires a secret (unknown to the adversary) to evaluate BF queries, and thus would not applicable in our setting. Naor and Yogev additionally provide a construction secure against unbounded adversaries, which, however, requires to know the precise set \(\mathcal S\) upfront. This is not the case in our application, and we leave the study of BFs in adversarial environments for application in BFE for future work.
2.2 Formal Model of a BFKEM
Subsequently, we introduce the formal model for BFKEM, which is a KEM-variant of puncturable encryption (PE) [17, 20, 31, 33] with the difference that with BFKEM we tolerate a non-negligible correctness error. Our Definition 2 is a variant of the one in [33], except that we allow the key generation to take the additional parameters m and k (of the BF) as input, which specify the correctness error. As already mentioned in Introduction, resorting to present BFKEMs instead of BFE does not represent any limitation.
Definition 2
(BFKEM) A Bloom filter key encapsulation scheme (BFKEM) with key space \(\mathcal {K}\) is a tuple \(\mathsf (KGen,Enc, Punc, Dec)\) of \(\mathsf PPT\) algorithms:
- \({\mathsf {KGen}}(1^\lambda ,m,k):\):
-
Takes as input a security parameter \(\lambda \), parameters m and k and outputs a secret and public key \((\mathsf {sk},\mathsf {pk})\) (we assume that \(\mathcal {K}\) is implicit in \(\mathsf {pk} \), and that \(\mathsf {pk} \) is implicit in \(\mathsf {sk} \)).
- \(\mathsf {Enc}(\mathsf {pk}):\):
-
Takes as input a public key \(\mathsf {pk} \) and outputs a ciphertext C and a symmetric key \(\mathsf {K}\).
- \(\mathsf {Punc}(\mathsf {sk},C):\):
-
Takes as input a secret key \(\mathsf {sk} \), a ciphertext C and outputs an updated secret key \(\mathsf {sk} '\).
- \(\mathsf {Dec}(\mathsf {sk},C):\):
-
Takes as input a secret key \(\mathsf {sk} \), a ciphertext C and deterministically computes and outputs a symmetric key \(\mathsf {K}\) or \(\bot \) if decapsulation fails.
Correctness We start by defining correctness of a BFKEM scheme. Basically, here one requires that a ciphertext can always be decapsulated with unpunctured secret keys. However, we allow that if punctured secret keys are used for decapsulation, then the probability that the decapsulation fails is bounded by some non-negligible function in the scheme’s parameters m, k.
Definition 3
(Correctness) We require that the following holds for all \(\lambda , m,k\in \mathbb {N}\) and any  .
.
For any (arbitrary interleaved) sequence of invocations of

where \(j \in \{1, \ldots , n\}\), \(\mathsf {sk} _{1} := \mathsf {sk} \), and  , it holds that
, it holds that
where  and \(\epsilon (\cdot )\) is a negligible function in \(\lambda \). The probability is over the random coins of \({\mathsf {KGen}}\), \(\mathsf {Punc}\), and \(\mathsf {Enc}\).
and \(\epsilon (\cdot )\) is a negligible function in \(\lambda \). The probability is over the random coins of \({\mathsf {KGen}}\), \(\mathsf {Punc}\), and \(\mathsf {Enc}\).
Remark 1
The bound \(\left( 1-e^{- \frac{(n+1/2)k}{m-1}}\right) ^k\) is motivated by the bound achievable by Bloom filters, cf. Equation (1) and the subsequent discussion.
2.3 Additional Properties of a BFKEM
In this section, we will define additional properties of a BFKEM that we will use for the application to 0-RTT key exchange from [33] and to construct a CCA-secure BFKEM via the Fujisaki–Okamoto (FO) transformation, as described in Sect. 3.2. We will show below that our constructions of CPA-secure BFKEMs satisfy these additional properties, and thus are suitable for our variant of the FO transformation, and to construct 0-RTT key exchange.
Extended correctness Intuitively, we first require an extended variant of correctness which demands that (1) decapsulation always yields a failure when attempting to decapsulate under a secret key previously punctured for that ciphertext. This is analogous to [33]. Second, we additionally demand that (2) decapsulating an honest ciphertext with the unpunctured key does always succeed and (3) if decryption does not fail, then the decapsulated value must match the key returned by the \(\mathsf {Enc}\) algorithm, for any key \(\mathsf {sk} '\) obtained from applying any sequence of puncturing operations to the initial secret key \(\mathsf {sk} \).
Definition 4
(Extended Correctness) We require that the following holds for all \(\lambda , m, k, n\in \mathbb {N}\) and any  .
.
For any (arbitrary interleaved) sequence of invocations of

where \(j \in \{1, \ldots , n\}\), \(\mathsf {sk} _{1} := \mathsf {sk} \), and  , it holds that:
, it holds that:
-
1.
Impossibility of false-negatives:
\(\mathsf {Dec}(\mathsf {sk} _{n+1},C_j)=\bot \) for all \(j \le n\).
-
2.
Perfect correctness of the initial secret key:
\(\mathsf {Dec}(\mathsf {sk},C) = \mathsf {K}\) for all
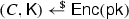 .
. -
3.
Semi-correctness of punctured secret keys:
If \(\mathsf {Dec}(\mathsf {sk} _{j+1},C) \ne \bot \) then \(\mathsf {Dec}(\mathsf {sk} _{j+1},C) = \mathsf {Dec}(\mathsf {sk},C)\).
Separable randomness We require that the encapsulation algorithm \(\mathsf {Enc}\) essentially reads the key \(\mathsf {K}\) in  directly from its random input tape. Intuitively, this will later enable us to make the randomness r used by the encapsulation algorithm \(\mathsf {Enc}\) dependent on the key \(\mathsf {K}\) computed by \(\mathsf {Enc}\).
directly from its random input tape. Intuitively, this will later enable us to make the randomness r used by the encapsulation algorithm \(\mathsf {Enc}\) dependent on the key \(\mathsf {K}\) computed by \(\mathsf {Enc}\).
Definition 5
(Separable Randomness) Let \(\mathsf {BFKEM}= ({\mathsf {KGen}},\mathsf {Enc},\mathsf {Punc},\mathsf {Dec})\) be a BFKEM. We say that \(\mathsf {BFKEM}\)has separable randomness, if one can equivalently write the encapsulation algorithm \(\mathsf {Enc}\) as

for uniformly random \((r,\mathsf {K}) \in \{0,1\}^{\rho +\lambda }\), where \(\mathsf {Enc}(\cdot ;\cdot )\) is a deterministic algorithm whose output is uniquely determined by \(\mathsf {pk} \) and the randomness \((r,\mathsf {K}) \in \{0,1\}^{\rho +\lambda }\).
Remark We note that one can generically construct a separable BFKEM from any non-separable BFKEM. Given a non-separable BFKEM with encapsulation algorithm \(\mathsf {Enc}\), a separable BFKEM with encryption algorithm \(\mathsf {Enc}'\) can be obtained as follows:
- \(\mathsf {Enc}'(\mathsf {pk}; (r,\mathsf {K}')):\):
-
Run
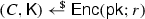 , set \(C':= (C,\mathsf {K}\oplus \mathsf {K}')\) return \((C', \mathsf {K}')\).
, set \(C':= (C,\mathsf {K}\oplus \mathsf {K}')\) return \((C', \mathsf {K}')\).
We need separability in order to apply our variant of the FO transformation, which is the reason why we have to make it explicit. Alternatively, we could have started from a non-separable BFKEM and applied the above construction. However, this adds an additional component to the ciphertext, while the construction given in Sect. 3.1 will already be separable, such that we can avoid this overhead.
Publicly checkable puncturing Finally, we need that it is efficiently checkable whether the decapsulation algorithm outputs \(\bot = \mathsf {Dec}(\mathsf {sk},C)\), given not the secret key \(\mathsf {sk} \), but only the public key \(\mathsf {pk} \), the ciphertext C to be decrypted, and the sequence \(C_1, \ldots , C_w\) at which the secret key \(\mathsf {sk} \) has been punctured.
Definition 6
(Publicly Checkable Puncturing) Let \(\mathcal {Q} = (C_1, \ldots , C_w)\) be any list of ciphertexts. We say that \(\mathsf {BFKEM}\)allows publicly checkable puncturing, if there exists an efficient algorithm \(\mathsf {CheckPunct} \) with the following correctness property.
-
1.
Run
 .
. -
2.
Compute
 and \(\mathsf {sk} = \mathsf {Punc}(\mathsf {sk},C_i)\) for \(i \in [w]\).
and \(\mathsf {sk} = \mathsf {Punc}(\mathsf {sk},C_i)\) for \(i \in [w]\). -
3.
Let C be any string. We require that
$$\begin{aligned} \bot = \mathsf {Dec}(\mathsf {sk},C) \iff \bot = \mathsf {CheckPunct} (\mathsf {pk},\mathcal {Q}, C). \end{aligned}$$
From a high-level perspective, this additional property will be necessary to simulate the decryption oracle properly in the CCA security experiment when our variant of the FO transformation is applied. Together with the second and third property of Definition 4, it replaces the perfect correctness property required in the original FO transformation.
Min-entropy of ciphertexts Following [37], we require that ciphertexts of a randomness-separable BFKEM have sufficient min-entropy, even if \(\mathsf {K}\) is fixed:
Definition 7
(\(\gamma \)-Spreadness) Let \(\mathsf {BFKEM}= ({\mathsf {KGen}},\mathsf {Enc},\mathsf {Punc},\mathsf {Dec})\) be a randomness-separable BFKEM with ciphertext space \(\mathcal C\). We say that \(\mathsf {BFKEM}\) is \(\gamma \)-spread, if for any honestly generated \(\mathsf {pk} \), any key \(\mathsf {K}\) and any \(C \in \mathcal C\)

2.4 Security Definitions
We define three security properties for BFKEMs. The two “standard” security notions are indistinguishability under chosen-plaintext (\(\mathsf {IND}\text {-}\mathsf {CPA}\)) and chosen-ciphertext (\(\mathsf {IND}\text {-}\mathsf {CCA}\)) attacks. In addition, we define one-wayness under chosen-plaintext attacks (\(\mathsf {OW}\text {-}\mathsf {CPA}\)). The latter is the weakest notion among the ones considered in this paper and implied by both \(\mathsf {IND}\text {-}\mathsf {CPA}\) and \(\mathsf {IND}\text {-}\mathsf {CCA}\), but sufficient for our generic construction of \(\mathsf {IND}\text {-}\mathsf {CCA}\)-secure BFKEMs.
Indistinguishability-based security Figure 2 defines the \(\mathsf {IND}\text {-}\mathsf {CPA}\) and \(\mathsf {IND}\text {-}\mathsf {CCA}\) experiments for BFKEMs. The experiments are similar to the security notions for conventional KEMs, but the adversary can arbitrarily puncture the secret key via the \(\mathsf {Punc}\) oracle and retrieve the punctured secret key via the \(\mathsf Corr\) oracle, once it has been punctured on the challenge ciphertext \(C^*\).
Definition 8
(Indistinguishability-Based Security of BFKEM) For \(\mathsf T \in \{\mathsf {IND}\text {-}\mathsf {CPA}, \mathsf {IND}\text {-}\mathsf {CCA} \}\), we define the advantage of an adversary \(\mathcal {A}\) in the \(\mathsf T\) experiment \(\mathbf{Exp}^{\mathsf {T}}_{\mathcal {A},{\mathsf {BFKEM}}}(\lambda ,m,k)\) as
A Bloom filer key-encapsulation scheme \(\mathsf BFKEM\) is \(\mathsf T\in \{\mathsf {IND}\text {-}\mathsf {CPA},\mathsf {IND}\text {-}\mathsf {CCA} \}\) secure, if \(\mathbf{Adv}^{\mathsf {T}}_{\mathcal {A},{\mathsf {BFKEM}}}(\lambda ,m,k)\) is a negligible function in \(\lambda \) for all \(m,k>0\) and all PPT adversaries \(\mathcal {A}\).
One-wayness under chosen-plaintext attack Figure 3 defines the \(\mathsf {OW}\text {-}\mathsf {CPA}\) experiment. The experiment is similar to the \(\mathsf {IND}\text {-}\mathsf {CPA}\) experiment, except that the goal of the adversary is to recover the encapsulated key, given a random challenge ciphertext.
Definition 9
(One-Wayness Under Chosen-Plaintext Attack) We define the advantage of an adversary \(\mathcal {A}\) in experiment \(\mathbf{Exp}^{\mathsf {OW}\text {-}\mathsf {CPA}}_{\mathcal {A},{\mathsf {BFKEM}}}(\lambda ,m,k)\) as
A \(\mathsf {BFKEM}\) is \(\mathsf {OW}\text {-}\mathsf {CPA} \) secure, if \(\mathbf{Adv}^{\mathsf {OW}\text {-}\mathsf {CPA}}_{\mathcal {A},{\mathsf {BFKEM}}}(\lambda ,m,k)\) is a negligible function in \(\lambda \) for all \(m,k>0\) and all PPT adversaries \(\mathcal {A}\).
Relation to “standard KEM security” We would like to point out that it is possible to remove both the puncture and corrupt oracle and immediately send the secret key (punctured at the challenge ciphertext) to the adversary. However, this security definition is only equivalent to our security definition if an adversary cannot detect in which order ciphertexts have been punctured. That is, this security definition only provides reasonable security for schemes where the secret key does not reveal the order of puncturings. A formalization of this can be found in [26].
3 BFKEM Constructions
In this section, we present different \(\mathsf {BFKEM}\)constructions. We start with a CPA-secure version inspired by the hashed Boneh–Franklin identity-based encryption (IBE) scheme [12] in Sect. 3.1 and then show how we can obtain a CCA secure variant via the Fujisaki–Okamoto (FO) transform [25] in the random oracle model (ROM) in Sect. 3.2. Then, in Sect. 3.3 we present a construction of a CPA-secure \(\mathsf {BFKEM}\)from ciphertext-policy attribute-based encryption (CP-ABE) schemes and discuss how to obtain CCA security via the FO transform in the ROM. Finally, in Sect. 3.4 we present a CPA secure \(\mathsf {BFKEM}\)from identity-based broadcast encryption (IBBE) and discuss how to obtain CCA security via the FO transform in the ROM or the CHK transform [16] without requiring random oracles.
3.1 BFKEM from Hashed IBE
Construction In the sequel, let  , and \(g_T = e(g_1,g_2)\). We will always assume that all algorithms described below implicitly receive these parameters as additional input. Let \(\mathsf {B}= ({\mathsf{BFGen}}, {\mathsf{BFUpdate}}, {\mathsf{BFCheck}})\) be a Bloom filter for set \(\mathbb {G}_1\). Furthermore, let \(G: \mathbb {N}\rightarrow \mathbb {G}_2\) and \(E: \mathbb {G}_T \rightarrow \{0,1\}^\lambda \) be cryptographic hash functions (which will be modeled as random oracles [7] in the security proof).
, and \(g_T = e(g_1,g_2)\). We will always assume that all algorithms described below implicitly receive these parameters as additional input. Let \(\mathsf {B}= ({\mathsf{BFGen}}, {\mathsf{BFUpdate}}, {\mathsf{BFCheck}})\) be a Bloom filter for set \(\mathbb {G}_1\). Furthermore, let \(G: \mathbb {N}\rightarrow \mathbb {G}_2\) and \(E: \mathbb {G}_T \rightarrow \{0,1\}^\lambda \) be cryptographic hash functions (which will be modeled as random oracles [7] in the security proof).
Let \(\mathsf {BFKEM}= ({\mathsf {KGen}},\mathsf {Enc},\mathsf {Punc},\mathsf {Dec})\) be defined as follows.
- \(\underline{{\mathsf {KGen}}(1^\lambda , m,k)}:\):
-
This algorithm first generates a Bloom filter instance by running
 . Then, it chooses
. Then, it chooses  and computes and returns $$\begin{aligned} \mathsf {sk}:= (T, (G (i)^\alpha )_{i \in [m]}) \text { and } \mathsf {pk}:= (g^{\alpha }_1, H). \end{aligned}$$
and computes and returns $$\begin{aligned} \mathsf {sk}:= (T, (G (i)^\alpha )_{i \in [m]}) \text { and } \mathsf {pk}:= (g^{\alpha }_1, H). \end{aligned}$$
Remark The reader familiar with the Boneh–Franklin IBE scheme [12] may note that the secret key contains m elements of \(\mathbb {G}_2\), each essentially being a secret key of the Boneh–Franklin scheme for “identity” i, \(i \in [m]\), with respect to “master public-key” \(g^{\alpha }_1\).
- \(\underline{\mathsf {Enc}(\mathsf {pk})}:\):
-
This algorithm takes as input a public key \(\mathsf {pk} \) of the above form. It samples a uniformly random key
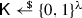 and exponent
and exponent 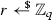 . Then, it computes \(i_j := H_j(g^{r}_1)\) for \((H_j)_{j \in [k]} := H\), then \(y_j = e(g^{\alpha }_1,G(i_j))^r \text { for } j \in [k]\), and finally $$\begin{aligned} C := \left( g^{r}_1, (E (y_j) \oplus \mathsf {K})_{j \in [k]} \right) . \end{aligned}$$
. Then, it computes \(i_j := H_j(g^{r}_1)\) for \((H_j)_{j \in [k]} := H\), then \(y_j = e(g^{\alpha }_1,G(i_j))^r \text { for } j \in [k]\), and finally $$\begin{aligned} C := \left( g^{r}_1, (E (y_j) \oplus \mathsf {K})_{j \in [k]} \right) . \end{aligned}$$It outputs \((C,\mathsf {K}) \in (\mathbb {G}_1 \times \{0,1\}^{k\lambda }) \times \{0,1\}^\lambda \).
Remark Note that for each \(j \in [k]\), the tuple \((g^{r}_1, E (y_j) \oplus \mathsf {K})\) is essentially a “hashed Boneh–Franklin IBE” ciphertext, encrypting \(\mathsf {K}\) for “identity” \(i_j = H_j(g^{r}_1)\) and with respect to master public key \(g^{\alpha }_1\), where the identity is derived deterministically from a “unique” (with overwhelming probability) ciphertext component \(g^{r}_1\). Thus, the ciphertext C essentially consists of k Boneh–Franklin ciphertexts that share the same randomness r, each encrypting the same key \(\mathsf {K}\) for an “identity” derived deterministically from \(g^{r}_1\).
Note also that this construction of \(\mathsf {Enc}\) satisfies the requirement of separable randomness from Definition 5. Furthermore, ciphertexts are \(\gamma \)-spread according to Definition 7 with \(\gamma = \log _2 p\), because \(g^{r}_1\) is uniformly distributed over \(\mathbb {G}_1\).
- \(\underline{\mathsf {Punc}(\mathsf {sk},C)}:\):
-
Given a ciphertext \(C := \left( g^{r}_1, (E (y_j) \oplus \mathsf {K})_{j \in [k]} \right) \) and secret key \(\mathsf {sk} = (T, (\mathsf {sk} [i])_{i \in [m]})\), the puncturing algorithm first computes \(T' = {\mathsf{BFUpdate}}(H, T,g^{r}_1)\). Then, for each \(i \in [m]\) it defines
$$\begin{aligned} \mathsf {sk} '[i] := {\left\{ \begin{array}{ll} \mathsf {sk} [i] &{} \text { if } T'[i] = 0,~\text {and} \\ \bot &{} \text { if } T'[i] = 1, \end{array}\right. } \end{aligned}$$where \(T'[i]\) denotes the i-th bit of \(T'\). Finally, this algorithm returns
$$\begin{aligned} \mathsf {sk} ' := (T', (\mathsf {sk} '[i])_{i \in [m]}). \end{aligned}$$
Remark Note that the above procedure is correct even if the procedure is applied repeatedly with different ciphertexts C, since the \({\mathsf{BFUpdate}}\) algorithm only changes bits of T from 0 to 1, but never from 1 to 0. So we can delete a secret key element \(\mathsf {sk} [i]\) once \(T'[i]\) has been set to 1. Furthermore, we have \(\mathsf {sk} '[i] = \bot \iff T'[i] = 1\). Intuitively, this will ensure that we can use this key to decrypt a ciphertext \(C := \left( g^{r}_1, (E (y_j) \oplus \mathsf {K})_{j \in [k]} \right) \) if and only if \({\mathsf{BFCheck}}(H,T,g^{r}_1) = 0\), where (H, T) is the Bloom filter instance contained in the public key. Note also that the puncturing algorithm essentially only evaluates k universal hash functions \(H = (H_j)_{j \in [k]}\) and then deletes a few secret keys, which makes this procedure extremely efficient. Finally, observe that the filter state T can be efficiently re-computed given only public information, namely the list of hash functions H contained in \(\mathsf {pk} \) and the sequence of ciphertexts \(C_1, \ldots , C_w\) on which a secret key has been punctured. This yields the existence of an efficient \(\mathsf {CheckPunct} \) according to Definition 6.
- \(\underline{\mathsf {Dec}(\mathsf {sk},C)}:\):
-
Given a secret key \(\mathsf {sk} = (T, (\mathsf {sk} [i])_{i \in [m]})\) and a ciphertext \(C := (C[0], C[i_1], \ldots , C[i_k] )\) it first checks whether \({\mathsf{BFCheck}}(H, T, C[0]) = 1\), and outputs \(\bot \) in this case. Otherwise, note that \({\mathsf{BFCheck}}( H, T, C[0]) = 0\) implies that there exists at least one index \(i^*\) with \(\mathsf {sk} [i^*] \ne \bot \). It picks the smallest index \(i^* \in \{i_1, \ldots , i_k\}\) such that \(\mathsf {sk} [i^*] = G (i^*)^\alpha \ne \bot \), computes
$$\begin{aligned} y_{i^*} := e(g^{r}_1, G (i^*)^\alpha ), \end{aligned}$$and returns \(\mathsf {K}:= C[i^*] \oplus E (y_{i^*})\).
Remark If \({\mathsf{BFCheck}}(H, T_n, C[0]) = 0\), then the decryption algorithm performs a “hashed Boneh–Franklin” decryption with a secret key for one of the identities. Note that \(\mathsf {Dec}(\mathsf {sk} _n, C) \ne \bot \iff {\mathsf{BFCheck}}(H, T, C[0]) = 0\), which guarantees the first extended correctness property required by Definition 4. It is straightforward to verify that the other two extended correctness properties of Definition 4 hold as well.
Design choices We note that we have chosen to base our BFKEM on hashed Boneh–Franklin IBE instead of standard Boneh–Franklin for two reasons. First, it allows us to keep ciphertexts short and independent of the size of the binary representation of elements of \(\mathbb {G}_T\). This is useful, because the recent advances for computing discrete logarithms in finite extension fields [39] apply to the target group of state-of-the-art pairing-friendly elliptic curve groups. Recent assessments of the impact of these advances by Menezes et al. [42] as well as Barbulescu and Duquesne [4] suggest that for currently used efficient curve families such as BN [6] or BLS [5] curves a conservative choice of parameters for the 128 bit security level yields sizes of \(\mathbb {G}_T\) elements of \(\approx 4600{-}5500\) bits. The hash function allows us to “compress” these group elements in the ciphertext to 128 bits (the size of a symmetric encryption key). Even if future research enables the construction of bilinear maps where elements of \(\mathbb {G}_T\) can be represented by \(2\lambda \) bits for \(\lambda \)-bit security (which is optimal), it is still preferable to hash group elements to \(\lambda \) bits to reduce the ciphertext by a factor of about 2. Second, by modeling \(E \) as a random oracle, we can reduce security to a weaker complexity assumption.
Correctness error of this scheme We will now explain that the correctness error of this scheme is essentially identical to the false-positive probability of the Bloom filter, up to a statistically small distance which corresponds to the probability that two independent ciphertexts share the same randomness r.
For \(m,k \in \mathbb {N}\), let  , let
, let  denote the set of all valid ciphertext with respect to \(\mathsf {pk} \). Let \({\mathcal {S}} = (C_1, \ldots , C_n)\) be a list of n ciphertexts, where
denote the set of all valid ciphertext with respect to \(\mathsf {pk} \). Let \({\mathcal {S}} = (C_1, \ldots , C_n)\) be a list of n ciphertexts, where  , and run \(\mathsf {sk} _i = \mathsf {Punc}(\mathsf {sk} _{i-1}, C_i)\) for \(i \in [n]\) to determine the secret key \(\mathsf {sk} _n\) obtained from puncturing \(\mathsf {sk} _0\) iteratively on all ciphertexts \(C_i \in {\mathcal {S}}\).
, and run \(\mathsf {sk} _i = \mathsf {Punc}(\mathsf {sk} _{i-1}, C_i)\) for \(i \in [n]\) to determine the secret key \(\mathsf {sk} _n\) obtained from puncturing \(\mathsf {sk} _0\) iteratively on all ciphertexts \(C_i \in {\mathcal {S}}\).
Now let us consider the probability

that a newly generated ciphertext \(C^* \not \in {\mathcal {S}}\) is not correctly decrypted by \(\mathsf {sk} _n\). To this end, let \(C^*[0] = g^{r^*}_1\) denote the first component of ciphertext \(C^* = (g^{r^*}_1, C_1^*, \ldots , C_k^*)\), and likewise let \(C_i[0]\) denote the first component of ciphertext \(C_i\) for all \(C_i \in {\mathcal {S}}\). Writing \(\mathsf {sk} _n = (T_n, (\mathsf {sk} _n[i])_{i \in [m]})\) and \(\mathsf {pk} = (g^{\alpha }_1, H)\), one can now verify that we have \(\mathsf {Dec}(\mathsf {sk} _n, C^*) \ne \mathsf {K}^* \iff {\mathsf{BFCheck}}(H, T_n, C^*[0]) = 1\), because \({\mathsf{BFCheck}}(H, T_n, C^*[0]) = 0\) guarantees that there exists at least one index j such that \(\mathsf {sk} _n[H_j(C^*[0])] \ne \bot \), so correctness of decryption follows essentially from correctness of the Boneh–Franklin scheme. Thus, we have to consider the probability that \({\mathsf{BFCheck}}(H, T_n, C^*[0]) = 1\). We distinguish between two cases:
-
1.
There exists an index \(i \in [n]\) such that \(C^*[0] = C_i[0]\). Note that this implies immediately that \({\mathsf{BFCheck}}(H, T_n, C^*[0]) = 1\). However, recall that \(C^*[0] = g^{r^*}_1\) is a uniformly random element of \(\mathbb {G}_1\). Therefore the probability that this happens is upper bounded by n/q, which is negligibly small.
-
2.
\(C^*[0] \ne C_i[0]\) for all \(i \in [n]\). In this case, as explained in Sect. 2.1, the soundness of the Bloom filter guarantees that
$$\begin{aligned} \mathsf {Pr}[{\mathsf{BFCheck}}(H, T_n, C^*[0]) = 1] \le \left( 1-e^{- \frac{(n+1/2)k}{m-1}}\right) ^k \le 2^{-k}. \end{aligned}$$
In summary, the correctness error of this scheme from the discussion in Sect. 2.1 is approximately \(2^{-k} + n/q\). Since n/q is negligibly small, this essentially amounts to the correctness error of the Bloom filter, which in turn depends on the number of ciphertexts n, and the choice of parameters m, k.
Flexible instantiability of this scheme Our scheme is highly parameterizable in the sense that we can adjust the size of keys and ciphertexts by adjusting the correctness error (determined by the choice of parameters m, k that in turn determine the false-positive probability of the Bloom filter) of our scheme.
Additional properties As already explained in the remarks after the description of the individual algorithms of \(\mathsf {BFKEM}\), the scheme satisfies the requirements of Definitions 4, 5, 6, and 7.
IND-CPAsecurity. We base \(\mathsf {IND}\text {-}\mathsf {CPA}\) security on a bilinear computational Diffie–Hellman variant in the bilinear groups generated by \(\mathsf {BilGen}\).
Definition 10
(BCDH [12]) We define the advantage of adversary \(\mathcal {A}\)in solving the BCDH problem with respect to \(\mathsf {BilGen}\)as

where  , and
, and  .
.
Theorem 1
From each efficient adversary \(\mathcal {B}\)that issues u queries to random oracle \(E \), we can construct an efficient adversary \(\mathcal {A}\)with
Proof
Algorithm \(\mathcal {A}\)receives as input a BCDH-challenge tuple \((g^{r}_1, g^{\alpha }_1, g^{\alpha }_2, h_2)\). It runs adversary \(\mathcal {B}\) as a subroutine by simulating the \(\mathbf{Exp}^{\mathsf {IND}\text {-}\mathsf {CPA}}_{\mathcal {B},\mathsf {BFKEM}}(\lambda ,m,k)\) experiment, including random oracles \(G \) and \(E \), as follows.
First, it defines \({\mathcal {Q}} := \emptyset \), runs  , and defines the public key as \(\mathsf {pk}:= (g^{\alpha }_1, H)\). Note that this public key is identically distributed to a public key output by \({\mathsf {KGen}}(1^\lambda , m, k)\). In order to simulate the challenge ciphertext, the adversary chooses a random key
, and defines the public key as \(\mathsf {pk}:= (g^{\alpha }_1, H)\). Note that this public key is identically distributed to a public key output by \({\mathsf {KGen}}(1^\lambda , m, k)\). In order to simulate the challenge ciphertext, the adversary chooses a random key  and k uniformly random values
and k uniformly random values  , \(j \in [k]\) and defines the challenge ciphertext as \(C^* := (g_1^r, (Y_j)_{j \in [k]})\). Finally, it outputs \((\mathsf {pk}, C^*, \mathsf {K})\) to \(\mathcal {B}\).
, \(j \in [k]\) and defines the challenge ciphertext as \(C^* := (g_1^r, (Y_j)_{j \in [k]})\). Finally, it outputs \((\mathsf {pk}, C^*, \mathsf {K})\) to \(\mathcal {B}\).
Whenever \(\mathcal {B}\)queries \(\mathsf {Punc}(\mathsf {sk}, \cdot )\) on input \(C = (C[0], \ldots )\), then \(\mathcal {A}\)updates T by running \(T = {\mathsf{BFUpdate}}(H,T,C[0])\), and \({\mathcal {Q}}\leftarrow {\mathcal {Q}}\cup \{C \}\).
Whenever a random oracle query to \(G: \mathbb {N}\rightarrow \mathbb {G}_2\) is made (either by \(\mathcal {A}\)or \(\mathcal {B}\)), with input \(\ell \in \mathbb {N}\), then \(\mathcal {A}\)responds with \(G (\ell )\), if \(G (\ell )\) has already been defined. If not, then \(\mathcal {A}\)chooses a random integer  , and returns \(G (\ell )\), where
, and returns \(G (\ell )\), where
This definition of \(G \) allows \(\mathcal {A}\)to simulate the \(\mathsf{Corr}\) oracle as follows. When \(\mathcal {B}\)queries \(\mathsf{Corr}\), then it first checks whether \(C^*\in {\mathcal {Q}}\), and returns \(\bot \) if this does not hold. Otherwise, note that we must have \(\forall j \in [k] : T[H_j(g_1^r)] = 0\), where \(H = (H_j)_{j \in [k]}\) and \(T[\ell ]\) denotes the \(\ell \)-th bit of T. Thus, by the simulation of \(G \) described above, \(\mathcal {A}\)is able to compute and return \(G (\ell )^\alpha = (g_2^{r_\ell })^\alpha = (g_2^\alpha )^{r_\ell }\) for all \(\ell \) with \(\ell \not \in \{H_j(g_1^r) : j \in [k]\}\), and therefore in particular for all \(\ell \) with \(T[\ell ]=1\). This enables the perfect simulation of \(\mathsf{Corr}\).
Finally, whenever \(\mathcal {B}\)queries random oracle \(E: \mathbb {G}_T \rightarrow \{0,1\}^\lambda \) on input y, then \(\mathcal {A}\)responds with \(E (y)\), if \(E (y)\) has already been defined. If not, then \(\mathcal {A}\)chooses a random string  , assigns \(E (y) := Y\), and returns \(E (y)\). Now we have to distinguish between two types of adversaries.
, assigns \(E (y) := Y\), and returns \(E (y)\). Now we have to distinguish between two types of adversaries.
-
1.
A Type-1 adversary \(\mathcal {B}\)never queries \(E \) on input of a value y, such that there exists \(j \in [k]\) such that \(y = e(g_1^\alpha , G (H_j(g_1^r)))^r\). Note that in this case the value \(Y_j' := E (e(g_1^\alpha , G (H_j(g_1^r)))^r)\) remains undefined for all \(j \in [k]\) throughout the entire experiment. Thus, information-theoretically, a Type-1 adversary receives no information about the key encrypted in the challenge ciphertext \(C^*\), and thus can only have advantage \(\mathbf{Adv}^{\mathsf {IND}\text {-}\mathsf {CPA}}_{{\mathcal {B}},{\mathsf {BFKEM}}}(\lambda ,m,k)=0\), in which case the theorem holds trivially.
-
2.
A Type-2 adversary queries \(E (y)\) such that there exists \(j \in [k]\) with \(y = e(g_1^\alpha , G ( H_j(g_1^r)))^r\). \(\mathcal {A}\)uses a Type-2 adversary to solve the BCDH challenge as follows. At the beginning of the game, it picks two indices
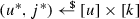 uniformly random. When \(\mathcal {B}\)outputs y in its \(u^*\)-th query to \(E \), then \(\mathcal {A}\)computes and outputs \(W := y \cdot e(g_1^\alpha , g_2^{r})^{-r_\ell }\). Since \(\mathcal {B}\)is a Type-2 adversary, we know that at some point it will query \(E (y)\) with \(y = e(g_1^\alpha , G (H_j(g_1^r)))^r\) for some \(j \in [k]\). If this is the \(u^*\)-th query and we have \(j = j^*\), which happens with probability 1/(uk), then we have $$\begin{aligned} W&= y \cdot e(g_1^r, g_2^{\alpha })^{-r_\ell } = e(g_1^\alpha , G (H_j(g_1^r)))^r\cdot e(g_1^\alpha , g_2^{r})^{-r_\ell } \\&= e(g_1^\alpha , h_2 \cdot g_2^{r_\ell })^r \cdot e(g_1^\alpha , g_2^{r})^{-r_\ell } = e(g_1^\alpha , h_2)^r \cdot e(g_1^\alpha , g_2^{r_\ell })^{r}\cdot e(g_1^\alpha , g_2^{r})^{-r_\ell } \end{aligned}$$
uniformly random. When \(\mathcal {B}\)outputs y in its \(u^*\)-th query to \(E \), then \(\mathcal {A}\)computes and outputs \(W := y \cdot e(g_1^\alpha , g_2^{r})^{-r_\ell }\). Since \(\mathcal {B}\)is a Type-2 adversary, we know that at some point it will query \(E (y)\) with \(y = e(g_1^\alpha , G (H_j(g_1^r)))^r\) for some \(j \in [k]\). If this is the \(u^*\)-th query and we have \(j = j^*\), which happens with probability 1/(uk), then we have $$\begin{aligned} W&= y \cdot e(g_1^r, g_2^{\alpha })^{-r_\ell } = e(g_1^\alpha , G (H_j(g_1^r)))^r\cdot e(g_1^\alpha , g_2^{r})^{-r_\ell } \\&= e(g_1^\alpha , h_2 \cdot g_2^{r_\ell })^r \cdot e(g_1^\alpha , g_2^{r})^{-r_\ell } = e(g_1^\alpha , h_2)^r \cdot e(g_1^\alpha , g_2^{r_\ell })^{r}\cdot e(g_1^\alpha , g_2^{r})^{-r_\ell } \end{aligned}$$and thus W is a solution to the given BCDH instance. Note that \(r_\ell \) is chosen in the simulation and therefore known. \(\square \)
OW-CPA-Security. The following theorem can either be proven analogous to Theorem 1, or based on the fact that \(\mathsf {IND}\text {-}\mathsf {CPA}\) security implies \(\mathsf {OW}\text {-}\mathsf {CPA}\) security. Therefore, we give it without proof.
Theorem 2
From each efficient adversary \(\mathcal {B}\)that issues u queries to random oracle \(E \), we can construct an efficient adversary \(\mathcal {A}\)with
Remark 2
The construction presented above allows to switch the roles of \(\mathbb {G}_1\) and \(\mathbb {G}_2\), i.e., to switch all elements in \(\mathbb {G}_1\) to \(\mathbb {G}_2\) and vice versa. This might be beneficial regarding the size of the secret key when instantiating our construction using a bilinear group where the representation of elements in \(\mathbb {G}_2\) requires more space than the representation of elements in \(\mathbb {G}_1\).
3.2 CCA Security of the BFKEM from Hashed IBE via Fujisaki–Okamoto
We obtain a CCA-secure BFKEM by adopting the Fujisaki–Okamoto (FO) transformation [25] to the BFKEM setting. Since the FO transformation does not work generically for any BFKEM, we have to use the additional requirements on the underlying BFKEM that are defined in Sect. 2.3. These additional properties enable us to overcome the difficulty that the original Fujisaki–Okamoto transformation from [25] requires perfect correctness. We remark that Hofheinz et al. [38] give a new, modular analysis of the FO transformation, which also works for public key encryption schemes with negligible correctness error; however, it is not applicable to BFKEMs, because, due to their non-negligible correctness error, the bounds given in [38] provide insufficient security in this case.
Construction Let \(\mathsf {BFKEM}= ({\mathsf {KGen}},\mathsf {Enc},\mathsf {Punc},\mathsf {Dec})\) be a BFKEM with separable randomness according to Definition 5. This means that we can write \(\mathsf {Enc}\) equivalently as  for uniformly random
for uniformly random  . In the sequel, let R be a hash function (modeled as a random oracle in the security proof), mapping \(R : \{0,1\}^* \rightarrow \{0,1\}^{\rho +\lambda }\). We construct a new scheme \(\mathsf {BFKEM}' = ({\mathsf {KGen}}',\mathsf {Enc}',\mathsf {Punc}',\mathsf {Dec}')\) as follows.
. In the sequel, let R be a hash function (modeled as a random oracle in the security proof), mapping \(R : \{0,1\}^* \rightarrow \{0,1\}^{\rho +\lambda }\). We construct a new scheme \(\mathsf {BFKEM}' = ({\mathsf {KGen}}',\mathsf {Enc}',\mathsf {Punc}',\mathsf {Dec}')\) as follows.
- \(\underline{{\mathsf {KGen}}'(1^\lambda , m,k)}:\):
-
This algorithm is identical to \({\mathsf {KGen}}\).
- \(\underline{\mathsf {Enc}'(\mathsf {pk})}:\):
-
Algorithm \(\mathsf {Enc}'\) samples
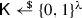 . Then it computes \((r,\mathsf {K}') := R(\mathsf {K}) \in \{0,1\}^{\rho +\lambda }\), runs
. Then it computes \((r,\mathsf {K}') := R(\mathsf {K}) \in \{0,1\}^{\rho +\lambda }\), runs  , and returns \((C,\mathsf {K}')\).
, and returns \((C,\mathsf {K}')\). - \(\underline{\mathsf {Punc}'(\mathsf {sk},C)}:\):
-
This algorithm is identical to \(\mathsf {Punc}\).
- \(\underline{\mathsf {Dec}'(\mathsf {sk},C)}:\):
-
This algorithm first runs
 , and returns \(\bot \) if \(\mathsf {K}= \bot \). Otherwise, it computes \((r,\mathsf {K}') = R(\mathsf {K})\), and checks consistency of the ciphertext by verifying that \((C,\mathsf {K}) = \mathsf {Enc}(\mathsf {pk};(r,\mathsf {K}))\). If this does not hold, then it outputs \(\bot \). Otherwise it outputs \(\mathsf {K}'\).
, and returns \(\bot \) if \(\mathsf {K}= \bot \). Otherwise, it computes \((r,\mathsf {K}') = R(\mathsf {K})\), and checks consistency of the ciphertext by verifying that \((C,\mathsf {K}) = \mathsf {Enc}(\mathsf {pk};(r,\mathsf {K}))\). If this does not hold, then it outputs \(\bot \). Otherwise it outputs \(\mathsf {K}'\).
Correctness error and extended correctness Both the correctness error and the extended correctness according to Definition 4 are not affected by the Fujisaki–Okamoto transform. Therefore, these properties are inherited from the underlying scheme. The fact that the first property of Definition 4 is satisfied makes the scheme suitable for the application to 0-RTT key establishment.
IND-CCA-security. The security proof reduces security of our modified scheme to the \(\mathsf {OW}\text {-}\mathsf {CPA}\) security of the scheme from Sect. 3.
Theorem 3
Let \(\mathsf {BFKEM}=({\mathsf {KGen}},\mathsf {Enc},\mathsf {Punc},\mathsf {Dec})\) be a BFKEM scheme that satisfies the additional properties of Definitions 4 and 6, and which is \(\gamma \)-spread according to Definition 7. Let \(\mathsf {BFKEM}' = ({\mathsf {KGen}}',\mathsf {Enc}',\mathsf {Punc}',\mathsf {Dec}')\) be the scheme described in Sect. 3.2. From each efficient adversary \(\mathcal {A}\)that issues at most \(q_\mathcal {O}\) queries to oracle \({\mathcal {O}}\) and \(q_R\) queries to random oracle R, we can construct an efficient adversary \(\mathcal {B}\)with
Proof
We proceed in a sequence of games. In the sequel, \({\mathcal {O}_i}\) is the implementation of the decryption oracle in Game i.
Game 0
This is the original \(\mathsf {IND}\text {-}\mathsf {CCA}\) security experiment from Definition 8, played with the scheme described above. In particular, the decryption oracle \({\mathcal {O}_0}\) is implemented as follows (we omit the check for \(C = C^*\)):

Recall that \(\mathsf {K}_0\) denotes the encapsulated key computed by the \(\mathsf {IND}\text {-}\mathsf {CCA}\) experiment. \(\mathsf {K}_0\) is uniquely defined by the challenge ciphertext \(C^*\) via \(\mathsf {K}_0 := \mathsf {Dec}(\mathsf {sk} _0,C^*)\), where \(\mathsf {sk} _0\) is the initial (non-punctured) secret key, since the scheme satisfies extended correctness (Definition 4, second property). Let \(A_0\) denote the event that \(\mathcal {A}\)ever queries \(\mathsf {K}_0\) to random oracle R. Note that \(\mathcal {A}\)has zero advantage in distinguishing \(\mathsf {K}'\) from random, until \(A_0\) occurs, because R is a random function. Thus, we have \(\mathsf {Pr}[A_0] \ge \mathbf{Adv}^{\mathsf {IND}\text {-}\mathsf {CCA}}_{{\mathcal {A}},{\mathsf {BFKEM}'}}(\lambda ,m,k)\). In the sequel, we denote with \(A_i\) the event that \(\mathcal {A}\)ever queries \(\mathsf {K}_0\) to random oracle R in Game i.
Game 1
This game is identical to Game 0, except that after computing  and checking whether \(\mathsf {K}\ne \bot \), the experiment additionally checks whether the adversary has ever queried random oracle R on input \(\mathsf {K}\), and returns \(\bot \) if not. More precisely, the experiment maintains a list
and checking whether \(\mathsf {K}\ne \bot \), the experiment additionally checks whether the adversary has ever queried random oracle R on input \(\mathsf {K}\), and returns \(\bot \) if not. More precisely, the experiment maintains a list
to record all queries \(\mathsf {K}\) made by the adversary to random oracle R, along with the corresponding response \((r,\mathsf {K}') = R(\mathsf {K})\). The decryption oracle \({\mathcal {O}_1}\) uses this list as follows (boxed statements highlight changes to \(\mathcal {O}_0\)):

Note that Games 0 and 1 are perfectly indistinguishable, unless \(\mathcal {A}\)ever outputs a ciphertext C with \(\mathcal {O}_1(C) = \bot \), but \(\mathcal {O}_0(C) \ne \bot \). Note that this happens if and only if \(\mathcal {A}\)outputs C such that \(C = \mathsf {Enc}(\mathsf {pk}; (r,\mathsf {K}))\), where r is the randomness defined by \((r,\mathsf {K}') = R(\mathsf {K})\), but without prior query of \(R(\mathsf {K})\).
The random oracle R assigns a uniformly random value \(r \in \{0,1\}^\rho \) to each query, so, by the \(\gamma \)-spreadness of \(\mathsf {BFKEM}\), the probability that the ciphertext C output by the adversary “matches” the ciphertext produced by \(\mathsf {Enc}(\mathsf {pk}; (r,\mathsf {K}))\) is \(2^{-\gamma }\). Since \(\mathcal {A}\)issues at most \(q_\mathcal {O}\) queries to \(\mathcal {O}_1\), this yields \(\mathsf {Pr}[A_1] \ge \mathsf {Pr}[A_0] - {q_\mathcal {O}}/{2^\gamma }\).
Game 2
We make a minor conceptual modification. Instead of computing \((r,\mathsf {K}') = R(\mathsf {K})\) by evaluating R, \(\mathcal {O}_2\) reads \((r,\mathsf {K}')\) from list \(L_R\). More precisely:

By definition of \(L_R\) it always holds that \((r,\mathsf {K}') = R(\mathsf {K})\) for all \((\mathsf {K},(r,\mathsf {K}')) \in L_R\). Indeed \((r,\mathsf {K}')\), is uniquely determined by \(\mathsf {K}\), because \((r,\mathsf {K}') = R(\mathsf {K})\) is a function. Since R is only evaluated by \(\mathcal {O}_1\) if there exists a corresponding tuple \((\mathsf {K},(r,\mathsf {K}')) \in L_R\) anyway, due to the changes introduced in Game 1, oracle \(\mathcal {O}_2\) is equivalent to \(\mathcal {O}_1\) and we have \(\mathsf {Pr}[A_2] = \mathsf {Pr}[A_1]\).
Game 3
This game is identical to Game 2, except that whenever \(\mathcal {A}\)queries a ciphertext C to oracle \(\mathcal {O}_3\), then \(\mathcal {O}_3\) first runs the \(\mathsf {CheckPunct}\) algorithm associated with \(\mathsf {BFKEM}\)(cf. Definition 6). If \(\mathsf {CheckPunct} (\mathsf {pk},\mathcal {Q},C)=\bot \), then it immediately returns \(\bot \). Otherwise, it proceeds exactly like \(\mathcal {O}_2\). More precisely:

Recall that by public checkability (Definition 6) we have \(\bot = \mathsf {Dec}(\mathsf {sk},C) \iff \bot = \mathsf {CheckPunct} (\mathsf {pk},\mathcal {Q}, C)\). Therefore, the introduced changes are conceptual, and \(\mathsf {Pr}[A_3] = \mathsf {Pr}[A_2]\).
Game 4
We modify the secret key used to decrypt the ciphertext. Let \(\mathsf {sk} _0\) denote the initial secret key generated by the experiment (that is, before any puncturing operation was performed). \(\mathcal {O}_4\) uses \(\mathsf {sk} _0\) to compute  instead of
instead of  , where \(\mathsf {sk} \) is a possibly punctured secret key. More precisely:
, where \(\mathsf {sk} \) is a possibly punctured secret key. More precisely:

For indistinguishability from Game 3, we show that \(\mathcal {O}_4(C) = \mathcal {O}_3(C)\) for all ciphertexts C. Let us first consider the case \(\mathsf {Dec}(\mathsf {sk},C) = \bot \). Then, public checkability guarantees that \(\mathcal {O}_4(C) = \mathcal {O}_3(C) = \bot \), due to the fact that \(\mathsf {Dec}(\mathsf {sk},C) = \bot \iff \mathsf {CheckPunct} (\mathsf {pk},\mathcal {Q}, C) = \bot \).
Now let us consider the case \(\mathsf {Dec}(\mathsf {sk},C) \ne \bot \). In this case, the semi-correctness of punctured keys (third requirement of Definition 4) guarantees that \(\mathsf {Dec}(\mathsf {sk},C) = \mathsf {Dec}(\mathsf {sk} _0,C) = \mathsf {K}\ne \bot \).
After computing \(\mathsf {Dec}(\mathsf {sk} _0,C)\), \(\mathcal {O}_4\) performs exactly the same operations as \(\mathcal {O}_3\) after computing \(\mathsf {Dec}(\mathsf {sk},C)\). Thus, in this case both oracles are perfectly indistinguishable, too. This yields that the changes introduced in Game 4 are purely conceptual, and we have \(\mathsf {Pr}[A_4] = \mathsf {Pr}[A_3]\).
Remark Due to the fact that we are now using the initial secret key to decrypt C, we have reached a setting where, due to the perfect correctness of the initial secret key \(\mathsf {sk} _0\), essentially a perfectly correct encryption scheme is used—except that the decryption oracle implements a few additional abort conditions. Thus, we can now basically apply the standard Fujisaki–Okamoto transformation, but we must show that we are also able to simulate the additional abort imposed by the additional consistency checks properly. To this end, we first replace these checks with equivalent checks before applying the FO transformation.
Game 5
We replace the consistency checks performed by \(\mathcal {O}_4\) with an equivalent check. More precisely, \(\mathcal {O}_5\) works as follows:

This is equivalent, so that we have \(\mathsf {Pr}[A_5] = \mathsf {Pr}[A_4]\).
Game 6
Observe that in Game 5 we check whether there exists a tuple \((r,\mathsf {K}')\) with \((\mathsf {K},(r,\mathsf {K}')) \in L_R\) and \((C,\mathsf {K}) = \mathsf {Enc}(\mathsf {pk};(r,\mathsf {K})\), where \(\mathsf {K}\) must match the secret key computed by  .
.
In Game 6, we relax this check. We test only whether there exists any tuple \((\tilde{\mathsf {K}},(\tilde{r}, \tilde{\mathsf {K}}')) \in L_R\) such that \((C,\tilde{\mathsf {K}}) = \mathsf {Enc}(\mathsf {pk};(\tilde{r},\tilde{\mathsf {K}})\) holds. Thus, it is not explicitly checked whether \(\tilde{\mathsf {K}}\) matches the value  . Furthermore, the corresponding value \(\tilde{\mathsf {K}}'\) is returned. More precisely:
. Furthermore, the corresponding value \(\tilde{\mathsf {K}}'\) is returned. More precisely:

By the perfect correctness of the initial secret key \(\mathsf {sk} _0\), we have
so that we must have \(\mathsf {K}= \tilde{\mathsf {K}}\). \(\mathcal {O}_6\) is equivalent to \(\mathcal {O}_5\), and \(\mathsf {Pr}[A_6] = \mathsf {Pr}[A_5]\).
Game 7
This game is identical to Game 6, except that we change the decryption oracle again. Observe that the value \(\mathsf {K}\) computed by  is never used by \(\mathcal {O}_6\). Therefore, the computation of
is never used by \(\mathcal {O}_6\). Therefore, the computation of  is obsolete, and we can remove it. More precisely, \(\mathcal {O}_7\) works as follows.
is obsolete, and we can remove it. More precisely, \(\mathcal {O}_7\) works as follows.

We have only removed an obsolete instruction, which does not change the output distribution of the decryption oracle. Therefore, \(\mathcal {O}_7\) simulates \(\mathcal {O}_6\) perfectly, and we have \(\mathsf {Pr}[A_7] = \mathsf {Pr}[A_6]\).
Reduction to OW-CPA-security. Now we are ready to describe the \(\mathsf {OW}\text {-}\mathsf {CPA}\)-adversary \(\mathcal {B}\). \(\mathcal {B}\)receives \((\mathsf {pk},C^*)\). It samples a uniformly random key  and runs the \(\mathsf {IND}\text {-}\mathsf {CCA}\)-adversary \(\mathcal {A}\)as a subroutine on input \((\mathsf {pk},C^*,\mathsf {K}')\). Whenever \(\mathcal {A}\)issues a \(\mathsf {Punc}\)- or \(\mathsf{Corr}\)-query, then \(\mathcal {B}\)forwards this query to the \(\mathsf {OW}\text {-}\mathsf {CPA}\)-experiment and returns the response. In order to simulate the decryption oracle \(\mathcal {O}\), adversary \(\mathcal {B}\) implements the simulated oracle \(\mathcal {O}_7\) from Game 7 described above. When \(\mathcal {A}\)terminates, then \(\mathcal {B}\) picks a uniformly random entry
and runs the \(\mathsf {IND}\text {-}\mathsf {CCA}\)-adversary \(\mathcal {A}\)as a subroutine on input \((\mathsf {pk},C^*,\mathsf {K}')\). Whenever \(\mathcal {A}\)issues a \(\mathsf {Punc}\)- or \(\mathsf{Corr}\)-query, then \(\mathcal {B}\)forwards this query to the \(\mathsf {OW}\text {-}\mathsf {CPA}\)-experiment and returns the response. In order to simulate the decryption oracle \(\mathcal {O}\), adversary \(\mathcal {B}\) implements the simulated oracle \(\mathcal {O}_7\) from Game 7 described above. When \(\mathcal {A}\)terminates, then \(\mathcal {B}\) picks a uniformly random entry  , and outputs \(\hat{\mathsf {K}}\).
, and outputs \(\hat{\mathsf {K}}\).
Analysis of the reduction Let \(\hat{Q}\) denote the event that \(\mathcal {A}\)ever queries \(\mathsf {K}_0\) to random oracle R. Note that \(\mathcal {B}\) simulates Game 7 perfectly until \(A_7\) occurs; thus, we have \(\mathsf {Pr}[\hat{Q}] \ge \mathsf {Pr}[A_7]\). Summing up, the probability that the value \(\hat{\mathsf {K}}\) output by \(\mathcal {B}\)matches the key encapsulated in \(C^*\) is therefore at least
\(\square \)
Remark on the tightness Alternatively, we could have based the security of our \(\mathsf {IND}\text {-}\mathsf {CCA}\)-secure scheme on the \(\mathsf {IND}\text {-}\mathsf {CPA}\) (rather than \(\mathsf {OW}\text {-}\mathsf {CPA}\)) security of \(\mathsf {BFKEM}'\). In this case, we would have achieved a tighter reduction, as we would have been able to avoid guessing the index  , at the cost of requiring stronger security of the underlying scheme.
, at the cost of requiring stronger security of the underlying scheme.
From IND-CCA-secure KEMs to IND-CCA-secure encryption. It is well known that \(\mathsf {IND}\text {-}\mathsf {CCA}\)-secure KEMs can be generically transformed into \(\mathsf {IND}\text {-}\mathsf {CCA}\)-secure encryption schemes, by combining it with a CCA-secure symmetric encryption scheme [25]. This construction applies to BFKEMs as well.
3.3 BFKEM from CP-ABE
We now present an alternative, generic construction of a BFKEM from ciphertext-policy attribute-based encryption (CP-ABE) [8]. In particular, the construction can be instantiated with any small-universe (i.e., bounded) CP-ABE schemeFootnote 3 that is adaptively secure, supports at least OR-policies, and allows to encrypt messages from an exponentially large space. We note that since the formulation of KEMs in context of ABE is not widely used, we opt to start from a CP-ABE scheme which we implicitly turn into a KEM in the construction via the folklore compiler to obtain KEMs from encryptions schemes.
In contrast to the basic BFKEM construction in Sect. 3.1, we are able to generically obtain constant-size ciphertexts (independent of the parameters m and k) if the underlying CP-ABE scheme beyond possessing the aforementioned properties, is also compact, i.e., provides constant-size ciphertexts, (as, e.g., [2, 18] which are obtained from static and parameterized assumptions, respectively). Compact-size ciphertexts come at the cost of increased secret key size in existing schemes (at least quadratic in the number of attributes). However, for forward-secret 0-RTT key-exchange storage cost at the server is less expensive than communication bandwidth and thus can be considered a viable trade-off.
CP-ABE Before we describe our construction let us briefly recall CP-ABE. Therefore, let \(\mathbb {U}\) be the universe of attributes and we require only small-universe constructions, i.e., \(\mathbb {U}\) is fixed at setup and \(|\mathbb {U}|\) is polynomially bounded in the security parameter \(\lambda \) (in our BFKEM construction we will have \(|\mathbb {U}|=m\)). Intuitively, in a CP-ABE scheme secret keys are issued with respect to attribute sets \(\mathbb {U}'\subseteq \mathbb {U}\) and messages are encrypted with respect to access structures (policies) defined over \(\mathbb {U}\). Decryption works iff the attributes in the secret key satisfy the policy used to produce the ciphertext. Let us discuss this a bit more formally.
Definition 11
(Access Structure [8]) Let \(\mathbb {U}\) be the attribute universe. A collection \(\mathbb {A}\in 2^{\mathbb {U}}\) of non-empty sets is an access structure on \(\mathbb {U}\). The sets in \(\mathbb {A}\) are called the authorized sets, and the sets not in \(\mathbb {A}\) are called the unauthorized sets. A collection \(\mathbb {A}\in 2^{\mathbb {U}}\) is called monotone if \(\forall ~B,C \in \mathbb {A}:\) if \(B\in \mathbb {A}\) and \(B\subseteq C\), then \(C\in \mathbb {A}\).
Subsequently, we do not require arbitrary monotone access structures, but only OR-policies (i.e., threshold policies with threshold 1). In particular, for some attribute set \(\mathbb {U}':=(u_1,\ldots ,u_n)\subseteq \mathbb {U}\) we consider policies of the form \(u_1~ \text {OR}~\ldots ~\text {OR}~u_n\), representing an access structure \(\mathbb {A}:=2^{\mathbb {U}'}\setminus \emptyset \).
Definition 12
(CP-ABE) A ciphertext-policy attribute-based encryption scheme is a tuple \(\mathsf {CP}\text {-}\mathsf {ABE}= (\mathsf Setup, KGen, Enc, Dec)\) of \(\mathsf PPT\) algorithms:
- \(\mathsf{Setup}(1^\lambda ,\mathbb {U}):\):
-
Takes as input a security parameter \(\lambda \) and an attribute universe description \(\mathbb {U}\) and outputs a master secret and public key \((\mathsf {msk},\mathsf {mpk})\). We assume that all subsequent algorithms will implicitly receive the master public key \(\mathsf {mpk} \) (public parameters) as input which implicitly fixes a message space \(\mathcal {M}\).
- \(\mathsf{KGen}(\mathsf {msk},\mathbb {U}'):\):
-
Takes as input the master secret key \(\mathsf {msk} \) and a set of attributes \(\mathbb {U}'\subseteq \mathbb {U}\) and outputs a secret key \(\mathsf {sk} _{\mathbb {U}'}\).
- \(\mathsf{Enc}(M,\mathbb {A}):\):
-
Takes as input a message \(M\in \mathcal {M}\) and an access structure \(\mathbb {A}\) and outputs a ciphertext C.
- \(\mathsf{Dec}(\mathsf {sk} _{\mathbb {U}'},C):\):
-
Takes as input a secret key \(\mathsf {sk} _{\mathbb {U}'}\) and a ciphertext C and outputs a message M or \(\bot \) in case of decryption does not work.
Correctness of CP-ABE requires that for all \(\lambda \), all attribute sets \(\mathbb {U},\) all  , all \(M\in \mathcal {M}\), all \(\mathbb {A}\in 2^{\mathbb {U}}\setminus \emptyset \), all \(\mathbb {U}'\in \mathbb {A}\), all
, all \(M\in \mathcal {M}\), all \(\mathbb {A}\in 2^{\mathbb {U}}\setminus \emptyset \), all \(\mathbb {U}'\in \mathbb {A}\), all  we have that \(\mathsf {Pr}[\mathsf{Dec}(\mathsf {sk} _{\mathbb {U}'},\mathsf{Enc}(M,\mathbb {A}))=M]=1\).
we have that \(\mathsf {Pr}[\mathsf{Dec}(\mathsf {sk} _{\mathbb {U}'},\mathsf{Enc}(M,\mathbb {A}))=M]=1\).
Security of CP-ABE Figure 4 defines adaptive \(\mathsf IND\)-\(\mathsf T\) with \(\mathsf{T} \in \{\mathsf{CPA}, \mathsf{CCA}\}\) security for CP-ABE. We stress that we use a formalization for small-universe schemes where the size of \(\mathbb {U}\) is polynomially bounded in the security parameter \(\lambda \) (for large universe \(\mathbb {U}\) is not required for \(\mathsf Setup\)). We denote this value by n and consider the attribute set to be \(\mathbb {U}=\{1,\ldots ,n\}\).
Definition 13
(\(\mathsf{IND}\)-\(\mathsf{T}\) Security of CP-ABE) We define the advantage of an adversary \(\mathcal {A}\) in the \(\mathsf IND\)-\(\mathsf T\) experiment \(\mathbf{Exp}^{\mathsf {IND\text {-}T}}_{\mathcal {A},\mathsf {CP}\text {-}\mathsf {ABE}}(\lambda ,n)\) as
A ciphertext-policy attribute-based encryption scheme \(\mathsf {CP}\text {-}\mathsf {ABE}\) is \(\mathsf IND\)-\(\mathsf T\), \(\mathsf{T} \in \{\mathsf{CPA}, \mathsf{CCA}\}\), secure, if \(\mathbf{Adv}^{\mathsf {IND\text {-}T}}_{\mathcal {A},\mathsf {CP}\text {-}\mathsf {ABE}}(\lambda ,n)\) is a negligible function in \(\lambda \) for all \(n>0\) and all PPT adversaries \(\mathcal {A}\).
Intuition of the BFKEM construction The intuition of constructing a CPA-secure BFKEM from CP-ABE is very simple. Basically, we map the indices m in \(T\in \{0,1\}^m\) of a Bloom filter (H, T) to the attribute universe \(\mathbb {U}\). Then, we generate for every attribute \(i\in [m]\) (we consider \(\mathbb {U}=\{1,\ldots ,m\}\)) a secret key \(\mathsf {sk} _{\{i\}}\), set our secret key of the BFKEM scheme to be \(\mathsf {sk}:=(T,(\mathsf {sk} _{\{1\}},\ldots ,\mathsf {sk} _{\{m\}}))\) and delete \(\mathsf {msk} \). Encryption is with respect to the attributes given by the indices \(\mathcal {I}\) obtained from sending a randomly sampled tag r through the hash functions \(H_j\), \(j\in [k]\) of the Bloom filter. Decryption works by using one secret key \(\mathsf {sk} _{\{i\}}\) indexed by \(\mathcal {I}\). Puncturing a ciphertext simply amounts to discarding all the secret keys \(\mathsf {sk} _{\{i\}}\) indexed by \(\mathcal {I}\).
Construction Subsequently, we describe the generic CPA-secure BFKEM construction from a CP-ABE scheme \(\mathsf ABE\). We, thereby, require a CP-ABE with exponentially large message space \(\mathcal {M}\) and assume that the key space \(\mathcal K\) of the BFKEM scheme is equivalent to \(\mathcal {M}\).
- \(\underline{{\mathsf {KGen}}(1^\lambda ,m,k)}:\):
-
Runs
 . Then it runs
. Then it runs 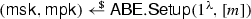 , and for all
, and for all  . Finally it sets and outputs $$\begin{aligned} \mathsf {sk}:= (T, (\mathsf {sk} _{\{i\}})_{i \in [m]}) \text { and } \mathsf {pk}:= (\mathsf {mpk}, (H_j)_{j \in [k]}). \end{aligned}$$
. Finally it sets and outputs $$\begin{aligned} \mathsf {sk}:= (T, (\mathsf {sk} _{\{i\}})_{i \in [m]}) \text { and } \mathsf {pk}:= (\mathsf {mpk}, (H_j)_{j \in [k]}). \end{aligned}$$ - \(\underline{\mathsf {Enc}(\mathsf {pk})}:\):
-
Takes as input a public key \(\mathsf {pk} \). It samples uniformly at random a key
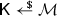 , as well as a value
, as well as a value  , computes \(\forall j\in [k]: i_j=H_j(r)\), sets \(\mathbb {U}'= \{i_1,\ldots ,i_k\}\) and \(\mathbb {A}=2^{\mathbb {U}'}\setminus \emptyset \). Finally, it computes
, computes \(\forall j\in [k]: i_j=H_j(r)\), sets \(\mathbb {U}'= \{i_1,\ldots ,i_k\}\) and \(\mathbb {A}=2^{\mathbb {U}'}\setminus \emptyset \). Finally, it computes  and outputs \((C, \mathsf {K})\) where ciphertext \(C:=(r,C')\).
and outputs \((C, \mathsf {K})\) where ciphertext \(C:=(r,C')\).
Remark We remark that if a CP-ABE is used where \(\mathcal K\) and \(\mathcal M\) are different, one can use standard randomness extraction techniques to extract a key \(k \in \mathcal{K}\) from a uniformly random message \(m \in \mathcal{M}\).
- \(\underline{\mathsf {Punc}(\mathsf {sk},C)}:\):
-
Takes as input a secret key \(\mathsf {sk}:=(T, (\mathsf {sk} _{\{i\}})_{i \in [m]})\) and ciphertext \(C:=(r,C')\). It computes
 and for each \(i \in [m]\) it defines $$\begin{aligned} \mathsf {sk} '_{\{i\}} := {\left\{ \begin{array}{ll} \mathsf {sk} _{\{i\}} &{} \text { if } T'[i] = 0,~\text {and} \\ \bot &{} \text { if } T'[i] = 1, \end{array}\right. } \end{aligned}$$
and for each \(i \in [m]\) it defines $$\begin{aligned} \mathsf {sk} '_{\{i\}} := {\left\{ \begin{array}{ll} \mathsf {sk} _{\{i\}} &{} \text { if } T'[i] = 0,~\text {and} \\ \bot &{} \text { if } T'[i] = 1, \end{array}\right. } \end{aligned}$$where \(T'[i]\) denotes the i-th bit of \(T'\). Finally, it returns an updated secret key \(\mathsf {sk} '=(T',(\mathsf {sk} '_{\{i\}})_{i \in [m]})\).
- \(\underline{\mathsf {Dec}(\mathsf {sk},C)}:\):
-
Takes as input a secret key \(\mathsf {sk} \) and a ciphertext \(C:=(r,C')\). It computes \(\forall j\in [k]: i_j=H_j(r)\) and takes the first element \(sk_{\{i_j\}}\) from \((\mathsf {sk} _{\{i\}})_{i \in [m]}\) with \(sk_{\{i_j\}}\ne \bot \). If such an \(sk_{\{i_j\}}\) exists it outputs
 and \(\bot \) otherwise.
and \(\bot \) otherwise.
Correctness error of this scheme Under the same argumentation as in the correctness proof in Sect. 3.1, we obtain that the correctness error is approximately \( 2^{-k} + n/2^{\lambda }\).
CPA security We directly relate the CPA security of our construction to the hardness of breaking CPA security for the underlying CP-ABE.
Theorem 4
From each efficient adversary \(\mathcal B\) against CPA security of our BFKEM, we can construct an efficient adversary \(\mathcal A\) which breaks CPA security of the underlying CP-ABE, with
Proof
We present a reduction which uses an adversary \(\mathcal B\) against CPA security of the BFKEM to break CPA security of the CP-ABE. First, we engage with a CPA challenger for a CP-ABE with respect to universe [m] to obtain \(\mathsf {mpk} \). Then, we complete the setup by running the following \(\mathsf{KeyGen}'\) algorithm and obtain \(\mathsf {pk} \):
- \(\mathsf{KeyGen'}(\mathsf {mpk}, m, k):\):
-
Runs
 , sets $$\begin{aligned} \mathsf {pk}:= (\mathsf {mpk}, (H_j)_{j \in [k]}), \end{aligned}$$
, sets $$\begin{aligned} \mathsf {pk}:= (\mathsf {mpk}, (H_j)_{j \in [k]}), \end{aligned}$$and outputs \(\mathsf {pk} \).
Then, we choose  ,
,  , and compute \(\forall j \in [k]: i_j = H_j(r)\), set \(\mathbb {U}' = \{i_1, \dots , i_k\}\), let \(\mathbb {A} = 2^{\mathbb {U}'}\setminus \emptyset \). We output \((\mathsf {K}_0, \mathsf {K}_1, \mathbb {A})\) to the challenger to obtain \(C'^*\). We start \(\mathcal B\) on \((\mathsf {pk}, (r, C'^*), \mathsf {K}_0)\) and simulate the oracles as follows:
, and compute \(\forall j \in [k]: i_j = H_j(r)\), set \(\mathbb {U}' = \{i_1, \dots , i_k\}\), let \(\mathbb {A} = 2^{\mathbb {U}'}\setminus \emptyset \). We output \((\mathsf {K}_0, \mathsf {K}_1, \mathbb {A})\) to the challenger to obtain \(C'^*\). We start \(\mathcal B\) on \((\mathsf {pk}, (r, C'^*), \mathsf {K}_0)\) and simulate the oracles as follows:
- \(\mathsf{Punc}(\mathsf {sk}, C):\):
-
Set \(\mathtt{P} \leftarrow \mathtt{P} \cup \{C\}\), and \(T \leftarrow \mathsf{BFUpdate}((H_j)_{i\in [k]}, T, r)\).
- \(\mathsf{Corr}:\):
-
If \(C^* \notin \mathtt{P}\) return \(\bot \). Otherwise, \(\forall j\in [k]: i_j = T[j]\), and, for all \(i_j = 0\) obtain \(\mathsf {sk} _{j} \leftarrow \mathsf{KGen}(j)\) using the key generation oracle provided by the challenger and return \(\mathsf {sk} \leftarrow (T, \{\mathsf {sk} _{j}\}_{j \in [k], i_j = 0})\).
If \(\mathcal B\) eventually outputs a bit \(b^*\) we output \(b^*\) to break CPA security of the CP-ABE scheme with the same probability as \(\mathcal B\) breaks the CPA security of the BFKEM. Note that the \(\mathsf{Corr}\) oracle can only be called after the challenge ciphertext \(C^*\), and, therefore r, is determined. This ensures that we only request “allowed” keys via the \(\mathsf KGen\) oracle provided by the challenger. \(\square \)
Obtaining CCA security The construction satisfies the additional properties of Definitions 4, 5, and 6 with the same arguments as in Sect. 3.1. Additionally, \(\gamma \)-spreadness (Definition 7) is given by construction: The randomness r is chosen uniformly at random from \(\{0,1\}^\lambda \). Thus, we can apply the Fujisaki–Okamoto [25] transform the same way as done in Sect. 3.2 to achieve CCA security.
3.4 BFKEM from IBBE
In this section, we present our generic construction of a BFKEM from any identity-based broadcast encryption (IBBE) scheme. We note that taking the path via IBBE allows us to simultaneously obtain small ciphertexts and small public keys.
Identity-Based Broadcast Encryption We recall the basic definition of IBBE and its security.
Definition 14
(IBBE) An identity-based broadcast encryption (IBBE) scheme is a tuple \(\mathsf {IBBE} = (\mathsf {Setup}, \mathsf {Extract}, \mathsf {Enc}, \mathsf {Dec})\) consisting of four probabilistic polynomial-time algorithms with the following properties:
- \(\mathsf {Setup} (1^\lambda , k):\):
-
Takes as input the security parameter \(\lambda \) and the maximal number of receivers k and outputs a master public key \(\mathsf {pk} \) and a master secret key \(\mathsf {msk} \). We assume that \(\mathsf {pk} \) implicitly defines the identity space \(\mathcal ID\).
- \(\mathsf {Extract} (\mathsf {msk}, \mathsf {ID} _i):\):
-
Takes as input the master secret key \(\mathsf {msk} \) and an user identity \(\mathsf {ID} _i\) and outputs and user private key \(\mathsf {sk} _{\mathsf {ID} _i}\).
- \(\mathsf {Enc} (\mathsf {pk}, \mathcal {S}):\):
-
Takes as input the master public key \(\mathsf {pk} \) and a set of user identities \(\mathcal {S}\) and outputs a ciphertext C and a key \(\mathsf {K}\).
- \(\mathsf {Dec} (\mathsf {sk} _{\mathsf {ID} _i}, \mathcal {S}, C):\):
-
Takes as input a user secret key \(\mathsf {sk} _{\mathsf {ID} _i}\), a set of user identities \(\mathcal {S}\) and a ciphertext C and outputs the key \(\mathsf {K}\).
Correctness for IBBE requires that for all \(\lambda \), for all polynomially bounded k in \(\lambda \), for all  , for all \(\mathcal{S} = \{\mathsf {ID} _1, \dots , \mathsf {ID} _i\} \in \mathcal{ID}^i\) with \(i \le k\), for all
, for all \(\mathcal{S} = \{\mathsf {ID} _1, \dots , \mathsf {ID} _i\} \in \mathcal{ID}^i\) with \(i \le k\), for all  , it holds for all \(\mathsf {ID} _\mathcal{S} \in \mathcal{S}\) that
, it holds for all \(\mathsf {ID} _\mathcal{S} \in \mathcal{S}\) that
Definition 15
(\(\mathsf {IND}\text {-}\mathsf {sID}\text {-}\mathsf {CPA}\)-security of IBBE) We define the advantage of an adversary \(\mathcal {A}\) in the \(\mathsf {IND}\text {-}\mathsf {sID}\text {-}\mathsf {CPA}\) experiment \(\mathbf{Exp}^{\mathsf {IND}\text {-}\mathsf {sID}\text {-}\mathsf {CPA}}_{{\mathcal {A}},\mathsf {IBBE}}(\lambda , k)\) as
We say that an identity-based broadcast encryption scheme \(\mathsf {IBBE}\) is \(\mathsf {IND}\text {-}\mathsf {sID}\text {-}\mathsf {CPA}\)-secure, if the advantage \(\mathbf{Adv}_{\mathcal {A}, \mathsf {IBBE}}^{\mathsf {IND}\text {-}\mathsf {sID}\text {-}\mathsf {CPA}}(\lambda , k)\) is a negligible function in \(\lambda \) for all \(k > 0\) and all PPT adversaries \(\mathcal {A}\).
Construction Let \(\mathsf {B}= ({\mathsf{BFGen}}, {\mathsf{BFUpdate}}, {\mathsf{BFCheck}})\) be a Bloom filter and let \(\mathsf {IBBE}\) = (\(\mathsf {Setup}\), \(\mathsf {Extract}\), \(\mathsf {Enc}\), \(\mathsf {Dec}\)) be an identity-based broadcast encryption scheme. We construct a Bloom filter key encapsulation mechanism \(\mathsf {BFKEM}\)= (\({\mathsf {KGen}}, \mathsf {Enc}, \mathsf {Punc}, \mathsf {Dec}\)) as follows:
\(\underline{{\mathsf {KGen}}(\lambda , m, k)}:\) The key generation algorithm generates a Bloom filter instance by running  and generates an IBBE instance by invoking
and generates an IBBE instance by invoking  . For each \(i \in [m]\) it calls
. For each \(i \in [m]\) it calls

Finally, it sets
Remark Observe that the maximum number of recipients is set to the Bloom filter’s optimal number of universal hash functions k and the user identity space is bound to the Bloom filter’s entries m.
\(\underline{\mathsf {Enc}(\mathsf {pk})}:\) Given a public key \(\mathsf {pk} = (H, \mathsf {pk} _\mathsf {IBBE})\), it samples a random value  and generates indices \(i_j := H_j(r)\) for \((H_j)_{j \in [k]} := H\). Then, it invokes
and generates indices \(i_j := H_j(r)\) for \((H_j)_{j \in [k]} := H\). Then, it invokes  , where \(\mathcal {S} := \{i_j\}_{j \in [k]}\). Finally, it outputs \((C, \mathsf {K})\), where ciphertext \(C := (r, C')\).
, where \(\mathcal {S} := \{i_j\}_{j \in [k]}\). Finally, it outputs \((C, \mathsf {K})\), where ciphertext \(C := (r, C')\).
\(\underline{\mathsf {Punc}(\mathsf {sk}, C)}:\) Given a secret key \(\mathsf {sk} = (T, (\mathsf {sk} _i)_{i \in [m]})\) and a ciphertext \(C = (r, C')\), it invokes \(T' = {\mathsf{BFUpdate}}(H, T, r)\) and defines
Finally, the algorithm returns \(\mathsf {sk} ' = (T', (\mathsf {sk} '_i)_{i \in [m]})\).
Remark From an IBBE’s point of view, the puncturing procedure removes participants from the broadcast network by deleting their respective user private keys.
\(\underline{\mathsf {Dec}(\mathsf {sk}, C)}:\) The input is a secret key \(\mathsf {sk} = (T, (\mathsf {sk} _i)_{i \in [m]})\) and ciphertext \(C = (r, C')\). Again, let \(\mathcal {S} := \{i_j\}_{j \in [k]}\). If \({\mathsf{BFCheck}}(H, T, r) = 0\), then the algorithm returns \(\bot \). Else, there exists at least one index \(n \in \mathcal {S}\) such that \(\mathsf {sk} _{n} \ne \bot \). The algorithm picks the smallest index n that meets the previous requirements, computes
and returns \(\mathsf {K}\).
Remark This algorithm essentially checks, if an user secret key of the user identities in set \(\mathcal {S}\) still exists. If so, the ciphertext can be decrypted.
Correctness error With exactly the same arguments as for the scheme from Sect. 3.1, one can verify that the correctness error of this scheme is essentially identical to the false positive probability of the Bloom filter, unless a given ciphertext \(C = (r, C')\) has a value of r which is identical to the value of r of any previous ciphertext. Since r is uniformly random in \(\{0,1\}^\lambda \), this probability is approximately \(2^{-k} + n \cdot 2^{-\lambda }\).
IND-CPA-security. We prove the \(\mathsf {IND}\text {-}\mathsf {CPA}\) security of our construction, if the IBBE is \(\mathsf {IND}\text {-}\mathsf {sID}\text {-}\mathsf {CPA}\)-secure.
Theorem 5
From each efficient adversary \(\mathcal {B}\)against \(\mathsf {IND}\text {-}\mathsf {CPA}\) security of our BFKEM, we can construct an efficient algorithm \(\mathcal {A}\)against the \(\mathsf {IND}\text {-}\mathsf {sID}\text {-}\mathsf {CPA}\) security of the underlying IBBE scheme with advantage
Proof
We proceed by presenting a reduction which uses an adversary \(\mathcal {B}\)against the \(\mathsf {IND}\text {-}\mathsf {CPA}\) security of the BFKEM to break the \(\mathsf {IND}\text {-}\mathsf {sID}\text {-}\mathsf {CPA}\) security of the IBBE. The reduction together with \(\mathcal {B}\)then forms \(\mathcal {A}\). In order to engage with the \(\mathsf {IND}\text {-}\mathsf {CPA}\) Challenger (\(\mathcal {C}\)henceforth), we need to commit to a set of recipients \(\mathcal {S}^*\) we will attack.
We generate a new Bloom filter instance by invoking  and sample an additional random value
and sample an additional random value  . Next, we compute indices \(i_j := H_j(r^*)\) where \((H_j)_{j \in [k]} := H\) are the k universal hash functions of the Bloom filter. We define \(\mathcal {S}^* := \{i_j\}_{j \in [k]}\) and forward the set to \(\mathcal {C}\). Note that \(|\mathcal {S}| = k\).
. Next, we compute indices \(i_j := H_j(r^*)\) where \((H_j)_{j \in [k]} := H\) are the k universal hash functions of the Bloom filter. We define \(\mathcal {S}^* := \{i_j\}_{j \in [k]}\) and forward the set to \(\mathcal {C}\). Note that \(|\mathcal {S}| = k\).
The challenger \(\mathcal {C}\)generates a master public key \(\mathsf {pk} \) and a master secret key \(\mathsf {msk} \) by invoking \(\mathsf {IBBE}.\mathsf {Setup} (\lambda , k)\) and sends us the master public key \(\mathsf {pk} \). Additionally, \(\mathcal {C}\)prepares a challenge by running  and sampling
and sampling  , where \(\mathcal {K}\) is the symmetric key space. The challenger sends us the challenge \((C', \mathsf {K}_b)\), where b is a bit drawn uniformly at random.
, where \(\mathcal {K}\) is the symmetric key space. The challenger sends us the challenge \((C', \mathsf {K}_b)\), where b is a bit drawn uniformly at random.
We will initialize the adversary \(\mathcal {B}\)with input \((\mathsf {pk}, C^* = (r^*, C'), \mathsf {K}_b)\). In the sequel, \(\mathcal {B}\)has access to several oracles, which we simulate as follows:
-
\(\mathsf {Punct}(C = (r, C'))\): We invoke \(T := {\mathsf{BFUpdate}}(H, T, r)\) and set \(\mathcal {Q} := \mathcal {Q} \cup \{C\}\).
-
\(\mathsf {Corr}:\) If \(C^* \notin \mathcal {Q}\), return \(\bot \). Else query \(\mathsf {sk} _j := \mathsf {Extract}(j)\) for all \(j \in [k]\) such that \(T[j] = 0\). Note that we are allowed to call \(\mathsf {Extract}\) on all user identities, since puncturing at \(C^*\) removes all troublesome secret keys. We return \((T, \{\mathsf {sk} _j\}_{j \in [k] \wedge T[j] = 0})\) to \(\mathcal {A}\).
Eventually, \(\mathcal {B}\)will output a bit \(b^*\) which we will forward to the challenger \(\mathcal {C}\). Since all queries are perfectly simulated, we get
This concludes the proof. \(\square \)
CCA security \(\mathsf {IND}\text {-}\mathsf {CCA} \) security can be achieved with the modified Fujisaki–Okamoto transformation described in Sect. 3.2. The IBBE-based construction satisfies the additional properties of Definitions 4, 5, and 6 with the same arguments as in Sect. 3.1. Additionally, \(\gamma \)-spreadness (Definition 7) is given by construction: The randomness r is chosen uniformly at random from \(\{0,1\}^\lambda \).
Separable randomness is not achieved as the symmetric key \(\mathsf {K}\) algebraically depends on the IBBE (i.e., the symmetric key \(\mathsf {K}\) is chosen by the IBBE and not by the generic construction).Footnote 4 It is, however, possible to transform any non-separable BFKEM into a separable BFKEM as shown in Sect. 2.3. Note that this transformation adds an additional component of size \(\lambda \) to the ciphertext.
Thus, we can apply the Fujisaki–Okamoto transform the same way as done in Sect. 3.2 to achieve CCA security. One notable drawback is that the transformation requires that the encapsulation procedure be run once during each decapsulation. Should the encapsulation procedure be computationally expensive and should the application strive for high efficiency, it might be worth considering a different approach for achieving \(\mathsf {IND}\text {-}\mathsf {CCA}\) security.
A different approach to achieve \(\mathsf {IND}\text {-}\mathsf {CCA}\) security for our construction would be to directly use an \(\mathsf {IND}\text {-}\mathsf {sID}\text {-}\mathsf {CCA}\)-secure IBBE. This can for example be achieved by using a variant of the CHK transformation [16] sketched in [22]. The basic idea is to derive one of the broadcasted identities from a verification key of a strongly unforgeable one-time signature (sOTS) scheme, which then in turn is used to sign the ciphertext. A reasonable choice for the signature scheme might be the Boneh–Lynn–Shacham signature scheme [13], which is strongly unforgeable due to its unique ciphertexts, or the sOTS due to Groth [32] which avoids pairing evaluations. Drawbacks of the transformation include an expansion of the ciphertext as both the signature verification key and the signature must be included. A formal description and security proof of the transformation can be found in [26].
4 Time-Based Bloom Filter Encryption
For a standard BFKEM scheme, we have to update the public key after the secret key has been punctured n-times, because otherwise the false-positive probability would exceed an acceptable bound. In this section, we describe a construction of a scheme where the lifetime of the public key is split into time slots. Ciphertexts are associated with time slots, which assumes loosely synchronized clocks between sender and receiver of a ciphertext. The main advantage is that for a given bound on the correctness error, we are able to handle about the same number of puncturings per time slot as the basic scheme during the entire life time of the public key. We call this approach time-based Bloom filter encryption. It is inspired by the time-based approach used to construct puncturable encryption in [31, 33], which in turn is inspired by the construction of forward-secure public-key encryption by Canetti, Halevi, and Katz [15].
Note that a time-based BFKEM (TB-BFKEM) scheme can trivially be obtained from any BFE scheme, by assigning an individual public/secret key pair for each time slot. However, if we want to split the life time of the public key into, say, \(2^t\) time slots, then this would of course increase the size of keys by a factor \(2^t\). Since we want to enable a fine-grained use of time slots, to enable a very large number of puncturings over the entire lifetime of the public key without increasing the false positive probability beyond an unacceptable bound, we want to have \(2^t\) as large as possible, but without increasing the size of the public key beyond an acceptable bound. To this end, we give a direct construction which increases the size of secret keys only by an additive amount of additional group elements, which is only logarithmic in the number of time slots. Thus, for \(2^t\) time slots we have to add merely about t elements to the secret key, while the size of public keys remains even constant. Recall also that due to the time slots, a TB-BFKEM helps to counter message suppression attacks by achieving a form of delayed forward secrecy.
4.1 Formal Model of TB-BFKEM
Likewise to considering our BFKEMs as an instantiation of a puncturable KEM with non-negligible correctness error, we can view the time-based approach analogously as an instantiation of a forward-secret BFKEM [33] with non-negligible correctness error, henceforth referred to as TB-BFKEM. We chose to align our model with the existing formal framework for puncturable forward-secret KEMs. It is essentially our BFKEM Definition 2, augmented by time slots and an additional algorithm \(\mathsf {PuncInt}\) that allows to puncture a secret key not with respect to a given ciphertext in a given time slot, but with respect to an entire time slot.
Definition 16
(TB-BFKEM) A puncturable forward-secret key encapsulation (TB-BFKEM) scheme is a tuple of the following \(\mathsf PPT\) algorithms:
- \({\mathsf {KGen}}(1^\lambda ,m,k,t):\):
-
Takes as input a security parameter \(\lambda \), parameters m and k for the Bloom filter, and a parameter t specifying the number of time slots. It outputs a secret and public key \((\mathsf {sk},\mathsf {pk})\), where we assume that the key-space \(\mathcal {K}\) is implicit in \(\mathsf {pk} \) and that \(\mathsf {pk} \) is implicit in \(\mathsf {sk} \).
- \(\mathsf {Enc}(\mathsf {pk},\tau ):\):
-
Takes as input a public key \(\mathsf {pk} \) and a time slot \(\tau \) and outputs a ciphertext C and a symmetric key \(\mathsf {K}\).
- \(\mathsf {PuncCtx}(\mathsf {sk},\tau ,C):\):
-
Takes as input a secret key \(\mathsf {sk} \), a time slot \(\tau \), a ciphertext C and outputs an updated secret key \(\mathsf {sk} '\).
- \(\mathsf {Dec}(\mathsf {sk},\tau ,C):\):
-
Takes as input a secret key \(\mathsf {sk} \), a time slot \(\tau \), a ciphertext C and deterministically computes and outputs a symmetric key \(\mathsf {K}\) or \(\bot \) if decapsulation fails.
- \(\mathsf {PuncInt}(\mathsf {sk},\tau ):\):
-
Takes as input a time slot \(\tau \) and a secret key \(\mathsf {sk} \) for any time slot \(\le \tau \), and outputs an updated secret key \(\mathsf {sk} '\) for the time slot \(\tau + 1\).
Correctness Essentially, the correctness definition is based on that of a BFKEM, but additionally considers time slots (see also [33]).
Definition 17
(Correctness) We require that the following holds for all \(\lambda , m,k,t\in \mathbb {N}\), for all \(z\in \mathbb {N}\) with \(z\le t\), and any  .
.
-
For any ordered sequence \(\tau _1, \ldots , \tau _z\) with \(1 \le \tau _{1}< \ldots < \tau _{z} \le t\) and

where \(i \in \{1, \ldots , z\}\) and \(\mathsf {sk} _1 := \mathsf {sk} \), and
-
for any arbitrary interleaved sequence of invocations of

where \(j \in \{1, \ldots , n\}\), \(\mathsf {sk} _{z+1,1} := \mathsf {sk} _{z+1}\), and

it holds that
where  and \(\epsilon (\cdot )\) is a negligible function in \(\lambda \). The probability is over the random coins of \({\mathsf {KGen}}\) and the random coins of \(\mathsf {Enc}\) used to compute \(C_{1}, \ldots , C_n\) and \(C^*\).
and \(\epsilon (\cdot )\) is a negligible function in \(\lambda \). The probability is over the random coins of \({\mathsf {KGen}}\) and the random coins of \(\mathsf {Enc}\) used to compute \(C_{1}, \ldots , C_n\) and \(C^*\).
4.2 Additional Properties of a TB-BFKEM
Again, we will require additional properties for the TB-BFKEM, similar to those from Sect. 2.3.
Definition 18
(Extended Correctness) We require that the following holds for all \(\lambda , m,k,t,n\in \mathbb {N}\), for all \(z\in \mathbb {N}\) with \(z\le t\), and any  .
.
-
For any ordered sequence \(\tau _1, \ldots , \tau _z\) with \(1 \le \tau _1< \ldots < \tau _z \le t\) and

where \(i \in \{1, \ldots , z\}\) and \(\mathsf {sk} _1 := \mathsf {sk} \), and
-
for any arbitrary interleaved sequence of invocations of

where \(j \in \{1, \ldots , n\}\), \(\mathsf {sk} _{z+1,1} := \mathsf {sk} _{z+1}\), and

it holds that:
-
1.
No false-negatives in the current time interval:
\(\mathsf {Dec}(\mathsf {sk} _{z+1,n+1},\tau _{z}+1,C_{j})=\bot \) for all \(j\in [n]\)
-
2.
No false-negatives with respect to ciphertexts from previous intervals:
\(\mathsf {Dec}(\mathsf {sk} _{z+1,n+1},\tau ^*,C)=\bot \) for all
 with \(\tau ^* < \tau _{z}+1\).
with \(\tau ^* < \tau _{z}+1\). -
3.
Perfect correctness of the initial secret key:
\(\mathsf {Dec}(\mathsf {sk},\tau ,C) = \mathsf {K}\) for all \(1 \le \tau \le t\) and all
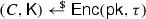 .
. -
4.
Semi-correctness of punctured secret keys:
For all \(1 \le \tau \le t\) holds: If \(\mathsf {Dec}(\mathsf {sk} _{z+1, j+1},\tau ,C) \ne \bot \) then \(\mathsf {Dec}(\mathsf {sk} _{z+1, j+1},\tau ,C) = \mathsf {Dec}(\mathsf {sk},\tau ,C)\).
Definition 19
(Separable Randomness) Let \(\mathsf {TB}\text {-}\mathsf {BFKEM}= ({\mathsf {KGen}},\mathsf {Enc},\mathsf{Punc}\mathsf{Ctx}, \mathsf {Dec}, \mathsf {PuncInt})\) be a TB-BFKEM. We say that \(\mathsf {TB}\text {-}\mathsf {BFKEM}\)has separable randomness, if one can equivalently write the encapsulation algorithm \(\mathsf {Enc}\) as

for uniformly random \((r,\mathsf {K}) \in \{0,1\}^{\rho +\lambda }\), where \(\mathsf {Enc}(\cdot ,\cdot ;\cdot )\) is a deterministic algorithm whose output is uniquely determined by \(\mathsf {pk} \), \(\tau \) and the randomness \((r,\mathsf {K}) \in \{0,1\}^{\rho +\lambda }\).
Definition 20
(Publicly Checkable Puncturing) Let \(\{\mathcal {Q} _{\tau _j}\}_{j=1}^k\) be any list of lists of ciphertexts \(\{(C_{\tau {_j},1}, \ldots , C_{\tau {_j},w_j})\}_{j=1}^k\). We say that \(\mathsf {TB}\text {-}\mathsf {BFKEM}\)allows publicly checkable puncturing, if there exists an efficient algorithm \(\mathsf {CheckPunct} \) with the following correctness property.
-
1.
Run
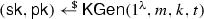 .
. -
2.
For \(j\in [k]\) do
-
Compute
 and \(\mathsf {sk} = \mathsf {PuncCtx}(\mathsf {sk},\tau _j,C_i)\) for \(i \in [w_j]\).
and \(\mathsf {sk} = \mathsf {PuncCtx}(\mathsf {sk},\tau _j,C_i)\) for \(i \in [w_j]\). -
Compute

-
-
3.
Let C and \(\tau \) be any string. We require that
$$\begin{aligned} \bot = \mathsf {Dec}(\mathsf {sk},\tau ,C) \iff \bot = \mathsf {CheckPunct} (\mathsf {pk},\tau ,\{\mathcal {Q} _{\tau _j}\}_{j=1}^k, C). \end{aligned}$$
Definition 21
(\(\gamma \)-Spreadness) Let \(\mathsf {TB}\text {-}\mathsf {BFKEM}= ({\mathsf {KGen}},\mathsf {Enc},\mathsf {PuncCtx},\mathsf {Dec},\mathsf{Punc}\mathsf{Int})\) be a randomness-separable TB-BFKEM with ciphertext space \(\mathcal C\). We say that it is \(\gamma \)-spread, if for any honestly generated \(\mathsf {pk} \), any key \(\mathsf {K}\), any \(\tau \) and any \(C \in \mathcal C\)

4.3 Security Definitions
The security of a TB-BFKEM scheme is defined in a selective-time experiment, where the adversary has to commit to a time slot \(\tau ^*\) to attack before seeing the parameters of the scheme. We present the \(\mathsf {IND}\text {-}\mathsf {CPA}\) and \(\mathsf {IND}\text {-}\mathsf {CCA}\) experiments in Fig. 6.
Definition 22
(\(\mathsf s\text {-}T\)-Security of TB-BFKEM) We define the advantage of an adversary \(\mathcal {A}\) in the \(\mathsf s\text {-}T\) experiment \(\mathbf{Exp}^{\mathsf {s\text {-}T}}_{\mathcal {A},{\mathsf {TB}\text {-}\mathsf {BFKEM}}}(\lambda ,m,k,t)\) as
A puncturable forward-secret key-encapsulation scheme \(\mathsf {TB}\text {-}\mathsf {BFKEM}\) is \(\mathsf {s\text {-}T}\), \(\mathsf{T} \in \{{\mathsf {IND}\text {-}\mathsf {CPA}}, {\mathsf {IND}\text {-}\mathsf {CCA}}\}\), secure, if \(\mathbf{Adv}^{\mathsf {s\text {-}T}}_{\mathcal {A},{\mathsf {TB}\text {-}\mathsf {BFKEM}}}(\lambda ,m,k,t)\) is a negligible function in \(\lambda \) for all \(m,k, t>0\) and all PPT adversaries \(\mathcal {A}\).
4.4 A Generic Time-Based BFKEM Construction
Before we can present our construction, we recall hierarchical identity-based key encapsulation schemes (HIB-KEMs). HIB-KEMs represent a building block of our construction.
HIB-KEMs Below we present the basic definition and the security properties of HIB-KEMs.
Definition 23
A \((t'+1)\)-level hierarchical identity-based key encapsulation scheme (\(\mathsf {HIB}\text {-}\mathsf {KEM}\)) with identity space \(\mathcal {D}^{\le t'+1}\), ciphertext space \(\mathcal {C}\), and key space \(\mathcal {K}\)consists of the following four algorithms:
- \(\mathsf {HIBGen}(1^\lambda ):\):
-
Takes as input a security parameter and outputs a key pair \((\mathsf {mpk}, \mathsf {sk} _\varepsilon )\). We say that \(\mathsf {mpk} \) is the master public key, and \(\mathsf {sk} _\varepsilon \) is the level-0 secret key.
- \(\mathsf {HIBDel}(\mathsf {sk} _{\mathbf {d}'}, d):\):
-
Takes as input secret key \(\mathsf {sk} _{\mathbf {d}'}\) and \(d\in \mathcal {D}\), and outputs a secret key \(\mathsf {sk} _{\mathbf {d}'|d}\). (We refer to | as concatenation.)
- \(\mathsf {HIBEnc}(\mathsf {mpk}, \mathbf {d}):\):
-
Takes as input the master public key \(\mathsf {mpk} \) and an identity \(\mathbf {d} \in \mathcal {D}^{\le t'+1}\) and outputs a ciphertext \(C \in \mathcal {C}\) and a key \(\mathsf {K}\in \mathcal {K}\).
- \(\mathsf {HIBDec}(\mathsf {sk} _{\mathbf {d}},C):\):
-
Takes as input a secret key \(\mathsf {sk} _{\mathbf {d}}\) and a ciphertext C, and outputs a value \(\mathsf {K}\in \mathcal {K}\cup \{\bot \}\), where \(\bot \) is a distinguished error symbol.
Correctness for \(\mathsf {HIB}\text {-}\mathsf {KEM}\). We require that for all \(\lambda \in \mathbb {N}\), for all  , for all \(d \in \mathcal {D}\), for all
, for all \(d \in \mathcal {D}\), for all  , for all \(\mathbf {d}\in \mathcal {D}^{\le t'+1}\), for all
, for all \(\mathbf {d}\in \mathcal {D}^{\le t'+1}\), for all  , we have that \(\mathsf {HIBDec}(\mathsf {sk} _{\mathbf {d}},C)=K\) holds.
, we have that \(\mathsf {HIBDec}(\mathsf {sk} _{\mathbf {d}},C)=K\) holds.
Security definition for \(\mathsf {HIB}\text {-}\mathsf {KEM}\). As for our generic construction, we will essentially follow the proof strategy of the \(\mathsf {BFKEM}\)construction and thus will rely on the weak notion of one-wayness under selective-ID and chosen-plaintext attacks (OW-sID-CPA) for \(\mathsf {HIB}\text {-}\mathsf {KEM}\). We note that any IND-sID-CPA-secure \(\mathsf {HIB}\text {-}\mathsf {KEM}\)also satisfies this notion of OW-sID-CPA security.
Definition 24
(OW-sID-CPA Security of HIB-KEM) We define the advantage of an adversary \(\mathcal {A}\) in the OW-sID-CPA experiment \(\mathbf{Exp}^{\mathsf {OW}\text {-}\mathsf {sID}\text {-}\mathsf {CPA}}_{{\mathcal {A}},\mathsf {HIB}\text {-}\mathsf {KEM}}(\lambda )\) as
We call a \(\mathsf {HIB}\text {-}\mathsf {KEM}\)OW-sID-CPA-secure, if \(\mathbf{Adv}^{\mathsf {OW\text {-}sID\text {-}CPA}}_{{\mathcal {A}},{\mathsf {HIB}\text {-}\mathsf {KEM}}}(\lambda )\) is a negligible function in \(\lambda \) for all PPT adversaries \(\mathcal {A}\).
Time slots We will construct a TB-BFKEM scheme that allows to use \(t=2^{t'}\) time slots. We associate the i-th time slot with the string in \(\{0,1\}^{t'}\) that corresponds to the canonical \(t'\)-bit binary representation of integer i.
Following [15, 31, 33], each time slot forms a leaf of an ordered binary tree of depth \(t'\). The root of the tree is associated with the empty string \(\epsilon \). We associate the left-hand descendants of the root with bit string 0, and the right-hand descendant with 1. Continuing this way, we associate the left descendant of node 0 with 00 and the right descendant with 01, and so on. We continue this procedure for all nodes, until we have constructed a complete binary tree of depth \(t'\). Note that two nodes at level \(j\le t'\) of the tree are siblings if and only if their first \(j-1\) bits are equal and that each bit string in \(\{0,1\}^{t'}\) is associated with a leaf of the tree. Note also that the leafs in the tree are ordered, in the sense that the leftmost leaf is associated with \(0^{t'}\), its right neighbor with \(0^{t'-1}1\), and so on.
Intuition of the construction The basic idea behind the construction combines the binary tree approach of [15, 31, 33] with the BF-KEM construction described in Sect. 3.1. We use a HIB-KEM with identity space
Each bit vector \(\tau \in \mathcal {D}_1 \times \cdots \times \mathcal {D}_{t'} = \{0,1\}^{t'}\) corresponds to one time slot, and we set \(\mathcal {D}_{t'+1} = [m]\), where m is the size of the Bloom filter. The hierarchical key delegation property of the HIB-KEM enables the following features:
First, given a HIB-KEM key \(\mathsf {sk} _\tau \) for some “identity” (= time slot) \(\tau \in \{0,1\}^{t'}\), we can derive keys for all Bloom filter bits from \(\mathsf {sk} _\tau \) by computing

Second, in order to advance from time slot \(\tau \) to \(\tau +1\), we first compute

As soon as we have computed all Bloom filter keys for time slot \(\tau \), we “puncture” the tree “from left to right,” such that we are able to compute all \(\mathsf {sk} _{\tau '}\) with \(\tau ' > \tau \), but not any \(sk_{\tau '}\) with \(\tau ' \le \tau \). Here, we proceed exactly as in [15, 31, 33]. That is, in order to puncture at time slot \(\tau \), we first compute the HIB-KEM secret keys associated with all right-hand siblings of nodes that lie on the path from node \(\tau \) to the root (if existent), and then we delete all secret keys associated with nodes that lie on the path from node \(\tau \) to the root, including \(\mathsf {sk} _\tau \) itself. This yields a new secret key, which contains m level-\((t'+1)\) HIB-KEM secret keys plus at most \(t'\) HIB-KEM secret keys for levels \(\le t'\), even though we allow for \(2^{t'}\) time slots.
Construction Let \((\mathsf {HIBGen}, \mathsf {HIBDel}, \mathsf {HIBEnc}, \mathsf {HIBDec})\) be a \((t'+1)\)-level HIB-KEM with key space \(\mathcal {K}\)and identity space \(\mathcal {D}= \mathcal {D}_1 \times \cdots \times \mathcal {D}_{t'+1}\), where \(\mathcal {D}_1 = \cdots = \mathcal {D}_t = \{0,1\}\), \(\mathcal {D}_{t'+1} = [m]\), and m is the size of the Bloom filter. Since we will only need selective security, one can instantiate such a HIB-KEM very efficiently, for example in bilinear groups based on the Boneh–Boyen–Goh [11] scheme, or based on lattices [1]. In the sequel, we will write \(\{0,1\}^{t'}\) shorthand for \(\mathcal {D}_1 \times \cdots \times \mathcal {D}_{t'}\), but keep in mind that the HIB-KEM supports more fine-grained key delegation. Let \(\mathsf {B}= ({\mathsf{BFGen}}, {\mathsf{BFUpdate}}, {\mathsf{BFCheck}})\) be a Bloom filter for set \(\{0,1\}^\lambda \). Furthermore, let \(G' : \mathcal {K}\rightarrow \{0,1\}^\lambda \) be a hash function (which will be modeled as a random oracle [7] in the security proof).
We define \(\mathsf {TB}\text {-}\mathsf {BFKEM}= ({\mathsf {KGen}},\mathsf {Enc},\mathsf {PuncCtx},\mathsf {Dec},\mathsf {PuncInt})\) as follows.
\(\underline{{\mathsf {KGen}}(1^\lambda , m,k, t={2^{t'}})}:\) This algorithm first runs  to generate a Bloom filter, and
to generate a Bloom filter, and  to generate a key pair. Finally, the algorithm generates the keys for the first time slot. To this end, it first computes the HIB-KEM key for identity \(0^{t'}\) by recursively computing
to generate a key pair. Finally, the algorithm generates the keys for the first time slot. To this end, it first computes the HIB-KEM key for identity \(0^{t'}\) by recursively computing

Footnote 5 Then, it computes the m Bloom filter keys for time slot \(0^{t'}\) by computing

and setting \(\mathsf {sk} _\mathsf {Bloom}:= (\mathsf {sk} _{0^{t'}|d})_{d \in [m]}\). Finally, it punctures the secret key \(\mathsf {sk} _\epsilon \) at position \(0^{t'}\), by computing

and setting \(\mathsf {sk} _\mathsf {time}:= (\mathsf {sk} _{0^{d-1}|1})_{d \in [t']}\). The algorithm outputs
\(\underline{\mathsf {Enc}(\mathsf {mpk}, \tau )}:\) On input \(\mathsf {mpk} \) and time slot identifier \(\tau \in \{0,1\}^{t'}\), this algorithm first samples a random string  and a random key
and a random key  . Then, it defines k HIB-KEM identities as \(\mathbf {d}_j := (\tau ,H_j(c)) \in \mathcal {D}\quad \text {for}\quad j \in [k]\), and generates k HIB-KEM key encapsulations as
. Then, it defines k HIB-KEM identities as \(\mathbf {d}_j := (\tau ,H_j(c)) \in \mathcal {D}\quad \text {for}\quad j \in [k]\), and generates k HIB-KEM key encapsulations as

Finally, it outputs the ciphertext \(C := (c, (C_j, G'(\mathsf {K}_j) \oplus \mathsf {K})_{j \in [k]})\).
Note that the ciphertexts essentially consists of \(k+1\) elements of \(\{0,1\}^\lambda \), plus k elements of \(\mathcal {C}\), where k is the Bloom filter parameter.
\(\underline{\mathsf {PuncCtx}(\mathsf {sk},C)}:\) Given a ciphertext \(C := (c, (C_j, G'(\mathsf {K}_j) \oplus \mathsf {K})_{j \in [k]})\), and secret key \(\mathsf {sk} = (T, \mathsf {sk} _\mathsf {Bloom}, \mathsf {sk} _\mathsf {time})\) where \(\mathsf {sk} _\mathsf {Bloom}= (\mathsf {sk} _{\tau |d})_{d \in [m]}\), the puncturing algorithm first computes \(T' = {\mathsf{BFUpdate}}((H_j)_{j \in [k]},T,c)\). Then, for each \(i \in [m]\), it defines
where \(T'[i]\) denotes the i-th bit of \(T'\). Finally, this algorithm sets \(\mathsf {sk} _\mathsf {Bloom}' = (\mathsf {sk} '_{\tau |d})_{d \in [m]}\) and returns \(\mathsf {sk} ' = (T', \mathsf {sk} _\mathsf {Bloom}', \mathsf {sk} _\mathsf {time})\).
Remark We note again that the above procedure is correct even if the procedure is applied repeatedly, with the same arguments as for the construction from Sect. 3.1. Also, the puncturing algorithm essentially only evaluates k universal hash functions and then deletes a few secret keys, which makes this procedure extremely efficient.
\(\underline{\mathsf {Dec}(\mathsf {sk},C)}:\) Given \(\mathsf {sk} = (T, \mathsf {sk} _\mathsf {Bloom}, \mathsf {sk} _\mathsf {time})\) where \(\mathsf {sk} _\mathsf {Bloom}= (\mathsf {sk} _{\tau |d})_{d \in [m]}\) and ciphertext \(C := (c, (C_j, G_j)_{j \in [k]})\). If \(\mathsf {sk} _{\tau |H_j(c)} = \bot \) for all \(j \in [k]\), then it outputs \(\bot \). Otherwise, it picks the smallest index j such that \(\mathsf {sk} _{\tau |H_j(c)} \ne \bot \), computes
and returns \(\mathsf {K}= G_j \oplus G'(\mathsf {K}_j)\).
Remark Again we have \(\mathsf {Dec}(\mathsf {sk}, C) \ne \bot \iff {\mathsf{BFCheck}}(H, T, c) = 0\), which guarantees extended correctness in the sense of Definition 18.
\(\underline{\mathsf {PuncInt}(\mathsf {sk},\tau )}:\) Given a secret key \(\mathsf {sk} = (T, \mathsf {sk} _\mathsf {Bloom}, \mathsf {sk} _\mathsf {time})\) for time interval \(\tau ' \le \tau \), the time puncturing algorithm proceeds as follows. First, it resets the Bloom filter by setting \(T := 0^m\). Then, it uses the key delegation algorithm to first compute \(\mathsf {sk} _{\tau }\). This key can be computed from the keys contained in \(\mathsf {sk} _\mathsf {time}\), because \(\mathsf {sk} \) is a key for time interval \(\tau ' \le \tau \). Then, it computes

and redefines \(\mathsf {sk} _\mathsf {Bloom}:= (\mathsf {sk} _{\tau |d})_{d \in [m]}\). Finally, it updates \(\mathsf {sk} _\mathsf {time}\) by computing the HIB-KEM secret keys associated with all right-hand siblings of nodes that lie on the path from node \(\tau \) to the root and adds the corresponding keys to \(\mathsf {sk} _\mathsf {time}\). Then, it deletes all keys from \(\mathsf {sk} _\mathsf {time}\) that lie on the path from \(\tau \) to the root.
Remark Note that puncturing between time intervals may become relatively expensive. Depending on the choice of Bloom filter parameters, in particular on m, this may range between \(2^{15}\) and \(2^{25}\) HIBKEM key delegations. However, the main advantage of BFKEM over previous constructions of puncturable encryption is that these computations must not be performed “online,” during puncturing, but can actually be computed separately (for instance, parallel on a different computer, or when a server has low workload, etc.).
Correctness error of this scheme Note that within each time slot we can use the same argumentation as for the scheme from Sect. 3.1 and one can verify that the correctness-error probability of this scheme is essentially identical to the false-positive probability of the Bloom filter, unless a given ciphertext \(C = (c, (C_j, G_j)_{j \in [k]})\) has a value of c which is identical to the value of c of any previous ciphertext. Since c is uniformly random in \(\{0,1\}^\lambda \), this probability is bounded by \(\left( 1-e^{- \frac{(n+1/2)k}{m-1}}\right) ^k + n\cdot 2^{-\lambda }\). Furthermore, due to the perfect correctness of the underlying \(\mathsf {HIB}\text {-}\mathsf {KEM}\)scheme, this yields the error-correctness bound of \(\mathsf {TB}\text {-}\mathsf {BFKEM}\).
More formally, we have that for all \(\lambda , m,k,t'\in \mathbb {N}\), for all \(t=2^{t'}\), for all \(z\in \mathbb {N}\) with \(z\le t\), and any  :
:
-
For any ordered sequence \(\tau _1, \ldots , \tau _z\in \{0,1\}^{t'}\) and

where \(i \in \{1, \ldots , z\}\) and \(\mathsf {sk} _1 := \mathsf {sk} \), and
-
for any arbitrary interleaved sequence of invocations of
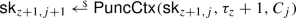
where \(j \in \{1, \ldots , n\}\), \(\mathsf {sk} _{z+1,1} := \mathsf {sk} _{z+1}\), and
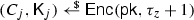
it holds that
where  , due to the perfect correctness of \(\mathsf {HIB}\text {-}\mathsf {KEM}\), the bounded false-positive probability property of the underlying Bloom filter (depending on m and k, see Section 2.1), and the bounded negligible loss \(n\cdot 2^{-\lambda }\) occurred due to collisions of uniform c-values in the ciphertexts.
, due to the perfect correctness of \(\mathsf {HIB}\text {-}\mathsf {KEM}\), the bounded false-positive probability property of the underlying Bloom filter (depending on m and k, see Section 2.1), and the bounded negligible loss \(n\cdot 2^{-\lambda }\) occurred due to collisions of uniform c-values in the ciphertexts.
Concerning the extended correctness, see that
-
1.
\(\mathsf {Dec}(\mathsf {sk} _{z+1,n+1},\tau _{z}+1,C_{j})=\bot \) for all \(j\in [n]\), i.e., no false-negatives in the current time interval due to the perfect-completeness property of the BF \(\mathsf {B}\) and deleting the respective \(\mathsf {HIB}\text {-}\mathsf {KEM}\) secret keys.
-
2.
\(\mathsf {Dec}(\mathsf {sk} _{z+1,n+1},\tau ^*,C)=\bot \) for all
 with \(\tau ^* < \tau _{z}+1\), i.e., no false-negatives with respect to ciphertexts from previous intervals due to the security properties of \(\mathsf {HIB}\text {-}\mathsf {KEM}\).
with \(\tau ^* < \tau _{z}+1\), i.e., no false-negatives with respect to ciphertexts from previous intervals due to the security properties of \(\mathsf {HIB}\text {-}\mathsf {KEM}\). -
3.
\(\mathsf {Dec}(\mathsf {sk},\tau ,C) = \mathsf {K}\) for all \(1 \le \tau \le t\) and all
 , i.e., perfect correctness of the initial secret key due to the perfect correctness property of \(\mathsf {HIB}\text {-}\mathsf {KEM}\)and perfect completeness of \(\mathsf {B}\).
, i.e., perfect correctness of the initial secret key due to the perfect correctness property of \(\mathsf {HIB}\text {-}\mathsf {KEM}\)and perfect completeness of \(\mathsf {B}\). -
4.
For all \(1 \le \tau \le t\) holds: If \(\mathsf {Dec}(\mathsf {sk} _{z+1, j+1},\tau ,C) \ne \bot \) then \(\mathsf {Dec}(\mathsf {sk} _{z+1, j+1},\tau ,C) = \mathsf {Dec}(\mathsf {sk},\tau ,C)\), i.e., semi-correctness of punctured secret keys due to perfect correctness property of \(\mathsf {HIB}\text {-}\mathsf {KEM}\)and perfect completeness of \(\mathsf {B}\).
CPA Security Below we state theorem for CPA security of our scheme.
Theorem 6
From each efficient adversary \(\mathcal {B}\)that issues u queries to random oracle \(G'\), we can construct an efficient adversary \(\mathcal {A}\)with
The proof is almost identical to the proof of Theorem 1 and a straightforward reduction to the security of the underlying HIB-KEM. We sketch it below.
Proof
(Sketch). We sketch the proof of Theorem 6. Recall that a ciphertext has the form
Essentially, one argues exactly as in Theorem 1 that the adversary receives no information about the key \(\mathsf {K}\) encapsulated by the Bloom filter encryption scheme, unless it ever queries \(\mathsf {K}_j\) to random oracle \(G'\) for some \(j \in [k]\). Therefore, assume that \(\mathcal {B}\)queries some \(\mathsf {K}_j\) to \(G'\) in its \(u^*\)-th query.
At the beginning of the reduction, \(\mathcal {A}\)first guesses index  and
and  . It also samples the random string
. It also samples the random string  used for the challenge BFKEM ciphertext at the beginning of the game, generates a Bloom filter
used for the challenge BFKEM ciphertext at the beginning of the game, generates a Bloom filter

and requests a challenge ciphertext for identity \(d^* = (\tau ^*|H_j(c))\), where \(\tau ^*\) is the time slot selected by \(\mathcal {B}\). The challenge ciphertext received back from the HIB-KEM experiment is then embedded in the TB-BFKEM challenge ciphertext. The \(\mathsf {PuncCtx}\) and \(\mathsf {PuncInt}(\mathsf {sk},\cdot )\) queries of \(\mathcal {B}\)can trivially be simulated by \(\mathcal {A}\). The \(\mathsf{Corr}\) queries can be answered using the \(\mathsf {HIBDel}\)oracle provided by the OW-sID-CPA security experiment of the HIB-KEM.
When \(\mathcal {B}\)makes its \(u^*\)-th query to \(G'\) on value \(\mathsf {K}'\), then \(\mathcal {A}\)terminates and outputs \(\mathsf {K}'\). We know that any non-trivial adversary \(\mathcal {B}\)queries \(\mathsf {K}_j\) to \(G'\) for some j. If \(\mathcal {A}\)has guessed \(u^*\) and j correctly, which happens with probability 1/(uk), then it holds that \(\mathsf {K}' = \mathsf {K}_j\), which yields the claim. \(\square \)
CCA Security In order to apply the Fujisaki–Okamoto [25] transform in the same way as done in Sect. 3.2 to achieve CCA security, we need to show that the time based variants of the properties presented in Sect. 2.3 are satisfied (i.e., Definitions 18, 19, 20, and 21). First, using a full-blown HIBE as a starting point yields a separable HIB-KEM as discussed in Sect. 2.3. Hence, the separable randomness (Definition 19) is satisfied. Moreover, the publicly checkable puncturing (Definition 20) is given by construction (as in Sect. 3.1). Regarding extended correctness (Definition 18), the impossibility of false-negatives is given by construction, the perfect correctness of the non-punctured secret key is given by the perfect correctness of the HIBE and the semi-correctness of punctured secret keys is given by construction. Finally, \(\gamma \)-spreadness (Definition 21) is also given by construction: the ciphertext component c is chosen uniformly at random from \(\{0,1\}^\lambda \). Consequently, all properties are satisfied. We note that one could omit c in the ciphertext if the concretely used HIBE ciphertexts are already sufficiently random. Considering the HIBE of Boneh–Boyen–Goh [11], HIBE ciphertexts are of the form \((g^r,(h_1^{I_1}\cdots h_t^{I_t}\cdot h_0)^r,H(e(g_1,g_2)^r)\oplus \mathsf {K})\), for honestly generated fixed group elements \(g,g_1,g_2,h_0,\ldots ,h_t\), universal hash function H, fixed \(\mathsf {K}\) and fixed integers \(I_1,\ldots ,I_t\). Consequently, we have that the ciphertext has at least min-entropy \(\log _2 q\) with q being the order of the groups. We want to mention that also many other HIBE construction satisfy the required properties, including, for example [19, 27, 48].
Remark on CCA Security Alternatively to applying the FO transform to a TB-BFKEM satisfying the additional properties of extended correctness, separable randomness, publicly checkable puncturing and \(\gamma \)-spreadness to obtain CCA security, we can add another HIBE level to obtain IND-CCA security via the CHK transform [15] in the standard model, and thus to avoid random oracles if required.Footnote 6
5 Forward-Secret 0-RTT Key Exchange
In [33] (with full version in [34]), Günther, Hale, Jager, and Lauer (GHJL) provide a formal model for forward-secret one-pass key exchange (FSOPKE) by extending the one-pass key exchange [36] by Halevi and Krawczyk. They provide a security model for FSOPKE which requires both forward secrecy and replay protection from the FSOPKE protocol and captures unilateral authentication of the server and mutual authentication simultaneously.
We recap the definition of FSOPKE with a slightly adapted \({\mathsf {KGen}}\) and correctness notion to allow for a non-negligible correctness error, which constitutes the main difference to the work of [33, 34]. We remark that we do not change the security model of [34, Sec. 3.2] (i.e., the new input parameters added to \({\mathsf {KGen}}\) do only affect FSOPKE correctness and not the FSOPKE security model).
In particular, we now take into account the maximum number of server and client runs \(n\in \mathbb {N}\) and a false-positive probability p of succeeding the runs (in computing the same session key for a particular time step). Looking ahead, this changes are necessary to instantiate FSOPKE with our TB-BFKEM. (See Sec. 2.1 for parameter selections of n and p and corresponding BF parameter m and k if one wants to instantiate the FSOPKE with a BF.)
Definition 25
(FSOPKE) An FSOPKE scheme \(\mathsf{FSOPKE}\) providing mutual or unilateral (server-only) authentication consists of the \(\mathsf PPT\) algorithms \(\mathsf (FSOPKE.KGen, FSOPKE.RunC, FSOPKE. RunS, \mathsf{FSOPKE}. TimeStep)\):
- \(\mathsf{FSOPKE}.{\mathsf {KGen}}(1^\lambda ,r,\tau _{max},n,p):\):
-
Takes as input a security parameter \(1^\lambda \), a role \(r\in \{\mathsf {server},\mathsf {client} \}\), the maximum number of time slots \(\tau _{max}\in \mathbb {N}\), and the maximum number of server and client runs \(n\in \mathbb {N}\) with false-positive probability p, outputs public and secret keys \((\mathsf {pk},\mathsf {sk})\) for a specific role r (we assume that the key-space \(\mathcal {K}\) is implicit in \(\mathsf {pk} \)).
- \(\mathsf{FSOPKE}.\mathsf {RunC} (\mathsf {sk},\mathsf {pk}):\):
-
Takes as input a secret key \(\mathsf {sk} \), a public key \(\mathsf {pk} \), and outputs a (potentially modified) secret key \(\mathsf {sk} '\), a session key \(\mathsf {K}\in \{0,1\}^*\cup \{\bot \}\), and a message \(M \in \{0,1\}^*\cup \{\bot \}\).
- \(\mathsf{FSOPKE}.\mathsf {RunS} (\mathsf {sk},\mathsf {pk},M):\):
-
Takes as input a secret key \(\mathsf {sk} \), a public key \(\mathsf {pk} \), and a message \(M \in \{0,1\}^*\) and outputs a (potentially modified) secret key \(\mathsf {sk} '\) and a session key \(\mathsf {K}\in \{0,1\}^*\cup \{\bot \}\).
- \(\mathsf{FSOPKE}.\mathsf {TimeStep} (\mathsf {sk},r):\):
-
Takes as input a secret key \(\mathsf {sk} \) and an according role \(r\in \{\mathsf {client},\mathsf {server} \}\) and outputs a (potentially modified) secret key \(\mathsf {sk} '\).
Server and client flow within an FSOPKE scheme A server and a client are engaging in an FSOPKE scheme as follows. According to their role, a server (i.e., when the role is \(\mathsf {server} \)) and a client (i.e., when the role is \(\mathsf {client} \)) execute
to generate initial public and private keys for a server and client, respectively (where \(\lambda \), \(\tau _{max}\), n, and p are pre-determined). For all \(i\in [\tau _{max}]\) and \(j\in [n]\), by executing \(\mathsf {sk} _{s,i+1,1}\leftarrow \mathsf{FSOPKE}.\mathsf {TimeStep} (\mathsf {sk} _{s,i,j},\mathsf {server})\) and \(\mathsf {sk} _{c,i+1,1}\leftarrow \mathsf{FSOPKE}.\mathsf {TimeStep} (\mathsf {sk} _{c,i,j}, \mathsf {client})\), the server and the client progresses from one time slot i to the next slot \(i+1\) to receive (potentially modified) secret keys \(\mathsf {sk} _{s,i+1,1}\) and \(\mathsf {sk} _{c,i+1,1}\), respectively.
Similarly, within a time step \(i\in [\tau _{max}]\) and for all \(j\in [n-1]\), the client proceeds with
for client’s private key \(\mathsf {sk} _{c,i,j}\) and a server’s public key \(\mathsf {pk} _{s}\), to receive a (potentially modified) secret key \(\mathsf {sk} _{c,i,j+1}\), a session key \(\mathsf {K}_{c,i,j}\), and a message \(M \) (e.g., a ciphertext) which is transmitted to the server (associated with \(\mathsf {pk} _{s}\)). The server obtains \(M \) and executes
for the server’s secret key \(\mathsf {sk} _{s,i,j}\) and the client’s public key \(\mathsf {pk} _{c}\) to receive a (potentially modified) secret key \(\mathsf {sk} _{s,i,j+1}\) and a session key \(\mathsf {K}_{s,i,j}\).
By our adapted correctness notion of the FSOPKE (see Definition 26 below), we have that \(\mathsf {K}_{c,i,j}=\mathsf {K}_{s,i,j}\) except with potentially non-negligible probability (bounded by \(\mu (n,p)+\varepsilon (\lambda )\), for a potential non-negligible function \(\mu (\cdot ,\cdot )\) that only depends on n and p, as well as a negligible function \(\varepsilon (\cdot )\) that depends on \(\lambda \)).
Definition 26
((Non-negligible) correctness of FSOPKE) For all \(\lambda ,\tau _{max},n\in \mathbb {N}\) and false-positive probability p, for all
for all \(i\in [\tau _{max}-1]\) and all \(j\in [n]\), for any
for all \(j\in [n-1]\) and \(i\in [\tau _{max}]\), for any
for all \(j''\in [n]\) and \(i''\in [\tau _{max}]\), we have that
where \(\mu (\cdot ,\cdot )\) is some (possibly non-negligible) function that depends on n and p, and \(\varepsilon (\cdot )\) is a negligible function that depends on \(\lambda \).
Security of FSOPKE The security model of FSOPKE is the same as in defined in [34, Section 3.2], and we omit it here. (See that the additional parameter n and p only affect correctness.) All security guarantees from [34, Theorem 2] directly translate to our FSOPKE construction and we restate the security claim in Corollary 1. (However, we have to argue about the correctness property of our FSOPKE construction where we now allow for a potential non-negligible correctness probability depending on \(\lambda ,n\), and p compared to perfect correctness of the FSOPKE scheme of [34, Definition 12].)
5.1 Construction of an Unilateral FSOPKE Scheme from a TB-BFKEM
The unilateral-authenticatedFootnote 7 FSOPKE construction in [33, 34] builds on PFSKEM; our TB-BFKEM is defined analogously (cf. Definition 16), but we have to account for the non-negligible correctness errors (in particular, for parameters n and p).
Let \({\mathsf {TB}\text {-}\mathsf {BFKEM}}=({\mathsf {KGen}},\mathsf {Enc},\mathsf {PuncCtx},\mathsf {Dec},\mathsf {PuncInt})\) be a TB-BFKEM. We construct an FSOPKE \(\mathsf{FSOPKE} =\mathsf (FSOPKE.KGen, FSOPKE.RunC, FSOPKE. RunS, \mathsf{FSOPKE}. TimeStep)\) as follows:
-
\(\underline{\mathsf{FSOPKE}.{\mathsf {KGen}}(1^\lambda ,r,\tau _{max},n,p)}:\) On input security parameter \(1^\lambda \), role \(r\in \{\mathsf {server},\mathsf {client} \}\), maximum number of time steps \(\tau _{max}\in \mathbb {N}\), maximum number of server and client runs \(n\in \mathbb {N}\) with false-positive probability p, proceed as follows:
-
if \(r=\mathsf {server} \), then compute \((PK,SK_{1,1})\leftarrow {\mathsf {KGen}}(1^\lambda , m,k,\tau _{max})\) (for suitable choices of m, k according to Sec. 2.1 depending on n and p) and set \(\mathsf {pk} _{s}:=(PK, \tau _{max})\) and \(\mathsf {sk} _{s,1,1}:=(SK_{1,1},1,\tau _{max})\), and output \((\mathsf {pk} _s,\mathsf {sk} _{s,i,1})\).
-
if \(r=\mathsf {client} \), then set \((\mathsf {pk} _c,\mathsf {sk} _{c,1,1}):=(\bot ,1)\).
-
-
\(\underline{\mathsf{FSOPKE}.\mathsf {RunC} (\mathsf {sk} _{c,i,j},\mathsf {pk} _s)}:\) Outputs \((\mathsf {sk} _{c,i,j+1},\mathsf {K}_{c,i,j},M)\) as follows: for \(\mathsf {sk} _{c,i,j}=i\) and \(\mathsf {pk} _s=(PK, \tau _{max})\), if \(i>\tau _{max}\), then set \((\mathsf {sk} _{c,i,j+1},\mathsf {K}_{c,i,j},M):=(\mathsf {sk} _{c,i,j},\bot ,\bot )\), otherwise obtain \((C,\mathsf {K}_{c,i,j})\leftarrow \mathsf {Enc}(\mathsf {pk} _s,i)\) and set \((\mathsf {sk} _{c,i,j+1},\mathsf {K}_{c,i,j},M):=(\tau ,\mathsf {K}_{c,i,j}, C)\).
-
\(\underline{\mathsf{FSOPKE}.\mathsf {RunS} (\mathsf {sk} _{s,i,j},\mathsf {pk} _c,M)}:\) Outputs \((\mathsf {sk} _{s,i,j+1},\mathsf {K}_{s,i,j})\) as follows: for \(\mathsf {sk} _{s,i,j}=(SK_{i,j}, i,\tau _{max})\) and \(\mathsf {pk} _c=\bot \), if \(SK_{i,j},=\bot \) or \(i>\tau _{max}\), then set \((\mathsf {sk} _{s,i,j+1},\mathsf {K}_{s,i,j}):=(\mathsf {sk} _{s,i,j},\bot )\) and abort. Obtain \(\mathsf {K}_{s,i,j}\leftarrow \mathsf {Dec}(SK_{i,j},M)\). If \(\mathsf {K}_{s,i,j}=\bot \), then set \((\mathsf {sk} _{s,i,j+1},\mathsf {K}_{s,i,j})=(\mathsf {sk} _{s,i,j},\bot )\), otherwise obtain \(SK_{i,j+1}\leftarrow \mathsf {PuncCtx}(SK_{i,j},M)\) and set \((\mathsf {sk} _{s,i,j+1},\mathsf {K}_{s,i,j})=((SK_{i,j+1},i,\tau _{max}),\mathsf {K}_{s,i,j})\).
-
\(\underline{\mathsf{FSOPKE}.\mathsf {TimeStep} (\mathsf {sk} _{\{s,c\},i,j},r)}:\) Outputs \(\mathsf {sk} _{\{s,c\},i+1,1}\) as follows:
-
if \(r=\mathsf {server} \), then for \(\mathsf {sk} _{s,i,j}=(SK_{i,j}, i,\tau _{max})\): if \(i\ge \tau _{max}\), then set \(\mathsf {sk} _{s,i+1,1}:=(\bot ,i+1,\tau _{max})\) and abort, otherwise compute \(SK_{i+1,1}\leftarrow \mathsf {PuncInt}(SK_{i,j},i)\) and set \(\mathsf {sk} _{s,i+1,1}:=(SK_{i+1,1},i+1,\tau _{max})\) and abort.
-
if \(r=\mathsf {client} \), then for \(\mathsf {sk} _{c,i,j}=i\), set \(\mathsf {sk} _{c,i+1,1}:=i+1\).
-
Correctness of \(\mathsf{FSOPKE} \). Since the underlying TB-BFKEM scheme \(\mathsf {TB}\text {-}\mathsf {BFKEM}\)has a potential non-negligible error correctness that is bounded by \(\mu '(m,k)+\varepsilon '(\lambda )\), this directly translates to the correctness of the FSOPKE scheme \(\mathsf{FSOPKE}\) in the sense that the \(\mathsf {TB}\text {-}\mathsf {BFKEM}\)-decapsulation \(\mathsf {Dec}\) fails with potential non-negligible probability \(\mu (n,p)+\varepsilon (\lambda )\le \mu '(m,k)+\varepsilon '(\lambda )\) which in turn translates to \(\mathsf{FSOPKE}.\mathsf {RunS} \) returning \((\mathsf {sk} _{s,i,j+1},\mathsf {K}_{s,i,j}\ne \mathsf {K}_{c,i,j})\) with potential non-negligible probability depending on \(\lambda ,n\), and p.
Security guarantees hold due to [34, Theorem 2]. (In particular, see that the parameters n and p we introduce in our FSOPKE definition above only affect the correctness error of the FSOPKE and all FSOPKE security guarantee are required to be independent not only of the time steps (as discussed in [34]), but also independent of n and p.) We state the following corollary:
Corollary 1
Let \(\mathsf {TB}\text {-}\mathsf {BFKEM}\) be a TB-BFEKEM as defined in Definition 16 with advantage function \(\mathbf{Adv}^{\mathsf {s\text {-}IND\text {-}CCA}}_{\mathcal {A},{\mathsf {TB}\text {-}\mathsf {BFKEM}}}(\lambda ,m,k,t)\) (cf. Definition 22). For any PPT adversary \(\mathcal {B}\) in the \(\mathsf {FSOPKE\text {-}sec}\) security experiment defined in [34, Definition 11], we have
for \(\mathsf{FSOPKE} \)’s advantage function \(\mathbf{Adv}^{\mathsf {FSOPKE\text {-}sec}}_{\mathcal {B},{\mathsf{FSOPKE}}}(\lambda )\) as defined in [34, Definition 11], for \(\tau _{max}\) the maximum number of time slots per session, \(n_{\mathcal {I}}\) the maximum number of identities, and \(n_s\) the maximum number of sessions (where \(n_{\mathcal {I}}\) and \(n_s\) are given as in [34, Sec. 3.2]). Furthermore, m and k depend on n and p as described in Sect. 2.1.
6 Analysis
BFKEM. Finally, we compare our different BFKEM instantiations as presented in Sect. 3 regarding their time and space complexity (also see Table 2). Regarding computational efficiency of \(\mathsf Dec\) and \(\mathsf Punc\), all schemes are roughly the same. The space complexity in the direct construction is optimal with respect to the size of public and secret keys, and we achieve ciphertexts of size O(k). Our construction based on CP-ABE can achieve constant size ciphertexts when instantiated with an ABE scheme that achieves constant size ciphertexts. We, however, note that all ABE schemes achieving constant size ciphertext we are aware of (i.e., [2, 18]) come at the cost of large public and secret keys. Those key sizes also carry over to our BFKEM construction. Finally, our construction from IBBE can be viewed as the dual to our direct construction in terms of space complexity. That is, the scheme based on IBBE is optimal regarding the size of ciphertexts and secret keys, while it requires O(k) sized public keys.
When taking concrete values regarding space complexity into account, our IBBE based construction is the favorable one. In particular, when we use the IBBE by Delerablée [22] (for convenience we recall it in “Appendix D”), we obtain ciphertexts \(C \in \{0,1\}^\lambda \times \mathbb {G}_1 \times \mathbb {G}_2\) and secret keys \(\mathsf {sk} \in \{0,1\}^m \times \mathbb {G}_1^m\). That is, ciphertexts are shorter and secret key entries are only half the size of the ones in our direct construction. It is, however, important to note that those efficiency gains come at the cost of a stronger assumption (whose validity was analyzed in the generic bilinear group model in [22]).
TB-BFKEM. In Table 3, we provide an overview of all existing practically instantiable approaches to construct a PFSKEM and compare them to the TB-BFKEM proposed in this paper.Footnote 8 We compare all schemes for an arbitrary number \(\ell \) of time slots, where for sake of simplicity we assume \(\ell =2^t\) for some integer t, (corresponding to our time-based BFKEM) and only count the expensive cryptographic operations, i.e., such as group exponentiations and pairings.
To quickly summarize the schemes: The most interesting characteristic of our approach compared to previous approaches is that our scheme allows to offload all expensive operations to an offline phase, i.e., to the puncturing of time intervals. Here, in addition to the \(O(w^2)\) operations which are common to all existing approaches, we have to generate a number of keys, linear in the size m of the Bloom filter. We believe that accepting this additional overhead in favor of blazing fast online puncturing and decryption operations is a viable tradeoff. For the online phase, our approach has a ciphertext size depending on k (where \(k=10\) is a reasonable choice), decryption depends on k, the secret key shrinks with increasing amount of puncturings and one does only require to securely delete secret keys during puncturing.Footnote 9 In contrast, decryption and puncturing in GHJL is highly inefficient and takes several seconds to minutes on decent hardware for reasonable deployment parameters as it involves a large amount of \(O(\lambda ^2)\) HIBE delegations and consequently expensive group operations. In the GM scheme,Footnote 10 puncturing is efficient, but the size of the secret key and thus cost of decryption grows in the number of puncturings p. Hence, it gets impractical very soon. More precisely, cost of decryption requires a number of pairing evaluations that depends on the number of puncturings and can be in the order of \(2^{20}\) for realistic deployment parameters.
7 Conclusion
In this paper, we introduced the new notion of Bloom filter encryption as a variant of puncturable encryption which tolerates a non-negligible correctness error. We presented various BFKEM constructions. The first one is a simple and very efficient construction which builds upon ideas known from the Boneh–Franklin IBE. It achieves constant size public keys. The second one is a generic construction from CP-ABEs, where a suitable choice of the CP-ABE achieves constant size ciphertexts are available. Those constant size ciphertexts, however, come at the cost of larger keys in existing schemes. The third one is a generic construction from IBBEs, which can be instantiated with the IBBE by Delerablée [22]. This instantiation simultaneously yields constant size ciphertexts and compact public keys. Furthermore, we extended the notion of BFKEM to the forward-secrecy setting and also presented a construction of what we call a time-based BFKEM (TB-BFKEM). This construction is based on HIBEs and in particular can be instantiated very efficiently using the Boneh–Boyen–Goh HIBE [11]. Our time-based BFKEM can directly be used to instantiate forward-secret 0-RTT key exchange (fs 0-RTT KE) as in [33].
From a practical viewpoint, our motivation stems from the observation that forward-secret 0-RTT KE requires very efficient decryption and puncturing. Our framework—for the first time—allows to realize practical forward-secret 0-RTT KE, even for larger server loads: while we only require to delete secret keys upon puncturing, puncturing in [33] requires, besides deleting secret-key components, additional computations in the order of seconds to minutes on decent hardware. Likewise, when using [31] in the forward-secret 0-RTT KE protocol given in [33], one requires computations in the order of the current number of puncturings upon decryption, while we achieve decryption independent of this number. Finally, we believe that BFE will find applications beyond forward-secret 0-RTT KE protocols.
Notes
We note that [24] uses the same techniques as in GHJL.
We discuss below why this is not only tolerable, but actually a very reasonable approach for applications like 0-RTT key exchange.
Note that any large universe CP-ABE scheme yields a small-universe CP-ABE scheme but not vice versa.
Depending on the instantiation, it might still be possible to directly achieve separable randomness. For this to work, the IBBE would need separable keys, that is, if we can equivalently write
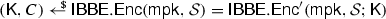 for uniformly random
for uniformly random  , where \(\mathsf {Enc} '\) is a deterministic algorithm. This property is not necessarily given for IBBEs.
, where \(\mathsf {Enc} '\) is a deterministic algorithm. This property is not necessarily given for IBBEs.Implicitly, we set \(\varepsilon :=0^0\).
We note, however, that one cannot straightforwardly apply the CHK transform in a black-box way, but needs to take care that all k \(\mathsf {HIB}\text {-}\mathsf {KEM}\)ciphertexts \(C_j\), \(j\in [k]\) need to use the same verification key of the strong one-time signature used to sign the overall ciphertext.
That is server-side authentication only.
First, note that all constructions have to implement a secure-delete functionality for secret keys within puncturing anyways. Second, note that the question regarding which data structures to choose so that implementations can actually benefit from the shrinking keys is out of scope here. Note that low-level optimizations for sparse files are typically implemented by modern operating systems and file systems [28]. This way one would even benefit when the memory for the secret keys is allocated as a single monolithic block and the deleted keys are simply zeroed out.
Although GM supports an arbitrary number d of tags in a ciphertext, we consider the scheme with only using a single tag (which is actually favorable for the scheme) to be comparable to GHJL as well as our approach.
References
S. Agrawal, D. Boneh, X. Boyen, Efficient lattice (H)IBE in the standard model, in: H. Gilbert (ed.) EUROCRYPT 2010. LNCS, vol. 6110 (Springer, Heidelberg, Germany, French Riviera, May 30–June 3, 2010), pp. 553–572
N. Attrapadung, G. Hanaoka, S. Yamada, Conversions among several classes of predicate encryption and applications to ABE with various compactness tradeoffs, in T. Iwata, J.H. Cheon (eds.) ASIACRYPT 2015, Part I. LNCS, vol. 9452 (Springer, Heidelberg, Germany, Auckland, New Zealand, Nov 30–Dec 3, 2015), pp. 575–601
N. Aviram, K. Gellert, T. Jager, Session resumption protocols and efficient forward security for TLS 1.3 0-RTT, in Y. Ishai, V. Rijmen (eds.) EUROCRYPT 2019, Part II. LNCS, vol. 11477 (Springer, Heidelberg, Germany, Darmstadt, Germany, May 19–23, 2019), pp. 117–150
R. Barbulescu, S. Duquesne, Updating key size estimations for pairings. Journal of Cryptology 32(4), 1298–1336 (2019)
P.S.L.M. Barreto, B. Lynn, M. Scott, Constructing elliptic curves with prescribed embedding degrees, in S. Cimato, C. Galdi, G. Persiano (eds.) SCN 02. LNCS, vol. 2576 (Springer, Heidelberg, Germany, Amalfi, Italy, Sep 12–13, 2003), pp. 257–267
P.S.L.M. Barreto, M. Naehrig, Pairing-friendly elliptic curves of prime order, in B. Preneel, S. Tavares (eds.) SAC 2005. LNCS, vol. 3897 (Springer, Heidelberg, Germany, Kingston, Ontario, Canada, Aug 11–12, 2006), pp. 319–331
M. Bellare, P. Rogaway, Random oracles are practical: a paradigm for designing efficient protocols, in D.E. Denning, R. Pyle, R. Ganesan, R.S. Sandhu, V. Ashby (eds.) ACM CCS 93. (ACM Press, Fairfax, Virginia, USA, Nov 3–5, 1993), pp. 62–73
J. Bethencourt, A. Sahai, B. Waters, Ciphertext-policy attribute-based encryption, in 2007 IEEE Symposium on Security and Privacy. (IEEE Computer Society Press, Oakland, CA, USA, May 20–23, 2007), pp. 321–334
O. Blazy, E. Kiltz, J. Pan, (Hierarchical) identity-based encryption from affine message authentication, in J.A. Garay, R. Gennaro (eds.) CRYPTO 2014, Part I. LNCS, vol. 8616 (Springer, Heidelberg, Germany, Santa Barbara, CA, USA, Aug 17–21, 2014), pp. 408–425
B.H. Bloom, Space/time trade-offs in hash coding with allowable errors. Commun. ACM 13(7), 422–426 (1970)
D. Boneh, X. Boyen, E.J. Goh, Hierarchical identity based encryption with constant size ciphertext, in R. Cramer (ed.) EUROCRYPT 2005. LNCS, vol. 3494 (Springer, Heidelberg, Germany, Aarhus, Denmark, May 22–26, 2005), pp. 440–456
D. Boneh, M.K. Franklin, Identity-based encryption from the Weil pairing, in J. Kilian (ed.) CRYPTO 2001. LNCS, vol. 2139 (Springer, Heidelberg, Germany, Santa Barbara, CA, USA, Aug 19–23, 2001), pp. 213–229
D. Boneh, B. Lynn, H. Shacham, Short signatures from the Weil pairing, in: C. Boyd (ed.) ASIACRYPT 2001. LNCS, vol. 2248 (Springer, Heidelberg, Germany, Gold Coast, Australia, Dec 9–13, 2001), pp. 514–532
C. Boyd, K. Gellert, A modern view on forward security. Comput. J. (2020), to appear
R. Canetti, S. Halevi, J. Katz, A forward-secure public-key encryption scheme, in E. Biham (ed.) EUROCRYPT 2003. LNCS, vol. 2656 (Springer, Heidelberg, Germany, Warsaw, Poland, May 4–8, 2003), pp. 255–271
R. Canetti, S. Halevi, J. Katz, Chosen-ciphertext security from identity-based encryption, in C. Cachin, J. Camenisch (eds.) EUROCRYPT 2004. LNCS, vol. 3027 (Springer, Heidelberg, Germany, Interlaken, Switzerland, May 2–6, 2004), pp. 207–222
R. Canetti, S. Raghuraman, S. Richelson, V. Vaikuntanathan, Chosen-ciphertext secure fully homomorphic encryption, in Public-Key Cryptography—PKC 2017 (2017), pp. 213–240
C. Chen, J. Chen, H.W. Lim, Z. Zhang, D. Feng, S. Ling, H. Wang, Fully secure attribute-based systems with short ciphertexts/signatures and threshold access structures, in E. Dawson (ed.) CT-RSA 2013. LNCS, vol. 7779 (Springer, Heidelberg, Germany, San Francisco, CA, USA, Feb 25–Mar 1, 2013), pp. 50–67
J. Chen, H. Wee, Fully, (almost) tightly secure IBE and dual system groups, in: R. Canetti, J.A. Garay (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043 (Springer, Heidelberg, Germany, Santa Barbara, CA, USA, Aug 18–22, 2013), pp. 435–460
A. Cohen, J. Holmgren, R. Nishimaki, V. Vaikuntanathan, D. Wichs, Watermarking cryptographic capabilities, in D. Wichs, Y. Mansour (eds.) 48th ACM STOC. (ACM Press, Cambridge, MA, USA, Jun 18–21, 2016), pp. 1115–1127
F. Dallmeier, J.P. Drees, K. Gellert, T. Handirk, T. Jager, J. Klauke, S. Nachtigall, T. Renzelmann, R. Wolf, Forward-secure 0-RTT goes live: implementation and performance analysis in QUIC. Cryptology ePrint Archive, Report 2020/824 (2020), https://eprint.iacr.org/2020/824
C. Delerablée, Identity-based broadcast encryption with constant size ciphertexts and private keys, in K. Kurosawa (ed.) ASIACRYPT 2007. LNCS, vol. 4833 (Springer, Heidelberg, Germany, Kuching, Malaysia, Dec 2–6, 2007), pp. 200–215
D. Derler, T. Jager, D. Slamanig, C. Striecks, Bloom filter encryption and applications to efficient forward-secret 0-RTT key exchange, in J.B. Nielsen, V. Rijmen (eds.) EUROCRYPT 2018, Part III. LNCS, vol. 10822 (Springer, Heidelberg, Germany, Tel Aviv, Israel, Apr 29–May 3, 2018), pp. 425–455
D. Derler, S. Krenn, T. Lorünser, S. Ramacher, D. Slamanig, C. Striecks, Revisiting proxy re-encryption: forward secrecy, improved security, and applications, in M. Abdalla (ed.) PKC 2018. LNCS, Springer (2018)
E. Fujisaki, T. Okamoto, Secure integration of asymmetric and symmetric encryption schemes, in M.J. Wiener (ed.) CRYPTO’99. LNCS, vol. 1666 (Springer, Heidelberg, Germany, Santa Barbara, CA, USA, Aug 15–19, 1999), pp. 537–554
K. Gellert, Construction and security analysis of 0-RTT protocols. PhD thesis (2020)
C. Gentry, A. Silverberg, Hierarchical ID-based cryptography, in Y. Zheng (ed.) ASIACRYPT 2002. LNCS, vol. 2501 (Springer, Heidelberg, Germany, Queenstown, New Zealand, Dec 1–5, 2002), pp. 548–566
D. Giampaolo, Practical File System Design with the Be File System. Morgan Kaufmann Publishers Inc., 1st edn (1998)
A. Goel, P. Gupta, Small subset queries and bloom filters using ternary associative memories, with applications, in V. Misra, P. Barford, M.S. Squillante (eds.) SIGMETRICS 2010, Proceedings of the 2010 ACM SIGMETRICS International Conference on Measurement and Modeling of Computer Systems, New York, New York, USA, 14–18 June 2010 (ACM, 2010), pp. 143–154. https://doi.org/10.1145/1811039.1811056
V. Goyal, O. Pandey, A. Sahai, B. Waters, Attribute-based encryption for fine-grained access control of encrypted data, in A. Juels, R.N. Wright, S. De Capitani di Vimercati (eds.) ACM CCS 2006 (ACM Press, Alexandria, Virginia, USA, Oct 30–Nov 3, 2006), pp. 89–98, available as Cryptology ePrint Archive Report 2006/309
M.D. Green, I. Miers, Forward secure asynchronous messaging from puncturable encryption, in 2015 IEEE Symposium on Security and Privacy (IEEE Computer Society Press, San Jose, CA, USA, May 17–21, 2015), pp. 305–320
J. Groth, Simulation-sound NIZK proofs for a practical language and constant size group signatures, in X. Lai, K. Chen (eds.) ASIACRYPT 2006. LNCS, vol. 4284 (Springer, Heidelberg, Germany, Shanghai, China, Dec 3–7, 2006), pp. 444–459
F. Günther, B. Hale, T. Jager, S. Lauer, 0-RTT key exchange with full forward secrecy, in: J. Coron, J.B. Nielsen (eds.) EUROCRYPT 2017, Part III. LNCS, vol. 10212 (Springer, Heidelberg, Germany, Paris, France, Apr 30–May 4, 2017), pp. 519–548
F. Günther, B. Hale, T. Jager, S. Lauer, 0-RTT key exchange with full forward secrecy. Cryptology ePrint Archive, Report 2017/223 (2017), http://eprint.iacr.org/2017/223
B. Hale, T. Jager, S. Lauer, J. Schwenk, Simple security definitions for and constructions of 0-RTT key exchange, in D. Gollmann, A. Miyaji, H. Kikuchi (eds.) ACNS 17. LNCS, vol. 10355 (Springer, Heidelberg, Germany, Kanazawa, Japan, Jul 10–12, 2017), pp. 20–38
S. Halevi, H. Krawczyk, One-pass HMQV and asymmetric key-wrapping, in D. Catalano, N. Fazio, R. Gennaro, A. Nicolosi (eds.) PKC 2011. LNCS, vol. 6571 (Springer, Heidelberg, Germany, Taormina, Italy, Mar 6–9, 2011), pp. 317–334
D. Hofheinz, K. Hövelmanns, E. Kiltz, A modular analysis of the Fujisaki-Okamoto transformation. In: Y. Kalai, L. Reyzin (eds.) TCC 2017, Part I. LNCS, vol. 10677 (Springer, Heidelberg, Germany, Baltimore, MD, USA, Nov 12–15, 2017), pp. 341–371
D. Hofheinz, K. Hövelmanns, E. Kiltz, A modular analysis of the fujisaki-okamoto transformation. Cryptology ePrint Archive, Report 2017/604 (2017), http://eprint.iacr.org/2017/604
T. Kim, R. Barbulescu, Extended tower number field sieve: A new complexity for the medium prime case, in M. Robshaw, J. Katz (eds.) CRYPTO 2016, Part I. LNCS, vol. 9814 (Springer, Heidelberg, Germany, Santa Barbara, CA, USA, Aug 14–18, 2016), pp. 543–571
S. Lauer, K. Gellert, R. Merget, T. Handirk, J. Schwenk, T0RTT: non-interactive immediate forward-secret single-pass circuit construction, in Proceedings on Privacy Enhancing Technologies, vol. 2020, no. 2 (2020), pp. 336–357
S. Lovett, E. Porat, A space lower bound for dynamic approximate membership data structures. SIAM J. Comput. 42(6), 2182–2196 (2013)
A. Menezes, P. Sarkar, S. Singh, Challenges with assessing the impact of NFS advances on the security of pairing-based cryptography. IACR Cryptology ePrint Archive 2016, 1102 (2016), http://eprint.iacr.org/2016/1102
M. Naor, E. Yogev, Bloom filters in adversarial environments, in R. Gennaro, M.J.B. Robshaw (eds.) CRYPTO 2015, Part II. LNCS, vol. 9216 (Springer, Heidelberg, Germany, Santa Barbara, CA, USA, Aug 16–20, 2015), pp. 565–584
R. Ostrovsky, A. Sahai, B. Waters, Attribute-based encryption with non-monotonic access structures, in P. Ning, S. De Capitani di Vimercati, P.F. Syverson (eds.) ACM CCS 2007. (ACM Press, Alexandria, Virginia, USA, Oct 28–31, 2007), pp. 195–203
E. Rescorla, The Transport Layer Security (TLS) Protocol Version 1.3. RFC 8446 (2018), https://rfc-editor.org/rfc/rfc8446.txt
S.F. Sun, A. Sakzad, R. Steinfeld, J.K. Liu, D. Gu, Public-key puncturable encryption: Modular and compact constructions, in A. Kiayias, M. Kohlweiss, P. Wallden, V. Zikas (eds.) Public-Key Cryptography—PKC 2020 (Springer International Publishing, Cham, 2020), pp. 309–338
M. Thomson, J. Iyengar, QUIC: a UDP-based multiplexed and secure transport. Internet-Draft draft-ietf-quic-transport-02, Internet Engineering Task Force (Mar 2017), https://datatracker.ietf.org/doc/html/draft-ietf-quic-transport-02, work in Progress
B. Waters, Dual system encryption: realizing fully secure IBE and HIBE under simple assumptions, in S. Halevi (ed.) CRYPTO 2009. LNCS, vol. 5677 (Springer, Heidelberg, Germany, Santa Barbara, CA, USA, Aug 16–20, 2009), pp. 619–636
D.J. Wu, A. Taly, A.D. Shankar, Boneh, Privacy, discovery, and authentication for the internet of things, in I.G. Askoxylakis, S. Ioannidis, S.K. Katsikas, C.A. Meadows (eds.) ESORICS 2016, Part II. LNCS, vol. 9879 (Springer, Heidelberg, Germany, Heraklion, Greece, Sep 26–30, 2016), pp. 301–319
Acknowledgements
We thank the anonymous reviewers of the Journal of Cryptology for their valuable comments. This research was supported by the European commission through H2020 under grant agreement \(\hbox {n}^{{\circ }}\)644962 (Prismacloud), grant agreement \(\hbox {n}^{{\circ }}\)653454 (Credential), \(\hbox {n}^{{\circ }}\)802823 (Rewocrypt), ECSEL-JU 2018 program under grant agreement \(\hbox {n}^{{\circ }}\)826610 (Comp4Drones), project IoT4CPS funded by the Austrian “ICT of the future” program of the Austrian Research Promotion Agency (FFG) and the Federal Ministry of Austria for Climate Action, Environment, Energy, Mobility, Innovation and Technology (BMK), by the Austrian Science Fund (FWF) and netidee SCIENCE under grant agreement P31621-N38 (Profet), and the German Research Foundation (DFG), project JA 2445/2-1.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Hugo Krawczyk.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This is a major extension of a paper which appears in Advances in Cryptology - Eurocrypt 2018 - 37th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Tel Aviv, Israel, April 29–May 3, 2018, Proceedings.
David Derler: Work done while with Graz University of Technology.
Appendices
A Formal Definitions for Bloom Filter Encryption
Definition 27
(Bloom Filter Encryption) A Bloom filter encryption (BFE) scheme is a tuple \(\mathsf (KGen,Enc, Punc, Dec)\) of \(\mathsf PPT\) algorithms:
- \({\mathsf {KGen}}(1^\lambda ,m,k):\):
-
Takes as input a security parameter \(\lambda \), parameters m and k and outputs a secret and public key \((\mathsf {sk},\mathsf {pk})\).
- \(\mathsf {Enc}(\mathsf {pk},M):\):
-
Takes as input a public key \(\mathsf {pk} \), a message \(M\in \mathcal {M}\) and outputs a ciphertext C.
- \(\mathsf {Punc}(\mathsf {sk},C):\):
-
Takes as input a secret key \(\mathsf {sk} \), a ciphertext C and outputs an updated secret key \(\mathsf {sk} '\).
- \(\mathsf {Dec}(\mathsf {sk},C):\):
-
Takes as input a secret key \(\mathsf {sk} \), a ciphertext C and outputs a message \(M\in \mathcal {M}\) or \(\bot \) if decryption fails.
Definition 28
(Correctness) We require that the following holds for all \(\lambda , m,k\in \mathbb {N}\), all arbitrary sequences of messages \((M_1,\ldots ,M_n,M^*)\in \mathcal {M}^{n+1}\) and any  .
.
For any (arbitrary interleaved) sequence of invocations of

where \(j \in \{1, \ldots , n\}\), \(\mathsf {sk} _{1} := \mathsf {sk} \), and  , it holds that
, it holds that
where  and \(\epsilon (\cdot )\) is a negligible function in \(\lambda \). The probability is over the random coins of \({\mathsf {KGen}}\), \(\mathsf {Punc}\), and \(\mathsf {Enc}\).
and \(\epsilon (\cdot )\) is a negligible function in \(\lambda \). The probability is over the random coins of \({\mathsf {KGen}}\), \(\mathsf {Punc}\), and \(\mathsf {Enc}\).
Note that the correctness is essentially our BFKEM definition ported to the encryption setting. As in Sect. 2.3, we can define the extended correctness, separable randomness, publicly checkable puncturing and \(\gamma \)-spreadness. As this is straightforward, we do not explicitly repeat the definitions here.
Security notions Subsequently, in Fig. 8, we define the \(\mathsf {IND}\text {-}\mathsf {CPA}/\mathsf {IND}\text {-}\mathsf {CCA} 2\)-experiment for BFE. The experiment is identical to \(\mathsf {IND}\text {-}\mathsf {CPA}/\mathsf {IND}\text {-}\mathsf {CCA} 2\) security for conventional public-key encryption, but in addition, the adversary in the second phase can arbitrarily puncture the secret key and retrieve the punctured secret key as long as the key has been punctured on the challenge ciphertext \(C^*\). This still should not help the adversary to obtain any information about the message hidden in \(C^*\).
Definition 29
(\(\mathsf IND\)-\(\mathsf T\) Security of BFE) We define the advantage of an adversary \(\mathcal {A}\) in the \(\mathsf IND\)-\(\mathsf T\)-experiment \(\mathbf{Exp}^{\mathsf {IND\text {-}T}}_{\mathcal {A},\mathsf {BFE}}(\lambda ,m,k)\) as
A Bloom filter encryption scheme \(\mathsf {BFE}\) is \(\mathsf IND\)-\(\mathsf T\)-secure, \(\mathsf{T} \in \{\mathsf {IND}\text {-}\mathsf {CPA},\mathsf {IND}\text {-}\mathsf {CCA} 2\}\), if \(\mathbf{Adv}^{\mathsf {IND\text {-}T}}_{\mathcal {A},\mathsf {BFE}}( \lambda ,m,k)\) is a negligible function in \(\lambda \) for all \(m,k>0\) and all PPT adversaries \(\mathcal {A}\).
B Proof of Lemma 1
We begin by computing the expected number of bits set to one in the BF after \(\alpha \) random elements have been added. Let \(T_0 = b_0 b_1 \ldots b_m\) be the sequence of bits of a BF with size m. After initialization, we have \(b_i := 0\) for all \(i \in [m]\). With each added element, we set up to k bits to one, that is we sample k elements \(a_1, \ldots , a_k \in [m]\) with replacement and set \(b_{a_i} := 1\). At the end of \(\alpha \) time steps, we have at most \(\alpha k\) bits equal to one and at least 1 bit equal to one. Let \(X_i^t\) be the event that \(b_i\) is set at time t, that is, \(X_i^t = 1 \implies b_i = 1\) has already been set to one at time t. Thus, the number bits set to one after \(\alpha \) time steps is
To compute the expected number of bits set to one at time t, we need to compute the expected value of each \(X_i\). Then, the expected number of bits set to one after \(\alpha \) time steps is
We can now bound the probability by applying a simple combinatorial argument. When choosing a random bit \(b_i\), we have a probability of \(X^\alpha /m\) to choose an index i with \(b_i = 1\). Independently repeating this process k times, leads us to the expected false-positive probability of a random element \(u \in \mathcal {U}\) being recognized by the Bloom filter:
\(\square \)
C Growth of the False-Positive Probability
Figures 9, 10, and 11 show the growth of the false-positive probability after \(\alpha \) elements have been added to a Bloom filter with \(n \in {2^{16}, 2^{24}, 2^{30}}\) for \(k \in \{8, 11, 17, 21\}\). Note that both axes are scaled logarithmically.
D Identity-based Broadcast Encryption with Constant Size Ciphertexts and Private Keys
The subsequent construction is the identity-based broadcast encryption scheme by Delerablée [22]. The main advantages of her scheme are the constant size ciphertexts and private keys.
Let  be public parameters of a bilinear map \(e : \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\) with prime orders p and \(|p| = \lambda \). Let \(\mathcal {H} : \mathbb {Z}_q^* \rightarrow \mathbb {Z}_q^*\) be a cryptographic hash function. We construct an identity-based broadcast encryption scheme \(\mathsf {IBBE}\) = (\(\mathsf {Setup}\), \(\mathsf {Extract}\), \(\mathsf {Enc}\), \(\mathsf {Dec}\)) as follows:
be public parameters of a bilinear map \(e : \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\) with prime orders p and \(|p| = \lambda \). Let \(\mathcal {H} : \mathbb {Z}_q^* \rightarrow \mathbb {Z}_q^*\) be a cryptographic hash function. We construct an identity-based broadcast encryption scheme \(\mathsf {IBBE}\) = (\(\mathsf {Setup}\), \(\mathsf {Extract}\), \(\mathsf {Enc}\), \(\mathsf {Dec}\)) as follows:
\(\underline{\mathsf {Setup} (\lambda , k)}:\) The key generation algorithm chooses two generators \(g_1 \in \mathbb {G}_1\) and \(g_2 \in \mathbb {G}_2\) and a secret value  . Finally, we set and output the public key \(\mathsf {pk} \) and master secret key \(\mathsf {msk} \) as
. Finally, we set and output the public key \(\mathsf {pk} \) and master secret key \(\mathsf {msk} \) as
\(\underline{\mathsf {Extract} (\mathsf {msk}, \mathsf {ID})}:\) The key extraction algorithm takes as input the master secret key \(\mathsf {msk} = \gamma \) and an identity \(\mathsf {ID}\). Output is an extracted secret key
\(\underline{\mathsf {Enc} (\mathsf {pk}, \mathcal {S})}:\) Given a public key \(\mathsf {pk} = (w, v, g_2^\gamma , \ldots , g_2^{\gamma ^k})\) and a set of identities \(\mathcal {S} = \{\mathsf {ID} _j\}_{j \in [s]}\) with \(s \le k\), it samples a symmetric key \(\mathsf {K}\) by choosing a secret value  and computing \(\mathsf {K}:= v^\rho = e(g_1, g_2)^\rho \). Finally, the algorithm computes a ciphertext \(C = (c_1, c_2)\) with
and computing \(\mathsf {K}:= v^\rho = e(g_1, g_2)^\rho \). Finally, the algorithm computes a ciphertext \(C = (c_1, c_2)\) with
It outputs \((\mathsf {K}, C)\).
\(\underline{\mathsf {Dec} (\mathsf {sk} _{\mathsf {ID} _j}, \mathcal {S}, C)}:\) Given a ciphertext \(C = (c_1, c_2)\), it computes
and returns \(\mathsf {K}\).
Note that indeed the ciphertext is \(C \in \mathbb {G}_1 \times \mathbb {G}_2\) and an extracted secret key is \(\mathsf {sk} _{\mathsf {ID} _j} \in \mathbb {G}_1\).
Remark on computation of \(p_{i,\mathcal {S}}\). The decapsulation algorithm uses a function p whose description is dependent of \(\gamma \). However, neither \(\gamma \) nor any other secret value is needed to compute it. Instead, we can compute \(g_2^{p_{i,\mathcal {S}}}\) by only using public values.
Let \(c_v(a_1, \ldots , a_n)\) be a function that on input of n values returns the sum of all possible pairwise distinct v-combinations of the input values, i.e., \(c_2(a, b, c) = ab + ac + bc\), and let \(\mathcal {S}_i= \{\mathcal {H}(\mathsf {ID} _j) | j \in \mathcal {S} \setminus \{i\}\}\). Then, we can rewrite
In our case, it suffices to compute
As \(s \le k\), all \(g_2^\gamma \)-like values are publicly known and thus, \(g_2^{p_{i,\mathcal {S}}}\) is computable without any secret knowledge. The given argument also holds for the computation of ciphertext \(c_2\) in the key encapsulation.
Security of the IBBE In [22], Delerablée also analyzes the security of the above scheme under the so called (g, f, F)-GDDHE assumption. This is a variant of a generalization of the Diffie–Hellman exponent assumption introduced in [11] and analyzed in the generic bilinear group model in [22]. For the sake of completeness, we restate the theorem from [22].
Theorem 7
From each efficient adversary \(\mathcal {B}\)against \(\mathsf {IND}\text {-}\mathsf {sID}\text {-}\mathsf {CPA}\) security of the IBBE scheme, we can construct an efficient algorithm \(\mathcal {A}\)against the (g, f, F)-GDDHE assumption with advantage
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Derler, D., Gellert, K., Jager, T. et al. Bloom Filter Encryption and Applications to Efficient Forward-Secret 0-RTT Key Exchange. J Cryptol 34, 13 (2021). https://doi.org/10.1007/s00145-021-09374-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00145-021-09374-3





 and define
and define 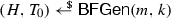 with
with 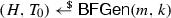 ,
, 
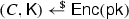 .
.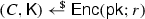 , set
, set  .
. and
and 

 . Then, it chooses
. Then, it chooses  and computes and returns
and computes and returns 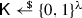 and exponent
and exponent 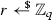 . Then, it computes
. Then, it computes 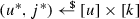 uniformly random. When
uniformly random. When 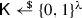 . Then it computes
. Then it computes  , and returns
, and returns  , and returns
, and returns 
 . Then it runs
. Then it runs 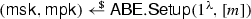 , and for all
, and for all  . Finally it sets and outputs
. Finally it sets and outputs 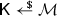 , as well as a value
, as well as a value  , computes
, computes  and outputs
and outputs  and for each
and for each  and
and  , sets
, sets 






 with
with 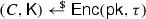 .
.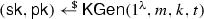 .
. and
and 



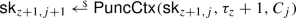
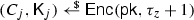
 with
with  , i.e., perfect correctness of the initial secret key due to the perfect correctness property of
, i.e., perfect correctness of the initial secret key due to the perfect correctness property of 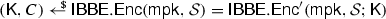 for uniformly random
for uniformly random  , where
, where 


