Classification and comparison of on-line video summarisation methods

Abstract

Many methods exist for generating keyframe summaries of videos. However, relatively few methods consider on-line summarisation, where memory constraints mean it is not practical to wait for the full video to be available for processing. We propose a classification (taxonomy) for on-line video summarisation methods based upon their descriptive and distinguishing properties such as feature space for frame representation, strategies for grouping time-contiguous frames, and techniques for selecting representative frames. Nine existing on-line methods are presented within the terms of our taxonomy and subsequently compared by testing on two synthetic data sets and a collection of short videos. We find that success of the methods is largely independent of techniques for grouping time-contiguous frames and for measuring similarity between frames. On the other hand, decisions about the number of keyframes and the selection mechanism may substantially affect the quality of the summary. Finally, we remark on the difficulty in tuning the parameters of the methods “on-the-fly”, without knowledge of the video duration, dynamic or content.

Introduction

Video summaries aim to provide a set of frames that accurately represent the content of a video in a significantly condensed form. Applications arise in various disciplines [13], including security [9], entertainment [1, 18, 37], browsing [29], retrieval [8] and lifelogging [22, 27]. Proposed algorithms and systems are often tailored to the specific domain. Truong and Venkatesh [35] describe and categorise existing solutions for video summarisation. Comprehensive surveys also exist for application- or approach-specific solutions, e.g. egocentric videos [12] and lifelogging [7], and context-based summaries [23].

Most solutions are based on identifying segments (shots/ scenes/ events or other time units of interest) within a video, by detecting significant change in the content information [14, 21, 22, 40, 41], or grouping the frames into clusters (not necessarily time-contiguous) [11, 18, 19, 29, 42]. Frames are selected from the identified segments based on temporal location, [2, 21, 30, 36], representativeness [11, 18, 19, 29, 40,41,42], or the relative values of the metric for identifying changes in the video stream [1, 14, 22].

The summaries generated are typically in the form of static keyframe sets, e.g. [22], or dynamic video skims, e.g. [37]. In addition, methods may either consider the time-stamp of frames, or content only. Time-aware methods may include a frame that is similar to an existing keyframe if it represents a shot distinct in time, e.g. [18]. Time-oblivious methods ignore any later frames that are similar to an existing keyframe from earlier in the video [11, 19, 29, 42]. The appropriate choice for the form of the summary depends on the application.

Many of the methods used for generating video summaries are computationally expensive; for example, requiring complex pre-processing [27], using high-level feature extraction [9], or selecting the frames through iterative, or multi-stage algorithms [20, 27, 37]. Methods typically also assume that the full video is available for processing. Here we are interested in on-line summarisation, where keyframes are selected for the summary before the entire video has been captured or received. On-line methods have been proposed that address different constraints, e.g. memory [4, 15], latency [1, 3, 31] or processing power [15, 28]. With such constraints, the traditional high-level feature extraction, such as through convolutional neural networks (CNN) [4], may be infeasible. Similarly, elaborate summary selection methods may not be applicable on-line.

Lightweight wearable cameras allow consumers to capture a continuous stream of images from their daily activities [5]. Examples of possible applications include recording first-person sport video footage [24], maintaining records for law enforcement purposes [10], monitoring social interactions [39], training medical professionals [33] and creating appealing travelling logs [6] or personalised summaries [17, 38]. Selecting a summary for such a video on-the-fly would make it possible to keep recording for a long time within the limited resources of the wearable device. Methods for on-line video summarisation considered in this study can potentially be used for this process.

To develop a method fit for this application, it is first instructive to understand and assess existing on-line video summarisation methods. We wish to identify the aspects of methods that influence performance and the restrictions inherent in on-line applications.

Fig. 1

A classification of on-line video summarisation methods

Here, we propose a classification of on-line video summarisation methods by identifying their most relevant descriptive properties. We investigate nine on-line summarisation methods by specifying them in the terms of the proposed classification, and subsequently apply them to synthetic data with an objectively “best” solution available, and to a collection of real videos. The rest of the paper is organised as follows. Section 2 introduces the classification system, and Sect. 3 describes the methods. The experiments are presented in Sect. 4, and the conclusion, in Sect. 5.

A classification of on-line video summarisation methods

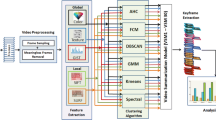
Truong and Venkatesh [35] provide a useful classification of video summarisation methods, which we adapt here for on-line video summarisation. Figure 1 shows our proposed classification.

All methods contain the same basic components:

• Feature representation Video frames are described as n-dimensional vectors in some feature space, $\mathbf{x}\in \mathbb {R}^n$. The choice of a feature space may be an integral element of a summarisation method [32], or the method may be independent of feature space [35]. Some existing methods use relatively complex features, e.g. CNN [4, 15]. However, for an on-line application, features that are less computationally expensive and require less memory are preferable. Examples of such feature spaces are the HSV histogram as a colour descriptor [1, 3, 32] and textural descriptors such as the CENTRIST feature space [28].

• Similarity How representative a keyframe is can be measured by how similar it is to the frames from which it is selected. To evaluate similarity between frames, we can use the feature representation in $\mathbb {R}^n$ and metrics defined on this space. Examples of such metrics are the Euclidean or Cosine distances [15, 31]; the volume of the convex hull of a set of frames [4]; the correlation between two frames [3]; the degree of linear independence between batches of frames [1]; the orthogonal projection of a frame onto the span of existing keyframes [28]; and the intersection of colour histogram bins [32]. Finally, some methods use statistical measures, such as the likelihood that a frame belongs to a distribution of existing frames, or the equivalence of two sets of frames in terms of mean and variance [34].

• Grouping strategies Representative frames are selected from groups of frames, which may or may not be time-contiguous. The groups can be created from the data stream either explicitly, e.g. clustering [4, 15], or implicitly, e.g. change detection [1, 3]. Gaussian mixture models (GMM) group the frames into a fixed [31] or variable [34] number of Gaussian distributions.

• Frame selection Particular frames are selected to represent each group. The criterion for selecting a frame can be its location within the cluster; typically the most central frame is chosen [4, 15]. Alternatively, frames can be selected based on their location within a shot, e.g. the first [1] or middle frame [32]. Some methods consider each frame within a group and progressively select keyframes based on some condition, e.g. the difference to existing keyframes [31].

• Set management In on-line video summarisation, the frames are acquired one by one, as the stream is being processed. We distinguish between two approaches for the keyframe set management: fixed and dynamic. According to the “fixed” approach, once a frame has been included in the summary, it cannot be replaced or removed [1, 3, 15, 28, 31, 32, 35]. Conversely, in the “dynamic” approach, frames may be dropped or replaced [4]. Dynamic management may not be practical in applications where latency is a constraint, and keyframes must be transmitted as soon as they are selected.

• Summary form Video summaries can be either in the form of skims (dynamic summary) [3, 31, 37] or keyframe sets (static summary) [1, 3, 4, 15, 28, 32] . In this study, we focus primarily on methods that generate static keyframe sets.

• Number of keyframes With an on-line application, the total number of frames will typically not be known beforehand. Deciding on the number of keyframes a priori may not be practical but is often done so as to ensure that the summary is suitable for the human viewer or complies with the on-line constraints [4]. Post-processing trims down an excessive keyframe set selected by the on-line method [4, 37]; termed a posteriori in the diagram. Finally, the summary may stay as extracted by the on-line method [1, 3, 15, 28, 31, 32, 34, 35], with the number of keyframes not known until the summarisation is complete.

• Running memory Some methods only need to store the current keyframe set [4, 28, 35], whereas others have potentially larger memory requirements such as buffering an entire shot in addition to maintaining the keyframe set [3, 32]. Methods that process frames in batches will need to hold the full batch in memory [1, 15, 34].

Methods included in the comparison study

We review and compare nine methods for on-line video summarisation. The methods are tested on two synthetic data sets, and video data from the VSUMM project [11]. Table 1 categorises the methods according to the classification given in Fig. 1, described in Sect. 2. Here, we give a brief description of each method.

Shot-boundary detection (SBD)

Abd-Almageed [1] uses change in the rank of the feature space matrix, formed by a sliding window of frames, to identify shot boundaries. The first frame in a shot is selected as a keyframe. The method parameters are the window size and a threshold on the rank for identifying change.

Table 1 Description of the methods included in the comparisons in terms of the classification in Fig. 1 (in alphabetical order of the first author)

Zero-mean normalised cross-correlation (ZNCC)

Almeida et al. [3] also look for shot boundaries. They compare the similarities between consecutive frames, using the zero-mean normalised cross-correlation as a measure of distance. Once shots have been identified, a predefined parameter determines whether or not the shot should be included in the summary. Keyframes are selected at uniform intervals throughout a shot. The authors define the desired interval size in terms of the full video length, which typically will not be known in the on-line case. They apply their method in the compressed domain, where it can produce either keyframe sets or skims.

Diversity promotion (DIV)

The approach taken by Anirudh et al. [4] is to group frames into clusters while simultaneously maximising the diversity between the clusters. They use the volume of the convex hull of the keyframe set as a measure of diversity. Incoming frames replace existing keyframes as cluster centres if doing so increases the diversity of the keyframe set. This diversity measure introduces a constraint on the number of keyframes in relation to the feature space size; the number of keyframes must be greater than the feature space dimensionality. The authors recommend the use of PCA to reduce a high-dimensional feature space. However, it is not clear how they calculate the principal components for data in an on-line manner.

Submodular convex optimisation (SCX)

Elhamifar and Kaluza [15] process frames in batches, and propose a “randomised greedy algorithm for unconstrained submodular optimisation” to select representative frames for each batch. These representatives can be a combination of existing keyframes and new keyframes from within the batch itself. In their experiment on videos, they pre-process the data to extract shots and use these as batches. An alternative choice, such as a fixed batch size, will have to be used in a true on-line setting. Similarly, their experiment defines a regularisation parameter in terms of the maximum observed distance between frames; a value that will not be available when running the method on-line.

Minimum sparse reconstruction (MSR)

The MSR method [28] uses the orthogonal projection of a frame onto the span of the current keyframe set to calculate the percentage of reconstruction for the frame. A predefined threshold then determines whether the frame is adequately represented by existing keyframes, or it is added to the keyframe set. The use of the orthogonal projection forces a constraint on the number of keyframes used for reconstruction, which is limited to the number of dimensions of the feature space. Once the maximum number of frames is reached, only the keyframes that best represent the others in the set are used to calculate the percentage of reconstruction.

Gaussian mixture model (GMM)

Ou et al. [31] use the components of a Gaussian mixture model to define clusters of frames. Each new frame is assigned to the nearest cluster, provided it is sufficiently close to the cluster mean, or otherwise forms a new cluster. The number of clusters is fixed, so any new clusters replace an existing one. Two parameters for the method interact to determine how long clusters are remembered for. This memory affects whether non-contiguous, similar frames are grouped together or not. This method has substantially more parameters to tune than the other methods. The number of clusters, and the initial variance and weight for new clusters must be defined, in addition to the two learning-rate parameters. The authors describe the algorithm as a method for video skimming rather than keyframe selection.

Histogram intersection (HIST)

Rasheed and Shah [32] propose a multi-pass algorithm that first detects shot boundaries, and then explore scene dynamics. For the on-line scenario here, we consider just the shot-boundary detection. The detection algorithm uses the intersection of HSV histograms for consecutive frames. An overlap below a predefined threshold defines a shot boundary. Once a full shot has been identified, frames from the shot are sequentially added to the keyframe set if they are not sufficiently similar to any existing shot keyframes.

Merged Gaussian mixture models (MGMM)

Similar to Ou et al., Song and Wang [34] sequentially update a GMM to describe the distribution of a data stream. However, rather than a fixed number of clusters, their method allows new ones to be added if necessary and also provides a mechanism for combining statistically equivalent clusters.

The MGMM method is for clustering a generic on-line data stream. For a comparison with video summarisation methods, we add an additional step of selecting a representative from each cluster as a keyframe. At each stage of processing, the frame closest to each cluster mean is stored as the current keyframe. Frames may be replaced if a subsequent frame is closer to the mean. As the cluster means are dynamic, the final set of keyframes may not be the optimal set that would be chosen if the full data set is kept in memory, and the keyframes selected at the end of processing.

Sufficient content change (SCC)

The change-detection algorithm from Truong and Venikatesh [35] selects the first frame sufficiently different to the last keyframe as the next keyframe. Unlike the other change-detection algorithms, this method does not require a buffer of all frames that have appeared within a shot so far. Only the keyframe set is stored in memory. The authors describe this algorithm in terms of a generic content change function. Here, we implement the algorithm using Euclidean, Minkowski or Cosine distance.

Experiments

Data

We test each of the nine methods on two synthetic data sets and subsequently illustrate their performance on the 50 real videos from the VSUMM collection [11].¹

The first data set reproduces the example of Elhamifar et al. [16]. The data consists of three clusters in 2-dimensional space as illustrated in Fig. 2. Each point represents a frame in the video. The three clusters come in succession, but the points within each cluster are generated independently from a standard normal distribution. The order of the points in the stream is indicated by a line joining every pair of consecutive points. The time tag is represented as the grey intensity. Earlier points are plotted with a lighter shade. The “ideal” selected set is shown with red target markers.

Fig. 2

Synthetic data set #1. The time tag is represented as the grey intensity. Earlier points are plotted with a lighter shade. The “ideal” selected set is shown with red target markers

The second synthetic data set, shown in Fig. 3, follows a similar pattern, but the clusters are less well-defined, they have different cardinalities, and the features have non-zero covariance. Data set #2 is also larger, containing 250 points, compared to 90 in data set #1. The difference in cluster size and total number of points between the two data sets will guard against over-fitting of parameters that may be sensitive to shot and video length.

Fig. 3

Synthetic data set #2. The time tag is represented as the grey intensity. Earlier points are plotted with a lighter shade. The “ideal” selected set is shown with red target markers

For both data sets, we add two dimensions of random noise (from the distribution $\mathscr {N}(0, 0.5)$). A higher-dimensional feature space is used so that the MSR method is not penalised by being constrained to a maximum of two keyframes for reconstruction. The additional dimensions and noise also make the synthetic examples a more realistic test for the methods.

Finally, we use the 50 videos from the VSUMM collection, and five ground-truth summaries for each video. Since the choice of feature representation may have serendipitous effect on some methods, we experiment with two basic colour descriptors: the HSV histogram and the RGB moments. These two spaces are chosen in view of the on-line desiderata. HSV histograms and RGB colour moments are among the most computationally inexpensive and, at the same time, the most widely used spaces. For the HSV histogram, each frame is divided uniformly into a 2-by-2 grid of blocks (sub-images). For each of the four resulting blocks, we calculate a histogram using eight bins for hue (H), and two bins each for saturation (S) and value (V). For the RGB colour space, we divide the frame into 3-by-3 blocks. For each block, we calculate the mean and the standard deviation of each colour, which gives 54 features in total for the frame.

For the four methods (DIV, SCX, MSR, GMM) developed using a specific feature space, other than colour histograms, we extract the original features (CNN, Centrist, MPEG7 colour layout) for the VSUMM collection. These original features are used to test whether using an alternative feature space leads to an unfair representation of the performance of a method.

Table 2 Parameters for the nine methods tested, the ranges used for tuning the methods to synthetic data set #1, and the parameter value that generates the best result

Evaluation metrics

The aim of video summarisation is to produce a comprehensive representation of the video content, in as few frames as possible. If the video is segmented into units (events, shots, scenes, etc.), the frames must allow for distinguishing between the units with the highest possible accuracy [25]. Therefore, we use three complementary objective measures of the quality of the summary:

$$\begin{aligned}&\text{ Cardinality }:K = |P| \end{aligned}$$

(1)

$$\begin{aligned}&\text{ Approximation } \text{ error }:J = \sum _{i=1}^Nd(\mathbf{x}_i,\mathbf{p}_i^*)\end{aligned}$$

(2)

$$\begin{aligned}&\text{ Accuracy }:A = \text{1-nn }(P) \end{aligned}$$

(3)

where $X=\langle \mathbf{x}_1,\ldots ,\mathbf{x}_N\rangle$ is the sequence of video frames, N is the total number of frames in the video, $P=\{\mathbf{p}_1,\ldots ,\mathbf{p}_K\}$ is the selected set of keyframes, $\mathbf{p}_i^*$ is the keyframe closest to frame $\mathbf{x}_i$, d is the Euclidean distance, and 1-nn(P) is the resubstitution classification accuracy in classifying X using P as the reference set. To obtain a good summary, we strive to maximise A while minimising J and K.

For the tests on synthetic data, we can evaluate the results of the summaries against the distributions used to generate the data. However, we acknowledge that what constitutes an adequate summary for a video is largely subjective. If user-derived ground-truth is available for a video, one possible way to validate an automatic summary is to compare it with the ground truth. The match between the summaries obtained through the nine examined on-line methods and the ground truth is evaluated using the approach proposed by De Avila et al. [11]. According to this approach, an F-measure is calculated (large values are preferable) using 16-bin histograms of the hue value of the two compared summaries [26].

Experimental protocol

We first tune parameters by training each method on the synthetic data set #1. Table 2 shows the parameters and their ranges for the nine methods.

Some methods have a parameter that defines the number of frames in a batch. For these methods, we define an upper limit of the batch size to represent the inherent on-line constraints of memory and processing. This limit ensures that tuning the batch size does not cause it to increase to an essentially off-line, full dataset implementation.

We extract the Pareto sets for the three criteria described in Sect. 4.2 and sort them in decreasing order of accuracy, A. Results with equal accuracy are arranged by increasing values of K (smaller sets are preferable), and then, if necessary, by increasing values of J (sets with lower approximation error are preferable). As A and J achieve their optimal values by including all frames as keyframes, we discount solutions that select more than ten keyframes.

An example of the results of training the SCX method on data set #1 is shown in Table 3.

Table 3 The Pareto sets for the SCX method trained on data set #1, describing the optimal combinations of accuracy, cardinality of the keyframe set, and approximation error

To assess the robustness of the method parameters across different data samples, the best parameters for each method, as trained on data set #1, are used to produce summaries for an additional 40 randomly generated data sets: 20 samples following the same cluster size and distributions as data set #1 (Fig. 2), and 20 samples following the cluster distributions of data set #2 (Fig. 3). We can think of the first 20 samples as “training”, and the latter 20 samples as “testing”, and place more value on the testing performance.

For all 40 data sets, the results for the methods are ranked one to nine; a lower rank indicates a better result. Tied results share the ranks that would have been assigned without the tie. For example, if there is a tie between the top two methods, they both receive rank 1.5.

We next illustrate the work of the algorithms on real videos separately on the HSV and the RGB feature spaces described in Sect. 4.1. We tune the parameters of each method on video #21 of the VSUMM database. The ranges described in Table 2 are used for parameters that are independent of the feature space and number of data points. Ranges for parameters that are sensitive to the magnitude and cardinality of the data are adjusted appropriately. The parameter combination taken forward is the one that maximises the average F-measure obtained from comparing the summary from the method and the five ground-truth summaries. We then select the more successful of the two feature spaces and use the optimal parameter set for each algorithm to generate summaries for the full set of VSUMM videos. The F-measures are calculated for the comparisons of each video, method and ground-truth summary, and the average for each method compared.

Finally, we repeat the training and testing on the VSUMM database using the original features used by the methods, where applicable. As methods may have been developed and tuned to use a specific feature space, this procedure ensures that methods are not disadvantaged by using the colour-based features.

Results

The relative performance of the methods on the synthetic data sets is shown in Fig. 4. The merging Gaussian mixture model method consistently generates one of the best summaries. While the method (MGMM) still performs relatively well on the data set #2 examples, it suffers from some over-fitting of its batch-size parameter on data set #1.

The SCX and SCC methods also perform relatively well, and are reasonably robust across changes in the data distribution. This robustness is demonstrated by the relative sizes of the grey and black parts of the bar for these methods; the SCX method receives better ranks on data set #2 than on data set #1, and the SCC method performs equally well across the two data sets.

The relatively poor performance of the GMM method may be due to the fact that this algorithm is designed to generate video skims, and therefore tends to return a higher number of keyframes than other methods. The MSR method is potentially affected by constraints from the low feature space dimensionality.

Fig. 4

Average rank for each method for summaries of 40 randomly generated data sets (20 each following the cluster distributions of data sets #1 and #2). On each data set, summaries from all methods are compared and ranked. Better methods receive lower rank

Fig. 5

Average F-measure for each method compared to five user ground-truth summaries for video #21. Method summaries are generated using HSV and RGB feature spaces. Summaries are matched using histograms of hue values for the selected frames

Table 4 Method parameters tuned on VSUMM video #21 using HSV histogram and RGB moments to represent frames

The comparison of the two features spaces on VSUMM video #21 is shown in Fig. 5 and Table 4. Sensitivity to the respective feature space can be observed both in terms of the optimal parameter values found (Table 4) and the quality of the match to the ground-truth summaries (Fig. 5):

• Some methods (GMM, ZNCC, SCC, DIV) perform quite differently when the two different feature spaces are used, with a significantly better average F-measure with one of the spaces.

• The two methods that perform relatively well on the synthetic data sets (MGMM and SCX) generate very similar results when HSV and RGB features are used.

• For most methods, including those with very different results (e.g. GMM), the tuned parameters are similar for both feature spaces.

• However, parameters directly related to the feature space are naturally very sensitive to a change in features. For example, the optimum distance threshold parameter for the SCC method is 516 in RGB space, compared to 6 in HSV space.

Table 5 Average number of frames and F-measure for summaries generated by each method of the 50 VSUMM videos using RGB moments, and average F-measure with the features originally used with the method

Most of the methods perform better with the RGB moment features. Therefore, we use these features and the corresponding tuned parameters to generate summaries for the full set of VSUMM videos. Table 5 shows the average F-measure across all VSUMM videos, and the median number of frames selected.

The method generating the best results on the synthetic data (MGMM), again produces relatively good summaries for the videos. The MSR method performs markedly better on the real videos, with a higher-dimensional feature space, than on the synthetic data. The SCX method has the highest average F-measure. As an illustration of the results, the summary generated by this method for video #29 is shown in Fig. 6 in comparison to the ground-truth summary from user 3. The method matches 7 of 8 frames selected by this user (shown next to the SCX frames in Fig. 6).

There is little difference in the performance of the methods using their original features, compared to RGB moments, both in terms of average F-measure and overall ranking. The SCX method maintains the highest average F-measure, and although the average score for the GMM method improves, it still remains lower than the other methods. The DIV method scores a lower average F-measure when the original features are used, highlighting the importance of considering simple, efficient feature spaces.

Fig. 6

Comparison of VSUMM video #29 summaries from ground-truth user #3 and the SCX method. The matches have been calculated using the 16-bin histogram method with threshold 0.5 [11]. The F-measure for the match is 0.88

Three observations can be made from the video summaries:

• The F-measures in Table 5 are generally low compared to those reported in the literature for other video summarisation methods. This difference is to be expected because here we compare on-line methods which do not have access to the whole collection of frames.

• Most methods are highly sensitive to their parameter values. The optimal values tuned on video #21 are not directly transferable to the remaining videos. Most methods (ZNCC, MSR, GMM, HIST, SCC) typically select too few keyframes. This indicates the importance of tuning. In the on-line scenario, data for tuning will not be available, especially the segment labels needed for calculating A.

• Most methods are tested using a different feature representation than that recommended by the authors (HSV histograms are used in only three of the methods: SBD, ZNCC, HIST; none of the methods use RGB features). However, the relative performances do not appear to be overly sensitive to the choice of feature space.

Conclusion

This paper proposes a classification of on-line video summarisation methods that incorporates feature representation, strategies for comparing and grouping frames, and the size, selection and management of frames.

Our experiments highlight the difficulty in pre-tuning the parameters of on-line video summarisation algorithms. This limitation suggests that algorithms are needed which are more robust to their parameter fluctuations, and ideally should adapt with the streaming data.

The relative performance of the methods appears to be independent of the strategy for grouping the frames into segments or clusters and of the similarity measure used. We note that, according to our experiments, no strategy or measure produced consistently good or consistently bad summaries. The methods that select the cluster centres as the keyframe set produce better summaries than those that select keyframes conditionally. Perhaps unsurprisingly, the method that decides the number of keyframes a priori, tends to perform less well than those that can continue to add keyframes as required, suggesting that on-line algorithms need flexibility to adapt the number of keyframes to the data. This requirement must be balanced with the memory restrictions inherent in on-line video summarisation.

The videos used for testing have well-defined shots, providing a relatively easy summarisation task. The performance of the methods may be different on other types of video, e.g. where the shots are less clearly defined or the variability within shots is greater. Examples of such type of data are egocentric videos and lifelogging photo streams.