Abstract
Automatic artery/vein (A/V) classification is one of the important topics in retinal image analysis. It allows the researchers to investigate the association between biomarkers and disease progression on a huge amount of data for arteries and veins separately. Recent proposed methods, which employ contextual information of vessels to achieve better A/V classification accuracy, still rely on the performance of pixel-wise classification, which has received limited attention in recent years. In this paper, we show that these classification methods can be markedly improved. We propose a new normalization technique for extracting four new features which are associated with the lightness reflection of vessels. The accuracy of a linear discriminate analysis classifier is used to validate these features. Accuracy rates of 85.1, 86.9 and 90.6% were obtained on three datasets using only local information. Based on the introduced features, the advanced graph-based methods will achieve a better performance on A/V classification.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The fundus image is a direct optical capture of the human retina, including landmarks like the optic disk, the macula and, most importantly, the retinal circulation system.
The simple and low-cost fundus image acquisition offers great potential for the images to be used in large-scale screening programs and relative statistical analysis. Many clinical studies on retinal vascular changes reveal that biomarkers like vessel tortuosity and vessel caliber are associated with the development of diabetic retinopathy, glaucoma, hypertension and other cardiovascular diseases [1,2,3]. In addition, previous works on retinal fractal dimension [4] and vascular tortuosity [5] implied that traditional retinal biomarkers might reveal more information for disease progression if they were measured separately on arteries and veins. Therefore, A/V classification is a necessary step for the measurement of retinal vascular biomarkers, such as central artery equivalent and central vein equivalent and artery-to-vein diameter ratio (AVR) [6, 7]. However, the analysis of separated trees of artery and vein has received limited attention, and it is still open for investigation. Arterial and venous vessels behave differently under pathological conditions [8]. Therefore, the separation of arteries and veins on the retinal images provides new information apart from the usual biomarkers. Several works on separating retinal arteries and veins have been proposed in the literature [9,10,11,12,13,14,15]. From the recent works, we can summarize the workflow for an artery/vein (A/V) classification system. It starts by importing a color fundus image. Then the vessel segmentation is applied to extract the vascular network. For each vessel pixel, multiple features based on the various color channels are extracted and used for a supervised A/V classification, called pixel-wise classification [13]. The label of each vessel centerline, or vessel segment, is determined by averaging the labels of its pixels, called the segment-wise classification [11, 14]. Finally, the result of segment-wise classification is corrected by using contextual information extracted from the vascular structure, like vessels connecting with each other have the same label and in crossovers they have opposite labels [9, 10, 12].
During the last few years, the application of graph-based approaches to classify arteries and veins has become popular in retinal image analysis [9,10,11,12]. A graph of the vascular tree represents the topological structure of the vessels. By including rules like arteries only cross the veins, it improves the result of pixel-wise classification. However, although the technique is powerful, it still relies on a good pixel-wise classification to draw the final decision. Additionally, if errors were made during the vessel graph construction, the labeling for the entire tree would go wrong. Therefore, a robust pixel-wise classification still plays an important role in A/V separation, as it affects the performance of graph-based approaches and can be used to correct the incorrect graph construction. In recent years, new features that give better image pattern representation have been applied in fields such as object identification and classification [16, 17]. In the field of retinal A/V classification, traditional normalized color intensities are still being used. For instance, the feature set used in the framework proposed by Dashtbozorg et al. [9] is based on the normalized RGB and HSB, where the normalization technique was proposed by Foracchia et al. [18] in 2005. The method by Vinayak et al. [11] extracts four features which are the mean and standard deviation of the green and hue channels. In addition, Estrada et al. [12] obtain the local RGB intensity and compute the mean color value of the three channels. The framework proposed by Hu et al. [10] uses a similar method by Niemeijer et al. [13] where the feature vector is based on the red, green, hue, saturation and brightness intensities, which are normalized to zero mean and unit standard deviation.
It turns out that the pixel-wise A/V classification has been relatively overlooked and can be further improved. In this paper, we propose new intensity-based features for the pixel-wise A/V classification. These features exploit new luminosity reflection properties of the vessel tissues in terms of different color channels, and turn out to have better performance in discriminating retinal arteries from veins, and improve the result of A/V classification methods.
The rest of the paper is organized as follows: In Sect. 2, we introduce the details of the proposed reflection features. In Sect. 3, we compare these features with the most often used features, such as raw and normalized RGB, HSB and Lab color channels. Section 4 is the discussion and Sect. 5 gives the conclusion.
2 Methodology
Blood in arteries contains oxygenated hemoglobin, while blood in veins contains deoxygenated hemoglobin, which have good discrimination on the light spectrum. The oxygenated hemoglobin absorbs less light with wavelengths between 600 and 800 nm than deoxygenated hemoglobin. Thus on color retinal images arteries are often brighter than veins in the red channel, because more light is reflected by the oxygenated hemoglobin. This difference is used in many A/V classification approaches to primarily assign A/V labels or probabilities of being arteries and veins to vessel pixels.
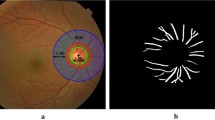
Retinal images often suffer from local luminosity and contrast variation (see Fig. 1), which is mainly due to non-uniform illumination and the irregular retinal surface. It seriously affects the A/V separation if the raw intensity values of the image color channels are used. In order to overcome this illumination variation, many approaches have been proposed in the literature for image preprocessing [18,19,20,21]. In this paper, we base our new approach on two of them for optimal artery/vein separation, which are the luminosity normalization method proposed by Foracchia et al. [18] and the method motivated by the Retinex approach proposed by Jobson et al. [21].
2.1 Luminosity normalization
The intensity of a retinal image f(x, y) can be modeled by an illumination–reflection model:
where r(x, y) is the reflection property of a material with regard to the absorbed light wavelength and l(x, y) is the general luminosity around a local area, which causes the inhomogeneous pixel intensity. The arteries and veins show discrimination in terms of r(x, y), so we need to eliminate the l(x, y) from the above model and compare the reflection property directly for A/V separation. The normalization method proposed by Foracchia et al. [18] is described by the following formula:
In the above equation, the numerator is the pixel intensity at position (x, y). The denominator is the mean filter applied to the n \(\times \) n neighbors around (x, y). Since l(x, y) is the image luminosity caused by the remote light source, we assume l(x, y) within a certain region has little change, so the above equation can be simplified through:
This method divides the local pixel intensity by the average intensity within its neighborhood to cancel the luminosity factor. The result \(N_1\left( x,y \right) \) is then the direct relation between local reflection and the average reflection inside its \(n \times n\) neighbors.
2.2 Retinex normalization
Another method that eliminates the term l(x, y) is motivated by the single-scale retinex (SSR) method proposed by Jobson et al. [21]. The SSR approach separates the two components by a logarithm transformation which is described by the following equation:
where I(x, y) is the original image intensity at position (x, y) , \(G(x,y,\sigma )\) is the Gaussian surrounding of (x, y) with scale \( \sigma \) and \( * \) denotes the convolution operation. In our work, we first compute the logarithm on the original image and then apply a mean filter instead of a Gaussian filter to it. The subtraction of the two results yields the luminosity invariant image:
The summation represents a mean filter applied to the neighborhood around a pixel. The luminosity is almost the same in its neighborhood. So the above equation is simplified as:
Finally, we take the exponential to both sides and obtain to the final form:
This method uses the logarithmic transformation to subtract the local luminosity component by its surrounding. The result \(N_2\left( x,y \right) \) indicates the ratio of reflection properties between the local pixel \(\left( x,y \right) \) and the root of the multiplication inside its \(n \times n\) neighbor.
2.3 The reflection property
Note that the most discriminative feature for artery/vein classification is \( N_{optimal} = r(x,y)\), where the reflection property of vessel is measured alone. The two normalization strategies eq.(3) and (7) eliminate the luminosity term l(x,y), but at the same time two denominators which compute the arithmetic and geometric average for background tissue and vessel reflection are added, respectively, and rescale the term r(x, y) (nonlinear transformation). This results in histogram shifting on the pixel intensity of artery and vein. In order to avoid the undesired transformation, and improving the discrimination between arteries and veins, we propose a set of new features which are computed based on the described two normalization methods.
We consider an \(n\,\times \,n\) window placed on an image patch which includes both vessel and background tissue. Inside the window, the reflection property \(r(x_i,y_i)\) has two clusters: the background tissue \(r_b(x,y)\) and vessel tissue \(r_v(x,y)\). By replacing eq. (3) and (7) with the \(r_b(x,y)\) and \(r_v(x,y)\), \(N_1(x,y)\) and \(N_2(x,y)\) become:
where \(n_b\) and \(n_v\) are the number of background pixels and vessel pixels in the \(n\,\times \,n\) window and r(x, y) is at the center of the window. For these two equations, we raise both sides to the power of -1, which flips the fraction upside down, and move r(x, y) into the summation and multiplication, respectively:
In the sliding window, we assume that \(r_b(x,y)\) for all background pixels is approximately equal; thus, the ratio \(\frac{r_b(x,y)}{r(x,y)}\) of each background pixel is approximately equal to a constant value \(\overline{r_b}\). And the same of each vessel pixel \(\frac{r_v(x,y)}{r(x,y)}\) are approximately equal to a constant value \(\overline{r_v}\). Now eq. (11) and (12) can be rewritten as:
Let a constant value a \(\left( 0<a<1 \right) \) represent the ratio between the number of background pixels and the total number of pixels contained in the window \(\left( a = \frac{n_b}{n^2}\right) \), the above two equations become:
Since a can be estimated from a vessel binary segmentation of the image, the above two equations contain two unknown variables. From them, we can solve two solutions, where one is larger than one and the other is approximately equal to one. If the center r(x, y) is a vessel pixel, \(\overline{r_b}\) is the solution that is larger than one \(( |\overline{r_b}| > 1)\), because the background reflection \(r_b(x,y)\) is usually higher than the vascular reflection r(x, y). Similarly, \(\overline{r_v}\) is the solution which is close to one \((|\overline{r_v}| \approx 1) \) because \(r_v(x,y)\) is approximately equal to r(x, y).
\(\overline{r_b}\) is the approximate of \(\frac{r_b(x,y)}{r(x,y)}\) and \(\overline{r_v}\) is the approximate of \(\frac{r_v(x,y)}{r(x,y)}\) for each pixel in the patch. But in our A/V classification, we use \(\overline{r_b}^{-1}\) and \(\overline{r_v}^{-1}\) as features instead of using \(\overline{r_b}\) and \(\overline{r_v}\) in order to keep them linear with respect to r(x, y) . Besides using \(\overline{r_b}^{-1}\) and \(\overline{r_v}^{-1}\), \(\frac{\overline{r_b}}{\overline{r_v}}\) and \(\frac{\overline{r_v}}{\overline{r_b}}\) are also computed, where \(\frac{\overline{r_b}}{\overline{r_v}}=\frac{r_b(x,y)}{r_v(x,y)}\) and \(\frac{\overline{r_v}}{\overline{r_b}}=\frac{r_v(x,y)}{r_b(x,y)}\) are the ratios between the background reflection and the vessel reflection, with the local term r(x, y) eliminated. In Fig. 2a, we show a small patch taken from a retinal image with high luminosity variation. For this patch, we obtain the \(N_1\) and \(\overline{r_b}^{-1}\) as well as the corresponding intensity profiles for an artery and a vein as shown in Fig. 2b, c. As we can see in the profile plots, the discrimination between the artery and the vein is better in the \(\overline{r_b}^{-1}\) channel. Specifically, at the central reflection part, \(\overline{r_b}^{-1}\) gives a better separation on the two vessels, while the intensity profiles of the raw red and the normalized red are almost overlapped.
3 Experimental Results
To validate our proposed reflection property features, we use retinal images from three datasets. The INSPIRE-AVR [22] (referred as INSPIRE) contains 40 optic disc-centered images with resolution 2392 \(\times \) 2048. A/V labels for the vessel centerlines are provided by Dashtbozorg et al. [9]. The second dataset consists of 45 optic disc-centered images with size of 3744\(\,\times \) 3744, acquired in the Ophthalmology Department of the Academic Hospital Maastricht (AZM) in the Netherlands. These images were captured by a NIDEK AFC-230 non-mydriatic auto fundus camera (referred as NIDEK), and the A/V labels of the vessel centerlines were provided by an expert using the “NeuronJ” software [23]. The third dataset is the VICAVR dataset [24] (referred as VICAVR) containing 58 images. From this dataset, the four images with different resolutions compared to the dataset description are discarded, and the remained 54 images with size 768 \(\times \) 576 are used. The pixel coordinates with A/V labeled are provided by three different experts, while we used the ones from expert 1 as reference.
For the INSPIRE dataset, half of the images are used for training and the rest are used for testing. For the NIDEK dataset, 25 images are used for training and 20 images are used for testing. For the VICAVR dataset, since the amount of ground truth is much less than the previous two datasets, we apply a 5-fold cross-validation to examine the features. For every vessel pixel, we extract the raw RGB, HSB and Lab color intensities. Then for each color intensity, we compute the normalized intensity using the method proposed in [18] and our reflection features including \(\overline{r_b}^{-1}\), \(\overline{r_v}^{-1}\), \(\frac{\overline{r_b}}{\overline{r_v}}\) and \(\frac{\overline{r_v}}{\overline{r_b}}\). For every pixel in total 54 (9 \(\times \) 6) features (see Table 1) are extracted. These features are validated by calculating the accuracy of a supervised linear discriminate analysis (LDA) classifier , as it is a simple technique with good performance on pixel-wise artery/vein classification [9, 13]:
where TP, TN, FP and FN represent the true positive, true negative, false positive and false negative, respectively, given by the confusion matrix of the classifier. The decision boundary of the classifier is set to 0.5 in all experiments. Due to the variation among different images, we apply the following normalization to correct the bias shifting for the feature values:
where \(f_v\), \( \mu (f_v) \) and \(\sigma (f_v)\) are the original feature obtained from one image and the corresponding mean value and standard deviation, and thus, \( \widetilde{f_v} \) is the normalized feature with zero mean and unit standard deviation.
In Table 1, we compare the pixel-wise classification accuracy of the original \(I_r\) and the normalized \(I_n\) intensity of the RGB, HSB and Lab channels with our proposed reflection features on the INSPIRE, NIDEK and VICAVR datasets. Table 2 shows the pixel-wise accuracy of using the normalized intensity combined with the four reflection features for each color channel. Moreover, we measure the performance of the segment-wise classification with the LDA using the combined feature sets. First for each pixel (x, y), the probability value of being an artery \(P_{a}(x,y)\) is obtained using the pixel-wise classification. Afterward, the type of each vessel segment is determined by calculating the average of probability values \(\overline{P_{a}}\) of the pixels belonging to the same segment. If \(\overline{P_{a}}\) is higher than 0.5, the vessel segment is labeled as an artery and otherwise it is labeled as a vein. Finally, the A/V label of segment is used to update the label of pixels. The last column of Table 2 shows the accuracy of using the combination of normalized intensities and the four reflection features. In Table 3, we compare the performance obtained using both the normalized and the reflection features with the most recent works on retinal artery/vein classification. We discuss the comparison in the next section.
4 Discussion
The validation on three datasets shows that using an individual raw color intensity can hardly classify the pixels as artery and vein, since the accuracies are mostly around 50%. It implies that the intensities, with the effect of luminosity variation, have no discrimination between arteries and veins. When the luminosity factor is eliminated from the reflection–illumination model and the nonlinear histogram transformation is avoided, the accuracy increases. On the INSPIRE dataset, \(\overline{r_b}^{-1}\) and \(\frac{\overline{r_b}}{\overline{r_v}}\) features of both red and brightness channels improve the classification accuracy by about 20%. Moreover, these two features computed on the L channel improve the accuracy by 14%. On the other hand, we can notice that the accuracy of \(\overline{r_v}^{-1}\) computed over all the channels is still less than 60%. These results are anticipated because the feature takes the ratio between the vascular pixel and the local pixel inside the sliding window, so if the center of the window is placed on a vessel, \(\overline{r_v}^{-1}\) is always approximately equal to 1 giving no discrimination between arteries and veins.
Additionally, similar results are found in the NIDEK dataset. As we can see in Table 1, the raw intensities can hardly discriminate arteries from veins, while the proposed features still help improving the performance. The accuracy of using \(\overline{r_b}^{-1}\) of both red and brightness increases to 74.5%, and \(\frac{\overline{r_b}}{\overline{r_v}}\) increases to 72.1%. The results of L and b channels increase to 73.2 and 70.8% for \(\overline{r_b}^{-1}\) and 72.1 and 69.7% for \(\frac{\overline{r_b}}{\overline{r_v}}\). Figure 3 shows the histogram of raw red intensity, corresponding \(\overline{r_b}^{-1}\), \(\overline{r_v}^{-1}\) and \(\frac{\overline{r_b}}{\overline{r_v}}\) for all pixels of the 45 NIDEK images. As we can see from the plots, compared with the raw red intensity, the reflection features, \( \overline{r_b}^{-1}\) and \( \frac{\overline{r_b}}{\overline{r_v}} \), provide better separations on pixels of arteries and veins.
What is more, in Fig. 4, we show four patches taken from different NIDEK images with their corresponding A/V labeling, the pixel-wise classification of using nine raw intensities (third row), nine normalized intensities (fourth row), nine \(\overline{r_b}^{-1}\) features (fifth row) and the combination of the normalized and reflection features (sixth row). As we can see from the results, the classification of using raw intensities is highly affected by the shadow of the images. The normalized intensities avoid the effect of illumination variation, while this involves undesired histogram shifting. This effect is significant when training a classifier with a large volume of training set.
Our proposed reflection features not only eliminate the luminosity effect, but also avoid the histogram shifting. Thus a more robust classifier is trained, as we can see from the 5th and 6th rows in Fig. 4.
Comparison of A/V pixel-wise classifications by using different feature subsets. First row: small patches taken from the test images of the NIDEK dataset; second row: the A/V labels that are used as reference; third row: pixel-wise classifications using nine raw intensities; fourth row: pixel-wise classifications using nine normalized intensities using the normalization method by [18]; fifth row: pixel-wise classifications of using the combination of reflection features \(\overline{r_b}^{-1}\) computed based on each color channels; last row: pixel-wise classifications using total 45 features including all the normalized intensities and the reflection features
Comparison of A/V pixel-wise and segment-wise classifications of using different feature subsets. a: the original patch. f: the A/V labeling. b–e: the pixel-wise classification of using raw intensities, normalized intensities, proposed reflection features and the combination of normalized intensities and reflection features. g–j: the corresponding segment-wise classification, where the label of each segment is determined be averaging the label of pixels of it. Yellow color represents a wrongly classified vessel segment. a Raw patch, b \( I_{r} \), c \(I_n\), d reflection features, e \(I_n\) and reflection features, f Ground truth, g \( I_{r} \), h \(I_n\)(i)reflection features, (j)\(I_n\) and reflection features (color figure online)
Beside the comparison with pixel-wise classification, Fig. 5 shows the segment-wise classification of using the raw intensities, the normalized intensities, the reflection features and the combination of normalized and reflection features. As we can see from the patches, a better pixel-wise classification yields a better segment-wise classification. It means that a contextual-based A/V classification approach can still be improved by using a better pixel-wise classification.
In the VICAVR dataset, the reflection features also outperform the raw and normalized intensities. Specifically, the accuracy of \(\overline{r_b}^{-1}\) computed on the green and hue channel reaches 82.9 and 80.6%. The \(\frac{\overline{r_b}}{\overline{r_v}}\) computed on these two intensities has 84.9 and 82.5% accuracy, respectively. The accuracy of these two reflection features computed on L and b channels is relatively low, but still better than the corresponding raw and normalized values.
Table 2 shows the accuracy of LDA classifier using the combination of the normalized intensities with the four reflection features for every color channel separately. Beside the ones that are not discriminative at all, the combination of features generally yields higher accuracy than using the individual ones. The last column shows the performance of joining all normalized intensities with the reflection features of all channels. As we can see, the A/V classification gets further improved among all datasets, where we achieve 79.3, 77.3 and 87.6% accuracy with using only local intensities as features.
Moreover, we apply the segment-wise classification for all datasets, which can be considered as using simple contextual information to improve the result of pixel-wise classification. As we can see in the last column of Table 2, we obtained the best A/V separation accuracy. In the INSPIRE and NIDEK datasets, it achieves the accuracy of 85.1 and 86.9%, respectively, when all the features are used. For the VICAVR, the accuracy increases from 87.6 to 90.6% (Fig. 6).
The results in Table 2 suggest that using the combination of the proposed reflection features and the traditional normalized intensities yields a better classification than using each of them alone. To investigate the relevant contribution of the features to the final classification, we conduct a 100-rounds greedy forward feature selection on the 54 features using the INSPIRE dataset. At each round, the centerline pixels of the 40 images are randomly assigned to ten groups, and then a 10-fold cross-validation is used to validate the improvement of adding each feature to the feature subset. The number of times that each feature being selected is counted and illustrated in Fig. 6. As we can see from the polar plot, 13 features get selected more than 75 times out of 100, which includes one raw intensity, four normalized intensities and eight reflection features: \(\overline{r_b}^{-1}\) on the red, green, blue and a channels, \(\frac{\overline{r_b}}{\overline{r_v}}\) on the brightness channel and \(\frac{\overline{r_v}}{\overline{r_b}}\) on the green, brightness and a channels. The feature selection result implies that these eight proposed reflection features have robust predictive power on artery/vein discrimination in combination with other traditional features. It benefits future studies as fewer features need to be extracted with no degradation in performance.
Polar plot for a 100-rounds greedy forward feature selection result on the 54 features using the INSPIRE dataset. Different colors represent different categories of the features including the original intensities, the normalized intensities and the four proposed reflection features (color figure online)
In Fig. 7, we plot the ROC curves for the three datasets. In this figure, the blue curves represent the feature subset of all raw intensities. The red curves are all normalized intensities. The green curves are all reflection features, and the purple curves indicate the combination of normalized intensities and the reflection features. As we compare the ROC curves with respect to different datasets, the reflection features outperform the conventional normalized intensities, which reach the AUC of 0.87, 0.84 and 0.95 for the INSPIRE, NIDEK and VICAVR datasets, respectively. We also observe that joining the normalized features with the reflection features gives small improvements, where the AUC increment for the purple curves compared to the green curves is less than 0.01.
In Table 3, we show a comparison between using the proposed features and the most recent methods on the classification performance of vessel centerline pixels. On the INSPIRE dataset, after applying the voting procedure as described in Sect. 3, we achieved an accuracy of 85.1% and an AUC of 0.87. The AUC value is higher than the value of 0.84 obtained by Niemeijer et al. [13], where the same segment-wise classification procedure was used. Our achieved accuracy of 85.1% is slightly higher than the result (84.9%) reported by Dashtbozorg et al. [9], but lower than the result (90.9%) reported by Estrada et al. [12]. Note that both techniques are based on graph analysis, which exploit branching and crossing patterns to build the whole vascular network for the final pixel classification. On the VICAVR dataset, we obtain an accuracy of 90.6%, which is better than the values achieved by Vazquez et al. [25] (88.80%) and Dashtbozorg et al. [9] (89.80%) on the same dataset. The table implies that the combination of the proposed features and the graph-based techniques may lead to a better performance.
However, the proposed reflection features have several limitations compared to the conventional luminosity normalization methods. First of all, the procedure for solving eq. 13 takes longer time than the traditional methods, especially for images with large resolution, where more centerline pixels are taken into account. Our method needs to find the solution pixel by pixel, while the traditional ones are convolution based. Therefore, it is not ready yet for automatic A/V classification large-scale study. This limitation can be solved by introducing parallel computing and using a precomputed lookup table for eq. 13 in future applications. Secondly, in recent works, features like the vessel intensity profile and intensity distribution within a certain neighborhood [9, 13, 26] are used, while in this paper, we only examine and compare the local values of pixel. It is interesting for future work to look at the reflection properties along one vessel segment or within a small neighborhood.
5 Conclusion
In this paper, we describe how to cancel the effect of luminosity variation on retinal arteries and veins separation. To solve this problem, we proposed four new features that avoid the affect of image lightness inhomogeneity. Moreover, the features compute the relation between the lightness reflection of vessel pixels and background pixels, and thus, the tissue lightness reflection properties of arteries and veins can be better discriminated. We tested our features on three datasets. The results show that the features outperform the traditional illumination normalization methods, which have been widely used in the recently proposed A/V classification approaches. Furthermore, the accuracy of using the introduced features with a segment-wise classification is comparable with recent works, which rely on using the sub/full vascular tree to improve the artery/vein separation. Therefore, we believe that our proposed features combined with advanced graph-based methods will achieve superior performance on retinal artery/vein classification.
References
Rasmussen, M., Broe, R., Frydkjaer-Olsen, U., Olsen, B., Mortensen, H., Peto, T., Grauslund, J.: Retinal vascular geometry and its association to microvascular complications in patients with type 1 diabetes: the Danish cohort of pediatric diabetes 1987 (dcpd1987). Graefe’s Arch. Clin. Exp. Ophthalmol. 255(2) pp. 293–299 (2016)
Cheng, S.M., Lee, Y.F., Ong, C., Yap, Z.L., Tsai, A., Mohla, A., Nongpiur, M.E., Aung, T., Perera, S.A.: Inter-eye comparison of retinal oximetry and vessel caliber between eyes with asymmetrical glaucoma severity in different glaucoma subtypes. Clin. Ophthalmol. (Auckland, NZ) 10, pp. 1315–1321 (2016)
Seidelmann, S.B., Claggett, B., Bravo, P.E., Gupta, A., Farhad, H., Klein, B.E., Klein, R., Di Carli, M.F., Solomon, S.D.: Retinal vessel calibers in predicting long-term cardiovascular outcomes: The atherosclerosis risk in communities study. Circulation 136(4), pp. CIRCULATIONAHA–116 (2016)
Huang, F., Dashtbozorg, B., Zhang, J., Bekkers, E.J., Abbasi-Sureshjani, S., Berendschot, T., ter Haar Romeny, B.M.: Reliability of using retinal vascular fractal dimension as a biomarker in the diabetic retinopathy detection. J. Ophthalmol. 2016, pp. 1–13 (2016)
Bekkers, E.J., Zhang, J., Duits, R., ter Haar Romeny, B.M.: Curvature based biomarkers for diabetic retinopathy via exponential curve fits in SE(2). In: Proceedings of the Ophthalmic Medical Image Analysis Second International Workshop, OMIA 2015, held in Conjunction with MICCAI 2015, pp. 113–120. Iowa Research Online (2015)
Dashtbozorg, B., Mendonça, A.M., Penas, S., Campilho, A.: Retinacad, a system for the assessment of retinal vascular changes. In: 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, pp. 6328–6331. IEEE (2014)
ter HaarRomeny, B.M., Bekkers, E.J., Zhang, J., Abbasi-Sureshjani, S., Huang, F., Duits, R., Dashtbozorg, B., Berendschot, T., Smit-Ockeloen, I., Eppenhof, K.A.J., Feng, J., Hannink, J., Schouten, J., Tong, M., Wu, H., van Triest, H.W., Zhu, S., Chen, D., He, W., Xu, L., Han, P., Kang, Y.: Brain-inspired algorithms for retinal image analysis. Mach. Vis. Appl. 255(2), pp. 293–299 (2016)
Flammer, J., Konieczka, K.: Retinal venous pressure: the role of endothelin. EPMA J. 6(21), 1--12 (2015)
Dashtbozorg, B., Mendonça, A.M., Campilho, A.: An automatic graph-based approach for artery/vein classification in retinal images. IEEE Trans. Image Process. 23(3), pp. 1073–1083 (2014)
Hu, Q., Abràmoff, M.D., Garvin, M.K.: Automated construction of arterial and venous trees in retinal images. J. Med. Imaging 2(4), 1–6 (2015)
Joshi, V.S., Reinhardt, J.M., Garvin, M.K., Abramoff, M.D.: Automated method for identification and artery-venous classification of vessel trees in retinal vessel networks. PloS One 9(2), 1–12 (2014)
Estrada, R., Allingham, M.J., Mettu, P.S., Cousins, S.W., Tomasi, C., Farsiu, S.: Retinal artery-vein classification via topology estimation. IEEE Trans. Med. Imaging 34(12), 2518–2534 (2015)
Niemeijer, M., Xu, X., Dumitrescu, A.V., Gupta, P., van Ginneken, B., Folk, J.C., Abramoff, M.D.: Automated measurement of the arteriolar-to-venular width ratio in digital color fundus photographs. IEEE Trans. Med. Imaging 30(11), 1941–1950 (2011)
Vázquez, S., Barreira, N., Penedo, M.G., Saez, M., Pose-Reino, A.: Using retinex image enhancement to improve the artery/vein classification in retinal images. In: International Conference Image Analysis and Recognition, pp. 50–59 (2010)
Dashtbozorg, B., Mendonça, A.M., Campilho, A.: Automatic classification of retinal vessels using structural and intensity information. In: Iberian Conference on Pattern Recognition and Image Analysis, pp. 600–607 (2013)
Yanikoglu, B., Aptoula, E., Tirkaz, C.: Automatic plant identification from photographs. Mach. Vis. Appl. 25(6), 1369–1383 (2014)
Sinha, A., Banerji, S., Liu, C.: New color GPHOG descriptors for object and scene image classification. Mach. Vis. Appl. 25(6), 361–375 (2014)
Foracchia, M., Grisan, E., Ruggeri, A.: Luminosity and contrast normalization in retinal images. Med. Image Anal. 9(3), 179–190 (2005)
Varnousfaderani, E.S., Yousefi, S., Belghith, A., Goldbaum, M.H.: Luminosity and contrast normalization in color retinal images based on standard reference image. In: SPIE Medical Imaging, pp. 1–6 (2016)
Mustafa, W.A., Yazid, H., Yaacob, S.B.: Illumination correction of retinal images using superimpose low pass and gaussian filtering. In: 2nd International Conference on Biomedical Engineering, pp. 1–4 (2015)
Jobson, D.J., Rahman, Z.U., Woodell, G.A.: A multiscale retinex for bridging the gap between color images and the human observation of scenes. IEEE Trans. Image Process. 6(7), 965–976 (1997)
Niemeijer, M., Xu, X., Dumitrescu, A., Gupta, P., van Ginneken, B., Folk, J., Abramoff, M.: INSPIRE-AVR: Iowa normative set for processing images of the retina-artery vein ratio. http://webeye.ophth.uiowa.edu/component/k2/item/270 (2011)
Meijering, E., Jacob, M., Sarria, J.C., Steiner, P., Hirling, H., Unser, M.: Design and validation of a tool for neurite tracing and analysis in fluorescence microscopy images. Cytom. Part A 58(2), 167–176 (2004)
VICAVR: VARPA images for the computation of the arterio/venular ratio. http://www.varpa.es/vicavr.html (2010)
Vazquez, S., Cancela, B., Barreira, N., Penedo, M.G., Saez, M.: On the automatic computation of the arterio-venous ratio in retinal images: Using minimal paths for the artery/vein classification. In: 2010 International Conference on Digital Image Computing: Techniques and Applications (DICTA), pp. 599–604. IEEE (2010)
Zamperini, A., Giachetti, A., Trucco, E., Chin, K.: Effective features for artery-vein classification in digital fundus images. In: Computer-Based Medical Systems (CBMS), 2012 In: 25th International Symposium on, pp. 1–6. IEEE (2012)
Acknowledgements
The work is part of the Hé Programme of Innovation Cooperation, which is financed by the Netherlands Organization for Scientific Research (NWO), dossier No. 629.001.003.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Huang, F., Dashtbozorg, B. & Romeny, B.M.t.H. Artery/vein classification using reflection features in retina fundus images. Machine Vision and Applications 29, 23–34 (2018). https://doi.org/10.1007/s00138-017-0867-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00138-017-0867-x