SAPS 3—From evaluation of the patient to evaluation of the intensive care unit. Part 2: Development of a prognostic model for hospital mortality at ICU admission

Abstract

Objective

To develop a model to assess severity of illness and predict vital status at hospital discharge based on ICU admission data.

Design

Prospective multicentre, multinational cohort study.

Patients and setting

A total of 16,784 patients consecutively admitted to 303 intensive care units from 14 October to 15 December 2002.

Measurements and results

ICU admission data (recorded within ±1 h) were used, describing: prior chronic conditions and diseases; circumstances related to and physiologic derangement at ICU admission. Selection of variables for inclusion into the model used different complementary strategies. For cross-validation, the model-building procedure was run five times, using randomly selected four fifths of the sample as a development- and the remaining fifth as validation-set. Logistic regression methods were then used to reduce complexity of the model. Final estimates of regression coefficients were determined by use of multilevel logistic regression. Variables selection and weighting were further checked by bootstraping (at patient level and at ICU level). Twenty variables were selected for the final model, which exhibited good discrimination (aROC curve 0.848), without major differences across patient typologies. Calibration was also satisfactory (Hosmer-Lemeshow goodness-of-fit test Ĥ=10.56, p=0.39, Ĉ=14.29, p=0.16). Customised equations for major areas of the world were computed and demonstrate a good overall goodness-of-fit.

Conclusions

The SAPS 3 admission score is able to predict vital status at hospital discharge with use of data recorded at ICU admission. Furthermore, SAPS 3 conceptually dissociates evaluation of the individual patient from evaluation of the ICU and thus allows them to be assessed at their respective reference levels.

Introduction

One of the crucial steps in the evaluation of risk-adjusted outcomes is the choice of the reference database for estimating adequate reference lines for the analyzed variables. For the SAPS 3 to reflect the standard of practices and outcome in intensive care at the beginning of the 21st century, we decided to collect data from a large sample of intensive care units (ICUs) worldwide. Other models have restricted data collection to large ICUs in Europe or North America—SAPS II [1], MPM II [2], APACHE II [3] and APACHE III [4], a strategy that minimizes the heterogeneity of the sample but restricts the generalization of the results.

At the statistical level, there is also a need for change, in order to take into account the hierarchic nature of our data [5, 6]. Current general outcome prediction models do not consider the existence of clinical and nonclinical factors, aggregated at the ICU level, that can have an important impact on prognosis. Instead, they assume that these factors are either not important or are randomly distributed throughout large samples and that the variation between ICUs is small. This assumption is not likely to be borne out at the ICU level for either nonclinical factors (e.g. organization and management, organizational culture) or clinical factors (e.g. clinical management, diagnostic and therapeutic strategies). If the variation between ICUs is not negligible, it will compromise the stability of the equations used to compute predicted mortality. Furthermore, the published models consider the relation between performance and severity of illness to be constant, and that may not be the case, since performance can vary within ICUs according to the severity of illness of the patients [7, 8]. To overcome this problem, we chose to adopt a new strategy for the development of the SAPS 3 score and to apply statistical modelling techniques that control for the clustering of patients within ICUs instead of assuming the independence of observations. Conceptually, the SAPS 3 admission core comprises the following parts:

First, the SAPS 3 ADMISSION SCORE, represented by the arithmetic sum of three subscores, or boxes:

• Box I: What we know about the patient characteristics before ICU admission: age, previous health status, co-morbidities, location before ICU admission, length of stay in the hospital before ICU admission, and use of major therapeutic options before ICU admission.

• Box II: What we know about the circumstances of ICU admission: reason(s) for ICU admission, anatomic site of surgery (if applicable), planned or unplanned ICU admission, surgical status and infection at ICU admission.

• Box III: What we know about the presence and degree of physiologic derangement at ICU admission (within 1 h before or after admission).

Second, the SAPS 3 PROBABILITY OF DEATH during a certain period of time (in the case of the main model, the probability of death at hospital discharge).

Given our objective of evaluating not only individual patient outcome but also the effectiveness of ICU practices, we focused the model on data available at ICU admission or shortly thereafter. This model will be completely open and available free of any direct or indirect charges to the scientific community.

Methods and statistical analysis

Primary variable selection

Based on the SAPS 3 Hospital Outcome Cohort as described in Part 1 of this report, continuous predictive variables were categorized in mutually exclusive categories based on smoothed curves such as LOWESS [9], showing the univariate dependence of hospital mortality on the predictive variables. Classes of categorical variables were also collapsed according to their univariate hospital mortality levels using multidimensional tables and clinical judgment as appropriate, depending on the nature of the data. Additively, regression trees (MART) [10] were applied to check the cutoffs.

Missing values were coded as the reference or “normal” category for each variable. When dual data collection was used—maximum and minimum values recorded during a certain time period—missing maximum values of a variable were replaced by the minimum, if documented, and vice versa. Some regression imputations were performed if noticeable correlations to available values could be exploited. For a detailed description of data collection and handling, see Part 1 of this report.

Selection of variables was done according to their association with hospital mortality, together with expert knowledge and definitions used in other severity of illness scoring systems. The objective of using this combination of techniques rather than regression-based criteria alone was to reach a compromise between over-sophistication of the model and knowledge from sources beyond the sample with its specific case mix and ICU characteristics.

Cross validation

For being able to cross-validate the model, we randomly extracted five roughly equal-sized parts based on number of patients from the database, as suggested previously [11]. In a second approach, partitioning was based on ICUs and not on patients. It was thus possible to run the model-building procedure five times in each of the two approaches, each time taking four parts of the sample as a development set and the remaining one as the validation set. This allowed to estimate the variability of prediction resulting from the construction process of the prognostic score. A further check of the stability of the predictions was made by partitioning the sample according to major patient characteristics, such as surgical status and infection status.

The quality of predictions in the validation sets was assessed by looking at the goodness-of-fit in terms of the p values for the Hosmer-Lemeshow tests Ĉ and Ĥ [13] and the discriminative capability of the models by the use of the area under the receiver operating characteristic (aROC) curve [14, 15]. Another criterion to judge the appropriateness of the model was the fit in certain subsamples, defined according to major patient typologies [16].

Reducing model complexity

To reduce the complexity of the model classes, we concentrated on logistic regression. In the first step a stepwise logistic regression was used to identify the significant predictors in each of the five subsamples. A threshold of 0.01 for the p value was generally applied for inclusion in the model to separate irrelevant predictors [12]. At this stage we also evaluated if interactions among these predictors would influence results. Interactions, however, did not make a valuable contribution for the prediction.

Significant predictors (n=70) were in a second step entered into a logistic regression model. The criterion for a predictor to enter the model was homogeneity across the five model-building processes: in principle, predictors should enter the model in all five development sets, but depending on the frequency of the predictor in the samples, the magnitude of the effect, and medical reasoning, some predictors were included if they appeared in the model in at least three subsamples. An example is the presence of Acquired Immunodeficiency Syndrome (AIDS): it was selected as a comorbidity in only 81 patients (0.48%), but the mortality—without controlling for other variables—in these patients was 42%. By taking all the above steps to identify the set of predictors, although deliberately not using any formal numeric criterion, we reduced the complexity of the model to minimize the amount of overfitting: This process resulted in 61 item classes (representing 20 variables) remaining in the final model.

Using the parameter estimates from the logistic regression as starting values, a multilevel model was applied in the next step, using patient characteristics as fixed effects and ICUs as a random effect. Estimates were again calculated for the five development sets (for both, patient and ICU -based development subsamples).

At this stage it was checked if rounding of coefficients (which allows for an easier manual computation of the score) would influence results, which was found not to be the case. Consequently, this was the approach chosen for the final construction of the SAPS 3 admission score sheet.

The stability of the processes of variable selection and reducing complexity was further checked by bootstraping with replacement the total sample 100 times, both at patient level and at ICU level.

Predicting hospital mortality

After this step was completed, a shrinking power transformation was applied. This procedure uses log-transformation of the score to reduce the influence of extreme score values (outliers) on the mortality prediction. For this purpose, the SAPS 3 score and the transformed log (SAPS 3 + g) scores were used to predict hospital mortality. Conventional logistic regression was used in the evaluation of this step because of convergence problems for the corresponding multilevel model in a few subsamples. The best shrinkage model then was selected (excluding the trivial model with the SAPS 3 score as the single predictor) by checking which of the terms in the model contributed best to the prediction and was moreover stable over the respective validation sets and specific subsamples. This procedure was applied on both, patient and ICU -based subsamples.

After finishing these steps of cross-validation, the final estimates for the selected predictors of the SAPS 3 score as well as the selected shrinkage procedure were then calculated from the total sample of patients.

To arrive at the customised models for each major geographic region, specific customised equations were calculated, relating, by logistic regression, the transformed log (SAPS 3 + g) admission scores computed as described above to the vital status at hospital discharge. This process allows both the intercept and the slope of the curve relating the SAPS 3 admission score to change across different regions. The goodness-of-fit of these equations was evaluated by means of the same methodology used for the global sample.

SAS for Windows, version 8.02 (SAS Institute Inc., Cary, NC, USA) and MLwiN version 1.10.0007 (Centre for Multilevel Modelling, Institute of Education, London, UK) and the R Software Package (http://www.r-project.org) were used for the development of the model.

Results

Based on the methodology described, 20 variables were selected for the SAPS 3 admission score (Tables 1 and 2):

• Five variables for evaluating Box I: age, co-morbidities, use of vasoactive drugs before ICU admission, intrahospital location before ICU admission, and length of stay in the hospital before ICU admission;

• Five variables for evaluating Box II: reason(s) for ICU admission, planned/unplanned ICU admission, surgical status at ICU admission, anatomic site of surgery, and presence of infection at ICU admission and place acquired;

• Ten variables for evaluating Box III: lowest estimated Glasgow coma scale, highest heart rate, lowest systolic blood pressure, highest bilirubine, highest body temperature, highest creatinine, highest leukocytes, lowest platelets, lowest hydrogen ion concentration (pH), and ventilatory support and oxygenation.

Table 1 SAPS 3 admission scoresheet—Part 1

Table 2 SAPS 3 admission scoresheet – Part 2

An estimation of the variability of the coefficients in the overall sample and in the five disjoint subsamples is given in Table E8 of the Electronic Supplementary Material (ESM), together with their respective coefficients (unrounded and rounded) and p values. The SAPS 3 admission score can thus, in theory, vary from a minimum of 0 points to a maximum of 217 points. The distribution of the SAPS 3 admission score in our sample is presented in Fig. 1. The minimum value observed was 5, and the maximum value was 124, with a mean of 49.9±16.6 (mean ± SD) and a median of 48 (38–60). The highest explanatory power came from Box I, with Box II and Box III being less important for the outcome; the three boxes represent 50%, 22.5% and 27.5%, respectively, of the total Nagelkerke’s R-Square. The relationship between the SAPS 3 and vital status at hospital discharge is given by the equation:

Logit = −32.6659 +ln(SAPS 3 score +20.5958) ×7.3068

and the probability of mortality by the equation:

Probability of death = e^logit/(1+e^logit).

Fig. 1

Distribution of the SAPS 3 admission score in the SAPS 3 database

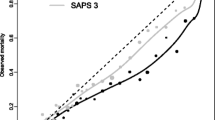
The relationship between the SAPS 3 admission score and the respective probability of death in the hospital is described in Fig. 2. Overall, no combined discrepancy between observed and expected outcomes across all of the strata was outside sampling variability as demonstrated a Hosmer-Lemeshow goodness-of-fit test Ĥ of 10.56 (p=0.39) and a Hosmer-Lemeshow goodness-of-fit test Ĉ of 14.29 (p=0.16) (Figs. 3, 4 and Table E9, ESM). The overall discriminatory capability of the model, as measured by aROC curve, was 0.848. The goodness-of-fit according to major patient typologies (surgical status, trauma, and infection) can be found in Table 3. Calibration and discrimination presented differences across different geographic areas: the best predictive results were achieved in patients from Northern Europe (observed-to-expected [O/E] mortality ratio 0.96 [0.83–1.09]) and the worst predictive results were obtained in patients from Central and South America (O/E mortality ratio, 1.30 [1.23–1.37]); see also Table 4 and Fig. 5 and Appendix B in the ESM.

Fig. 2

Relationship between the SAPS 3 admission score and the respective probabilities of hospital mortality

Fig. 3

Hosmer-Lemeshow goodness-of-fit test Ĉ in the overall sample. Predicted risk of hospital death, observed hospital mortality rate, and the corresponding number of patients per decile are shown. Columns: Number of patients; squares: mean SAPS 3-predicted mortality per decile; circles: mean observed mortality per decile

Fig. 4

Hosmer-Lemeshow goodness-of-fit test Ĥ in the overall sample. Predicted risk of hospital death, observed hospital mortaliy rate, and the corresponding number of patients per decile are shown. Columns: Number of patients; squares: mean SAPS 3-predicted mortality per decile; circles: mean observed mortality per decile

Table 3 Performance of the model across major patient typologies

Table 4 Performance of the model in the global sample and in different geographic areas

Fig. 5

Observed-to-expected (O/E) mortality ratios by region. Observed-to-expected (O/E) mortality ratios are shown by region. Bars indicate 95% confidence intervals

For a more precise estimation of the probability of death in the hospital across the different geographic regions, specific customised equations were calculated (Table 5). This customised approach allows each ICU to choose its own reference line for the prediction of hospital mortality: either the overall SAPS 3 hospital mortality sample or its own regional subsample. This approach can be supplemented in the future by customised equations at the country level if data are available and if a more precise estimation of outcome in a specific setting is needed. The overall goodness-of-fit of these customised equations for each region is presented in Table 5. A complete list of the number of patients and the respective O/E mortality ratios by country, according to the global equation and the regional equations, are presented in Tables E10 and E11 of the ESM, with point estimates varying at the global level from 0.68 (0.56–0.80) to 2.05 (1.27–2.82). Most O/E ratios are close to the identity line, as expected for a stable model.

Table 5 Customized SAPS 3 admission equations for the different geographic areas

Discussion

We have presented the results of a large multicentric, multinational study aimed at updating the SAPS II model. This study was necessary for several reasons. First, the reference line used by SAPS II was derived from a database collected in the early 1990s; since that time, there have been changes in the prevalence of major diseases and in the availability and use of major diagnostic and therapeutic methods that are associated with a shift toward poor calibration of older models such as SAPS II and APACHE III [17, 18]. Second, SAPS II was developed from a database built exclusively from patients in Europe and North America. This sample may not be representative of the case mix and medical practices that constitute the reality of intensive care medicine in the rest of the world (e.g. Australasia or South America), where variability in structures and organization is probably related to outcome [19].

Third, since computation of predicted mortality is based on a reference database, the user should be able to choose between them, i.e., a global database, which provides a broader comparison at the potential cost of less relevance to local conditions, and a regional database, which provides a better comparison with ICUs in geographic proximity but at the cost of losing comparability with ICUs in other parts of the world. A third possibility could be added—a country-representative database—but such a database would raise the problem of whether the ICUs selected were representative of a certain country.

Fourth, the development of computers in recent years has created easy access to strong computational power. One of the implications of this is that it is now possible to develop a new outcome prediction model, based on digital data acquisition and analysis, with minimal differences in definitions and application criteria. These advances were coupled with extensive automatic logical and error-checking capabilities and the availability of data collection manuals online. Moreover, developers of the SAPS 3 model could take advantage of computer-intensive methods of data selection and analysis, such as the use of additive partition trees and logistic regression with random effects. Several new statistical techniques have been used in recent years to allow a more stable prediction of outcome, such as genetic algorithms and artificial neural networks [20, 21], dynamic microsimulation techniques [22], and first- and second-level customization strategies [23–25]. However, the value of these techniques is for the moment limited, usually because they are based on regional databases [24–26] that prevent extrapolation to other settings; moreover, their superiority in even the regional setting still needs to be established.

Finally, the SAPS 3 conceptually dissociates evaluation of the individual patient from evaluation of the ICU. Thus, for individual patient assessment, the system separates the relative contributions to prognosis of (i) chronic health status and previous therapy, (ii) the circumstances related to ICU admission, and (iii) the presence and degree of physiologic dysfunction. It is interesting to note that one half of the predictive power of the model is achieved with Box I, i.e., with the information that is available before ICU admission. The prognostic capabilities of the model can be further improved by 22.5% by using data related to the circumstances of the ICU admission (Box II), and by another 27.5% by the incorporation of physiologic data (Box III). These numbers are different from those published by Knaus et al. [4] but are based on what we have learned in the last years about prognostic determinants in the critically ill patient.

For performance evaluation, several reference lines should be used, with risk-adjusted mortality in different patient typologies and not only O/E mortality ratios at hospital discharge in the overall ICU population [27]. The results of the SAPS 3 study showing that different O/E ratios were observed in different regions of the world should be explored further, since, apart from regional differences in case mix (not taken into account by the model), they can also be related to regional variations in structures and organization of acute medical care, to different lifestyles (e.g., prevalence of obesity, or alcohol and tobacco use) and/or—though less likely—to genetic differences among populations.

We would like to re-emphasize that the model presented here is based exclusively on data (including physiologic data) available within 1 h of ICU admission and calibrated for manual data acquisition; consequently, it should be expected to overestimate mortality when an automatic patient data management system with a high sampling rate is used [28, 29]. Limiting acquisition of physiologic data to the hour of ICU admission should minimise the impact of this factor when compared with models based on the most deranged data from the first 24 h after ICU admission, probably at the expense of a small decrease in the ROC curve, a greater sensitivity to the exact time point at which admission to ICU occurs, and therefore more reliant on the assumption that measured physiology alone (as opposed to changes in physiology) predict outcome. It also allows the prediction of mortality to be done before ICU interventions take place. This gives the SAPS 3 admission model a major advantage over existing systems, such as the SAPS II or the APACHE II and III, since all these systems can be affected by the so-called Boyd and Grounds effect: the occurrence of more abnormal physiologic values during the first 24 h in the ICU, leading to an increase in computed severity of illness and a corresponding increase in predicted mortality. These increases may, however, be due not to a greater intrinsic severity of illness of the patient but to the provision of suboptimal care in the first 24 h of ICU admission, when a stable patient may be allowed to deteriorate [30].

Further studies should be done of factors occurring after ICU admission that influence risk-adjusted mortality. We should keep however in mind that this approach comes with one potential pitfall: a possible decrease in the amount of data available for the computation of the model; also, the shorter time period for data collection can eventually increase the likelihood of missing physiological data and the reliance on the assumption that missing physiological data are normal. This effect should be small, considering the widespread availability of monitoring and point-of-case analysers.

Having demonstrated the internal validity of the SAPS 3 admission model by the extensive use of cross-validation techniques, we should stress that external validation is also necessary. The fact that the overall database was not collected to be representative of the global case-mix (and especially the case-mix of specific regional areas or patient typologies such as specific diseases) should be empirically tested. Furthermore, the rate of deterioration of our estimates over time should be followed by the appropriate use of temporal validation, especially to avoid what Popovich called grade inflation [18].

The SAPS 3 system was developed to be used free of charge by the scientific community; no proprietary information regarding the scientific content is retained. All the coefficients needed for the computation of outcome probabilities are available in the published material. The SAPS 3 can even be computed manually, using a simple scoresheet, although it was designed to be integrated into computerised data acquisition and storage systems that allow the automatic check of the quality of the registered data.

In conclusion, we can say that at the end of this stage of the project, we have been able to overcome some of the problems inherent in current risk-adjustment systems. We have minimized user-dependent problems through the publication of careful, detailed definitions and criteria for data collection [31]. We have also addressed the patient-dependent problems by expanding the reference database and making it more representative of reality, in order to include the maximum possible range of variations for patient-centred variables and resulting patient-centred outcomes. This approach was complemented by the development of specific customised equations for major areas of the world, allowing ICUs to choose a reference line for outcome prediction—the global database or the regional database for their own area.

Users of these models should keep in mind that benchmarking is a process of comparing an ICU with a reference population. The appropriate choice of reference population is difficult, and we cannot simply change it because the observed-to-predicted mortality rate is not the one we want. For this reason, the choice should depend on the objective of the benchmark: more precise estimation will need local or regional equations, developed from a more homogeneous case mix. A generalisable estimation will, on the other hand, need more global equations developed from a more representative case mix.

Last but not least, we have successfully addressed some of the problems of prognostic model development, especially those related to the underlying statistical assumptions for the use of specific methods for selection and weighting of variables and the conceptual development of outcome prediction models. In the future, multi-level modelling with varying slopes (and not just random intercepts) might be able to give a better answer to researchers but for the moment they would make the models to complex to be managed outside a research environment.