Introduction

Porphyry Cu–Mo ± Au deposits provide approximately 75% Cu, 50% Mo, 20% Au of the world’s resources, and significant amounts of Re, Ag, and other metal resources to support societal development (Sillitoe 2010). Porphyry Cu–Mo mineralization was recognized in the late 1960s to early 1970s in the Delamerian Orogen (Hosking 1970; Langsford 1971; Morris 1977), which is predominantly located in the southeast of South Australia (Fig. 1a). The Delamerian Orogen was proximal to an Andean-style convergent subduction belt active from middle Cambrian to early Ordovician along the eastern margin of the Archean-Proterozoic Australian craton (Preiss 2000; Kemp et al. 2009; Cayley 2011; Foden et al. 2020). No economically important porphyry-style deposits have been discovered in this early Paleozoic magmatic arc during the past five decades, largely due to limited exploration activity and deficits in geological understanding of the regional mineral systems. The recent discovery of the Thursday’s Gossan Cu–Mo ± Au deposit, associated with porphyritic intrusions in the adjacent Stavely Arc of Victoria (28.3 Mt at 0.75% Cu and 0.11 g/t Au; Stavely Minerals 2022), has led to renewed attention to explore porphyry-style ore deposits in the Delamerian greenfield province.

Fig. 1
figure 1

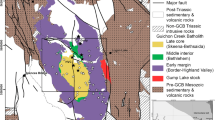
(modified from Gravestock et al. 2012). b-d. Sketch geologic maps for Delamerian porphyry prospects highlighting studied drill hole sites. b. Anabama Hill, adapted from McDonald (1992). c. Netley Hill, adapted from Hosking (1970). d. Bendigo, adapted from Langsford (1973). Inset showing the Orogenic belts of eastern Australia after Foden et al. (2020). Legend for b, c, and d are same as that included in Fig. d

a. Simplified geologic map of the Delamerian Orogen in South Australia.

Full size image

During the past decades, increasing interest has been paid to in situ chemical analysis of magmatic minerals, including zircon and apatite, and its application to identifying the presence of, or potential for porphyry-style mineralization (e.g., Ballard et al. 2002; Belousova et al. 2006; Dilles et al. 2015; Bouzari et al. 2016; Lu et al. 2016, 2019; Mao et al. 2016; Nathwani et al. 2020; Parra-Avila et al. 2022). These minerals are defined as porphyry indicator minerals (Celis et al. 2013; Bouzari et al. 2016; Cooke et al. 2020). Trace and rare earth elements (REEs) in zircon such as Th, U, Y, Ce, Eu, Gd, and Yb, have been found to discriminate the metallogenic fertility of causative magmas genetically related to porphyry mineralization (Ballard et al. 2002; Chelle-Michou et al. 2014; Dilles et al. 2015; Shen et al. 2015; Lu et al. 2016; Lee et al. 2017, 2020; Loader et al. 2017; Nathwani et al. 2021; Paolillo et al. 2022; Parra-Avila et al. 2022). Apatite can directly archive the volatile signatures (e.g., S and Cl) of magmatic systems from which it crystallizes, which can distinguish mineralized intrusions from barren plutons (Chelle‑Michou and Chiaradia 2017; Richards et al. 2017; Zhu et al. 2018; Cao et al. 2021; Xu et al. 2021; Parra-Avila et al. 2022; Xie et al. 2023). Analyses of these minerals can provide crucial information to determine whether studied magmatic suites in a porphyry prospect are hydrous, oxidized, and sulfur-rich – all of which are prerequisites to exsolving fluids for extensive hydrothermal alteration and porphyry-style mineralization (Richards 2003, 2015; Seedorff et al. 2005; Sillitoe 2010; Cooke et al. 2014). Therefore, zircon and/or apatite chemistry are regarded as robust tools utilized on a district- to regional-scale at an early exploration stage, with the aim to target intermediate to felsic complexes or individual intrusions within such complexes (Bouzari et al. 2016; Loader et al. 2017; Cooke et al. 2020; Xing et al. 2020; Li et al. 2021; Nathwani et al. 2021; Parra-Avila et al. 2022), which are likely to host porphyry Cu–Mo ± Au ore deposits.

Geologic context

The Delamerian Orogen is the westernmost and earliest episode of the Tasmanides accretionary orogenic systems (~ 520–230 Ma; Fig. 1a) that form the eastern third of the Australian continent (Foster and Gray 2000; Preiss 2000; Kemp et al. 2009; Cayley 2011; Johnson et al. 2016; Foden et al. 2020). The orogen is best exposed in South Australia, known as the Adelaide Fold Belt, and extends eastwards to the Grampians-Stavely Belt in western Victoria (Fig. 1a; Foster and Gray 2000; Cayley 2011; Schofield 2018), and northeast to Loch Lilly-Kars-Koonenberry Belt in New South Wales (Fig. 1a; Greenfield et al. 2011; Johnson et al. 2016).

The Delamerian Orogen comprises Neoproterozoic to Cambrian sedimentary rock packages, with lesser intercalated volcanic units, which formed during successive phases of rift and sag events at the margin of the Archean-Proterozoic crust of southern Australia (Preiss 2000; Foden et al. 2006, 2020; Robertson et al. 2015; Lloyd et al. 2020). The Cambrian volcano-sedimentary rocks include the Normanville Group and succeeding Kanmantoo Group that were deposited in a deepening rift system on the eastern edge of the Neoproterozoic (Adelaidean) rift system (Fig. 1a; Preiss 2000; Foden et al. 2002, 2020; Betts et al. 2018; Lloyd et al. 2020, 2022). These Neoproterozoic to Cambrian rocks experienced multiple episodes of deformation and greenschist to amphibolite facies metamorphism from the middle to late Cambrian (i.e., the Delamerian Orogeny, 514–490 Ma; Foden et al. 2006), as a result of initial subduction of the Pacific oceanic crust and the imbrication and thickening of the Adelaide Superbasin during outboard volcanic arc development (Cayley 2011; Greenfield et al. 2011; Betts et al. 2018; Robertson et al. 2015; Schofield 2018; Foden et al. 2020). Syn-tectonic S- and I-type plutons and granitic sheets (~ 514–490 Ma) intruded the Neoproterozoic and Cambrian rocks during the early phases of the Delamerian Orogeny, while largely A-type granitic bodies were intruded late and subsequent to the main orogenic activity (490–470 Ma; Turner et al. 1992; Foden et al. 2006, 2020).

Porphyry and skarn Cu–Mo ± Au prospects recognized in the Delamerian Orogen (Fig. 1) include Anabama Hill, Blue Rose, Netley Hill, Cronje Dam, Bendigo, Colebatch, and Wild Horse in South Australia (Hosking 1970; Langsford 1971; Morris 1977). This porphyry Cu belt stretches southeast towards the Stavely Arc in Victoria, evidenced by the discovery of the Thursday’s Gossan and Junction porphyry Cu–Au deposits associated with porphyritic stocks from 505 to 498 Ma (Duncan et al. 2018; Stavely Minerals 2022). As opposed to Cambrian counterparts, Baatar et al. (2020) argued that Devonian monzonitic porphyries in the Loch Lilly-Kars Belt of New South Wales have the greater metallogenic potential for porphyry mineralization.

Detailed descriptions of hydrothermal alteration, vein stages, and mineralization regarding these prospects can be found in Hong et al. (2023), and concise summaries of related intrusive rocks, mineralization ages, hydrothermal alteration, and sulfide associations are listed in ESM2 Table S1. Granodiorite batholiths are the dominated intrusive phases, and diorite porphyry, monzonite, dacite porphyry and/or granite host sulfide mineralization and hydrothermal alteration (Fig. 1b-d). These intrusions have zircon U-Pb ages ranging from 490 to 465 Ma (Hong et al. 2023). Molybdenite Re-Os chronology revealed two porphyry Cu-Mo mineralization events at ca. 480 Ma and 470–460 Ma, respectively, with the later prevailing at Anabama Hill, Netley Hill, and Bendigo (Hong et al. 2023). Hydrothermal alteration and mineralization in the Delamerian prospects are comparable to typical porphyry Cu-Mo deposits, with Cu-bearing sulfides being hosted by multiple veins, stockworks, and minor breccias. These prospects are characterized by intense muscovite-quartz-pyrite assemblages (phyllic alteration) that commonly overprint weak to moderate K-feldspar ± biotite alteration (potassic) and chlorite-epidote ± albite alteration (propylitic; Fig. 1b-d). Zircon and apatite crystals were separated from drill core and hand specimen samples for in situ micro-analyses. These rocks include the granodiorite, diorite, monzogranite and dacite porphyry from Anabama Hill, granodiorite, diorite, biotite granite and K-feldspar granite from Netley Hill, and granodiorite, biotite granite and porphyritic diorite from Bendigo prospect, as well as the Colebatch granite.

Analytical techniques

SEM-BSE-CL imaging and EPMA analysis

Zircon and apatite grains were hand-picked from heavy mineral concentrates of crushed granitic rocks under a petrographic microscope. Selected mineral grains were placed on double-sided tape and then set into 2.5-cm diameter epoxy blocks. These mounts were polished using clean sandpaper and polishing cloths down to 1 μm diamond grade. Additional six samples from Anabama Hill and Bendigo were prepared as polished 2.5-cm rock blocks for apatite analyses (see details in ESM A1). In order to reveal internal textures and inclusions within individual grains prior to micro-analyses, cathodoluminescence (CL) and backscatter electron (BSE) images of investigated minerals were collected simultaneously on a Hitachi SU3800 SEM at Adelaide Microscopy in the University of Adelaide. For both minerals, the SEM was operated at voltage of 15 to 20 kV, spot intensity of 80, and sample depth of 10 to 15 mm.

Major element and halogen compositions for apatite were performed on a Cameca SX-Five electron probe microanalyzer (EPMA), equipped with five tunable wavelength-dispersive spectrometers at Adelaide Microscopy. The instrument runs PeakSite v6.2 software for microscope operation, and Probe for EPMA software (distributed by Probe Software Inc.) was used for all data acquisition and processing. The EPMA was operated with a 10-kV excitation voltage, 15–20 nA beam current, and 5-µm beam diameter during the apatite sessions. Analytical elements include Ca, P, Si, Fe, Mn, Na, F, Cl, and S. Oxygen was calculated by stoichiometry, assuming that all Fe was Fe2+. Matrix corrections of Armstrong-Love/Scott w(ρz) and Henke mass absorption coefficients were used for data reduction. Beam damage and alkali element migration in silicate analyses were minimized using a defocused electron beam, in addition to use of the mean atomic number background correction (Donovan et al. 2016) over traditional two-point background interpolation. This reduces the aforementioned effects of beam damage and element migration and their subsequent impact on the quality of analysis. Mobile elements (e.g., Na, F, and Cl) were analyzed first on the detector and the time-dependent intensity correction feature of Probe for EPMA was used, aimed to monitor and review post-analysis. All individual results for major and halogen elements of apatite are presented in Electronic Supplementary Material (ESM) A1.

LA-ICP-MS analysis

Both zircon and apatite trace element analyses were performed at Adelaide Microscopy, using an Agilent 7900x quadrupole ICP-MS with a RESOlution 193 nm ArF excimer laser system. Instrument mass bias and drift were corrected using standard materials analyzed after every 20–30 unknowns. For zircon session, the GJ zircon (Jackson et al. 2004) was used as the primary standard to correct for Pb/U and Pb/Th mass bias, down hole fractionation, and instrument drift, whereas zircons 91,500 and Plesovice were used as secondary standards. NIST610 glass was used as an external standard for trace element analysis (Pearce et al. 1997). Each zircon analysis began with a 30 s blank gas measurement followed by a further 30 s of analysis time when the laser was switched on. Zircons were analyzed with 30 μm spots and NIST610 glass with 43 μm spots, using a repetition rate of 5 Hz and an energy density of approximately 2 J/cm2 (3.5 J/cm2 for NIST610). A flow of He carrier gas (0.38 L/min) carried particles ablated by the laser out of the sample chamber to be mixed with Ar gas (1.01 L/min), before transport to the plasma torch. LA-ICP-MS data reduction was conducted using LADR software (https://norsci.com/ladr). Representative analytical zircon spots with CL images can be referred to Hong et al. (2023).

Zirconium was used as the internal standard with an assumed stoichiometric concentration of 49.29 wt%. 238U/206Pb age outliers apparently above or below the array of a 238U/206Pb age population are explained due to inheritance or Pb loss and thus were removed. Analyses with age discordance > 5% were discarded (discordance = 100 × [(207Pb/235Uage) – (238U/206Pbage)] / [207Pb/235Uage]). Silicon content > 185,000 ppm and U > 4,000 ppm are most likely due to micro-scale inclusions (e.g., silicates and/or U-rich minerals) within zircons. Results with Ti > 50 ppm were interpreted as ablation of Ti-Fe oxide inclusions. Lanthanum > 1 ppm commonly reflects apatite inclusions in zircon (e.g., Lu et al. 2016). Taking the approximately 0.2 ppm analytical uncertainty (2σ) into account, analyses with La < 1.2 ppm were considered free of apatite inclusions. Light rare earth element index (LREE-I = [Dy/Nd]+[Dy/Sm]) < 10 was used to screen out zircon grains that underwent apparent alteration (Bell et al. 2016). Individual trace element results for analyzed trace elements in standards and zircon samples, including U-Pb ages are tabulated in ESM A2.

For apatite session, the 401 apatite (Thompson et al. 2016) was used as the primary standard to correct for mass bias, down hole fractionation, and instrument drift. NIST612 glass (Pearce et al. 1997) was used as an external standard for trace element determination. Each apatite analysis began with a 30 s blank gas measurement followed by a further 40 s of analysis time when the laser was switched on. Apatite grains were analyzed with 30 μm spots and NIST612 glass with 43 μm spots, using a repetition rate of 5 Hz and an energy density of approximately 3.5 J/cm2. Related parameters for He and Ar gas flow are same to the zircon session described above. Representative analytical spots with CL-BSE images are presented in ESM1 Fig. S1.

Stable time-resolved LA-ICP-MS spectra were typically chosen to start at 35 s and end at 70 s using LADR. Spectra with anomalous spikes were interpreted as ablation of inclusions in the apatite and were then avoided. All apatite mineral data were normalized to 97.5 wt% oxides, with Ca used as the internal standard. Results with Ca of 36.5–40.5 wt% and P of 15.5–19.5 wt% are considered as apatite. High Si (normally > 1 wt%), Al (> 1000 ppm), Fe (> 2500 ppm), Mg (> 1000 ppm), Na (> 1500 ppm), Ti (> 100 ppm), and Zr (> 200 ppm) are interpreted as accidental ablation of mineral inclusions within apatite, and therefore these data have been screened out. A total of 305 apatite results were retained after discarding > 90 analyses due to the contamination of microscale inclusions. Individual results and detection limits for analyzed trace elements in apatite can be found in ESM A3.

Analytical results

Zircon composition

After data processing and screening a total of 360 analyses, 163 LA-ICP-MS results were retained. The chondrite-normalized (McDonough and Sun 1995) rare earth elements (REEs) in zircon from each intrusive phase show typical convex-upward patterns (Fig. 2), characterized by strongly enriched heavy REEs, depleted light REEs, prominent positive Ce anomalies (CeN/NdN = 1.3–45), and weak to moderate negative Eu anomalies (Eu/Eu* = 0.2–0.78). Granodiorite intrusions from the Anabama Hill, Netley Hill, and Bendigo prospects display similar REE patterns and compositions (Fig. 2a, c, and e), as do the porphyritic diorite plutons (Fig. 2a, c, and f). Zircons from the dacite porphyry at Anabama Hill and biotite porphyry from Bendigo have higher REE abundances than other intermediate-felsic counterparts, with medians of 1,827 and 2,936 ppm, respectively (ESM2 Table S2). Zircon from the A-type Colebatch granite is characterized by their slightly low Ce/Ce* values (12.9–23.7) and remarkably negative Eu anomalies (median Eu/Eu* 0.02–0.40; Fig. 2f; ESM2 Table S4).

Fig. 2
figure 2

Chondrite-normalized (McDonough and Sun 1995) rare earth element diagrams for zircon from each intrusive rock. Anabama Hill prospect: (a) granodiorite and diorite porphyry, (b) monzogranite and dacite porphyry. Netley Hill prospect: (c) granodiorite and diorite porphyry, (d) red K-feldspar granite and biotite porphyry. Bendigo: (e) granodiorite and biotite granite, and (f) diorite porphyry. Colebatch granite included in panel (f). Each line pattern represents an average value of analyses of each granite. The grey fields represent the maximum and minimum ranges

Full size image

Ti-in-zircon thermometer of Ferry and Watson (2007) was used to calculate temperatures for each intrusive phase, assuming a TiO2 activity of 0.7 and SiO2 activity of 1 that reflect titanite and titanomagnetite saturation (Claiborne et al. 2010). The Ti-in zircon temperatures for the Anabama Hill granodiorite range from 846 to 674 °C (Fig. 3a), with a median of 735 ± 56 °C (ESM2 Table S4), whereas the plagioclase-phyric diorite is slightly hot and has temperature variations between 620 and 910 °C (median 765 ± 78 °C). The monzogranite at Anabama Hill appears to have a similar temperature range to the diorite, averaging at 762 ± 47 °C (706–854 °C). The dacite porphyry is slightly cool with temperatures from 870 to 694 °C (median 740 ± 46 °C). In the Netley Hill prospect, the temperatures for the red, K-feldspar-bearing granite (median 816 ± 57 °C) are shown 50–100 °C higher than those for the granodiorite (773 ± 58 °C), porphyritic diorite (770 ± 38 °C), and biotite-phyric granite (730 ± 41 °C). The Bendigo granodiorite (750 ± 47 °C) and biotite granite (780 ± 39 °C) appear to be slightly hotter than the diorite porphyry (median 728 ± 52 °C) from the same district (Fig. 3a). Ti-in-zircon thermometer estimates a temperature range of 865 to 650 °C (median 734 ± 66 °C) for the Colebatch granite.

Fig. 3
figure 3

Representative plots showing zircon trace elements or ratios as a function of Hf variations. (a) Hf vs. temperatures, (b) Hf vs. 238U/206Pb age, (c) Hf vs. Eu/Eu*, (d) Hf vs. CeN/(Nd2/Sm)N, (e) Hf vs. Th/U, and (f) Hf vs. Yb/Gd (chondrite-normalized)

Full size image

Our analyses show that Hf in zircon from the Delamerian porphyry prospects mostly range from 8,500 to 16,000 ppm, Th of 50–2,000 ppm, and U of 75–3,000 ppm. Hafnium contents in zircon increase consistently with decreasing crystallization temperatures, Th/U ratios, and Eu/Eu* values (Fig. 3a, c, and e), and correlate positively with CeN/(Nd2/Sm)N and YbN/GdN ratios (Fig. 3d and f). Generally, 238U/206Pb ages in zircon decrease with Hf concentrations from 8,500 to 15,000 ppm, although there is a peak age of 510 Ma at a Hf value of ca. 11,000 ppm (Fig. 3b).

Apatite composition

BSE and CL images have been collected to reveal the internal textures and generations of the apatite crystals in this study and representative BSE-CL images for analyzed apatite crystals are presented in ESM1 Figure S1. Most of the apatite crystals are characterized by homogenous massive CL-bright domains (ESM1 Fig. S1) that may locally have thin oscillatory zoned rims (ESM1 Figs. S1 k and n), characteristic of igneous zoning features (Bouzari et al. 2016). A small amount of apatite crystals displays irregularly patchy zoning with dark CL features grown on CL-bright cores (ESM1 Fig. S1 i), crosscutting CL-dark cracks (ESM1 Figs. S1 a, f, g, and l), and/or porous textures filled with rare earth element-rich inclusions. These apatite crystals are classified as alteration apatite with hydrothermal origin (Bouzari et al. 2016) and were not analyzed for major and trace element compositions.

All apatite crystals have F abundances over 1.75 wt%, with the highest value to 4.5 wt%, and thus the apatite from the Delamerian prospects exclusively belongs to the fluorapatite group (Pasero et al. 2010). The excess F contents in apatite > 3.77 wt% (maximum values theoretically) could be ascribed to analysis facet parallel to apatite’s c-axis. Atom per formula (apfu) calculations are based on 12.5 oxygen equivalents and for those with excess F, calculated OH and Cl are omitted. At Anabama Hill, apatite crystals in the granodiorite and diorite have equivalent F (average ~ 4.02 wt%), Cl (~ 0.01 wt%), and SO3 (0.02 wt%), with XCl/OH of 0.02–0.04 and XF/OH of 10.3–15.1 (Fig. 4), whereas the monzogranite and dacite porphyry have lower F (average 3.42 and 3.79 wt%, respectively) and XF/OH of 6.9–11.4, but higher Cl (0.03 and 0.012 wt%) and SO3 (0.07 and 0.02 wt%) contents in apatite (Fig. 4a–c; ESM2 Table S3). There is a decreasing trend for F in apatite from granodiorite (3.88 ± 0.37 wt%; median XF/OH of 12.1), diorite porphyry (3.84 ± 0.42 wt%; median XF/OH of 7.82), to porphyritic aplite (3.63 ± 0.57 wt%; median XF/OH of 7.41) at Netley Hill, but their Cl and SO3 mostly fluctuate around 0.01 wt% and 0.02–0.03 wt%, respectively (Fig. 4a–b). At the Bendigo prospect, the apatite from the young diorite porphyry contains higher averaged Cl (~ 0.23 wt%; XCl/OH of 0.15) and SO3 (~ 0.14 wt%), and lower F contents (~ 3.02 wt%; XF/OH of 3.9) than from the granodiorite (averages of 0.01, 0.09, and 3.62 wt%) and biotite granite (averages of 0.02, 0.06, and 3.94 wt%; Fig. 4a–c). The Colebatch apatite shows relatively low F (3.30 wt%; XF/OH of 5.57) and high Cl (0.07 wt%; XCl/OH of 0.06) and SO3 (0.09 wt%) abundances compared to those from other prospects (Fig. 4a–c). The positive linear trend defined by XF/OH and XCl/OH ratios implies a volatile-undersaturated character for apatite from the Delamerian porphyry prospects (Fig. 4c; cf. Meng et al. 2021).

Fig. 4
figure 4

Halogen element variations in apatite analyzed by EMPA from Delamerian porphyry prospects. (a) Cl vs. F, (b) Cl vs. SO3, and (c) XF/XOH vs. XCl/XOH. Abbreviations Ap = Apatite, DL = Detection limit. XF, XCl, and XOH calculated by atom per formula (apfu)

Full size image

EMPA shows that MnO, SiO2, FeO, and Na2O in apatite from the Delamerian plutons are mostly below 0.41, 0.21, 0.22, and 0.13 wt%, respectively (Supplementary Material A1), and a large percentage of the total analyses are below respective detection limits (e.g., ~ 40% for MnO, 45% for SiO2, 50% for FeO). LA-ICP-MS analyses reveal Mn as the most abundant trace element in apatite, ranging from 110 to 10,900 ppm and averaging at 1,970 ppm (Fig. 5a; ESM2 Table S3). Yttrium in apatite ranges from 130 to 5,350 ppm and averages at 1,070 ppm (Fig. 5b). The light REEs (La to Gd) in apatite commonly have median values from 100 to 780 ppm, whereas heavy REEs (Tb to Lu) typically average 10–40 ppm (Fig. 6; ESM2 Table S3). The Sr, Fe, Na, Mg, and Si contents in apatite are typically few hundreds of ppm on average (Fig. 5d–h), and U, Th, As, V, and Pb concentrations typically several to tens of ppm (Fig. 5i–l). Other apatite trace elements, including Al, Ba, Cu, Ti, Rb, Zn, and Zr, commonly have median values below 0.65 ppm, whereas Cr, Hf, Mo, Nb, Ta, and W typically have concentrations < 0.05 ppm on average. Approximate 30–90% of LA-ICP-MS analyses on these elements are below detection limits (ESM A3).

Fig. 5
figure 5

Percentile box plots showing compositions and variations of representative trace elements in apatite from different intrusions of the Delamerian porphyry prospects. (a) Mn, (b) Y, (c) total REEs, (d) Sr, (e) Fe, (f) Mg, (g) Na, (h) Si, (i) U, (j) Th, (k) As, and (l) V. Host rock types and prospect names are labelled in panels (g) and (j), respectively

Full size image
Fig. 6
figure 6

Rare earth element plots for apatite from the Delamerian porphyry prospects. Anabama Hill prospect: (a) granodiorite and diorite porphyry, and (b) monzogranite and dacite porphyry. Netley Hill prospect: (c) granodiorite and diorite porphyry. Bendigo prospect: (d) granodiorite, (e) biotite granite, and (f) diorite porphyry. (g) Colebatch granite. All LA-ICP-MS apatite results normalized to the Chondrite element values from McDonough and Sun (1995)

Full size image

Overall, apatite crystals from the granodiorite, diorite porphyry and monzogranite at Anabama Hill and Netley Hill show similar abundances for each trace element (Fig. 5). Apatite crystals in the dacite porphyry at Anabama Hill are evidently depleted in Mn, Fe, Mg, Na, and Y, and enriched in Si, REEs, U, Th, As, V, and Pb relative to other granitoids from the two prospects (Fig. 5). At Bendigo, apatite Mn, Sr, and Y contents increase sequentially from the granodiorite, diorite porphyry, to the biotite granite, whereas Fe, Na, Si, REEs, U, Th, and V mostly decrease in concentration (Fig. 5). Apatite crystals from the Colebatch granite are characterized by relatively high Si, Y, U, As, and V, and low Mn, Sr, Fe, and Mg concentrations (Fig. 5).

Apatite from the Delamerian porphyry prospects displays similar REE fractionation patterns to magmatic apatite typically from unaltered rocks in porphyry Cu systems (Fig. 6; Bouzari et al. 2016; Parra-Avila et al. 2022). Apatite crystals from the granodiorite and diorite porphyry at Anabama Hill have comparable flat REE patterns (Fig. 6a), with variably negative to positive Eu anomalies (average Eu/Eu* = 0.72–1.24). The monzogranite and dacite porphyry have identical apatite REE patterns, but a wider REE composition range (690–4,200 ppm) than those from the granodiorite and diorite porphyry (Fig. 6a–b). Rare earth elements in apatite from the granodiorite and diorite at Netley Hill define a typical ‘V’-shaped pattern, with prominently negative Eu anomalies (average 0.35 ± 0.3) and slight enrichment of light REEs (Fig. 6c). Apatite crystals from the Bendigo Granite show distinctive right-inclined REE patterns, with light REE enrichments and negative Eu anomalies (Fig. 6d–f). The Colebatch apatite is characterized by a V-shaped REE pattern with prominent negative Eu anomalies (0.4 ± 0.1) and characteristic Y (900–5,350 ppm) and Lu (20–140 ppm) enrichments (Figs. 5b and 6g). No evident Ce anomalies occur in apatite from the Delamerian porphyry prospects (Fig. 6; ESM2 Table S4).

Discussion

Magmatic evolution

Zircon perspective

Correlations between increasing Hf contents and cooling temperatures in zircon have been used to record an elevated degree of magmatic evolution of intermediate-felsic magmas (Miller and Wooden 2004; Gagnevin et al. 2010; Dilles et al. 2015; Lee et al. 2017). Our data from the Delamerian Orogen indicate that decreasing crystallization temperatures, Eu/Eu*, and Th/U correlate systematically with increasing Hf content in zircon (Fig. 3). These data suggest that both the Anabama and Bendigo granitic complexes underwent an increased degree of magmatic evolution and fractionation, consistent with the presence of early intermediate compositions to later felsic compositions (Fig. 3a, c, and e).

The biotite granite at Netley Hill has the highest U and Th contents and lowest Th/U ratios (average 0.58; due to the higher partition coefficient for Th than U; Fig. 3e), which is consistent with a normal fractionation trend with Th and U enriched in the residual melts (e.g., Miller and Wooden 2004; Gagnevin et al. 2010). This is also supported by the increasing Yb/Gd ratios with Hf in zircon (Fig. 3f). However, in contrast with the normal fractional crystallization trend, zircon from the dacite porphyry at Anabama has similar U contents to the diorite and granodiorite, but relatively low Th and Th/U (Fig. 3e). This implies replenishing pulses or variable assimilation of the intermediate melts into the dacite porphyritic melt (cf. Gagnevin et al. 2010; Lee et al. 2017; Paolillo et al. 2022). Although limited in analyses, zircon crystals from the Bendigo diorite porphyry record higher Th, U, and Hf contents and lower Th/U than those in the granodiorite and biotite granite (Fig. 3e), illustrating a more evolved melt crystallized later under lower temperatures than other intrusions at Bendigo (Fig. 3a–b). Elevated Th and U and low Th/U generally with increasing Hf concentrations in the Colebatch zircon (Fig. 3e) are ascribed to prolonged plagioclase crystallization and is supported by their prominent negative Eu anomalies (average Eu/Eu* = 0.09; Fig. 3c).

To investigate fractional crystallization of different minerals and/or mineral assemblages equilibrated with magmatic melts from the Delamerian Orogen, empirical Rayleigh modelling has been performed as functions of Yb/Gb and Eu/Eu* in zircon (Fig. 7). The modelling started at the average composition of the Anabama granodiorite (see details in ESM A2). Partition coefficients between melt and plagioclase are from Dunn and Sen (1994), amphibole from Klein et al. (1997), apatite and zircon from Sano et al. (2002), titanite from Bachmann et al. (2005), and garnet from Burnham and Berry (2017). Single mineral and mixed mineral fractionation curves are calculated using formulas from Loader et al. (2017). Zircon populations in granodiorite from both the Anabama Hill and Netley Hill are characterized by low-moderate Yb/Gd (8.3–20) and high-intermediate Eu/Eu* ratios (> 0.4), implying initial high-temperature amphibole and apatite crystallization in the deep magma chamber (Fig. 7a–b). Increasing Yb/Gd (20–39.7) with decreasing Eu/Eu* (< 0.4) suggests a late titanite crystallization (up to 0.3%) with cooling (Fig. 7a–b). The diorite porphyries from both prospects have experienced distinct fractional crystallization controlled by amphibole (< 60%), garnet (< 15%), and minor apatite (< 0.6%; Fig. 7a–b). Monzogranite and K-feldspar granite phases from the Anabama Granite likely have undergone similar crystallization trends to their diorite counterpart (Fig. 7a–b). The dacite porphyry and biotite granite show limited variations in Eu/Eu* (0.3–0.5) and may have experienced minor apatite (< 0.4%) or titanite crystallization (< 0.15%; Fig. 7a–b) at Anabama Hill. The granodiorite, diorite porphyry, and biotite granite from the Bendigo prospect are consistently characterized by fractional crystallization dominated by amphibole (< 50%) under high temperature, with lesser influence due to apatite (< 0.8%) and/or titanite (< 0.15%) crystallization with cooling (Fig. 7c). In contrast to the Anabama and Bendigo granite suites, the A-type Colebatch granite is distinct by extensive plagioclase crystallization up to 90% (Fig. 7d).

Fig. 7
figure 7

Rayleigh fractionation modelling in terms of Yb/Gb and Eu/Eu* in zircon showing crystallization behaviors of different mineral or mineral assemblages in parental melt. (a) Anabama Hill, (b) Netley Hill, (c) Bendigo, and (d) Colebatch. Average values of the Anabama granodiorite are taken as the starting point of Rayleigh modelling. Partition coefficients between mineral and melt are from Klein et al. (1997; amphibole), Sano et al. (2002; apatite and zircon), Burnham and Berry (2017; garnet), Dunn and Sen (1994; plagioclase), and Bachmann et al. (2005; titanite). Single mineral and mixed mineral fractionation models are calculated using formulas from Loader et al. (2017). The numbers on each modelling curve represent crystallization percentages of the relevant mineral (black curve) or mixed mineral assemblage (blue curve). Abbreviations Amp = Amphibole, Ap = Apatite, Grt = Garnet, Pl = Plagioclase, Ttn = Titanite, Zrn = Zircon

Full size image

Our zircon geochemical modeling reveals that garnet-amphibole crystallization dominated the fractionation of the intermediate to felsic components of the Anabama Granite, whereas amphibole crystallization prevailed during the fractionation of the Bendigo Granite, with additional minor apatite and/or titanite crystallization influencing this (Fig. 7). These characteristics are consistent with a number of hornblende phenocrysts observed by previous petrographic studies (Langsford 1971; McDonald 1992), both indicating that both Anabama and Bendigo granites contain high magmatic water content, a prerequisite that potentially generates porphyry Cu–Mo ± Au deposits (Sillitoe 2010; Richards 2011; Cooke et al. 2014; Loucks 2014).

Apatite perspective

Similar to zircon, apatite chemical composition is determined by melt composition, temperature-pressure conditions, oxidation state, and relative timing of its crystallization to other mineral phases (Belousova et al. 2002; Mao et al. 2016; Nathwani et al. 2020; Bromiley 2021; Parra-Avila et al. 2022). Apatite crystals from the Anabama Hill and Netley Hill prospects have average Mn concentrations of 900–2,740 ppm, as compared to a lower Mn content of 190–17,90 ppm (average = 545 ppm) from the Bendigo prospect (Fig. 5a). These values are consistent with porphyry Cu–Mo ± Au deposits that commonly have apatite with high Mn contents (MnAp) of 330–11,000 ppm (Mao et al. 2016). Experimental studies show that MnAp concentrations are controlled mainly by melt structure and composition (Stokes et al. 2019), and apatite that crystallizes from evolved magmas typically contains high Mn concentrations (Bromiley 2021). This increasing MnAp trend is recorded in the intermediate granodiorite, diorite porphyry, to felsic granite (except the Anabama dacite porphyry) of the Delamerian porphyry prospects (Fig. 8a). Magnesium contents in apatite correlate positively with Mn, but both Mg and Fe generally have lower concentrations in more felsic intrusions (e.g., Fig. 8a). The coherent decreases of Mg and Fe in apatite during the evolution of the Anabama porphyry systems (Fig. 5e–f) are likely ascribed to continuous amphibole crystallization (Parra-Avila et al. 2022). Consistent with the presence of amphibole (or hornblende) phenocrysts in the sulfide mineralization-hosting porphyritic diorite, apatite from this diorite porphyry records the highest Mg and Fe among intrusive suites at Bendigo (e.g., Figs. 5e–f and 8a).

Fig. 8
figure 8

Representative trace elements and ratios in apatite showing magmatic evolution. (a) Mn vs. Mg, (b) Sr vs. Y, (c) Mg vs. Sr/Y, and (d) Sr/Y vs. Eu/Eu*

Full size image

The general negative correlation between Y and Sr in apatite (Fig. 8b) can be attributed to progressive Y enrichment and Sr depletion led by plagioclase crystallization during increasing magmatic fractionation (Bromiley 2021). This is contrasted with the zircon REE modelling that implies an amphibole-dominated crystallization at depth (Fig. 7). Perhaps, trace element compositions in apatite from the Delamerian porphyry prospects record the relatively extensive plagioclase crystallization in the shallow crust (Nathwani et al. 2020; Bromiley 2021). Consequently, Y increases and Sr decreases in apatite from intermediate to more felsic granite plutons at each prospect. There are a few exceptions such as from the Anabama and Bendigo granites that have high Sr and low Y (Fig. 8b), which are probably inherited from their primitive magmas at depth (cf. Nathwani et al. 2020).

Low Mg (< 670 ppm) and Sr/Y ratios (< 5) characterize the apatite crystals from Delamerian porphyry systems (Fig. 8c), implying that the intermediate-felsic host magmas experienced fractional crystallization principally in the shallow crust, since apatite crystallizing early from a near-liquidus melt in the lower crust typically contains high Mg (up to 4,000 ppm) and Sr/Y (up to 10; Nathwani et al. 2020). Plagioclase crystallization can lower Sr/Y and cause negative Eu anomalies during shallow crustal melt evolution, whereas amphibole ± garnet crystallization leads to elevated Sr/Y ratios and high Eu/Eu* under high magmatic water conditions (Richards et al. 2012; Loucks 2014). Accordingly, the low Sr/Y and Mg contents in apatite (Fig. 8c) may indicate that the Delamerian intrusive suites had experienced relatively extensive plagioclase crystallization in the shallow crust. However, the prominent Sr/Y increase with positive Eu/Eu* (Fig. 8d) and slight Sr/Y increase with decreasing Mg in apatite in both Anabama and Bendigo samples (Fig. 8c), mostly follow the trends defined by amphibole fractional crystallization. Potentially, these low Mg apatite crystals with high Sr/Y and Eu/Eu* values recorded primitive melt signatures with high Sr/Y and Eu/Eu*, driven by amphibole-dominated fractional crystallization at depth (cf. Nathwani et al. 2020). Extremely low Mg, Sr/Y, and Eu/Eu* in apatite from the A-type Colebatch granite highlight extensive plagioclase fractionation, in agreement with the zircon chemistry and trace-element modelling (Figs. 7 and 8c–d).

Low Mn, Y, Sr, Na, Fe, and Mg concentrations characterize apatite from the dacite porphyry at Anabama Hill (Fig. 5) and highlight that the dacite dikes may have greater metallogenic fertility than other igneous phases. These trace elements could have been exsolved from ore-associated magmas and progressively enriched in magmatic-hydrothermal fluids, causing their depletions in magmatic apatite that directly crystallized from ore-associated melts rather than replacement apatite modified by hydrothermal fluids (Cao et al. 2021). High concentrations of pathfinder elements in apatite, including high REEs, Si, Th, As, and V (Fig. 5c, h, j, k, and l), provide additional evidence for the porphyry mineralization potential of dacite dikes at Anabama Hill (cf. Mao et al. 2016; Xu et al. 2021; Parra-Avila et al. 2022). Elevated As and V contents might be incorporated into apatite at a relatively high oxygen fugacity state (presented as As5+ and V5+), whereas REEs, Th, and Si coupled with S6+ can substitute a small fraction of Ca and P into the apatite’s structure (cf. Parra-Avila et al. 2022).

Moderately high oxidation

Zircon Ce and Eu anomalies have been shown by experimental studies to relate to melt oxygen fugacity (Burnham and Berry 2012, 2014; Trail et al. 2012; Burnham et al. 2015), although the trace elements can also be affected by melt compositions, temperature, pressure, and co-crystallizing minerals (Burnham et al. 2015; Loader et al. 2017, 2022). Nevertheless, these studies indicate that more oxidized systems tend to have zircon with stronger positive Ce anomalies and intermediate negative Eu anomalies. These findings have important implications for exploration of porphyry-style Cu–Mo ± Au deposits that typically originate from hydrous, oxidized arc magmas (Candela and Piccoli 2005; Sillitoe 2010; Richards et al. 2012; Wilkinson 2013; Cooke et al. 2014; Loucks 2014). Much lower Ce4+/Ce3+ ratios (average 1.22 ± 0.51) were detected in zircon from barren Paleozoic granitoids of the Australia’s Lachlan Orogen (Belousova et al. 2006). Zircon from porphyry Cu deposits in the Central Asian Orogenic Belt has Ce4+/Ce3+ ratios mostly above 120, strengthening such a positive correlation between oxygen fugacity (represented as Ce4+/Ce3+ ratios) and Cu endowment (Shen et al. 2015). It is challenging to accurately determine the Ce anomalies (Ce/Ce* calculated as CeN/[(LaN×PrN)]0.5) due to La and Pr concentrations in zircon close to or below their detection limits (e.g., Belousova et al. 2006; Chelle-Michou et al. 2014; Shen et al. 2015), and Ce4+/Ce3+ ratios are complicated to calculate using the lattice-strain model by Ballard et al. (2002). Alternatively, chondrite-normalized Ce/Nd ratio in zircon was proposed to estimate the Ce anomaly (Chelle-Michou et al. 2014; Loader et al. 2017) and this approach is adopted in this study (Figs. 3d and 9a; ESM2 Table S4).

Fig. 9
figure 9

Selected zircon trace elements and ratios for magma fertility assessment for the Delamerian porphyry prospects. (a) CeN/(Nd2/Sm)N vs. Eu/Eu*, (b) Dy/Yb vs. Eu/Eu*, (c) (Ce/Nd)/Y vs. 1000 × (Eu/Eu*)/Y, and (d) (Ce/Nd)/Y vs. Eu/Eu*. The fields for fertile and barren magmas are from Lee et al. (2017) and Lu et al. (2016)

Full size image

The Eu anomalies (Eu/Eu*) in zircon have been proposed to be a proxy for either magmatic oxidation state (Shen et al. 2015; Lee et al. 2017, 2020), hydration state (Lu et al. 2016), or SO2 degassing (Dilles et al. 2015). Distinctive Eu/Eu* ratios in zircon (> 0.4) characterize the ore-forming magmas associated with porphyry Cu–Mo ± Au deposits in Central Asia, Chile, Peru, and North America (Dilles et al. 2015; Shen et al. 2015; Lee et al. 2017, 2020). Lu et al. (2016) proposed that zircon from porphyry Cu–Mo ± Au systems have Eu/Eu* > 0.3. Based on a large global dataset, Lu et al. (2016) also proposed that zircons from fertile magmatic suites have collectively higher 1000×(Eu/Eu*)/Y (> 1) and (Ce/Nd)/Y (> 0.01), and lower Dy/Yb (< 0.3) ratios than barren pluton suites. More than 90% of zircon analyses from the Anabama Hill, Netley Hill, and Bendigo prospects plot in the fertile fields of porphyry mineralization in terms of Eu/Eu*, 1000×(Eu/Eu*)/Y, and (Ce/Nd)/Y (Fig. 9c–d), whereas only about 50% of zircon results plot into the fertile field defined by Dy/Yb and Eu/Eu* (Fig. 9b). The observed patterns in Ce and Eu anomalies in zircon from the three prospects are interpreted as a consequence of the prevalent garnet ± amphibole crystallization and suppression of plagioclase at hydrous and/or oxidized conditions (Richards 2011; Chelle-Michou et al. 2014; Loucks 2014; Dilles et al. 2015; Shen et al. 2015; Lu et al. 2016; Lee et al. 2017, 2020). Contrastingly, the A-type Colebatch granite is suggested to have a low potential for porphyry mineralization (Fig. 9).

Oxygen fugacity of the intrusive rocks from the Delamerian Orogen has been quantitively estimated using Ce, Ti, and initial U concentrations in zircon by adopting the approach of Loucks et al. (2020), irrespective of temperature, water content, and melt composition (Fig. 10a). The calculated oxygen fugacity values are presented in terms of fO2 relative to the fayalite-magnetite-quartz (FMQ) buffer. The granodiorite, porphyritic diorite, monzogranite, and dacite porphyritic dike at Anabama Hill have ΔFMQ values from 1.6 to 3.1 (average 2.1 ± 0.4), 0.87 to 2.62 (average 1.9 ± 0.5), 0.97 to 2.37 (average 1.8 ± 0.4), to -0.2 to 2.4 (average 1.3 ± 0.7; Fig. 10a). In the Netley Hill prospect, the granodiorite, K-feldspar granite, and biotite granite have near-identical ΔFMQ values, with averages of 1.3 ± 0.6 to 1.5 ± 0.6, whereas the ΔFMQ is slightly higher for the porphyritic diorite, with an average of 1.9 ± 0.5 ranging between 0.4 and 2.7 (Fig. 10a). The granodiorite and biotite granite from the Bendigo prospect have ΔFMQ compositions similar to comparable lithologies from the Anabama Hill prospect, with averages of 1.3 ± 0.4 and 1.2 ± 0.5 (ESM2 Table S4). The Bendigo diorite dikes have lower average ΔFMQ (0.7 ± 0.9), which fluctuates considerably from − 0.5 to 2.3 (Fig. 10a). The Colebatch granite from the Padthaway Ridge have the lowest ΔFMQ value of 0.4 ± 1.1 (-1.8 to 2.0). Except for the A-type Colebatch granite, all intrusions from the Delamerian porphyry prospects have ΔFMQ values into the range for subduction-related magmas typically defined by FMQ + 0.5 to + 2 (Rowe et al. 2009; Zimmer et al. 2010; Brounce et al. 2014; Richards 2015). These results highlight a moderate magmatic oxidation state of the Delamerian porphyry systems, which could be inherited from fO2 state of the parental magmas during post-subduction processes of the Delamerian Orogeny (ca. 514–490 Ma; Foden et al. 2006; Foden et al. 2020; Hong et al. 2023). About 24% of the zircon analyses yield high ΔFMQ values from 2 up to 3.1 (Fig. 10a). This is likely ascribed to prolonged magmatic evolution during cooling that can exert an important influence on magma redox state (cf. Burnham and Berry 2014; Burnham et al. 2015; Loader et al. 2017, 2022), or may have resulted from SO2 degassing to the exsolving magmatic-hydrothermal fluids accompanied with the reduction of S4+ from S6+ (sulfate), oxidizing the remnant melt (Dilles et al. 2015).

Fig. 10
figure 10

(a) Oxidation states plotted against temperatures estimated based on zircon geochemistry. The oxidation states are expressed in terms of fO2 relative to the fayalite-magnetite-quartz (FMQ) reference buffer. Zircon ΔFMQ is calculated from Loucks et al. (2020): ΔFMQ = 3.998 (± 0.124) × log [Ce/\(\sqrt{(Ui\times Ti)}\)] + 2.284 (± 0.101). Inset shows mean values of ΔFMQ and temperature with standard deviation uncertainty (error bar) for each intrusive rock. The ΔFMQ area for typical arc magmas from Zimmer et al. (2010) and Richards (2015). (b) Oxidation states plotted against temperatures estimated based on apatite Mn contents. Apatite saturation temperatures (AST) are calculated from whole-rock SiO2 and P2O5 concentrations using the equation of Piccoli and Candela (1994). Mn-in-apatite oxybarometer is using the equation of Miles et al. (2014): log fO2 = − 0.0022 (± 0.0003) Mn (ppm) – 9.75 (± 0.46). ASTs are 50–150 °C higher than Ti-in-zircon temperatures for respective rock type, in agreement with relatively early apatite crystallization in intermediate-felsic magmas (cf. Piccoli and Candela 1994)

Full size image

Apatite Eu and Ce anomalies have also been argued to correlate with magmatic oxygen fugacity of the silicate melts from which it crystallizes (cf. Bromiley 2021). Under increasing oxidation conditions, negative Eu anomalies decrease progressively, in contrast to increasing negative Ce anomalies in apatite (Bromiley 2021). The narrow range of Ce/Ce* values in apatite from the Delamerian porphyry prospects (0.99–1.22; ESM2 Table S4) restricts the application to track magmatic oxidation. Apatite Eu/Eu* values range widely from 0.2 to 4 among the Delamerian samples (ESM2 Table S4), which are strongly affected by feldspar crystallization (Eu2+ incorporation) – they are more likely to highlight magmatic sources and evolution (cf. Belousova et al. 2002; Chu et al. 2009; Mao et al. 2016; Nathwani et al. 2020; Bromiley 2021). There has been increasing use of MnAp contents as an oxybarometer to quantitively estimate oxidation states of silicic magmas (Miles et al. 2014; Mao et al. 2016; Richards et al. 2017). The Mn-in-apatite oxybarometry yields fO2 results distinctly contrasting with the zircon oxybarometer for the Delamerian porphyry prospects, with the highest oxidation state of ΔFMQ + 3.5 on average for the A-type Colebatch (Fig. 10b). The Mn-in-apatite oxybarometry provides ΔFMQ values of 1.6 ± 1, 2.4 ± 0.4, and 1.8 ± 0.9 for the Bendigo biotite granite, granodiorite, and diorite porphyry, largely compatible with those yielded by zircon chemistry (Fig. 10b). However, this oxybarometer yields significantly lower mean ΔFMQ values, ranging from − 4.8 to + 0.5 for intrusions from the Anabama Hill and Netley Hill prospects (Fig. 10b). These discrepant results indicate the unreliability of the Mn-in-apatite oxybarometer, consistent with recent studies that MnAp contents are predominantly controlled by melt structure rather than magmatic redox (Stokes et al. 2019; Bromiley 2021).

Sulfur and chlorine contents

The formation of porphyry Cu–Mo ± Au deposits typically relate to magmatic-hydrothermal fluids exsolved from hydrous, moderately oxidized, intermediate to felsic melts that also contain high S and Cl concentrations. These halogen elements efficiently scavenge and enrich metals as complexing ligands in fluids (Richards 2003; Candela and Piccoli 2005; Seedorff et al. 2005; Sillitoe 2010; Cooke et al. 2014; Loucks 2014). Volatile elements may be incorporated into apatite lattice structure, and therefore S and Cl concentrations are commonly used to assess metallogenic fertility. Apatite Cl and S concentrations reportedly cannot distinguish mineralized magmas from barren intrusions in the Gangdese porphyry copper belt of Tibet (Li et al. 2021), and low SO3 contents (mean < 0.61 wt%) was revealed in magmatic apatite associated with the Huojihe porphyry Mo deposit of NE China (Xing et al. 2020). However, many workers have emphasized that higher Cl and S in apatite characterize well-mineralized porphyry Cu–Mo ± Au deposits, e.g., 0.25 ± 0.17 wt% SO3 in apatite from the Carmen de Andacollo Cu–Au deposit of northern Chile (Richards et al. 2017), high SO3 (0.28–0.32 wt% vs. 0.03–0.11 wt% in mineralized and barren intrusions) and Cl (0.82–1.47 wt% vs. 0.02–0.51wt.%) at Red Chris Cu–Au deposit of British Columbia (Zhu et al. 2018), higher Cl (average 0.17 wt% vs. 0.04 wt%) and SO3 (average 0.19 wt% vs. 0.10 wt%) from fertile magmas than barren suites from post-subduction porphyry provinces (Xu et al. 2021), and increasing Cl (1.5–3 wt%) and S concentrations (up to 0.7 wt% SO3) in apatite from the Pliocene Cu–Au porphyries at Tampakan of Philippines (Parra-Avila et al. 2022). Even for the Paleoproterozoic Haib porphyry Cu deposit in Namibia, relatively high S contents (0.11–0.27 wt%) were detected in apatite (Meng et al. 2021). In general, apatite crystals from Phanerozoic porphyry Cu systems have relatively high SO3 contents (average 0.30 ± 0.07 wt%), which are likely inherited from causative intermediate to felsic arc magmas with SiO2 > 52 wt% in Circum-Pacific ring (average 0.38 ± 0.07 wt% SO3 in apatite; Meng et al. 2021 and references therein).

Apatites from granodiorite, diorite porphyry, to dacite porphyry and aplite at Anabama Hill and Netley Hill, and from granodiorite, biotite granite to diorite porphyry at Bendigo yield Cl contents that increase positively with S and negatively with F (Fig. 4a–c). Overall, apatite from the porphyritic diorite at Bendigo has the highest Cl and S values (Fig. 4a–c). These trends are consistent with the argument that F is compatibly partitioned into co-existing silicate melt (Webster et al. 2014). The sulfur trend is inverse to the expected pattern of evolving from mafic to felsic composition, as S solubility decreases linearly with FeO and thus is expected to become depleted in felsic melt (Wallace and Carmichael 1992). Alternatively, S and Cl are more likely incorporated into a magmatic volatile phase (Zajacz et al. 2012; Webster et al. 2014), which are potentially exsolved into a magmatic-hydrothermal fluid, or high S contents in ore-associated felsic magmas can result from recharge by transcrustal S-rich mafic melts or evaporitic sulfate sources (cf. Keith et al. 1997). Sulfur contents in apatite fluctuate as a complex function of magmatic temperature, oxidation state, and sulfur fugacity (Peng et al. 1997; Parat and Holtz 2004; Konecke et al. 2017, 2019) and S concentrations in apatite are generally proportional to those in the magmatic melts. Using a revised approach by Meng et al. (2021), magmatic S contents are estimated to be 37.3 ± 9, 49.3 ± 17, 134 ± 83, and 65.8 ± 16 ppm on average for the Anabama granodiorite, diorite, monzogranite, and dacite porphyry, 345 ± 278, 281 ± 178, and 909 ± 474 ppm for the Bendigo granodiorite, biotite granite, and diorite porphyry (ESM2 Table S4).

Similarly, the Cl abundances in apatite are dependent on melt composition, Cl content, temperature and/or pressure of the system (Webster et al. 2014; Webster and Piccoli 2015; Li and Hermann 2017). The crystallization sequence of amphibole/hornblende and apatite is not well constrained for the intrusions from the Delamerian prospects, considering lack of petrographic evidence. However, Cl concentrations in melts calculated for the mineralized porphyries at Coroccohuayco porphyry-skarn deposit in Peru are 0.2–0.3 wt% based on Cl in apatite, higher than those based on Cl in amphibole (~ 0.10 wt%; Chelle‑Michou and Chiaradia 2017). The crystallization of hornblende/amphibole therefore does not significantly affect the Cl uptake into apatite in granitic magmas. Nevertheless, using Cl–OH exchange equations in apatite by Li and Hermann (2017), magmatic Cl contents in equilibrium with apatite are calculated to be 0.30 ± 0.24, 0.56 ± 0.85, 0.64 ± 0.89, and 0.36 ± 0.61 wt% on average for the Anabama granodiorite, diorite, monzogranite, and dacite porphyry, and 0.45 ± 0.47, 1.02 ± 1.13, and 3.01 ± 1.54 wt% for the Bendigo granodiorite, biotite granite, and diorite porphyry (ESM2 Table S4).

The S (0.02–0.56 wt% SO3) and Cl (0.01–0.58 wt% Cl) in apatite from the Delamerian porphyry systems are significantly lower than those from porphyry deposits in subducted magmatic arcs (normally 0.12–0.60 wt% SO3 and 0.2–3.0 wt% Cl). Recent studies have shown that zircon-hosted apatite inclusions prior to volatile exsolution commonly contain relatively high magmatic Cl and SO3 contents essential to potential porphyry Cu–Mo ± Au mineralization (Sun et al. 2023; Huang et al. 2024). All the apatite crystals analyzed in this study were separated and hand-picked from intrusive rocks and they probably occur as microphenocrysts in groundmass or as inclusions hosted by plagioclase and biotite. Consequently, these apatites could have lower Cl and SO3 contents than those hosted by zircon, due to fluid exsolution or re-equilibrium with post-exsolution melt (e.g., Sun et al. 2023; Huang et al. 2024). This is one of the likely reasons that apatites from the Delamerian porphyry prospects have significantly lower S and Cl signatures than those from typical porphyry Cu deposits in magmatic arcs. Although S and Cl compositions analyzed by apatite in this study might not best record the magmatic volatile budgets and evolution of the Delamerian porphyry systems, the low S and Cl signatures in magmas from the Delamerian porphyry prospects are, alternatively, consistent with their emplacement in a post-subduction setting, to which they have been ascribed (Cayley 2011; Johnson et al. 2016; Foden et al. 2020; Hong et al. 2023). In this environment, slab rollback and/or back-arc extension could have led to the development of magma from upwelling asthenosphere (sulfur-undersaturated), distal to the subduction arc with sufficient oxidized sulfur supply (Richards 2009; Wallace and Edmonds 2011; Richards et al. 2017). Magmas derived from a post-subduction setting may retain some arc geochemical signatures, but more likely, they have compositions similar to primitive intra-plate magmas with relatively poor S and/or Cl contents (Kimura and Yoshida 2006; Wallace and Edmonds 2011; Timm et al. 2012). Nevertheless, Cl and S in apatite illustrates gradual enrichment of Cl and S contents in causative magmas, which again identify the monzogranite and dacite porphyries at Anabama Hill and diorite porphyries at Bendigo as having good potential for porphyry-style mineralization.

Conclusions

Micro-analytical results of zircon and apatite from diverse granitic intrusions of four prospects have been used to evaluate the metallogenic fertility in terms of porphyry-style mineralization in the early Paleozoic Delamerian orogenic belt, South Australia. Zircon analyses from the Anabama Hill, Netley Hill, and Bendigo prospects have relatively high Eu/Eu* (> 0.3), 1000×(Eu/Eu*)/Y (> 1) and (Ce/Nd)/Y (> 0.01), and low Dy/Yb (< 0.3), which mostly fall into the fields defined by fertile magmas for porphyry Cu–Mo ± Au deposits globally. Key trace elements in zircon, e.g., Ti, Th, U, Hf, Gd, and Yb, imply elevated degrees of magmatic evolution from intermediate granodiorite to more felsic granite. Rayleigh fractionation modelling using Eu/Eu* and Yb/Gd ratios in zircon highlight that Anabama and Bendigo granite complexes had undergone prevalent (garnet ±) amphibole crystallization surpassing plagioclase crystallization under hydrous conditions, consistent with high REEs, Th, As, V, Sr/Y, and Eu/Eu*, and low Mg signatures detected in apatite. Zircon and/or apatite oxybarometers estimate a moderately high oxidation state ranging from ΔFMQ + 1 to + 3 for intrusive suites from these prospects. Apatite has elevated magmatic S and Cl components within monzogranite and dacite porphyries at Anabama Hill and diorite porphyry at Bendigo. Together, these data support the igneous phases of monzogranite and dacite porphyries at Anabama Hill and diorite porphyry at Bendigo as being the most fertile and likely to relate to Cu–Mo porphyry-style mineralization. Our study indicates that the prospects in Delamerian Orogen have positive indicators for porphyry-style mineralization and should encourage further exploration in this greenfield province.