Abstract
Laser ablation-inductively coupled plasma-mass spectrometry and electron-probe microanalysis were used to investigate the trace-element contents of sphalerite, chalcopyrite and pyrite from the Plaka Pb–Zn–Ag deposit. Using petrographic observations, the analytical results could be linked to the temporal evolution of the Plaka ore-forming system. Sphalerite chemistry reliably records the temperature and fS2 evolution of the system, with estimated formation temperatures reproducing the microthermometric results from previous fluid-inclusion studies. Chalcopyrite chemistry also shows systematic variations over time, particularly for Cd, Co, Ge, In, Sn and Zn concentrations. Measurable pyrite was only found in association with early high-temperature mineralisation, and no clear trends could therefore be identified. We note, however, that As and Se contents in pyrite are consistent with formation temperatures estimated from co-existing sphalerite. Statistical analysis of the sphalerite data allowed us to identify the dominant geological controls on its trace-element content. The three investigated factors temperature, fS2, and sample location account for > 80% of the observed variance in Mn, Fe, Co, Ga, Ge, In, Sb and Hg concentrations, and > 60% of the observed variance in Cd and Sn concentrations. Only for Cu and Ag concentrations is the explained variance < 50%. A similarly detailed analysis was not possible for chalcopyrite and pyrite. Nevertheless, comparison of the results for all three investigated minerals indicates that there are some systematic variations across the deposit which may be explained by local differences in fluid composition.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The trace-element signatures of sulfide minerals are quickly becoming important tools in the study of hydrothermal mineral deposits (Cook et al. 2016; Fontboté et al. 2017). This is because they can record critical information on both the physical and chemical conditions of ore formation, as demonstrated by several recent studies (Deditius et al. 2014; Frenzel et al. 2016, 2020; Keith et al. 2018). However, the field is still young, and relatively little work has been done to systematically link changes in sulfide trace-element chemistry to the evolution of individual ore-forming systems (e.g. Sykora et al. 2018; Bauer et al. 2019; Godefroy-Rodriguez et al. 2020). Studies which simultaneously investigate the chemistry of multiple co-existing sulfide minerals are even rarer (e.g. George et al. 2016).
In this work, we used laser ablation-inductively coupled plasma-mass spectrometry (LA-ICP-MS) and electron-probe microanalysis (EPMA) to investigate trace-element concentrations in sphalerite, chalcopyrite and pyrite in Pb–Zn–Ag ores from different parts of the Plaka deposit, Lavrion, Greece. The Plaka deposit is characterised by an evolution from high- to low-temperature sulfide mineralisation styles (Voudouris et al. 2008). This evolution is reasonably well constrained (Voudouris et al. 2008), making it an excellent case study to: (1) examine changes in the trace-element signatures of the investigated minerals with ore-forming conditions and (2) test the applicability of existing geochemical tools such as the GGIMFis (= Ga, Ge, In, Mn and Fe in phalerite) geothermometer (Frenzel et al. 2016) at the scale of a single deposit.
Geological setting
District geology
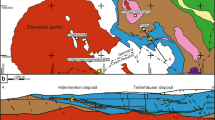
The Lavrion area is located 50 km southeast of Athens (Fig. 1A) and belongs to the Attic-Cycladic Crystalline Belt, a metamorphic terrain formed between the Late Cretaceous and Late Miocene (Altherr et al., 1982, Katzir et al. 2000; Bröcker et al. 2004; Bröcker and Keasling 2006; Scheffer et al. 2016). Two tectonic units dominate the geology of the area. They are separated by a large detachment fault (Fig. 1A).
Geological overview: A simplified geological map of the Lavrion ore district (modified after Marinos and Petrascheck, 1956, Scheffer et al. 2016; Voudouris et al. 2021). B Geological sketch map of the Plaka area (modified after Papanikolaou and Syskakis 1991); 1, porphyry-type mineralised granodiorite; 2, skarn-style mineralisation; 3, Breccia-style mineralisation; 4, skarn-free carbonate replacement mineralisation; 5, Vein 80
The basal Kamariza Unit is composed of a sequence of Triassic to Early Jurassic metasedimentary rocks. It is subdivided into three members: The Lower Marble, Kamariza Schist and Upper Marble (Fig. 1A; Marinos and Petrascheck 1956, Photiades and Carras, 2001, Scheffer et al. 2016).
The Lavrion Unit overlies the Kamariza Unit and consists of the Lavrion Schist, marbles and a meta-ophiolite (Photiades and Carras, 2001). During peak metamorphism, both units reached blueschist facies conditions (Scheffer et al. 2016). However, they later retrogressed mostly to greenschist facies mineral assemblages (Scheffer et al. 2016).
Several occurrences of granite and granodiorite laccoliths, pipes, dikes and sills are exposed across the Lavrion district (Marinos and Petrascheck 1956; Skarpelis 2007; Papanikolaou and Syskakis 1991; Skarpelis et al. 2008). The most important of these is the Plaka intrusion (Fig. 1B), an I-type granodiorite surrounded by an extensive contact metamorphic aureole of calc-silicate hornfels in the Kamariza schists (Fig. 1B; Baltatzis 1981). Field relationships indicate that magmatism was broadly synchronous with the post-metamorphic development of the large detachment fault, with available radiometric dates suggesting an absolute age of 9.7–8.1 Ma (Skarpelis et al. 2008; Liati et al. 2009).
Mineralisation
The Lavrion district is famous for its long mining history, starting before 3000 bc (Conophagos 1980; Roald and Webster 2018) and ending in the 1970s (Marinos and Petrascheck 1956). Two major mining centres were located at Plaka and Kamariza, but several other sulfide deposits occur in the district (Fig. 1A). Overall, about 2.3 Mt of Pb, 1.12 Mt of Zn and 7.8 kt of Ag were produced from the district (Conophagos 1980). However, not all Zn originally contained in the ores was extracted, so that a reasonable estimate of the original Zn:Pb ratio in the ores is ~ 1:1.
The major economic mineralisation styles are skarn-hosted and skarn-free carbonate-replacement Pb–Zn–Ag ores, as well as vein-type Pb–Zn-Ag ores (Marinos and Petrascheck 1956; Leleu et al. 1973; Economou et al. 1981; Voudouris 2005; Skarpelis 2007; Voudouris et al. 2008; Bonsall et al. 2011; Berger et al. 2013; Scheffer et al. 2017, 2019). Minor porphyry-style Cu-Mo and breccia-hosted Pb–Zn–Ag mineralisation also occur (Voudouris et al. 2008), but these latter mineralisation styles have never been of economic interest. Besides Pb, Zn and Ag, the ores also contain significant concentrations of Cu, Fe, As, Sb, Bi and Au (Voudouris et al. 2008).
Mineralisation appears to be linked to Late Miocene magmatism (Marinos and Petrascheck, 1956, Voudouris et al. 2008; Bonsall et al. 2011). This is particularly clear in the Plaka area where the different mineralisation styles developed after hornfels formation in and around the Plaka granodiorite, mostly in the Kamariza Schist and Upper Marble formations (Leleu et al. 1973; Economou et al. 1981; Fig. 1B).
Fluid-inclusion studies indicate a two-stage evolution of the Plaka mineralising system. Early fluids were high-temperature and high-salinity magmatic fluids (~ 360 °C, < 40 wt.% NaCleq) that mostly deposited early porphyry-style, skarn and carbonate-replacement mineralisation. These were followed by low-temperature and lower-salinity (< 250 °C, < 10 wt.% NaCleq) fluids of mixed origin responsible for the formation of late Ag-rich vein-hosted assemblages (Voudouris et al. 2008; Bonsall et al. 2011; Scheffer et al. 2019).
Sulfide parageneses in all four Pb–Zn-dominated mineralisation styles (skarn-hosted and skarn-free carbonate-replacement, breccia-hosted and vein-type) are similar, starting with early pyrrhotite followed by pyrite, sphalerite, chalcopyrite, galena and sometimes arsenopyrite (Voudouris et al. 2008). This early paragenesis corresponds to the early high-temperature fluids. Vein-type mineralisation additionally contains a later paragenetic stage comprising base-metal sulfides, as well as native arsenic, sulfosalts and various silver minerals (Voudouris et al. 2008). This later paragenesis corresponds to the lower-temperature fluids. Sphalerite occurs across both paragenetic stages and evolved from iron-rich to iron-poor compositions as the system cooled (Voudouris et al. 2008).
Materials and methods
Samples
Six samples of carbonate-replacement and vein-style mineralisation were selected for detailed investigation (Table ESM1.1; Fig. 2). The material was collected during an earlier sampling campaign from the surface and underground galleries at Plaka (Voudouris et al. 2008). Sampling locations are shown in Fig. 1B. Polished rounds (ø 25 mm) were prepared from all samples at the National and Kapodistrian University of Athens. The focus during sample selection was on material containing abundant sphalerite associated with other sulfides. Sphalerite is currently the best understood sulfide mineral in terms of the geological controls on its trace-element content (e.g. Lusk and Calder 2004; Frenzel et al. 2016, 2020) and was therefore of the greatest interest for this study.
Sample photographs: A pyrrhotite-rich skarn-free carbonate replacement-style mineralisation (sample 65); B pyrite, sphalerite and galena in marble, skarn-free carbonate replacement-style mineralisation (sample 46); C pyrrhotite with chalcopyrite and sphalerite, skarn-free carbonate replacement-style (sample 38); D mixed vein-style/carbonate replacement-style mineralisation (samples FL8012/15); E galena and sphalerite in carbonate vein (sample PLA-7). See Fig. 1 and Table ESM 1.1 for sample locations and descriptions. Mineral abbreviations are identical to those used in Table ESM 1.1. Cal, calcite; Qz, quartz; Sd, siderite
Petrography
Initial petrographic characterisation was performed under reflected light using a Nikon Eclipse LV100 Pol microscope, equipped with a Prior Proscan III motorised stage. Optical scans at a resolution of ~ 3 μm/px were recorded on all samples for further documentation using the same instrument. To identify unknown minerals and clarify paragenetic relationships, samples were then carbon coated and examined using an FEI Quanta 450F scanning electron microscope equipped with a Bruker Quantax EDX detector, housed at Adelaide Microscopy (University of Adelaide).
Electron-probe microanalysis
Sphalerite compositions were determined quantitatively using a Cameca SX-Five EPMA, equipped with five tunable wavelength-dispersive spectrometers, located at the University of Adelaide. The instrument ran the PeakSite v6.2 software for microscope operation, and the Probe for EPMA software (distributed by Probe Software Inc.) for all data acquisition and processing. Operating conditions were 20 kV/30 nA with a defocused beam diameter of 3 µm.
The full list of analysed elements along with primary and interference standards are given in Tables ESM1.2 to ESM1.4 in the Electronic supplementary material (ESM). Matrix corrections of Armstrong-Love/Scott φ(ρz) (Armstrong 1988) and Henke MACs were used for data reduction. Due to the complexity of off-peak interferences in sulfide minerals, all elements were acquired using a multipoint background fit, excepting Cu and Ni, which were acquired using a traditional 2-point linear fit.
Beam damage and element migration (e.g. for Cd, In) were monitored by using the Time Dependent Intensity (TDI) correction feature of Probe for EPMA (e.g. Donovan and Rowe 2005). The decay of X-ray counts over time was measured and modelled to return a t = 0 intercept, and from this a concentration could be calculated. Upon visual inspection, the X-ray counts did not appear to decay over time and thus no correction was applied.
Laser ablation-inductively coupled plasma-mass spectrometry
The trace-element contents of sphalerite, chalcopyrite and pyrite were analysed using an ESI NWR213 solid state laser, coupled to an Agilent 7900 ICP-MS at the University of Adelaide. The system used He as the carrier gas, which was mixed with Ar for plasma generation in the ICP-MS. Where possible, a minimum of 5 spot analyses were performed on each mineral generation in each sample. The following isotopes were monitored during each measurement (30 s background, 50 s ablation): 55Mn, 57Fe, 59Co, 60Ni, 63Cu, 66Zn, 69 Ga, 72Ge, 73Ge, 75As, 77Se, 107Ag, 111Cd, 113In, 115In, 118Sn, 121Sb, 125Te, 202Hg, 205Tl, 208Pb and 209Bi. Ablation spot size was generally 50 μm. An ablation pulse frequency of 10 Hz and fluence of 3.5 J/mm2 were used. In some samples, mineral grain sizes and intergrowth relationships required the use of smaller spot sizes down to 25 µm to avoid inclusions.
Data reduction was done using the Iolite software package (Woodhead et al. 2007; Paton et al. 2011). To convert measured count rates to concentrations, the 66Zn signal was used as the internal standard for sphalerite, while 57Fe was used for chalcopyrite and pyrite. Average Zn concentrations for each sphalerite generation in each sample were taken from EPMA measurements. Stoichiometric Fe concentrations were used for pyrite and chalcopyrite. MASS-1 (Wilson et al. 2002) was used as the external standard for all elements. In addition, two measurements on NIST SRM 610 (NIST 2012) were included with every standard block for quality control. A block of two to three standard measurements was inserted before and after every 20 to 30 sample measurements. Off-line corrections were made for the isobaric interferences of 113Cd on 113In and 115Sn on 115In in both the samples and the standard, using raw count rates and the natural abundance ratios of the relevant isotopes. Interferences of 56Fe16O and 57Fe16O (cf. Belissont et al. 2014) on 72Ge and 73Ge, respectively, were monitored by comparing the measured abundance ratio of 72Ge to 73Ge in the sample to the natural ratio expected for the two isotopes. If significant deviations (more than 50% relative) of 72Ge/73Ge from the natural value of 3.5 occurred, the measurement was designated as below detection limit, with the highest of the two reported concentration values as the detection limit. In general, interferences did not appear to be a problem for Ge measurements, as also noted by Belissont et al. (2014). Even in Fe-rich, Ge-poor sphalerites, spurious concentrations produced by the interference of Fe–O species on Ge never exceeded ~ 0.5 µg/g. The official reference value of 58 ppm Ge was used for the MASS-1 standard (cf. Belissont et al. 2014), and count rates on MASS-1 always showed the correct 72Ge/73Ge ratio within 10% relative of the expected natural value.
Since the Iolite software produces unrealistically low detection limits in cases where background counts are below the minimum count rate (50 cps in our case), median detection limits for the affected elements were estimated assuming a count detection limit of twice the minimum count rate—i.e. 100 cps. This procedure was applied to the following elements: Co, Ni, Cu, Ga, Ge, Se, Ag, Cd, In, Sn, Sb, Tl and Pb.
Estimation of ore-forming conditions from sphalerite composition
Sphalerite formation temperatures were estimated using the GGIMFis geothermometer (Frenzel et al. 2016). This is based on an empirical relationship between sphalerite composition and formation temperature and is described by the following equation:
with
where \(\mathrm{ln}(x)\) denotes the natural logarithm (base e), and \({c}_{i}\) is the concentration of trace element \(i\) in sphalerite, given in units of µg/g for Ga, Ge, Mn and In, and in wt.% for Fe. The relationship was calibrated using mean sphalerite compositions and microthermometric data for 51 hydrothermal base-metal sulfide deposits, formed between 100 and 400 °C (cf. Frenzel et al. 2016). Uncertainties on absolute temperatures estimated from (1) are generally on the order of ± 50 °C across the entire calibration range. The GGIMFis geothermometer is expected to work well for the estimation of average formation temperatures for individual deposits, as well as distinct mineralisation events within deposits (cf. Frenzel et al. 2016; Bauer et al. 2019). Its ability to capture smaller-scale variations in formation temperatures—e.g., across an individual sphalerite grain—has not yet been tested.
In addition to formation temperatures, we also estimated the sulfur fugacities which prevailed during sphalerite formation. To do so, we first recalculated the measured Fe-contents in sphalerite to mol.% FeS using the Fe/Zn ratios determined by LA-ICP-MS. We then used these concentrations to estimate the FeS-activity in the sphalerite,\(\left[FeS \left(sp\right)\right]\), from
where \(FeS\) is the Fe-content in sphalerite (mol.% FeS), and \(Fe{S}_{max}\) is the temperature- and pressure-dependent maximum solubility of FeS in sphalerite when in contact with metallic Fe and troilite, described by:
where \(T\) is temperature in Kelvin, and \(p\) is pressure in kbar (Barton and Toulmin 1966; Balabin and Urusov 1995). A formation pressure of 0.2 ± 0.1 kbar (cf. Voudouris et al. 2008) and formation temperatures estimated from the GGIMFis geothermometer were used in Eq. (4). Finally, the resultant FeS-activities were combined with GGIMFis temperatures to calculate fS2 values, including uncertainties, using:
Equations (3) to (5) are based on a re-fitting of the data from Barton and Toulmin (1966), Scott and Barnes (1971), Scott and Kissin (1973), Balabin and Urusov (1995) and Lusk and Calder (2004) as described in detail in ESM 1.
This estimation procedure for fS2 relies on the assumption that Fe contents in sphalerite are buffered by pyrite. Pyrite is present in most samples and is generally an abundant and widely distributed mineral at Plaka. It occurs throughout the complete paragenetic sequence (Voudouris et al. 2008). It is always present with Sp I in our samples, but not generally with Sp II (cf. “Results”). Nevertheless, its general abundance across the deposit means that the fluids involved in the precipitation of Sp II would have been in contact with pyrite on their way, and generally in close proximity to, the site of mineralisation, even if pyrite and sphalerite did not precipitate together. This means that pyrite-buffering is a reasonable assumption in the present case. The same working principle was adopted by Barton et al. (1977) for their classic study of the Creede district, Colorado.
Results
The following sections briefly summarise the key petrographic observations made on the investigated samples, as well as the corresponding results for sulfide mineral chemistry.
Petrography
Overall, the paragenetic sequence in all investigated samples is similar. Note, however, that not all parts of the sequence described below occur in each sample. For instance, sample PLA-7 only contains minerals of the late vein-related paragenesis, while sample 46 only contains minerals of the early carbonate-replacement paragenesis. Mineral names and/or abbreviations in combination with Roman numerals are used to indicate distinctive mineral generations occurring consistently across samples.
Quartz is generally the first hydrothermal mineral, occurring mostly as isolated crystals and clusters of euhedral grains. This is followed by an early pyrrhotite (Po I), now completely replaced by pyrite and/or marcasite (Fig. 3B, C). An assemblage comprising Fe-rich sphalerite (Sp I) ± galena (Gn I) ± pyrrhotite (Po II) ± chalcopyrite (Ccp I) succeeds Po I, often in association with siderite (Fig. 3B). Sphalerite I is generally characterised by abundant small inclusions of chalcopyrite (‘disease’, Barton and Bethke 1987, Fig. 3F), while Ccp I is characterised by small star-shaped inclusions of sphalerite (Fig. 3D). Pyrrhotite II is often partially replaced by Ccp I, as well as intimate intergrowths of sphalerite and pyrite (Fig. 3B). Euhedral to massive pyrite (Py I) concludes this early stage.
Representative micrographs illustrating textural relationships between different mineral generations: A late siderite-rich vein with Fe-poor sphalerite II crosscutting mineralised host rock with Fe-rich sphalerite I and chalcopyrite I (reflected light; sample FL8015); B early pyrrhotite I replaced by pyrite and overgrown by later siderite, pyrrhotite II and chalcopyrite I, with pyrrhotite II partially replaced by pyrite and sphalerite (reflected light; sample FL8012); C late sulfides (tetrahedrite, sphalerite II, chalcopyrite II) in vein fill and as replacements (reflected light; FL8012); D star-shaped exsolutions of sphalerite in chalcopyrite I (high-contrast BSE image; sample 38); E Fe-rich sphalerite I overgrown by Fe-poor sphalerite II, round spots are LA-ICP-MS craters (high-contrast BSE image; sample FL8012; F Fe-rich sphalerite I cross-cut by veinlets of Fe-poor sphalerite II, and showing chalcopyrite disease (high-contrast BSE image; sample FL8012). Mineral abbreviations are identical to those used in Table ESM 1.1 and Fig. 2. Roman numerals indicate mineral generations
In some samples (38, 65, FL8012, FL8015), this first mineralisation stage is partially overprinted by a second stage, characterised by Fe-poor sphalerite (Sp II) ± galena (Gn II) ± chalcopyrite (Ccp II) ± argentiferous tetrahedrite (~ 1–20 wt.% Ag, EDX) (Fig. 3A, C, E). This second stage mostly occurs in veins (Fig. 3A), but can also partially overprint earlier carbonate-replacement ores (Fig. 3C, E). Unlike those of the first stage, the sphalerite and chalcopyrite associated with this stage are generally free of abundant mineral inclusions.
These observations are consistent with the descriptions of Voudouris et al. (2008) and confirm that the major mineralisation stages at Plaka are well covered by the investigated sample suite.
Trace elements in sphalerite
Table 1 summarises the results of the sphalerite LA-ICP-MS analyses in terms of the geometric means for each sphalerite generation in each sample, accompanied by the lower and upper bounds of the corresponding 95% confidence intervals. These statistics were calculated by replacing all values below the detection limit (B.D.L.) with the respective detection limit (cf. van den Boogaart and Tolosana-Delgado, 2013) and omitting values affected by mineral inclusions.
Elements not shown in Table 1 were either mostly below or around detection limit (Ni, Se, Te, Tl, Bi) or were largely hosted by inclusions (As, Pb). A summary of EPMA results (Table ESM1.5) as well as files with the detailed documentation and analytical results for each EPMA/LA-ICP-MS measurement spot are included in the ESM.
It is apparent from Table 1 that there are systematic compositional differences between sphalerite I and sphalerite II. Where both generations occur in the same sample, concentrations of Fe, Mn, Co and In are generally higher in sphalerite I. Concentrations of Ga, Ge, Sn, Sb and Hg, on the other hand, show the opposite behaviour. Finally, Cu, Ag and Cd concentrations do not show clear systematic differences between the two sphalerite generations across samples. Another interesting observation is that high concentrations of Co and In appear to be restricted to sphalerite I in samples collected from the southern part of the deposit—i.e. in or close to Vein 80 (samples 38, FL8012, FL8015 and PLA-7; cf. Table ESM1.1).
Formation temperatures estimated from the GGIMFis geothermometer (Frenzel et al. 2016) are consistent with the chemical differences described above (Table 2). Namely, sphalerite I appears to have formed at a substantially higher temperature (276 ± 54 to 373 ± 61 °C on average) than sphalerite II (182 ± 50 to 212 ± 49 °C on average) in all samples. While relatively large uncertainties are attached to the estimates of absolute temperatures (Table 2), the differences between the two generations are well constrained, as shown by the substantial differences in PC1* values, which do not overlap at all between the generations, even across samples. This agrees well with previous observations from fluid inclusion studies which suggest the formation of sphalerite I is associated with early high-temperature fluids (~ 360 °C), while sphalerite II is associated with later low-temperature fluids (< 250 °C) (Voudouris et al. 2008).
Average sulfur fugacities estimated from GGIMFis temperatures and Fe contents in sphalerite (detailed procedures and assumptions in ESM1) also reveal some differences between the two sphalerite generations (Table 2). Specifically, sphalerite I seems to have formed at somewhat higher absolute sulfur fugacity (mean log10fS2 values between − 11.9 ± 2.9 and − 8.1 ± 2.2) than sphalerite II (mean log10fS2 values between − 16.3 ± 3.7 and − 14.2 ± 3.1). However, these differences are less pronounced than for the temperatures.
Trace elements in chalcopyrite
A summary of the chalcopyrite data is presented in Table 3. Again, the data for elements that were largely around or below minimum detection limit (Mn, Ni, As, Sb, Te, Hg, Tl), or mostly hosted in inclusions (Pb), are not shown in this table. Complete results for each measurement spot are included in ESM2.
Similar to sphalerite, there are systematic chemical differences between the two generations of chalcopyrite. While Zn, Cd, In, Sn and Bi are generally higher in chalcopyrite I, Ge and Co are higher in chalcopyrite II. For Ga, Se and Ag, there are no systematic differences. It is also apparent that high Co and In concentrations are again restricted to samples originating from the southern part of the deposit—i.e. in and around Vein 80. The same appears to be true for Se, Bi and Ag.
Trace elements in pyrite
The pyrite data are summarised in Table 4. Unlike sphalerite and chalcopyrite, only one generation of pyrite could be analysed in each sample. This was the early euhedral pyrite occurring slightly later than sphalerite I and chalcopyrite I in most samples. While it is apparent that pyrite compositions differ markedly from sample to sample, there are no clear systematic differences between samples taken from different parts of the deposit, except in terms of their Se contents. These are higher for the two samples taken in the south, in or around Vein 80. Furthermore, the only sample containing measurable Bi concentrations in pyrite is FL 8012, also from the south.
Discussion
Below, we briefly discuss the implications of our results for the evolution of the Plaka ore-forming system. We then focus on the LA-ICP-MS results for each mineral, how they relate to this evolution, and which implications this has for the overall behaviour of the different trace elements during ore formation.
Evolution of the Plaka ore-forming system
While the temperature and salinity evolution of the ore-forming fluids at Plaka was previously constrained through microthermometric measurements by Voudouris et al. (2008), the additional determination of sulfur fugacities in this contribution (Table 2) enables a discussion in terms of the fS2–T paths of the fluids (Einaudi et al. 2003).
Figure 4 shows the position of the different Plaka sphalerite generations in fS2–T space, relative to important mineral reaction lines. Despite the relatively high uncertainties in terms of their absolute formation temperatures, there are clear differences between the two sphalerite generations. While sphalerite I falls on the boundary between the low-sulfidation and intermediate-sulfidation fields, sphalerite II lies well within the intermediate-sulfidation field. Furthermore, the evolutionary trend defined by the two sphalerite generations follows the “rock buffer” of Einaudi et al. (2003) rather than the sulfur-gas buffer. This indicates that the ore fluids cooled in equilibrium with the magmatic and metamorphic country rocks, and that this was the main driver for the observed changes in ore-forming conditions (cf. Einaudi et al. 2003), in addition to mixing with meteoric and/or marine waters (cf. Voudouris et al 2008).
Sulfur fugacity-inverse temperature plot adapted from Einaudi et al. (2003) showing the location of the two sphalerite generations from Plaka relative to different mineral reaction lines (in black), the sulfur gas (S-gas) and rock buffers of Einaudi et al. (2003) (in grey), and isolines describing the variation in sphalerite Fe contents according to the model used in this publication (in red; cf. ESM1). The thick black arrow indicates the evolution of the mineralising fluids at Plaka. Ellipses delineating the fields for Sp I and Sp II at Plaka correspond to 95% confidence intervals. Mineral abbreviations: Bn, bornite; Cv, covellite; Dg, digenite; Fe, native iron; Lo, löllingite. All other abbreviations as in Table ESM 1.1 and Fig. 2
Sphalerite data
We showed earlier that mean sphalerite formation temperatures estimated from the GGIMFis geothermometer are consistent with the known evolution of the Plaka mineralising system, i.e., sphalerite I corresponds to the early high-temperature stage while sphalerite II corresponds to the later low-temperature stage. An interesting question is whether a similar relationship also holds true at the small scale—i.e., at the scale of individual LA-ICP-MS spot measurements.
To explore this, Fig. 5 compares the distribution of GGIMFis temperatures obtained from individual LA-ICP-MS spot analyses to previously determined fluid-inclusion (FI) homogenisation temperatures in associated gangue minerals. It is evident that the GGIMFis temperatures reproduce the distribution of FI homogenisation temperatures, both in terms of the central tendency and spread of the high- and low-temperature populations. Given that sphalerite occurs throughout the entire paragenetic sequence of the deposit (cf. petrography section; Voudouris et al. 2008), and that LA-ICP-MS and microthermometric data are sampled at a similar scale (10 s of µm), this suggests that, indeed, sphalerite chemistry may record small-scale variations in sphalerite formation temperatures. This is an important result since the original analysis by Frenzel et al. (2016), as well as later work by Bauer et al. (2019), only showed that the GGIMFis geothermometer is applicable at the scale of entire ore deposits and/or temporally and physically very distinct mineralisation events within the same deposit.
Comparison between the distributions of: A homogenisation temperatures in different minerals associated with early and late base-metal mineralisation at Plaka and B GGIMFis temperatures determined from sphalerite trace element compositions according to Frenzel et al. (2016)
We made further use of this result, in conjunction with the estimated sulfur fugacities for each measurement spot, to investigate the dominant controls on the observed variations in sphalerite composition. To get a first impression of the trends present in the dataset, we plotted trace-element concentrations for the individual measurement spots against temperature (Fig. 6) and a value describing variations in sulfur fugacity corrected for temperature-driven changes (Fig. 7). The correction of the temperature effect on sulfur fugacity before plotting was necessary since a substantial proportion of the total variance in \({\mathrm{log}}_{10}(f{S}_{2})\) values appear to be due to changes in temperature (Fig. 8A), probably in consequence of the cooling-driven evolution of the ore forming system (cf. previous section). This means it would not have been possible to distinguish between the specific effects of temperature and sulfur fugacity without an appropriate correction. The correction was done by fitting a model of the following form to the dataset:
where \(D\) and \(E\) are constants. The residuals of this model correspond to the corrected \(df{S}_{2}\) values used in Fig. 7 and the further modelling. The fitted values for coefficients \(D\) and \(E\) are indicated in Fig. 8A.
Trace element concentrations in sphalerite as a function of GGIMFis temperature for individual LA-ICP-MS spot analyses: A Fe, B Mn, C In, D Ga, E Ge, F Cd, G Co, H Ag, I Hg, J Sb, and K Sn. Symbol sizes are larger than typical analytical uncertainties. A.D.L., above detection limit (i.e., measurable); B.D.L., below detection limit. Copper has been omitted from this and the following figures since it does not show clear relationships with any of the investigated explanatory variables (cf. Table 5)
Trace element concentrations in sphalerite as a function of corrected log-sulfur fugacity, dfS2, for individual LA-ICP-MS spot analyses: A Fe, B Mn, C In, D Ga, E Ge, F Cd, G Co, H Ag, I Hg, J Sb, and K Sn. Symbol sizes are larger than typical analytical uncertainties. A.D.L., above detection limit (i.e., measurable); B.D.L., below detection limit
Plot of \({\mathrm{log}}_{10}(f{S}_{2})\) against inverse GGIMFis temperature for individual measurement spots (A), showing strong linear correlation. B The residuals (dfS2 values) after subtraction of the fitted relationship indicated in (A) and Eq. (6)
Figures 6 and 7 already indicate that some trace-element concentrations correlate strongly with temperature (e.g. Fe, Mn, Ga, Hg) and/or \(df{S}_{2}\) (e.g. Ge, In), while others show no such clear trends (e.g. Cd). However, it is also apparent that various complexities are present within the dataset. For instance, Co concentrations seem to correlate with temperature in samples from the southern part of the deposit (Fig. 6C, black, green and blue symbols), while samples from the northern part fall off this trend (red and yellow symbols). In fact, clear groupings are observed for individual samples for nearly all elements. These groupings illustrate the variable effects of differences between sample locations (cf. Dmitrijeva et al. 2018).
Separating the effects of temperature, dfS2, and sample location by standard correlation analysis is nearly impossible. Therefore, we used linear mixed-effects models (cf. Winter 2013) of the following form to quantify the different effects:
where \({c}_{i}\) denotes the concentration of trace element \(i\), \(T\) denotes the estimated GGIMFis temperature in Kelvin,\(df{S}_{2}\) denotes a corrected value for \({\mathrm{log}}_{10}(f{S}_{2})\) after de-correlation with \(1/T\), and \(Sample\) is a categorical variable describing on which sample a measurement spot was obtained. The notation used in Eq. (7) corresponds to that used in the R software suite (R Core Team 2017) to describe linear mixed-effects models. The same notation is employed in Dmitrijeva et al. (2018) and Godefroy-Rodriguez et al. (2020). Temperature and \(df{S}_{2}\) are treated as fixed effects, while \(Sample\) is treated as a random effect. Interaction terms between the different variables were not included in the modelling.
The main reason for using linear mixed-effects models was, first, that the dataset is not balanced. That is, different numbers of observations are available from each sample and for each sphalerite generation (cf. Table 1). This can lead to distortions in the fitting of linear models unless it is properly accounted for (cf. Winter 2013; Dmitrijeva et al. 2018). The second reason was the necessity to account for random signals introduced into the dataset by variations between sample locations which are not related to variations in the fixed effects \(T\) and \(df{S}_{2}\), and which would otherwise cause distortions in the results. For instance, the different Co concentrations between samples from the northern and southern parts of the deposit described above (cf. Figure 6C) are a manifestation of such effects. This was accounted for in the models by including \(Sample\) as a random effect (cf. discussions in Dmitrijeva et al. 2018; Godefroy-Rodriguez et al. 2020). Effectively, the \(Sample\) variable can be thought of as a proxy for the (temperature- and sulfur fugacity-corrected) location dependence of sphalerite compositions, giving a compound measure for the variance due to both larger (kilometre) and smaller (decimetre)-scale effects.
Table 5 summarises the results of the modelling for each element, providing p-values for each of the fixed effects, as well as R2 values for the fixed and random effects. Unfortunately, it is not mathematically possible to give separate estimates of R2 for each of the fixed effects (cf. Godefroy-Rodriguez et al. 2020). A graphical representation of the overall goodness of fit for each element is provided in Fig. 9, where observed values are plotted versus predicted ones.
Comparison between fitted and observed trace-element concentrations in sphalerite, according to the model described in the main text (Eq. (7); cf. Tables 5 and 6): A Mn, B Co, C Ga, D Ge, E Ag, F Cd, G In, H Sn, I Sb, and J Hg. Indicated R2 values correspond to R2 (total) in Table 5. A.D.L., above detection limit (i.e., measurable); B.D.L., below detection limit. Note that displaced stacks of values for individual samples (e.g. F) essentially reflect the effect of \(Sample\) in the models. Also note that the true relationship between Ge concentrations and the explanatory variables considered here is probably stronger, since the relatively large proportion of B.D.L. values tends to obscure part of the relationship. Iron has been omitted from this figure since its behaviour, by definition, is perfectly explained by temperature and sulfur fugacity
The results in Table 5 can be interpreted as follows: the p-values provide a measure of statistical significance: the smaller the p-value, the more probable the existence of a relationship with the respective explanatory variable. In the present case, p-values below 2 × 10−3 were considered to indicate statistically significant relationships. The R2 values, on the other hand, provide a measure of the proportion of the total variance explained by a given part of the model. Specifically, R2 (1/T + dfS2) corresponds to the proportion of the variance explained by temperature and fS2, while R2 (Sample) corresponds to the proportion of the variance explained by the effects of sampling/locality. R2 (Total) is the sum of the two previous values and describes the goodness of fit for the overall model. Thus, the R2 (Sample) value of 0.67 for Co means that differences between localities account for 67% of the observed variance in Co concentrations, while the R2 (1/T + dfS2) value of 0.27 means that temperature and sulfur fugacity account for 27%. The sum of these two values is 94% which corresponds to the proportion of the variance in Co concentrations explained by the overall model, i.e. R2 (Total).
Considering first the R2 values for the overall models, there are three broad groups of trace elements: (1) those whose variability is well explained by the models (R2 > 0.80)—i.e. Mn, Fe, Co, Ga, Ge, In, Sb and Hg; (2) those whose variability is accounted for in large parts (R2 > 0.60), while considerable uncertainties remain—i.e. Sn and Cd; (3) and, finally, those whose variability is only explained to some degree by the model (R2 < 0.50), and for which the main cause(s) of the observed variability cannot currently be determined—i.e. Cu and Ag. Within these groups, great variability exists in terms of the dominant geological control(s), as indicated by the highly variable R2 values for \((1/T + df{S}_{2})\) and Sample.
Several features of the results are worth noticing. First, it is of considerable interest that several elements (Mn, Co, Ge, In, Sb and maybe Hg) in addition to Fe show statistically significant relationships with \(df{S}_{2}\). These effects have never been described before. Unfortunately, the degree to which \(df{S}_{2}\) influences trace-element concentrations can only be assessed qualitatively, since separate R2 values cannot be calculated. In general, the relationships with \(df{S}_{2}\) appear to be weaker or less well constrained than those with \(T\), as indicated by the larger p-values for \(df{S}_{2}\).
Second, it is interesting that some temperature dependence is seen here for all trace elements, except Cu and Cd. This probably reflects the general importance of cooling in the evolution of the Plaka ore-forming system (cf. previous section).
Third, the results for \(Sample\) highlight the considerable effects of sample location on some trace-element concentrations, even after correction is made for the effects of temperature and sulfur fugacity. The most striking cases are Co, where this accounts for 67% of the observed variance, Cd, where it accounts for 65% and In, where it accounts for 61%. These effect sizes are similar in magnitude to those reported for hematite in the Middleback Ranges iron deposits, and pyrite in the Kalgoorlie gold district (Dmitrijeva et al. 2018; Godefroy-Rodriguez et al. 2020).
While the exact reasons for such location-dependent effects remain unclear, it is likely that they reflect local variations in the physico-chemical parameters of ore formation not accounted for in the modelling—e.g. pH, fO2 and fluid composition. Potential explanations for such local differences include variations in host-rock composition, relative position with respect to the major hydrothermal feeder zones of the deposit, as well as compositional differences between locally introduced fluid pulses.
Finally, Table 6 shows the model coefficients for the dependence of different elements on \(T\) and \(df{S}_{2}\). These provide an idea of the direction and degree in which changes in these parameters affect specific elements. Of particular interest here are the slopes with respect to \(df{S}_{2}\) for Mn, Co, Ge, In, Sb and Hg, since they provide direct indications for the relevant reaction mechanisms involved in their incorporation into the sphalerite (cf. ESM1 for the discussion on Fe). For instance, a slope of + 0.5 with \(df{S}_{2}\) indicates the consumption of around 0.5 S2 molecules per atom of trace element incorporated into the sphalerite, while a slope of − 0.5 indicates the release of 0.5 S2 molecules. These balances in turn indicate changes in the oxidation state of either the respective trace element or sulfur during the reaction.
Below, we give some tentative reactions which may explain the observed slopes for Mn, Co, Ge and Hg, and which would be compatible with the probable speciation(s) of these elements in the hydrothermal fluids, some host rocks and/or buffer minerals (Varekamp and Buseck 1984; Calvert and Pedersen 1996; Wood and Samson 2006; Liu et al. 2011), as well as their binding states in sphalerite (Grammatikopoulos et al. 2006; Cook et al. 2009; Bonnet et al. 2017):
Note that the observed slope of Hg concentrations with \(df{S}_{2}\) is smaller than ~ 0.5, as indicated by reaction (11). This may be due to some of the Hg being present in solution as Hg2+ (cf. Varekamp and Buseck 1984) which can be directly incorporated into sphalerite without any participation of S2 in the reaction.
For indium, a coupled substitution reaction with Cu (cf. Johan 1988), buffered by chalcopyrite and pyrite may explain the positive sign of the slope but would predict a smaller absolute value of ~ 0.25:
For Sb, however, reactions compatible with both the indicated slopes with \(df{S}_{2}\) and its speciation cannot presently be devised. Antimony is generally thought to occur with an oxidation state of + III in the hydrothermal fluids and sphalerite (Pokrovski et al. 2006; Wood and Samson 2006; Cook et al. 2012; Belissont et al. 2014). While native Sb or stibarsen could buffer its incorporation into sphalerite, the corresponding reaction should produce the opposite of the observed trend since it would consume S2. Therefore, the cause for the observed trend in Sb concentrations remains unclear.
For the other elements for which no statistically significant relationships with \(df{S}_{2}\) were found, it is probable that the oxidation states of these elements in the fluid and sphalerite are the same, that their incorporation is not associated with other elements whose oxidation state changes, or that their concentrations are not buffered by pyrite. Therefore, no consumption or release of S2 is required for their incorporation into the sphalerite structure.
Last but not least, the slopes with \(1/T\) are also interesting since they indicate the direction in which temperature affects the different trace elements. Referring back to Table 6, concentrations of Mn, Fe, Co and In increase with temperature, while concentrations of Ga, Ge, Ag, Sn, Sb and Hg decrease. Concentrations of Cu and Cd are not affected. It is worth noting that the results for Cu, Cd, Ga, Ge, In, Mn and Fe are similar to those obtained for the global dataset of Frenzel et al. (2016). That is, the concentrations of Mn, Fe and In increase with temperature, those of Ga and Ge decrease, and those of Cu and Cd are not affected. Only Co and Ag differ from their respective global trends, showing some dependence on \(T\) in the present dataset, but none in the global data of Frenzel et al. (2016). This may be due to differences in the dominant geological controls at different scales of observation. For instance, differences in background signals (e.g. source rock composition) may be more important at the global scale and thus reduce the observable strength of the temperature signal when compared to observations at the local scale. Note that the strength of the local relationships of Co and Ag with \(T\) at Plaka is quite weak, with R2 values of < 0.27 and < 0.23, respectively (cf. Table 5). This would support such an interpretation.
Chalcopyrite data
In general, chalcopyrite chemistry is not sufficiently well understood to enable a similarly detailed discussion as the sphalerite data. Particularly the dependence of trace-element concentrations on formation conditions has not yet been constrained, neither globally nor at the scale of individual ore deposits (George et al. 2016, 2018). Therefore, we must restrict ourselves to (1) noting that all measured trace-element concentrations in chalcopyrite from Plaka fall well within the range reported for other magmatic-hydrothermal deposits (cf. Cook et al. 2011; George et al. 2016, 2018) and (2) comparing the observed trends in chalcopyrite compositions with those described for sphalerite above. Regarding this last point, the discussion below is separated into temporal and spatial trends. Temporal trends refer to the differences between mineral generations within individual samples, while spatial trends refer to systematic differences between samples, particularly those from the southern and northern parts of the deposit (cf. “Results”).
In terms of temporal trends, it is interesting to note that some trace elements (Ge, In, maybe Ag) show the same trends in chalcopyrite as they do in sphalerite, while others show opposite trends (Co, Sn) (cf. Tables 1 and 3). A third group (Cd, Ga) shows dissimilar, but not opposite, behaviours.
While it is probable that the observed differences between the two chalcopyrite generations reflect a general control by fluid evolution, just as they do for sphalerite, it is not clear which exact factors cause the observed trends. Only one constraint can be derived from the present data: where the concentration of a specific trace element in chalcopyrite changes in the opposite direction compared to sphalerite during cooling, it is likely that a change in fluid composition—in particular, the relative activity of the trace element in question—is not the dominant cause for the observed behaviour, since this should have produced similar trends. The reason for this is that changes in the activity of a given trace-element in the fluid should always produce changes in the same direction for all minerals into which the element is incorporated (cf. McIntire 1963). For instance, if the activity of \(C{o}_{aq}^{2+}\) in the fluid increases, everything else staying the same, then its concentration in all co-existing minerals would be expected to increase. This response can be overruled, however, by simultaneous changes in partitioning behaviour, e.g. through temperature- or pressure-induced changes in the equilibrium partitioning constants, or due to kinetic effects (cf. McIntire 1963). Changes in the activity ratios of the major elements typically replaced by trace elements in the two minerals, i.e. Fe to Zn or Cu to Zn in the case of chalcopyrite and sphalerite, are another possibility to independently change the relative rates of incorporation for the different trace elements (cf. McIntire 1963; Frenzel et al. 2016 for detailed discussion).
Opposite behaviour between sphalerite and chalcopyrite at Plaka is only observed for Sn and Co. Therefore, it is likely that changes in the activities of Sn and Co in the fluids between the earlier and later mineralisation phases are not the main driver for the observed temporal behaviour of these two elements. Instead, this is likely to be driven by other factors such as temperature changes.
For the other trace elements, no further constraints can be derived from the observed trends. Concentration changes in the same direction can be due to any number of factors, from changes in the activity of the relevant trace element itself, to changes in temperature, Fe, Cu and Zn activities or kinetic factors influencing trace-element incorporation. Clearly, there is a need for further work to improve the general understanding of chalcopyrite chemistry to better constrain the causes of the observed temporal trends.
In terms of spatial trends, it is interesting that some trace elements behave similarly in coexisting sphalerite and chalcopyrite. Particularly, Co and In show systematically higher concentrations in samples from the southern part of the deposit (cf. “Results”). The most probable explanation for these trends are differences in fluid composition between the locations. That is, fluids in the southern part of the deposit may have had higher activities of Co and In. In turn, these higher activities may reflect either differences in background signals (e.g. host rock compositions) or fluid pathways (e.g. proximity to fluid source, interaction with different rocks during ascent) between the locations. Finally, it is interesting to note in this context, that the partitioning of In between coexisting chalcopyrite and sphalerite at Plaka is similar to that reported from other deposits (George et al. 2016; Carvalho et al. 2018; Frenzel et al. 2019). That is, sphalerite, with one exception, contains between 1 and 10 times higher In concentrations than coexisting chalcopyrite (cf. Tables 1 and 3).
Pyrite data
As for chalcopyrite, the current understanding of the physicochemical controls on pyrite composition in hydrothermal systems remains limited. Despite the relatively large amounts of analytical data collected over the past 30 years (e.g. Bajwah et al. 1987; Reich et al. 2005; Large et al. 2009; Genna and Gaboury 2015; Steadman et al. 2021), no meta-analysis has ever been conducted to systematically constrain the differences between different deposit types or the relationships with important physical parameters such as formation temperature. Furthermore, there is no comprehensive quantitative understanding of the thermodynamic controls for any of the common trace elements in pyrite such as exists, for instance, for Fe in sphalerite. Experimental data are only available for As and Au incorporation at low temperatures (Kusebauch et al. 2018, 2019). Theoretical predictions exist for Se at constant fluid composition (Huston et al. 1995). Broad correlations between formation temperatures and some trace elements (As, Au, Se) in natural pyrites have also been reported, but only from a limited number of Cu–Au deposits (Deditius et al. 2014; Keith et al. 2018). At present, it is not clear whether these relationships apply to pyrite in Pb–Zn deposits.
Given these limitations, we must restrict ourselves to some general comments on the Plaka data. First, we note that the observed As and Se concentrations in pyrite I would be compatible with formation temperatures above 300 °C, if indeed the relationships reported by Deditius et al. (2014) and Keith et al. (2018) apply here. This would be consistent with the other temperature data (GGIMFis, FI thermometry) available for the early high-temperature phase with which pyrite I is associated.
Second, the average Co/Ni ratio of pyrite I varies between 1 and 10 (Table 4). This fits the magmatic-hydrothermal origin of the ores (Bajwah et al. 1987; Gregory et al. 2015).
Finally, it is worth noting that pyrite composition also shows some systematic differences between the southern and northern parts of the deposit, some of which coincide with the trends already described for sphalerite and chalcopyrite. Specifically, higher Co concentrations in both sphalerite and chalcopyrite from the southern part of the deposit are also reflected in pyrite. Higher Se concentrations in pyrite from the south mirror the trend observed in chalcopyrite. Again, these features probably reflect systematic differences in the activities of the respective elements in the ore-forming fluids, with similar causes as discussed for chalcopyrite above.
Conclusions
Overall, this article has highlighted the great scientific potential which studies of sulfide mineral chemistry have in constraining both the evolution of hydrothermal ore-forming systems, as well as the behaviour of different trace elements within them. Not only was it possible to reconstruct the T–fS2 evolution of the Plaka system using sphalerite chemistry, with results that are consistent with previous fluid-inclusion studies, but it was also possible to gain important insights into the geological controls on the temporal and spatial distribution of several trace elements within the ore-forming system. Some of the results, such as the fS2 dependence of Mn, Co, Ge and Hg concentrations in sphalerite, even provided new insights into the potential incorporation mechanisms of these elements into sulfide minerals.
Some of the insights reported in this paper, particularly with respect to the spatial distribution of trace elements within the deposit, could only be achieved by combining data from several minerals and comparing them in terms of the observed spatial and temporal trends. This demonstrates that there are some clear advantages in multi-mineral studies compared to the single-mineral ones which have mostly been the standard in the field so far (e.g. Cook et al. 2009; George et al. 2015, 2018; Keith et al. 2018). Particularly, the combination of data on well understood minerals, such as sphalerite, with data on less well-understood minerals, such as chalcopyrite and pyrite, may prove a powerful approach to yield important new insights into ore-forming processes in the future.
Data availability
All analytical data are included with this article in electronic supplements. Sample material used for this article is stored by M. Frenzel and P. Voudouris and can be made available on request.
Code availability
No programs were written for this contribution.
Change history
06 November 2021
Springer Nature’s version of this paper was updated to present the Open Access funding note.
References
Altherr R, Kreuzer H, Wendt I, Lenz H, Wagner G, Keller J, Harre W, Hohndorf A (1982) A late Oligocene/Early Miocene high temperature belt in the Attic-Cycladic crystalline complex (SE Pelagonian, Greece). Geol Jb 23:97–164
Armstrong JT (1988) Quantitative analysis of silicate and oxide minerals: comparison of Monte Carlo, ZAF, and φ(ρz) procedures. In: Newbury DE (ed) Microbeam Analysis. San Fransisco Press, San Francisco, pp 239–246
Bajwah ZU, Seccombe PK, Offler R (1987) Trace element distribution Co: Ni ratios and genesis of the Big Cadia iron-copper deposit, New South Wales, Australia. Miner Deposita 22:292–300
Balabin AI, Urusov VS (1995) Recalibration of the sphalerite cosmobarometer: experimental and theoretical treatment. Geochim Cosmochim Ac 59:1401–1410
Baltatzis E (1981) Contact metamorphism of the calc-silicate hornfels from Plaka area, Laurium, Greece. N Jb Miner Mh 11:481–488
Barton PB, Bethke PM (1987) Chalcopyrite disease in sphalerite: pathology and epidemiology. Am Mineral 72:451–467
Barton PB, Bethke PM, Roedder E (1977) Environment of ore deposition in the Creede mining district, San Juan Mountains, Colorado. Part III. Progress toward interpretation of the chemistry of the ore-forming fluid for the OH Vein. Econ Geol 72:1–24
Barton PB, Toulmin P (1966) Phase relations involving sphalerite in the Fe-Zn-S system. Econ Geol 61:815–849
Bauer ME, Burisch M, Ostendorf J, Krause J, Frenzel M, Seifert T, Gutzmer J (2019) Trace element geochemistry of sphalerite in contrasting hydrothermal systems of the Freiberg District, Germany: Insights from LA-ICP-MS analysis, near-infrared light microthermometry of sphalerite-hosted fluid inclusions, and sulfur isotope geochemistry. Miner Deposita 54:237–262
Belissont R, Boiron M-C, Luais B, Cathelineau M (2014) LA-ICP-MS analyses of minor and trace elements and bulk Ge isotopes in zone Ge-rich sphalerites from the Noailhac-Saint-Salvy deposit (France): insights into incorporation mechanisms and ore deposition processes. Geochim Cosmochim Ac 126:518–540
Berger A, Schneider DA, Grasemann B, Stockli D (2013) Footwall mineralization during late Miocene extension along the West Cycladic detachment system, Lavrion, Greece. Terra Nova 25:181–191
Bonnet J, Cauzid J, Testemale D, Kieffer I, Proux O et al (2017) Characterization of germanium speciation in sphalerite (ZnS) from Central and Eastern Tennessee, USA, by X-ray absorption spectroscopy. Minerals 7:79
Bonsall TA, Spry PG, Voudouris PC, Tombros S, Seymour KS, Melfos V (2011) The geochemistry of carbonate-replacement Pb-Zn-Ag mineralization in the Lavrion district, Attica, Greece: fluid inclusion, stable isotope, and rare earth element studies. Econ Geol 106:619–651
Bröcker M, Keasling A (2006) Ionprobe U-Pb zircon ages from the high-pressure/low-temperature mélange of Syros, Greece: age diversity and the importance of pre-Eocene subduction. J Metam Geol 24:615–631
Bröcker M, Bieling D, Hacker B, Gans P (2004) High-Si phengite records the time of greenschist facies overprinting: implications for models suggesting mega-detachments in the Aegean Sea. J Metam Geol 22:427–442
Calvert SE, Pedersen TF (1996) Sedimentary geochemistry of manganese; implications for the environment of formation of manganiferous black shales. Econ Geol 91:36–47
Carvalho JRS, Relvas JMRS, Pinto AMM, Frenzel M, Krause J, Gutzmer J, Pacheco N, Fonseca R, Santos S, Caetano P, Reis T, Goncalves M (2018) Indium and selenium distribution in the Neves-Corvo deposit, Iberian Pyrite Belt, Portugal. Mineral Mag 82:S5–S41
Conophagos C (1980) The ancient Lavrion and the Greek techniques for silver production. Hellados Publishers, Athens, p 458
Cook NJ, Ciobanu CL, Pring A, Skinner W, Shimizu M, Danyushevsky L, Saini-Eidukat B, Melcher F (2009) Trace and minor elements in sphalerite: a LA-ICP-MS study. Geochim Cosmochim Ac 73:4761–4791
Cook NJ, Ciobanu CL, Danyushevsky LV, Gilbert S (2011) Minor and trace elements in bornite and associated Cu-(Fe)-sulfides: A LA-ICP-MS study. Geochim Cosmochim Ac 75:6473–6496
Cook NJ, Ciobanu CL, Brugger J, Etschmann B, Howard DL, de Jonge MD, Ryan C, Paterson D (2012) Determination of the oxidation state of Cu in substituted Cu-In-Fe-bearing sphalerite via µ XANES spectroscopy. Am Mineral 97:476–479
Cook NJ, Ciobanu CL, George L, Zhu Z-Y, Wade B, Ehrig K (2016) Trace element analysis of minerals in magmatic-hydrothermal ores by laser ablation inductively-coupled plasma mass spectrometry: approaches and opportunities. Minerals 6:111
Deditius AP, Reich M, Kesler SE, Utsunomiya S, Chryssoulis SL et al (2014) The coupled geochemistry of Au and As in pyrite from hydrothermal ore deposits. Geochim Cosmochim Ac 140:644–670
Dmitrijeva M, Metcalfe AV, Ciobanu CL, Cook NJ, Frenzel M, Keyser WM, Johnson G, Ehrig K (2018) Discrimination and variance structure of trace element signatures in Fe-oxides: a case study of BIF-mineralisation from the Middleback Ranges, South Australia. Math Geosci 50:381–415
Donovan JJ, Rowe M (2005) Techniques for improving quantitative analysis of mineral glasses. Geochimica et Cosmochimica Acta, supplement 69(10):A589
Dunn OJ (1961) Multiple comparisons among means. J Am Stat Assoc 59:52–64
Economou M, Skounakis S, Papathanassiou K (1981) Magnetite deposits of skarn type from the Plaka area of Laurium, Greece. Chem Erde 40:241–252
Einaudi MT, Hedenquist JW, Inan EE (2003) Sulfidation state of fluids in active and extinct hydrothermal systems: transition from porphyry to epithermal environments. In: Simmons SF, Graham I (eds) Volcanic, geothermal, and ore-forming fluids: rulers and witnesses of processes within the Earth, SEG Special Publication, vol. 10, Society of Economic Geologists, Littleton, Co., pp. 285–313
Fontboté L, Kouzmanov K, Chiaradia M, Pokrovski GS (2017) Sulfide minerals in hydrothermal deposits. Elements 13:97–103
Frenzel M, Hirsch T, Gutzmer J (2016) Gallium, germanium, indium, and other minor and trace elements in sphalerite as a function of deposit type – a meta-analysis. Ore Geol Rev 76:52–78
Frenzel M, Bachmann K, Carvalho JRS, Relvas JMRS, Pacheco N, Gutzmer J (2019) The geometallurgical assessment of by-products – geochemical proxies for the complex mineralogical deportment of indium at Neves-Corvo, Portugal. Miner Deposita 54:959–982
Frenzel M, Cook NJ, Ciobanu CL, Slattery AD, Wade BP, Gilbert S, Ehrig K, Burisch M, Verdugo-Ihl MR, Voudouris P (2020) Halogens in hydrothermal sphalerite record origin of ore-forming fluids. Geology 48:766–770
Genna D, Gaboury D (2015) Deciphering the hydrothermal evolution of a VMS system by LA-ICP-MS using trace elements in pyrite: an example from the Bracemac-McLeod deposits, Abitibi, Canada, and implications for exploration. Econ Geol 110:2087–2108
George LL, Cook NJ, Ciobanu CL (2016) Partitioning of trace elements in co-crystallized sphalerite-galena-chalcopyrite hydrothermal ores. Ore Geol Rev 77:97–116
George LL, Cook NJ, Ciobanu CL, Wade BP (2015) Trace and minor elements in galena: a reconnaissance LA-ICP-MS study. Am Mineral 100:548–569
George LL, Cook NJ, Crowe BBP, Ciobanu CL (2018) Trace elements in hydrothermal chalcopyrite. Miner Mag 82:59–88
Godefroy-Rodriguez M, Hagemann S, Frenzel M, Evans NJ (2020) Laser ablation ICP-MS trace element systematics of hydrothermal pyrite in gold deposits of the Kalgoorlie district, Western Australia. Miner Deposita 55:823–844
Grammatikopoulos TA, Valeyev O, Roth T (2006) Compositional variation in Hg-bearing sphalerite from the polymetallic Eskay Creek deposit, British Columbia, Canada. Chem Erde-Geochem 66:307–314
Gregory DD, Large RR, Halpin JA, Baturina EL, Lyons TW, Wu S et al (2015) Trace element content of sedimentary pyrite in black shales. Econ Geol 110:1389–1410
Huston DL, Sie SH, Suter GF, Cooke DR, Both RA (1995) Trace elements in sulfide minerals from Eastern Australian volcanic-hosted massive sulfide deposits. Part I. Proton microprobe analyses of pyrite, chalcopyrite, and sphalerite, and Part II. Selenium levels in pyrite: comparison with δ34S values and implications for the source of sulfur in volcanogenic hydrothermal systems. Econ Geol 90:1167–1196
Johan Z (1988) Indium and germanium in the structure of sphalerite: an example of coupled substitution with copper. Miner Petrol 39:211–229
Katzir Y, Avigad D, Matthews A, Garfunkel Z, Evansm BW (2000) Origin, HP/LT metamorphism and cooling of ophiolitic mélanges in southern Evia (NW Cyclades), Greece. J Metamorph Geol 18:699–718
Keith M, Smith DJ, Jenkin GRT, Holwell DA, Dye MD (2018) A review of Te and Se systematics in hydrothermal pyrite from precious metal deposits: Insights into ore-forming processes. Ore Geol Rev 96:269–282
Kusebauch C, Gleeson SA, Oelze M (2019) Coupled partitioning of Au and As into pyrite controls formation of giant Au deposits. Sci Adv 5:eaav5891. https://doi.org/10.1126/sciadv.aav5891
Kusebauch C, Oelze M, Gleeson SA (2018) Partitioning of arsenic between hydrothermal fluid and pyrite during experimental siderite replacement. Chem Geol 500:136–147
Large RR, Danyushevsky L, Hollit C, Maslennikov V, Meffre S et al (2009) Gold and trace element zonation in pyrite using a laser imaging technique: implications for the timing of gold in orogenic and Carlin-style sediment-hosted deposits. Econ Geol 104:635–668
Leleu M, Morikis A, Picot P (1973) Sur des mineralisations de type skarn au Laurium (Grece). Miner Deposita 8:259–263
Liati A, Skarpelis N, Pe-Piper G (2009) Late Miocene magmatic activity in the Attic-Cycladic belt of the Aegean (Lavrion, SE Attica, Greece): Implications for the geodynamic evolution and timing of ore deposition. Geol Mag 146:732–742
Liu W, Borg SJ, Testemale D, Etschmann B, Hazemann J-L, Brugger J (2011) Speciation and thermodynamic properties for cobalt chloride complexes in hydrothermal fluids at 35–440°C and 600 bar: an in-situ XAS study. Geochim Cosmochim Ac 75:1227–1248
Lusk J, Calder BOE (2004) The composition of sphalerite and associated sulfides in reactions of the Cu-Fe-Zn-S, Fe-Zn-S and Cu-Fe-S system at 1 bar and temperatures between 250 and 535°C. Chem Geol 203:319–345
Marinos G, Petrascheck WE (1956) Laurium/Laurion. Geological and Physical Research Reports, vol 4. Institute for Geology and Subsurface Research, Athens, p 246
McIntire WL (1963) Trace element partition coefficients – a review of theory and applications in geology. Geochim Cosmochim Ac 27:1209–1264
NIST (2012) Certificate of analysis – Standard Reference Material 610 – trace elements in glass. National Institute of Standards & Technology, Gaithersburg
Papanikolaou DJ, Syskakis D (1991) Geometry of acid intrusives in Plaka, Laurium and relation between magmatism and deformation. Bull Geol Soc Greece 25:355–368
Paton C, Hellstrom J, Paul B, Woodhead J, Hergt J (2011) Iolite: freeware for the visualisation and processing of mass spectrometric data. J Anal at Spectrom 26:2508–2518
Photiades A, Carras N (2001) Stratigraphy and geological structure of the Lavrion area (Attica, Greece). Bull Geol Soc Greece 34:103–109
Pokrovski GS, Borisova AY, Roux J, Hazemann J-L, Petdang A, Tella M, Testemale D (2006) Antimony speciation in saline hydrothermal fluids: a combined X-ray absorption fine structure spectroscopy and solubility study. Geochim Cosmochim Ac 70:4196–4214
R Core Team (2017) R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna
Reich M, Kesler SE, Utsunomiya S, Palenik CS, Chryssoulis SL, Ewing RC (2005) Solubility of gold in arsenian pyrite. Geochim Cosmochim Ac 69:2781–2796
Roald R, Webster M (2018) Exploring Thorikos. Department of Archeology, Ghent University, Ghent, 72 p
Scheffer C, Vanderhaeghe O, Lanari P, Tarantola A, Ponthus L, Photiades A, France L (2016) Syn- to post-orogenic exhumation of metamorphic nappes: structure and thermobarometry of the western Attic-Cycladic Metamorphic Complex (Lavrion, Greece). J Geodyn 96:174–193
Scheffer C, Tarantola A, Vanderhaeghe O, Voudouris P, Rigaudier T, Photiadis A, Morin D, Alloucherie A (2017) The Lavrion Pb-Zn-Fe-Cu-Ag detachement-related district (Attica, Greece): structural control on hydrothermal flow and element transfer-deposition. Tectonophysics 717:607–627
Scheffer C, Tarantola A, Vanderhaeghe O, Voudouris P, Spry PG, Rigaudier T, Photiades A (2019) The Lavrion Pb-Zn-Ag-rich Vein and Breccia Detachment-Related Deposits (Greece): involvement of Evaporated Seawater and Meteoric Fluids during Post-Orogenic Exhumation. Econ Geol 114:1415–1442
Scott SD, Barnes HL (1971) Sphalerite geothermometry and geobarometry. Econ Geol 66:653–669
Scott SD, Kissin SA (1973) Sphalerite composition in the Zn-Fe-S system below 300°C. Econ Geol 68:475–479
Skarpelis N (2007) The Lavrion deposit (SE Attika, Greece): geology, mineralogy and minor elements chemistry. N Jb Miner Abh 183:227–249
Skarpelis N, Tsikouras B, Pe-Piper G (2008) The Miocene igneous rocks in the Basal unit of Lavrion (SE Attica, Greece): petrology and geodynamic implications. Geol Mag 145:1–15
Steadman JA, Large RR, Olin PH, Danyushevsky LV, Meffre S et al (2021) Pyrite trace element behavior in magmatic-hydrothermal environments: an LA-ICPMS imaging study. Ore Geol Rev 128:103878
Sykora S, Cooke DR, Meffre S, Stephanov AS, Gardner K, Scott R, Selley D, Harris AC (2018) Evolution of trace element compositions from porphyry-style and epithermal conditions at the Lihir gold deposit: implications for ore genesis and mineral processing. Econ Geol 113:193–208
Varekamp JC, Buseck PR (1984) The speciation of mercury in hydrothermal systems, with application to ore deposition. Geochim Cosmochim Ac 48:177–185
Wilson SA, Ridley WI, Koenig AE (2002) Development of sulfide calibration standards for the laser ablation inductively-coupled plasma mass spectrometry technique. J Anal Atom Spectrom 17:406–409
Winter B (2013) Linear models and linear mixed effects models in R with linguistic applications. arXiv preprint https://arxiv.org/abs/1308.5499
Wood SA, Samson IM (2006) The aqueous geochemistry of gallium, germanium, indium and scandium. Ore Geol Rev 28:57–102
Woodhead J, Hellstrom J, Hergt JM, Greig A, Maas R (2007) Isotopic and elemental imaging of geological materials by laser ablation inductively coupled plasma-mass spectrometry. Geostand Geoanal Res 31:331–343
Van den Boogaart KG, Tolosana-Delgado R (2013) Analyzing compositional data with R. Springer-Verlag, Berlin
Voudouris P (2005) Gold and silver mineralogy of the Lavrion deposit Attika, Greece. In: Mao J, Bierlein FP (eds) Mineral deposit research: Meeting the global challenge, vol 2. Springer Verlag, Berlin, pp 1089–1092
Voudouris P, Melfos V, Mavrogonatos C, Photiades A, Moraiti E et al (2021) The Lavrion mines: a unique site of geological and mineralogical heritage. Minerals 11:76
Voudouris P, Melfos V, Spry PG, Bonsall TA, Tarkian M, Economou-Eliopoulos M (2008) Mineralogical and fluid inclusion constraints on the evolution of the Plaka intrusion-related ore system, Lavrion, Greece. Miner Petrol 93:79–110
Acknowledgements
We gratefully acknowledge support from the German Academic Exchange Service (DAAD) in funding the first author’s stay in Adelaide, where most of this work was conducted. Finally, we thank Dr. Guillaume Barré and one anonymous reviewer for their constructive comments that helped to significantly improve this manuscript.
Funding
Open Access funding enabled and organized by Projekt DEAL. M. Frenzel’s position was funded by the German Academic Exchange Service (DAAD) for the duration of his stay in Adelaide in 2017/18.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
All authors declare that they have no conflicts of interest or competing interests in the publication of this work.
Additional information
Editorial handling: A. R. Cabral.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Frenzel, M., Voudouris, P., Cook, N.J. et al. Evolution of a hydrothermal ore-forming system recorded by sulfide mineral chemistry: a case study from the Plaka Pb–Zn–Ag Deposit, Lavrion, Greece. Miner Deposita 57, 417–438 (2022). https://doi.org/10.1007/s00126-021-01067-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00126-021-01067-y