Abstract
A recombinant inbred line (RIL) population, derived from two Arabidopsis thaliana accessions, and the corresponding testcrosses with these two original accessions were used for the development and validation of machine learning models to predict the biomass of hybrids. Genetic and metabolic information of the RILs served as predictors. Feature selection reduced the number of variables (genetic and metabolic markers) in the models by more than 80% without impairing the predictive power. Thus, potential biomarkers have been revealed. Metabolites were shown to bear information on inherited macroscopic phenotypes. This proof of concept could be interesting for breeders. The example population exhibits substantial mid-parent biomass heterosis. The results of feature selection could therefore be used to shed light on the origin of heterosis. In this respect, mainly dominance effects were detected.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The main objective of the work presented in this article is to develop methods which serve to improve the prediction of hybrid properties based on their potential parents, a fundamental aspect in many breeding programs. Today breeders often use genetic information to identify specific lines whose progeny are likely to manifest positive traits (McCouch 2004). The aim is to accelerate the otherwise laborious process of quality assessment and selection.
We focus on the development and validation of machine learning methods designed to improve the prediction of traits of new crosses using molecular data from different sources. Molecular data often are described by a huge number of features, the importance of which for the traits under investigation is generally not known. We present a procedure that combines variables/feature selection with regression and dimensionality reduction. The selected variables serve as potential biomarkers allowing the prognosis of progeny properties.
Several methods have been developed to predict hybrid performance in maize using genetic markers (Maenhout et al. 2009; Reif et al. 2003; Schrag et al. 2007; Schrag et al. 2009a, b; Vuylsteke et al. 2000) or gene expression analysis (Frisch et al. 2009). A combination of genetic markers with morphological characters, isozymes, and proteins was employed for the same purpose in oilseed rape (Yu et al. 2005). We present a proof of concept of a new complementary approach that involves the utilization of metabolite profiles as predictors in addition to SNP markers and the introduction of a new feature selection procedure.
The detection of important markers is closely related to the understanding of the interactions between them and the resulting implications for the progeny traits. The advancement of this understanding is a further objective of the present study.
The introduction of hybrids was a successful development in plant breeding, especially with respect to yield (Birchler et al. 2003). This is due to the effect called heterosis, which describes the superiority of heterozygous hybrids in comparison to their homozygous parents (Shull 1948). Three hypotheses have been put forward in early studies to explain this phenomenon: the dominance (Bruce 1910; Davenport 1908), overdominance (Crow 1948; Hull 1945), and epistasis hypothesis (Powers 1944; Williams 1959). However, in spite of enormous efforts, the molecular basis of this phenomenon remains largely obscure.
For the validation of our procedure we chose a recombinant inbred line (RIL) population derived from Arabidopsis accessions Col-0 and C24 (Törjék et al. 2006) and the heterozygous testcrosses of its lines with both parents. This population meets the following requirements of a validation population: it has been genotyped using SNP markers (Törjék et al. 2006), manifests significant biomass heterosis (Meyer et al. 2009), shows sufficient variance of the trait in the crosses and consists of a sufficient number of genotypes. In addition a large amount of established biochemical knowledge on the population is available (Lisec et al. 2008, 2009; Meyer et al. 2007). Especially, quantitative trait loci (QTL) for biomass per se, biomass heterosis, and metabolites are known. Furthermore, we performed for the present study a QTL analysis for testcross biomass per se. The simple design of the testcross population with one parent being kept constant facilitates both, prediction and interpretation. A further advantage of using Arabidopsis thaliana is the existence of comprehensive databases such as AraCyc (www.arabidopsis.org/biocyc/), which contain information about predicted and experimentally determined pathways, reactions, compounds, genes, and enzymes.
We previously developed a procedure to predict mid-parent heterosis from a combination of SNP markers and metabolite profiles of the homozygous population (Gärtner et al. 2009). This multivariate procedure combined regression, dimensionality reduction, and feature selection methods. In the work presented here, we predict directly the biomass of the hybrids, from data obtained from the parents. The predicted trait—in contrast to the mid-parent heterosis—and its predictors are entirely derived from different genotypes allowing for the validation of the method.
Methods and materials
The recombinant inbred line population and testcrosses
The homozygous RIL population was created from a reciprocal cross between the Arabidopsis thaliana accessions C24 and Col-0. F2 plants were propagated by single seed descent to the F8 generation. A set of 110 SNP markers served for the genotyping of the RIL population (Törjék et al. 2003; Törjék et al. 2006). In the present study, we included 359 RILs and 718 testcrosses with both parents, for which both genetic and metabolic data were available.
Plant cultivation
All plants were grown together under controlled conditions in 1:1 mixture of GS 90 soil and vermiculite (Gebrüder Patzer, Sinntal-Jossa, Germany), under long-day regime (16 h fluorescent light at 20°C and 60% relative humidity/8 h darkness at 18°C and 75% humidity (Lisec et al. 2008)). Six plants of the same line were grown in one pot.
Shoot dry weight
The shoot dry weight was measured 15 days after sowing (DAS). Mean shoot dry weight in milligram per plant was estimated by using the linear mixed model G + E:E·G + E·GC + E·GC·T where E is experiment, G is genotype, GC is growth chamber, and T is tray (Meyer et al. 2007; Piepho et al. 2003).
Metabolite data
The metabolite profiles for each line were measured by gas chromatography–mass spectrometry (GC–MS). The samples for this measurement were harvested simultaneously with those for the dry weight measurement at 15 DAS. The details of measurement and GC–MS analysis are described by Lisec et al. (2006). The metabolite profiles contain 181 different metabolites. Since the lines were measured on different days the effect of detector sensitivity were corrected by dividing the intensity of each metabolite by the median of all intensities of that metabolite per measurement day. The normalization was done as described by Lisec et al. (2008).
Search for gene metabolite connections
We used the AraCyc 4.5 database to connect metabolites, SNP markers, and genes as described by Lisec et al. (2009) and identified genes directly involved in the conversion of the respective metabolite. For such a gene, the closest SNP marker is regarded to be associated with that metabolite. Alternatively the SNP markers closest to the metabolic QTL found by Lisec et al. (2008) were included.
QTL analyses
The QTL analyses for the biomass of the testcrosses followed the approach described by Meyer et al. (2009). Composite interval mapping (CIM) was performed using the software package PLABQTL (Utz and Melchinger 1996). Cofactors were automatically selected by forward stepwise regression. Empirical logarithm of the odds (LOD) thresholds were determined by 1,000 permutations (Churchill and Doerge 1994). The genetic map used in all QTL analyses is based on the map presented by Törjék et al. (2006), with additional SNP markers (Meyer et al. 2009).
Machine learning procedure
The objective of the study presented here is to learn to predict the biomass of the progeny from molecular data of the ancestors. The machine learning procedure to achieve this purpose is divided into two parts: (i) variable or feature selection and (ii) regression. In the first step, the molecular quantities that are best suited to predict the trait are identified in order to reduce the number of variables without compromising the predictive power of the data set—defined here as the correlation between estimated and measured trait. In the second step, regression models are estimated using only the selected variables. Here, the actual prediction is performed.
The variables selection was subjected to a robustness evaluation. The combination of feature selection and regression was subjected to cross validation and permutation tests.
Variable selection methods
The variables selection method used in the present study is a modification of the approach described by Gärtner et al. (2009). In both approaches the variables are first ordered according to the same measure of importance. In the second step the actual selection takes place.
The variables are ordered according to their variables importance in the projection (VIP) (Chong and Jun 2005; Pérez-Enciso and Tenenhaus 2003). The VIP method is based on the partial least squares (PLS) approach (Eriksson et al. 2001; Wold 1975). PLS looks for linear combinations of the original predictor variables that maximize the covariance with a dependent variable also called response. These combinations, called PLS components, are orthogonal, in our application. Thus, by taking only a small number h of components PLS can be used for dimensionality reduction. There are different ways to determine h, as explained below.
The weight of the jth original variable in the linear combination resulting in the ith PLS component is denoted by w ij . The VIP of the jth variable depends basically on the sum of the squared w ij (i = 1,…, h) multiplied by the correlation of the ith PLS component with the response.
In the approach by Gärtner et al. (2009) the VIP of each original variable is calculated on the basis of the complete data set. The number of PLS components h in the corresponding PLS model is determined by maximizing the squared correlation between the true dry weight and the dry weight predicted in cross validation. Afterward, subsets of variables are considered, the size of which varies between 1 and the total number of variables. The kth subset comprises the variables with the kth highest VIPs. For several subsets PLS regression models are tested using cross validation. This cross validation is performed in the training set only and is repeated for each training set. Thus, two different subsets are determined: a set with maximal predictive power and another set, the predictive power of which is not significantly lower than that of the maximal set. In order to estimate the significance of the deviation from the maximal value, confidence intervals are calculated by jackknife procedures. The minimal set is the set of selected variables that will be used in the subsequent prediction procedure.
The modified procedure proposed here also calculates the VIP of each original variable, but the determination of the number h of PLS components in the corresponding PLS model is achieved by applying F tests. The modified procedure starts with the maximum VIP variable. For the next variable in the VIP order an F test is performed, which decides if the new variable yields additional information about the response, i.e., the null hypothesis of the test states that the regression coefficient of the new variable is zero. The F statistic we used is defined by \( {{F = {\text{RSS}}( {\beta_{k} } ) - {\text{RSS}}( {\beta_{k + 1} } )}/ {( {{{{\text{RSS}}( {\beta_{k + 1} })}/{( {n - k - 2})}}} )}} \), RSS denoting the residual sum of squares for the models expressed by the coefficient vectors β k and βk+1, and k and k + 1 representing the number of variables already selected. If the P value for the new variable is lower than 0.05 the variable is included in the subset, if not, the next variable in the VIP order is tested as described above.
Regression methods
The choice of the regression model depends on the properties of predictor data. Since the two procedures of variables selection differ, we used two different regression models.
The variable selection method by Gärtner et al. (2009) does not consider orthogonality directly. Therefore, a dimensionality reduction method rendering the predictor matrix orthogonal was required. Gärtner et al. (2009) used PLS regression.
For the data sets generated by the modified approach we applied, in addition to the PLS regression, ordinary least squares (OLS) models, which maximize the correlation between a combination of the predictor variables and the response. The advantage of this method lies in its unbiased estimation of the model. The disadvantage is that correlation and co-linearity of the predictors result in a large variance of the estimation. However, since the selection of variables is biased to orthogonal variables, the application of OLS models is appropriate.
Evaluation of the robustness of the feature selection
We tested the robustness of the feature selection against possible loss of information by the reduction of the number of lines by applying bootstrap-like resamplings. In the first test, 1077 (= 3 × 359) samples were drawn with replacement from the set of all (359) RILs. This specific number of samples was chosen because the expected proportion of lines drawn at least once was then approximately 95%. Thus, 18 lines were expected not to be included in the resampled sets. For the second test, 359 samples were drawn from the set of all RILs, thus in average around 35% of the lines were left out. The resampling was replicated 100 times in both cases. Variable selection was performed on the generated data sets as described in the previous sections.
We also evaluated the effect of small perturbations. For this purpose one observation was removed from the original data set 20 times. The question whether some of the selected markers could be replaced by others if there are only small changes in the data set was approached that way.
Cross validation
The cross validation was performed according to the leave-one-out (LOO) procedure: the predictor matrix X n×p (with n number of samples, i.e., RILs; and p number of variables, i.e., SNP or metabolites) and the response, i.e., the dry weight vector, are divided into subsets. All but one subset are used to train a model including feature selection and regression. The model is then applied to the remaining subset in order to predict response Y of the test set. The pseudo code displayed in Supplmentary Fig. 1 illustrates this procedure.
Permutation tests
Permutation tests were performed to determine the statistical significance of the estimation of the response (i.e., the dry weight) from the predictor data sets. The null hypothesis assumes that there is no relationship between the considered set of markers and the testcross dry weight. Therefore, the dry weight vectors were permuted 1,000 times. The complete machine learning procedure as described above, including the variables selection, was applied to each of these permutated dry weight vectors, while the marker set remained unchanged. For each permutation the correlation between the permutated vector and its prediction was calculated. These correlations were compared to the predictive power of the procedure, when applied to the real data. The significance of the procedure is measured by a P value, which is defined as the number of random correlations higher than the predictive power divided by the number of permutations: (number of R perm,i > R true/number of permutations). The procedure of permutation test is represented by the pseudo code in Supplementary Fig. 2.
Results
The parental dry weight as predictor for hybrid biomass
The biomass ratio of the biggest to the smallest RIL is 1.8, the corresponding ratios of C24 and Col-0 testcrosses are 2.6 and 3.3, respectively. The mean dry weight values are 1.08, 1.59, and 1.55 mg plant−1 for RILs, C24, and Col-0 testcrosses, respectively. The power of the prediction of the testcross biomass from parental biomass was evaluated separately for the C24 and the Col-0 testcross population. Since only the RIL parent has a variable dry weight in this experimental set-up, the Pearson correlation of the RIL dry weight with the biomass of both types of testcrosses is considered as a measure for predictive power. For the C24 testcrosses that correlation is very low (0.21) but still statistically significant (P value = 6 × 10−5). The corresponding correlation with Col-0 testcrosses biomass is even lower (0.08 with a P value of 0.11).
Prediction of dry weight of testcrosses by parental molecular data from different sources of the parents
The following four data sets were used as predictors: metabolite profiles containing relative levels of 181 metabolites, 110 SNP markers, the combination of SNP markers and metabolite profiles, the combination of SNP markers, metabolites, and the RIL dry weight. All mentioned predictor variables are measurements on RIL parents only. In the following, we refer to these sets as METAB, SNP, METAB-SNP, and METAB-SNP-DW. The response to be predicted was the dry weight of the C24 testcrosses and the dry weight of the Col-0 testcrosses.
Before applying the feature selection, the predictive power of the predictor complete sets was determined using the OLS and the PLS regression method. A cross validation was performed as described in the “Methods” part. The best result was obtained for the C24 testcross population using the SNP data set (R = 0.48). For all other data sets much lower values were obtained, especially in the case the OLS regression is applied (Table 1).
Using our modified feature selection method we sought to minimize the size of biomarker sets without significantly lowering the predictive power in cross validation. The predictive power of each data set/combination is given in Table 1. For the METAB-SNP set the OLS prediction with feature selection is improved in comparison to or equally good as the PLS results for the complete data set. Figure 1 illustrates these results and their application using the example of the combination of parental SNP markers, metabolites, and dry weight as predictors for biomass in C24 testcrosses. We have shown that the plants predicted to be the 10% biggest C24 testcrosses applying the OLS regression method had indeed a significantly higher mean value (1.79 mg) than the entire C24 testcross population (1.59 mg). This was done by a one sample t test. The P value was lower than 10−16. This indicates a significant biomass difference of the population mean as compared to the value 1.79 mg.
Plot of the dry weight observed in the C24 testcrosses against the dry weight predicted by the METAB-SNP-DW set after variables selection. The vertical line indicates the 90% quantile of the predicted dry weight values. Thus, the testcrosses corresponding to the data points to the right of this line have been predicted to be the biggest 10% of the crosses. The horizontal line indicates the 90% quantile of the true biomass values
Statistical significance of the procedure
The statistical significance of the OLS regression results including our new variable selection procedure was evaluated by permutation tests as described in the “Methods” section. The highest P value was 0.085 for the metabolite data set applied to C24 testcrosses. For all other potential biomarker sets the P value was smaller than 0.001 in both testcross set-ups.
For the METAB set permutation tests with 100 permutations were performed using PLS and the variable selection method of Gärtner et al. (2009). P values of 0.04 and 0.02 were calculated for the Col-0 and C24 effect, respectively.
The detected markers
The set of variables selected from the METAB-SNP set contained six metabolites and six SNP markers for the C24 testcrosses’ biomass and 12 metabolites and three SNP markers for the Col-0 testcrosses’ biomass. The overlap between the two testcross set-ups comprises one metabolite and one SNP marker. All three SNP markers found for the Col-0 effect, and five of six SNP markers found for the C24 effect in the METAB-SNP set were also selected in the SNP set. Lists of the selected markers are arranged in the Supplementary Tables 1–3.
Robustness of the selected marker sets
To evaluate the effect of small changes one observation was removed randomly 20 times from the METAB-SNP set. The whole procedure was then applied to the reduced data set and the selected features for each repetition were stored. Eight of the 12 selected C24 testcross markers were identified in all 20 subsets. Two further markers were used more than 10 times. A further 31 markers were detected at least once. The corresponding numbers for the Col-0 effect are three, eight, and 39 (Supplmentary Table 3). The predictive power for the reduced sets ranged from 0.535 to 0.564 for C24 and from 0.451 to 0.483 for Col-0.
The results of robustness evaluation of the METAB-SNP variable selection by bootstrap-like resamplings in the case of the threefold resampling is presented in Supplmentary 5. For the C24 effect eight markers were found at least 90 times. Six of these markers belong to the 12 markers detected in the real data set (cf. Supplmentary Table 3). This includes the only marker that was detected 100 times (see Supplmentary Table 5). For the Col-0 effect four markers were detected at least 90 times including two of the selected markers (cf. Supplmentary Table 3). One SNP marker from chromosome 4 was found 100 times. This marker also belongs to the set of markers detected within the real data set.
With the second, more stringent resampling strategy (see “Methods and materials” part), one marker for the C24 effect and two markers for the Col-0 effect were found at least 90 times. One metabolite marker of unknown chemical identity was selected for both effects. For the Col-0 effect the SNP marker MASC04123 located on chromosome 4 was selected in addition. Both markers were also detected within the real data set.
Methods comparison
We compared our results to those obtained applying the method proposed by Gärtner et al. (2009). For this purpose the variables selected by their method were subjected to a cross validation, i.e., the variables selection is not included in the cross validation. The procedure is similar to those explained by the pseudocode for the permutation loop. Therefore, the markers selected by the new feature selection were subjected to the same kind of cross validation. Here, only the results for PLS regression were compared (Table 2). In most cases the predictive power is similar for both methods.
However, for the C24 effect metabolites have a higher predictive power, if the procedure by Gärtner et al. (2009) is applied, whereas the application of the new approach on SNP markers yields better or equally good results. In most cases fewer variables are needed when the new approach is employed (Table 2). There is large overlap between the markers detected with both methods. Notably, all of the markers robust against small changes are found with both methods.
Selected metabolites and SNP markers connected to them
We found in the AraCyc 4.5 database all genes connected directly to the metabolites of known chemical identity selected from the METAB-SNP set. In the second step we found for each such gene the SNP closest to it on the chromosome. Using an F test we determined, whether integrating the set of these SNPs in the reduced METAB-SNP model (excluding the metabolites of known chemical identity) significantly raises the predictive power.
For the Col-0 testcrosses 22 SNPs were linked to six metabolites from the METAB-SNP set. The F test resulted in a P value of 0.23, the inclusion of the six metabolites in a P value of 0.02. For the C24 effect 12 SNPs were determined as belonging to four metabolites. The corresponding P values are 0.65 and 0.04.
Alternatively, the SNPs closest to the QTL found for those metabolites by Lisec et al. (2008) were used, allowing us to include also SNPs for metabolites of unknown chemical identity. For the Col-0 effect four SNPs were linked to the 11 metabolites from the METAB-SNP selection. There was no significant gain in information by the inclusion of the SNPs (P value 0.18) in contrast to the inclusion of the metabolites (see above). For the C24 effect we found eight SNPs belonging to the six metabolites. Again the F test yielded no significant P value (0.57) for the inclusion of the set of SNPs, while a P value of 3 × 10−4 was obtained for the inclusions of the metabolites.
Comparison with per se, biomass heterosis, and testcross biomass QTL
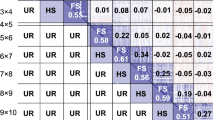
The SNP markers selected as important features were compared to the SNP markers closely linked to detected biomass QTL (Meyer et al. 2009). The results are summarized in Table 3. We found that four of the eight SNP markers selected from the SNP set for the prediction of dry weight in Col-0 testcrosses, are co-locating with one of the seven per se biomass QTL. The only Col-0 QTL for biomass heterosis is co-located with one of the markers selected from the SNP set.
For the C24 testcrosses three out of nine SNP markers selected are also in the support intervals of per se biomass QTL. For the six C24 QTL for biomass heterosis we found three co-located SNP markers with the variables selection.
In addition, a QTL search for the testcross biomass was performed in the present study with the same methods as used by Meyer et al. (2009), cf. Chap. “Methods and materials”. We found six QTL for the C24 testcrosses and two for the Col-0 testcrosses (Supplmentary Table 4). The markers co-locating with QTL are indicated by arrows in Fig. 2. One SNP marker on chromosome 1 is found for both effects. The signs of the impact of the markers obtained from the feature selection on the hybrid biomass indicate in the most cases a biomass increase when the corresponding position is heterozygous. There are two exceptions for the C24 effect, but the corresponding markers are less important than the others. One marker on chromosome 1 for both effects shows a decrease in the hybrid biomass, if the RIL parent had a C24 allele at this position.
The SNP markers located in the support intervals of the testcross biomass QTL were used to predict the corresponding dry weight in cross validation. The predictive power of these predictors was determined with 0.48 and 0.37 for C24 and Col-0, respectively. Since the same response trait (i.e., testcross dry weight) was used these results could be in principle compared to the predictive power of the markers obtained by feature selection. However, the cross validation did not include the QTL search. Therefore, the SNPs detected by the feature selection were subjected to the same kind of cross validation (i.e., the feature selection is not included in the cross validation). Their predictive power is then 0.54 and 0.45 for the C24 and Col-0 effect, respectively.
Discussion
We developed a new feature selection method that represents a complementary approach to previous works in the field (e.g., Frisch et al. 2009; Maenhout et al. 2009; Schrag et al. 2007, 2009a, b; Yu et al. 2005). For the proof of concept presented here we used a model population of Arabidopsis, therefore a direct comparison with the more agricultural applications of these authors is difficult. However, the predictive power and the reduction of the number of markers achieved by our procedure indicate its potential usefulness for breeding programs. Additionally, metabolites are introduced as useful markers.
We employed three types of potential predictors: macroscopic phenotypes, genetic markers, and metabolites. The small amount of variance of the hybrid biomass explained by the parents’ biomass shows the insufficiency of phenotypic markers as good predictors. The application of machine-learning procedures to molecular data is therefore a relevant alternative for the prediction of hybrid performance in this population.
We could show that the prediction of the trait under investigation is clearly increased by the use of SNP markers and metabolite profiles in comparison to the use of parent dry weight only. Permutation tests showed with one exception, that the metabolites significantly predict the testcross biomass. We conclude therefore that these substances are potential biomarkers for hybrid performance.
With our procedure we were able to reduce the number of variables employed for at least one of the two testcross classes from 291 SNP markers and metabolites to 12 features. The markers found by feature selection prove to be robust against small changes in the data set. Some markers are exchangeable without compromising the predictive power. Overall, only a small proportion of the available markers are used, e.g., for the C24 effect 31 out of 291. A much smaller number (eight and four for the C24 and Col-0 effect, respectively) of markers are robust against the loss of about 5% of the lines and only two markers are robust against greater changes as shown by the results of the bootstrap-like resampling.
The selection of small sets of markers is important for three reasons. First, the prediction of the trait could be improved for most of the predictor sets (see Table 1). Second, the selection of a small set of markers reduces the cost of measurement. Finally, a targeted measurement of metabolite concentrations will result in a higher accuracy. The selection of few important metabolites enables such targeted measurements. This in turn is likely to improve the predictive power of the procedure.
The modification of our original method (Gärtner et al. 2009) lowers the number of variables necessary to make predictions with a nearly equal predictive power. As described above, this is advantageous for the direct application in breeding. However, when we are interested not only in the prediction of an observed effect but in an explanation of it in molecular terms, it is reasonable to take into account also markers that improve the prediction only slightly. Therefore, the markers identified by the method of Gärtner et al. (2009) should be considered in such investigations, e.g., modelling approaches. Furthermore, the modified method has the tendency to fail in case of predictors with considerable measurement errors. This is shown by the worse results for the metabolites in the case of the C24 testcrosses, where a significant prediction was computed with our original method.
The metabolites of known chemical identity found to be important in the METAB-SNP set, could be related to SNP markers using information from the AraCyc 4.5 database. In contrast to the metabolites, this set of SNP markers does not add to the predictive power of the set of SNP markers found to be important. The use of SNP markers derived from metabolic QTL lead to the same conclusion. The metabolite concentrations can not be explained sufficiently by a linear combination of the genes known to be related to these metabolites.
The SNP markers found by feature selection overlap substantially with the QTL determined by Meyer et al. (2009). This is also true for the testcross biomass QTL determined in the present study. Mainly dominance effects are found. The only QTL found for both C24 and Col-0 shows additive effects. The predictive power of the SNP marker set detected by the variables selection is clearly higher than that of the combination of QTL. This shows that our method can find new interesting regions on the chromosomes, represented by the SNP markers. In our approach interactions between SNP markers are not considered and therefore, epistasis could not be detected, directly. However, the role of the metabolites as presented above nevertheless clearly indicates the presence of epistasis.
To improve our approach, we plan to include gene interaction in our model. Here, the knowledge of important metabolites and their connection to genes will be helpful. The use of more complex populations, i.e., derived from more than two accessions, would be a further possibility to test our method. In combination these two applications will increase the area of potential applications of our procedure for plant breeders.
References
Birchler JA, Auger DL, Riddle NC (2003) In search of the molecular basis of heterosis. Plant Cell 15:2236–2239
Bruce AB (1910) The Mendelian theory of heredity and the augmentation of vigor. Science 32:627–628
Chong I-G, Jun C-H (2005) Performance of some variable selection methods when multicollinearity is present. Chemometr Intell Lab 78:103–112
Churchill GA, Doerge RW (1994) Empirical threshold values for quantitative trait mapping. Genetics 138:963–971
Crow JF (1948) Alternative hypotheses of hybrid vigor. Genetics 33:477–487
Davenport CB (1908) Degeneration, albinism and inbreeding. Science 28:454–455
Eriksson L, Johansson E, Kettaneh-Wold N, Wold S (2001) Multi- and megavariate data analysis, Principles and applications. Umetrics Academy, Umeå, Sweden
Frisch M, Thiemann A, Fu J, Schrag TA, Scholten S, Melchinger AE (2009) Transcriptome-based distance measures for grouping of germplasm and prediction of hybrid performance in maize. Theor Appl Genet (this issue)
Gärtner T, Steinfath M, Andorf S, Lisec J, Meyer RC, Altmann T, Willmitzer L, Selbig J (2009) Improved heterosis prediction by combining information on DNA- and metabolic markers. PLoS ONE 4:e5220
Hull FH (1945) Recurrent selection for specific combining ability in corn. J Am Soc Agron 37:134–135
Lisec J, Schauer N, Kopka J, Willmitzer L, Fernie AR (2006) Gas chromatography mass spectrometry-based metabolite profiling in plants. Nat Protoc 1:387–396
Lisec J, Meyer RC, Steinfath M, Redestig H, Becher M, Witucka-Wall H, Fiehn O, Törjék O, Selbig J, Altmann T, Willmitzer L (2008) Identification of metabolic and biomass QTL in Arabidopsis thaliana in a parallel analysis of RIL and IL populations. Plant J 53:960–972
Lisec J, Steinfath M, Meyer RC, Melchinger AE, Selbig J, Willmitzer L, Altmann T (2009) Identification of heterotic metabolite QTL in Arabidopsis thaliana RIL and IL populations. Plant J. doi:10.1111/j.1365-313X.2009.03910.x
Maenhout S, De Baets B, Haesaert G (2009) Prediction of maize single-cross hybrid performance: support vector machine regression versus best linear prediction. Theor Appl Genet (this issue)
McCouch S (2004) Diversifying selection in plant breeding. PLoS Biol 2:e347
Meyer RC, Steinfath M, Lisec J, Becher M, Witucka-Wall H, Törjék O, Fiehn O, Eckardt A, Willmitzer L, Selbig J, Altmann T (2007) The metabolic signature related to high plant growth rate in Arabidopsis thaliana. Proc Natl Acad Sci USA 104:4759–4764
Meyer RC, Kusterer B, Lisec J, Steinfath M, Becher M, Scharr H, Melchinger AE, Selbig J, Schurr U, Willmitzer L, Altmann T (2009) QTL analysis of early stage heterosis for biomass in Arabidopsis. Theor Appl Genet. doi:10.1007/s00122-009-1074-6
Pérez-Enciso M, Tenenhaus M (2003) Prediction of clinical outcome with microarray data: a partial least squares discriminant analysis (PLS-DA) approach. Hum Genet 112:581–592
Piepho HP, Büchse A, Emrich K (2003) A hitchhiker’s guide to mixed models for randomized experiments. J Agron Crop Sci 189:310–322
Powers L (1944) An expansion of Jones’ theory for the explanation of heterosis. Am Nat 78:275–280
Reif JC, Melchinger AE, Xia XC, Warburton ML, Hoisington DA, Vasal SK, Srinivasan G, Bohn M, Frisch M (2003) Genetic distance based on simple sequence repeats and heterosis in tropical maize populations. Crop Sci 43:1275–1282
Schrag TA, Maurer HP, Melchinger AE, Piepho HP, Peleman J, Frisch M (2007) Prediction of single-cross hybrid performance in maize using haplotype blocks associated with QTL for grain yield. Theor Appl Genet 114:1345–1355
Schrag TA, Möhring J, Maurer HP, Dhillon BS, Melchinger AE, Piepho HP, Sørensen AP, Frisch M (2009a) Molecular marker-based prediction of hybrid performance in maize using unbalanced data from multiple experiments with factorial crosses. Theor Appl Genet 118:741–751
Schrag TA, Möhring J, Kusterer B, Dhillon BS, Melchinger AE, Piepho HP, Frisch M (2009b) Hybrid performance prediction in maize using molecular markers and joint analyses of hybrids and parental inbreds. Theor Appl Genet (this issue)
Shull GH (1948) What is “Heterosis”? Genetics 33:439–446
Törjék O, Berger D, Meyer RC, Müssig C, Schmid KJ, Sörensen TR, Weisshaar B, Mitchell-Olds T, Altmann T (2003) Establishment of a high-efficiency SNP-based framework marker set for Arabidopsis. Plant J 36:122–140
Törjék O, Witucka-Wall H, Meyer RC, von Korff M, Kusterer B, Rautengarten C, Altmann T (2006) Segregation distortion in Arabidopsis C24/Col-0 and Col-0/C24 recombinant inbred line populations is due to reduced fertility caused by epistatic interaction of two loci. Theor Appl Genet 113:1551–1561
Utz HF, Melchinger AE (1996) PLABQTL: A program for composite interval mapping of QTL. J Quant Trait Loci 2 (online)
Vuylsteke M, Kuiper M, Stam P (2000) Chromosomal regions involved in hybrid performance and heterosis: their AFLP(R)-based identification and practical use in prediction models. Heredity 85:208–218
Williams W (1959) Heterosis and the genetics of complex characters. Nature 184:527–530
Wold H (1975) Soft modelling by latent variables. Academic Press, London, UK
Yu CY, Hu SW, Zhao HX, Guo AG, Sun GL (2005) Genetic distances revealed by morphological characters, isozymes, proteins and RAPD markers and their relationships with hybrid performance in oilseed rape (Brassica napus L.). Theor Appl Genet 110:511–518
Acknowledgments
We thank Anke Kalkbrenner, Cindy Marona, Melanie Teltow, and Monique Zeh for excellent technical assistance and Katrin Seehaus and Dirk Zerning for plant cultivation. This project was supported by research grants of the Deutsche Forschungsgemeinschaft (German Research Foundation) under priority research program “Heterosis in Plants” to T.A. and R.C.M. (AL387/6-1, AL387/6-2, AL387/6-3), to L.W. (WI 550/3-2, WI 550/3-3), and to J.S. and M.S. (SE611/3-1), a grant of the European Community to T.A. (QLG2-CT-2001-01097), by the European Commission Framework Programme 6, Integrated Project: AGRON-OMICS—LSHG-CT-2006-037704, and by the Max Planck Society.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by M. Frisch.
Contribution to the special issue “Heterosis in Plants”.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Steinfath, M., Gärtner, T., Lisec, J. et al. Prediction of hybrid biomass in Arabidopsis thaliana by selected parental SNP and metabolic markers. Theor Appl Genet 120, 239–247 (2010). https://doi.org/10.1007/s00122-009-1191-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00122-009-1191-2