Abstract
The avian feather combines mechanical properties of robustness and flexibility while maintaining a low weight. Under periodic and random dynamic loading, the feathers sustain bending forces and vibrations during flight. Excessive vibrations can increase noise, energy consumption, and negatively impact flight stability. However, damping can alter the system response, and result in increased stability and reduced noise. Although the structure of feathers has already been studied, little is known about their damping properties. In particular, the link between the structure of shafts and their damping is unknown. This study aims at understanding the structure-damping relationship of the shafts. For this purpose, laser Doppler vibrometry (LDV) was used to measure the damping properties of the feather shaft in three segments selected from the base, middle, and tip. A combination of scanning electron microscopy (SEM) and micro-computed tomography (µCT) was used to investigate the gradient microstructure of the shaft. The results showed the presence of two fundamental vibration modes, when mechanically excited in the horizontal and vertical directions. It was also found that the base and middle parts of the shaft have higher damping ratios than the tip, which could be attributed to their larger foam cells, higher foam/cortex ratio, and higher percentage of foam. This study provides the first indication of graded damping properties in feathers.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Flight has given the animals survival advantages, by providing efficient locomotion and various habitats (Clark 2013). In avians, wings consisted of the flight feathers needed to sustain the dynamic force and vibration during the flapping (Greenewalt 1960). Excessive vibrations can lead to more consumed energy, noise, and negatively impact flight stability. It is reasonable to hypothesize that feathers of wings have undergone adaptations to develop several mechanisms to mitigate vibrations.
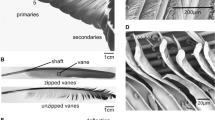
Feathers originated in theropod dinosaurs as simple filaments of varying lengths and diameters (Clark 2013). Feathers of modern birds, in contrast, evolved into complex hierarchically organized epidermal structures (Prum 1999; Bragulla and Hirschberg 2003). During feather evolution, pennaceous vanes for flight and display, and fluffy plumulaceous branches evolved for thermoregulation (Chang et al. 2019). Typical bird flight feathers consist of a shaft and two vanes (Fig. 1). The shaft is composed of a rigid outer shell and an inner foam-like structure, which shows a longitudinal gradient of cell sizes (Bonser and Purslow 1995). The vane consists of numerous barbs aligned parallel to each other, but at some angle to the shaft (Prum 1999; Clark 2013). The barbs are loosely connected by the elaborate system of hooklets and, when separated by an external force, they can easily re-establish their connections (Ennos et al. 1995; Butler and Johnson 2004; Kovalev et al. 2013; Gao et al. 2013; Chen et al. 2016; Sullivan et al. 2016).
Similar to other flyers such as dragonfly and damselfly, oscillations might negatively influence the stability (Rajabi et al. 2011, 2016). Hence, damping or energy dissipation is present in such a dynamic system. Damping alters the response of the system and results in desirable effects, such as stability and enhanced controllability (De Silva 1999). Therefore, it is plausible to hypothesize that there are structural mechanisms that enhance the damping properties of feathers and, thereby, reduce unwanted oscillations during flight.
Concerning the feather shaft, damping-related loss factors (tan δ) of swan, eagle, owl, and pigeon have been previously measured (Bonser and Purslow 1995; Gao et al. 2014). Loss factor, the ratio of loss modulus to storage modulus, is a parameter that presents the viscoelasticity and the damping capacity. For a small damping ratio, the loss factor is twice the damping ratio, tan δ = 2 ζ (Hansen 2018). A low damping ratio ranging from 0.015 to 0.035 has been revealed for bending of the swan feathers (Bonser and Purslow 1995), while the damping ratio of owl flight shafts has been estimated to be 0.804 ± 0.119, which is larger than those of gold eagle 0.543 ± 0.037 and pigeon 0.448 ± 0.041 (Gao et al. 2014). However, a systematic understanding of the relationship between gradient structure and damping property of feathers is still far from being achieved.
Feather, as a mechanical structure, is lightweight and combines this feature with specific robustness and flexibility (Raspet 1960; Prum 1999). This combination is supposed to be the result of the specific hierarchical organization at the macro-, micro-, and nano-scales (Yang et al. 2013). It has been suggested that the mechanical properties of the shaft are mainly dominated by the properties of the outer cortex (Purslow and Vincent 1978; Bachman et al. 2012). Inside of the cortex, foams are known to be a design strategy to enhance mechanical stability by energy absorption (Bonser and Purslow 1995; Banhart and Baumeister 1998; Bonser 2001; Gao et al. 2014).
In this study, we aimed to understand the contribution of the gradient foam-filled shaft to the damping behavior of primaries. Measurements, using laser Doppler vibrometry (LDV), were performed on specimens selected from different shaft regions, to study variations of damping properties along the shafts. A combination of scanning electron microscopy (SEM) and micro-computed tomography (µCT) was used to explore the correlation between the shaft morphology, its microstructure, and measured damping properties.
Materials and methods
Sample preparation
Adult female pigeons Columba livia were taken from the collection of the Zoological Institute of Kiel University, Germany. Preliminary experiments showed the presence of more than one oscillatory mode in vibrations of deflected feather shafts after release. Hence, to facilitate the data analysis, we introduced a simple manipulation to the system: the oscillations were studied with a mass attached to the free distal end of each segment. In this way, only two resonance frequencies were observed in the deflected shafts after release.
For further studies, the primary flight feathers were cut out from the wing (Fig. 1a). Primary feathers 1–6 (165–180-mm length) were sectioned, and 18 shaft specimens were used for damping tests. Vanes were cut from the feathers using a razor blade. The shaft was transversely sectioned in 50-mm-long intervals from the tip, dividing the shaft into three parts (Fig. 1b). The most basal part of the shaft, the calamus, was excluded from the experiments. The basal part of the specimens was embedded in epoxy resin and then mechanically fixed (Fig. 2b, black triangles). Primary feather 7 (160-mm length) was used for μCT analysis.
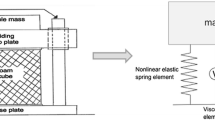
Damping measurements. The oscillation of the shaft specimen was measured using a velocity-sensitive laser Doppler vibrometry (LDV). (a) Experimental setup: feather specimen (1), support (2), objective lens (3), video monitor (4), waveform analysis equipment (5), and software control (6). (b) Excitation of oscillations of the feather shaft segments by its tip deflection and abrupt release vertically (upper panel) perpendicularly to the vane, and horizontally in the plane of the vane (lower panel)
Damping test
In this study, damping tests were performed under room temperature 20–22 °C and humidity 40–45%. Damping tests were conducted on the basal, middle, and tip segments of the shaft. The test specimens were mechanically fixed at their basal parts in a 3D micro-manipulator. To reduce the oscillation decay and to simplify the frequency analysis, as mentioned earlier, an extra mass (of 2.015 g) was attached at the free distal end of the specimens. The specimens were excited to oscillate by releasing from an initial deflection of 15 mm. The oscillations were excited in the vertical (perpendicular to the vane) and horizontal (parallel to the vane) directions (Fig. 2b). The decaying oscillation velocity was measured using a laser Doppler vibrometer (Polytec, Waldbronn, Germany) (Fig. 2a). The experimental setup including the mechanical supporters holding the feather specimen and the laser displacement sensor is shown in Fig. 2a. The oscillation velocity was recorded with a sampling rate of 5 kHz and observed in one direction, perpendicular or parallel to the vane plane. The original experimental recordings were then converted from the analysis software package Spike2 (CED, version 4.24) (Cambridge Electronic Design Limited, Cambridge, England) to the software Origin Pro 8.0 (OriginLab, MA, USA).
Feather morphology
An SEM Hitachi S-4800 (Hitachi High-Technology, Tokyo, Japan) was used at an acceleration voltage of 3 kV to study the feather microstructure at different levels of the shaft. Dry samples were attached to aluminum stubs using adhesive tape and then sputter-coated with 8-nm gold–palladium using a Leica EM SCD 500 (Leica Microsystems, Mannheim, Germany).
Skyscan 1172 µCT (Bruker microCT, Kontich, Belgium) was used for three-dimensional scanning of shaft specimens (1 primary feather, 8 segments). The X-ray voltage and current were set to 40 kV and 250 μA, respectively. The NRecon software (SkyScan, Kontich, Belgium) was used to reconstruct structures from the 3D data of µCT scans. The segmentation was performed using the image analysis software Amira (FEI Visualization Sciences Group, Bordeaux, France).
Fitting of oscillation curves
In this study, the equation of under-damped oscillations was employed to describe the damping behavior of the shaft. For shaft segments with a terminal mass, the oscillations behavior is under-damped. The motion of the shaft end can be described by the following equation (Rao 2010):
where X and t are the displacement and time, β is the damping coefficient, A is the initial amplitude, ω is the circular frequency, and φ is the phase angle. The presence of two vibration modes (frequencies) was observed in experiments on oscillating shaft segments. Therefore, a second term for the second vibration mode as well as an offset, A0, was added to Eq. 2:
where indices 1 and 2 refer to the first and second vibration modes. To perform the fit of experimental curves with Eq. 2, the initial values of the fit parameters were determined as follows. Fast Fourier transformation (FFT) was employed to estimate the first (ω1) and second (ω2) frequencies and initial phases φ1 and φ2 of the shaft segments. Initial amplitudes A1 and A2 were taken equal to half of the peak value in the experimental velocity–time curve.
However, the damping coefficient, β, is related to the frequency (Beards 1996), while the damping ratio, ζ, is frequency independent. The damping ratio was calculated using Eq. 3:
To compare our results with those previously reported in the reference (Bonser and Purslow 1995; Gao et al. 2014), the damping ratios will be further presented.
Results and discussion
Damping properties of shaft segments
After deflecting the free end of the shaft specimens, they started to oscillate. The velocity of the oscillations decreased over time until they stopped. The oscillations of all shaft segments showed typical characteristics of an under-damped regime (Fig. 3). The decay times of the shaft specimens are roughly 1 s at the base, 3 s in the middle, and 12 s at the tip. The power spectra of the velocity-decay time curves calculated using fast Fourier transform (FFT) are illustrated in Fig. 3b, d, f. Two frequencies were observed in all segments: 54.66 ± 17.37 Hz and 66.62 ± 9.91 Hz at the base, 29.46 ± 1.75 Hz and 38.14 ± 4.16 Hz in the middle, 6.46 ± 0.40 Hz and 8.16 ± 1.41 Hz at the tip of the shaft.
The comparison of damping ratios of the shaft segments in the horizontal and vertical deflections (as Fig. 2b) is illustrated in Fig. 4. Under both deflections, the damping ratios of the 1st mode at the base are higher than those in the middle and tip segments. In the 2nd mode, in contrast, the maximum values of the damping ratios were observed in the middle segment. The damping ratio in the horizontal direction was higher than that in the vertical direction.
Damping ratios of (a) the 1st (lower) frequency and (b) the 2nd (higher) frequency oscillations in different segments of the feather shaft under vertical and horizontal deflections. Measurements were performed for 6 feather shafts, 18 segments, and repeated three times. nS indicates no significant difference according to the results of the two-way ANOVA test
As seen, the damping ratios of primary feather shafts from the pigeon range from 0.268 to 0.034 in the 1st mode, and 0.127 to 0.032 in the 2nd mode (Fig. 4). Our results are lower than the previous data obtained from a uniaxial tensile test (Gao et al. 2014), where the of the pigeon shafts was found to be 0.448. This difference can be due to the use of different specimens and measurement techniques.
Feather shaft morphology
Cortex morphology
The three-dimensional reconstructions based on μCT data show structural variations of the cortex (Fig. 5). The diameter and the cross-sectional area decrease continuously from the feather base towards its tip. The shape of the cortex varies from an almost circular shape at the base, to a rectangle in the middle, and finally to an ellipse at the tip. It is known that, given the same cross-sectional area, square cross-sections show higher bending rigidity and are superior in maintaining the original shape under deformation, in comparison to circular sections, which become oval-shaped upon flexing (Prum and Williamson 2001; Wang and Meyers 2016). The square shape with a high area moment of inertia, using a larger amount of material, would be mechanically favorable in bending, but also heavier. Taking into account that feathers are anchored to the bone, the circular base has grown from cylindrical feather follicles perhaps providing better mechanical connectivity (Prum and Williamson 2001; Wang and Meyers 2016). However, to achieve improved resistance to forces applied to the feather during flight at a minimal weight, the cross-sectional shape of the feather transforms to a square in the middle, and then to a more elliptical shape at the tip.
In the interior dorsal surface of the cortex, ridges are running from 1/4 to 3/4 of the feather length (Fig. 5). At the base of the shaft, next to the calamus, two dorsal ridges are present. In the middle of the feather, four ridges appear. The ridges transform into a serrated structure and disappear at the tip. The ridges are likely to contribute to a tight bonding between the stiff cortex and flexible medulla by increasing the interfacial area (Zhang et al. 2012).
Along the shaft, the thickness of the cortex changes (Fig. 6). This decreasing thickness may enhance the damping performance, as shown for the stick insect antenna with a longitudinal thickness gradient (Rajabi et al. 2011). The feather cortex has also a radial gradient of the thickness in cross-section. The cortex is thicker on the dorsal and ventral sides if compared with the lateral sides (Table 1). This difference could be explained by a potential need to resist higher levels of stress experienced by the dorsal and ventral bending during flight (Sullivan et al. 2016). The mechanical behavior of the shaft is mainly determined by the cortex (Bonser and Purslow 1995; Lingham-Soliar et al. 2010; Liu et al. 2015). The flexural stiffness depends on the second moment of the area and Young’s modulus, which in turn depends on the keratin bundles formed in the cortex (Lingham-Soliar et al. 2010; Liu et al. 2015).
SEM images of transverse sections of shaft segments taken at 150–100 mm (base), 100–50 mm (middle), and 50–0 mm (tip) away from the tip. (a, d, g, j) Basal region. (b, e, h, k) Middle region. (c, f, i, l) Tip of the shaft. (a–c) Scale bars: 1 mm. (d–f) Scale bars: 50 μm. (g–i) Scale bars: 10 μm. (j–l) Scale bars: 5 μm
Medullary foam structure
The shaft is filled with foam cells. The shape and morphology of foam cells demonstrate a gradient (Figs. 6 and 7). At the base, the foam cells are relatively large with a diameter of about 27.09 ± 1.08 µm. Their size decreases to 21.35 ± 0.40 µm in the middle, and to 18.21 ± 0.46 µm at the tip (a decrease of ~ 15% and ~ 32%, respectively). The cells are polyhedrally or spherically shaped, and the walls (membranes) are very thin (~ 0.08-µm thickness). The SEM analysis also revealed that the walls and struts are closely packed in the septa. The fragmentary or columnar struts interconnect the foam cells and strengthen the cell interfaces. The continuous wall likely serves as the primary load supporter increasing the stability of the foams. The cell walls are made of irregularly orientated and curved weaving fibers (Fig. 6j–l). The fibers of cells merge with the fibrils composing the cortex, which enhance the mechanical stiffness of the medulla foam.
Bird wings in general and feathers, in particular, are simultaneously robust and light enough to meet the mechanical demands to generate aerodynamic forces (Pennycuick 1968). The shaft is an important part, which consists of medullary foam and cortex (Sullivan et al. 2017). The tubular structure is perhaps the simplest solution to maximize the stiffness at a minimal weight (Bonser 2001). However, a tubular structure is likely to fail by buckling (Bonser 2001). The foam-like lightweight medulla within the shaft is much less stiff than the cortex but also contributes to the mechanical performance of the shaft (Purslow and Vincent 1978; Bonser 2001; Lingham-Soliar et al. 2010). It has been previously shown that the removal of the medulla reduces the stiffness of the shafts by 16% (Bonser 2001). The estimated Young’s modulus of the foam showed considerable variation, ranging from 5 MPa to 1.58 GPa (Bonser 2001). The foam is expected to delay the onset of buckling under compression (Bonser 2001) and bending (Purslow and Vincent 1978) by transferring the stress from the cortical layer to medulla foams. The foams are also likely to dissipate energy and, thereby, contribute to the damping properties of the feathers.
Effect of cortex and gradient foam structure
Similar to other dynamic systems, unwanted oscillations could reduce the aerodynamic performance in flying animals (Rajabi et al. 2011, 2016; Alexander 2015). It is known that bird wings have vibration-sensitive mechanoreceptors, either at the follicle or Herbst corpuscles (Bruecker et al. 2016). Apart from the active control of energy-consuming muscles and neural systems (Alexander 2015), the feathers with damping capability could help to passively minimize undesirable vibrations. The flight feathers are anchored to the ulna and metacarpals/phalanges, where they are supplemented with muscles and sensors (Kondo et al. 2018). The higher damped base of the shaft assures the stability of the wing bone under oscillations.
A gradient of damping properties is present in the shaft. The observed structural gradients, both of the cortex wall and foams, are assumed to be responsible for the different damping properties of the three segments of the shaft. The cortex consists of multiple layers of aligned collagen fibers (Liu et al. 2015). It is plausible to assume that friction between these fibers and layers may contribute to the damping properties. The presence of ridges increases the cortex-foam interface and therein leads to increased friction between them. The filled medulla, which occupies a large part of the shaft’s cross-section, is assumed to strongly contribute to the damping properties of the shaft. The damping ratio following the size of foam cell and area ratio of the foam/cortex change in the 1st vibration mode (Figs. 4a and 7a, c). It means that the larger foam cells and the higher area ratio between foam and cortex are, the higher is the damping ratio. The higher percentage of foam structure is proportional to the higher damping ratio in the 2nd vibration mode (Figs. 4b and 7b).
Bending, shear, and buckling are the main deformation modes in the foam structure (Vincent and Owers 1986; Gibson et al. 1989; Gibson and Ashby 1997). During shaft bending, the cells situated remote from the central axis experience the highest stress (Nillsson and Nillsson 2002). At small strains, the walls elastically bend, the foam cells/struts undergo the shear deformation, and cell walls may experience no stretching. At large strains, beyond a critical value, the cells may collapse by elastic buckling and plastic yielding or even fracture. At higher strains, the cells collapse and undergo densification with rapidly increasing stiffness (Triantafillou et al. 1989; Gibson and Ashby 1997). Several mechanisms participate in the energy dissipation in foams (Schwaber 1973). Foams dissipate deformation energy across layers, reduce possible crack propagation, and delay the local buckling (Vincent and Owers 1986; Bonser 2001). The cell walls which are composed of curved weaving fibrils absorb energy known as intrinsic damping (Andersson et al. 2010). The fiber-composite cells dissipate energy by fiber pullout (Gibson and Ashby 1997). The difference under the two deflections may depend on the anisotropy of the cortex and foam-like medulla structure. The cell sizes, relative density, and anisotropy have proven to be important parameters governing the mechanical properties of the foam (Gibson and Ashby 1997).
Consequently, the combination of the cortex and the gradient foam makes the feather shaft a lightweight structure with varied damping properties. The higher damped base anchored to the bone assures the wing stability under oscillations. To decay the oscillations in flapping, avian feathers have reached certain levels of damping due to their specialized macrostructures and microstructures.
Conclusions
The feather shaft represents natural gradient material with damping properties that have been previously oversimplified in the literature. This paper provides the first indication of the graded damping properties of the shaft in feathers. Under horizontal and vertical deflections, the damping ratios at the base are highest in the 1st mode, and the maximum values were observed in the middle of the shaft in the 2nd mode. The higher damping of the base and the middle of the shaft close to the bone assures the stability of the wing under oscillations. SEM and µCT analyses were used to investigate the gradient microstructure of the shaft. The closed-cell medulla is based on curved weaving fibrils with hierarchical levels of porosity. The energy dissipation of the shaft is likely due to the deformations and the densification of foam cells. The higher damping properties are influenced by the larger foam cells, higher area percentage of the foam, and higher area ratio between the foam and cortex. This study represents the first step in exploring damping mechanisms in bird feathers. It also offers an interesting design that may inspire technical structures with adjustable damping properties.
References
Alexander DE (2015) On the wing: insects, pterosaurs, birds, bats and the evolution of animal flight. Oxford, UK
Andersson A, Lundmark S, Magnusson A, Maurer FHJ (2010) Vibration and acoustic damping of flexible polyurethane foams modified with a hyperbranched polymer. J Cell Plast 46(1):73–93
Bachmann T, Emmerlich J, Baumgartner W, Schneider JM, Wagner H (2012) Flexural stiffness of feather shafts: geometry rules over material properties. J Exp Biol 215(3):405–415
Banhart J, Baumeister J (1998) Deformation charateristics of metal foams. J Mater Sci 33:1431–1440
Beards CF (1996) Structural vibration: analysis and damping. London, UK
Bonser RHC, Purslow PP (1995) The Young’s modulus of feather keratin. J Exp Biol 198:1029–1033
Bonser RHC (2001) The mechanical performance of medulla foam from feathers. J Mater Sci Lett 20:941–942
Bragulla H, Hirschberg RM (2003) Horse hooves and bird feathers: two model systems for studying the structure and development of highly adapted integumentary accessory organs - the role of the dermo-epidermal interface for the micro-architecture of complex epidermal structures. J Exp Zool B Mol Dev Evol 298(1):140–151
Bruecker C, Schlegel D, Triep M (2016) Feather vibration as a stimulus for sensing incipient separation in falcon diving flight. Nat Resour J 7(7):411–422
Butler M, Johnson AS (2004) Are melanized feather barbs stronger? J Exp Biol 207(2):285–293
Chang WL, Wu H, Chiu YK et al (2019) The making of a flight feather: bio-architectural principles and adaptation. Cell 179(6):1409–1423
Chen Q, Gorb SN, Kovalev A, Li Z, Pugno N (2016) An analytical hierarchical model explaining the robustness and flaw-tolerance of the interlocking barb-barbule structure of bird feathers. Europhys Lett 116(2):24001
Clarke J (2013) Feathers before flight. Science 340(6133):690–692
De Silva CW (1999) Vibration: fundamentals and practice. Boca Raton, USA
Ennos AR, Hickson JRE, Roberts A (1995) Functional morphology of the vanes of the flight feathers of the pigeon Columba livia. J Exp Biol 198(5):1219–1228
Gao JL, Zhang GQ, Guan L, Chu JK, Kong DY, Bi YT (2013) Structure and mechanical property of Asio otus feather barbs. Key Eng Mater 562–565:914–919
Gao JL, Chu JK, Guan L, Shang HX, Lei ZK (2014) Viscoelastic characterization of long-eared owl flight feather shaft and the damping ability analysis. Shock Vib 709367
Gibson LJ, Ashby MF, Zhang J, Triantafillou TC (1989) Failure surfaces for cellular materials under multiaxial loads - I. Modeling Int J Mech Sci 31(9):635–663
Gibson LJ, Ashby MF (1997) Cellular solids: structure and properties. Cambridge, UK
Greenewalt CH (1960) The wings of insects and birds as mechanical oscillators. Proc Am Philos Soc 104(6):605–611
Hansen C (2018) Foundations of vibroacoustics. Boca Raton, USA
Kondo M, Sekine T, Miyakoshi T, Kitajima K, Egawa S, Seki R, Abe G, Tamura K (2018) Flight feather development: its early specialization during embryogenesis. Zoological Lett 4(1):2
Kovalev A, Filippov AE, Gorb SN (2013) Unzipping bird feathers. J R Soc Interface 11:20130988
Lingham-Soliar T, Bonser RHC, Wesley-Smith J (2010) Selective biodegradation of keratin matrix in feather rachis reveals classic bioengineering. Proc R Soc B 277:1161–1168
Liu ZQ, Jiao D, Meyers MA, Zhang ZF (2015) Structure and mechanical properties of naturally occurring lightweight foam-filled cylinder- the peacock’s tail coverts shaft and its components. Acta Biomater 17:137–151
Nillsson E, Nillsson AC (2002) Prediction and measurement of some dynamic properties of sandwich structure with honeycomb and foam cores. J Sound Vib 251(3):409–430
Pennycuick CJ (1968) Power requirements for horizontal flight in the pigeon Columba livia. J Exp Biol 49(3):527–555
Prum RO (1999) Development and evolutionary origin of feathers. J Exp Zool 285(4):291–306
Prum RO, Williamson S (2001) Theory of the growth and evolution of feather shape. J Exp Zool 291(1):30–57
Purslow PP, Vincent JFV (1978) Mechanical properties of primary feathers from the pigeon. J Exp Biol 72(1):251–260
Rajabi H, Moghadami M, Darvizeh A (2011) Investigation of microstructure, natural frequencies and vibration modes of dragonfly wing. J Bionic Eng 8(2):165–173
Rajabi H, Shafiei A, Darvizeh A, Dirks JH, Appel E, Gorb SN (2016) Effect of microstructure on the mechanical and damping behaviour of dragonfly wing veins. R Soc Open Sci 3:160006
Rao SS (2010) Mechanical vibrations. New Jersey, USA
Raspet A (1960) Biophysics of bird flight. Science 132(3421):191–200
Schwaber DM (1973) Impact behavior of polymeric foams: a review. Polymer-Plast Technol Eng 2(2):231–249
Sullivan TN, Pissarenko A, Herrera SA, Kisailus D, Lubarda VA, Meyers MA (2016) A lightweight biological structure with tailored stiffness: the feather vane. Acta Biomater 41:27–39
Sullivan TN, Wang B, Espinosa HD, Meyers MA (2017) Extreme lightweight structures: avian feathers and bones. Mater Today 20(7):377–391
Triantafillou TC, Zhang J, Shercliff TL, Gibson LJ, Ashby MF (1989) Failure surfaces for cellular materials under multiaxial loads – II Comparison of models with experiment. Int J Mech Sci 31(9):665–678
Vincent JFV, Owers P (1986) Mechanical design of hedgehog spines and porcupine quills. J Zool 210(1):55–75
Wang B, Meyers MC (2016) Light like a feather: a fibrous natural composite with a shape changing from round to square. Adv Sci 4(3):1600360
Yang W, Chao C, McKittrick J (2013) Axial compression of a hollow cylinder filled with foam: a study of porcupine quills. Acta Biomater 9(2):5297–5304
Zhang YM, Yao H, Oritz C, Xu JQ, Dao M (2012) Bio-inspired interfacial strengthening strategy through geometrically interlocking designs. J Mech Behav Biomed Mater 15:70–77
Acknowledgements
The authors would like to thank all the related members of the Institute of Functional Morphology and Biomechanics at Kiel University, Germany, and the Institute of Bioinspired Structure and Surface Engineering at Nanjing University of Aeronautics and Astronautics, China.
Funding
Open Access funding enabled and organized by Projekt DEAL. This work was financially supported by Chinesisch-Deutsches Zentrum für Wissenschaftsförderung to SNG and ZDD (Grant no. GZ1154).
Author information
Authors and Affiliations
Contributions
S.N.G. designed and coordinated the study; K.D., A.K., H.R., C.F.S., and S.N.G. designed the experiment; K.D. performed the experiment, carried out the statistical analysis, and wrote the manuscript; All authors analyzed the data, discussed the results, edited the manuscript, and gave final approval for publication.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Communicated by: Matthias Waltert
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Deng, K., Kovalev, A., Rajabi, H. et al. The damping properties of the foam-filled shaft of primary feathers of the pigeon Columba livia. Sci Nat 109, 1 (2022). https://doi.org/10.1007/s00114-021-01773-7
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00114-021-01773-7