Abstract
The high-cycle fatigue behaviour of a timber-to-timber connection with self-tapping screws is examined with the fasteners under bending due to their alignment lateral to the load direction. The cyclic tests were carried out with a sinusoidal non-reversed load (\(R=0.1\)) with a loading frequency of 5 Hz. The examined connection is designed for the quasistatic failure mechanism with two plastic hinges per shear plane according to Johansen’s theory (European Yield Model), which is mirrored in the observed fatigue failure. Based on 30 cyclic tests on four nominal stress levels \(\left( S=\left\{ 0.47,\;0.41,\;0.31,\;0.20 \right\} \right) \) in the finite-life regime the respective Wöhler-curve is obtained, showing high conformity with the test data due to a consideration of the specific density of the individual specimens. It is shown that the examined fasteners show a superior fatigue behaviour under bending compared to axial loading. A simple safe-side approach for the application of Wöhler-curves for axial loading of threaded fasteners to the present case of fastener bending is proposed, extending the field of possible applications for the results of existing and future studies of the behaviour under axial loading.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the light of a growing societal and political demand for more sustainable solutions in the construction sector, timber constructions are increasingly considered for high/performance structures that are subjected to repeated loading, for example, towers for wind energy plants (cf. Röhm et al. 2015; Schröder 2015; Christian and Aicher 2016; Gräfe et al. 2017; Sieder and Schröder 2019), heavy duty road bridges (cf. Rantakokko and Salokangas 2000; Flach and Frenette 2004; Meyer et al. 2005; Lefebvre and Richard 2014), or elevator shafts (cf. Abrahamsen and Malo 2014; Malo et al. 2016; Abrahamsen 2017). Constituting an essential advancement in timber construction fastener technology, self-tapping screws can make a crucial contribution to the fulfillment of the structural challenges that arise with the new application fields.
However, little is known about the behaviour of connections with these fasteners in the high-cycle fatigue regime, which is a decisive limit state in the design of the described structures. Previous studies on this subject are highly limited and consider either small conventional timber and furniture screws that are not suitable for high-performance structural engineering applications (Burmester and Hoffmann 1970; Trübswetter 1973; Bröker and Krause 1991), or consider the fastener itself under axial loading (Ringhofer 2017; Ringhofer et al. 2019; Niebuhr and Sieder 2020) or connections with primarily axial loading of the fasteners (Stamatopoulos and Malo 2017).
Connections with self-tapping screws are predominantly realised with an inclined orientation of the fasteners with regard to the load direction to achieve mainly axial loading in the screws. This configuration yields higher strength and stiffness values than a lateral orientation of the fasteners which subjects them predominantly to bending. If, however, fatigue failure is considered, threaded metallic fasteners under bending generally show a behaviour that is superior to that under axial tension (cf., e.g., Schaumann and Marten 2009) which could privilege the lateral orientation of the fastener in cases where material fatigue needs consideration. In this contribution, a timber-to-timber connection with self-tapping screws under mainly lateral loading will be examined to form a first empirical basis for the comparison of the fatigue performance of timber connections with lateral and axial loading of the fasteners.
A previous study (Niebuhr and Sieder 2020) that examined the same fasteners under axial loading will later be complemented by an ongoing examination of the withdrawal behaviour of the fasteners in spruce wood. That way, all possible failure mechanisms of connections with an inclined orientation of the fasteners have been examined, allowing for a full characterisation of these connections, which can then be compared to connections with lateral loading as examined in this contribution.
2 Material and methods
2.1 Material
The examined fasteners are fully threaded self-tapping screws with a nominal outer thread diameter of \(d_n=6\) mm and length \(l=120\) mm with a cylindric head according to ETA-12/0114 (2017). In a sample with 23 specimens, the mean values of outer thread diameter, core diameter, flank inclination angle, head diameter and pitch have been determined as \(d=5.96\) mm, \(d_c=4.01\) mm, \(\nu =39.59^\circ \), \(d_k=8.15\) mm, and \(p=3.60\) mm. The tensile strength of the material was determined as \(\sigma _{u,mean}=1236.9\) N/mm\(^2\) with \(CV_{\sigma u}=1.36\%\) in a previous study (Niebuhr and Sieder 2020).
The wooden specimens were manufactured from kiln dried spruce wood (Picea abies). Prior to specimen manufacturing, the material was stored in standard climate 20/65 (DIN 50014:2018-08 2018) until mass equilibrium was reached, and was stored in the same climate between manufacturing and testing. All specimens with visible imperfections such as knots, checks, excessive slope of grain etc. were neglected so that small clear specimens can be assumed. All tests were performed in standard climate 23/50 (DIN 50014:2018-08 2018). The mean density of the specimens was determined as \(\rho _{N,mean}=473.9\) kg/m\(^3\) with \(CV_{\rho }=11.06\%\). Figure 1 shows the distribution of \(\rho _N\) for all specimens, divided into the test series samples.
Distribution of the specimen density at standard climate 20/65 (DIN 50014:2018-08 2018)
2.2 Test setup
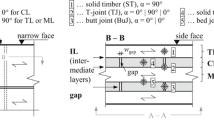
The examined connection is a timber-to-timber connection with mainly lateral loading of the screws, i.e. the screws are oriented perpendicular to the load direction; the test setup is shown in Fig. 2.
The load is introduced as a compression force on the middle member and the outer members are supported vertically. To prevent unwanted axial forces in the fasteners due to the excentric load introduction into the side members, steel profiles have been set out to act as horizontal supports for the outer members, shown as ideal horizontal supports in Fig. 2. To ensure that the fasteners bear as much of the outer load as possible, the surface between middle and outer members has been lined with a thin PTFE-layer (\(t=0.20\) mm) to minimise friction. Thin plywood battens (also lined with PTFE) were set out in the lower part of the specimens to prevent a rotation of the members around the fastener axis. The displacement in the shear planes was measured with four inductive displacement sensors, one on each side of each shear plane, see Fig. 2. Any mentioned displacement value is a mean value of these four points.
Spacings and edge distances of the fasteners fulfill the requirements in ETA-12/0114 (2017); the thickness of the outer members and the penetration depth in the middle member were chosen in accordance with Eq. (NA.110) of the German National Annex to EN 1995-1-1:2004+A1:2008 (2008) (DIN EN 1995-1-1/NA:2013-08 2013) to ensure two plastic hinges per shear plane according to Johansen’s theory (European Yield Model, cf. Johansen 1949):
Based on the mean density of the specimen material, the embedment strength was assumed as \(f_{h,mean}=26.7\) N/mm\(^2\) according to Blaß et al. (2006). The fastener yield moment was assumed as the characteristic value in ETA-12/0114 (2017), \(M_{y,Rk}=16{,}000\) Nmm, because a mean value was not available. As the chosen test setup is planned to be used in a later study with inclined screws, the penetration depth in the middle member was increased by \(1.17\cdot d=7\) mm in accordance with Pirnbacher et al. (2009), who proposed considering the influence of the fastener tip on the withdrawal behaviour of self-tapping screws with a reduction factor \(k_{length}=1.17\cdot d\). This is not assumed to influence the behaviour under lateral loading considerably and was done to ensure maximal comparability between the tests with fasteners aligned perpendicular to the load direction and later tests with inclined fasteners.
Preliminary to the cyclic tests, the quasistatic capacity of the specimens was determined in 13 ramp tests according to EN 26891:1991-07 (1991) (Series Lstat).
2.3 Experimental programme
The fatigue behaviour of the considered connection was examined in three series of cyclic tests as shown in Table 1. The stress level \(S=F_{max}/F_{ult}\) was determined with the quasistatic ultimate capacity \(F_{ult,mean}\) from Series Lstat. The ratio between minimal and maximal loading (stress ratio) was set to \(R=0.1\)which is close to the most damaging non-reversing loading for timber structures (cf. empirical data by, e.g., Sterr 1963; Tsai and Ansell 1990; Bonfield and Ansell 1991; Bond and Ansell 1998 or general assessments by Kreuzinger and Mohr 1994 and Smith et al. 2003). Reversed loading was omitted to keep the load introduction simple. The chosen loading frequency is \(f=5\,Hz\) in all cyclic tests. Because the load cycle numbers at failure in the first tests were smaller than the commonly assumed threshold for high-cycle fatigue phenomena of metallic specimens (\(N<1.0E4\), see e.g., Collins 1993), the stress level of the subsequent tests in that series was adjusted and the first tests are separately considered as Series Ldyn,0. All cyclic tests were performed as force-controlled tests with sinusoidal loading at MFPA Leipzig GmbH on a walter + bai servo-hydraulic test rig (type LFV-5) with a maximum capacity of 7.5 kN. In compliance with the quasistatic reference tests the chosen termination criterion is a displacement of \(u=15\) mm.
3 Results
3.1 Quasistatic tests
Figure 3 shows the array of \(F-u\)- curves of the quasistatic tests. Note, that the discontinuity at ca. 5.5 kN is the transition from force-controlled testing to displacement-controlled testing. In all tests, the displacement threshold of \(u=15\) mm was decisive for the determination of the ultimate capacity, which was determined as
The individual results of the quasistatic tests in Series Lstat are given in Table 2. An evaluation of the opened specimens after testing showed plastic deformation in the fasteners at 47 of the 52 expected plastic hinge locations (ca. 90%). However, as the tests were not aborted at \(u=15\) mm but were continued up to \(u\approx 20\) mm, a proportion of these observed plastic hinges might have formed after reaching the respective ultimate capacity.
Influence of \(\rho _{N}\) on \(F_{ult}\) (\(\rho _{N,mean,i}\) acc. to Eq. 3)
As shown in Fig. 4, the observed ultimate capacity shows a distinct dependence on the density of the individual specimen, which can satisfactorily be explained by the influence of the specimen density on the embedment strength. In order to estimate the individual quasistatic capacity of each specimen in the cyclic test series, a linear regression was performed on the results from Series Lstat, yielding the following relation between specimen density and quasistatic capacity (\(R^2=0.9147\)):
Here, a mean value for the density of the individual specimens (each comprised of three wooden members: two side members [sm] and one middle member [mm]) was assumed. First, the individual geometric mean density for both shear planes was calculated analogous to the consideration of different densities when determining \(K_{ser}\), cf. EN 1995-1-1:2004+A1:2008 (2008) 7.1 (2); then, the arithmetic mean of the values for both shear planes was determined:
In the subsequent description of the results of the cyclic tests, the stress level will be individually evaluated for each test, determining the quasistatic capacity with Eq. 2 and the individual mean density of the respective specimen. These individually determined stress levels are indicated with an asterisk \(S^*\).
3.2 Cyclic tests
3.2.1 Failure modes
In all cases, ultimate failure in the cyclic tests occurred through tear off of the screws due to the cyclic bending. Failure was observed at two points in each screw, one on each side of the shear plane, analogous to the desired pairs of plastic hinges according to Johansen’s theory under ultimate quasistatic load, see Fig. 5.
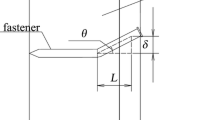
While in most cases full separation was observed, in a few cases failure occured only as a distinct crack on the tension side of the screw. With decreasing stress level, the location of the points of failure was observed to be closer to the shear plane, see Fig. 6.
Figure 7 shows the progression of the deformations at maximum load during cyclic testing. To compensate for the different magnitudes of load cycle numbers and deformations, the graphs of all tests are normalised with regard to both axes. The load cycle numbers are displayed relative to the individual ultimate load cycle number \(N_{i}/N\) and the deformations are displayed relative to the mean deformation \(u_{mean}\) between \(0.15\cdot N\) and \(0.75\cdot N\) of every test during which the deformations are quite stable. The individual values of \(u_{mean}\) are given in Table 3.
3.2.2 Load cycle numbers
The load cycle numbers at failure of the individual tests are given in Table 3 and displayed in Fig. 8. In Fig. 8, the four tested load levels (cf. Table 1) cannot readily be identified, because the ordinate displays the individual stress levels \(S^*\), determined with \(F_{ult,i}\) according to Eq. 2. This yields an individual effective stress level for each specimen, even though the absolute loading is the same within each series Ldyn,i.
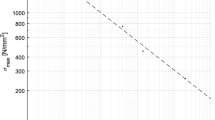
Since failure essentially occurs in the metallic fasteners, assuming a linear relation between the logarithmic values of loading and load cycle numbers was identified as the most promising approach for a continuous description of the test results. A linear regression was performed with the logarithmic \(S^*-N\)-data, yielding the following relation for a failure probability of \(P_A=50\,\%\) (\(R^2=0.939\)):
Although the linear regression is based on the double-logarithmic data, a linear scale is chosen for the ordinate (\(S^*\)) in Fig. 8 to comply with the common form of \(S-N\)-curves in timber construction. The chosen \(S^*-N\)-relation also accounts for a possible influence of the fatigue behaviour of the embedment in the wood. Beyond that, an evaluation of the stress amplitude in the fasteners (the ordinary approach in the evaluation of metal fatigue) is only possible with limited reliability. Both of these aspects will be further discussed in Sect. 4. Analogous to the pearl string method in DIN 50100:2016-12 (2016), the standard deviation of the logarithmic load cycle numbers at failure over all tests was determined as \({\tilde{s}}_{logN,corr}=0.1922\) (corrected according to Martin et al. 2011 to compensate for the limited sample size). This approach is based on the assumption that the respective standard deviation is constant in the finite-life regime. A summary of the different testing and evaluation approaches in DIN 50100:2016-12 (2016) and the underlying assumptions has been given by Masendorf and Müller (2018).
To allow for a comparison of the given test results in bending and the results in axial tension from an earlier study (Niebuhr and Sieder 2020), the axial bending stresses in the fasteners shall be assessed. The analytical determination of the cross-sectional screw properties is not trivial and has been described extensively by Ringhofer (2017). Figure 9 shows the chosen coordinates and the considered cross-section. For the fastener given here (see Sect. 2), the moments of inertia have been determined as
With the location of the cross-section’s local centre of gravity (\(y_s=0/z_s=-0.22\,mm\)), the section moduli are
Considered cross-section and coordinates for the determination of cross-sectional properties (adapted from Ringhofer 2017)
To estimate the bending moment in the fasteners during the cyclic tests, a simple numerical beam-on-springs-model was used (implemented in the software package DLUBAL RFEM). The fasteners were modelled as cylindric beams with linear elastic behaviour (\(E=210\) GPa) and diameter \(d=d_c=4.01\) mm. The embedment was modelled with discrete nonlinear spring elements (spaced 1 mm apart), estimating the load-slip behaviour with the following equation:
Equation 7 is taken from Blaß et al. (2006) for the chosen geometric conditions. Initial slip \(w_s=0.022\) mm is considered in \(w'=w-w_s\). To account for the pronounced influence of the specimen density on \(f_h\), the specimens were grouped into five classes with respect to their mean density \(\rho _{N,mean,i}\). For each class, a nominal embedment strength and respective load-slip diagram was estimated and considered in the numerical determination of the bending moments:
Figure 10 shows the assumed load-slip diagrams.
The determined location of the maximal bending moment in the screw is shown in Fig. 6. It can be seen that the distance between the shear plane and the theoretical location of the maximal bending moment increases with increasing stress level \(S^*\). However, the observed distance between location of failure and shear plane is generally smaller than between the shear plane and the numerically determined location of the maximal bending moment, see also Fig. 5. Possible reasons for this discrepancy will be discussed in Sect. 4.
4 Discussion
4.1 Progression of deformation
As seen in Fig. 7, the deformations at \(F_{max}\) of most specimens are stable for most of the fatigue life and a considerable rise in deformations is observed only shortly before ultimate failure. In a small number of tests, however, an abrupt rise of deformations is seen considerably before ultimate failure, followed by a stabilisation on a higher deformation level. Obviously, considerable damage has occured before ultimate failure in these tests, with ultimate failure probably only deferred by the redundant nature of the chosen test setup with two fasteners.
A possible approach to considering this phenomenon is to choose a different termination criterion in the fatigue tests, for example, a certain deformation increment between load cycles or a smaller absolute deformation. However, because the stress level in the fatigue tests is defined by the quasistatic ultimate capacity determined in Series Lstat, compliance between the failure criteria in the static and dynamic test series is prioritised, which is why the original failure criterion (\(u=15\) mm) was maintained in the fatigue tests. As the described premature damaging occured only in a small fraction of the tests, the effective influence on the overall evaluation is assumed to be small.
4.2 Location of failure
Quantitatively, the observed shift of the location of failure towards the shear plane with decreasing stress level \(S^*\) as shown in Fig. 6 is plausible, given that the embedment stiffness decreases with increasing embedment stress (cf. Fig. 10). For smaller stress levels the embedment stiffness is higher in relation to the bending stiffness of the fastener, which is assumed to be constant in the linear elastic regime. With increasing embedment stiffness, the location of the maximal bending moment moves closer to the shear plane, ultimately yielding the ideal bearing-type connection assumed for bolted steel connections, where no bending in the fastener is considered (Petersen 2013).
As mentioned, a discrepancy between the observed location of failure and the theoretical location of the maximal bending moment in the fastener was observed (cf. Figs. 5, 6 ). On average, the failure location is \({\varDelta }_{u\vert M}=3.72\) mm closer towards the shear plane than the numerically estimated maximal bending moment. Considering the individual values of \({\varDelta }_{u\vert M}\) for all fatigue tests, given in Table 3 as a mean value of the four failure locations per specimen, the discrepancy tends to be bigger for smaller stress levels \(S^*\). While the reason(s) for the observed discrepancy could not definitively be found, some possible explanations will be discussed:
-
1.
Deficiencies in the numerical simulation Obviously, the chosen numerical beam-on-springs-model is a gross simplification of the reality, especially with regard to the fatigue behaviour of the embedment of the fastener in the wood. However, given that the standard deviations for the load-slip-curve parameter given by Blaß et al. (2006) are small, the estimation of this behaviour is thought to be sufficiently accurate.
-
2.
Gaping shear plane Due to imperfect manufacturing and possibly also due to unexpected (and unnoticed) lateral deformations during testing, an open gap between side members and middle member of the specimens (in the shear plane) cannot be neglected. At a minimum, the members are kept at a certain distance by the PTFE-layer, although this alone (\(t=0.20\) mm) is not enough to justify the observed discrepancy \({\varDelta }_{u\vert M}\). However, considering any gaping joint yields a maximal bending moment that lies closer to the shear plane, allowing to assign a partly explanation to this aspect.
-
3.
Random scatter of crack initiation nuclei in the fastener The location of a fatigue crack in metals is bound to the existence of a crack initiation nucleus in the material such as dislocations and vacancies (Forsyth 1969). A certain proportion of these points is assumed to be randomly distributed along the idealised longitudinal axis of the fastener (disregarding geometrical effects such as notches formed by the thread and other effects such as work hardening). In a previous study of the fatigue behaviour of the given fasteners under axial tensile loading (Niebuhr and Sieder 2020), failure was observed to occur anywhere between the 2nd and 22nd thread (counting from head to tip), which is assumed to be reasoned by the natural scatter of crack initiation nuclei. The same can be applied here, certainly explaining some of the scatter of the location of failure. Additionally, with increasing deformation, an increasing proportion of the external load is borne as axial forces in the fasteners due to the rope effect, reducing the relative influence of the bending stresses in the fastener due to superposition of the stresses. However, as the observed failure locations are generally on one side of the theoretical location, natural scatter alone is an unsufficient explanation for the discrepancy.
-
4.
Influence of geometric and metallurgical notches Given that the surface geometry of the specimen has a major influence on the crack initiation, a deviation of the failure locations in the magnitude of the thread pitch \(p=3.60\) mm would be plausible as this is the interval in which the geometric shape of the fastener repeats along the axis. However, the scatter range is about three times bigger than that (cf. Fig. 6), moreover, the deviation is only to one side of the theoretical location, see above.
-
5.
Accumulated deformation in the wood close to the shear plane Smith et al. (2003) describe that under compressive fatigue loading parallel to grain an accumulation of deformations can be observed in spruce wood (findings based on Gong 2000). Assuming that this is also valid for the given embedment in the wood (the load is oriented parallel to the grain as well), the aforementioned gaping shear plane effect might be considerably intensified by local fatigue damage of the wood fibers close to the shear plane (cf. Fig. 11), effectively leading to the described gaping shear plane without an externally visible gap. This effect would assign a non-negligible influence on the behaviour of the connection to the fatigue behaviour of the wood, as it governs the alteration of the fastener loading during the progression of the test.
Given the described discrepancy between the location of failure and the theoretical location of the maximum bending moment, the determination of axial bending stresses in the fastener must be discussed. Due to the uncertainties described above, the exact magnitude of the bending moment in the fastener at the location of failure is unknown. Additionally, the appropriate section moduli of the screw are unknown as the orientation of the screw (with regard to rotation around its longitudinal axis) is unspecified; Eq. 6 gives only the extreme values. Hence, the axial bending stresses in the fastener at the location of failure are estimated as a limit value consideration, determining the minimal and maximal realistic magnitude of the stress amplitudes for every specimen.
The maximum limit value of the bending moment in the fastener \(M_{max}\) is assumed as the maximum value from the simulation, regardless of its location. The minimum limit value \(M_{loc}\) is assumed as the value from the simulation at the point where failure was observed in the test. Both values are shown in Fig. 5. As to the section moduli, the minimal and maximal values from Eq. 6, \(W_y\) and \(W_z\), are used, corresponding to the most favourable and most unfavourable axial orientation of the fastener (cf. Fig. 9). With these quantities, the minimum limit value of the axial bending stress at maximum external force \(F_{max}\) is determined with the minimal bending moment and the maximal section modulus:
Accordingly, the maximum limit value at maximum external force \(F_{max}\) is determined with the maximal bending moment and the minimal section modulus:
All of these considerations were undertaken for the stresses under the maximal external force in the load cycle \(F_{max}\). Neglecting some of the aforementioned nonlinearities, the stresses at \(F_{min}=F_{max}\cdot R\) are assumed as
which yields
for the limit values of the stress amplitude. Equation 11 was used to determine the axial bending stress amplitudes in Fig. 12, showing the minimal and maximal values as a range of uncertainty. A linear regression of the logarithmic \(\sigma _a-N\)-data yielded the following relations for the minimum \((R^2=0.955)\) and maximum \((R^2=0.945)\) limit values:
4.3 Comparison axial tension and bending
Figure 12 shows the derived \(\sigma _a - N\)-Wöhler-curves in the classical double-logarithmic form for metals, displaying the stress amplitude on the ordinate. The results are compared to the corresponding Wöhler-curve for the tested screw under axial tension from an earlier study (Niebuhr and Sieder 2020). It is obvious that the observed behaviour under bending is superior to that under comparable axial tension. This complies with existing findings on the behaviour of steel bolts that have been extensively examined for applications with combined loading such as bolted ring flange joints in towers for wind energy plants (cf. Agatonovic 1973; Frank 1980; Kampf 1997; Seidel 2001; Alt 2005; Berger et al. 2008; Schaumann and Marten 2009; Eichstädt 2019). As stated by the named authors, and shown in Fig. 12, the fatigue behaviour of threaded fasteners under bending and under combined axial and bending loading can be characterised on the safe side using a Wöhler-curve for pure axial loading, as long as for combined loading the additional stress due to the bending component is considered in the determination of the stress in the fastener. This approach will be used in the next section.
4.4 Verification and design
At first, the Wöhler-curve given for nailed connections in EN 1995-1-1:2004+A1:2008 (2008) shall be viewed as it might be considered appropriate for the verification of connections with self-tapping screws. As seen in Fig. 8, the EC-curve lies on the unsafe side of the obtained test results, clearly dismissing it for a verification of the tested fastener. This can satisfactorily be explained by the negative influence of the geometric notch that is formed by the threads as well as metallurgical notches formed during manufacturing of the fasteners. Hence, a dedicated design curve for self-tapping screws or threaded fasteners in general is necessary.
Obviously, for the specific examined fastener, Eq. 4 yields the most accurate verification of timber-to-timber connections with lateral loading of the fastener. However, as described in Sect. 1, empirical data for the fatigue behaviour of threaded fasteners in timber construction is primarily available and easier obtainable for axial loading. Hence, a simple safe-side approach for the verification of lateral fastener loading using axial Wöhler-curves is presented to allow for a utilisation of this more readily available type of data if connections with other fasteners shall be assessed.
As mentioned in the previous section, an axial Wöhler-curve is sufficient for a safe-side estimation of the fatigue behaviour of the fastener under bending. These curves generally describe a \(\sigma _a-N\)-relation which will be transferred into an \(S-N\)-form in order to comply with the common form in timber construction. The stress amplitude from Eq. 11 is rearranged and multiplied with the minimum value of the section modulus to derive a respective maximum bending moment in the description of the material behaviour:
For a simplified estimation of the bending moment in a fastener under a given external force, a linear approach is proposed. It is based on the ultimate capacity \(F_{ult}\) (determined with a method of choice, e.g., according to EN 1995-1-1:2004+A1:2008, 2008) and the yield moment of the fastener \(M_{y,R}\) (e.g., as given in the respective technical assessment). The bending moment in the fastener is assumed to decrease linearly with decreasing external loading which yields
for the maximum force in a load cycle, yielding
and thus (Eq. 13\(\rightarrow \)14)
Assuming \(M_{y,Rk}=16{,}000\) Nmm for the examined fastener, this approach estimates the numerically estimated bending moment at the failure location \(M_{loc}\) with a mean error of 2.0% (\(CV=10.59\%\)). Considering the extent of the conservativeness of the \(\sigma _{a,axial}\)-curve compared to the \(\sigma _{a,lateral}\)-curve in Fig. 12, this approach can be seen as reasonable.
Exemplarily, the proposed approach will be shown for the examined fastener, as the Wöhler-curve for axial loading is available from an earlier study (Niebuhr and Sieder 2020). There, the \(\sigma _a-N\)-relation for failure in the threaded part of the fastener was determined as
Considering Eq. 15 and \(W_{z}=\pm 6.5\) mm\(^3\) (Eq. 6), Eq. 16 can be written as
Figure 8 shows the Wöhler-curve given by Eq. 17. Clearly, the simplified approach yields a highly conservative estimation of the behaviour under lateral loading. However, if no other empirical data is available for a specific fastener, but a lateral orientation is desirable (e.g., because of space limitation in the members), the proposed approach enables a safe-side estimation of the fatigue behaviour.
5 Conclusion
The fatigue behaviour of a timber-to-timber connection with self-tapping screws under lateral loading was examined in the finite-life regime. The design of the connection was successfully aimed at a decisive quasistatic failure mode with two plastic hinges per shear plane according to Johansen’s theory, which was mirrored in fatigue failure. The Wöhler-curve for the examined connection was obtained on the basis of 30 fatigue tests with load cycle numbers ranging from 5.00E3 to 2.97E6, whereby the consideration of the individual density of the specimens enabled a continuous description of the results with a high accuracy.
An inspection of the obtained results with regard to the stress in the fastener enabled a comparison with the behaviour of the fastener under axial loading. The general understanding that the fatigue behaviour of threaded fasteners under bending is superior to that under axial loading could be confirmed for the examined fastener. On this basis, a simple safe-side approach for the utilisation of axial Wöhler-curves for connections with lateral loading of the fastener was proposed, allowing to use these results for a wider range of applications.
As described in Sect. 1, a full comparison between connections with lateral and axial loading of the examined fastener has to consider results from an ongoing examination of the withdrawal behaviour of the screw. This will allow for a qualitative and quantitative assessment of the superiority of either configuration with regard to fatigue failure.
Apart from this, it has to be emphasised that an unreserved validity of the obtained results is only given for the specific screw that was examined. Differences in geometry, material, manufacturing and other aspects (cf. Ringhofer 2017) certainly influence the behaviour of different fasteners. For axial loading, this assumption has been confirmed by Niebuhr and Sieder (2020), comparing their test data with similar data from Ringhofer et al. (2019), although a certain affinity of the behaviour of the considered screws was apparent. An extensive experimental study of a wide variety of screws might enable a general description of this type of fasteners, similar to the detail categories in EN 1993-1-9:2005 + AC:2009 (2009) or the respective general consideration of nailed connections and connections with dowels in EN 1995-1-1:2004+A1:2008 (2008). The results given here are only one of many contributions that are neccessary for this extensive study.
Availability of data and material
Not applicable.
Code availability
Not applicable.
References
Abrahamsen RB (2017) Mjøstårnet—construction of an 81 m tall timber building. In: Proc 23. int Holzbau-forum 2017
Abrahamsen RB, Malo KA (2014) Structural design and assembly of Treet—a 14-storey timber residential building in Norway. In: WCTE 2014 conf proc
Agatonovic P (1973) Verhalten von Schraubenverbindungen bei zusammengesetzter Betriebsbeanspruchung [Behaviour of bolted connections under combined fatigue loading] (in German). PhD thesis, Technische Universität Berlin
Alt A (2005) Dauerfestigkeitsprüfung und Dauerfestigkeit von Schraube-Mutter-Verbindungen unter kombinierter Zug- und Biegebelastung [Fatigue limit and fatigue limit evaluation of bolt and nut connections under combined tension and bending] (in German). PhD thesis, Technische Universität Berlin
Berger C, Schaumann P, Stolle C, Marten F (2008) Experimentelle Ermittlung von Wöhlerlinien großer Schrauben [Fatigue strength of high strength bolts with large diameters] (in German): Report ZP 52-5-16.125-1231/06. DIBt, Berlin
Blaß HJ, Bejtka I, Uibel T (2006) Tragfähigkeit von Verbindungen mit selbstbohrenden Holzschrauben mit Vollgewinde [Strength of connections with self-tapping full-threaded timber screws] (in German). Univ.-Verl. Karlsruhe
Bond IP, Ansell MP (1998) Fatigue properties of jointed wood composites: part I statistical analysis, fatigue master curves and constant life diagrams. J Mater Sci 33(11):2751–2762. https://doi.org/10.1023/A:1017565215274
Bonfield PW, Ansell MP (1991) Fatigue properties of wood in tension, compression and shear. J Mater Sci 26(17):4765–4773. https://doi.org/10.1007/BF00612416
Bröker FW, Krause HA (1991) Orientierende Untersuchungen über das Haltevermögen dynamisch beanspruchter Holzschrauben [Orienting exaxmination of the capacity of timer screws under danymic loading] (in German). Holz Roh Werkst 49(10):381–384. https://doi.org/10.1007/BF02608920
Burmester A, Hoffmann A (1970) Schraubenhaltevermögen von Kiefern- und Fichtenholz unter langdauernder statischer und dynamischer Belastung [Pull-out capacity of pine and spruce under static and dynamic loading] (in German). Die Holzbearbeitung HOB 17(5):9–11
Christian Z, Aicher S (2016) Fatigue behaviour of timber composites and connections for ultra high wooden towers. In: WCTE 2016 conf proc
Collins JA (1993) Failure of materials in mechanical design: analysis, prediction, prevention, 2nd edn. Wiley, New York
DIN 50014:2018-08 (2018) Normalklimate für Vorbehandlung und/oder Prüfung—Festlegungen [Standard atmospheres for conditioning and/or testing—specifications] (in German)
DIN 50100:2016-12 (2016) Load controlled fatigue testing—execution and evaluation of cyclic tests at constant load amplitudes on metallic specimens and components (in German) https://doi.org/10.15488/5157
DIN EN 1995-1-1/NA:2013-08 (2013) National Annex—Nationally determined parameters—Eurocode 5: design of timber structures—Part 1-1: general—common rules and rules for buildings (in German)
Eichstädt R (2019) Fatigue assessment of large-size bolting assemblies for wind turbine support structures. PhD thesis, Universität Hannover. https://doi.org/10.15488/5157
EN 1993-1-9:2005 + AC:2009 (2009) Eurocode 3: design of steel structures—part 1-9: fatigue
EN 1995-1-1:2004+A1:2008 (2008) Eurocode 5: design of timber structures—part 1-1: general—common rules and rules for buildings
EN 1995-2:2004 (2004) Eurocode 5: design of timber structures—part 2: bridges
EN 26891:1991-07 (1991) Timber structures; joints made with mechanical fasteners; general principles for the determination of strength and deformation characteristics (ISO 6891:1983)
ETA-12/0114 (2017) European Technical Assessment: SPAX self-tapping screws
Flach M, Frenette CD (2004) Wood-concrete-composite-technology in bridge construction. In: WCTE 2004 conf proc, pp 289–294
Forsyth PJE (1969) The physical basis of metal fatigue. Blackie & Son, London
Frank KH (1980) Fatigue strength of anchor bolts. J Struct Div 106(6):1279–1293
Gong M (2000) Failure of spruce under compressive low-cycle fatigue loading parallel to grain. PhD thesis, University of New Brunswick
Gräfe M, Bert C, Winter S (2017) Prestressed CLT wind-turbine towers. Bautech 94(11):804–811. https://doi.org/10.1002/bate.201700080
Johansen KW (1949) Theory of timber connections. IABSE Publ 9:249–262. https://doi.org/10.1002/bate.201700080
Kampf M (1997) Dauerhaltbarkeit von Schrauben unter kombinierter Zug- und Biegebelastung [Fatigue limit of bolts under combined tension and bending] (in German). PhD thesis, Technische Universität Berlin
Kreuzinger H, Mohr B (1994) Holz und Holzverbindungen unter nicht vorwiegend ruhenden Einwirkungen [Timber and timber connections under repeated loading] (in German): Report. Technische Universität München
Lefebvre D, Richard G (2014) Design and construction of a 160-metre-long wood bridge in Mistissini, Québec. In: Proc 20 int Holzbau-forum 2014
Malo KA, Abrahamsen RB, Bjertnæs MA (2016) Some structural design issues of the 14-storey timber framed building Treet in Norway. Eur J Wood Wood Prod 74(3):407–424. https://doi.org/10.1007/s00107-016-1022-5
Martin A, Hinkelmann K, Esderts A (2011) Zur Auswertung von Schwingfestigkeitsversuchen im Zeitfestigkeitsbereich—Teil 2 [On the evaluation of fatigue tests in the finite-life regime—part 2] (in German). Mater Test 53(9):513–521. https://doi.org/10.3139/120.110256
Masendorf R, Müller C (2018) Execution and evaluation of cyclic tests at constant load amplitudes—DIN 50100:2016. Mater Test 60(10):961–968. https://doi.org/10.3139/120.111238
Meyer L, Morzier C, Tissot JB (2005) Holz-Beton-Verbundbrüclen für den 40t-Verkehr im Kanton Freiburg (Schweiz) [40-ton wood-concrete composite bridges in Canton Fribourg] (in German). In: Proc 11. int Holzbau-forum 2005
Niebuhr P, Sieder M (2020) High-cycle fatigue behavior of a self-tapping timber screw under axial tensile loading. J Fail Anal Prev 20(2):580–589. https://doi.org/10.1007/s11668-020-00863-4
Petersen C (2013) Stahlbau [Steel construction] (in German). Springer, Wiesbaden https://doi.org/10.1007/s11668-020-00863-4
Pirnbacher G, Brandner R, Schickhofer G (2009) Base parameters of self-tapping screws: CIB-W18: paper 42-7-1. Dübendorf
Rantakokko T, Salokangas L (2000) Design of the Vihantasalmi Bridge, Finland. Struct Eng Int 10(3):150–152. https://doi.org/10.2749/101686600780481590
Ringhofer A (2017) Axially loaded self-tapping screws in solid timber and laminated timber products. PhD thesis, TU Graz
Ringhofer A, Augustin M, Schickhofer G (2019) Basic steel properties of self-tapping timber screws exposed to cyclic axial loading. Constr Build Mater 211:207–216
Röhm J, Brand S, Kunz F (2015) Hoher Züblin-Windkraft-Turm aus Holz [Züblin wooden wind power tower] (in German). In: Proc 21 int Holzbau-forum 2015
Schaumann P, Marten F (2009) Fatigue resistance of high strength bolts with large diameters. In: Proc int symp for steel struct
Schröder C (2015) Ermüdungsbeanspruchte Brettsperrholz-Bauteile am Beispiel eines Turms für Windkraftanlagen [Wooden and wood hybrid towers for wind turbines in the multi-megawatt class] (in German). In: Proceeding 21. int Holzbau-forum
Seidel M (2001) Zur Bemessung geschraubter (Ringflanschverbindungen von Windenergieanlagen [On the verification of bolted ring flange connections in wind energy plants] (in German). PhD thesis, Universität Hannover
Sieder M, Schröder C (2019) TimberTower: Erfahrungen aus Konstruktion und Betrieb der ersten Windkraftanlage mit Holzturm [TimberTower: Experience from construction and operation of the first wind energy plant with wooden tower] (in German). In: Proc 25. Int Holzbau-Forum 2019, pp 259–272
Smith I, Landis E, Gong M (2003) Fracture and fatigue in wood. Wiley, Chichester
Stamatopoulos H, Malo KA (2017) Fatigue strength of axially loaded threaded rods embedded in glulam at \(45^\circ \) to the grain. In: Proc int conf on timber bridges 2017
Sterr R (1963) Untersuchungen zur Dauerfestigkeit von Schichtholzbalken [Investigations on the fatigue resistance of laminated wood beams] (in German). Holz Roh Werkst 21(2):47–61. https://doi.org/10.1007/BF02609715
Trübswetter T (1973) Klammern als Holzverbinder bei wechselnden Lasten [Tacks as timber fasteners under alternating loading] (in German). HK Holz- und Kunststoffverarbeitung 7(5)
Tsai KT, Ansell MP (1990) The fatigue properties of wood in flexure. J Mater Sci 25(2):865–878. https://doi.org/10.1007/BF03372174
Acknowledgements
The authors wish to thank SPAX International GmbH & Co. KG for the provision of the tested fasteners.
Funding
Open Access funding enabled and organized by Projekt DEAL. This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—397985109. The tested fasteners were provided by SPAX International GmbH & Co. KG.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Niebuhr, P., Sieder, M. High-cycle fatigue behaviour of a timber-to-timber connection with self-tapping screws under lateral loading. Eur. J. Wood Prod. 79, 785–796 (2021). https://doi.org/10.1007/s00107-021-01699-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00107-021-01699-x