Abstract
In this study, the relatively new picture frame method applied to wood is compared with three established shear test methods, namely the experimental modal analysis, the square plate twist method and the torsion test. For the investigations, the wood species European beech (Fagus sylvatica L.) and spruce (Picea abies L. Karst.) were used and the shear tests were conducted in LR and RL direction. The results show comparable shear moduli for beech and spruce in the range of 931–1289 Nmm−2 and 495–842 Nmm−2, respectively. In contrast to the theory of linear elastic orthotropic materials, significant differences in the results of the picture frame method between LR and RL direction were observed for spruce.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
There is currently no valid European standard for determining the shear modulus of small clear wood samples. Many methods of direct or indirect determination have been investigated in the past. Indirect methods are used to determine the shear modulus as a by-product when measuring other mechanical properties such as bending tests (Brabec et al. 2017). A detailed literature review is given by Brabec et al. (2017) and Krüger et al. (2018). The following test methods are currently known for testing shear modulus of wood: torsion test (Stamer and Siegelschmidt 1935; Schwab and Polaczek 1977; Grimsel 1999; Brabec et al. 2017); off-axis tension test (Yoshihara and Ohta 2000; Xavier et al. 2004); three-point bending with different width/span ratios (Yoshihara et al. 1998); standard four-point bending with shear field evaluation between upper and lower support (DIN EN 408 2012; Brandner et al. 2008); four-point asymmetric bending (Yoshihara and Kubojima 2002); Iosipescu test (Xavier et al. 2004; Yoshihara et al. 2001); Arcan test (Müller et al. 2015; Xavier et al. 2009); rolling shear test setup according to ASTM D1037 (Sretenovic et al. 2004); square-plate twist test (Bodig and Jayne 1982; Yoshihara and Sawamura 2006); picture frame method (Krüger et al. 2018); experimental modal analysis (Nakao and Okano 1987; Yoshihara 2009) and methods using ultrasonic waves (Bucur and Archer 1984; Keunecke et al. 2007; Hering et al. 2012; Longo et al. 2018). Only a few of these methods produce a quite uniform shear deformation state (Arcan, Iosipescu, Torsion, picture frame).
Krüger et al. (2018) showed, in the application to wood, a new method for the determination of shear properties. An established method, the picture frame method for fibre-reinforced composites (DIN SPEC 4885 2014), was used and adapted to wood. It is suitable for investigating both shear modulus and shear strength. There is currently no direct comparison of this new method with other established methods for determining the shear modulus of wood. For this reason, the aim of this paper is to compare the new picture frame method with three other test methods, namely experimental modal analysis, square-plate twist method and torsion test. The focus of this study is only the shear modulus and not the shear strength, because non-destructive tests are also used (modal analysis, square plate twist method).
2 Materials and methods
2.1 Materials
The wood species European beech (Fagus sylvatica L.) and spruce (Picea abies L. Karst.) were used for the investigations. The samples were cut from kiln dried boards as clear square plates with dimension longitudinal (L) × radial (R) × tangential (T) = 150 × 150 × 3 mm3. Prior to testing, the samples were conditioned at 20 °C and 65% relative humidity (rh) until equilibrium moisture content (EMC) in adsorption had been achieved. The determination of EMC was conducted according to DIN EN 13183-1 (2002).
Ten replicates were used for determining the shear modulus by experimental modal analysis (EMA) and afterwards by plate-twist method (PTM). Then, the square plates were cut into strips of 30 mm width for torsion test and samples for picture frame method (PFM) (Fig. 1). Two PFM specimens were cut out of one square plate to obtain one sample each for LR and RL directions and to check whether there is a significant difference between the directions.
2.2 Experimental modal analysis
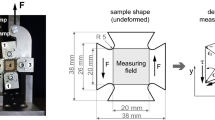
EMA is a nondestructive method for determining the properties of a structure (mode shape, eigenfrequencies and damping). To measure the complex vibrations of the structure, impulse or shaker excitation is required at different measuring points and the response is measured with an acceleration sensor (Fig. 2 left). To this end, the samples were divided into a 5 × 5 measuring point pattern with 30 mm spacing. In total, there were 25 measuring points for imaging the sample structure. The specimens were suspended from rubber bands located at the four corners to realize free boundary condition. The excitation of a measuring point was provided using an impact hammer. The complex vibrations were measured by an accelerometer located at the lower left corner of the sample on the rear side of a measuring point (Fig. 2 left). The position of the accelerometer was the same for all measuring points, while the impact hammer was roving over the measuring pattern. Each point was excited five times to average the frequency response function (FRF) and thus, minimize the error of manual exciting. In sum of all FRFs, the mode shapes of the structures and their corresponding eigenfrequencies can be estimated. The shear modulus can be calculated with the resonant frequency of the [1, 1]-mode, which is the torsional vibration mode (Fig. 2 right), according to Nakao and Okano (1987):
where ρ is the density, x and y are the dimension in L and R directions, h is the thickness of the sample and fr is the resonant frequency of the torsional vibration mode.
2.3 Plate-twist method
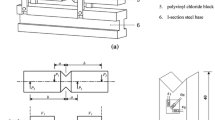
The PTM is a method for determining the in-plane shear modulus of a square plate and is standardized in DIN EN ISO 15310 (2005) for testing fiber-reinforced plastic composites. The principle of the method is to realize shear deformations under bending conditions. The result of the method is an analog deformation of the specimen as it occurs due to the torsional vibration mode of the EMA (Fig. 2 right). The square plate rests on two points of a diagonal and is loaded by the simultaneous movement of two load points on the opposite diagonal (Fig. 3).
The supporting and loading points are located close to the corners. The specimen is loaded until a bending deformation of half the thickness of the specimen is reached. During the test, the provided load and deflection of the loading points will be recorded. DIN EN ISO 15310 (2005) specifies a ratio s of the test span S to the plate diagonal D
This ratio s should be 0.95, which cannot be realized due to the drilled holes near the corners for supporting the rubber straps for EMA testing. Yoshihara and Sawamura (2006) found that comparable results can be measured up to a reduction in the ratio s to 0.85. Therefore, a ratio of s = 0.85 was chosen for these measurements. According to DIN EN ISO 15310 (2005), the in-plane shear modulus can be calculated as follows:
where x and y are the dimensions in L and R direction, h is the thickness of the sample, ΔF is the applied load difference between two points within the linear range, Δw is the corresponding deflection difference, and K is a geometric correction factor. If the ratio s is different to 0.95, K will be calculated as follows:
The thickness of the specimen differs from the standard, which is 4 mm. The specimen used for the PFM should not be thicker than 3 mm to ensure that the maximum allowed force of the apparatus is not exceeded. Therefore, a specimen thickness for all performed tests was defined to be 3 mm. The ratio of specimen length to thickness was 50, which is much greater than the required ratio of equal or greater than 35. With increasing length to thickness ratio, the effect of through-to-thickness shear deflections will be reduced (Yoshihara and Sawamura 2006), so the determination of the shear modulus will be more accurate.
The test was carried out on a universal testing machine (Inspekt 10, Hegewald & Peschke, Nossen, Germany). The testing speed was 1 mm min−1. The applied load was measured with a 500 N load cell. The deflection of the sample was measured by the crosshead movement of the testing machine.
2.4 Picture frame method
The PFM is relatively new in the application to wood. This method is usually used for fiber-reinforced plastic composites and is specified in detail in DIN SPEC 4885 (2014). The principle of this method is to convert uniaxial tensile loads acting on the picture frame into shear loads and leads to a quite uniform shear deformation of the specimen (Fig. 4). A detailed description of the conducted PFM is given by Krüger et al. (2018). The shear strain γ can be calculated by measuring the deformation of the opposite corners (ε1 and ε2) within the measuring field as follows:
The in-plane shear modulus can then be determined as follows:
where τ is the shear load, which is defined as the quotient of the applied tensile load and the cross-sectional area of the specimen within the measuring field.
Two samples were cut out of each square plate used for EMA and PTM. Thus, the shear modulus of both directions GLR and GRL could be tested. The first index refers to the loading direction (y direction), while the second index indicates the direction perpendicular to the loading direction parallel to the surface of the specimen (x direction).
The test was carried out on a universal testing machine (Inspekt 10, Hegewald & Peschke, Nossen, Germany). The test was stopped after the ultimate strength had been reached. The testing speed was 2 mm min−1. The applied load was measured with a 10 kN load cell. For the strain measurement, an optical measurement system (Video extensometer ME 46 of Messphysik, Fürstenfeld, Austria) was used. A black contrast speckle pattern was applied to the measuring field of the specimen surface.
2.5 Torsion test
Figure 5 shows the test setup for the torsion test. During the test, both ends of the specimen are fixed clamped in the torsional axis direction. On one side, there is a rigid clamp. On the opposite side, a bearing is disposed with a degree of freedom of rotation around the longitudinal axis of the specimen. The distance between the clamps is 120 mm, the clamping length is 15 mm. A torque is applied via a disc attached centrally to the bearing. For this purpose, a thin rope is attached to the circumference of the disc, which is connected to the cross beam of the universal testing machine (Inspekt 10, Hegewald & Peschke, Nossen, Germany). By moving the cross beam, a tensile force is applied and thus a torque T is generated on the specimen.
Due to the elongation of the thin rope and the bearing clearance, it is necessary to correct the recorded cross beam movement by a machine stiffness correction performed on a steel specimen. This allows the twisting angle α to be calculated as the quotient of the corrected cross beam travel w and the radius of the rotating disc (r = 100 mm). The preload force was 1 N and the crosshead speed was 50 mm min−1 (43.6°min−1). The applied load was measured with a 500 N load cell. The test was stopped after reaching a twist angle of 10°.
The apparent shear modulus Ga can be calculated according to Sumsion and Rajapakse (1979) as follows:
where l is the distance between the clamps, J is the cross section moment of inertia of second degree and ΔT/Δα is the gradient from applied torque and twisting angle. For rectangular cross section, J is calculated according to Sumsion and Rajapakse (1979) as:
where b is the width and h is the thickness of the specimen. For small values of h/b, the torsional parameter β according to Sumsion and Rajapakse (1979) can be approximated as follows:
Ga is a mixture of both shear moduli GLR and GLT (Bodig and Jayne 1982). For a small slenderness ratio, here h/b = 0.1, it can be assumed that the influence of the l–h shear plane can be neglected, so that Ga is equivalent to GLR or GRL.
To measure the shear modulus in LR direction as well as in RL direction, where the first index refers to the longitudinal axis of the specimen, half of the square plates was cut parallel to the L direction and the other half in R direction (Fig. 1).
3 Results and discussion
Figure 6 shows the results of the shear modulus of the applied test methods. PTM, EMA and PFM show comparable mean values with a low standard deviation for beech and spruce in the range of 973–1061 Nmm−2 and 563–577 Nmm−2, respectively. The results of the torsion test in RL direction are equivalent to those of the other test methods, beech—998 Nmm−2 and spruce—495 Nmm−2. However, the mean values in LR direction are about 25–40% higher than the other test results, beech—1289 Nmm−2 and spruce—842 Nmm−2. A comparison of the shear moduli determined in this study with literature references is shown in Table 1 for beech and in Table 2 for spruce.
For spruce it can be seen that Yoshihara and Ohta (2000) achieved similar shear modulus of 600 Nmm−2 with torsion test, as well as Sretenovic et al. (2004) with the rolling shear test setup (540 Nmm−2) and Müller et al. (2015) with the Arcan test (541–556 Nmmm−2). Results of Yoshihara et al. (2001) show significantly higher values of 1040–1070 Nmm−2 determined by torsion test and Iosipescu test for Sitka spruce (Picea sitchensis Carr.). Dahl and Malo (2009) also determined values of 734–754 Nmm−2 using the Arcan test, which are about 20–35% higher at a significantly lower density (398 kgm−3) than those of the present study (463 kgm−3).
For beech, it can be seen that Krüger et al. (2018), Brabec et al. (2017) and Grimsel (1999) achieved comparable shear moduli of 953–1021 Nmm−2, but the literature values determined by dynamic test methods with ultrasonic waves (Hering et al. 2012 and Bucur and Archer 1984) and resonant ultrasound spectroscopy (Longo et al. 2018) are about 25–50% higher than those of this study.
Contrary to the general fact that dynamic test methods like ultrasonic waves or EMA achieve higher values than static methods (torsion test, PTM, PFM, Arcan test, Iosipescu test), the results of EMA are similar to PTM and PFM. Hearmon and Barkas (1941) also achieved similar results of 975 Nmm−2 using a dynamic test method with torsional vibration.
A comparison of the two directions LR and RL is only possible for the PFM and torsion test. In these methods, the load direction of the test setup corresponds to the direction of the shear forces. PTM and EMA cannot differentiate a direction due to the indirect measuring principle for inducing shear forces by bending conditions.
The results of the present study show lower shear moduli in RL direction than in LR direction for beech of 931–998 Nmm−2 (RL) and 973–1289 Nmm−2 (LR) and for spruce of 495–537 Nmm−2 (RL) and 584–842 Nmm−2 (LR). The difference between the directions is not as big for PFM as for the torsion test (see Fig. 6). Both Müller et al. (2015) and Dahl and Malo (2009) could not find any significant differences between LR and RL direction by statistical analysis. A comparable statistical analysis (Mann–Whitney test, p < α = 0.05) of the present results showed that only for beech tested by PFM, no significant differences could be confirmed (p = 0.076). For spruce tested by PFM (p = 0.003) and for the torsion test (beech, spruce—p = 0.008), the results between the directions differ significantly, which is contrary to the theory of linear elastic orthotropic materials, where the material behaves symmetrically within each plane.
The significant differences for PFM between LR and RL direction for spruce may be explained by the fact that in LR direction, the wood rays are arranged perpendicularly to the load direction. Due to the movement of the right clamping jaw of the picture frame to which the crosshead of the testing machine is attached and the loading being initiated into the picture frame, shear stress is induced to the specimen parallel to the load direction (Fig. 4). The wood rays prevent shear-caused sliding of the annual rings by locking them and acting like a bolt (Mattheck and Bethge 1998; Burgert et al. 1999). On the other hand, the wood rays run parallel to the loading direction in RL direction, so that the sliding of the annual rings is not hindered by the rays as much as in LR direction.
The determined shear modulus by torsion test is always a combined modulus of both torsion surfaces (Bodig and Jayne 1982). In LR configuration, the second torsion surface is the LT plane, and in RL configuration, it is the RT plane. While the slenderness ratio h/b of the torsion specimen is small and thus the determined shear modulus is significantly affected by the larger area (LR or RL), an influence of the second torsion surface cannot be excluded. The shear modulus in LT direction is similar to the LR plane, but in RT direction, it is significantly lower than in LR direction. This causes the difference of the determined shear moduli in LR and RL direction. If the specimen thickness was reduced or the specimen width increased, the difference between the directions would be smaller. Furthermore, the difference between RL direction and LR direction for spruce can be explained by the fact that in an RL configuration, the grip end effect is much more pronounced than in an LR configuration. In an RL configuration, the annual rings run perpendicular to the torsion axis and parallel to the clamping jaws. Due to the large inhomogeneity caused by large density differences at the annual ring interfaces, this leads to greater deformations than in LR configuration, where the annual rings run parallel to the torsion axis. For beech, the density differs not as much within an annual ring, which corresponds to a lower influence of the grip end effect between RL and LR direction.
Bachtiar et al. (2017) examined the shear moduli by Arcan tests on all six shear planes of walnut wood (LR, RL, LT, TL, RT and TR) at different moisture contents. The indexing of the shear moduli does not correspond to the indexing in the present study, so that GLR, for example, corresponds to GRL assignment of Bachtiar et al. (2017). For a better understanding, their shear moduli assignment will be transposed to the definition of the present study. The results of Bachtiar et al. (2017) show constantly 5–12% higher shear moduli in LR and TL direction than in RL and LT direction, respectively. Only for RT and TR directions, there is no clear trend. This is in line with the PFM results for beech and spruce, where GLR has a higher modulus of about 5–10% compared to GRL.
4 Conclusion
The shear modulus of beech and spruce was obtained in this study by four different test methods. One of the methods was PFM, which was proven as the adequate method for determination of shear modulus of wood.
In conclusion, the PFM provides comparable results to PTM and EMA as well as to literature values determined by torsion, Arcan or Iosipescu tests. The advantage of PFM compared to other test methods for determining the shear properties of wood is that both shear modulus and shear strength can be determined simultaneously in all anatomical directions of wood due to the relatively small specimen dimensions.
In future measurements with PFM, an optical full-field measuring method should be used to enable a strain evaluation of the full shear field on the specimen surface. In this way, it could be verified whether the shear state is quite uniform. Currently, only pointwise evaluation with the video extensometer is possible.
It should also be further investigated whether there is a significant difference between the mutual configuration ij and ji within the shear planes LR–RL, LT–TL and TR–RT and whether it depends on the tested wood species with their anatomical differences.
For further evaluation of the PFM, direct comparison to other shear test methods such as Arcan or Iosipescu test should be made.
References
Bachtiar EV, Rüggeberg M, Hering S, Kaliske M, Niemz P (2017) Estimating shear properties of walnut wood: a combined experimental and theoretical approach. Mater Struct 50:248. https://doi.org/10.1617/s11527-017-1119-2
Bodig J, Jayne BA (1982) Mechanics of wood and wood composites, 712nd edn. Van Nostrand Reinhold, New York
Brabec M, Lagaňa R, Milch J, Tippner J, Sebera V (2017) Utilization of digital image correlation in determining of both longitudinal shear moduli of wood at single torsion test. Wood Sci Technol 51:29–45. https://doi.org/10.1007/s00226-016-0848-7
Brandner R, Freytag B, Schickhofer G (2008) Determination of shear modulus by means of standardized four-point bending tests. CIB-W18:1–13
Bucur V, Archer RR (1984) Elastic constants for wood by an ultrasonic method. Wood Sci Technol 18(4):255–265. https://doi.org/10.1007/BF00353361
Burgert I, Bernasconi A, Eckstein D (1999) Evidence for the strength function of rays in living trees. Holz Roh- Werkst 57:397–399. https://doi.org/10.1007/s001070050367
Dahl KB, Malo KA (2009) Nonlinear shear properties of spruce softwood: experimental results. Wood Sci Technol 43:539–558. https://doi.org/10.1007/s00226-009-0247-4
DIN EN 13183-1 (2002) Moisture content of a piece of sawn timber Part 1: determination by oven dry method. DIN German Institute of Standardization, Berlin
DIN EN 408 (2012) Timber structures—Structural timber and glued timber—Determination of some physical and mechanical properties. DIN German Institute of Standardization, Berlin
DIN EN ISO 15310 (2005) Fibre-reinforced composites—Determination of the in-plane shear modulus by the plate twist method. DIN German Institute of Standardization, Berlin
DIN SPEC 4885 (2014) Fibre-reinforced plastic composites—Shear test method using a shear frame for the determination of the in-plane shear stress/shear strain response and shear modulus. DIN-German-Institute of Standardization, Berlin
Grimsel M (1999) Mechanisches Verhalten von Holz. Struktur- und Parameteridentifikation eines anisotropen Werkstoffes (Mechanical behaviour of wood. Structure and parameter identification of an anisotropic material). Dissertation TU Dresden
Hearmon RFS, Barkas WW (1941) The effect of grain direction on the Young’s moduli and rigidity moduli of beech and Sitka spruce. Proc Phys Soc 53:674–680
Hering S, Keunecke D, Niemz P (2012) Moisture-dependent orthotropic elasticity of beech wood. Wood Sci Technol 46:927–938. https://doi.org/10.1007/s00226-011-0449-4
Keunecke D, Sonderegger W, Pereteanu K, Lüthi T, Niemz P (2007) Determination of Young’s and shear moduli of common yew and Norway spruce by means of ultrasonic waves. Wood Sci Technol 41:309–327. https://doi.org/10.1007/s00226-006-0107-4
Krüger R, Buchelt B, Wagenführ A (2018) New method for determination of shear properties of wood. Wood Sci Technol 52(6):1555–1568. https://doi.org/10.1007/s00226-018-1053-7
Longo R, Laux D, Pagano S, Delaunay T, Le Clézio E, Arnould O (2018) Elastic characterization of wood by resonant ultrasound spectroscopy (RUS): a comprehensive study. Wood Sci Technol 52(2):383–402. https://doi.org/10.1007/s00226-017-0980-z
Mattheck C, Bethge K (1998) The structural optimization of trees. Naturwissenschaften 85:1–10. https://doi.org/10.1007/s001140050443
Müller U, Ringhofer A, Brandner R, Schickhofer G (2015) Homogeneous shear stress field of wood in an Arcan shear test configuration measured by means of electronic speckle pattern interferometry: description of the test setup. Wood Sci Technol 49(6):1123–1136. https://doi.org/10.1007/s00226-015-0755-3
Nakao T, Okano T (1987) Evaluation of modulus of rigidity by dynamic plate shear testing. Wood Fiber Sci 19(4):332–338
Schwab E, Polaczek P (1977) Bestimmung der Schubmoduln von Holz durch statische Torsionsversuche Beitrag zur Neufassung DIN 52190 (Determination of the shear modulus of wood by static torsion tests Contribution to the new version of DIN 52190). Holz Roh- Werkst 35(1):23–27. https://doi.org/10.1007/BF02611182
Sretenovic A, Müller U, Gindl W, Teischinger A (2004) New shear assay for the simultaneous determination of shear strength and shear modulus in solid wood: finite element modelling and experimental results. Wood Fiber Sci 36(3):302–310
Stamer J, Siegelschmidt H (1935) Elastische Formänderungen der Hölzer (Elastic deformations of wood). Zeitschrift des Vereins deutscher Ingenieure 77 Heft 10:503–505
Sumsion HT, Rajapakse YDS (1979) Simple torsion test for determining the shear moduli of orthotropic composites. J Compos Technol Res 1(4):8–11
Xavier JC, Garrido NM, Oliveira M, Morais JL, Camanho PP, Pierron F (2004) A comparison between the Iosipescu and off-axis shear test methods for the characterization of Pinus Pinaster Ait. Compos A 35(7–8):827–840. https://doi.org/10.1016/j.compositesa.2004.01.013
Xavier JC, Oliveira M, Morais J, Pinto T (2009) Measurement of the shear properties of clear wood by the Arcan test. Holzforschung 63:217–225. https://doi.org/10.1515/HF.2009.034
Yoshihara H (2009) Edgewise shear modulus of plywood measured by square-plate twist and beam flexure methods. Constr Build Mater 23(12):3537–3545. https://doi.org/10.1016/j.conbuildmat.2009.06.041
Yoshihara H, Kubojima Y (2002) Measurement of the shear modulus of wood by asymmetric four-point bending tests. J Wood Sci 48(1):14–19. https://doi.org/10.1007/BF00766232
Yoshihara H, Ohta M (2000) Estimation of the shear strength of wood by uniaxial-tension tests of off-axis specimens. J Wood Sci 46(2):159–163. https://doi.org/10.1007/BF00777364
Yoshihara H, Sawamura Y (2006) Measurement of the shear modulus of wood by the square-plate twist method. Holzforschung 60:543–548. https://doi.org/10.1515/HF.2006.090
Yoshihara H, Kubojima Y, Nagaoka K, Ohta M (1998) Measurement of the shear modulus of wood by static bending tests. J Wood Sci 44(1):15–20. https://doi.org/10.1007/BF00521869
Yoshihara H, Ohsaki H, Kubojima Y, Ohta M (2001) Comparison of shear stress/shear strain relations of wood obtained by Iosipescu and torsion tests. Wood Fiber Sci 33(2):275–283
Acknowledgements
Open Access funding provided by Projekt DEAL. The authors would like to thank the colleagues of the Institute of Aerospace Engineering of the Technische Universität Dresden for providing the picture frame and their kind support during its application.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Krüger, R., Wagenführ, A. Comparison of methods for determining shear modulus of wood. Eur. J. Wood Prod. 78, 1087–1094 (2020). https://doi.org/10.1007/s00107-020-01565-2
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00107-020-01565-2