Abstract
Effective utilization of structural timber requires grading and indicating properties (IPs) that are able to predict strength with high accuracy and machines that are able to measure the underlying board properties at a speed that corresponds to the production speed of sawmills. The aim of this research is to assess the performance of a new machine strength grading method/procedure which was recently approved for the European market and to compare the performance of it with the performance of other available techniques. The novel method is based on laser scanning utilizing the tracheid effect, in combination with data from dynamic excitation and weighing. Applied indicating properties are defined in detail and results presented include assessment of the repeatability, coefficients of determination between IPs and grade determining properties, and examples of the yield achieved in different strength classes and combinations of strength classes. The investigated sample comprised more than 900 pieces of timber of Norway spruce (Picea abies) from Sweden, Norway and Finland. For this sample the coefficient of determination between the IP to bending strength and the measured bending strength was as high as R 2 = 0.69, while the coefficient of determination between dynamic modulus of elasticity (MOE) and measured bending strength was R 2 = 0.53. The yield in high strength classes, C35 and above, becomes about twice as high using the new method/procedure compared to machines using dynamic MOE as IP. A comparison of the performance with what has been presented for machines that are based on X-ray in combination with dynamic excitation indicates that the new method/procedure will surpass such machines as well.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Effective utilization of structural timber requires grading using indicating properties (IPs) that are able to predict strength with high accuracy, and machines that are able to measure the underlying board properties at a speed that corresponds to the production speed of sawmills. Many of the methods and machines used on the market today utilize longitudinal dynamic modulus of elasticity (MOE) for prediction of edgewise bending strength. The vibration signal from dynamic excitation, the weight and the dimensions of the board can be measured fast and accurately with machines that are comparatively inexpensive, and the dynamic MOE representing an averaged value of the entire board is calculated using a simple equation. However, the relationship between longitudinal dynamic MOE and bending strength is rather weak. For Norway spruce the coefficient of determination, R 2, between longitudinal dynamic MOE and edgewise bending strength is about 0.5 which results in poor yield in high strength classes. Flatwise bending machines have been used since the 1960’s and are still available on the market. Over a span of about 1 m, and moving along the board, the bending stiffness is determined using for example three point bending and on the basis of this an MOE, valid for flatwise bending and representing a certain part of the board, is calculated. Thus, such machines give some information regarding the stiffness variation along the board, and the grading is based on the relationship between the lowest flatwise MOE found along the board and the edgewise bending strength. The speed with which the board passes through the machine may induce vibrations which can disturb the measurement results, and the application of three-point bending implies that the determined bending stiffness is affected by the board’s shear properties. Thus, when grading Norway spruce at production speed the grading principle of such machines results in a grading accuracy that is comparable with the one achieved using grading machines based on dynamic MOE, see Johansson (2003) and Oscarsson (2014).
There are grading machines on the market that combine X-ray techniques with dynamic MOE and these represent the most accurate strength grading that has been utilized on the market in recent years. The information added by the X-ray technique is high resolution information of the variation of density within a board which means that knot measures can be derived and used in definitions of IPs. In an extensive study performed by Hanhijärvi and Ranta-Maunus (2008), comprising more than 1000 pieces of Norway spruce (Picea abies) and 1000 pieces of Scots pine (Pinus sylvestris), mostly from Finland but also from North-Western Russia, assessments of various strength grading machines and IPs to tension and bending strength were performed. The machine/IP that showed the best performance was “GoldenEye + Viscan” of the company Microtec (Microtec 2015). On the basis of dynamic excitation, X-ray and knowledge of dimensions, it gives information on longitudinal resonance frequency, board density, board dimensions and knot parameters that are used in combination for the establishment of an IP to bending strength. For the spruce timber loaded to failure in bending the machine/IP gave an R 2 to bending strength of 0.64. When dynamic MOE (also assessed by equipment from the same company) was calculated on the basis of resonance frequency and board density, and on resonance frequency alone, R 2 of 0.57 and 0.48, respectively, were achieved for the same timber. For the sample of Scots pine the improvement in grading accuracy using “GoldenEye + Viscan”, rather than dynamic MOE alone, was larger than what it was for the sample of Norway spruce. Other studies that give examples of the performance of the same or similar equipment are Bacher (2008) and Nocetti et al. (2010).
Olsson et al. (2013) suggested a strength grading method based on dot laser scanning, which gives high resolution information of the fibre orientation on board surfaces, to be used in combination with knowledge of dynamic MOE. Based on the fibre orientation, basic material wood properties, and cross-sectional integration schemes, a new IP defined as the lowest local edgewise bending MOE found along a board was established. A comparison of coefficients of determination of the new, suggested IP and dynamic MOE, respectively, to bending strength was performed and the result was advantageous for the new IP. The new method/equipment also provides profiles of how stiffness and strength varies along a board. However, the investigation only comprised a small sample of 105 boards of one dimension, 45 × 145 × 3600 mm3, and the examination of the boards was not performed under production conditions or at production speed. Between 2013 and 2015 the method was examined in a large-scale study involving cooperation with both manufacturers of equipment for grading and sawmilling companies. The timber sample examined was composed such that the results could be used as the basis for a formal approval of the method for the European market. The study was supervised by SP Technical Research Institute of Sweden and considered all parts that would be needed for an approval and successful market introduction, such as assessment of repetitiveness, significance of grading speed, determination of settings and evaluation of yield in different strength classes, etcetera. The results of the study are made available to the research society through the present paper. Definitions of IPs involved are defined in detail.
In addition to the research group at Linnaeus University in Sweden, a number of research groups in Europe are active in research aiming at new and accurate methods and IPs for machine strength grading, or at improvements of regulations for how grading methods should be assessed and setting values determined. Among these is a research group at TU Wien which, on the basis of X-ray and reconstruction of knots in 3D, recently has suggested new IPs for strength grading, for example, Lukacevic et al. (2015). Another group, based in France and involving several universities and institutes, has suggested grading on the basis of X-ray in combination with fibre orientation information from tracheid effect scanning, for example Viguier et al. (2015). Further, a group in Munich has recently published work on assessment of grading methods in use and on derivation of settings, for example Rais and Van de Kuilen (2015).
2 Materials and measurement methods
2.1 Sampling of material
The investigation was aimed not only at a thorough assessment of the method suggested by Olsson et al. (2013) but also at a formal approval of it, i.e. fulfilment of requirements of initial type testing according to the European Standard EN 14081-2, and derivation of settings for a growth area covering Sweden, Norway and Finland. Therefore, the sampling and the preparation of the timber for testing, including drying aiming at 12 % moisture content (MC), was performed in accordance with the requirements laid down in the standard.
To derive machine settings that are valid for a new machine type, a minimum total number of 900 timber pieces originating from at least four different sub-samples shall, according to EN 14081-2, clause 6.2.2, be sampled. Each sub-sample shall consist of at least 100 pieces of one or more board cross-sections. The pieces shall be representative for the material to be graded in production, which in practice, and in most cases, mean that they shall not be pre-graded. The sub-samples shall be distributed over a chosen geographic area with the purpose of reflecting the variation of growth conditions. The principles on which this distribution is based are not laid down in detail in the standard, but sampling guidelines (Anon 2012) have been issued by TG1 which is a technical group set up under technical committee TC 124, Working Group 2 within the European Committee for Standardization.
The present sample was divided into five subsamples representing timber from (1) northern Sweden, (2) mid Sweden, (3) southern Sweden, (4) Norway, and (5) Finland and included dimensions ranging from 30 to 70 mm in thickness and from 70 to 245 mm in depth. The locations from which the timber was fetched for the subsamples are marked on the map shown in Fig. 1.
It is stated in EN 384 (2010), clause 5.2, that when assessing bending strength the critical section, i.e. the section along the board at which failure is expected to occur, shall be in a position that can be tested, that is within the loading heads in a four point bending test as described in EN 408 (2010). Therefore, boards having their critical section closer to one of the ends than about 6.5 times the board depth were discarded. Hence, in order to assess at least 900 pieces, about twice the number had to be sampled in a first stage. The number of boards from each region fulfilling the requirement with respect to the criterion on the position of the critical section and actually evaluated with respect to the grade determining properties, i.e. bending strength, mean MOE and density, are presented in Table 1. The grade determining properties referred to are defined in clause 3.5 of EN 14081-2 (2010) for the strength classes of EN 338 (2009). The criterion employed for which section along each board that was regarded as the critical one is based on a calculated local MOE in bending defined in Sect. 3.1 below.
2.2 Measurements and equipment for IP determining data
The IPs utilized in the grading method are based on local fibre orientation on the four longitudinal faces of the board and on the board longitudinal resonance frequency and mass assessed as described below. In addition, knowledge of the MC of the timber was required, and for each dimension and sawmill represented in the investigation the MC of about ten pieces was determined using a resistive moisture transducer. Then, the average value of the MC was used for all the boards of the same dimension from the same sawmill.
2.2.1 Resonance frequency and mass
The equipment employed for measurements of longitudinal resonance frequency and mass of each board was a Precigrader strength grading machine (Dynalyse 2015). When a board passes the machine it is excited by means of a hammer blow at one of the board ends. The response in terms of the sound in the time domain is captured by means of two microphones, and by fast Fourier transform of the sound the lowest resonance frequency corresponding to the first longitudinal mode of vibration is extracted. The board weight is determined by means of a balance placed in the production line. The length of the board is also measured by means of a distance meter. Figure 2 shows a Precigrader strength grading machine in action and boards fed by it in transversal direction in a production line. The distance meter is shown at the far end of the line.
2.2.2 Fibre orientation on wood surfaces
A WoodEye 5 scanner (WoodEye 2015) equipped with four sets of dot lasers and multi-sensor cameras, one set for each longitudinal surface of the board fed through the scanner, was used for collecting high resolution data regarding fibre orientation in the plane of each of the scanned surfaces. In the scanner, fibre orientation data is obtained by means of the so-called tracheid effect which means that the wood fibres in softwood conduct concentrated light better in the direction of the fibres than across (Matthews and Beech 1976; Soest et al. 1993). This results in the light intensity distribution around a laser dot entering the shape of an ellipse for which the major principal axis is oriented in the direction of the wood fibres. This provides a practical method for measuring variations in grain angle on a wood surface. Figure 3 shows (a) a WoodEye 5 scanner, (b) a part of a wood surface including a knot, (c) the spread of light from the laser dots on the wood surface, (d) the fibre orientation on the wood surface calculated by identifying the major principal axis of each light spot using image analysis. Within the knot, where fibres are actually directed almost perpendicular to the surface, the light spots become almost circular in shape and hence the calculated fibre direction in the plane of the surface becomes uncertain. The resolution obtained in the transverse direction of the board surfaces is dependent on the grid installed on the dot laser source. In this investigation the chosen grid resulted in a transversal resolution of 4.4 mm. The resolution obtained in the longitudinal direction, i.e. along the board, depends on the speed of the boards fed through the scanner and on the sampling frequency of the cameras. Scanning was performed at two different speeds, namely 200 m/min, giving a resolution in longitudinal direction of 3.5 mm, and 450 m/min giving a resolution in longitudinal direction of 4.4 mm. For safety reasons the lower speed was mainly used, since no safe cordon was arranged during scanning, but actions were taken to verify that the speed employed had no significance for the indicating properties calculated on the basis of data from scanning. This is further commented upon in Sects. 4.1 and 5.2 below. Furthermore the scanner determines length, thickness and depth of the board and these dimension measures are used in the definitions of the IPs as described in Sect. 3.2.

Figure b–d originate from Petersson (2010)
a WoodEye 5 scanner, b part of a wood surface including a knot, c spread of light from laser dots on the wood surface, d fibre orientation on wood surface calculated by identifying the major principal axis of each light spot using image analysis.
2.3 Determination and requirements of grade determining properties
The measurements and calculations performed for the grade determining properties, i.e. the properties that are decisive for the strength class to which a board should be graded were carried out as follows.
2.3.1 Modulus of elasticity, MOE
In Fig. 4, the test arrangement for a four point bending test according to EN 408 is displayed. On the basis of such a test both a local and a global MOE may be calculated and they are defined, respectively, as
and
where a = distance between one of the point loads and the closest support (EN 408 allows a = 6 ± 1.5 h, but here a = 6 h is used), F = total loading (two load levels, F1 and F2, respectively), l 1 = span for determination of local MOE (= 5 h), I = second moment of inertia (bh 3/12), \( \bar{w} \) = centre deflection of the span l 1 (D in relation to C and E), l = distance between the supports (18 h), w = centre deflection of the span l (D in relation to A and B), b = thickness of the board, h = depth of the board, G = shear modulus.
When E local and E global have been determined in accordance with Eqs. (1) and (2), a correction with respect to MC is performed. According to EN 384, clause 5.3.4.2, it shall be done such that the MOE is adjusted with 1 % for each per cent deviation from 12 % MC. Thus, corrected values are calculated as
where u is the MC (%) of the board determined for a piece of clear wood cut out from the board close to the position of failure in the four point bending test described in EN 408. It should be noted that for specimens with MC above 18 % the correction of MOE is limited to 6 %, which means that MC above 18 % is disregarded.
The stiffness property to be considered when grading timber into strength classes is defined as (EN 384, clause 5.3.2)
where E i is the ith value of E global,corr and n is the number of boards in the sample. For each of the strength classes defined in EN 338 there is a required value of average MOE which means that \( \bar{E} \) of the boards, 1 to n, assigned to a strength class must exceed this required value. Note that the influence of shear in Eq. (2) shall be ignored by taking G as infinite, since Eq. (5), implicitly, takes account of the shear deformation.
2.3.2 Bending strength
The bending strength f m is calculated as
where F max is the maximum value of F and the other parameters included in the equation are defined in the previous section. This bending strength is then corrected with respect to the depth of the board according to EN 384, clause 5.3.4.3 as
where
The correction term k h is thus equal to unity for a board of depth 150 mm. The basic requirement on strength in grading is that 95 % of the boards assigned to a strength class shall have a value of \( f_{\text{m,corr}} \) that exceeds the characteristic strength of the class as defined in EN 338.
2.3.3 Density
The piece of wood cut out for determination of moisture content of each board is also used for calculation of board density. According to EN 384, clause 8, a density, corrected with respect to moisture content, shall be calculated as
where u is the moisture content determined as described in Sect. 2.3.1 above. The basic requirement on density in grading is that 95 % of the boards assigned to a strength class shall have a value of \( \rho_{\text{corr}} \) that exceeds the characteristic density of the class as defined in EN 338.
3 Calculation model and definitions of indicating properties
The principles of the assessed grading method are given in brief in Sect. 3.1. A complete account of the method is given by Olsson et al. (2013). The IPs employed for grading are formally defined in Sect. 3.2 below.
3.1 Determination of local MOE valid for bending
Wood is an orthotropic material having very high stiffness and strength in the fibre direction, whereas the performance of these properties is much poorer in other directions. The local stiffness in the longitudinal direction of the board is thus strongly dependent on the local fibre orientation. Knowledge of the spatial distribution of the material orientation and the stiffness properties of the material everywhere within the board makes it possible to calculate the local stiffness in the longitudinal direction of the board and, by integration, to calculate the stiffness properties on the cross-sectional level. It has been shown by several researchers over the years (Oscarsson et al. 2014) that knowledge of local MOE, measured over a few centimetres, would enable more accurate prediction of bending strength than what more global measures of MOE, such as axial dynamic board MOE or MOE determined by means of flatwise bending machines, do. However, techniques for determination of high resolution MOE along a board have not been implemented in sawmill production. Now, when high resolution data of local fibre orientation is available, as described in Sect. 2.2.2, this possibility can actually be utilized. However, since the fibre direction is scanned on the surface, the information regarding the material orientation within the boards is limited. Thus, certain assumptions have to be made before the cross-sectional stiffness properties can actually be calculated and used in the definitions of IPs. In the presented grading method, it is therefore assumed that
-
The density (ρ) and the MOE in the fibre direction (E l) are constant within a board,
-
An initial, nominal value of the MOE in the fibre direction (E l,0) as well as nominal values of other material parameters are assumed, see Table 2,
Table 2 Nominal material parameters employed (Norway spruce), values originating from Dinwoodie (2000) -
When a value of E l that should be valid for an examined board is determined, it is assumed that the relationships between the other board stiffness parameters (E r, E t, G lr, G lt, and G rt) and their corresponding nominal values (E r,0, E t,0, G lr,0, G lt,0, G rt,0) are the same as the relationship between E l and E l,0. Regarding notation of the stiffness parameters, E and G represent MOE and shear modulus, respectively, and indices l, r and t, represent longitudinal, radial and tangential direction, respectively. Poisson’s ratios, displayed in Table 2, are denoted as v.
-
Fibre directions measured on the wood surface (Fig. 5a) are located in the longitudinal-tangential plane of the wood material,
Fig. 5 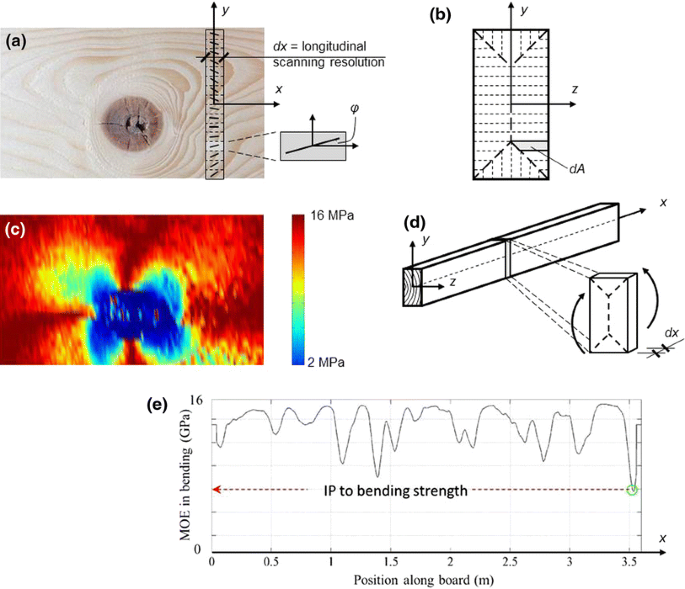
Figure a–d from Oscarsson et al. (2014)
a Local fibre directions scanned on a member’s surface by means of a row of laser dots, b cross-section divided into sub-areas implying that the exhibited angle φ and corresponding MOE in the longitudinal direction, E x(x,y,z), is valid within the volume dA × dx, c distribution of E x(x,y,z), d segment of length dx for which the edgewise bending MOE is calculated by stiffness integration over the segment’s cross-section, and e a bending MOE profile, each value along the graph representing the average edgewise bending MOE of the surrounding 90 mm, and the lowest value along the profile defining the IP to bending strength.
-
The fibre direction coincides with the wood surface, i.e. the out of plane angle is set to zero, and
-
The fibre direction measured on a surface is valid to a certain depth, which means that the fibre angle φ highlighted in Fig. 5a, and the corresponding local MOE, i.e. E x(x,y,z), is assumed to be valid within the volume defined by the area dA (Fig. 5b) times the length dx (Fig. 5a, d).
On the basis of the described assumptions, the edgewise bending MOE of the segment shown in Fig. 5d can be calculated by stiffness integration over the segment’s cross-section. Information that originates from the dynamic excitation and weighing is used to get a value of E l which is assumed to be representative for the board investigated.
The maximum resolution of the determined bending MOE profile is mainly dependent on the speed of the scanning, but even for very fast scanning the bending stiffness is evaluated for sections along the board being only a few millimetres apart (as mentioned above, a resolution of 4.4 mm can be achieved for scanning at a speed of 450 m/minute). Figure 5e shows a bending MOE profile where the value shown in each position along the board is the average MOE of the surrounding 90 mm long section. The lowest MOE along the profile is used as the indicating property to the board bending strength.
3.2 Definitions of indicating properties
Different IPs for the grade determining properties density, MOE and bending strength are defined and may be utilized for grading. The first one is intended for prediction of ρ corr and it is defined as
where m is the mass (m) of the board registered by the Precigrader, L, h and b are the length, depth and thickness of the board registered by the WoodEye 5 and u s is the MC (%) measured by a device in the line of production or manually supplied by an operator. A value of u s representative for the batch, as defined in EN 14081-1 (2005), being graded is sufficient. However, it is specified for the machine that the mean MC of the batch shall be between 10 and 20 % and the MC of individual pieces shall not deviate by more than four percentage points from the mean.
The second IP may be used for prediction of MOE and it is defined as
where f is the resonance frequency (Hz) corresponding to the first mode of axial vibration of the board determined by Precigrader and the other parameters are defined in the same way as for IP density.
The third IP is used for prediction of bending strength, f m,corr, and it can also be used for prediction of MOE. It is defined as
where E b,90 is the lowest bending MOE over a 90 mm long section of the board determined on the basis of information from WoodEye 5 and Precigrader as described above in Sect. 3.1 and illustrated in Fig. 5e. During development of the grading method different lengths of sections to be considered for lowest bending MOE were evaluated and a length of about 90 mm gave the highest coefficient of determination between the IP to bending strength and the bending strength. This length is, however, the only parameter that was adjusted empirically to optimize the accuracy of the method when it was developed. Moreover, the coefficient of determination is not very sensitive to the length of the section. For example, if 70 or 110 mm is used, rather than 90 mm, the coefficient of determination between IP and bending strength decreases with less than one percentage point. A brief study on the significance of the section length is presented in Oscarsson (2014), pp. 62–63.
4 Grading and regulations
As described in Sect. 2 the presented investigation concerns a formal approval of the current grading method. Thus, all the requirements of initial type testing according to EN 14081-2 must be fulfilled. The requirements and evaluation with respect to repeatability are described in Sect. 4.1 below and the procedure for calculation of setting values for different strength classes are set out in brief in Sect. 4.2.
4.1 Requirements and assessment of repeatability and significance of scanning speed
If the same board is graded repeatedly the measured data should result in the same calculated IPs and the board should be assigned to the same strength class each time but, of course, some tolerances must always be allowed for. In EN 14081-2, clause 6.2.5, it is stated that a repeatability check including at least 100 boards of one size must be performed. The boards shall be passed through the machine five times and each time the IPs shall be determined. The feed speed shall be equivalent with the machine’s critical feed speed, i.e. the maximum speed at which the machine is intended to operate in commercial grading. The range of the IP value considered shall then be divided into n intervals, each containing approximately the same number of boards, representing fictitious grades. The most frequent grade assigned to each board over the five passes shall be designated its optimum grade. Then a so called size matrix is established and the number in each cell represents the number of times a board with a certain optimum grade is assigned to a certain assigned grade. Numbers in the diagonal represent correctly graded boards, i.e. when the board is assigned to the optimum grade, while off-diagonal numbers represent erroneously graded boards. An elementary cost matrix is also established and filled with penalty factors. In the cells in the diagonal these factors are set to zero. In cells adjacent to the diagonal the factors are set to 1, two steps away from the diagonal they are set to 2 and so on. A global cost matrix is then established such that each cell in it contains the product of the number in the corresponding cells of the size matrix and the elementary cost matrix divided by the sum of the numbers in all cells for the assigned grade of the size matrix. The requirement is that no number in the global cost matrix may exceed 0.1. If this requirement is fulfilled the method is regarded accurate enough for grading n − 1 strength classes simultaneously in production. Table 3 shows examples of a size matrix, an elementary cost matrix and a global cost matrix, respectively, for a case when 100 boards were graded five times and divided in n = 3 classes. In this case no number in the global cost matrix exceeds 0.1 which means that n − 1 = 2 classes may be graded simultaneously in production.
In the repeatability check of the present method 120 boards of dimension 45 × 145 × 3600 mm3 were included. Each board passed a Precigrader and a WoodEye 5 scanner five times at a speed of 450 m/min which is the critical feed speed of the approved version of the grading method. The boards were oriented in the following way for the different passes through the scanner:
-
1.
Pith side up, root end first
-
2.
Pith side up, top end first
-
3.
Pith side down, root end first
-
4.
Pith side down, top end first
-
5.
For each board the orientation of pith side and root end were chosen at random.
The results of the reliability check are presented in Sect. 5 below.
In addition to the repeatability check for the speed 450 m/min, the 120 boards also passed through the scanner at a speed of 200 m/min, so that it could be evaluated whether the speed had any significance for the calculated indicating properties. This was important since the boards utilized for determination of settings were scanned at a speed of 200 m/min and the method should be approved for the speed 450 m/min. Results of the speed check are also presented in Sect. 5 below.
4.2 Calculation of settings for strength classes
When using the timber sample for calculation of settings, i.e. minimum requirements for the values of the IPs for a board to be assigned to a strength class defined in EN 338, requirements on the three grade determining properties bending strength, mean MOE and density must be fulfilled. In principle this means that at least 95 % of the boards graded to a class must be stronger than the characteristic strength of that class, that the density of at least 95 % of the boards must be higher than the characteristic density of the class and that the average MOE must be higher than 95 % of the required average MOE of the class. However, it is stated in EN 14081-2, clause 6.2.2, with reference to EN 384, that for strength classes up to C30 the requirements on strength that must be exceeded by 95 % of the boards is not \( f_{\text{m,corr}} \), which it is for higher strength classes, but \( f_{\text{m,corr}} \) /1.12. This adjustment is done on machine strength graded timber only, in order to compensate for larger uncertainties in visually strength graded timber of corresponding strength classes.
In addition to the main principle explained above, EN 14081-2 and the standards that it refers to contain a number of additional requirements. In short these can be summarized as follows:
-
When settings are calculated at least 0.5 % of the sample, and not less than five pieces, must be rejected.
-
At least 20 pieces must be assigned to each strength class being graded.
-
Requirements on the sample, where one subsample at a time is excluded, must be fulfilled.
-
Cost matrices shall be established and considered.
-
A certain country check must be performed.
All the requirements specified in EN 14081-2 are considered for the calculated setting values and for the yield in different strength classes that are presented below.
5 Results and discussion
5.1 Properties decisive for the grade determining properties
A summary of the results for the properties defined in Sect. 3.2 is given in Table 4. Mean values, standard deviation and coefficient of variation are presented and it can be concluded that the quality of the timber is similar to what has been reported in other studies on Norway spruce from these countries, e.g. Johansson et al. (1992) and Hanhijärvi and Ranta-Maunus (2008). Regarding the relationships between the different properties in terms of coefficient of determination these are, as well as the coefficients of determination to the IP values, reported in Sect. 5.3 below.
5.2 Repeatability check and significance of scanning speed on indicating properties
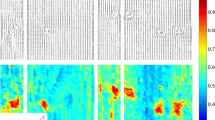
Repeatability checks using a sample of 120 boards, see Sect. 4.1, were performed for all three IPs being defined, namely, IP fb, IP MOE and IP density and the results were satisfactory. For all three IPs the repeatability allowed for five classes or more, including rejects, to be graded simultaneously while fulfilling the requirements stipulated for the global cost matrix as described in Sect. 4.1. This means that four classes plus reject may be graded simultaneously using this method, which is more than what is generally done in any commercial grading process today. Figure 6 shows an example of a result from the evaluation, the repeatability check on IP fb for the cases with four classes, including rejects, graded simultaneously. On the horizontal axis each board’s average value of five runs through the machine is displayed and on the vertical axis the value of each run of each board is shown. The vertical lines mark the borders between fictitious strength classes. A blue mark (+) indicates a run of a board through the machine where it was graded to its optimum grade while a red mark (□) indicates an assignment to a different grade. Note that optimum grade is defined as the most common class assignment of the five runs of each board which means that the optimum grade for a particular board is not necessarily represented by a position within any of the four large diagonal squares of the grid indicated in Fig. 6. Of course, the risk that a board, in one or several runs, is graded into a different grade than the optimum grade is higher if the IP value of the board is close to a border between two classes, i.e. close to one of the vertical lines in Fig. 6. The size matrix, the elementary cost matrix and the global cost matrix corresponding to the repeatability check shown in Fig. 6 are shown in Table 5. Each red square in Fig. 6 contributes to an increased number in one of the off-diagonal cells of the size matrix. Since no cell in the global cost matrix exceeds 0.1 the repeatability check shows an acceptable result.
Result of a repeatability check on IP fb. On the horizontal axis each board’s average value of five runs through the machine is displayed and on the vertical axis the value of each run of each board is displayed. The vertical lines mark the borders between fictitious strength classes. Blue marks (+) indicate boards graded to its optimum grade while red marks (□) indicate boards graded differently
Regarding the significance of the scanning speed, 200 or 450 m/minute, comparisons showed that there was no significant difference in results when the 120 boards were scanned in these two different speeds. When the boards were scanned in 200 and 450 m/min, respectively, in the same orientation through the scanner, and the same set of resonance frequencies and masses were used for calculating IP fb, then the coefficient of determination between the two sets was as high as 0.998. This can be compared with the coefficients of determination between any two runs in the repeatability check presented above where the speed 450 m/min was used and the boards were oriented in different ways and associated with different sets of measured resonance frequencies and masses. Then the coefficients of determination between two runs were in the range of 0.97–0.98. Thus, it was proved that the scanning speed of 450 m/min gives the same values of IP fb as the speed 200 m/min does. Thus, 450 m/min is a verified speed.
5.3 Regression analysis
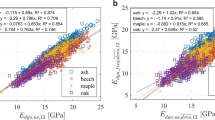
The relationships and coefficients of determination between IP fb and f m,corr, and between dynamic MOE, denoted as IP MOE, and f m,corr are presented in Fig. 7. For the relationship between IP fb and f m,corr a linear regression coefficient of determination of 0.69 was achieved. For a slightly curved, exponential function of the relationship R 2 = 0.70 was reached. The linear regression coefficient of determination between IP MOE and f m,corr was R 2 = 0.53. Table 6 shows R 2 (numbers in bold), including an approximate 95 % confidence interval, between each of the grade determining properties and the indicating properties involved. The R 2 of 0.69 (0.70) between IP fb and f m,corr for this large and representative sample of Norway spruce was even slightly higher than the corresponding R 2 of 0.68 reported for the small sample of 105 boards investigated when this IP was first introduced by Olsson et al. (2013). A comparison with the R 2 of 0.53 for IP MOE is relevant since dynamic MOE are used by Precigrader and several other grading machines on the market for prediction of bending strength. Furthermore, the R 2 between f m,corr and E local,corr was R 2 = 0.62 and between f m,corr and E global,corr it was R 2 = 0.64, which means that IP fb gives better prediction of f m,corr than either of these static bending MOEs. Thus, IP fb is indeed an effective IP for prediction of bending strength of Norway spruce. The scatter plot displayed in Fig. 7a, and the inserted equation representing the line of regression, also show that there is an almost direct proportionality between IP fb and predicted bending strength.
As shown by the results presented in Table 6, IP fb can be used for prediction of E local,corr and E global,corr with approximately the same accuracy as when IP MOE is used for this purpose. IP MOE, which represents a global measure of MOE, is slightly more effective for prediction of E global,corr (R 2 = 0.84) than what IP fb is (R 2 = 0.82), while IP fb, which is a local measure of MOE, is more effective for prediction of E local,corr (R 2 = 0.76) than what IP MOE is (R 2 = 0.69). It should be noted, however, that IP fb is a very poor IP for prediction of ρ corr (R 2 = 0.33). For the purpose of predicting density IP MOE is much better (R 2 = 0.53) and, of course, IP density is the best one of the three IPs investigated (R 2 = 0.84).
5.4 Yield in strength classes
From a practical and commercial point of view, a grading method is judged by the yield obtainable in different strength classes, given the quality of the assessed timber. Table 7 shows, for the investigated timber, examples of yield in some different single and combined strength classes using the IPs defined herein. The first column specifies the strength class or class combination considered. The second column gives the yield obtained using IP MOE, i.e. axial dynamic MOE, as IP to all three grade determining properties. The third column gives the yield obtained using IP fb for prediction of all the grade determining properties, and the fourth column gives the yield obtained using IP fb as IP to both f m,corr and to E global,corr (the latter one determines the grade determining property \( \bar{E} \), see Eq. 5) but IP density for prediction of ρ corr. The fifth column shows the yield that could be obtained with a “perfect machine”, i.e. a machine able to predict all the grade determining properties perfectly. As explained in Sect. 4.2, yields are calculated considering all the rules set down in EN 14081-2. Furthermore, when class combinations are considered herein, i.e. when so-called double grade is performed, as much timber as possible is graded into the highest class, even if a higher total value could have been obtained by downgrading a few pieces to the lower class, in order to decrease the number of rejects.
Not surprisingly, since spruce timber that is representative for Sweden, Norway and Finland is of high quality, the maximum yield of 99.5 % was obtained for all the IPs investigated when grading C24 as single class. High yield was also obtained for the classes TR26 and C30, but here a small difference to the advantage of IP fb, as compared to IP MOE, is noted. For the high classes, C35 and C40, there is a considerable improvement in yield using IP fb rather than IP MOE, the yield becoming almost twice as high. However, from a commercial point of view it is rarely interesting to grade such high classes in single grade, since the number of rejects then becomes rather high. Instead high strength classes are often graded together with a low class and two combinations examined here are C35/C18 and C40/C24. In both cases IP fb performs much better than what IP MOE does, giving about twice as high yield in the higher strength class and still very few rejects. A comparison of using IP fb alone, or both IP fb and IP density for grading, the numbers in columns three and four of Table 7 show that yields become higher when IP density is used for prediction of ρ corr, especially when grading C40. Of course, this is not very surprising since IP fb is a poor IP to ρ corr and density may be a significant grade determining property for high strength classes.
The yield when using the imaginary “perfect machine”, see the fifth column of Table 7, shows the potential of further improvements of grading machines and IPs. The grading method examined herein gives, however, almost as large improvement in yield, in comparison with machines using dynamic MOE as IP to the grade determining properties, as the “perfect machine” would give in comparison with the examined grading method. For example, dynamic MOE as IP gives a yield of 14.5 % in the class C40, when graded in combination with C24. The new method gives a yield of 30.3 % and the “perfect machine” would be able to give 47.7 %.
Deepened analysis of what is governing the yield in different strength classes can be summarized as follows:
-
The ability to predict bending strength is governing the yield. As a matter of fact, for the classes and class combinations displayed in Table 7, and using IP MOE for prediction of strength, the requirements on density and MOE stated in the standard do not affect the yield at all, i.e. even if there were no requirements on density and MOE in the definitions of the strength classes the yield would not increase. This is, however, not always the case. For some samples requirements on density could be of great importance for settings and yield, since the properties of a few pieces of a sample may affect settings considerably. There is an element of chance.
-
When using IP fb for prediction of both strength and density (column three in Table 7) the yield is limited by requirements on density. However, if the density is accurately predicted using IP density (column four in Table 7) the yield is not significantly decreased due to requirements on density. Only in the strength class C40 the yield would increase from 30.3 to 31.6 % if the requirement on density was omitted in the definition of the class.
-
Requirements on MOE in the definitions of the strength classes do not limit the yield for any of the real grading methods or strength classes assessed.
-
For a perfect machine the requirements on density considerably limit the yield in high strength classes. For example, for the class C35 the yield would increase from 69.2 to 74.4 % if the requirement of density was omitted. If the same requirement was omitted for class C40, the yield would increase from 47.7 to 51.7 %.
-
Regarding other requirements for calculation of settings and yield, see Sect. 4.2, it is concluded that requirements on cost matrices, in a few cases, lead to slightly decreased yield. For example, when grading C30 using IP fb and IP density for prediction of strength and density, respectively, a requirement on the cost matrix brought about that the yield decreased from 97.1 to 96.8 %, i.e. three more pieces out of the 936 pieces included in the sample had to be rejected in order to fulfil requirements on the global cost matrix.
-
The so-called country check, which is an additional requirement decided by TG1 (Anon 2014) that shall be made when settings are derived for more than one country, did not have any impact on the yield presented in Table 7.
6 Conclusion and further work
The new strength grading method fulfils all the requirements laid down in EN 14081-2 and it has recently been approved for the European market. In the process for approval a timber sample of Norway spruce from Sweden, Norway and Finland was evaluated and the coefficient of determination achieved between the IP to bending strength and the measured bending strength was as high as R 2 = 0.69/0.70, while the corresponding relationship between dynamic MOE and measured bending strength was R 2 = 0.53. A comparable study of the performance of methods on the market was presented by Hanhijärvi and Ranta-Maunus (2008) and although conclusions should always be drawn with caution when comparing coefficients of determination between IPs and grade determining properties of different timber samples, the results of the different investigations indicate that the performance of the new method/procedure will surpass what is achieved by market leading techniques of recent years.
Regarding yield in strength classes the new method gives almost twice as high yield in high strength classes (C35 and above) compared to what grading methods based on dynamic MOE alone does. With timber of spruce from Sweden, Norway and Finland, grading C40 and C24 simultaneously, a yield as high as 30 % in the class C40 can be achieved while the rest of the timber (except the mandatory 0.5 % to be rejected) is graded into the class C24. This may be compared to the yield in the class C40 using dynamic MOE as IP of 15 % and the optimum yield that could be achieved using an imaginary “perfect machine” of 47 %.
Further work should comprise a large study on the performance of the new method when grading Norway spruce timber into T-classes, i.e. for prediction of tension strength of laminations for production of glulam, and also studies on the performance of the method for other species. Possibilities for further improvements of the method, e.g. as suggested by Hu et al. (2015) and Briggert et al. (2015) should also be developed, evaluated and possibly implemented in production.
References
Anon (2012) Guidelines for sampling a growth area for deriving machine settings. 6th DRAFT, 18 October. European Committee for Standardization/TC124/WG2/TG1
Anon (2014) TG1 decisions, 5 March. European Committee for Standardization/TC124/WG2/TG1
Bacher M (2008) Comparison of different machine strength grading principles. COST E53, 29–30 October 2008, Delft, The Netherlands, pp 183–193
Briggert A, Olsson A, Oscarsson J (2015) Three dimensional knot models based on surface laser scanning. In: Proceedings of the 19th international nondestructive testing and evaluation of wood symposium, 22–25 September 2015, Rio de Janeiro, Brazil
Dinwoodie JM (2000) Timber: its nature and behaviour. E & FN Spon, New Fetter Lane, London
Dynalyse AB (2015) Precigrader. http://dynalyse.se/precigrader/. Accessed 25 Jul 2015
EN 14081-1 (2005) Timber structures—strength graded structural timber with rectangular cross section—Part 1: general requirements
EN 14081-2 (2010) Timber structures—strength graded structural timber with rectangular cross section—Part 2: Machine grading; additional requirements for initial type testing. European Committee for Standardization
EN 338 (2009) Structural timber—strength classes. European Committee for Standardization
EN 384 (2010) Structural timber—determination of characteristic values of mechanical properties and density. European Committee for Standardization
EN 408 (2010) + A1 (2012) Timber structures—structural timber and glued laminated timber—determination of some physical and mechanical properties. European Committee for Standardization
Hanhijärvi A, Ranta-Maunus A (2008) Development of strength grading of timber using combined measurement techniques. Report of the Combigrade-project—phase 2. VTT Publication 686
Hu M, Johansson M, Olsson A, Oscarsson J, Enquist B (2015) Local variation of modulus of elasticity in timber determined on the basis of non-contact deformation measurement and scanned fibre orientation. Eur J Wood Prod 73(1):17–27
Johansson C-J (2003) Grading of timber with respect to mechanical properties. In: Thelandersson S, Larsen HJ (eds) Timber engineering. Wiley, Chichester, pp 23–43
Johansson C-J, Brundin J, Gruber R (1992) Stress Grading of Swedish and German Timber—a comparison of machine stress grading and three visual grading systems. SP Swedish National Testing and Research Institute, SP REPORT 1992:23
Lukacevic M, Füssl J, Eberhardsteiner J (2015) Discussion of common and new indicating properties for the strength grading of wooden boards. Wood Sci Technol 49(3):551–576
Matthews PC, Beech BH (1976) Method and apparatus for detecting timber defects. US Patent no. 3676384A
Microtec (2015). http://microtec.eu/. Accessed 25 Jul 2015
Nocetti M, Bacher M, Brunetti M, Crivellaro A, van de Kuilen J-W (2010) Machine grading of Italian structural timber: preliminary results on different wood species. In: Proceedings of the 11th world conference on timber engineering, Trentino, Italy 2010
Olsson A, Oscarsson J, Serrano E, Källsner B, Johansson M, Enquist B (2013) Prediction of timber bending strength and in-member cross-sectional stiffness variation on the basis of local wood fibre orientation. Eur J Wood Prod 71(3):319–333
Oscarsson, J (2014) Strength grading of structural timber and EWP laminations of Norway spruce—development potentials and industrial applications. Doctoral dissertation, no 170/2014, Linnaeus University, Växjö, Sweden
Oscarsson J, Olsson A, Enquist B (2014) Localized modulus of elasticity in timber and its significance for the accuracy of machine strength grading. Wood Fiber Sci 46(4):489–501
Petersson H (2010) Use of optical and laser scanning techniques as tools for obtaining improved FE-input data for strength and shape stability analysis of wood and timber. In: Proceedings of V European Conference on Computational Mechanics, Paris, France, May 16–21
Rais A, Van de Kuilen J-W (2015) Critical section effect during derivation of settings for grading machines based on dynamic modulus of elasticity. Wood Mat Sci Eng. doi:10.1080/17480272.2015.1109546
Soest J, Matthews PC, Wilson B (1993) A simple optical scanner for grain defects. In: Proceedings of 5th international conference on scanning technology and process control for the wood products industry, Atlanta, USA, October 25–27
Viguier J, Jehl A, Collet R, Bleron L, Meriaudeau F (2015) Improving strength grading of timber by grain angle measurement and mechanical modelling. Wood Mat Sci Eng 10(1):145–156
WoodEye AB (2015) WoodEye. http://woodeye.se/en/. Accessed 26 Aug 2015
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Olsson, A., Oscarsson, J. Strength grading on the basis of high resolution laser scanning and dynamic excitation: a full scale investigation of performance. Eur. J. Wood Prod. 75, 17–31 (2017). https://doi.org/10.1007/s00107-016-1102-6
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00107-016-1102-6