Abstract
The ring of periodic distributions on \(\mathbb {R}^{\texttt {d}}\) with usual addition of distributions, and with convolution is considered. Via Fourier series expansions, this ring is isomorphic to the ring \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) of all maps \(f:\mathbb {Z}^{\texttt {d}}\rightarrow \mathbb {C}\) of at most polynomial growth (that is, there exist a real number \(M>0\) and an integer \(\texttt {m}\ge 0\) such that \( |f(\varvec{n})|\le M(1+|\texttt{n}_1|+\cdots +|\texttt {n}_{\texttt {d}}|)^{\texttt {m}}\) for all \(\varvec{n}=(\texttt{n}_1,\cdots , \texttt {n}_{\texttt {d}})\in \mathbb {Z}^{\texttt {d}}\)), with pointwise operations. It is shown that finitely generated ideals in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) are principal, and ideal membership is characterised analytically. Calling an ideal in \(\mathcal {S}'(\mathbb {Z}^\texttt{d})\) fixed if there is a common index \(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\) where each member vanishes, the fixed maximal ideals are described, and it is shown that not all maximal ideals are fixed. It is shown that finitely generated (hence principal) prime ideals in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) are fixed maximal ideals. The Krull dimension of \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) is proved to be infinite, while the weak Krull dimension is shown to be equal to 1.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The aim of this article is to study ideals in a naturally arising ring in harmonic analysis and distribution theory, namely the ring \(\mathcal {D}'_{\textbf{V}}(\mathbb {R}^{\texttt {d}})\) of periodic distributions with the usual addition \(+\) of distributions on \(\mathbb {R}^{\texttt {d}}\), and with convolution \(*\) taken as multiplication. Via a Fourier series expansion, the ring \((\mathcal {D}'_{\textbf{V}}(\mathbb {R}^{\texttt {d}}),+,*)\) is isomorphic to the ring \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) consisting of all \(f:\mathbb {Z}^{\texttt {d}} \rightarrow \mathbb {C}\) of at most polynomial growth, with pointwise operations, and we recall this below.
1.1 Motivation
The structure of maximal and prime ideals in rings of analytic objects have been studied in many works. E.g., in [1], it was shown that a uniform algebra on a compact metric space has infinite Krull dimension and exactly \(2^c\) nonmaximal prime ideals. A simpler proof in the context of the ring \(H^\infty \) (of bounded and holomorphic functions in the unit disc with pointwise operations) was given in [13]. The Krull dimension and weak Krull dimension were also investigated in [7], for rings of holomorphic functions and of convolution algebras of measures, arising in control theory as classes of transfer functions or of impulse responses of stable systems. The question of determining the Krull dimension of rings of transfer functions and of impulse responses arises in the modern algebraic framework for solving the stabilisation problem in control theory, see [5]. In this article, we consider a natural convolution algebra of distributions, namely periodic distributions. There has been recent interest in periodic distributions; see e.g. [10]. We remark that the convolution of two Schwartz class distributions \(T_1,T_2\in \mathcal {S}'(\mathbb {R}^{\texttt {d}})\) is not well-defined in general, and so \(\mathcal {S}'(\mathbb {R}^{\texttt {d}})\) is not a convolution algebra. On the other hand, one may consider the convolution algebra \(\mathcal {E}'(\mathbb {R}^{\texttt {d}})\) of compactly supported distributions, and we leave this question for future work.
1.2 The Ring of Periodic Distributions
For background on periodic distributions and its Fourier series theory, we refer the reader to [3, Chap. 16] and [11, pp. 527–529].
Let \(\mathbb {N}=\{1,2,3,\cdots \}\) be the set of natural numbers, \(\mathbb {N}_0:=\mathbb {N}\cup \{0\}\), and \(\mathbb {Z}\) be the set of integers. Consider the space \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) of all complex valued maps on \(\mathbb {Z}^{\texttt {d}}\) of at most polynomial growth, that is,

where  for all \(\varvec{n}=(\texttt {n}_1,\cdots , \texttt {n}_{\;\!\texttt {d}})\in \mathbb {Z}^{\texttt {d}}\). Then \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) is a unital commutative ring with pointwise operations, and the multiplicative unit element \(1_{\mathbb {Z}^{\texttt {d}}}\) is the constant function \( \mathbb {Z}^{\texttt {d}}\ni \varvec{n}\mapsto 1\). Moreover, \((\mathcal {S}'(\mathbb {Z}^{\texttt {d}}),+,\cdot )\) is isomorphic as a ring, to the ring \((\mathcal {D}'_{\textbf{V}}(\mathbb {R}^{\texttt {d}}), +, *)\), where \(\mathcal {D}'_{\textbf{V}}(\mathbb {R}^{\texttt {d}})\) is the set of all periodic distributions (with periods described by \({\textbf{V}}\), see the definition below), with the usual pointwise addition of distributions, and multiplication taken as convolution of distributions.
for all \(\varvec{n}=(\texttt {n}_1,\cdots , \texttt {n}_{\;\!\texttt {d}})\in \mathbb {Z}^{\texttt {d}}\). Then \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) is a unital commutative ring with pointwise operations, and the multiplicative unit element \(1_{\mathbb {Z}^{\texttt {d}}}\) is the constant function \( \mathbb {Z}^{\texttt {d}}\ni \varvec{n}\mapsto 1\). Moreover, \((\mathcal {S}'(\mathbb {Z}^{\texttt {d}}),+,\cdot )\) is isomorphic as a ring, to the ring \((\mathcal {D}'_{\textbf{V}}(\mathbb {R}^{\texttt {d}}), +, *)\), where \(\mathcal {D}'_{\textbf{V}}(\mathbb {R}^{\texttt {d}})\) is the set of all periodic distributions (with periods described by \({\textbf{V}}\), see the definition below), with the usual pointwise addition of distributions, and multiplication taken as convolution of distributions.
Let \(\mathcal {D}(\mathbb {R}^d)\) denote the space of compactly supported infinitely many times differentiable complex valued functions on \(\mathbb {R}^{\texttt {d}}\), and \(\mathcal {D}'(\mathbb {R}^{\texttt {d}})\) the space of distributions on \(\mathbb {R}^{\texttt {d}}\). For \(\varvec{v}\in {{\mathbb {R}}}^{\texttt {d}}\), the translation operator \({\textbf{S}}_{{\varvec{v}}}:\mathcal {D}'(\mathbb {R}^{\texttt{d}})\rightarrow \mathcal {D}'(\mathbb {R}^{\texttt {d}})\), is defined by \(\langle {\textbf{S}}_{\varvec{v}}(T),\varphi \rangle = \langle T,\varphi (\cdot +\varvec{v})\rangle \) for all \(\varphi \in {\mathcal {D}}({\mathbb {R}}^{\texttt {d}})\). A distribution \(T\in {\mathcal {D}}'({\mathbb {R}}^{\texttt {d}})\) is called periodic with a period \(\varvec{v}\in {\mathbb {R}}^{\texttt {d}}\setminus \{\textbf{0}\}\) if \(T= {\textbf{S}}_{\varvec{v}}(T)\). Let \( {\textbf{V}}:=\{\varvec{v}_1, \cdots , \varvec{v}_{\texttt {d}}\} \) be a linearly independent set of \({\texttt {d}}\) vectors in \({\mathbb {R}}^{\texttt {d}}\). Let \({\mathcal {D}}'_{{\textbf{V}}}({\mathbb {R}}^{\texttt {d}})\) denote the set of all distributions T that satisfy \({\textbf{S}}_{\varvec{v}_{\texttt{k}}}(T)=T\) for all \({\texttt {k}}\in \{1,\cdots , \texttt {d}\}\). From [2, §34], T is a tempered distribution. Let \(\widehat{T}\) denote the Fourier transform of T. Taking Fourier transforms on both sides of \({\textbf{S}}_{\varvec{v}_{\texttt {k}}}(T)=T\), it follows that \( (1-e^{2\pi i \varvec{v}_{\texttt {k}} \cdot \varvec{y}})\widehat{T}=0\), for \( {\texttt{k}}\in \{1,\cdots , \texttt {d}\}\), \(\varvec{y}\in \mathbb {R}^d\). Then \( \widehat{T} = \sum _{\varvec{v}\in V^{-1} {\mathbb {Z}}^{\texttt {d}}} \alpha _{\varvec{v}}(T) \delta _{\varvec{v}}, \) for some scalars \(\alpha _{\varvec{v}}(T)\in {\mathbb {C}}\), and where V is the matrix with its rows equal to the transposes of the column vectors \({\varvec{v}_1, \cdots , \varvec{v}_{\texttt{d}}}\):  with \(V^{\text {t}}\) denoting the transpose of the matrix V. Also, in the above, \(\delta _{\varvec{v}}\) denotes the usual Dirac measure with support in \(\varvec{v}\), i.e., \( \langle \delta _{\varvec{v}}, \varphi \rangle =\varphi (\varvec{v})\) for all \( \varphi \in {\mathcal {D}}({\mathbb {R}}^{\texttt {d}})\). Then the Fourier coefficients \(\alpha _{\varvec{v}}(T)\) give rise to an element in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\), and vice versa, every element in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) is the set of Fourier coefficients of some periodic distribution. In fact, the ring \( (\mathcal {D}'_{\textbf{V}}(\mathbb {R}^{\texttt {d}}),+,*) \) of periodic distributions on \(\mathbb {R}^{\texttt {d}}\) is isomorphic to the ring \( (\mathcal {S}'(\mathbb {Z}^{\texttt {d}}),+,\cdot ). \)
with \(V^{\text {t}}\) denoting the transpose of the matrix V. Also, in the above, \(\delta _{\varvec{v}}\) denotes the usual Dirac measure with support in \(\varvec{v}\), i.e., \( \langle \delta _{\varvec{v}}, \varphi \rangle =\varphi (\varvec{v})\) for all \( \varphi \in {\mathcal {D}}({\mathbb {R}}^{\texttt {d}})\). Then the Fourier coefficients \(\alpha _{\varvec{v}}(T)\) give rise to an element in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\), and vice versa, every element in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) is the set of Fourier coefficients of some periodic distribution. In fact, the ring \( (\mathcal {D}'_{\textbf{V}}(\mathbb {R}^{\texttt {d}}),+,*) \) of periodic distributions on \(\mathbb {R}^{\texttt {d}}\) is isomorphic to the ring \( (\mathcal {S}'(\mathbb {Z}^{\texttt {d}}),+,\cdot ). \)
In [8], some algebraic-analytical properties of \((\mathcal {S}'(\mathbb {Z}^{\texttt {d}}),+,\cdot )\) were established; see also [6]. In this article, the structure of ideals in this ring is studied, akin to the investigation in [12] for a ring of entire functions.
1.3 Main Results and Organisation of the Article
-
In Sect. 2, we show that finitely generated ideals in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) are principal, and ideal membership is characterised analytically.
-
In Sect. 3, we describe fixed maximal ideals in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\), and it is shown that not all maximal ideals are fixed.
-
In Sect. 4, we show that finitely generated (and hence principal) prime ideals in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) are fixed maximal ideals. Also, the Krull dimension of \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) is proved to be infinite, while the weak Krull dimension is shown to be equal to 1.
2 Finitely Generated Ideals
Recall that in a commutative ring R, and element d is a divisor of \(r\in R\) if there exists a \(q\in R\) such that \(r=qd\).
Proposition 2.1
g is a divisor of f in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) if and only if there exist a real number \(M>0\) and a nonnegative integer \(\texttt {m}\) such that for all \(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\),  .
.
Proof
(‘If’ part:) Define \(d:\mathbb {Z}^{\texttt {d}}\rightarrow \mathbb {C}\) by
Thus for \(g(\varvec{n})\ne 0\), we have  , and this also holds trivially when \(g(\varvec{n})=0\), since the left-hand side is 0. Thus \(d\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\). Moreover, for \(g(\varvec{n})\ne 0\), we have \(d(\varvec{n})g(\varvec{n})=f(\varvec{n})\), and when \(g(\varvec{n})=0\), the inequality
, and this also holds trivially when \(g(\varvec{n})=0\), since the left-hand side is 0. Thus \(d\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\). Moreover, for \(g(\varvec{n})\ne 0\), we have \(d(\varvec{n})g(\varvec{n})=f(\varvec{n})\), and when \(g(\varvec{n})=0\), the inequality  yields \(f(\varvec{n})=0\) too, showing that \(d(\varvec{n})g(\varvec{n})=d(\varvec{n})0=0=f(\varvec{n})\). Hence \(dg=f\), as wanted.
yields \(f(\varvec{n})=0\) too, showing that \(d(\varvec{n})g(\varvec{n})=d(\varvec{n})0=0=f(\varvec{n})\). Hence \(dg=f\), as wanted.
(‘Only if’ part:) Suppose that \(d\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) is such that \(dg=f\). Since \(d\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\), there exist \(M>0\) and a nonnegative integer \(\texttt {m}\) such that  . So
. So  for all \(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\). \(\square \)
for all \(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\). \(\square \)
In particular, we have the following.
Corollary 2.2
Let \(f\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\). Then f is invertible in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) if and only if there exists a real number \(\delta >0\) and a nonnegative integer \(\texttt {m}\) such that for all \(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\), \(|f(\varvec{n})|\ge \delta (1+|\varvec{n}|)^{-\texttt {m}}\).
In a commutative ring R, given elements \(r_1,\cdots , r_{\texttt {K}}\in R\) (\(\texttt {K}\in \mathbb {N}\)), an element \(d\in R\) is called a greatest common divisor of \(r_1,\cdots , r_{\texttt {K}}\) if
\(\bullet \) d is a divisor of each \(r_{\texttt {k}}\), \(1\le \texttt {k}\le \texttt {K}\), and
\(\bullet \) whenever \(\widetilde{d}\) is a divisor of each \(r_{\texttt {k}}\), \(1\le \texttt {k}\le \texttt {K}\), then \(\widetilde{d}\) is a divisor of d.
The following result shows that every finite number of elements from \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) possesses a greatest common divisor. Moreover, while the greatest common divisor is not unique, it is unique up to multiplication by an invertible element in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) (see Proposition 2.4). Combined with Proposition 2.3 and Corollary 2.2, we obtain a complete characterisation of the set of greatest common divisors for any given finite collection of elements from \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\).
Proposition 2.3
Every finite number of elements \( f_1,\cdots , f_{\texttt {K}}\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) \((\texttt {K}\in \mathbb {N})\) have a greatest common divisor d, given by
Proof
Let \(d(\varvec{n})=\max \{|f_1(\varvec{n})|,\cdots , |f_{\texttt {K}}(\varvec{n})|\}\) for all \(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\). Clearly \(d\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\). As \(|f_{\texttt {k}}(\varvec{n})|\le |d(\varvec{n})|\) for all \(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\) and all \(\texttt {k}\in \{1,\cdots , \texttt {K}\}\), Proposition 2.1 implies that d is a common divisor of \(f_1,\cdots , f_{\texttt {K}}\).
If \(\widetilde{d}\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) is a common divisor of \(f_1,\cdots , f_{\texttt {K}}\), then by Proposition 2.1 again, there exist real \(M_{\texttt {k}}>0\) and positive integers \(\texttt{m}_{\texttt {k}}\), for each \(\texttt {k}\in \{1,\cdots , \texttt {K}\}\), such that  for all \({\varvec{n}}\in \mathbb {Z}^{\texttt {d}}\). Setting \(M:=\max \{M_1,\cdots , M_{\texttt {K}}\}\) and \(m:=\max \{\texttt {m}_1,\cdots , \texttt {m}_{\texttt {K}}\}\), we get
for all \({\varvec{n}}\in \mathbb {Z}^{\texttt {d}}\). Setting \(M:=\max \{M_1,\cdots , M_{\texttt {K}}\}\) and \(m:=\max \{\texttt {m}_1,\cdots , \texttt {m}_{\texttt {K}}\}\), we get  for all \(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\). By Proposition 2.1, \(\widetilde{d}\) divides d in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\). \(\square \)
for all \(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\). By Proposition 2.1, \(\widetilde{d}\) divides d in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\). \(\square \)
Proposition 2.4
If \(d,\widetilde{d}\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) are greatest common divisors of a finite number of elements \( f_1,\cdots , f_{\texttt {K}}\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) \((\texttt {K}\in \mathbb {N})\), then there exists an invertible element \(q\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) such that \(q\widetilde{d}=d\).
Proof
As d is a greatest common divisor of \(f_1,\cdots , f_{\texttt {K}}\), and since \(\widetilde{d}\) is a common divisor of \(f_1,\cdots , f_\texttt{K}\), it follows that \(\widetilde{d}\) divides d. So there exist a real number \(M>0\) and a nonnegative integer \(\texttt {m}\) such that

Upon interchanging the roles of \(\widetilde{d}\) and d, we also obtain as above that there exist a real number \(\widetilde{M}>0\) and a nonnegative integer \(\widetilde{\texttt {m}}\) such that

We have the following cases:
-
\(1^\circ \) \(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\) is such that \(d(\varvec{n})=0\). Then (\(\star \star \)) shows that \(\widetilde{d}(\varvec{n})=0\) too. Setting \(q(\varvec{n}):=1\), we obtain \(d(\varvec{n})=0=1(0)=q(\varvec{n})\widetilde{d}(\varvec{n})\). Moreover,
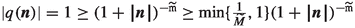 , and
, and  .
. -
\(2^\circ \) \(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\) is such that \(d(\varvec{n})\ne 0\). Then (\(\star \)) shows that \(\widetilde{d}(\varvec{n})\ne 0\) too. Setting \(q(\varvec{n}):=\frac{d(\varvec{n})}{\widetilde{d}(\varvec{n})}\), we have \(d(\varvec{n})=q(\varvec{n})\widetilde{d}(\varvec{n})\). From (\(\star \star \)),
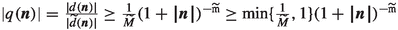 . Also, (\(\star \)) implies
. Also, (\(\star \)) implies 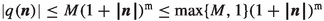 .
.
From the above, it follows that:
-
For all \(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\),
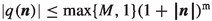 . So \(q\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\).
. So \(q\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\). -
For all \(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\), \(d(\varvec{n})=q(\varvec{n})\widetilde{d}(\varvec{n})\), and so \(d=q\widetilde{d}\).
-
For all \(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\),
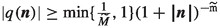 , and so by Corollary 2.2, q is invertible in \(S'(\mathbb {Z}^\texttt{d})\).
, and so by Corollary 2.2, q is invertible in \(S'(\mathbb {Z}^\texttt{d})\).
This completes the proof. \(\square \)
Recall that in a commutative ring R, the ideal \(\langle r_1,\cdots , r_{\texttt {K}}\rangle \) generated by \(r_1,\cdots , r_{\texttt {K}}\in R\) (\(\texttt {K}\in \mathbb {N}\)) is the set \(\{a_1 r_1+\cdots +a_{\texttt {K}}r_{\texttt {K}}: a_1,\cdots ,a_{\texttt {K}}\in R\}\).
Proposition 2.5
Let \(\langle f_1,\cdots , f_{\texttt {K}}\rangle \) denote the ideal generated \(\texttt {K}\in \mathbb {N}\) elements \( f_1,\cdots , f_{\texttt {K}}\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\). Then \(f\in \langle f_1,\cdots , f_\texttt{K}\rangle \) if and only if there exists an \(M>0\) and a nonnegative integer \(\texttt {m}\) such that

Proof
(‘If’ part:) For \(\texttt {k}\in \{1,\cdots , \texttt {N}\}\), define \(g_\texttt{k}:\mathbb {Z}^{\texttt {d}}\rightarrow \mathbb {C}\) by
If \(Q(\varvec{n}):= {{\sum \limits _{\texttt {j=1}}^{\texttt {K}} }} |f_\texttt{j}(\varvec{n})|^2\ne 0\), then (by Cauchy-Schwarz inequality in the last step),

So \(g_1,\cdots , g_{\texttt {K}}\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\). We claim that \(f_1g_1+\cdots +f_{\texttt {K}} g_{\texttt {K}}=f\). The evaluation of the left-hand side at an \(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\) such that \( Q(\varvec{n})\ne 0\) is easily seen to be \(f(\varvec{n})\) by the definition of \(g_1,\cdots , g_{\texttt {K}}\). On the other hand, if \(Q(\varvec{n})=0\), then each \(f_\texttt{k}(\varvec{n})=0\), and by the given inequality in the statement of the proposition, so is \(f(\varvec{n})=0\). Thus in this case the evaluations at \(\varvec{n}\) of both sides of \(f_1g_1+\cdots +f_{\texttt {K}} g_{\texttt {K}}=f\) are zeroes.
(‘Only if’ part:) If \(f\in \langle f_1,\cdots , f_\texttt{K}\rangle \), then there exist \(g_1,\cdots , g_{\texttt {K}}\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) such that \(f=f_1g_1+\cdots +f_{\texttt {K}} g_\texttt{K}\). Let \(M_{\texttt {k}}>0\) and \(\texttt {m}_{\texttt {k}}\in \mathbb {N}\cup \{0\}\), \(\texttt {k}\in \{1,\cdots , \texttt {K}\}\), be such that  (\(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\)). Then with \(M:=\max \{M_1,\cdots , M_{\texttt {K}}\}\) and \(\texttt {m}:=\max \{\texttt {m}_1,\cdots , \texttt {m}_{\texttt {K}}\}\), we get
(\(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\)). Then with \(M:=\max \{M_1,\cdots , M_{\texttt {K}}\}\) and \(\texttt {m}:=\max \{\texttt {m}_1,\cdots , \texttt {m}_{\texttt {K}}\}\), we get

\(\square \)
It follows from Propositions 2.3 and 2.5 that every finitely generated ideal \(\mathfrak {i}\) in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) is principal, that is, \(\mathfrak {i}\) is an ideal generated by one element.
Corollary 2.6
Every finitely generated ideal in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) is principal.
Proof
Let \(f_1,\cdots , f_{\texttt {K}}\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\). We will show that \(\langle f_1,\cdots , f_{\texttt {K}}\rangle =\langle d\rangle \), where \(d\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) is given by \(d(\varvec{n})=\max \{|f_1(\varvec{n})|,\cdots , |f_{\texttt {K}}(\varvec{n})|\}\) for all \(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\). That \(f_{\texttt {k}}\subset \langle d\rangle \) for each \(\texttt {k}\) is obvious as d divides \(f_{\texttt {k}}\), in turn showing \(\langle f_1,\cdots , f_{\texttt {K}}\rangle \subset \langle d\rangle \). For the reverse inclusion,
and so by Proposition 2.5, \(d\in \langle f_1,\cdots , f_{\texttt {K}}\rangle \). Thus we obtain that \(\langle d\rangle \subset \langle f_1,\cdots , f_{\texttt {K}}\rangle \). \(\square \)
3 Maximal Ideals
In a commutative ring R, an ideal \(\mathfrak {i}\) is proper if \(\mathfrak {i}\ne R\). We also recall that in a commutative ring R, an ideal \(\mathfrak {m}\) is maximal if it is maximal with respect to set inclusion amongst all proper ideals, that is, there are no other ideals contained between \(\mathfrak {m}\) and R.
Definition 3.1
An ideal \(\mathfrak {i}\) of \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) is fixed if there exists a \(\varvec{k}\in \mathbb {Z}^{\texttt {d}}\) such that for all \(f\in \mathfrak {i}\), \(f(\varvec{k})=0\).
Theorem 3.2
For \(\varvec{k}\in \mathbb {Z}^{\texttt {d}}\), let \(\mathfrak {m}_{\varvec{k}}:=\{f\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}}): f(\varvec{k})=0\}\).
Then \(\mathfrak {m}_{\varvec{k}}\) is a fixed maximal ideal of \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\).
Every fixed maximal ideal of \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) is equal to \(\mathfrak {m}_{\varvec{k}}\) for some \(\varvec{k}\in \mathbb {Z}^{\texttt {d}}\).
Proof
The fixedness of \(\mathfrak {m}_{\varvec{k}}\) is clear. We now show that maximality. As \(1_{\mathbb {Z}^{\texttt {d}}}\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}}){\setminus } \mathfrak {m}_{\varvec{k}}\), \(\mathfrak {m}_{\varvec{k}} \subsetneq \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\). Let \(\mathfrak {i}\) be an ideal such that \(\mathfrak {m}_{\varvec{k}}\subsetneq \mathfrak {i}\). Suppose that \(f\in \mathfrak {i}{\setminus } \mathfrak {m}_{\varvec{k}}\). Then \(f(\varvec{k})\ne 0\). Define \(g\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) by \(g=1_{\mathbb {Z}^\texttt{d}}-\frac{f}{f(\varvec{k})} \). As \(g(\varvec{k})=0\), we have \(g\in \mathfrak {m}_{\varvec{k}}\subset \mathfrak {i}\). Also, \(\frac{f}{f(\varvec{k})} \in \mathfrak {i}\). Thus \(1_{\mathbb {Z}^{\texttt {d}}} =g+\frac{f}{f(\varvec{k})} \in \mathfrak {i}\), i.e., \(\mathfrak {i}=\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\).
Next, let \(\mathfrak {m}\) be a fixed maximal ideal of \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\). Since \(\mathfrak {m}\) is fixed, there exists a \(\varvec{k}\in \mathbb {Z}^{\texttt {d}}\) such that \(\mathfrak {m}\subset \mathfrak {m}_{\varvec{k}}\subsetneq \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\). By the maximality of \(\mathfrak {m}\), we conclude that \(\mathfrak {m}= \mathfrak {m}_{\varvec{k}}\). \(\square \)
Example 3.3
(Non-fixed maximal ideals) Let \((\texttt {k}_{\texttt {j}})_{\texttt {j}\in \mathbb {N}}\) be any subsequence of the sequence of natural numbers. Set \(\varvec{k}_{\texttt {j}}=(\texttt {k}_\texttt{j},\cdots , \texttt {k}_{\texttt {j}})\in \mathbb {Z}^{\texttt {d}}\). Define \( \mathfrak {i}:=\{ f\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}}):\lim _{\texttt {j}\rightarrow \infty } e^{\texttt {k}_{\texttt {j}}} f(\varvec{k}_{\texttt {j}})=0\}. \) Then \(\mathfrak {i}\) is an ideal of \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\). (It is clear that if \(f,g\in \mathfrak {i}\), then \(f+g\in \mathfrak {i}\). If \(f\in \mathfrak {i}\) and \(g\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\), then there exist a real \(M>0\) and an \(\texttt {m}\in \mathbb {N}\cup \{0\}\) such that  for all \(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\), and so
for all \(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\), and so
showing that \(f g\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\).) Moreover, \(\mathfrak {i}\ne \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) since \(1_{\mathbb {Z}^{\texttt {d}}} \not \in \mathfrak {i}\): \(e^{\texttt {k}_{\texttt {j}}} |1_{\mathbb {Z}^\texttt{d}}(\varvec{k}_{\texttt {j}})| = e^{\texttt {k}_{\texttt {j}}} 1> 1\) for all \(n\in \mathbb {N}\). Hence there exists a maximal ideal \(\mathfrak {m}\) in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) such that \(\mathfrak {i}\subset \mathfrak {m}\). We note that for each \(\varvec{k}\in \mathbb {Z}^{\texttt {d}}\), \(\mathfrak {m}\ne \mathfrak {m}_{\varvec{k}}\): Define \(1_{\{\varvec{k}\}}:\mathbb {Z}^{\texttt {d}}\rightarrow \mathbb {C}\) by \(1_{\{\varvec{k}\}}(\varvec{n})=0\) for all \(\varvec{n}\ne \varvec{k}\) and \(1_{\{\varvec{k}\}}(\varvec{k})=1\). Then \(1_{\{\varvec{k}\}}\in \mathfrak {i} \subset \mathfrak {m}\), but \(1_{\{\varvec{k}\}}\not \in \mathfrak {m}_{\varvec{k}}\) as \(1_{\{\varvec{k}\}}(\varvec{k})=1\ne 0\). \(\Diamond \)
4 Prime Ideals
Recall that an ideal \(\mathfrak {p}\) of a commutative ring R is prime if \(\mathfrak {p}\subsetneq R\), and whenever \(a,b\in R\) are such that \(ab\in \mathfrak {p}\), then \(a\in \mathfrak {p}\) or \(b\in \mathfrak {p}\).
4.1 Finitely Generated (Hence Principal) Proper Prime Ideals
Theorem 4.1
Let \(\mathfrak {p}\) be a finitely generated proper prime ideal of \({\mathcal {S}}'(\mathbb {Z}^{\texttt {d}})\). Then there exists an \(\varvec{n}_*\in \mathbb {Z}^{\texttt {d}}\) such that
Proof
We carry out the proof in several steps.
Step 1. As every finitely generated ideal in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) is principal, suppose that \({{\mathfrak {p}\!=\!\langle d\rangle }}\) for some \(d\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\). For each \({{\varvec{n}\!\in \! \mathbb {Z}^{\texttt {d}}}}\), let \({{d(\varvec{n})\!=\!|d(\varvec{n})|e^{i\theta (\varvec{n})}}}\) for some \(\theta (\varvec{n})\in (-\pi ,\pi ]\). Define \(h\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) by \({{h(\varvec{n})=\sqrt{|d(\varvec{n})|}e^{i\theta (\varvec{n})/2}}}\) for all \(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\). Then \(h^2=d\in \mathfrak {p}\), and as \(\mathfrak {p}\) is prime, \(h\in \mathfrak {p}\).
Step 2. d has exactly one zero. We will now show that there exists an \(\varvec{n}_*\in \mathbb {Z}^{\texttt {d}}\) such that \(d(\varvec{n}_*)=0\). Suppose this is not true. Then by Step 1, \(d(\varvec{n})\ne 0\) for all \(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\). If \(h\in \mathfrak {p}\) is as in Step 2, then there exists a \(k\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) such that \(h=kd\), i.e., \(\sqrt{|d(\varvec{n})|}e^{i\theta (\varvec{n})/2}=|d(\varvec{n})| e^{i\theta (\varvec{n})} k(\varvec{n})\), which yields \(1=d(\varvec{n})(k(\varvec{n}))^2\) (\(\varvec{n}\in \mathbb {Z}^\texttt{d}\)). Thus \(dk^2=1_{\mathbb {Z}^{\texttt {d}}}\), showing that d is invertible in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\), contradicting the properness of the ideal \(\mathfrak {p}\).
Step 3. We now show that \(\mathfrak {p}= \{f\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}}):f(\varvec{n}_*)=0\}\) . That \(\mathfrak {p}\subset \{f\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}}):f(\varvec{n}_*)=0\}\) is clear. Let \(f\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) be such that \(f(\varvec{n}_*)=0\). Define \(g:\mathbb {Z}^\texttt{d}\rightarrow \mathbb {C}\) by
Then \(f=dg\) (note that \(f(\varvec{n})=d(\varvec{n})g(\varvec{n})\) for \(\varvec{n}\ne \varvec{n}_*\) follows from the definition of g, and \(f(\varvec{n}_*)=d(\varvec{n}_*) g(\varvec{n}_*)\) too since both sides are 0). As the h from Step 2 is in \(\mathfrak {p}\), there exists a \(k\in \mathcal {S}'(Z^{\texttt {d}})\) such that \(h=kd\), and so for all \(\varvec{n}\in \mathbb {Z}^{\texttt {d}}\), we get \(\sqrt{|d(\varvec{n})|} e^{i\theta (\varvec{n})/2} =|d(\varvec{n})| e^{i\theta (\varvec{n})} k(\varvec{n})\), giving \(1=|d(\varvec{n})||k(\varvec{n})|^2\). Hence for \(\varvec{n}\ne \varvec{n}_*\), \(\frac{1}{|d(\varvec{n})|}=|k(\varvec{n})|^2\le M(1+|\varvec{n}|)^{\texttt {m}} \) for some \(M>0\) and a nonnegative integer \(\texttt {m}\). This estimate shows that \(g\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\), and hence \(f=gd\in d\mathcal {S}'(\mathbb {Z}^{\texttt {d}})=\langle d\rangle =\mathfrak {p}\). \(\square \)
4.2 Krull Dimension
Recall that a finite chain of ideals is a list of ideals \(\mathfrak {i}_1,\cdots , \mathfrak {i}_{\texttt {K}}\) (\(\texttt {K}\in \mathbb {N}\)) such that \(\mathfrak {i}_1\subset \mathfrak {i}_2\subset \cdots \subset \mathfrak {i}_{\texttt {K}}\).
Definition 4.2
The Krull dimension of a commutative ring R is the supremum of the lengths of chains of distinct proper prime ideals of R.
Recall that the Hardy algebra \(H^\infty \) is the Banach algebra of bounded and holomorphic functions on the unit disc \(\mathbb {D}:=\{z\in \mathbb {C}: |z|<1\}\), with pointwise operations and the supremum norm \(\Vert \cdot \Vert _\infty \). In [13], von Renteln showed that the Krull dimension of \(H^\infty \) is infinite. We adapt the idea given in [13], to show that the Krull dimension of \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) is infinite too. A key ingredient of the proof in [13] was the use of a canonical factorisation of \(H^\infty \) elements used to create ideals with zeroes at prescribed locations with prescribed multiplicities. Instead, we will look at the zero set in \( \mathbb {Z}^{\texttt {d}}\) for \(f\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\), and use the notion of ‘zero-order’ introduced below.
If \(f\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) and \(\varvec{n}=(\texttt {n}_1,\cdots , \texttt{n}_{\texttt {d}})\in \mathbb {Z}^{\texttt {d}}\) is such that \(f(\varvec{n})=0\), then we define the zero-order \(m(f,\varvec{n})\) by
If \(f(\texttt {n}_1, \cdots , \texttt {n}_{\texttt {k}-1}, \texttt {n}_\texttt{k}\!+\!\texttt {j}, \texttt {n}_{\texttt {k}+1}, \cdots , \texttt {n}_{\texttt {d}})=0\) for all \(\texttt {j} \in \mathbb {N}\cup \{0\}\), and all \(\texttt {k}\in \{1,\cdots , \texttt {d}\}\), then we set \(m(f,\varvec{n})=\infty \). If \(f(\varvec{n})\ne 0\), then we set \(m(f,\varvec{n})=0\). Analogous to the multiplicity of a zero of a (not identically vanishing) holomorphic function, the zero-order satisfies the following property.
The multiplicity of a zero \(\zeta \) of the pointwise product of two holomorphic functions is the sum of the multiplicities of \(\zeta \) as a zero of each of the two holomorphic functions. For the zero-order, we have the following instead:
We will use the following known result; see [4, Theorem, §0.16, p.6].
Proposition 4.3
If \(\mathfrak {i}\) is an ideal in a ring R, \(M\subset R\) is a set that is closed under multiplication, and \(M\cap \mathfrak {i}=\emptyset \), then there exists an ideal \(\mathfrak {p}\) such that \(\mathfrak {i}\subset \mathfrak {p}\) and \(\mathfrak {p}\cap M=\emptyset ,\) and \(\mathfrak {p}\) maximal with respect to these properties. Moreover, such an ideal \(\mathfrak {p}\) is necessarily prime.
Theorem 4.4
The Krull dimension of \({\mathcal {S}}'(\mathbb {Z}^{\texttt {d}})\) is infinite.
Proof
For \(\texttt {i}\in \{1,\cdots , \texttt {d}\}\), let \(\varvec{e}_{\texttt {i}}\in \mathbb {Z}^{\texttt {d}}\) be the vector all of whose components are zeroes except for the \(\texttt {i}^{\text {th}}\) one, which is defined as 1. For \(\texttt {n}\in \mathbb {N}\), define \(f_{\texttt {n}}\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) by
Note that \(m(f_{\texttt {n}}, 2^{\texttt {k}} \varvec{e}_1)\ge \texttt {k}^{\texttt {n}+1}\), but for each fixed \(\texttt {n}\in \mathbb {N}\), there exists a \(\texttt {K}_\texttt{n}\in \mathbb {N}\cup \{0\}\) such that the gap between the indices,
and so \(m(f_{\texttt {n}},2^{\texttt {k}} \varvec{e}_1)=\texttt {k}^{\texttt {n}+1}\) for all \(\texttt {k}>\texttt {K}_{\texttt {n}}\). Hence
Let
The set \(\mathfrak {i}_*\) is nonempty since \(0\in \mathfrak {i}_*\). Clearly \(\mathfrak {i}_*\) is closed under addition, and \(f g\in \mathfrak {i}_*\) whenever \(f\in \mathfrak {i}_*\) and \(g\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\). So \(\mathfrak {i}_*\) is an ideal of \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\). For \(\texttt {n}\in \mathbb {N}\), define
Clearly \(f_{\texttt {n}} \in \mathfrak {i}_{\texttt {n}}\), and so \(\mathfrak {i}_{\texttt {n}}\) is not empty. Using (P1), we see that if \(f,g\in \mathfrak {i}_{\texttt {n}}\), then \(f+g\in \mathfrak {i}_{\texttt {n}}\). If \(g\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) and \(f\in \mathfrak {i}_{\texttt {n}}\), then (P2) implies that \(f g\in \mathfrak {i}_{\texttt {n}}\). Hence \(\mathfrak {i}_{\texttt {n}}\) is an ideal of \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\).
The identity element \(1_{\mathbb {Z}^{\texttt {d}}} \in M_{\texttt {n}}\) for all \(\texttt{n}\in \mathbb {N}\). If \(f,g \in M_{\texttt {n}}\), then it follows from (P2) that \(f g\in M_{\texttt {n}}\). Thus \(M_{\texttt {n}}\) is a nonempty multiplicatively closed subset of \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\).
It is easy to check that for all \(\texttt {n}\in \mathbb {N}\), \(\mathfrak {i}_{\texttt {n}+1}\subset \mathfrak {i}_{\texttt {n}}\) and \(M_\texttt{n}\subset M_{\texttt {n}+1}\). We now prove that the inclusions are strict for each \(\texttt {n}\in \mathbb {N}\). From Eq. (1), it follows that \(f_{\texttt {n}} \in \mathfrak {i}_{\texttt {n}}\) but \(f_{\texttt {n}} \not \in \mathfrak {i}_{\texttt {n}+1}\). Also \(f_{\texttt {n}} \in M_{\texttt{n}+1}\) and \(f_{\texttt {n}} \not \in M_{\texttt {n}}\).
Next we show that \(\mathfrak {i}_{\texttt {n}} \cap M_{\texttt {n}} =\emptyset \). Indeed, if \(f\in \mathfrak {i}_{\texttt {n}} \cap M_{\texttt {n}}\), then
a contradiction. But \(\mathfrak {i}_{\texttt {n}} \cap M_{\texttt {n}+1} \ne \emptyset \), since \(f_{\texttt {n}} \in \mathfrak {i}_{\texttt {n}} \) and \(f_\texttt{n}\in M_{\texttt {n}+1}\).
We will now show that the Krull dimension of \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) is infinite by showing that for all \(\texttt {N}\in \mathbb {N}\), we can construct a chain of strictly decreasing prime ideals \( \mathfrak {p}_{\texttt {N}+1}\subsetneq \mathfrak {p}_{\texttt {N}}\subset \cdots \subsetneq \mathfrak {p}_2 \subsetneq \mathfrak {p}_1 \) in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\).
Fix an \(\texttt {N}\in \mathbb {N}\). Applying Proposition 4.3 by taking \(\mathfrak {i}=\mathfrak {i}_{\texttt {N}+1}\) and \(M=M_{\texttt {N}+1}\), we obtain the existence of a prime ideal \(\mathfrak {p}=\mathfrak {p}_{\texttt {N}+1}\) in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\), which satisfies \(\mathfrak {i}_{\texttt {N}+1} \subset \mathfrak {p}_{\texttt{N}+1}\) and \(\mathfrak {p}_{\texttt {N}+1} \cap M_{\texttt {N}+1} =\emptyset \).
We claim the ideal \(\mathfrak {i}_{\texttt {N}}+\mathfrak {p}_{\texttt {N}+1}\) of \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) satisfies \({{(\mathfrak {i}_{\texttt {N}} +\mathfrak {p}_{\texttt {N}+1}) \cap M_{\texttt {N}} = \emptyset }}\). Let \(h=f+g \in \mathfrak {i}_{\texttt {N}}+\mathfrak {p}_{\texttt {N}+1}\), where \(f\in \mathfrak {i}_{\texttt {N}}\) and \(g\in \mathfrak {p}_{\texttt {N}+1}\). Since \(g\in \mathfrak {p}_{\texttt {N}+1}\), by the construction of \({\mathfrak {p}}_{\texttt {N}+1}\) it follows that \(g\not \in M_{\texttt{N}+1}\). But \(M_{\texttt {N}} \subset M_{\texttt {N}+1}\), and so \(g\not \in M_{\texttt {N}}\) as well. Thus there exists a subsequence \((\texttt {k}_{\texttt {j}})_{\texttt {j}\in \mathbb {N}}\) of \((\texttt {k})_{\texttt {k}\in \mathbb {N}}\) such that
From (P1), we obtain
As \(f\in \mathfrak {i}_{\texttt {N}}\), it follows that
Thus \(h\not \in M_{\texttt {N}}\). Consequently, \((\mathfrak {i}_{\texttt {N}} +\mathfrak {p}_{\texttt {N}+1}) \cap M_{\texttt {N}}=\emptyset \).
Clearly \(\mathfrak {i}_{\texttt {N}} \subset \mathfrak {i}_\texttt{N}+\mathfrak {p}_{\texttt {N}+1}\). Applying Proposition 4.3 again, now taking \(\mathfrak {i}=\mathfrak {i}_{\texttt {N}}+\mathfrak {p}_{\texttt {N}+1}\) and \(M=M_{\texttt {N}}\), we obtain the existence of a prime ideal \(\mathfrak {p}=\mathfrak {p}_{\texttt {N}}\) in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) such that \(\mathfrak {i}_{\texttt {N}}+\mathfrak {p}_{\texttt {N}+1} \subset \mathfrak {p}_{\texttt {N}}\) and \(\mathfrak {p}_{\texttt {N}} \cap M_{\texttt {N}} =\emptyset \). Thus \(\mathfrak {p}_{\texttt {N}+1}\subset \mathfrak {i}_\texttt{N}+ \mathfrak {p}_{\texttt {N}+1}\subset \mathfrak {p}_{\texttt {N}}\). The first inclusion is strict as \(f_{\texttt {N}}\in \mathfrak {i}_{\texttt {N}}\subset \mathfrak {i}_{\texttt {N}}+\mathfrak {p}_{\texttt {N}+1}\). But \(f_\texttt{N}\not \in \mathfrak {p}_{\texttt {N}+1}\) (since \(f_{\texttt {N}}\in M_{\texttt{N}+1}\) and \(\mathfrak {p}_{\texttt {N}+1}\cap M_{\texttt {N}+1} =\emptyset \) by the construction of \(\mathfrak {p}_{\texttt {N}+1}\)). Thus \(\mathfrak {p}_{\texttt {N}+1}\subsetneq \mathfrak {p}_{\texttt {N}}\).
Now consider the ideal \(\mathfrak {i}:=\mathfrak {i}_{\texttt{N}-1}+\mathfrak {p}_{\texttt {N}}\supset \mathfrak {i}_{\texttt {N}-1}\) of \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) and the multiplicatively closed set \(M:=M_{\texttt {N}-1}\) of \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\). Similar to the argument given above, we show below that \(\mathfrak {i}\cap M=(\mathfrak {i}_{\texttt {N}-1}+\mathfrak {p}_{\texttt {N}})\cap M_{\texttt{N}-1}=\emptyset \).
Let \(h=f+g \in \mathfrak {i}_{\texttt {N}-1}+\mathfrak {p}_{\texttt {N}}\), where \(f\in \mathfrak {i}_{\texttt {N}-1}\) and \(g\in \mathfrak {p}_\texttt{N}\). Since \(g\in \mathfrak {p}_{\texttt {N}}\), by the construction of \(\mathfrak {p}_{\texttt {N}}\), \(g\not \in M_{\texttt {N}}\supset M_{\texttt {N}-1}\), and so \(g\not \in M_{\texttt {N}-1}\). Thus there exists a subsequence \((\texttt {k}_{\texttt {j}})_{\texttt {j}\in \mathbb {N}}\) of \((\texttt {k})_{\texttt {k}\in \mathbb {N}}\) such that
As \(f\in \mathfrak {i}_{\texttt {N}-1}\),
Thus \(h\not \in M_{\texttt {N}-1}\). So \((\mathfrak {i}_{\texttt {N}-1} +\mathfrak {p}_{\texttt {N}}) \cap M_{\texttt {N}-1}=\emptyset \).
By Proposition 4.3, taking \(\mathfrak {i}=\mathfrak {i}_{\texttt {N}-1}+\mathfrak {p}_{\texttt {N}}\supset \mathfrak {i}_{\texttt {N}-1}\) and \(M=M_{\texttt {N}-1}\), there exists a prime ideal \(\mathfrak {p}=\mathfrak {p}_{\texttt {N}-1}\) in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) such that \(\mathfrak {i}_{\texttt{N}-1}+\mathfrak {p}_{\texttt {N}} \subset \mathfrak {p}_{\texttt {N}-1}\) and \(\mathfrak {p}_{\texttt {N}-1} \cap M_{N-1} =\emptyset \). Thus \(\mathfrak {p}_{\texttt {N}}\subset \mathfrak {i}_{\texttt {N}-1}+ \mathfrak {p}_{\texttt {N}}\subset \mathfrak {p}_{\texttt {N}-1}\), and again the first inclusion is strict (because \(f_{\texttt {N}-1}\in \mathfrak {i}_{\texttt {N}-1}\subset \mathfrak {i}_{\texttt{N}-1}+\mathfrak {p}_{\texttt {N}}\), \(f_{\texttt {N}-1}\in M_{\texttt {N}}\) and \(M_{\texttt {N}}\cap \mathfrak {p}_{\texttt {N}}=\emptyset \)).
Proceeding in this manner, we obtain the chain of distinct prime ideals \( \mathfrak {p}_{\texttt {N}+1} \subsetneq \mathfrak {p}_{\texttt {N}} \subsetneq \mathfrak {p}_{\texttt {N}-1} \subsetneq \cdots \subsetneq \mathfrak {p}_1. \) in \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\). As \(\texttt {N}\in \mathbb {N}\) was arbitrary, it follows that the Krull dimension of \(\mathcal {S}'(\mathbb {Z}^\texttt{d})\) is infinite. \(\square \)
4.3 Weak Krull Dimension
Recall the following definition from [9]:
Definition 4.5
The weak Krull dimension of a commutative ring R is the supremum of the lengths of chains of distinct proper finitely generated prime ideals of R.
Theorem 4.6
The weak Krull dimension of \({\mathcal {S}}'(\mathbb {Z}^{\texttt {d}})\) is 1.
Proof
Let \(\mathfrak p_1\) and \(\mathfrak p_2\) be finitely generated proper prime ideals in \({\mathcal {S}}'(\mathbb {Z}^{\texttt {d}})\) such that \(\mathfrak p_1\subset \mathfrak p_2\). For each \(\texttt {i}\in \{1,2\}\), by Proposition 2.3, there exists an \(\varvec{n}_\texttt{i}\in \mathbb {Z}^{\texttt {d}}\) such that \(\mathfrak {p}_{\texttt {i}}=\{f\in \mathcal {S}'(\mathbb {Z}^{\texttt {d}}):f(\varvec{n}_{\texttt {i}})=0\}\). But as \(\mathfrak p_1\subset \mathfrak p_2\), it follows that \(\varvec{n}_1=\varvec{n}_2\) (by considering the function which is zero at all \(\varvec{n}\in \mathbb {Z}^\texttt{d}{\setminus } \{\varvec{n}_2\}\) and equal to 1 at \(\varvec{n}_2\)), and so \(\mathfrak {p}_1=\mathfrak {p}_2\). So the weak Krull dimension of \(\mathcal {S}'(\mathbb {Z}^{\texttt {d}})\) is 1. \(\square \)
References
Dietrich, W.: Prime ideals in uniform algebras. Proc. Am. Math. Soc. 42, 171–174 (1974)
Donoghue, W., Jr.: Distributions and Fourier Transforms. Academic Press, New York and London (1969)
Duistermaat, J., Kolk, J.: Distributions: Theory and Applications. Birkhäuser, Boston (2010)
Gillman, L., Jerison, M.: Rings of Continuous Functions. D. Van Nostrand Company, Princeton, New Jersey (1960)
Quadrat, A.: On a generalization of the Youla-Kučera parametrization. II. The lattice approach to MIMO systems. Math. Control Signal Syst. 18(3), 199–235 (2006)
Roitman, M., Sasane, A.: On the Gleason-Kahane-Żelazko theorem for associative algebras. Res. Math. 78(1), 26 (2023)
Sasane, A.: On the Krull dimension of rings of transfer functions. Acta Appl. Math. 103(2), 161–168 (2008)
Sasane, A.: A potpourri of algebraic properties of the ring of periodic distributions. Bull. Belgian Math. Soc. 25(5), 755–776 (2018)
Tang, G.: Weak Krull dimension over commutative rings. In: Chen, J., Ding, N. (eds.) Advances in Ring Theory, pp. 215–224. Springer, New York (2005)
Toft, J., Nabizadeh, E.: Periodic distributions and periodic elements in modulation spaces. Adv. Math. 323, 193–225 (2018)
Trèves, F.: Topological Vector Spaces, Distributions and Kernels. Dover Publications, Mineola, NY (2006)
von Renteln, M.: Rings of entire functions with weighted Hadamard multiplication. Demonstr. Math. 10(3–4), 807–813 (1977)
von Renteln, M.: Primeideale in der topologischen algebra \(H^{\infty }(\beta )\). Math. Z. 157, 79–82 (1977)
Funding
No funding was received for conducting this study.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Hans G. Feichtinger.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sasane, A. Ideals in the Convolution Algebra of Periodic Distributions. J Fourier Anal Appl 30, 18 (2024). https://doi.org/10.1007/s00041-024-10078-y
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00041-024-10078-y
Keywords
- Krull dimension
- Prime ideals
- Maximal ideals
- Ring of periodic distributions
- Convolution
- Sequences of at most polynomial growth



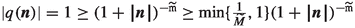 , and
, and  .
.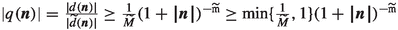 . Also, (
. Also, (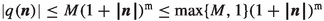 .
.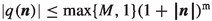 . So
. So 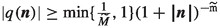 , and so by Corollary
, and so by Corollary