On Discrete Groups of Euclidean Isometries: Representation Theory, Harmonic Analysis and Splitting Properties

Abstract

We study structural properties and the harmonic analysis of discrete subgroups of the Euclidean group. In particular, we 1. obtain an efficient description of their dual space, 2. develop Fourier analysis methods for periodic mappings on them, and 3. prove a Schur-Zassenhaus type splitting result.

1 Introduction

The main objective of the present contribution is a study of various aspects of discrete subgroups of the Euclidean group ${\textrm{E}}(d)$ concerning their representations, harmonic analysis and splitting properties. Special cases of such groups are finite subgroups of the rotation group ${{\textrm{O}}}(d)$ and the crystallographic space groups. While these objects are very well studied, cf. e. g. [8, 10, 12, 16] for classic references and [36, 40] for some recent developments, the theory for general discrete groups of Euclidean isometries is considerably less developed. In a sense that is made precise below, they interpolate and combine aspects of finite rotation groups and space groups as they might be assumed to embed into a subgroup of ${{\textrm{O}}}(d_1)\oplus {\mathcal {S}}$ for some $d_2$-dimensional space group ${\mathcal {S}}$, where $d_1+d_2=d$. We will see that it is possible to identify a “translational part” of such a group featuring some properties analogous to those of a $d_2$-dimensional lattice. This will allow us to 1. obtain an efficient description of the dual space of discrete subgroups of ${\textrm{E}}(d)$, 2. to develop Fourier analysis methods for periodic mappings on them, and 3. to prove a Schur-Zassenhaus type splitting result with respect to the translational part.

It goes without saying that, besides of their intrinsic mathematical interest, Fourier methods have applications in a wide variety of different applications. For non-abelian groups, as in our case, a thorough understanding and manageable description of the dual space is decisive. In particular, for crystallographic space groups band representations have been provided in [3, 41], efficient computation schemes for the fast Fourier transform, wavelets with underlying crystal symmetry and, recently, the crystallographic phase retrieval problem have been addressed [5, 7, 18, 24, 25]. As a general source for background material with an emphasis on applications in solid state physics we mention [17]. We also refer to the recent contributions [30,31,32], where efficiency of the Fourier transform in the general non-abelian setting is investigated from an algorithmic perspective.

Our main motivation originates in a physical question on the stability of so-called Objective Structures. These particle systems were introduced by James in [20] as a far reaching generalization of lattice systems and have been deployed successfully to describe a remarkable number of important structures ranging from biology (parts of viruses) to nanoscience (carbon nanotubes).

In order to motivate and illustrate our investigations let us consider ${{\mathbb {Z}}}^d$ as the most basic and classical example of a lattice system. Localized mappings $u \in \ell ^1({{\mathbb {Z}}}^d)$ (say) can be conveniently analyzed in terms of their Fourier transform which in particular induces a resolution into plane waves ${\textrm{e}}^{2\pi {\textrm{i}}\langle k, \cdot \rangle }$, characterized by their wave vectors k, with dominant contributions from small wave numbers |k|. So as to account for lattice mappings with significant contributions from large wave numbers, a feasible strategy is to investigate N-periodic functions $u: {{\mathbb {Z}}}^d \rightarrow {{\mathbb {C}}}$, $N \in {{\mathbb {N}}}$, for which $u(x + N e_i) = u(x)$ for all $i \in \{1, \ldots , d\}$ in the asymptotic regime $N \rightarrow \infty$. Such a function might alternatively be looked at as a function on ${{\mathbb {Z}}}_N^d$ and is described by its discrete Fourier transform

$k \in \{0, \frac{1}{N}, \ldots , \frac{N-1}{N}\}^d$, as

Here the wave vectors k are eventually dense in the unit cell $[0,1]^d$ as the period N becomes larger and larger. In this way one obtains Fourier descriptions for all periodic functions which, upon truncating the maximal periodicity at finite N, lends itself to a directly controllable approximation in numerical simulations.

By a simple coordinate change such an analysis applies to general lattice systems $A {{\mathbb {Z}}}^d$, $A \in {{\,\mathrm{\textrm{GL}}\,}}(d, {{\mathbb {R}}})$, which are easily seen to be the orbit of a single point under the action of a discrete group of translations on ${{\mathbb {R}}}^d$. These point sets are of paramount interest in solid state physics where they might describe positions of atoms and molecules. More generally, an Objective Structure can be defined as the orbit of a single point under the action of a general discrete subgroup of the Euclidean group ${\textrm{E}}(d)$ on ${{\mathbb {R}}}^d$, cf. [20]. Those structures are thus characterized by the fact that any two points “see” an identical environment of other points, modulo a rigid motion.

One of the aims of the present contribution is to develop an extension of the above described Fourier analysis for discrete translation groups to general discrete groups of Euclidean isometries. While in principle a Fourier transform is defined on the dual space of such a group, an efficient description of these spaces appears to be missing. Moreover, the incorporation of periodic mappings with significant “long wave-length” contributions is non-trivial. In fact, due to a possible lack of periodicity, even the definition of a quantity that can be interpreted as a wave-length is not obvious. Our main goal is therefore, by exploiting the special structure of discrete subgroups of ${\textrm{E}}(d)$, to provide an efficient and extensive description of their dual spaces. In particular we identify a finite union of convex “wave vector domains” for each such space, which reflects the existence of an underlaying translational part of finite index.

We proceed to give a more detailed account of our results and a plan of the paper. In Sect. 2 we first collect basic definitions and properties of the Euclidean group and space groups and cite a characterization of discrete subgroups of the Euclidean group: Up to conjugation in ${\textrm{E}}(d)$ a discrete subgroup ${\mathcal {G}}$ of ${\textrm{E}}(d)$ embeds into a subgroup of ${{\textrm{O}}}(d_1) \oplus {\mathcal {S}}$ for a spacegroup ${\mathcal {S}} \subset E(d_2)$, where $d_1+d_2=d$, with surjective projection $\pi$ onto ${\mathcal {S}}$, cf. Fig. 1.

Fig. 1

Structure of a discrete subgroup of ${\textrm{E}}(d)$

Whereas the spacegroup ${\mathcal {S}}$ has a rich translation group ${\mathcal {T}}_{{\mathcal {S}}}$, this is in general not the case for ${\mathcal {G}}$. To overcome this problem, in Sect. 3 we fix a section ${\mathcal {T}}\subset {\mathcal {G}}$ of ${\mathcal {T}}_{{\mathcal {S}}}$, which, however, will not be a group in general. We also set ${\mathcal {F}}= \ker (\pi ) \cap {\mathcal {G}}$ and analyze ${\mathcal {T}}$ and ${\mathcal {F}}$ in some detail. A first remarkable fact then is that ${\mathcal {T}}^N$ (set of N-fold products of elements in ${\mathcal {T}}$) for suitable $N \in {{\mathbb {N}}}$ is a subgroup and even a normal divisor, see Theorem 3.11, which is essential in our later considerations on periodic functions.

In Sect. 4 we obtain our main results on the structure of representations of ${\mathcal {G}}$. We consider the subgroup ${\mathcal {T}}{\mathcal {F}}$ of ${\mathcal {G}}$, which corresponds to the set of preimages of ${\mathcal {T}}_{{\mathcal {S}}}$ under $\pi$, and analyze in detail the representations of ${\mathcal {T}}{\mathcal {F}}$ and the induced representations of ${\mathcal {T}}{\mathcal {F}}$ in ${\mathcal {G}}$. In Theorem 4.16 we prove that the latter decompose into a finite disjoint union $\bigsqcup _{\rho \in R}{{\mathbb {R}}}^{d_2}/{\mathcal {G}}_\rho$ of orbit spaces (or fundamental domains) of certain space groups ${\mathcal {G}}_\rho$ on ${{\mathbb {R}}}^{d_2}$ via

$$\begin{aligned} ({\mathcal {G}}_\rho \cdot k,\rho ) \mapsto {\textrm{Ind}}_{{\mathcal {T}}{\mathcal {F}}}^{\mathcal {G}}({\textrm{e}}^{-2\pi {\textrm{i}}\langle k, \cdot \rangle }\rho ), \end{aligned}$$

for a suitable finite $R \subset \widehat{{\mathcal {T}}{\mathcal {F}}}$. (More precisely, ${\textrm{e}}^{-2\pi {\textrm{i}}\langle k, \cdot \rangle }$ acts on the translation vector associated to an element of ${\mathcal {T}}{\mathcal {F}}$ after projection onto ${\mathcal {T}}_{{\mathcal {S}}}$.) This in particular allows for an interpretation of $\bigsqcup _{\rho \in R}{{\mathbb {R}}}^{d_2}/{\mathcal {G}}_\rho$ as a set of “generalized wave vectors” given in terms of a finite number of $\rho$’s and associated “classical” wave vectors $k \in {{\mathbb {R}}}^{d_2}/{\mathcal {G}}_\rho$ so that the “generalized plane wave”

$$\begin{aligned} {\textrm{e}}^{-2\pi {\textrm{i}}\langle k, \cdot \rangle }\rho \end{aligned}$$

induces a representation on ${\mathcal {G}}$. A version for periodic representations is given in Theorem 4.17 where the orbit spaces ${{\mathbb {R}}}^{d_2}/{\mathcal {G}}_\rho$ are replaced by suitable rescalings of $L_{\mathcal {S}}^*$, the dual lattice of translations in ${\mathcal {S}}$. As a result of Theorem 4.16, we obtain that – up to a negligible set – the whole dual space $\widehat{{\mathcal {G}}}$ is equal to the same set of induced representations. More precisely, for each $\rho \in R$ there is a zero-set $N_\rho \subset {{\mathbb {R}}}^{d_2}/{\mathcal {G}}_\rho$ (with respect to the Lebesgue-measure) and a zero-set $N\subset \widehat{{\mathcal {G}}}$ (with respect to the Plancherel-measure on $\widehat{{\mathcal {G}}}$) such that the above mapping is bijective when restricted to

$$\begin{aligned} \bigsqcup _{\rho \in R}({{\mathbb {R}}}^{d_2}/{\mathcal {G}}_\rho )\setminus N_\rho \rightarrow \widehat{{\mathcal {G}}}\setminus N, \end{aligned}$$

cf. Theorem 4.19. We remark that, as compared to general results in this direction obtained with the Mackey machine (see in particular [22, 23, 28] and also cp. Theorem A.5 below), we obtain an explicit labeling of representations with “wave vectors” in a finite union of convex domains in ${{\mathbb {R}}}^{d_2}$, which in turn are identified as fundamental domains of associated space groups.

In the following, comparatively elementary Sect. 5 we introduce an inner product space of functions that satisfy a suitable periodicity assumption. We then proceed to develop a harmonic analysis on such objects by defining the Fourier transform for both periodic and absolutely summable functions and formulating well-known theorems like the Plancherel formula within our setting.

In Sect. 6 we then address the question if ${\mathcal {G}}$ splits into a translational part (more precisely, some ${\mathcal {T}}^m \triangleleft {\mathcal {G}}$) and a finite complement. In general this is not the case. However, our main structural splitting result Theorem 6.7 provides such representations as semidirect products for quotient groups of ${\mathcal {G}}$ with respect to a series of eventually sparse normal subgroups: If in addition $n\in {{\mathbb {N}}}$ is coprime to m and $|{\mathcal {S}}/{\mathcal {T}}_{\mathcal {S}}|$, then there is a group ${\mathcal {H}}\le {\mathcal {G}}/{\mathcal {T}}^{nm}$ such that

$$\begin{aligned} {\mathcal {G}}/{\mathcal {T}}^{nm} = {\mathcal {T}}^m/{\mathcal {T}}^{nm}\rtimes {\mathcal {H}}, \end{aligned}$$

where ${\mathcal {T}}^m/{\mathcal {T}}^{nm} \cong {{\mathbb {Z}}}_n^{d_2}$. (Note that for space groups and $m = 1$ such a result is mentioned in [4, 14].)

Finally, Sect. A in the appendix collects some well-known definitions and theorems of harmonic analysis like the definition and basic properties of dual spaces and induced representations.

We close this introduction with an outlook to applications on the stability analysis of particle systems. Assuming that particles at different sites interact, one is naturally led to the question if an Objective Structure corresponds to a stable configuration. Similar questions are by now well understood in lattice systems, see, e. g., [19]: At equilibrium configurations the second order Taylor approximation of the configurational energy is conveniently analyzed in Fourier space and formulae for stability constants under rather generic interaction assumptions are available [11]. The results in the current contribution will indeed allow for an analogous characterization of stability constants for Objective Structures. This will be realized in the forthcoming contributions [37, 38], where we provide a characterization that even leads to a numerical algorithm for testing the stability of a given structure and to novel applications to nanotubes.

1.1 Notation

We will use the following notation. For all groups G and subsets $S_1,S_2\subset G$ we denote

$$\begin{aligned} S_1S_2:=\{s_1s_2\,|\,s_1\in S_1,s_2\in S_2\}\subset G \end{aligned}$$

the product of group subsets. For all $S\subset G$, $n\in {{\mathbb {Z}}}$ and $g\in G$ we denote

$$\begin{aligned} S^n&:=\{s^n\,|\,s\in S\}\subset G \end{aligned}$$

and

$$\begin{aligned} gS&:=\{gs\,|\,s\in S\}\subset G. \end{aligned}$$

For two groups G, H we write $H<G$ if H is a proper subgroup of G and $H\triangleleft G$ if H is a normal subgroup of G. For a subset S of a group G we write $\langle S\rangle$ for the subgroup generated by S.

For representations (and equivalence classes thereof), which are tacitly understood to be unitary and (in our setting without loss of generality) finite-dimensional, we use the symbol $\chi$ if they are one-dimensional and $\rho$ otherwise. Their dimensions are denoted $d_\rho$. The dual space of a group G is denoted $\widehat{G}$. If $H \triangleleft G$, the action of $g\in G$ on (equivalence classes of) representations $\rho$ of H is written as $g\cdot \rho (h):=\rho (g^{-1}h g)$ for $h\in H$.

Moreover, for $H \triangleleft G$ and $\rho \in \widehat{H}$ we denote by $G^\rho$ the stabilizer of $\rho$ in G and by $G \cdot \rho$ the orbit of $\rho$ with respect to this action. Likewise, $(G/H)^\rho$ is the stabilizer of $\rho$ in G/H and $(G/H) \cdot \rho$ the orbit of $\rho$ on $\widehat{H}$ with respect to the induced action of G/H on $\widehat{H}$.

Finally, let ${{\mathbb {N}}}$ be the set of all positive integers $\{1,2,\dots \}$, ${{\mathbb {Z}}}_n$ be the group ${{\mathbb {Z}}}/(n{{\mathbb {Z}}})$, $e_i$ be the $i^{\text {th}}$ standard coordinate vector $(0,\dots ,0,1,\dots ,0)\in {{\mathbb {R}}}^d$ and $I_n\in {{\mathbb {R}}}^{n\times n}$ be the identity matrix of size n. We use capital letters for matrices. For $A=(a_{ij})\in {{\mathbb {C}}}^{m\times n}$ and $B=(b_{ij})\in {{\mathbb {C}}}^{p\times q}$, their direct sum and their Kronecker product are

$$\begin{aligned} A\oplus B:=\bigg (\begin{matrix}A&{}0\\ 0&{}B\end{matrix}\bigg ) \in {{\mathbb {C}}}^{(m+p)\times (n+q)}, \qquad A\otimes B:=\begin{bmatrix} a_{11}B &{} \cdots &{} a_{1n}B\\ \vdots &{} \ddots &{} \vdots \\ a_{m1}B &{} \cdots &{} a_{mn}B \end{bmatrix}\in {{\mathbb {C}}}^{mp\times nq}, \end{aligned}$$

respectively. The Hermitian adjoint of A is denoted $A^H$. $\textrm{U}(n)$ is the group of all unitary matrices in ${{\mathbb {C}}}^{n\times n}$.

2 Discrete Groups of Euclidean Isometries

This preliminary section serves to collect some basics on the Euclidean group acting on ${{\mathbb {R}}}^d$ and of its discrete subgroups. We also introduce some general notation.

2.1 The Euclidean Group

Let $d\in {{\mathbb {N}}}$ be the dimension. We denote the set of all Euclidean distance preserving transformations of ${{\mathbb {R}}}^d$ into itself by the Euclidean group ${\textrm{E}}(d)$. The elements of ${\textrm{E}}(d)$ are called Euclidean isometries. It is well-known that the Euclidean group ${\textrm{E}}(d)$ can be described concretely as the outer semidirect product of ${{\mathbb {R}}}^d$ and ${{\textrm{O}}}(d)$, the orthogonal group in dimension d:

$$\begin{aligned} {\textrm{E}}(d)={{\textrm{O}}}(d)\ltimes {{\mathbb {R}}}^d. \end{aligned}$$

The group operation is given by

$$\begin{aligned} (A_1, b_1 )(A_2, b_2 )=(A_1A_2, b_1+A_1b_2 ) \end{aligned}$$

for all $(A_1, b_1 ),(A_1, b_2 )\in {\textrm{E}}(d)$, and the inverse of $(A, b )\in {\textrm{E}}(d)$ is

$$\begin{aligned} (A, b )^{-1}=(A^{-1}, -A^{-1}b ). \end{aligned}$$

Moreover, we define the maps

$$\begin{aligned} L:{\textrm{E}}(d)\rightarrow {{\textrm{O}}}(d), \quad&(A, b )\mapsto A \qquad \text {and} \\ \tau :{\textrm{E}}(d)\rightarrow {{\mathbb {R}}}^d, \quad&(A, b )\mapsto b \end{aligned}$$

and for all $(A, b )\in {\textrm{E}}(d)$ we call $L((A, b ))$ the linear component and $\tau ((A, b ))$ the translation component of $(A, b )$. Thus,

$$\begin{aligned} g=(I_d, \tau (g) )(L(g), 0 ) \end{aligned}$$

for every $g\in {\textrm{E}}(d)$. We call an Euclidean isometry $(A, b )$ a translation if $A=I_d$. All translations form the group of translations ${\textrm{Trans}}(d)$, which is the abelian subgroup of ${\textrm{E}}(d)$ given by

$$\begin{aligned} {\textrm{Trans}}(d):=\{I_d\}\ltimes {{\mathbb {R}}}^d. \end{aligned}$$

We call a set of translations linearly independent if their translation components are linearly independent. The natural group action of ${\textrm{E}}(d)$ on ${{\mathbb {R}}}^d$ is given by

$$\begin{aligned} (A, b )\cdot x:=Ax+b\qquad \text {for all }(A, b )\in {\textrm{E}}(d)\text { and }x\in {{\mathbb {R}}}^d. \end{aligned}$$

In this contribution we use a calligraphic font for subsets and particularly for subgroups of ${\textrm{E}}(d)$. For every group ${\mathcal {G}}<{\textrm{E}}(d)$ we denote the orbit of a point $x\in {{\mathbb {R}}}^d$ under the action of the group ${\mathcal {G}}$ by

$$\begin{aligned} {\mathcal {G}}\cdot x:=\{g\cdot x\,|\,g\in {\mathcal {G}}\}. \end{aligned}$$

We endow ${\textrm{E}}(d)$ with the subspace topology of the Euclidean space ${{\mathbb {R}}}^{d\times d}\times {{\mathbb {R}}}^d$ such that ${\textrm{E}}(d)$ is a topological group. It is well-known that a subgroup ${\mathcal {G}}<{\textrm{E}}(d)$ is discrete if and only if for every $x\in {{\mathbb {R}}}^d$ the orbit ${\mathcal {G}}\cdot x$ is discrete, see, e. g., [13, Exercise I.1.4]. In particular, every finite subgroup of ${\textrm{E}}(d)$ is discrete.

A discrete group ${\mathcal {G}}<{\textrm{E}}(d)$ is said to be decomposable if the group representation

$$\begin{aligned}&{\mathcal {G}}\rightarrow {{\,\mathrm{\textrm{GL}}\,}}(d+1,{{\mathbb {C}}})\\&(A,b)\mapsto \begin{pmatrix}A&{}b\\ 0&{}1\end{pmatrix} \end{aligned}$$

is decomposable, i. e., there is a decomposition of ${{\mathbb {R}}}^{n+1}$ into the direct sum of two proper subspaces invariant under $\{({\begin{matrix}A&{}b\\ 0&{}1\end{matrix}})\,|\,(A, b )\in {\mathcal {G}}\}$. If this is not the case, the discrete group ${\mathcal {G}}$ is called indecomposable, see, e. g., [12, Appendix A.3]. An indecomposable discrete group ${\mathcal {G}}<{\textrm{E}}(d)$ is also called a (d-dimensional) space group. Below we also present a (well-known) characterization of the space groups and the decomposable discrete subgroups of ${\textrm{E}}(d)$, respectively, which does not use representations.

In the physically important case $d=3$, all space groups and discrete decomposable subgroups of ${\textrm{E}}(3)$ are well-known and classified, see, e. g., [2] and [34], respectively.

2.2 Space Groups

The following theorem is well-known, see, e. g., [12, Appendix A.3].

Theorem 2.1

Let $d\in {{\mathbb {N}}}$ be the dimension and ${\mathcal {G}}< {\textrm{E}}(d)$ a discrete subgroup. The following are equivalent:

• (i) ${\mathcal {G}}$ is a space group.

• (ii) ${\mathcal {G}}$ contains d linearly independent translations.

• (iii) The subgroup of translations of ${\mathcal {G}}$ is generated by d linearly independent translations.

Also the following theorem is well-known.

Theorem 2.2

Let ${\mathcal {G}}$ be a d-dimensional space group and ${\mathcal {T}}$ its subgroup of translations. Then it holds:

• (i) The group ${\mathcal {T}}$ is a normal subgroup of ${\mathcal {G}}$ and isomorphic to ${{\mathbb {Z}}}^d$.

• (ii) The point group $L({\mathcal {G}})$ of ${\mathcal {G}}$ is finite.

• (iii) The map

  $$\begin{aligned}{\mathcal {G}}/{\mathcal {T}}\rightarrow L({\mathcal {G}}),\quad (A, a ){\mathcal {T}}\mapsto A\end{aligned}$$

  is bijective and particularly, also ${\mathcal {G}}/{\mathcal {T}}$ is finite.

Proof

(i) This is clear by Theorem 2.1. (ii) See, e. g., [13, Theorem I.3.1]. (iii) It is easy to see that the map is bijective and by (ii) the set ${\mathcal {G}}/{\mathcal {T}}$ is finite. $\square$

Corollary 2.3

Let ${\mathcal {G}}$ be a d-dimensional space group and ${\mathcal {T}}$ its subgroup of translations. Then for all $N\in {{\mathbb {N}}}$ the set ${\mathcal {T}}^N$ is a normal subgroup of ${\mathcal {G}}$ and isomorphic to ${{\mathbb {Z}}}^d$.

Proof

This is clear by Theorem 2.2(i). $\square$

2.3 Discrete Subgroups of the Euclidean Group

We recall that two subgroups ${\mathcal {G}}_1,{\mathcal {G}}_2<{\textrm{E}}(d)$ are termed conjugate subgroups under the group ${\textrm{E}}(d)$ if there exists some $g\in {\textrm{E}}(d)$ such that $g^{-1}{\mathcal {G}}_1 g={\mathcal {G}}_2$. Note that every such conjugation corresponds to a coordinate transformation in ${{\mathbb {R}}}^d$.

Now we may state the following well-known characterization of the discrete subgroups of ${\textrm{E}}(d)$. For this purpose for all $d_1,d_2\in {{\mathbb {N}}}$ we define the group homomorphism

$$\begin{aligned} \oplus :&{{\textrm{O}}}(d_1)\times {\textrm{E}}(d_2)\rightarrow {\textrm{E}}(d_1+d_2)\\&(A_1,(A_2, b_2 ))\mapsto A_1\oplus (A_2, b_2 ):=\bigg (\bigg (\begin{matrix}A_1&{}0\\ 0&{}A_2\end{matrix}\bigg ), \bigg (\begin{matrix}0\\ b_2\end{matrix}\bigg ) \bigg ). \end{aligned}$$

Theorem 2.4

Let $d\in {{\mathbb {N}}}$ be the dimension and ${\mathcal {G}}<{\textrm{E}}(d)$ be discrete. Then there exist $d_1,d_2\in {{\mathbb {N}}}_0$ such that $d=d_1+d_2$, a $d_2$-dimensional space group ${\mathcal {S}}$ and a discrete group ${\mathcal {G}}'<{{\textrm{O}}}(d_1)\oplus {\mathcal {S}}$ such that ${\mathcal {G}}$ is conjugate under ${\textrm{E}}(d)$ to ${\mathcal {G}}'$ and $\pi ({\mathcal {G}}')={\mathcal {S}}$, where $\pi$ is the natural surjective homomorphism ${{\textrm{O}}}(d_1)\oplus {\textrm{E}}(d_2)\rightarrow {\textrm{E}}(d_2)$, $A\oplus g\mapsto g$.

Proof

Let $d\in {{\mathbb {N}}}$ be the dimension and ${\mathcal {G}}<{\textrm{E}}(d)$ be discrete. If ${\mathcal {G}}$ is a space group, the assertion is trivial. If ${\mathcal {G}}$ is finite, then ${\mathcal {G}}$ is conjugate under ${\textrm{E}}(d)$ to a finite subgroup of ${{\textrm{O}}}(d)\ltimes \{0_d\}\cong {{\textrm{O}}}(d)$, see, e. g., [34, Section 4.12]. If ${\mathcal {G}}$ is an infinite decomposable discrete subgroup of ${\textrm{E}}(d)$, the assertion is proven in [12, A.4 Theorem 2]. $\square$

Remark 2.5

Here ${{\textrm{O}}}(d_1)\oplus {\mathcal {S}}$ is understood to be ${{\textrm{O}}}(d)$ if $d_1=d$ and to be ${\mathcal {S}}$ if $d_1=0$.

3 Translational Sections

Our first aim will be to efficiently describe the discrete group ${\mathcal {G}}<{\textrm{E}}(d)$ in terms of the range ${\mathcal {S}}$ and the kernel ${\mathcal {F}}$ of $\pi |_{\mathcal {G}}$. An important step will be to fix and analyze a section ${\mathcal {T}}\subset {\mathcal {G}}$ of the translation group ${\mathcal {T}}_{\mathcal {S}}$ of ${\mathcal {S}}$. The main result in this section is Theorem 3.11 which characterizes $m\in {{\mathbb {N}}}$ for which ${\mathcal {T}}^m \triangleleft {\mathcal {G}}$.

Definition 3.1

Let $d\in {{\mathbb {N}}}$ be the dimension. Let $d_1,d_2\in {{\mathbb {N}}}_0$ be such that $d=d_1+d_2$. Let ${\mathcal {S}}$ be a $d_2$-dimensional space group. Let ${\mathcal {G}}<{{{\textrm{O}}}(d_1)\oplus {\mathcal {S}}}$ be discrete such that $\pi ({\mathcal {G}})={\mathcal {S}}$, where $\pi$ is the natural surjective homomorphism ${{\textrm{O}}}(d_1)\oplus {\textrm{E}}(d_2)\rightarrow {\textrm{E}}(d_2)$, $A\oplus g\mapsto g$. Let ${\mathcal {F}}$ be the kernel of $\pi |_{\mathcal {G}}$ and ${\mathcal {T}}_{\mathcal {S}}$ be the subgroup of translations of ${\mathcal {S}}$. Let ${\mathcal {T}}\subset {\mathcal {G}}$ such that the map ${\mathcal {T}}\rightarrow {\mathcal {T}}_{\mathcal {S}}$, $g\mapsto \pi (g)$ is bijective.

Remark 3.2

• (i) By Theorem 2.4 for every discrete group ${\mathcal {G}}'<{\textrm{E}}(d)$ there exists some discrete group ${\mathcal {G}}$ as in Definition 3.1 such that ${\mathcal {G}}$ is conjugate to ${\mathcal {G}}'$ under ${\textrm{E}}(d)$.

• (ii) If $d_1=0$, we have $d_2=d$, ${\mathcal {G}}={\mathcal {S}}$, ${\mathcal {T}}={\mathcal {T}}_{\mathcal {S}}$ and ${\mathcal {F}}=\{{id}\}$. If $d_1=d$, we have $d_2=0$, ${\mathcal {G}}$ is finite, ${\mathcal {G}}={\mathcal {F}}$ and ${\mathcal {T}}=\{{id}\}$.

• (iii) The quantities d, $d_1$, $d_2$, ${\mathcal {F}}$, ${\mathcal {S}}$ and ${\mathcal {T}}_{\mathcal {S}}$ are uniquely defined by ${\mathcal {G}}$. In general for given ${\mathcal {G}}$ there is no canonical choice for ${\mathcal {T}}$, see Example 3.4.

• (iv) Let ${\mathcal {G}}$ be given. In general, for every choice of ${\mathcal {T}}$ the set ${\mathcal {T}}$ is not a subset of ${\textrm{Trans}}(d)$, see Example 3.3. Moreover, in general for every choice of ${\mathcal {T}}$ the set ${\mathcal {T}}$ is not a group and the elements of ${\mathcal {T}}$ do not commute, see Example 3.5.

• (v) Let ${\mathcal {G}}$ be given. One possible choice for ${\mathcal {T}}$ is the following. Let $t_1,\dots ,t_{d_2}\in {\mathcal {T}}_{\mathcal {S}}$ be such that $\{t_1,\dots ,t_{d_2}\}$ generates ${\mathcal {T}}_{\mathcal {S}}$. For all $i\in \{1,\dots ,d_2\}$ let $g_i\in {\mathcal {G}}$ such that $\pi (g_i)=t_i$. Upon this, we define

  $$\begin{aligned} {\mathcal {T}}=\{g_1^{n_1}\dots g_{d_2}^{n_{d_2}}\,|\,n_1,\dots ,n_{d_2}\in {{\mathbb {Z}}}\}.\end{aligned}$$

For the following examples for all angles $\alpha \in {{\mathbb {R}}}$ we define the rotation matrix

$$\begin{aligned} R(\alpha ):=\bigg (\begin{matrix}\cos (\alpha )&{}-\sin (\alpha )\\ \sin (\alpha )&{}\cos (\alpha )\end{matrix}\bigg )\in {{\textrm{O}}}(2). \end{aligned}$$

Example 3.3

(Helical groups) Let $d_1=2$, $d_2=1$, $\alpha \in {{\mathbb {R}}}$ be an angle, $n\in {{\mathbb {N}}}$,

$$\begin{aligned} {\mathcal {T}}=\Big \langle {R(\alpha )\oplus (I_1, 1 )}\Big \rangle ,\quad {\mathcal {F}}=\Big \langle {R(2\pi /n)\oplus (I_1, 0 )}\Big \rangle \quad \text {and}\quad {\mathcal {P}}= \Big \langle {\big ({\begin{matrix}1&{}0\\ 0&{}-1\end{matrix}}\big )\oplus (-I_1, 0 )}\Big \rangle . \end{aligned}$$

Then ${\mathcal {T}}$ is isomorphic to ${{\mathbb {Z}}}$, ${\mathcal {F}}$ is a cyclic group of order n, ${\mathcal {P}}$ is a group of order 2 and ${\mathcal {F}}{\mathcal {P}}$ a dihedral group of order 2n. Moreover, ${\mathcal {T}}$, ${\mathcal {T}}{\mathcal {F}}$, ${\mathcal {T}}{\mathcal {P}}$ and ${\mathcal {T}}{\mathcal {F}}{\mathcal {P}}$ are decomposable discrete subgroups of ${\textrm{E}}(3)$. If we have $\alpha \in {{\mathbb {R}}}\setminus (2\pi {{\mathbb {Q}}})$, the groups ${\mathcal {T}}$, ${\mathcal {T}}{\mathcal {F}}$, ${\mathcal {T}}{\mathcal {P}}$ and ${\mathcal {T}}{\mathcal {F}}{\mathcal {P}}$ are so-called helical groups, i. e. infinite discrete subgroups of the Euclidean group ${\textrm{E}}(3)$ which do not contain any translation except the identity.

Example 3.4

(The choice of ${\mathcal {T}}$ is not unique.) Let $t=(I_1, 1 )$, ${\mathcal {F}}_0=\{I_2,R(\pi )\}$, ${\mathcal {S}}={\mathcal {T}}_{\mathcal {S}}=\langle t\rangle$ and

$$\begin{aligned} {\mathcal {G}}=\Big \{(R(n\pi /2)F)\oplus t^n\,\Big |\, n\in {{\mathbb {Z}}}, F\in {\mathcal {F}}_0\Big \}<{\textrm{E}}(3). \end{aligned}$$

Then the choice $R(\pi /2)\oplus t\in {\mathcal {T}}$ as well as $R(3\pi /2)\oplus t\in {\mathcal {T}}$ is possible. In particular, the choice of ${\mathcal {T}}$ is not unique.

Example 3.5

We present a discrete group ${\mathcal {G}}<{\textrm{E}}(8)$ such that for every choice of ${\mathcal {T}}$ the set ${\mathcal {T}}$ is not a group and the elements of ${\mathcal {T}}$ do not commute.

Let $\alpha _1,\alpha _2\in {{\mathbb {R}}}\setminus (2\pi {{\mathbb {Q}}})$ be angles, $R_1=R(\alpha _1)$, $R_2=R(\alpha _2)$, $R_3=R(\pi /2)$, $S=({\begin{matrix}1&{}0\\ 0 &{}-1\end{matrix}})$, $t_1=(I_2, e_1 )$ and $t_2=(I_2, e_2 )$. Then we have $\langle R_1\rangle \cong {{\mathbb {Z}}}$, $\langle R_2\rangle \cong {{\mathbb {Z}}}$, and $\langle R_3,S\rangle <{{\textrm{O}}}(2)$ is a dihedral group. Let ${\mathcal {S}}={\mathcal {T}}_{\mathcal {S}}=\{t_1^{n_1}t_2^{n_2}\,|\,n_1,n_2\in {{\mathbb {Z}}}\}$,

$$\begin{aligned} {\mathcal {G}}:=\bigg \{\Big (R_1^{n_1}\oplus R_2^{n_2}\oplus (S^{n_1}R_3^{n_2+m})\Big )\oplus \big (t_1^{n_1}t_2^{n_2}\big )\,\bigg |\, n_1,n_2\in {{\mathbb {Z}}},m\in \{0,2\}\bigg \}<{\textrm{E}}(8) \end{aligned}$$

and $\pi :{\mathcal {G}}\rightarrow {\mathcal {S}}$ be the natural surjective homomorphism with kernel ${\mathcal {F}}=\{{id},(I_4\oplus R_3^2)\oplus {id}_{{\textrm{E}}(2)}\}$. Let ${\mathcal {T}}\subset {\mathcal {G}}$ such that the map ${\mathcal {T}}\rightarrow {\mathcal {T}}_{\mathcal {S}}$, $g\mapsto \pi (g)$ is bijective. Since $t_1,t_2\in {\mathcal {T}}_{\mathcal {S}}$, there exist $m_1,m_2\in \{0,2\}$ such that $t_1':=(R_1\oplus I_2\oplus (SR_3^{m_1}))\oplus t_1\in {\mathcal {T}}$ and $t_2':=(I_2\oplus R_2\oplus R_3^{1+m_2})\oplus t_2\in {\mathcal {T}}$. We have $t_1't_2'\ne t_2't_1'$ since

$$\begin{aligned} t_1't_2'(t_1')^{-1}(t_2')^{-1}= & {} \big (I_4\oplus (SR_3^{m_1}R_3^{1+m_2}R_3^{-m_1}SR_3^{-1-m_2})\big )\oplus {id}_{{\textrm{E}}(2)}\nonumber \\= & {} (I_4\oplus R_3^2)\oplus {id}_{{\textrm{E}}(2)}. \end{aligned}$$

(1)

Thus, the elements of ${\mathcal {T}}$ do not commute.

Now we suppose that ${\mathcal {T}}$ is a group. Since $\pi ^{-1}({id}_{{\textrm{E}}(2)})={\mathcal {F}}$ and by (1), we have $\pi ^{-1}({id}_{{\textrm{E}}(2)})\subset {\mathcal {T}}$. This contradicts the claim that $\pi |_{\mathcal {T}}$ is bijective. Thus, ${\mathcal {T}}$ is not a group.

For the remainder of this section we fix the dimension $d\in {{\mathbb {N}}}$, the discrete group ${\mathcal {G}}<{\textrm{E}}(d)$ and the quantities $d_1$, $d_2$, ${\mathcal {T}}$, ${\mathcal {F}}$, ${\mathcal {S}}$, ${\mathcal {T}}_{\mathcal {S}}$ as introduced by Definition 3.1. The following lemma collects some elementary properties.

Lemma 3.6

• (i) The group ${\mathcal {F}}$ is finite.

• (ii) For all $n\in {{\mathbb {N}}}$ the set ${\mathcal {T}}^n{\mathcal {F}}$ is independent of the choice of ${\mathcal {T}}$, and it holds

  $$\begin{aligned} {\mathcal {T}}^n{\mathcal {F}}\triangleleft {\mathcal {G}}. \end{aligned}$$

  In particular, it holds ${\mathcal {T}}{\mathcal {F}}\triangleleft {\mathcal {G}}$.

• (iii) The map ${\mathcal {G}}/{\mathcal {T}}{\mathcal {F}}\rightarrow {\mathcal {S}}/{\mathcal {T}}_{\mathcal {S}}$, $g{\mathcal {T}}{\mathcal {F}}\mapsto \pi (g){\mathcal {T}}_{\mathcal {S}}$ is a group isomorphism, where $\pi :{\mathcal {G}}\rightarrow {\mathcal {S}}$ is the natural surjective homomorphism with kernel ${\mathcal {F}}$. In particular, ${\mathcal {G}}/{\mathcal {T}}{\mathcal {F}}$ is finite.

• (iv) For all $n\in {{\mathbb {N}}}$ the map ${\mathcal {T}}_{\mathcal {S}}\rightarrow {\mathcal {T}}^n{\mathcal {F}}/{\mathcal {F}}$, $t\mapsto \varphi (t^n){\mathcal {F}}$ is a group isomorphism, where $\varphi :{\mathcal {T}}_{\mathcal {S}}^n\rightarrow {\mathcal {T}}^n$ is the canonical bijection. In particular, the group ${\mathcal {T}}{\mathcal {F}}/{\mathcal {F}}$ is commutative.

• (v) For all $n\in {{\mathbb {Z}}}\setminus \{0\}$ the map ${\mathcal {T}}\rightarrow {\mathcal {T}}^n$, $t\mapsto t^n$ is bijective.

Proof

Let $\pi :{\mathcal {G}}\rightarrow {\mathcal {S}}$ be the natural surjective homomorphism with kernel ${\mathcal {F}}$.

• (i) Since ${\mathcal {G}}$ is discrete, the group ${\mathcal {F}}$ is discrete. Moreover, ${\mathcal {F}}$ is a subgroup of ${{\textrm{O}}}(d_1)\oplus \{{id}_{{\textrm{E}}(d_2)}\}$. Thus, the group ${\mathcal {F}}$ is finite.

• (ii) Let $n\in {{\mathbb {N}}}$. The set ${\mathcal {T}}^n{\mathcal {F}}$ is the preimage of ${\mathcal {T}}_{\mathcal {S}}^n$ under $\pi$. Since ${\mathcal {T}}_{\mathcal {S}}^n$ is a normal subgroup of ${\mathcal {S}}$, the set ${\mathcal {T}}^n{\mathcal {F}}$ is a normal subgroup of ${\mathcal {G}}$.

• (iii) This is clear, since ${\mathcal {T}}{\mathcal {F}}$ is the preimage of ${\mathcal {T}}_{\mathcal {S}}$ under $\pi$.

• (iv) Let $n\in {{\mathbb {N}}}$. Since ${\mathcal {T}}_{\mathcal {S}}$ is isomorphic to ${{\mathbb {Z}}}^{d_2}$, the map $\varphi _1:{\mathcal {T}}_{\mathcal {S}}\rightarrow {\mathcal {T}}_{\mathcal {S}}^n$, $t\mapsto t^n$ is a group isomorphism. Since ${\mathcal {F}}$ is the kernel of $\pi$ and ${\mathcal {T}}^n{\mathcal {F}}$ the preimage of ${\mathcal {T}}_{\mathcal {S}}^n$ under $\pi$, the map $\varphi _2:{\mathcal {T}}^n{\mathcal {F}}/{\mathcal {F}}\rightarrow {\mathcal {T}}_{\mathcal {S}}^n$, $g{\mathcal {F}}\mapsto \pi (g)$ is an isomorphism. This implies the assertion, i. e. the map $\varphi _2^{-1}\circ \varphi _1$ is an isomorphism.

• (v) Let $n\in {{\mathbb {Z}}}\setminus \{0\}$. The map $\psi :{\mathcal {T}}\rightarrow {\mathcal {T}}^n$, $t\mapsto t^n$ is surjective. Since the map ${\mathcal {T}}_{\mathcal {S}}\rightarrow {\mathcal {T}}_{\mathcal {S}}^n$, $t\mapsto t^n$ is injective, the map $\psi$ is injective and thus, bijective.

$\square$

If ${\mathcal {T}}$ is a group, it is naturally isomorphic to ${\mathcal {T}}_{\mathcal {S}}$.

Lemma 3.7

Let $m\in {{\mathbb {Z}}}\setminus \{0\}$ such that ${\mathcal {T}}^m$ is a group. Then, the map

$$\begin{aligned} {\mathcal {T}}_{\mathcal {S}}\rightarrow {\mathcal {T}}^m, \quad t\mapsto \varphi (t)^m \end{aligned}$$

is a group isomorphism, where $\varphi :{\mathcal {T}}_{\mathcal {S}}\rightarrow {\mathcal {T}}$ is the canonical bijection. In particular, ${\mathcal {T}}^m$ is isomorphic to ${{\mathbb {Z}}}^{d_2}$.

Furthermore, for all $n\in {{\mathbb {Z}}}$ it holds

$$\begin{aligned} {\mathcal {T}}^{nm}\triangleleft {\mathcal {T}}^m. \end{aligned}$$

Proof

Let $m\in {{\mathbb {Z}}}\setminus \{0\}$ such that ${\mathcal {T}}^m$ is a group. Let $\pi :{\mathcal {T}}{\mathcal {F}}\rightarrow {\mathcal {T}}_{\mathcal {S}}$ be the natural surjective homomorphism with kernel ${\mathcal {F}}$. Let $\varphi$ be the inverse function of $\pi |_{\mathcal {T}}$, i. e. $\varphi :{\mathcal {T}}_{\mathcal {S}}\rightarrow {\mathcal {T}}$ is the canonical bijection. The map

$$\begin{aligned} \psi _1:{\mathcal {T}}_{\mathcal {S}}\rightarrow {\mathcal {T}}{\mathcal {F}}/{\mathcal {F}},\quad t\mapsto \varphi (t){\mathcal {F}}\end{aligned}$$

is an isomorphism. Since ${\mathcal {T}}{\mathcal {F}}/{\mathcal {F}}$ is isomorphic to ${{\mathbb {Z}}}^{d_2}$ and $({\mathcal {T}}{\mathcal {F}}/{\mathcal {F}})^m={\mathcal {T}}^m{\mathcal {F}}/{\mathcal {F}}$, the map

$$\begin{aligned} \psi _2:{\mathcal {T}}{\mathcal {F}}/{\mathcal {F}}\rightarrow {\mathcal {T}}^m{\mathcal {F}}/{\mathcal {F}},\quad t\mapsto t^m \end{aligned}$$

is an isomorphism. Since ${\mathcal {T}}^m$ is a group, the map

$$\begin{aligned} \psi _3:{\mathcal {T}}^m\rightarrow {\mathcal {T}}^m{\mathcal {F}}/{\mathcal {F}},\quad g\mapsto g{\mathcal {F}}\end{aligned}$$

is an isomorphism. The map

$$\begin{aligned} {\mathcal {T}}_{\mathcal {S}}\rightarrow {\mathcal {T}}^m,\quad t\mapsto \varphi (t)^m \end{aligned}$$

is equal to $\psi _3^{-1}\circ \psi _2\circ \psi _1$ and thus, an isomorphism.

Let $n\in {{\mathbb {Z}}}$. Since ${\mathcal {T}}^m$ is isomorphic to ${{\mathbb {Z}}}^{d_2}$, we have ${\mathcal {T}}^{mn}=({\mathcal {T}}^m)^n\triangleleft {\mathcal {T}}^m$. $\square$

We proceed to show that, albeit ${\mathcal {T}}$ is not a group in general, the situation is much better for special powers of ${\mathcal {T}}$.

Definition 3.8

We define the set

$$\begin{aligned} M_0:=\{m\in {{\mathbb {N}}}\,|\, {\mathcal {T}}^m \text { is a normal subgroup of }{\mathcal {G}}\}. \end{aligned}$$

Thus, the quotient group ${\mathcal {G}}/{\mathcal {T}}^m$ is well-defined if and only if $m\in M_0$.

Proposition 3.9

For all $m\in M_0$ the group ${\mathcal {T}}^m$ is a subgroup of the center of ${\mathcal {T}}{\mathcal {F}}$.

Proof

Let $m\in M_0$, $t\in {\mathcal {T}}$ and $g\in {\mathcal {T}}{\mathcal {F}}$. By Lemma 3.6(iv) there exists some $f\in {\mathcal {F}}$ such that

$$\begin{aligned} gt^m=t^mgf. \end{aligned}$$

Since $m\in M_0$, it follows

$$\begin{aligned} f=g^{-1}t^{-m}gt^m\in {\mathcal {T}}^m. \end{aligned}$$

Since ${\mathcal {T}}^m\cap {\mathcal {F}}=\{{id}\}$, we have $f={id}$, i. e. g and $t^m$ commute. $\square$

Lemma 3.10

The set $M_0$ is not empty.

Proof

Since ${\mathcal {F}}$ is a normal subgroup of ${\mathcal {G}}$, for all $g\in {\mathcal {G}}$ the map

$$\begin{aligned} \varphi _g:{\mathcal {F}}\rightarrow {\mathcal {F}},\quad f\mapsto g^{-1}fg \end{aligned}$$

is a group automorphism. Let n be the order of the automorphism group of ${\mathcal {F}}$. For all $g\in {\mathcal {G}}$ it holds $\varphi _g^{n}={id}$. Thus for all $g\in {\mathcal {G}}$ and $f\in {\mathcal {F}}$ we have

$$\begin{aligned} g^{n}f=fg^{n}, \end{aligned}$$

(2)

i. e. $g^{n}$ and f commute.

Now we show that for all $g,h\in {\mathcal {T}}{\mathcal {F}}$ the elements $g^{n|{\mathcal {F}}|}$ and h commute. Let $g,h\in {\mathcal {T}}{\mathcal {F}}$. Since ${\mathcal {T}}{\mathcal {F}}/{\mathcal {F}}$ is commutative, there exists some $f\in {\mathcal {F}}$ such that

$$\begin{aligned} h^{-1}g^{n}h=g^{n}f. \end{aligned}$$

With (2) it follows

$$\begin{aligned} h^{-1}g^{n|{\mathcal {F}}|}h=(h^{-1}g^{n}h)^{|{\mathcal {F}}|}=(g^{n}f)^{|{\mathcal {F}}|}=g^{n|{\mathcal {F}}|}f^{|{\mathcal {F}}|}=g^{n|{\mathcal {F}}|}. \end{aligned}$$

(3)

Now we show that ${\mathcal {T}}^{n|{\mathcal {F}}|^2}$ is a subgroup of ${\mathcal {T}}{\mathcal {F}}$. Let $t,s\in {\mathcal {T}}$. We have to show that $t^{n|{\mathcal {F}}|^2}s^{-n|{\mathcal {F}}|^2}\in {\mathcal {T}}^{n|{\mathcal {F}}|^2}$. Let $r\in {\mathcal {T}}$ and $f\in {\mathcal {F}}$ such that $ts^{-1}=rf$. Since ${\mathcal {T}}{\mathcal {F}}/{\mathcal {F}}$ is commutative, there exists some $e\in {\mathcal {F}}$ such that $t^{n|{\mathcal {F}}|}s^{-n|{\mathcal {F}}|}=r^{n|{\mathcal {F}}|}e$. By (3) and (2) we have

$$\begin{aligned} t^{n|{\mathcal {F}}|^2}s^{-n|{\mathcal {F}}|^2}=(t^{n|{\mathcal {F}}|}s^{-n|{\mathcal {F}}|})^{|{\mathcal {F}}|}=(r^{n|{\mathcal {F}}|}e)^{|{\mathcal {F}}|}=r^{n|{\mathcal {F}}|^2}e^{|{\mathcal {F}}|}=r^{n|{\mathcal {F}}|^2}\in {\mathcal {T}}^{n|{\mathcal {F}}|^2}. \end{aligned}$$

Now we show that ${\mathcal {T}}^{n|{\mathcal {F}}|^2}$ is a normal subgroup of ${\mathcal {G}}$. Let $g\in {\mathcal {G}}$ and $t\in {\mathcal {T}}$. We have to show that

$$\begin{aligned} g^{-1}t^{n|{\mathcal {F}}|^2}g\in {\mathcal {T}}^{n|{\mathcal {F}}|^2}. \end{aligned}$$

Since ${\mathcal {T}}^{n}{\mathcal {F}}$ is a normal subgroup of ${\mathcal {G}}$, there exist some $s\in {\mathcal {T}}$ and $f\in {\mathcal {F}}$ such that

$$\begin{aligned} g^{-1}t^{n}g=s^{n}f. \end{aligned}$$

By (2) we have

$$\begin{aligned} g^{-1}t^{n|{\mathcal {F}}|^2}g=(g^{-1}t^{n}g)^{|{\mathcal {F}}|^2}=(s^{n}f)^{|{\mathcal {F}}|^2} =s^{n|{\mathcal {F}}|^2}f^{|{\mathcal {F}}|^2}=s^{n|{\mathcal {F}}|^2}\in {\mathcal {T}}^{n|{\mathcal {F}}|^2}.\qquad \ \end{aligned}$$

$\square$

The following Theorem is a key observation on the structural decomposition of ${\mathcal {G}}$. Not only do we have the existence of exponents $m \in {{\mathbb {N}}}$ such that ${\mathcal {T}}^m \triangleleft {\mathcal {G}}$ as guaranteed by Lemma 3.10, but the set of such ‘good’ exponents will in fact be of the form $m_0{{\mathbb {N}}}$, $m_0\in {{\mathbb {N}}}$.

Theorem 3.11

There exists a unique $m_0\in {{\mathbb {N}}}$ such that $M_0=m_0{{\mathbb {N}}}$.

Proof

We define the set

$$\begin{aligned} {\widetilde{M_0}}:=\{m\in {{\mathbb {Z}}}\,|\,{\mathcal {T}}^m\text { is a normal subgroup of }{\mathcal {G}}\}. \end{aligned}$$

First we show that ${\widetilde{M_0}}$ is a subgroup of the additive group of integers ${{\mathbb {Z}}}$. It is clear that $0\in {\widetilde{M_0}}$. Let $n_1,n_2\in {\widetilde{M_0}}$. We have to show that $n_1-n_2\in {\widetilde{M_0}}$. Let $\varphi :{\mathcal {T}}_{\mathcal {S}}\rightarrow {\mathcal {T}}$ be the canonical bijection. By Proposition 3.9 and Lemma 3.7, for all $t,s\in {\mathcal {T}}_{\mathcal {S}}$ it holds

$$\begin{aligned} \varphi (t)^{n_1-n_2}\varphi (s)^{-(n_1-n_2)}&=\varphi (t)^{n_1}\varphi (s)^{-n_1}\varphi (t)^{-n_2}\varphi (s)^{n_2}=\varphi (ts^{-1})^{n_1}\varphi (ts^{-1})^{-n_2}\\&=\varphi (ts^{-1})^{n_1-n_2}\in {\mathcal {T}}^{n_1-n_2}, \end{aligned}$$

and thus, ${\mathcal {T}}^{n_1-n_2}$ is a group. It remains to show that ${\mathcal {T}}^{n_1-n_2}$ is a normal subgroup of ${\mathcal {G}}$. Without loss of generality we assume that $n_1,n_2\ne 0$, i. e. $n_1n_2\ne 0$. Let $g\in {\mathcal {G}}$ and $t\in {\mathcal {T}}$. Since ${\mathcal {T}}^{n_1},{\mathcal {T}}^{n_2}\triangleleft {\mathcal {G}}$, there exist some $s_1,s_2\in {\mathcal {T}}$ such that $gt^{n_1}g^{-1}=s_1^{n_1}$ and $gt^{n_2}g^{-1}=s_2^{n_2}$. Since $s_1^{n_1n_2}=gt^{n_1n_2}g^{-1}=s_2^{n_1n_2}$ and the map ${\mathcal {T}}\rightarrow {\mathcal {T}}^{n_1n_2}$, $r\mapsto r^{n_1n_2}$ is bijective, it holds $s_1=s_2$. Now we have

$$\begin{aligned} gt^{n_1-n_2}g^{-1}=(gt^{n_1}g^{-1})(gt^{n_2}g^{-1})^{-1}=s_1^{n_1-n_2}\in {\mathcal {T}}^{n_1-n_2}. \end{aligned}$$

By Lemma 3.10 and since $M_0\subset {\widetilde{M_0}}$, the group ${\widetilde{M_0}}$ is nontrivial. Since every nontrivial subgroup of ${{\mathbb {Z}}}$ is equal to $n{{\mathbb {Z}}}$ for some $n\in {{\mathbb {N}}}$, there exists a unique $m_0\in {{\mathbb {N}}}$ such that ${\widetilde{M_0}}=m_0{{\mathbb {Z}}}$. Now, we have

$$\begin{aligned} M_0={\widetilde{M_0}}\cap {{\mathbb {N}}}=m_0{{\mathbb {N}}}. \end{aligned}$$

$\square$

Remark 3.12

• (i) The proof of Lemma 3.10 shows that $m_0$ divides $|{\mathcal {F}}|^2|\textrm{Aut}({\mathcal {F}})|$, where $m_0\in {{\mathbb {N}}}$ is such that $M_0=m_0{{\mathbb {N}}}$ and $\textrm{Aut}({\mathcal {F}})$ is the automorphism group of ${\mathcal {F}}$. In particular, we have an upper bound for $m_0$.

• (ii) The group ${\mathcal {G}}$ is virtually abelian since for all $m\in M_0$ the index of the abelian subgroup ${\mathcal {T}}^m$ in ${\mathcal {G}}$ is $m^{d_2}|{\mathcal {F}}||{\mathcal {G}}/({\mathcal {T}}{\mathcal {F}})|$ and thus, finite.

Example 3.13

We give an example for which $m_0 = 4$, independent of the choice of ${\mathcal {T}}$. Let ${\mathcal {G}}$ be the group considered in Example 3.5. In terms of $t_{n_1,n_2,m}:=\big (R_1^{n_1}\oplus R_2^{n_2}\oplus (S^{n_1}R_3^{n_2+m})\big )\oplus t_1^{n_1}t_2^{n_2}$ for $n_1,n_2\in {{\mathbb {Z}}},m\in \{0,2\}$, the choices for ${\mathcal {T}}$ are explicitly given by

$$\begin{aligned} {\mathcal {T}}_\mu =\{t_{n_1,n_2,\mu (n_1,n_2)}\,|\,n_1,n_2\in {{\mathbb {Z}}}\}, \end{aligned}$$

where $\mu$ is any mapping $\mu :{{\mathbb {Z}}}^2\rightarrow \{0,2\}$. Using $SR_3=-R_3S$, $R_3^2=-I_2$ and $S^2=R_3^4=I_2$ we see that $t_{n_1,n_2,m}^2=\big (R_1^{2n_1}\oplus R_2^{2n_2}\oplus ((-1)^{(n_1+1)n_2}I_2)\big )\oplus t_1^{2n_1}t_2^{2n_2}$ and so ${\mathcal {T}}_\mu ^2$ is still not a group. (Notice that $t_{1,0,\mu (1,0)}^2 t_{0,1,\mu (0,1)}^2\ne t_{1,1,\mu (1,1)}^2$.) However, as $t_{n_1,n_2,m}^4=\big (R_1^{4n_1}\oplus R_2^{4n_2}\oplus I_2\big )\oplus t_1^{4n_1}t_2^{4n_2}$, we see that ${\mathcal {T}}_\mu ^4$ is a normal subgroup of ${\mathcal {G}}$. In view of Theorem 3.11 we have $m_0=4$.

Example 3.14

In this example we show that in general $M_0=m_0{{\mathbb {N}}}$, ${\mathcal {T}}^{m_0}$ and the index of ${\mathcal {T}}^{m_0}$ in ${\mathcal {G}}$ are dependent on the choice of ${\mathcal {T}}$. Let ${\mathcal {G}}$ be the group considered in Example 3.4. If we choose

$$\begin{aligned} {\mathcal {T}}=\Big \{R(n\pi /2)\oplus t^n\,\Big |\, n\in {{\mathbb {Z}}}\Big \}, \end{aligned}$$

then $m_0=1$, ${\mathcal {T}}^{m_0}={\mathcal {T}}$ and $|{\mathcal {G}}:{\mathcal {T}}^{m_0}|=2$. But if we choose

$$\begin{aligned} {\mathcal {T}}=\Big \{(R(n\pi /2)R(\pi ))\oplus t^n\,\Big |\, n\in {{\mathbb {Z}}}\Big \}, \end{aligned}$$

then $m_0=2$, ${\mathcal {T}}^{m_0}=\{R(n\pi )\oplus t^{2n}\,|\, n\in {{\mathbb {Z}}}\}$ and $|{\mathcal {G}}:{\mathcal {T}}^{m_0}|=4$.

4 Wave Vector Characterization of the Dual Space

We now study representations of ${\mathcal {T}}{\mathcal {F}}$ and their induced representations on ${\mathcal {G}}$. As all groups encountered here are virtually abelian (cp. Remark 3.12(ii)), we may and will restrict to finite-dimensional (unitary) representations in what follows, see e. g. [33]. The reader is referred to the last paragraph of Sect. 1 for notation and to Sect. A in the appendix for basic material on induced representations and the necessary background on standard Mackey analysis, adapted to our set-up of discrete subgroups of ${\textrm{E}}(d)$.

As ${\mathcal {T}}{\mathcal {F}}= \pi ^{-1}({\mathcal {T}}_{\mathcal {S}})$, where $\pi : {\mathcal {G}}\rightarrow {\mathcal {S}}$ is the natural surjective homomorphism, we are led to first considering characters on ${\mathcal {T}}{\mathcal {F}}$ by lifting those on ${\mathcal {T}}_{\mathcal {S}}$ (i. e., plane waves) via $\pi ^{-1}$.

Definition 4.1

For all $k\in {{\mathbb {R}}}^{d_2}$ we define the one-dimensional representation $\chi _k\in \widehat{{\mathcal {T}}{\mathcal {F}}}$ by

$$\begin{aligned} \chi _k(g):=\exp (2\pi {\textrm{i}}\langle k, \tau (\pi (g))\rangle )\qquad \text {for all }g\in {\mathcal {T}}{\mathcal {F}}, \end{aligned}$$

where $\pi :{\mathcal {T}}{\mathcal {F}}\rightarrow {\mathcal {T}}_{\mathcal {S}}$ is the natural surjective homomorphism.

Since ${\mathcal {T}}{\mathcal {F}}$ is a normal subgroup of ${\mathcal {G}}$, ${\mathcal {G}}$ acts on $\widehat{{\mathcal {T}}{\mathcal {F}}}$.

Lemma 4.2

For all $g\in {\mathcal {G}}$ and $k,k'\in {{\mathbb {R}}}^{d_2}$ it holds

$$\begin{aligned} \chi _k\chi _{k'}=\chi _{k+k'} \qquad \text {and} \qquad g\cdot \chi _k=\chi _{L(\pi (g))k}, \end{aligned}$$

where $\pi :{\mathcal {G}}\rightarrow {\mathcal {S}}$ is the natural surjective homomorphism.

Proof

Let $g\in {\mathcal {G}}$, $k,k'\in {{\mathbb {R}}}^{d_2}$ and $\pi :{\mathcal {G}}\rightarrow {\mathcal {S}}$ be the natural surjective homomorphism. For all $h\in {\mathcal {T}}{\mathcal {F}}$ it holds

$$\begin{aligned} \chi _k(h)\chi _{k'}(h)&=\exp (2\pi {\textrm{i}}\langle k, \tau (\pi (h))\rangle )\exp (2\pi {\textrm{i}}\langle k', \tau (\pi (h))\rangle )\\&=\exp (2\pi {\textrm{i}}\langle k+k', \tau (\pi (h))\rangle )\\&=\chi _{k+k'}(h) \end{aligned}$$

and

$$\begin{aligned} (g\cdot \chi _k)(h)&=\chi _k(g^{-1}hg)\\&=\exp (2\pi {\textrm{i}}\langle k, \tau (\pi (g^{-1}hg))\rangle )\\&=\exp (2\pi {\textrm{i}}\langle k, L(\pi (g^{-1}))\tau (\pi (h))\rangle )\\&=\exp (2\pi {\textrm{i}}\langle L(\pi (g))k, \tau (\pi (h))\rangle )\\&=\chi _{L(\pi (g))k}(h). \end{aligned}$$

$\square$

In our analysis of periodic representations below it will necessary to analyze representations that are trivial on ${\mathcal {T}}^n$, $n\in {{\mathbb {N}}}$. To this end, we recall that a set $L\subset {{\mathbb {R}}}^n$ is a lattice if L is a subgroup of the additive group ${{\mathbb {R}}}^n$ which is isomorphic to the additive group ${{\mathbb {Z}}}^n$, and which spans the real vector space ${{\mathbb {R}}}^n$. The dual lattice $L^*$ (also called the reciprocal lattice) of a lattice $L\subset {{\mathbb {R}}}^n$ is the set

$$\begin{aligned} \{x\in {{\mathbb {R}}}^n\,|\,\langle x, y\rangle \in {{\mathbb {Z}}}\text { for all }y\in L\}. \end{aligned}$$

This is indeed a lattice as well, see, e. g., [29, Chapter 1].

Definition 4.3

We define the lattice

$$\begin{aligned} L_{\mathcal {S}}:=\tau ({\mathcal {T}}_{\mathcal {S}})<{{\mathbb {R}}}^{d_2} \end{aligned}$$

and denote its dual lattice by $L_{\mathcal {S}}^*$.

Lemma 4.4

For all $n\in {{\mathbb {N}}}$ it holds

$$\begin{aligned} L_{\mathcal {S}}^*/n=\{k\in {{\mathbb {R}}}^{d_2}\,|\,\chi _k|_{{\mathcal {T}}^n}=1\}. \end{aligned}$$

Proof

Let $n\in {{\mathbb {N}}}$ and $\pi :{\mathcal {T}}{\mathcal {F}}\rightarrow {\mathcal {T}}_{\mathcal {S}}$ be the natural surjective homomorphism. First we show that $L_{\mathcal {S}}^*/n\subset \{k\in {{\mathbb {R}}}^{d_2}\,|\,\chi _k|_{{\mathcal {T}}^n}=1\}$. Let $k\in L_{\mathcal {S}}^*/n$. For all $t\in {\mathcal {T}}$ it holds $\tau (\pi (t^n))=n\tau (\pi (t))$ and thus,

$$\begin{aligned} \chi _k(t^n)=\exp (2\pi {\textrm{i}}\langle k, \tau (\pi (t^n))\rangle )=\exp (2\pi {\textrm{i}}\langle nk, \tau (\pi (t))\rangle )=1. \end{aligned}$$

Now we show that $\{k\in {{\mathbb {R}}}^{d_2}\,|\,\chi _k|_{{\mathcal {T}}^n}=1\}\subset L_{\mathcal {S}}^*/n$. Let $k\in {{\mathbb {R}}}^{d_2}$ such that $\chi _k|_{{\mathcal {T}}^n}=1$. Let $x\in L_{\mathcal {S}}$. There exists some $t\in {\mathcal {T}}$ such that $x=\tau (\pi (t))$. We have

$$\begin{aligned} \langle nk, x\rangle =\langle nk, \tau (\pi (t))\rangle =\langle k, \tau (\pi (t^n))\rangle \in {{\mathbb {Z}}}, \end{aligned}$$

where we used that $\chi _k(t^n)=1$ in the last step. Since $x\in L_{\mathcal {S}}$ was arbitrary, we have $k\in L_{\mathcal {S}}^*/n$. $\square$

In view of ${\mathcal {G}}$ and the characters of ${\mathcal {T}}{\mathcal {F}}$ acting on $\widehat{{\mathcal {T}}{\mathcal {F}}}$ we now proceed to introduce the following equivalence relation. It will allow us to partition $\widehat{{\mathcal {T}}{\mathcal {F}}}$ in such a way that in each equivalence class the elements are – modulo action of ${\mathcal {G}}$ – characterized by a “lifted plane wave” $\chi _k$.

Definition 4.5

We define the relation $\sim$ on $\widehat{{\mathcal {T}}{\mathcal {F}}}$ by

$$\begin{aligned} (\rho \sim \rho '):\Longleftrightarrow \;(\exists \,g\in {\mathcal {G}}\,\exists \,k\in {{\mathbb {R}}}^{d_2}: g\cdot \rho =\chi _k\rho '). \end{aligned}$$

Remark 4.6

One can also define an equivalence relation $\sim$ on the set of all representations of ${\mathcal {T}}{\mathcal {F}}$ by

$$\begin{aligned} (\rho \sim \rho '):\Longleftrightarrow \;([\rho ]\sim [\rho '])\qquad \text {for all representations }\rho , \rho '\text { on }{\mathcal {T}}{\mathcal {F}}. \end{aligned}$$

Lemma 4.7

The relation $\sim$ on $\widehat{{\mathcal {T}}{\mathcal {F}}}$ is an equivalence relation.

Proof

It is clear that $\sim$ is reflexive.

Now we show that $\sim$ is symmetric. Let $\rho ,\rho '\in \widehat{{\mathcal {T}}{\mathcal {F}}}$ such that $\rho \sim \rho '$. There exist some $g\in {\mathcal {G}}$ and $k\in {{\mathbb {R}}}^{d_2}$ such that $g\cdot \rho =\chi _k\rho '$. This implies

$$\begin{aligned} g^{-1}\cdot \rho '=(g^{-1}\cdot \chi _{-k})(g^{-1}\cdot (\chi _k\rho '))=\chi _{-L(\pi (g^{-1}))k}\rho , \end{aligned}$$

where $\pi :{\mathcal {G}}\rightarrow {\mathcal {S}}$ is the natural surjective homomorphism.

Now we show that $\sim$ is transitive. Let $\rho ,\rho ',\rho ''\in \widehat{{\mathcal {T}}{\mathcal {F}}}$ such that $\rho \sim \rho '$ and $\rho '\sim \rho ''$. There exist some $g,g'\in {\mathcal {G}}$ and $k,k'\in {{\mathbb {R}}}^{d_2}$ such that $g\cdot \rho =\chi _k\rho '$ and $g'\cdot \rho '=\chi _{k'}\rho ''$. This implies

$$\begin{aligned} (g'g)\cdot \rho =g'\cdot (\chi _k\rho ')=\chi _{L(\pi (g'))k+k'}\rho '', \end{aligned}$$

where $\pi :{\mathcal {G}}\rightarrow {\mathcal {S}}$ is the natural surjective homomorphism. $\square$

Definition 4.8

For all groups ${\mathcal {H}}\le {\mathcal {G}}$ and $N\in M_0$ such that ${\mathcal {T}}^N$ is a normal subgroup of ${\mathcal {H}}$, let ${\mathcal {H}}_N$ denote the quotient group ${\mathcal {H}}/{\mathcal {T}}^N$.

The following lemma gives an algorithm how we can determine a representation set of $\widehat{{\mathcal {T}}{\mathcal {F}}}/{\sim }$.

Lemma 4.9

Let $m\in {{\mathbb {N}}}$ such that $M_0=m{{\mathbb {N}}}$.

• (i) Every representation set of $\{\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}\,|\,\rho |_{{\mathcal {T}}^m}=I_{d_\rho }\}/{\sim }$ is a representation set of $\widehat{{\mathcal {T}}{\mathcal {F}}}/{\sim }$.

• (ii) The map

  $$\begin{aligned}\widehat{({\mathcal {T}}{\mathcal {F}})_m}\rightarrow \{\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}\,|\,\rho |_{{\mathcal {T}}^m}=I_{d_\rho }\},\quad \rho \mapsto \rho \circ \pi \end{aligned}$$

  where $\pi :{\mathcal {T}}{\mathcal {F}}\rightarrow ({\mathcal {T}}{\mathcal {F}})_m$ is the natural surjective homomorphism, is bijective. In particular, the set $\{\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}\,|\,\rho |_{{\mathcal {T}}^m}=I_{d_\rho }\}$ is finite.

• (iii) Let K be a representation set of $(L_{\mathcal {S}}^*/m)/L_{\mathcal {S}}^*$ and ${\mathcal {P}}$ be a representation set of ${\mathcal {G}}/({\mathcal {T}}{\mathcal {F}})$. Then, for all $\rho ,\rho '\in \{{\tilde{\rho }}\in \widehat{{\mathcal {T}}{\mathcal {F}}}\,|\,{\tilde{\rho }}|_{{\mathcal {T}}^m}=I_{d_{{\tilde{\rho }}}}\}$ it holds

  $$\begin{aligned} (\rho \sim \rho ')\iff (\exists \,g\in {\mathcal {P}}\,\exists \,k\in K: g\cdot \rho =\chi _k\rho '). \end{aligned}$$

Proof

Let $m\in {{\mathbb {N}}}$ such that $M_0=m{{\mathbb {N}}}$.

(i) Let R be a representation set of $\{\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}\,|\,\rho |_{{\mathcal {T}}^m}=I_{d_\rho }\}/{\sim }$. We have to show that for all $\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}$ there exists some $\rho '\in R$ such that $\rho \sim \rho '$. Let $\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}$. By Proposition 3.9 the group ${\mathcal {T}}^m$ is a subgroup of the center of ${\mathcal {T}}{\mathcal {F}}$ and thus, by Schur’s lemma for all $t\in {\mathcal {T}}^m$ there exists some $\lambda \in {{\mathbb {C}}}$ such that $|\lambda |=1$ and $\rho (t)=\lambda I_{d_\rho }$. Hence, there exists some one-dimensional representation $\chi \in \widehat{{\mathcal {T}}^m}$ such that $\rho |_{{\mathcal {T}}^m}=\chi I_{d_\rho }$.

There exists some $k\in {{\mathbb {R}}}^{d_2}$ such that $\chi |_{{\mathcal {T}}^m}=\chi _k|_{{\mathcal {T}}^m}$: By Lemma 3.7 the group ${\mathcal {T}}^m$ is isomorphic to ${{\mathbb {Z}}}^{d_2}$. Thus, there exist $t_1,\dots ,t_{d_2}\in {\mathcal {T}}^m$ such that $\{t_1,\dots ,t_{d_2}\}$ generates ${\mathcal {T}}^m$. For all $j\in \{1,\dots ,d_2\}$ there exists some $\alpha _j\in {{\mathbb {R}}}$ such that $\exp (2\pi {\textrm{i}}\alpha _j)=\chi (t_j)$. For all $i\in \{1,\dots ,d_2\}$ let $b_i\in {{\mathbb {R}}}^{d_2}$ such that

$$\begin{aligned} \langle b_i, \tau (\pi (t_j))\rangle =\delta _{ij}\qquad \text {for all }j\in \{1,\dots ,d_2\}, \end{aligned}$$

where $\pi :{\mathcal {T}}{\mathcal {F}}\rightarrow {\mathcal {T}}_{\mathcal {S}}$ is the natural surjective homomorphism. For $k=\sum _{i=1}^{d_2}\alpha _ib_i\in {{\mathbb {R}}}^{d_2}$ it holds $\chi |_{{\mathcal {T}}^m}=\chi _k|_{{\mathcal {T}}^m}$.

Thus, we have $\rho |_{{\mathcal {T}}^m}=\chi _k|_{{\mathcal {T}}^m}I_{d_\rho }$. Since $\chi _{-k}\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}$ and $(\chi _{-k}\rho )|_{{\mathcal {T}}^m}=I_{d_\rho }$, there exists some $\rho '\in R$ such that $\chi _{-k}\rho \sim \rho '$. There exist some $g\in {\mathcal {G}}$ and $l\in {{\mathbb {R}}}^{d_2}$ such that $g\cdot \rho '=\chi _l(\chi _{-k}\rho )$. This implies $\rho \sim \rho '$.

(ii) The first statement is clear from the general relation of the duals of a group and a quotient of it. The second follows from Remark 3.12(ii).

(iii) Let $\rho ,\rho '\in \widehat{{\mathcal {T}}{\mathcal {F}}}$ such that $\rho |_{{\mathcal {T}}^m}=I_{d_\rho }$, $\rho '|_{{\mathcal {T}}^m}=I_{d_{\rho '}}$ and $\rho \sim \rho '$. There exist some $g\in {\mathcal {G}}$ and $k\in {{\mathbb {R}}}^{d_2}$ such that $g\cdot \rho =\chi _k\rho '$. Let $h\in {\mathcal {P}}$ such that $g{\mathcal {T}}{\mathcal {F}}=h{\mathcal {T}}{\mathcal {F}}$. It holds $I_{d_\rho }=(g\cdot \rho )|_{{\mathcal {T}}^m}=(\chi _k\rho ')|_{{\mathcal {T}}^m}=\chi _k|_{{\mathcal {T}}^m}I_{d_{\rho '}}$. This implies $\chi _k|_{{\mathcal {T}}^m}=1$ and thus, $k\in (L_{\mathcal {S}}^*/m)$ by Lemma 4.4. Let $l\in K$ such that $lL_{\mathcal {S}}^*=kL_{\mathcal {S}}^*$. We have

$$\begin{aligned} h\cdot \rho =g\cdot \rho =\chi _k\rho '=\chi _l\rho ', \end{aligned}$$

where we used that ${\mathcal {T}}{\mathcal {F}}$ acts trivially on $\widehat{{\mathcal {T}}{\mathcal {F}}}$ in the first step and that $\chi _{k-l}=1$ since $k-l\in L_{\mathcal {S}}^*$ in the last step.

The other direction of the assertion is trivial. $\square$

Corollary 4.10

The set $\widehat{{\mathcal {T}}{\mathcal {F}}}/{\sim }$ is finite.

Proof

This is clear by Lemma 4.9. $\square$

As a final preparation, given $\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}$, we need specify the domain of wave vectors k for which $\chi _k\rho$ is to be considered. To this end we begin with the following definition.

Definition 4.11

For all $\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}$ we define the set

$$\begin{aligned} {\mathcal {G}}_\rho :=\Big \{(L(\pi (g)), k )\,\Big |\,g\in {\mathcal {G}},k\in {{\mathbb {R}}}^{d_2}:g\cdot \rho =\chi _k\rho \Big \}\subset {\textrm{E}}(d_2), \end{aligned}$$

where $\pi :{\mathcal {G}}\rightarrow {\mathcal {S}}$ is the natural surjective homomorphism.

Proposition 4.12

For all $\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}$ the set ${\mathcal {G}}_\rho$ is a space group and it holds

$$\begin{aligned} L_{\mathcal {S}}^*\le \big \{k\in {{\mathbb {R}}}^{d_2}\,\big |\,(I_{d_2}, k )\in {\mathcal {G}}_\rho \big \}\le L_{\mathcal {S}}^*/m, \end{aligned}$$

where $m\in {{\mathbb {N}}}$ is such that $M_0=m{{\mathbb {N}}}$.

Proof

Let $\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}$ and $m\in {{\mathbb {N}}}$ such that $M_0=m{{\mathbb {N}}}$. First we show that ${\mathcal {G}}_\rho$ is a subgroup of ${\textrm{E}}(d_2)$. Let $g_1,g_2\in {\mathcal {G}}_\rho$. We have to show that $g_1g_2^{-1}\in {\mathcal {G}}_\rho$. Let $\pi :{\mathcal {G}}\rightarrow {\mathcal {S}}$ be the natural surjective homomorphism. For all $i\in \{1,2\}$ let $h_i\in {\mathcal {G}}$ and $k_i\in {{\mathbb {R}}}^{d_2}$ such that $g_i=(L(\pi (h_i)), k_i )$ and $h_i\cdot \rho =\chi _{k_i}\rho$. It holds

$$\begin{aligned} (h_1h_2^{-1})\cdot \rho= & {} h_1\cdot (h_2^{-1}\cdot \rho )=h_1\cdot ((h_2^{-1}\cdot \chi _{-k_2})\rho )\\= & {} ((h_1h_2^{-1})\cdot \chi _{-k_2})(h_1\cdot \rho )=\chi _{k_1-L(\pi (h_1h_2^{-1}))k_2}\rho \end{aligned}$$

and thus,

$$\begin{aligned} g_1g_2^{-1}=(L(\pi (h_1h_2^{-1})), k_1-L(\pi (h_1h_2^{-1}))k_2 )\in {\mathcal {G}}_\rho . \end{aligned}$$

Let

$$\begin{aligned} {\mathcal {H}}:={\mathcal {G}}_\rho \cap {\textrm{Trans}}(d_2) \end{aligned}$$

be the group of all translations of ${\mathcal {G}}_\rho$. It is clear that $\tau ({\mathcal {H}})=\{k\in {{\mathbb {R}}}^{d_2}\,|\,(I_{d_2}, k )\in {\mathcal {G}}_\rho \}$.

Now we show that $\tau ({\mathcal {H}})\le L_{\mathcal {S}}^*/m$. Let $k\in \tau ({\mathcal {H}})$, i. e. $(I_{d_2}, k )\in {\mathcal {G}}_\rho$. There exists some $g\in {\mathcal {G}}$ such that $g\cdot \rho =\chi _k\rho$ and $L(\pi (g))=I_{d_2}$. The latter implies $\pi (g)\in {\mathcal {T}}_{\mathcal {S}}$ and thus, $g\in {\mathcal {T}}{\mathcal {F}}$. Since ${\mathcal {T}}{\mathcal {F}}$ acts trivially on $\widehat{{\mathcal {T}}{\mathcal {F}}}$ we thus have $\rho =\chi _k\rho$. Let ${\tilde{\rho }}$ be a representative of $\rho$. There exists some $T\in \textrm{U}(d_\rho )$ such that $T^H{\tilde{\rho }}(g)T=\chi _k(g){\tilde{\rho }}(g)$ for all $g\in {\mathcal {T}}{\mathcal {F}}$. Moreover, by Proposition 3.9 the set ${\mathcal {T}}^m$ is a subset of the center of ${\mathcal {T}}{\mathcal {F}}$ and hence, by Schur’s lemma ${\tilde{\rho }}(g)$ is a scalar multiple of $I_{d_\rho }$ for all $g\in {\mathcal {T}}^m$. Hence, we have $\chi _k(g)=1$ for all $g\in {\mathcal {T}}^m$ and $k\in L_{\mathcal {S}}^*/m$ by Lemma 4.4.

Now we show that $L_{\mathcal {S}}^*\le \tau ({\mathcal {H}})$. Let $k\in L_{\mathcal {S}}^*$. By Lemma 4.4 we have $\chi _k|_{\mathcal {T}}=1$. Since we also have $\chi _k|_{\mathcal {F}}=1$, we have $\chi _k=1$. Thus we have ${id}_{\mathcal {G}}\cdot \rho =\chi _k\rho$ and $(I_{d_2}, k )\in {\mathcal {H}}$, i. e. $k\in \tau ({\mathcal {H}})$.

Now we show that ${\mathcal {G}}_\rho$ is discrete. Since $\tau ({\mathcal {H}})$ is a subgroup of $L_{\mathcal {S}}^*/m$, the group ${\mathcal {H}}$ is discrete. Since $L({\mathcal {G}}_\rho )$ is a subgroup of the finite group $L({\mathcal {S}})$, the index $|{\mathcal {G}}_\rho :{\mathcal {H}}|=|L({\mathcal {G}}_\rho )|$ is finite. Hence, the group ${\mathcal {G}}_\rho$ is discrete (see, e. g., [34, Theorem 7.1]). Since $L_{\mathcal {S}}^*$ is a subgroup of $\tau ({\mathcal {H}})$, the group ${\mathcal {G}}_\rho$ contains $d_2$ linearly independent translations. By Theorem 2.1 the group ${\mathcal {G}}_\rho$ is a space group. $\square$

Lemma 4.13

For all $N\in M_0$ and $\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}$ such that $\rho |_{{\mathcal {T}}^N}=I_{d_\rho }$, the set $L_{\mathcal {S}}^*/N$ is invariant under ${\mathcal {G}}_\rho$, i. e. $\{g\cdot k\,|\,g\in {\mathcal {G}}_\rho ,k\in L_{\mathcal {S}}^*/N\}=L_{\mathcal {S}}^*/N$.

Proof

Let $N\in M_0$ and $\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}$ such that $\rho |_{{\mathcal {T}}^N}=I_{d_\rho }$. Let $k\in L_{\mathcal {S}}^*/N$ and $g\in {\mathcal {G}}_\rho$. We have to show that $g\cdot k\in L_{\mathcal {S}}^*/N$. Let $\pi :{\mathcal {G}}\rightarrow {\mathcal {S}}$ be the natural surjective homomorphism. There exist some $h\in {\mathcal {G}}$ and $l\in {{\mathbb {R}}}^{d_2}$ such that $g=(L(\pi (h)), l )$ and $h\cdot \rho =\chi _l\rho$. Since $\rho |_{{\mathcal {T}}^N}=I_{d_\rho }=(h\cdot \rho )|_{{\mathcal {T}}^N}$, we have $\chi _l|_{{\mathcal {T}}^N}=1$. We have

$$\begin{aligned} \chi _{g\cdot k}=\chi _{L(\pi (h))k+l}=(h\cdot \chi _k)\chi _l \end{aligned}$$

and thus, $\chi _{g\cdot k}|_{{\mathcal {T}}^N}=1$. By Lemma 4.4 we have $g\cdot k\in L_{\mathcal {S}}^*/N$. $\square$

Definition 4.14

Let ${\mathcal {H}}$ be a subgroup of ${\textrm{E}}(n)$. Then the set of all orbits of ${{\mathbb {R}}}^n$ under the action of ${\mathcal {H}}$ is written as ${{\mathbb {R}}}^n/{\mathcal {H}}$ and is called the quotient of the action or orbit space.

Remark 4.15

If a group ${\mathcal {H}}<{\textrm{E}}(n)$ is discrete, then the quotient space ${{\mathbb {R}}}^n/{\mathcal {H}}$ equipped with the orbit space distance function

$$\begin{aligned} {{\mathbb {R}}}^n/{\mathcal {H}}\times {{\mathbb {R}}}^n/{\mathcal {H}}\rightarrow [0,\infty ),\qquad (x,y)\mapsto {\textrm{dist}}(x,y) \end{aligned}$$

is a metric space whose topology is equal to the quotient topology, see, e. g., [35, §6.6].

We are finally in a position to state and prove our main results on the structure of ${\textrm{Ind}}_{{\mathcal {T}}{\mathcal {F}}}^{\mathcal {G}}(\widehat{{\mathcal {T}}{\mathcal {F}}})$. Note that the set R in the following theorems is finite due to Corollary 4.10.

Theorem 4.16

Let R be a representation set of $\widehat{{\mathcal {T}}{\mathcal {F}}}/{\sim }$. Then, the map

$$\begin{aligned}&\bigsqcup _{\rho \in R}{{\mathbb {R}}}^{d_2}/{\mathcal {G}}_\rho \rightarrow {\textrm{Ind}}_{{\mathcal {T}}{\mathcal {F}}}^{\mathcal {G}}(\widehat{{\mathcal {T}}{\mathcal {F}}}),\\&({\mathcal {G}}_\rho \cdot k,\rho )\mapsto {\textrm{Ind}}_{{\mathcal {T}}{\mathcal {F}}}^{\mathcal {G}}(\chi _k\rho ), \end{aligned}$$

where $\bigsqcup$ is the disjoint union, is bijective.

Proof

Let R be a representation set of $\widehat{{\mathcal {T}}{\mathcal {F}}}/{\sim }$. We define the map

$$\begin{aligned} \varphi :\bigsqcup _{\rho \in R}{{\mathbb {R}}}^{d_2}/{\mathcal {G}}_\rho \rightarrow {\textrm{Ind}}(\widehat{{\mathcal {T}}{\mathcal {F}}}), \qquad ({\mathcal {G}}_\rho \cdot k,\rho )\mapsto {\textrm{Ind}}(\chi _k\rho ). \end{aligned}$$

First we show that $\varphi$ is well-defined. Let $\rho \in R$, $k,k'\in {{\mathbb {R}}}^{d_2}$ and $g\in {\mathcal {G}}_\rho$ such that $k'=g\cdot k$. Let $\pi :{\mathcal {G}}\rightarrow {\mathcal {S}}$ be the natural surjective homomorphism. There exist some $h\in {\mathcal {G}}$ and $l\in {{\mathbb {R}}}^{d_2}$ such that $g=(L(\pi (h)), l )$ and $h\cdot \rho =\chi _l\rho$. We have

$$\begin{aligned} h\cdot (\chi _k\rho )=(h\cdot \chi _k)(h\cdot \rho )=\chi _{L(\pi (h))k+l}\rho =\chi _{k'}\rho \end{aligned}$$

and thus, ${\textrm{Ind}}(\chi _k\rho )={\textrm{Ind}}(\chi _{k'}\rho )$ by Proposition A.2.

Now we show that $\varphi$ is injective. Let $\rho ,\rho '\in {\mathcal {R}}$ and $k,k'\in {{\mathbb {R}}}^{d_2}$ such that ${\textrm{Ind}}(\chi _k\rho )={\textrm{Ind}}(\chi _{k'}\rho ')$. We have to show that $\rho =\rho '$ and ${\mathcal {G}}_\rho \cdot k={\mathcal {G}}_{\rho '}\cdot k'$. By Proposition A.2 there exists some $g\in {\mathcal {G}}$ such that $g\cdot (\chi _k\rho )=\chi _{k'}\rho '$. This is equivalent to $g\cdot \rho =\chi _{k'-L(\pi (g))k}\rho '$, which implies $\rho \sim \rho '$ and thus, $\rho =\rho '$. This implies that $(L(\pi (g)), k'-L(\pi (g))k )\in {\mathcal {G}}_\rho$ and thus,

$$\begin{aligned} {\mathcal {G}}_\rho \cdot k={\mathcal {G}}_{\rho '}\cdot \big ((L(\pi (g)), k'-L(\pi (g))k )\cdot k\big )={\mathcal {G}}_{\rho '}\cdot k'. \end{aligned}$$

Now we show that $\varphi$ is surjective. Let $\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}$. Let $\rho '\in R$ such that $\rho \sim \rho '$. There exist some $g\in {\mathcal {G}}$ and $k\in {{\mathbb {R}}}^{d_2}$ such that $g\cdot \rho =\chi _k\rho '$. By Proposition A.2 we have

$$\begin{aligned} \varphi (({\mathcal {G}}_{\rho '}\cdot k,\rho '))={\textrm{Ind}}(\chi _k\rho ')={\textrm{Ind}}(g\cdot \rho )={\textrm{Ind}}\rho . \end{aligned}$$

$\square$

There is also a version of this result for periodic representations.

Theorem 4.17

Let R be a representation set of $\{\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}\,|\,\rho |_{{\mathcal {T}}^m}=I_{d_\rho }\}/{\sim }$, where $m\in {{\mathbb {N}}}$ is such that $M_0=m{{\mathbb {N}}}$. Then the maps

• (i) $\begin{aligned}&\bigsqcup _{\rho \in R}\{k/N\,|\,k\in L_{\mathcal {S}}^*,N\in M_0\}/{\mathcal {G}}_\rho \rightarrow {\textrm{Ind}}(\{\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}\,|\,\exists \,N\in M_0:\rho |_{{\mathcal {T}}^N}=I_{d_\rho }\})\\&({\mathcal {G}}_\rho \cdot (k/N),\rho )\mapsto {\textrm{Ind}}(\chi _{k/N}\rho ) \end{aligned}$

• (ii) $\begin{aligned}&\bigsqcup _{\rho \in R}(L_{\mathcal {S}}^*/N)/{\mathcal {G}}_\rho \rightarrow {\textrm{Ind}}(\{\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}\,|\,\rho |_{{\mathcal {T}}^N}=I_{d_\rho }\})\\&({\mathcal {G}}_\rho \cdot k,\rho )\mapsto {\textrm{Ind}}(\chi _k\rho ), \end{aligned}$

where $\bigsqcup$ is the disjoint union, ${\textrm{Ind}}={\textrm{Ind}}_{{\mathcal {T}}{\mathcal {F}}}^{\mathcal {G}}$ and $N\in M_0$ in (ii) is arbitrary, are bijective.

Proof

Let $m\in {{\mathbb {N}}}$ such that $M_0=m{{\mathbb {N}}}$ and R be a representation set of $\{\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}\,|\,\rho |_{{\mathcal {T}}^m}=I_{d_\rho }\}/{\sim }$. By Lemma 4.9 the set R is a representation set of $\widehat{{\mathcal {T}}{\mathcal {F}}}/{\sim }$.

(i) We define the map

$$\begin{aligned} \psi&:\bigsqcup _{\rho \in R}\{k/N\,|\,k\in L_{\mathcal {S}}^*,N\in M_0\}/{\mathcal {G}}_\rho \rightarrow {\textrm{Ind}}(\{\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}\,|\,\exists \,N\in M_0:\rho |_{{\mathcal {T}}^N}=I_{d_\rho }\})\\&\quad ({\mathcal {G}}_\rho \cdot (k/N),\rho )\mapsto {\textrm{Ind}}(\chi _{k/N}\rho ). \end{aligned}$$

First we show that $\psi$ is well-defined. Let $\rho \in R$, $k\in L_{\mathcal {S}}^*$ and $N\in M_0$. Since ${\mathcal {T}}^N\subset {\mathcal {T}}^m$ and by Lemma 4.4, we have $(\chi _{k/N}\rho )|_{{\mathcal {T}}^N}=I_{d_\rho }$. By Lemma 4.13 for all $N\in M_0$ we have $(L_{\mathcal {S}}^*/N)/{\mathcal {G}}_\rho \subset {{\mathbb {R}}}^{d_2}/{\mathcal {G}}_\rho$ and thus, by Theorem 4.16 the map $\psi$ is well-defined.

Since the map of Theorem 4.16 is injective, also $\psi$ is injective.

It remains to show that $\psi$ is surjective. Let $\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}$ and $N\in M_0$ such that $\rho |_{{\mathcal {T}}^N}=I_{d_\rho }$. There exists some $\rho '\in R$ such that $\rho \sim \rho '$. There exist some $g\in {\mathcal {G}}$ and $k\in {{\mathbb {R}}}^{d_2}$ such that $g\cdot \rho =\chi _k\rho '$. We have $(g\cdot \rho )|_{{\mathcal {T}}^N}=I_{d_\rho }=\rho '|_{{\mathcal {T}}^N}$ and thus, $\chi _k|_{{\mathcal {T}}^N}=1$. By Lemma 4.4 we have $k\in L_{\mathcal {S}}^*/N$ and thus

$$\begin{aligned} \psi (({\mathcal {G}}_{\rho '}\cdot k,\rho '))={\textrm{Ind}}(\chi _k\rho ')={\textrm{Ind}}(g\cdot \rho )={\textrm{Ind}}\rho , \end{aligned}$$

by Proposition A.2. (ii) The proof is analogous to the proof of (i). $\square$

As a direct consequence of the above theorems we obtain:

Corollary 4.18

Let R be as in Theorem 4.16. For every $\sigma \in \widehat{{\mathcal {G}}}$ there exists a $\rho \in R$ and a $k\in {{\mathbb {R}}}^{d_2}$ such that $\sigma$ is a subrepresentation of ${\textrm{Ind}}_{{\mathcal {T}}{\mathcal {F}}}^{\mathcal {G}}(\chi _k\rho )$. If moreover R is as in Theorem 4.17 and $\rho |_{{\mathcal {T}}^N}=I_{d_\rho }$ for an $N \in M_0$, then k can be chosen in $L_{\mathcal {S}}^*/N$.

Proof

This is a direct consequence of Theorems 4.16 and 4.17 and Proposition A.3. $\square$

We finally address the natural question to what extent the induced representations labeled by $\bigsqcup _{\rho \in R}{{\mathbb {R}}}^{d_2}/{\mathcal {G}}_\rho$ from Theorem 4.16 are irreducible and exhaust the total dual space $\widehat{{\mathcal {G}}}$. To this end, we equip the orbit space ${{\mathbb {R}}}^{d_2}/{\mathcal {H}}$ of a $d_2$-dimensional space group ${\mathcal {H}}$ with the pushforward under the action of ${\mathcal {H}}$ of the $d_2$-dimensional Lebesgue-measure restricted to an associated fundamental domain. The dual space $\widehat{{\mathcal {G}}}$ of ${\mathcal {G}}$ shall be endowed with the Plancherel measure $\mu _{{\mathcal {G}}}$, which is characterized in our setting by $\sum _{g \in {\mathcal {G}}} |f(g)|^2 = \int _{\widehat{{\mathcal {G}}}} {\text {Tr}} \big ( \rho (f)^H \rho (f) \big ) \, \textrm{d}\mu _{{\mathcal {G}}}$ for all $f \in \ell ^1({\mathcal {G}})$, where $\rho (f) = \sum _{g \in {\mathcal {G}}} f(g) \rho (g) \in {{\mathbb {C}}}^{d_\rho \times d_\rho }$, cf., e. g., [15]. Without loss of generality we restrict to groups of infinite order as for $|{\mathcal {G}}| < \infty$ one has $d_2=0$, ${\mathcal {T}}= \{{id}\}$ and ${\mathcal {T}}{\mathcal {F}}= {\mathcal {G}}$.

Theorem 4.19

Suppose ${\mathcal {G}}$ is of infinite order. Let R be a representation set of $\{\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}\,|\,\rho |_{{\mathcal {T}}^m}=I_{d_\rho }\}/{\sim }$, where $m\in {{\mathbb {N}}}$ is such that $M_0=m{{\mathbb {N}}}$. There are a null-set $N\subset \widehat{{\mathcal {G}}}$ and null-sets $N_\rho \subset {{\mathbb {R}}}^{d_2}/{\mathcal {G}}_\rho$ for each $\rho \in R$ such that the mapping

$$\begin{aligned}&\bigsqcup _{\rho \in R}({{\mathbb {R}}}^{d_2}/{\mathcal {G}}_\rho )\setminus N_\rho \rightarrow \widehat{{\mathcal {G}}}\setminus N\\&({\mathcal {G}}_\rho \cdot k,\rho )\mapsto {\textrm{Ind}}_{{\mathcal {T}}{\mathcal {F}}}^{\mathcal {G}}(\chi _k\rho ), \end{aligned}$$

is bijective.

Remark 4.20

The proof shows that the $N_\rho$ can be chosen as $N_\rho = {\mathcal {G}}_\rho \cdot K$, where K is the Lebesgue null-set

$$\begin{aligned} K = \Big \{k\in {{\mathbb {R}}}^{d_2}\,\Big |\,\exists A\in L({\mathcal {S}})\setminus \{I_{d_2}\}:(A-I_{d_2})k\in L_{\mathcal {S}}^*/m\Big \}. \end{aligned}$$

Also note that, by Theorem 4.16 and Corollary 4.18, for any $\sigma \in N$ there is a $\rho \in R$ and a ${\mathcal {G}}_\rho \cdot k\in N_\rho$ such that $\sigma$ is a subrepresentation of ${\textrm{Ind}}_{{\mathcal {T}}{\mathcal {F}}}^{\mathcal {G}}(\chi _k\rho )$.

Lemma 4.21

Let K be as in Remark 4.20. Suppose $g\in {\mathcal {G}}$ and $k,k'\in {{\mathbb {R}}}^{d_2}$ are such that $L(\pi (g))k-k' \in L_{\mathcal {S}}^*/m$, where $m\in {{\mathbb {N}}}$ is such that $M_0=m{{\mathbb {N}}}$. Then we have $k\in K$ if and only if $k'\in K$.

Proof

Let $g\in {\mathcal {G}}$ and $k,k'\in {{\mathbb {R}}}^{d_2}$ such that $s\in L_{\mathcal {S}}^*/m$, where $B=L(\pi (g))$ and $s=Bk-k'$. Assume $k \in K$, say $(A-I_{d_2})k\in L_{\mathcal {S}}^*/m$ with $A\in L({\mathcal {S}})\setminus \{I_{d_2}\}$. Observe that also $BAB^T \in L({\mathcal {S}})\setminus \{I_{d_2}\}$ and that $L_{\mathcal {S}}^*/m$ is invariant under $L({\mathcal {S}})$, since $L({\mathcal {S}})\ltimes \{0_{d_2}\}<{\mathcal {G}}_{\chi _0}$ and by Lemma 4.13 with $\rho = \chi _0$. We thus get

$$\begin{aligned} (BAB^T-I_{d_2})k' = B(A-I_{d_2}) k - BAB^T s + s \in L_{\mathcal {S}}^*/m, \end{aligned}$$

i. e., $k' \in K$. If, conversely, $k' \in K$, then the same argument with g replaced by $g^{-1}$ and s replaced by $- B^T s$ yields $k \in K$. $\square$

As a consequence of this we have the following lemma.

Lemma 4.22

The set K defined in Remark 4.20 is invariant under ${\mathcal {G}}_\rho$ for any $\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}$ with $\rho |_{{\mathcal {T}}^m}=I_{d_\rho }$, where $m\in {{\mathbb {N}}}$ is such that $M_0=m{{\mathbb {N}}}$.

Proof

Let $k \in K$ and $g \in {\mathcal {G}}_\rho$, where $\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}$ with $\rho |_{{\mathcal {T}}^m}=I_{d_\rho }$. There exist some $h\in {\mathcal {G}}$ and $l\in {{\mathbb {R}}}^{d_2}$ such that $g=(L(\pi (h)), l )$ and $h\cdot \rho =\chi _l\rho$. Since $\rho |_{{\mathcal {T}}^m}=I_{d_\rho }=(h\cdot \rho )|_{{\mathcal {T}}^m}$, we have $\chi _l|_{{\mathcal {T}}^m}=1$ and so $l \in L_{\mathcal {S}}^*/m$ due to Lemma 4.4. Now Lemma 4.21 implies $g \cdot k = L(\pi (h)) k + l \in K$. $\square$

We now prove Theorem 4.19.

Proof

As in the proof of Theorem 4.17 we let $m\in {{\mathbb {N}}}$ such that $M_0=m{{\mathbb {N}}}$ and R be a representation set of $\{\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}\,|\,\rho |_{{\mathcal {T}}^m}=I_{d_\rho }\}/{\sim }$ so that R is a also representation set of $\widehat{{\mathcal {T}}{\mathcal {F}}}/{\sim }$ due to Lemma 4.9. Choose K as in Remark 4.20 and, for each $\rho \in R$, set $N_\rho ={\mathcal {G}}_\rho \cdot K$. We then claim that the following implication holds true for any $\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}$ with $\rho |_{{\mathcal {T}}^m}=I_{d_\rho }$, $k\in {{\mathbb {R}}}^{d_2}$ and $g\in {\mathcal {G}}{\setminus }{\mathcal {T}}{\mathcal {F}}$:

$$\begin{aligned} g\cdot (\chi _k\rho )=\chi _k\rho \implies k\in K. \end{aligned}$$

To see this fix such $\rho$, k and g with $g\cdot (\chi _k\rho )=\chi _k\rho$. Since $\rho |_{{\mathcal {T}}^m}=I_{d_\rho }$ we also have $g\cdot \chi _k|_{{\mathcal {T}}^m}=\chi _k|_{{\mathcal {T}}^m}$. Thus Lemmas 4.2 and 4.4 yield $(L(\pi (g))-I_{d_2})k\in L_{\mathcal {S}}^*/m$ and hence $k\in K$.

Since the point group $L({\mathcal {S}})$ is finite and the lattice $L_{\mathcal {S}}^*$ is countable, the Lebesgue measure of $K\subset {{\mathbb {R}}}^{d_2}$ is 0. As also ${\mathcal {G}}_\rho$ is countable for any $\rho \in R$, the sets $N_\rho \subset {{\mathbb {R}}}^{d_2}/{\mathcal {G}}_\rho$ are null-sets as well.

By Theorem 4.16 for each $\rho \in R$ and ${\mathcal {G}}_\rho \cdot k\in {{\mathbb {R}}}^{d_2}/{\mathcal {G}}_\rho$ there is a well-defined representation ${\textrm{Ind}}_{{\mathcal {T}}{\mathcal {F}}}^{\mathcal {G}}(\chi _k\rho )$. Combining Mackey’s irreducibility criterion stated in Theorem A.4 and the above claim we see that ${\textrm{Ind}}_{{\mathcal {T}}{\mathcal {F}}}^{\mathcal {G}}(\chi _k\rho )$ is irreducible for every $\rho \in R$ and ${\mathcal {G}}_\rho \cdot k\in ({{\mathbb {R}}}^{d_2}/{\mathcal {G}}_\rho ){\setminus } N_\rho$. We thus obtain that the mapping in the assertion of the theorem is well-defined and, upon choosing $N\subset \widehat{{\mathcal {G}}}$ suitably, also surjective. By Theorem 4.16 it is injective as well since, as noted above, R is also a representation set of $\widehat{{\mathcal {T}}{\mathcal {F}}}/{\sim }$.

We proceed to show that N is a null-set with respect to the Plancherel measure on $\widehat{{\mathcal {G}}}$. First note that, as ${\mathcal {T}}^m \cong {{\mathbb {Z}}}^{d_2}$, the dual space of ${\mathcal {T}}^m$ is $\widehat{{\mathcal {T}}^m} = \{\chi _k|_{{\mathcal {T}}^m}\,|\,k\in {{\mathbb {R}}}^{d_2}\}$, which by Lemma 4.4 can be identified with the flat torus ${{\mathbb {R}}}^{d_2}/(L_{\mathcal {S}}^*/m)$ whose Haar measure is the pushforward under the action of $L_{\mathcal {S}}^*/m$ of the $d_2$-dimensional Lebesgue-measure restricted to a unit cell of $L_{\mathcal {S}}^*/m$.

Let $\Omega$ be the $\mu _{{\mathcal {T}}^m}$-conull set $\{\chi _k|_{{\mathcal {T}}^m}\,|\,k\in {{\mathbb {R}}}^{d_2} {\setminus } K\} \subset \widehat{{\mathcal {T}}^m}$. Note that $\Omega$ is ${\mathcal {G}}$-invariant: For $g \in {\mathcal {G}}$ and $k \in {{\mathbb {R}}}^{d_2}$ Lemma 4.2 gives $g \cdot \chi _k|_{{\mathcal {T}}^m} = \chi _{k'}|_{{\mathcal {T}}^m}$ with $k' = L(\pi (g)) k$ and then Lemma 4.21 shows that $k \in K$ if and only if $k' \in K$. Trivially, each $\chi _k|_{{\mathcal {T}}^m}$ extends to $\chi _k$ on ${\mathcal {T}}{\mathcal {F}}$ and $g \cdot \chi _k|_{{\mathcal {T}}^m} = \chi _k|_{{\mathcal {T}}^m}$ for all $g \in {\mathcal {T}}{\mathcal {F}}$. Conversely, if $g \in {\mathcal {G}}{\setminus } {\mathcal {T}}{\mathcal {F}}$ and $k \in {{\mathbb {R}}}^{d_2} {\setminus } K$, then the above claim yields $g \cdot \chi _k|_{{\mathcal {T}}^m} \ne \chi _k|_{{\mathcal {T}}^m}$. As a consequence, ${\mathcal {G}}^{\chi _k|_{{\mathcal {T}}^m}} = {\mathcal {T}}{\mathcal {F}}$ and ${\mathcal {G}}_m^{\chi _k|_{{\mathcal {T}}^m}} = ({\mathcal {T}}{\mathcal {F}})_m$ whenever $k \in {{\mathbb {R}}}^{d_2} \setminus K$. Invoking Theorem A.5 we thus find that

$$\begin{aligned} \bigcup _{{\mathcal {G}}\cdot k \notin K/{\mathcal {G}}}\Big \{{\textrm{Ind}}_{{\mathcal {T}}{\mathcal {F}}}^{\mathcal {G}}(\chi _k \rho )\,\Big |\,\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}: \rho |_{{\mathcal {T}}^m}=I_{d_\rho }\Big \}, \end{aligned}$$

is a $\mu _{\mathcal {G}}$-conull subset of $\widehat{{\mathcal {G}}}$, where we also have used Lemma 4.9(ii) in order to pass from representations in $\widehat{({\mathcal {T}}{\mathcal {F}})_m}$ to representations in $\widehat{{\mathcal {T}}{\mathcal {F}}}$ that annihilate ${\mathcal {T}}^m$. To finish the proof it now suffices to show that

$$\begin{aligned}{} & {} \bigcup _{{\mathcal {G}}\cdot k\notin K/{\mathcal {G}}} \Big \{{\textrm{Ind}}_{{\mathcal {T}}{\mathcal {F}}}^{\mathcal {G}}(\chi _k\rho )\,\Big |\,\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}: \rho |_{{\mathcal {T}}^m}=I_{d_\rho }\Big \}\\{} & {} \quad \subset \bigsqcup _{\rho \in R}\big \{{\textrm{Ind}}_{{\mathcal {T}}{\mathcal {F}}}^{\mathcal {G}}(\chi _k\rho )\,\big |\,{\mathcal {G}}_\rho \cdot k\in ({{\mathbb {R}}}^{d_2}/{\mathcal {G}}_\rho ) \setminus N_\rho \big \}. \end{aligned}$$

Let $k\in {{\mathbb {R}}}^{d_2} {\setminus } K$ and $\rho \in \widehat{{\mathcal {T}}{\mathcal {F}}}: \rho |_{{\mathcal {T}}^m}=I_{d_\rho }$. Let $\rho '\in R$ such that $\rho '\sim \chi _k\rho$. There exists some $g\in {\mathcal {G}}$ and $k'\in {{\mathbb {R}}}^{d_2}$ such that $g\cdot (\chi _k \rho )=\chi _{k'}\rho '$. We have $\rho |_{{\mathcal {T}}^m}=I_{d_\rho }=\rho '|_{{\mathcal {T}}^m}$ and thus we have $\chi _{L(\pi (g))k}|_{{\mathcal {T}}^m}=\chi _{k'}|_{{\mathcal {T}}^m}$. So with Lemma 4.4 we get $L(\pi (g))k-k'\in L_{\mathcal {S}}^*/m$ and thus $k'\in {{\mathbb {R}}}^{d_2} \setminus K$ due to Lemma 4.21. By Lemma 4.22 we then have ${\mathcal {G}}_\rho \cdot k' \notin N_\rho$. The claim now follows from

$$\begin{aligned} {\textrm{Ind}}(\chi _k\rho )={\textrm{Ind}}(g\cdot (\chi _k\rho ))={\textrm{Ind}}(\chi _{k'}\rho '). \end{aligned}$$

$\square$

5 Harmonic Analysis of Periodic Functions

In this section we develop methods from Fourier analysis for periodic mappings on ${\mathcal {G}}$. We begin by defining a suitable notion of periodicity.

Definition 5.1

Let S be a set and $N\in M_0$. A function $u:{\mathcal {G}}\rightarrow S$ is called ${\mathcal {T}}^N$-periodic if

$$\begin{aligned} u(g)=u(gt)\qquad \text {for all }g\in {\mathcal {G}}\text { and }t\in {\mathcal {T}}^N. \end{aligned}$$

A function $u:{\mathcal {G}}\rightarrow S$ is called periodic if there exists some $N\in M_0$ such that u is ${\mathcal {T}}^N$-periodic.

We equip ${{\mathbb {C}}}^{m\times n}$ with the Frobenius inner product $\langle {{}\cdot {}}, {{}\cdot {}}\rangle$ defined by

$$\begin{aligned} \langle A, B\rangle :=\sum _{i=1}^m\sum _{j=1}^n a_{ij}\overline{b_{ij}}\qquad \text {for all }A,B\in {{\mathbb {C}}}^{m\times n} \end{aligned}$$

and let $\Vert {{}\cdot {}}\Vert$ denote the induced norm. We define the set

$$\begin{aligned} L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n}):=\{u:{\mathcal {G}}\rightarrow {{\mathbb {C}}}^{m\times n}\,|\,u\text { is periodic}\}. \end{aligned}$$

Remark 5.2

If ${\mathcal {G}}$ is finite and S a set, then every function from ${\mathcal {G}}$ to S is periodic and in particular, we have $L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})=\{u:{\mathcal {G}}\rightarrow {{\mathbb {C}}}^{m\times n}\}$.

The following Lemma shows that the above definition of periodicity is independent of the choice of ${\mathcal {T}}$.

Lemma 5.3

Let S be a set. A function $u:{\mathcal {G}}\rightarrow S$ is periodic if and only if there exists some $N\in {{\mathbb {N}}}$ such that

$$\begin{aligned} u(g)=u(gh)\qquad \text {for all }g\in {\mathcal {G}}\text { and }h\in {\mathcal {G}}^N. \end{aligned}$$

Proof

Let S be a set and $u:{\mathcal {G}}\rightarrow S$ be ${\mathcal {T}}^N$-periodic for some $N\in M_0$. By Theorem 3.11 the function u is ${\mathcal {T}}^{|{\mathcal {F}}| N}$-periodic. By Proposition 3.9 it holds

$$\begin{aligned} {\mathcal {G}}^{|{\mathcal {G}}/({\mathcal {T}}{\mathcal {F}})||{\mathcal {F}}| N}\subset ({\mathcal {T}}{\mathcal {F}})^{|{\mathcal {F}}| N}\subset ({\mathcal {T}}^N{\mathcal {F}})^{|{\mathcal {F}}|}={\mathcal {T}}^{|{\mathcal {F}}| N}{\mathcal {F}}^{|{\mathcal {F}}|}={\mathcal {T}}^{|{\mathcal {F}}| N}\subset {\mathcal {T}}^N \end{aligned}$$

and thus, we have

$$\begin{aligned} u(g)=u(gh)\qquad \text {for all }g\in {\mathcal {G}}\text { and }h\in {\mathcal {G}}^{|{\mathcal {G}}/({\mathcal {T}}{\mathcal {F}})||{\mathcal {F}}| N}. \end{aligned}$$

The other direction is trivial since by Theorem 3.11 for all $N\in {{\mathbb {N}}}$ there exists some $n\in {{\mathbb {N}}}$ such that $nN\in M_0$. $\square$

The following lemma characterizes the periodic functions on ${\mathcal {G}}$ with the aid of the quotient groups ${\mathcal {G}}/{\mathcal {T}}^N$.

Lemma 5.4

If $N\in M_0$ and $u:{\mathcal {G}}\rightarrow S$ is ${\mathcal {T}}^N$-periodic, then the function

$$\begin{aligned} {\mathcal {G}}_N\rightarrow S, \qquad g{\mathcal {T}}^N\mapsto u(g) \end{aligned}$$

is well-defined. Moreover, we have

$$\begin{aligned} L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})=\Big \{{\mathcal {G}}\rightarrow {{\mathbb {C}}}^{m\times n},g\mapsto u(g{\mathcal {T}}^N)\,\Big |\,N\in M_0,u:{\mathcal {G}}_N\rightarrow {{\mathbb {C}}}^{m\times n}\Big \}, \end{aligned}$$

and this space is a vector space.

Proof

This follows immediately from the definition of $L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})$. (Note that, if $u_i\in L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})$ is ${\mathcal {T}}^{N_i}$-periodic, $N_i\in M_0$, $i=1,2$, then $u_1+u_2$ is ${\mathcal {T}}^{N_1N_2}$-periodic.) $\square$

Definition 5.5

For all $N\in M_0$ let ${\mathcal {C}}_N$ be a representation set of ${\mathcal {G}}/{\mathcal {T}}^N$.

Remark 5.6

Let ${\mathcal {G}}$ be infinite. There exists some $m\in {{\mathbb {N}}}$ such that $M_0=m{{\mathbb {N}}}$ and there exist $t_1,\dots ,t_{d_2}\in {\mathcal {T}}^m$ such that $\{t_1,\dots ,t_{d_2}\}$ generates ${\mathcal {T}}^m$. Let ${\mathcal {C}}$ be a representation set of ${\mathcal {G}}/{\mathcal {T}}^m$. Then for all $N\in M_0$ a feasible choice for ${\mathcal {C}}_N$ is

$$\begin{aligned} {\mathcal {C}}_N=\Big \{t_1^{n_1}\dots t_{d_2}^{n_{d_2}}g\,\Big |\,n_1,\dots ,n_{d_2}\in \{0,\dots ,N/m-1\},g\in {\mathcal {C}}\Big \}. \end{aligned}$$

For this choice, for all $x\in {{\mathbb {R}}}^d$ and large $N\in M_0$ the set ${\mathcal {C}}_N\cdot x$ is similar to a cube which explains the nomenclature.

We equip the vector space $L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})$ with an inner product.

Definition 5.7

We define the inner product $\langle {{}\cdot {}},{{}\cdot {}}\rangle$ on $L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})$ by

$$\begin{aligned} \langle u,v\rangle :=\frac{1}{|{\mathcal {C}}_N|}\sum _{g\in {\mathcal {C}}_N}\langle u(g),v(g)\rangle \qquad \text {if }u\text { and }v\text { are }{\mathcal {T}}^N\text {-periodic} \end{aligned}$$

for all $u,v\in L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})$. We denote the induced norm by $\Vert {{}\cdot {}}\Vert _2$.

In order to define the Fourier transform we must choose a set of representatives for the periodic elements of $\widehat{{\mathcal {G}}}$.

Definition 5.8

Let ${\mathcal {E}}$ be a representation set of $\{\rho \in \widehat{{\mathcal {G}}}\,|\,\rho \text { is periodic}\}$.

Remark 5.9

For all $N\in M_0$ a representation $\rho$ of ${\mathcal {G}}$ is ${\mathcal {T}}^N$-periodic if and only if $\rho |_{{\mathcal {T}}^N}=I_{d_\rho }$, i. e., if it is of the form ${\bar{\rho }}\circ \pi _N$ for a representation ${\bar{\rho }}$ of ${\mathcal {G}}_N$ and $\pi _N$ denoting the natural surjective homomorphism from ${\mathcal {G}}$ to ${\mathcal {G}}_N$. We thus obtain

$$\begin{aligned} \big \{\rho \in \widehat{{\mathcal {G}}}\,\big |\,\rho \text { is }{\mathcal {T}}^N\text {-periodic}\big \}&=\big \{\rho \circ \pi _N\,\big |\,\rho \in \widehat{{\mathcal {G}}_N}\big \} \\ \end{aligned}$$

for all $N\in M_0$ and

$$\begin{aligned} \big \{\rho \in \widehat{{\mathcal {G}}}\,\big |\,\rho \text { is periodic}\big \}&=\big \{\rho \circ \pi _N\,\big |\,N\in M_0,\rho \in \widehat{{\mathcal {G}}_N}\big \}. \end{aligned}$$

Definition 5.10

For all $u\in L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})$ and for all periodic representations $\rho$ of ${\mathcal {G}}$ we define

where $N\in M_0$ is such that u and $\rho$ are ${\mathcal {T}}^N$-periodic and $\otimes$ denotes the Kronecker product.

Proposition 5.11

(The Plancherel formula) The Fourier transformation

is well-defined and bijective. Moreover, we have the Plancherel formula

Proof

We show that the well-known Plancherel formula for finite groups, see, e. g., [39, Exercise 5.7], implies the Plancherel formula of the proposition. Let $N\in M_0$ and $\pi _N:{\mathcal {G}}\rightarrow {\mathcal {G}}_N$ be the natural surjective homomorphism. The map

$$\begin{aligned} f_1:\{u:{\mathcal {G}}_N\rightarrow {{\mathbb {C}}}^{m\times n}\}\rightarrow \{u\in L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})\,|\,u\text { is }{\mathcal {T}}^N\text {-periodic}\}, \qquad u\mapsto u\circ \pi _N \end{aligned}$$

is bijective. Let ${\mathcal {E}}_N=\{\rho \,|\,\rho \text { is a representation of }{\mathcal {G}}_N, \rho \circ \pi _N\in {\mathcal {E}}\}$. We have $\{\rho \circ \pi _N\,|\,\rho \in {\mathcal {E}}_N\}=\{\rho \in {\mathcal {E}}\,|\,\rho \text { is }{\mathcal {T}}^N\text {-periodic}\}$. Thus the map

$$\begin{aligned} f_2:&\bigoplus _{\rho \in {\mathcal {E}},\ \rho \text { is }{\mathcal {T}}^N\text {-periodic}}{{\mathbb {C}}}^{(md_\rho )\times (nd_\rho )}\rightarrow \bigoplus _{\rho \in {\mathcal {E}}_N}{{\mathbb {C}}}^{(md_\rho )\times (nd_\rho )},\\&(A_\rho )_{\rho \in {\mathcal {E}},\ \rho \text { is }{\mathcal {T}}^N\text {-periodic}}\mapsto (A_{\rho \circ \pi _N})_{\rho \in {\mathcal {E}}_N} \end{aligned}$$

is bijective. By Remark 5.9 the set ${\mathcal {E}}_N$ is a representation set of $\widehat{{\mathcal {G}}_N}$. For all $u:{\mathcal {G}}_N\rightarrow {{\mathbb {C}}}^{m\times n}$ and $\rho \in {\mathcal {E}}_N$ we define By the Plancherel formula for finite groups, the Fourier transformation

is bijective and it holds for all $u,v:{\mathcal {G}}_N\rightarrow {{\mathbb {C}}}^{m\times n}$. The diagram

commutes, where the upper map is defined by Thus, the map

(4)

is bijective and we have

for all ${\mathcal {T}}^N$-periodic functions $u,v\in L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})$.

Since $N\in M_0$ was arbitrary, for all $u\in L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})$, for all $N\in M_0$ such that u is ${\mathcal {T}}^N$-periodic and $n\in {{\mathbb {N}}}$ it holds

(5)

By (5) for all $u\in L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})$ and $N\in M_0$ such that u is ${\mathcal {T}}^N$-periodic, we have

(6)

By (5) and (6) the Fourier transformation is well-defined and we have

for all $u,v\in L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})$. Moreover, since the map defined in (4) is injective and $L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})=\bigcup _{N\in M_0}\{u\in L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})\,|\,u\text { is } {\mathcal {T}}^N\text {-periodic}\}$, the Fourier transformation is injective. Analogously, the Fourier transformation is surjective. $\square$

Remark 5.12

• (i) The above proof also shows that for all $u:{\mathcal {G}}\rightarrow {{\mathbb {C}}}^{m\times n}$ and $N\in M_0$ such that u is ${\mathcal {T}}^N$-periodic, we have

  

  Moreover, for all $N\in M_0$ the map

  

  is bijective.

• (ii) It is easy to see that by the above proposition we have also a description of the completion of $L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})$ with respect to the norm $\Vert {{}\cdot {}}\Vert _2$. We have

  

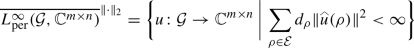
  and the map

  

  is bijective.

Lemma 5.13

Let $f\in L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})$, $g\in {\mathcal {G}}$ and $\tau _gf$ denote the translated function $f({{}\cdot {}}g)$. Then we have $\tau _gf\in L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})$ and

for all periodic representations $\rho$ of ${\mathcal {G}}$.

Proof

Let $f\in L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})$, $g\in {\mathcal {G}}$ and $\rho$ be a periodic representation. Let $N\in M_0$ such that f and $\rho$ are ${\mathcal {T}}^N$-periodic. The function $\tau _gf$ is ${\mathcal {T}}^N$-periodic and we have

where in the third step we made a substitution and used that ${\mathcal {C}}_N$ and ${\mathcal {C}}_Ng$ are representation sets of ${\mathcal {G}}/{\mathcal {T}}^N$ and that the function $h\mapsto f(h)\otimes \rho (hg^{-1})$ is ${\mathcal {T}}^N$-periodic. $\square$

Definition 5.14

For all $u\in L^1({\mathcal {G}},{{\mathbb {C}}}^{m\times n})$ and all representations $\rho$ of ${\mathcal {G}}$ we define

Remark 5.15

If the group ${\mathcal {G}}$ is finite, $\rho$ is a representation of ${\mathcal {G}}$ and $u\in L^1({\mathcal {G}},{{\mathbb {C}}}^{m\times n})=L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})$, then the Definitions 5.10 and 5.14 for differ by the multiplicative constant $|{\mathcal {G}}|$, but it will always be clear from the context which of the both definitions is meant. If ${\mathcal {G}}$ is infinite, then $L^1({\mathcal {G}},{{\mathbb {C}}}^{m\times n})\cap L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})=\{0\}$ and thus, there is no ambiguity.

Definition 5.16

For all $u\in L^1({\mathcal {G}},{{\mathbb {C}}}^{l\times m})$ and $v\in L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})$ we define the convolution $u*v\in L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{l\times n})$ by

$$\begin{aligned} u*v(g):=\sum _{h\in {\mathcal {G}}}u(h)v(h^{-1}g)\qquad \text {for all }g\in {\mathcal {G}}. \end{aligned}$$

Lemma 5.17

Let $u\in L^1({\mathcal {G}},{{\mathbb {C}}}^{l\times m})$, $v\in L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})$ and $\rho$ be a periodic representation of ${\mathcal {G}}$. Then

• (i) the convolution $u*v$ is ${\mathcal {T}}^N$-periodic if v is ${\mathcal {T}}^N$-periodic and

• (ii) we have

  

Proof

Let $u\in L^1({\mathcal {G}},{{\mathbb {C}}}^{l\times m})$, $v\in L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})$ and $\rho$ be a periodic representation of ${\mathcal {G}}$. Let $N\in M_0$ such that v and $\rho$ are ${\mathcal {T}}^N$-periodic. By Definition 5.16 it is clear that $u*v$ is ${\mathcal {T}}^N$-periodic and thus we have $u*v\in L_\textrm{per}^\infty ({\mathcal {G}},{{\mathbb {C}}}^{m\times n})$ as claimed in Definition 5.16. We have

$\square$

6 Quotient Groups as Semidirect Products

By Definition 3.8 for all $m\in M_0$ the group ${\mathcal {T}}^m$ is a normal subgroup of ${\mathcal {G}}$, but in general there does not exist any group ${\mathcal {H}}<{\mathcal {G}}$ such that ${\mathcal {G}}={\mathcal {T}}^m\rtimes {\mathcal {H}}$, see Example 6.1. In this section we determine for $m\in M_0$ and appropriate $N\in m{{\mathbb {N}}}$ a group ${\mathcal {H}}\le {\mathcal {G}}/{\mathcal {T}}^N$ such that

$$\begin{aligned} {\mathcal {G}}/{\mathcal {T}}^N={\mathcal {T}}^m/{\mathcal {T}}^N\rtimes {\mathcal {H}}, \end{aligned}$$

(7)

see Theorem 6.7. The proof is similar to the proof of the Schur-Zassenhaus theorem, see, e. g., [1]. If ${\mathcal {G}}$ is a space group, for appropriate $N\in {{\mathbb {N}}}$ the existence of a group ${\mathcal {H}}$ such that

$$\begin{aligned} {\mathcal {G}}/{\mathcal {T}}^N={\mathcal {T}}/T^N\rtimes {\mathcal {H}}\end{aligned}$$

(8)

is mentioned in [4, p. 299] and in [14, p. 376].

Example 6.1

(Symmorphic and nonsymmorphic space groups) Let ${\mathcal {G}}$ be a space group and ${\mathcal {T}}$ its subgroup of translations. If there exists a group ${\mathcal {H}}<{\mathcal {G}}$ such that ${\mathcal {G}}={\mathcal {T}}\rtimes {\mathcal {H}}$, then ${\mathcal {G}}$ is said to be a symmorphic space group, see e. g., [34, Section 9.1]. Otherwise, ${\mathcal {G}}$ is a nonsymmorphic space group.

Let $d=2$, $t_1=(I_2,e_1)$, $t_2=(I_2,e_2)$, ${id}=(I_2, 0 )$, $p_1=\big (\big ({\begin{matrix}1&{} 0 \\ 0&{} -1\end{matrix}}\big ), 0 \big )$ and $p_2=\big (\big ({\begin{matrix}1&{} 0 \\ 0&{} -1\end{matrix}}\big ), ({\begin{matrix}0.5 \\ 0 \end{matrix}}) \big )$. The space group

$$\begin{aligned} \big \{tp\,\big |\,t\in \langle t_1,t_2\rangle ,p\in \lbrace {id},p_1\rbrace \big \}<{\textrm{E}}(2) \end{aligned}$$

is symmorphic and equal to ${\mathcal {T}}\rtimes {\mathcal {H}}$ with ${\mathcal {T}}=\langle t_1,t_2\rangle$ and ${\mathcal {H}}=\langle p_1\rangle$. The space group

$$\begin{aligned} \big \{tp\,\big |\,t\in \langle t_1,t_2\rangle ,p\in \lbrace {id},p_2\rbrace \big \}<{\textrm{E}}(2) \end{aligned}$$

is nonsymmorphic, since it does not contain any element of order 2, but the order of the quotient group of the space group by its subgroup of all translations is 2.

In the following definition we define ${\mathcal {P}}_{\mathcal {S}}^{(n)}$ such that (8) is true for the choice ${\mathcal {H}}=\{g{\mathcal {T}}^N\,|\,g\in {\mathcal {P}}_{\mathcal {S}}^{(N)}\}$, see Corollary 6.9.

Definition 6.2

Let ${\tilde{\tau }}:L({\mathcal {S}})\rightarrow \tau ({\mathcal {S}})$ be a map such that $(P, {\tilde{\tau }}(P) )\in {\mathcal {S}}$ for all $P\in L({\mathcal {S}})$. We define the map

$$\begin{aligned} {{\bar{\tau }}}:L({\mathcal {S}})\times L({\mathcal {S}})\rightarrow \tau ({\mathcal {T}}_{\mathcal {S}}), \qquad (P,Q)\mapsto {\tilde{\tau }}(P)+P{\tilde{\tau }}(Q)-{\tilde{\tau }}(PQ). \end{aligned}$$

Furthermore, for all $n\in {{\mathbb {N}}}$ coprime to $|L({\mathcal {S}})|$ we define the set

$$\begin{aligned} {\mathcal {P}}_{\mathcal {S}}^{(n)}:=\bigg \{\bigg (P, {\tilde{\tau }}(P)-a(n)\sum _{Q\in L({\mathcal {S}})} {{\bar{\tau }}}(P,Q) \bigg )\,\bigg |\,P\in L({\mathcal {S}})\bigg \}\subset {\mathcal {S}}, \end{aligned}$$

where $a(n)=\max \big \{{{\tilde{a}}}\in \lbrace 0,-1,\dots \rbrace \,\big |\,\exists \,b\in {{\mathbb {Z}}}\text { such that }{{\tilde{a}}}|L({\mathcal {S}})|+bn=1\big \}$.

For all $n\in {{\mathbb {N}}}$ coprime to $|L({\mathcal {S}})|$ let ${\mathcal {P}}^{(n)}\subset {\mathcal {G}}$ be such that the map

$$\begin{aligned} {\mathcal {P}}^{(n)}\rightarrow {\mathcal {P}}_{\mathcal {S}}^{(n)}, \qquad g\mapsto \pi (g) \end{aligned}$$

is bijective, where $\pi :{\mathcal {G}}\rightarrow {\mathcal {S}}$ is the natural surjective homomorphism.

Remark 6.3

• (i) For all $P,Q\in L({\mathcal {S}})$ it holds

  $$\begin{aligned} (P, {\tilde{\tau }}(P) )(Q, {\tilde{\tau }}(Q) )=(I_{d_2}, {{\bar{\tau }}}(P,Q) )(PQ, {\tilde{\tau }}(PQ) ) \end{aligned}$$

  and thus, the map ${{\bar{\tau }}}$ is well-defined. Note that one could also use this equation as an equivalent definition for ${{\bar{\tau }}}$.

• (ii) By Remark 6.3(i) it is clear that, for symmorphic space groups and in contrast to non-symmorphic space groups, see Example 6.1, it is possible to choose ${\tilde{\tau }}$ such that ${{\bar{\tau }}}$ is equal to 0.

• (iii) If $n=1$, then $a(n)=0$ and ${\mathcal {P}}_{\mathcal {S}}^{(n)}=\{(P, {\tilde{\tau }}(P) )\,|\,P\in L({\mathcal {S}})\}$.

We now consider the group ${\mathcal {T}}^n{\mathcal {F}}{\mathcal {P}}^{(n)}$. Our motivation for this is the following: In general ${\mathcal {T}}$ is not a group and thus, in order to generalize (8) to (7), we replace ${\mathcal {T}}/{\mathcal {T}}^N$ by ${\mathcal {T}}^m/{\mathcal {T}}^N$. Then (8) will be true for the choice ${\mathcal {H}}={\mathcal {T}}^n{\mathcal {F}}{\mathcal {P}}^{(n)}$, see Theorem 6.7

Lemma 6.4

For all $n\in {{\mathbb {N}}}$ coprime to $|L({\mathcal {S}})|$ and for all $N\in (n{{\mathbb {N}}})\cap M_0$ it holds

$$\begin{aligned} {\mathcal {T}}^n{\mathcal {F}}{\mathcal {P}}^{(n)}\le {\mathcal {G}}\quad \text {and}\quad {\mathcal {T}}^N\triangleleft {\mathcal {T}}^n{\mathcal {F}}{\mathcal {P}}^{(n)}. \end{aligned}$$

Proof

Let $n\in {{\mathbb {N}}}$ be coprime to $|L({\mathcal {S}})|$.

First, we prove that ${\mathcal {T}}_{\mathcal {S}}^n{\mathcal {P}}_{\mathcal {S}}^{(n)}$ is a subgroup of ${\mathcal {S}}$. Let $t,s\in {\mathcal {T}}_{\mathcal {S}}^n$ and $p,q\in {\mathcal {P}}_{\mathcal {S}}^{(n)}$. We have to show that $tp(sq)^{-1}\in {\mathcal {T}}_{\mathcal {S}}^n{\mathcal {P}}_{\mathcal {S}}^{(n)}$. Clearly, it holds $tp(sq)^{-1}=tpq^{-1}s^{-1}(pq^{-1})^{-1}pq^{-1}$. Since ${\mathcal {T}}_{\mathcal {S}}^n\triangleleft {\mathcal {S}}$, we have $(pq^{-1})s^{-1}(pq^{-1})^{-1}\in {\mathcal {T}}_{\mathcal {S}}^n$, and hence, it suffices to show that $pq^{-1}\in {\mathcal {T}}_{\mathcal {S}}^n{\mathcal {P}}_{\mathcal {S}}^{(n)}$. Let $P=L(p)$, $Q=L(q)$ and $R=PQ^{-1}\in L({\mathcal {S}})$. Let $a=\max \big \{{{\tilde{a}}}\in \lbrace 0,-1,\dots \rbrace \,\big |\,\exists \,b\in {{\mathbb {Z}}}\text { such that }a|L({\mathcal {S}})|+bn=1\big \}$ and $b\in {{\mathbb {Z}}}$ such that $a|L({\mathcal {S}})|+bn=1$. We compute

$$\begin{aligned} pq^{-1}&=\bigg (P, {\tilde{\tau }}(P)-a\sum _{S\in L({\mathcal {S}})}{{\bar{\tau }}}(P,S) \bigg )\bigg (Q^{-1}, -Q^{-1}{\tilde{\tau }}(Q)+a\sum _{S\in L({\mathcal {S}})}Q^{-1}{{\bar{\tau }}}(Q,S) \bigg )\\&=\bigg (R, {\tilde{\tau }}(P)-PQ^{-1}{\tilde{\tau }}(Q)-a\sum _{S\in L({\mathcal {S}})}({{\bar{\tau }}}(P,S)-PQ^{-1}{{\bar{\tau }}}(Q,S)) \bigg )\\&=\bigg (R, {\tilde{\tau }}(R)-{{\bar{\tau }}}(PQ^{-1},Q)-a\sum _{S\in L({\mathcal {S}})}({{\bar{\tau }}}(P,S)-PQ^{-1}{{\bar{\tau }}}(Q,S)) \bigg )\\&=\bigg (R, {\tilde{\tau }}(R)-(a|L({\mathcal {S}})|+bn){{\bar{\tau }}}(PQ^{-1},Q)-a\sum _{S\in L({\mathcal {S}})}({{\bar{\tau }}}(P,S)-PQ^{-1}{{\bar{\tau }}}(Q,S)) \bigg )\\&=\Big (I_{d_2}, {{\bar{\tau }}}(R,Q) \Big )^{-bn}\bigg (R, {\tilde{\tau }}(R)-a\sum _{S\in L({\mathcal {S}})}({{\bar{\tau }}}(PQ^{-1},Q)+{{\bar{\tau }}}(P,S)-PQ^{-1}{{\bar{\tau }}}(Q,S)) \bigg )\\&=\Big (I_{d_2}, {{\bar{\tau }}}(R,Q) \Big )^{-bn}\bigg (R, {\tilde{\tau }}(R)-a\sum _{S\in L({\mathcal {S}})}({\tilde{\tau }}(PQ^{-1})-{\tilde{\tau }}(PS)+PQ^{-1}{\tilde{\tau }}(QS)) \bigg ). \end{aligned}$$

We use that $\sum _{S\in L({\mathcal {S}})}{\tilde{\tau }}(S)=\sum _{S\in L({\mathcal {S}})}{\tilde{\tau }}(TS)$ for all $T\in L({\mathcal {S}})$.

$$\begin{aligned} pq^{-1}&=\Big (I_{d_2}, {{\bar{\tau }}}(R,Q) \Big )^{-bn}\bigg (R, {\tilde{\tau }}(R)-a\sum _{S\in L({\mathcal {S}})}({\tilde{\tau }}(PQ^{-1})-{\tilde{\tau }}(PQ^{-1}S)+PQ^{-1}{\tilde{\tau }}(S)) \bigg )\\&=\Big (I_{d_2}, {{\bar{\tau }}}(R,Q) \Big )^{-bn}\bigg (R, {\tilde{\tau }}(R)-a\sum _{S\in L({\mathcal {S}})}{{\bar{\tau }}}(R,S) \bigg )\in {\mathcal {T}}_{\mathcal {S}}^n{\mathcal {P}}_{\mathcal {S}}^{(n)}. \end{aligned}$$

Thus, we have ${\mathcal {T}}_{\mathcal {S}}^n{\mathcal {P}}_{\mathcal {S}}^{(n)}\le {\mathcal {S}}$.

Let $\pi$ be the natural surjective homomorphism from ${\mathcal {G}}$ to ${\mathcal {S}}$ with kernel ${\mathcal {F}}$. It holds $\pi ^{-1}({\mathcal {T}}_{\mathcal {S}}^n{\mathcal {P}}_{\mathcal {S}}^{(n)})={\mathcal {T}}^n{\mathcal {F}}{\mathcal {P}}^{(n)}$ and thus, ${\mathcal {T}}^n{\mathcal {F}}{\mathcal {P}}^{(n)}$ is a subgroup of ${\mathcal {G}}$.

Now let $N\in (n{{\mathbb {N}}})\cap M_0$. Since n divides N, we have ${\mathcal {T}}^N\subset {\mathcal {T}}^n{\mathcal {F}}{\mathcal {P}}^{(n)}$. Since $N\in M_0$, we have ${\mathcal {T}}^N\triangleleft {\mathcal {T}}^n{\mathcal {F}}{\mathcal {P}}^{(n)}$. $\square$

Recall Definition 4.8.

Remark 6.5

Let $n\in {{\mathbb {N}}}$ be coprime to $|L({\mathcal {S}})|$. Let $m\in M_0$, $N=nm$ and $t_1,\dots ,t_{d_2}\in {\mathcal {T}}^n$ such that $\pi (\{t_1,\dots ,t_{d_2}\})$ generates ${\mathcal {T}}_{\mathcal {S}}^n$, where $\pi :{\mathcal {T}}{\mathcal {F}}\rightarrow {\mathcal {T}}_{\mathcal {S}}$ is the natural surjective homomorphism. Then, the map

$$\begin{aligned}&\{0,\dots ,m-1\}^{d_2}\times {\mathcal {F}}\times {\mathcal {P}}^{(n)}\rightarrow ({\mathcal {T}}^n{\mathcal {F}}{\mathcal {P}}^{(n)})_N,{} & {} ((n_1,\dots ,n_{d_2}),f,p)\mapsto t_1^{n_1}\dots t_{d_2}^{n_{d_2}}fp{\mathcal {T}}^N \end{aligned}$$

is bijective.

For Theorem 6.7 and its corollaries we need the groups ${\mathcal {G}}_N$, $({\mathcal {T}}^n{\mathcal {F}})_N$ and $({\mathcal {T}}^m)_N$ for appropriate $n,m,N\in {{\mathbb {N}}}$. These groups were already investigated in Sect. 3. The following lemma characterizes the elements and orders of the groups which will be needed for the proof of Theorem 6.7.

Lemma 6.6

Let $t_1,\dots ,t_{d_2}\in {\mathcal {T}}$ such that the set $\pi (\{t_1,\dots ,t_{d_2}\})$ generates ${\mathcal {T}}_{\mathcal {S}}$, where $\pi :{\mathcal {T}}{\mathcal {F}}\rightarrow {\mathcal {T}}_{\mathcal {S}}$ is the natural surjective homomorphism. For all $N\in M_0$ it holds

$$\begin{aligned}&{\mathcal {G}}_N=\Big \{t_1^{n_1}\dots t_{d_2}^{n_{d_2}}fp{\mathcal {T}}^N\,\Big |\,n_1,\dots ,n_{d_2}\in \{0,\dots ,N-1\},f\in {\mathcal {F}},p\in {\mathcal {P}}^{(1)}\Big \} \end{aligned}$$

and particularly $|{\mathcal {G}}_N|=N^{d_2}|{\mathcal {F}}||L({\mathcal {S}})|$.For all $n\in {{\mathbb {N}}}$ and $N\in (n{{\mathbb {N}}})\cap M_0$ it holds

$$\begin{aligned}&({\mathcal {T}}^n{\mathcal {F}})_N=\Big \{t_1^{nn_1}\dots t_{d_2}^{nn_{d_2}}f{\mathcal {T}}^N\,\Big |\,n_1,\dots ,n_{d_2}\in \{0,\dots ,(N/n)-1\},f\in {\mathcal {F}}\Big \} \end{aligned}$$

and particularly $|({\mathcal {T}}^n{\mathcal {F}})_N|=(N/n)^{d_2}|{\mathcal {F}}|$. Moreover, for all $n\in {{\mathbb {N}}}$ and $N\in (n{{\mathbb {N}}})\cap M_0$ it holds $({\mathcal {T}}^n{\mathcal {F}})_N\triangleleft {\mathcal {G}}_N$.For all $m\in M_0$ and $N\in m{{\mathbb {N}}}$ it holds

$$\begin{aligned}&({\mathcal {T}}^m)_N=\Big \{t_1^{mn_1}\dots t_{d_2}^{mn_{d_2}}{\mathcal {T}}^N\,\Big |\,n_1,\dots ,n_{d_2}\in \{0,\dots ,(N/m)-1\}\Big \}, \end{aligned}$$

$({\mathcal {T}}^m)_N$ is a subgroup of the center of $({\mathcal {T}}{\mathcal {F}})_N$ and particularly $|({\mathcal {T}}^m)_N|=(N/m)^{d_2}$.

Proof

Since ${\mathcal {P}}^{(1)}$ is a representation set of ${\mathcal {G}}/{\mathcal {T}}{\mathcal {F}}$, the map ${\mathcal {T}}\times {\mathcal {F}}\times {\mathcal {P}}^{(1)}\rightarrow {\mathcal {G}}$, $(t,f,p)\mapsto tfp$ is bijective. The assertions are clear by Lemma 3.6, Theorem 3.11, Lemma 3.7 and Proposition 3.9. $\square$

The following theorem characterizes the group ${\mathcal {G}}_N$ for appropriate $N\in {{\mathbb {N}}}$.

Theorem 6.7

Let $m\in M_0$. Let $n\in {{\mathbb {N}}}$ be coprime to m and $|L({\mathcal {S}})|$. Let $N=nm$. Then, we have

$$\begin{aligned} {\mathcal {G}}_N=({\mathcal {T}}^m)_N\rtimes ({\mathcal {T}}^n{\mathcal {F}}{\mathcal {P}}^{(n)})_N \end{aligned}$$

and $({\mathcal {T}}^m)_N$ is isomorphic to ${{\mathbb {Z}}}_n^{d_2}$.

Proof

Let $m\in M_0$. Let $n\in {{\mathbb {N}}}$ be coprime to m and $|L({\mathcal {S}})|$. Let $N=nm$. By Theorem 3.11 we have ${\mathcal {T}}^m\triangleleft {\mathcal {G}}$ and ${\mathcal {T}}^N\triangleleft {\mathcal {G}}$, and by Lemma 3.7 we have ${\mathcal {T}}^N\triangleleft {\mathcal {T}}^m$. Hence, we have

$$\begin{aligned} ({\mathcal {T}}^m)_N\triangleleft {\mathcal {G}}_N. \end{aligned}$$

(9)

By Lemma 3.7 the group ${\mathcal {T}}^m$ is isomorphic to ${{\mathbb {Z}}}^{d_2}$ and thus, $({\mathcal {T}}^m)_N$ is isomorphic to ${{\mathbb {Z}}}_n^{d_2}$. By Lemma 6.4 we have

$$\begin{aligned} ({\mathcal {T}}^n{\mathcal {F}}{\mathcal {P}}^{(n)})_N\le {\mathcal {G}}_N. \end{aligned}$$

(10)

For all $N\in {{\mathbb {N}}}$ and ${\mathcal {H}}\le {\mathcal {S}}$ such that ${\mathcal {T}}_{\mathcal {S}}^N$ is a subgroup of ${\mathcal {H}}$, we denote

$$\begin{aligned} {\mathcal {H}}_N:={\mathcal {H}}/{\mathcal {T}}_{\mathcal {S}}^N. \end{aligned}$$

Let $\pi :{\mathcal {G}}_N\rightarrow {\mathcal {S}}_N$ be the natural surjective homomorphism with kernel $\{g{\mathcal {T}}^N\,|\,g\in {\mathcal {F}}\}$. We have

$$\begin{aligned} \pi (({\mathcal {T}}^m)_N\cap ({\mathcal {T}}^n{\mathcal {F}}{\mathcal {P}}^{(n)})_N)&\subset \pi (({\mathcal {T}}^m)_N)\cap \pi (({\mathcal {T}}^n{\mathcal {F}}{\mathcal {P}}^{(n)})_N)\nonumber \\&=({\mathcal {T}}_{\mathcal {S}}^m)_N\cap ({\mathcal {T}}_{\mathcal {S}}^n{\mathcal {P}}_{\mathcal {S}}^{(n)})_N\nonumber \\&=({\mathcal {T}}_{\mathcal {S}}^m)_N\cap ({\mathcal {T}}_{\mathcal {S}}^n)_N\nonumber \\&=\{{id}\}, \end{aligned}$$

(11)

where in the third step we used that for all $p\in {\mathcal {P}}_{\mathcal {S}}^{(n)}$ such that $L(p)=I_{d_2}$ we have $p\in {\mathcal {T}}_{\mathcal {S}}^n$ and in the last step we used that the numbers $n^{d_2}$ and $m^{d_2}$ are coprime, $|({\mathcal {T}}_{\mathcal {S}}^m)_N|=n^{d_2}$, $|({\mathcal {T}}_{\mathcal {S}}^n)_N|=m^{d_2}$ and Lagrange’s theorem. By (11) and since $\pi |_{({\mathcal {T}}^m)_N}$ is injective, we have

$$\begin{aligned} ({\mathcal {T}}^m)_N\cap ({\mathcal {T}}^n{\mathcal {F}}{\mathcal {P}}^{(n)})_N=\{{id}\}. \end{aligned}$$

(12)

We have

$$\begin{aligned} |{\mathcal {G}}_N|=|\ker (\pi )||\pi ({\mathcal {G}}_N)|=|\{g{\mathcal {T}}^N\,|\,g\in {\mathcal {F}}\}||{\mathcal {S}}_N|=|{\mathcal {F}}||L({\mathcal {S}})| N^{d_2}, \end{aligned}$$

(13)

see Lemma 6.6, and

$$\begin{aligned} |({\mathcal {T}}^n{\mathcal {F}}{\mathcal {P}}^{(n)})_N|&=|\ker (\pi |_{({\mathcal {T}}^n{\mathcal {F}}{\mathcal {P}}^{(n)})_N})||\pi (({\mathcal {T}}^n{\mathcal {F}}{\mathcal {P}}^{(n)})_N)|\nonumber \\&=|{\mathcal {F}}||({\mathcal {T}}_{\mathcal {S}}^n{\mathcal {P}}_{\mathcal {S}}^{(n)})_N|=|{\mathcal {F}}||{\mathcal {P}}_{\mathcal {S}}^{(n)}||({\mathcal {T}}_{\mathcal {S}}^n)_N|=|{\mathcal {F}}||L({\mathcal {S}})| m^{d_2}, \end{aligned}$$

(14)

see Remark 6.5. By (13), (14) and since $({\mathcal {T}}^m)_N$ is isomorphic to ${{\mathbb {Z}}}_n^{d_2}$, we have

$$\begin{aligned} |{\mathcal {G}}_N|=|({\mathcal {T}}^m)_N||({\mathcal {T}}^n{\mathcal {F}}{\mathcal {P}}^{(n)})_N|. \end{aligned}$$

(15)

By (9), (10), (12) and (15) we have

$$\begin{aligned} {\mathcal {G}}_N=({\mathcal {T}}^m)_N\rtimes ({\mathcal {T}}^n{\mathcal {F}}{\mathcal {P}}^{(n)})_N. \end{aligned}$$

$\square$

Corollary 6.8

Let $m\in M_0$, ${{\tilde{n}}}\in {{\mathbb {N}}}$, $n={{\tilde{n}}}m|L({\mathcal {S}})|+1$ and $N=nm$. Then we have

$$\begin{aligned} {\mathcal {P}}_{\mathcal {S}}^{(n)}&=\bigg \{\bigg (P, {\tilde{\tau }}(P)+{{\tilde{n}}}m\sum _{Q\in L({\mathcal {S}})} {{\bar{\tau }}}(P,Q) \bigg )\,\bigg |\,P\in L({\mathcal {S}})\bigg \} \end{aligned}$$

and

$$\begin{aligned} {\mathcal {G}}_N&=({\mathcal {T}}^m)_N\rtimes ({\mathcal {T}}^{n}{\mathcal {F}}{\mathcal {P}}^{(n)})_N. \end{aligned}$$

Proof

Let $m\in M_0$, ${{\tilde{n}}}\in {{\mathbb {N}}}$, $n={{\tilde{n}}}m|L({\mathcal {S}})|+1$ and $N=nm$. In particular, n is coprime to m and $|L({\mathcal {S}})|$. We have

$$\begin{aligned}&\max \big \{{{\tilde{a}}}\in \lbrace 0,-1,\dots \rbrace \,\big |\,\exists \,b\in {{\mathbb {Z}}}\text { such that }{{\tilde{a}}}|L({\mathcal {S}})|+bn=1\big \}\\&\qquad \quad =\max \big \{{{\tilde{a}}}\in \lbrace 0,-1,\dots \rbrace \,\big |\,\exists \,b\in {{\mathbb {N}}}\text { such that }({{\tilde{a}}}+b{{\tilde{n}}}m)|L({\mathcal {S}})|+b=1\big \}\\&\qquad \quad =-{{\tilde{n}}}m \end{aligned}$$

and hence,

$$\begin{aligned} {\mathcal {P}}_{\mathcal {S}}^{(n)}=\bigg \{\bigg (P, {\tilde{\tau }}(P)+{{\tilde{n}}}m\sum _{Q\in L({\mathcal {S}})} {{\bar{\tau }}}(P,Q) \bigg )\,\bigg |\, P\in L({\mathcal {S}})\bigg \}. \end{aligned}$$

By Theorem 6.7 we have ${\mathcal {G}}_N=({\mathcal {T}}^m)_N\rtimes ({\mathcal {T}}^{n}{\mathcal {F}}{\mathcal {P}}^{(n)})_N$. $\square$

Corollary 6.9

Suppose that ${\mathcal {G}}$ is a space group. Let $N\in {{\mathbb {N}}}$ be coprime to $|L({\mathcal {G}})|$. Then we have

$$\begin{aligned} {\mathcal {G}}_N={\mathcal {T}}_N\rtimes \{g{\mathcal {T}}^N\,|\,g\in {\mathcal {P}}^{(N)}\}. \end{aligned}$$

Proof

Let ${\mathcal {G}}$ be a space group. We have ${\mathcal {F}}=\{{id}\}$ and $M_0={{\mathbb {N}}}$. For all $N\in {{\mathbb {N}}}$ coprime to $|L({\mathcal {G}})|$, we have $({\mathcal {T}}^N{\mathcal {P}}^{(N)})/{\mathcal {T}}^N=\{g{\mathcal {T}}^N\,|\,g\in {\mathcal {P}}^{(N)}\}$. Thus, Theorem 6.7 implies the assertion. $\square$

Corollary 6.10

Suppose that ${\mathcal {G}}$ is a space group. Let $n\in {{\mathbb {N}}}$ and $N=n|L({\mathcal {G}})|+1$. Then it holds

$$\begin{aligned}&{\mathcal {P}}^{(N)}=\bigg \{\bigg (P, {\tilde{\tau }}(P)+n\sum _{Q\in L({\mathcal {G}})} {{\bar{\tau }}}(P,Q) \bigg )\,\bigg |\, P\in L({\mathcal {G}})\bigg \} \end{aligned}$$

and

$$\begin{aligned}&{\mathcal {G}}_N={\mathcal {T}}_N\rtimes \{g{\mathcal {T}}^N\,|\,g\in {\mathcal {P}}^{(N)}\}. \end{aligned}$$

Proof

This is clear by Corollary 6.8 and Corollary 6.9. $\square$

Corollary 6.11

Suppose that ${\mathcal {G}}={\mathcal {T}}{\mathcal {F}}$. Let $m\in M_0$ and $n\in {{\mathbb {N}}}$ be coprime. Let $N=nm$. Then it holds

$$\begin{aligned} {\mathcal {G}}_N=({\mathcal {T}}^m)_N\times ({\mathcal {T}}^n{\mathcal {F}})_N. \end{aligned}$$

Proof

Suppose that ${\mathcal {G}}={\mathcal {T}}{\mathcal {F}}$. Let $m\in M_0$ and $n\in {{\mathbb {N}}}$ be coprime. We have ${\mathcal {S}}={\mathcal {T}}_{\mathcal {S}}$ and $L({\mathcal {S}})=\{I_{d_2}\}$. Without loss of generality we assume that ${\tilde{\tau }}=0$. We have ${{\bar{\tau }}}=0$ and ${\mathcal {P}}_{\mathcal {S}}^{(n)}=\{{id}\}$. Without loss of generality we assume that ${\mathcal {P}}^{(n)}=\{{id}\}$. By Theorem 6.7, Lemma 3.6(ii) and Proposition 3.9 we have ${\mathcal {G}}_N=({\mathcal {T}}^m)_N\times ({\mathcal {T}}^n{\mathcal {F}})_N$. $\square$

Induced Representations and Mackey Analysis

With the aim to keep our presentation largely self-contained, we recall some topics on induced representations and standard Mackey analysis in a short appendix. Our setting allows for a definition of induced representations as for finite groups, see, e. g., [39, Section 8.2]. (For general locally compact groups the definition is more complicated, see, e. g., [21, Chapter 2].) For notation we refer to the last paragraph of Sect. 1.

Definition A.1

Let ${\mathcal {H}}<{\textrm{E}}(d)$ be discrete and ${\mathcal {K}}$ be a subgroup of ${\mathcal {H}}$ such that the index $n=|{\mathcal {H}}:{\mathcal {K}}|$ is finite. Choose a complete set of representatives $\{h_1,\dots ,h_n\}$ of the left cosets of ${\mathcal {K}}$ in ${\mathcal {H}}$. Suppose $\rho :{\mathcal {K}}\rightarrow \textrm{U}(d_\rho )$ is a representation of ${\mathcal {K}}$. Let us introduce a dot notation in this context by setting

$$\begin{aligned} {\dot{\rho }}(g):={\left\{ \begin{array}{ll} \rho (g) &{} \text {if }g\in {\mathcal {K}}\\ 0_{d_\rho ,d_\rho } &{} \text {else} \end{array}\right. } \end{aligned}$$

for all $g\in {\mathcal {H}}$. The induced representation ${\textrm{Ind}}_{\mathcal {K}}^{\mathcal {H}}\rho :{\mathcal {H}}\rightarrow \textrm{U}(nd_\rho )$ is defined by

$$\begin{aligned} {\textrm{Ind}}_{\mathcal {K}}^{\mathcal {H}}\rho (g)=\begin{bmatrix}{\dot{\rho }}(h_1^{-1}gh_1)&{}\cdots &{}{\dot{\rho }}(h_1^{-1}gh_n)\\ \vdots &{}\ddots &{}\vdots \\ {\dot{\rho }}(h_n^{-1}gh_1)&{}\cdots &{}{\dot{\rho }}(h_n^{-1}gh_n)\end{bmatrix}\qquad \text {for all }g\in {\mathcal {H}}. \end{aligned}$$

The induced representation of an equivalence class of representations is the equivalence class of the induced representation of a representative. Moreover, let ${\textrm{Ind}}_{\mathcal {K}}^{\mathcal {H}}(\widehat{{\mathcal {K}}})$ denote the set of all induced representations of $\widehat{{\mathcal {K}}}$. We also write ${\textrm{Ind}}$ instead of ${\textrm{Ind}}_{\mathcal {K}}^{\mathcal {H}}$ if ${\mathcal {K}}$ and ${\mathcal {H}}$ are clear by context.

The following proposition is standard in Clifford theory.

Proposition A.2

Let ${\mathcal {H}}<{\textrm{E}}(d)$ be discrete and ${\mathcal {N}}$ be a normal subgroup of ${\mathcal {H}}$ such that the index $|{\mathcal {H}}:{\mathcal {N}}|$ is finite. Then the map

$$\begin{aligned} \widehat{{\mathcal {N}}}/{\mathcal {H}}\rightarrow {\textrm{Ind}}_{\mathcal {N}}^{\mathcal {H}}(\widehat{{\mathcal {N}}}), \qquad {\mathcal {H}}\cdot \rho \mapsto {\textrm{Ind}}_{\mathcal {N}}^{\mathcal {H}}\rho \end{aligned}$$

is bijective, where $\widehat{{\mathcal {N}}}/{\mathcal {H}}=\{{\mathcal {H}}\cdot \rho \,|\,\rho \in \widehat{{\mathcal {N}}}\}$.

Proof

That this mapping is well-defined and surjective follows, e. g., from [21, Proposition 2.39]. For its injectivity see, e. g., [9, Theorem 3.2(ii)]. $\square$

We also record the following well-known results on the relation of irreducible and induced representations adapted to our setting.

Proposition A.3

Let ${\mathcal {H}}<{\textrm{E}}(d)$ be discrete and ${\mathcal {K}}$ be a subgroup of ${\mathcal {H}}$ of finite index. Then every irreducible representation of ${\mathcal {H}}$ is a subrepresentation of a representation which is induced by an irreducible representation of ${\mathcal {K}}$.

Proof

Let $\rho$ be an irreducible representation of ${\mathcal {H}}$. Choose $\sigma \in \widehat{{\mathcal {K}}}$ such that $\sigma$ is a subrepresentation of $\rho$ restricted to ${\mathcal {H}}$. Then [27, Theorem 8.2] shows that $\rho$ is a subrepresentation of ${\textrm{Ind}}_{{\mathcal {K}}}^{{\mathcal {H}}}\sigma$. $\square$

The following is Mackey’s irreducibility criterion, cp. [26], which we state in a form that is directly implied by, e. g., [6, Theorem 1.1].

Theorem A.4

Let ${\mathcal {H}}<{\textrm{E}}(d)$ be discrete and ${\mathcal {N}}$ be a normal subgroup of ${\mathcal {H}}$ of finite index. Let $\rho$ be an irreducible representation of ${\mathcal {N}}$. Then ${\textrm{Ind}}_{{\mathcal {N}}}^{{\mathcal {H}}}\rho$ is irreducible if and only if for every $g\in {\mathcal {H}}\setminus {\mathcal {N}}$ the representations $g\cdot \rho$ and $\rho$ are not isomorphic.

We finally state a version of the Mackey machine (cf. [28]) in a form proven in [22, 23] and adapted to our setting of discrete subgroups of ${\textrm{E}}(d)$.

Theorem A.5

Let ${\mathcal {H}}<{\textrm{E}}(d)$ be discrete, ${\mathcal {N}}$ be a normal abelian subgroup of ${\mathcal {H}}$ of finite index with respective Plancherel measures $\mu _{{\mathcal {H}}}$ and $\mu _{{\mathcal {N}}}$ and set ${\mathcal {P}}= {\mathcal {H}}/{\mathcal {N}}$. Suppose there is an ${\mathcal {H}}$-invariant measurable $\mu _{\mathcal {N}}$-conull subset $\Omega \subset \widehat{{\mathcal {N}}}$ such that all $\sigma \in \Omega$ can be extended to a unitary representation ${\tilde{\sigma }}$ of ${\mathcal {H}}^\sigma$. For $\sigma \in \Omega$ and $\rho \in {\mathcal {P}}^\sigma$ define the unitary representation $\sigma \times \rho$ of ${\mathcal {H}}^\sigma$, acting on ${{\mathbb {C}}}^{d_\sigma d_\rho }$, by

$$\begin{aligned} (\sigma \times \rho )(g)={\tilde{\sigma }}(g)\otimes \rho (g{\mathcal {N}})\qquad \text {for all }g\in {\mathcal {H}}^\sigma . \end{aligned}$$

Then the set

$$\begin{aligned} \bigcup _{\mathcal {\mathcal {P}}\cdot \sigma \in \Omega /{\mathcal {P}}}\big \{{\textrm{Ind}}_{{\mathcal {H}}^\sigma }^{\mathcal {H}}(\sigma \times \rho )\,\big |\,\rho \in \widehat{{\mathcal {P}}^\sigma }\big \} \end{aligned}$$

is a $\mu _{\mathcal {H}}$-conull subset of $\widehat{{\mathcal {H}}}$.