1 Introduction

Let us consider the Gaussian \(\phi (t) = \mathrm{e}^{-\pi t^2}\), for \(t \in {\mathbb {R}}\). We may define the Gabor transform of a signal \(f \in L^2({\mathbb {R}})\) via

$$\begin{aligned} {\mathcal {V}}_\phi f(x,\omega ) = \int _{\mathbb {R}}f(t) \phi (t-x) \mathrm{e}^{-2\pi \mathrm{i}t \omega } \,\mathrm{d}t, \qquad (x,\omega ) \in {\mathbb {R}}^2. \end{aligned}$$

In this paper, we are interested in the uniqueness question of the Gabor phase retrieval problem which consists of recovering a function \(f \in L^2({\mathbb {R}})\) from the magnitude measurements

$$\begin{aligned} \left|{{\mathcal {V}}_\phi f(x,\omega )}\right|, \qquad (x,\omega ) \in S, \end{aligned}$$
(1)

where S is a subset of \({\mathbb {R}}^2\). We say that f is uniquely determined (up to a global phase factor) by the measurements (1) if for any \(g \in L^2({\mathbb {R}})\),

$$\begin{aligned} \left|{{\mathcal {V}}_\phi f(x,\omega )}\right| = \left|{{\mathcal {V}}_\phi g(x,\omega )}\right| \qquad (x,\omega ) \in S, \end{aligned}$$

implies that

$$\begin{aligned} f = \mathrm{e}^{\mathrm{i}\mu } g, \end{aligned}$$

for some \(\mu \in {\mathbb {R}}\). When \(S={\mathbb {R}}^2\), it is well-known that Gabor phase retrieval is uniquely solvable. In fact, this result holds true for any window function \(\psi \) for which \({\mathcal {V}}_\psi \psi \) is non-zero almost everywhere on \({\mathbb {R}}^2\). However, when S is a true subset of \({\mathbb {R}}^2\), the answer is less clear. In particular, measurements can only be collected on discrete sets S in applications. Thus, the question of uniqueness for Gabor phase retrieval is specifically interesting when S is discrete.

In recent work [1], we were able to show that real-valued, bandlimited signals in \(L^2({\mathbb {R}})\) are uniquely determined up to global phase from Gabor magnitude measurements (1) sampled on the discrete set \(S = (4B)^{-1} {\mathbb {Z}}\times \{0\}\), where \(B > 0\) is such that the bandwidth of the signal is contained in \([-B,B]\). While we were writing this paper, work by Grohs and Liehr [3] appeared showing that it is possible to recover compactly supported signals in \(L^4([-C/2,C/2])\) up to global phase from Gabor magnitude measurements (1) sampled on the discrete set \(S = {\mathbb {Z}}\times (2C)^{-1} {\mathbb {Z}}\). Finally, during the review process of this paper, the work [4] appeared. In [4], the authors generalise the findings proposed here to general short-time Fourier transform phase retrieval.

We focus on the general uniqueness question for Gabor phase retrieval:

Question 1

Is there any lattice \(S \subset {\mathbb {R}}^2\) such that all functions in \(L^2({\mathbb {R}})\) are uniquely determined up to global phase from Gabor magnitude measurements (1) sampled on S?

The main contribution of this paper is that we answer this question negatively: In particular, no matter how fine-grained the sampling lattice S, one will not be able to recover all functions in \(L^2({\mathbb {R}})\) from Gabor magnitude measurements (1) on S. Our answer to Question 1 is constructive in the sense that we are able to explicitly give functions \(f_{\pm } \in L^2({\mathbb {R}})\) which do not agree up to global phase but which satisfy

$$\begin{aligned} \left|{{\mathcal {V}}_\phi f_+(x,\omega )}\right| = \left|{{\mathcal {V}}_\phi f_-(x,\omega )}\right|, \qquad (x,\omega ) \in S. \end{aligned}$$

We note that the functions \(f_{\pm } \in L^2({\mathbb {R}})\) are well concentrated in both time and frequency and if \(S = a {\mathbb {Z}}\times b {\mathbb {Z}}\), \(a,b > 0\), is a rectangular lattice, then \(f_+\) and \(f_-\) can be constructed to be real-valued.

1.1 Basic Notions

We want to emphasise that the notation \(\phi \) is reserved for the Gaussian \(\phi (t) = \mathrm{e}^{-\pi t^2}\), for \(t \in {\mathbb {R}}\), throughout this paper.

We will encounter the fractional Fourier transform of a function \(f \in L^1({\mathbb {R}})\) defined by

$$\begin{aligned} {\mathcal {F}}_\alpha f(\omega ) := c_\alpha \mathrm {e}^{\pi \mathrm {i}\omega ^2 \cot \alpha } \int _{\mathbb {R}}f(t) \mathrm {e}^{\pi \mathrm {i}t^2 \cot \alpha } \mathrm {e}^{-2 \pi \mathrm {i}\frac{t \omega }{\sin \alpha }} \,\mathrm {d}t, \qquad \omega \in {\mathbb {R}}, \end{aligned}$$

for \(\alpha \in {\mathbb {R}}\setminus \pi {\mathbb {Z}}\), where \(c_\alpha \in {\mathbb {C}}\) is the square root of \(1 - \mathrm{i}\cot \alpha \) with positive real part, and by \({\mathcal {F}}_{2\pi k} f := f\) as well as \({\mathcal {F}}_{(2k+1)\pi } f(\omega ) := f(-\omega )\), for \(\omega \in {\mathbb {R}}\), where \(k \in {\mathbb {Z}}\) [5]. One may show that the fractional Fourier transform preserves the canonical inner product \((\cdot ,\cdot )\) on \(L^2({\mathbb {R}})\) in the sense that for all \(\alpha \in {\mathbb {R}}\) and \(f,g \in L^1({\mathbb {R}}) \cap L^2({\mathbb {R}})\) it holds that

$$\begin{aligned} (f,g) = ({\mathcal {F}}_\alpha f, {\mathcal {F}}_\alpha g). \end{aligned}$$

It follows that one may extend the fractional Fourier transform to \(L^2({\mathbb {R}})\) by a classical density argument. For the further understanding of this paper, it is essential to observe that the fractional Fourier transform rotates functions in the time–frequency plane in the following sense:

Lemma 1

(See [5, p. 424]) Let \(\alpha \in {\mathbb {R}}\) and \(f,g \in L^2({\mathbb {R}})\). It holds that

$$\begin{aligned} {\mathcal {V}}_{{\mathcal {F}}_\alpha g} {\mathcal {F}}_\alpha f (x,\omega ) ={\mathcal {V}}_g f (x \cos \alpha - \omega \sin \alpha , x \sin \alpha + \omega \cos \alpha ) \mathrm{e}^{\pi \mathrm{i}\sin \alpha \left( \left( x^2 - \omega ^2 \right) \cos \alpha -2 x\omega \sin \alpha \right) }, \end{aligned}$$

for \(x,\omega \in {\mathbb {R}}\).

In addition, as for the classical Fourier transform, it holds that the Gaussian \(\phi \) is invariant under the fractional Fourier transform in the sense that

$$\begin{aligned} {\mathcal {F}}_\alpha \phi = \phi , \qquad \alpha \in {\mathbb {R}}. \end{aligned}$$

One can see this by a direct computation using the classical result which can for instance be found on [2, p. 17].

In the following, we will denote by \(R_\alpha : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2\) the rotation of the time–frequency plane given by

$$\begin{aligned} R_\alpha (x,\omega ) := (x \cos \alpha - \omega \sin \alpha , x \sin \alpha + \omega \cos \alpha ), \qquad x,\omega \in {\mathbb {R}}. \end{aligned}$$

Additionally, we will use the standard notation for the family of time-shift operators \(\hbox {T}_{x} : L^2({\mathbb {R}}) \rightarrow L^2({\mathbb {R}})\), with \(x \in {\mathbb {R}}\), given by

$$\begin{aligned} \hbox {T}_{x} f(t) = f(t-x), \qquad t \in {\mathbb {R}}, \end{aligned}$$

and the family of modulation operators \(\hbox {M}_{\xi } : L^2({\mathbb {R}}) \rightarrow L^2({\mathbb {R}})\), with \(\xi \in {\mathbb {R}}\), given by

$$\begin{aligned} \hbox {M}_{\xi } f(t) = f(t) \mathrm{e}^{2\pi \mathrm{i}t \xi }, \qquad t \in {\mathbb {R}}, \end{aligned}$$

for \(f \in L^2({\mathbb {R}})\).

2 Main Result

Fig. 1
figure 1

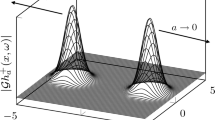
The functions defined in Eq. (2) with \(a=1\)

Full size image

Using the relation of the Gabor transform and the Bargmann transform [2] in conjunction with the Hadamard factorisation theorem allows us to design functions \(f_{\pm } \in L^2({\mathbb {R}})\) which do not agree up to global phase but which generate measurements (1) that agree when \(S \subset {\mathbb {R}}^2\) is chosen to be any set of infinitely many equidistant parallel lines. For the specific set \(S = a{\mathbb {Z}}\times {\mathbb {R}}\), with \(a > 0\), this construction leads us to consider the real-valued functions

$$\begin{aligned} f_{\pm }(t) := \mathrm{e}^{-\pi t^2} \left( \cos \left( \frac{\pi t}{a} \right) \pm \sin \left( \frac{\pi t}{a} \right) \right) , \qquad t \in {\mathbb {R}}, \end{aligned}$$
(2)

as depicted in Fig. 1. It is easy to see that \(f_+\) and \(f_-\) do not agree up to global phase: Consider for instance that

$$\begin{aligned} f_+\left( \frac{a}{4} \right) = \mathrm{e}^{-\frac{\pi a^2}{16}} \left( \cos \left( \frac{\pi }{4} \right) +\sin \left( \frac{\pi }{4} \right) \right) =\sqrt{2} \mathrm{e}^{-\frac{\pi a^2}{16}} \ne 0, \end{aligned}$$

as well as

$$\begin{aligned} f_-\left( \frac{a}{4} \right) = \mathrm{e}^{-\frac{\pi a^2}{16}} \left( \cos \left( \frac{\pi }{4} \right) -\sin \left( \frac{\pi }{4} \right) \right) = 0. \end{aligned}$$

Furthermore, it is not hard to compute the Gabor transforms of \(f_+\) and \(f_-\) and thereby verify the following lemma.

Lemma 2

Let \(a > 0\) and let \(f_\pm \in L^2({\mathbb {R}})\) be defined as in Eq. (2). Then, it holds that

$$\begin{aligned} \left|{{\mathcal {V}}_\phi f_+}\right| = \left|{{\mathcal {V}}_\phi f_-}\right| \text{ on } a {\mathbb {Z}}\times {\mathbb {R}}. \end{aligned}$$
(3)

Remark 1

It is immediate that the above lemma implies that

$$\begin{aligned} \left|{{\mathcal {V}}_\phi f_+}\right| = \left|{{\mathcal {V}}_\phi f_-}\right| \end{aligned}$$

continues to hold on \(a {\mathbb {Z}}\times b {\mathbb {Z}}\) no matter how small one chooses \(b > 0\).

Remark 2

As mentioned above, the functions \(f_+\) and \(f_-\) were constructed by considering what Eq. (3) implies for the Bargmann transforms \(F_+\) and \(F_-\) of \(f_+\) and \(f_-\). In particular, we applied Hadamard’s factorisation theorem to \(F_+\) and \(F_-\) and then followed ideas similar to the ones presented in [5, 6].

Proof of Lemma 2

Let us start by noting that

$$\begin{aligned} f_{\pm } = \left( \frac{1}{2} \pm \frac{1}{2\mathrm{i}} \right) \hbox {M}_{\frac{1}{2a}} \phi + \left( \frac{1}{2} \mp \frac{1}{2\mathrm{i}} \right) \hbox {M}_{-\frac{1}{2a}} \phi . \end{aligned}$$

By the linearity and the covariance property of the Gabor transform (see [2, Lemma 3.1.3 on p. 41]), we obtain

$$\begin{aligned} {\mathcal {V}}_\phi f_{\pm }(x,\omega ) = \left( \frac{1}{2} \pm \frac{1}{2\mathrm{i}} \right) {\mathcal {V}}_\phi \phi \left( x, \omega - \frac{1}{2a} \right) +\left( \frac{1}{2} \mp \frac{1}{2\mathrm{i}} \right) {\mathcal {V}}_\phi \phi \left( x, \omega + \frac{1}{2a} \right) , \end{aligned}$$

for \(x,\omega \in {\mathbb {R}}\). Using that the Gaussian is invariant under the Fourier transform, one may calculate that

$$\begin{aligned} {\mathcal {V}}_\phi \phi (x,\omega ) = \frac{1}{\sqrt{2}} \mathrm{e}^{-\pi \mathrm{i}x \omega } \mathrm{e}^{-\frac{\pi }{2} \left( x^2 + \omega ^2\right) } \end{aligned}$$

such that

$$\begin{aligned} {\mathcal {V}}_\phi f_{\pm }(x,\omega )= & {} \frac{1}{2 \sqrt{2}} ( 1 \mp \mathrm{i}) \mathrm{e}^{-\pi \mathrm{i}x \left( \omega - \frac{1}{2a} \right) } \mathrm{e}^{-\frac{\pi }{2} \left( x^2 +\left( \omega -\frac{1}{2a} \right) ^2 \right) }\\&+\frac{1}{2 \sqrt{2}} ( 1 \pm \mathrm{i}) \mathrm{e}^{-\pi \mathrm{i}x \left( \omega + \frac{1}{2a} \right) } \mathrm{e}^{-\frac{\pi }{2} \left( x^2 + \left( \omega +\frac{1}{2a} \right) ^2 \right) }. \end{aligned}$$

We might reformulate the above expression to

$$\begin{aligned} {\mathcal {V}}_\phi f_{\pm }(x,\omega ) = \frac{\mathrm{e}^{-\frac{\pi }{8a^2}}}{2 \sqrt{2}} \mathrm{e}^{-\pi \mathrm{i}x\omega } \mathrm{e}^{-\frac{\pi }{2}\left( x^2 + \omega ^2\right) } \left( ( 1 \mp \mathrm{i}) \mathrm{e}^{\frac{\pi }{2a}\left( \omega + \mathrm{i}x \right) } + ( 1 \pm \mathrm{i}) \mathrm{e}^{-\frac{\pi }{2a} \left( \omega + \mathrm{i}x \right) } \right) . \end{aligned}$$

If \(x = ak\), where \(k \in {\mathbb {Z}}\), and \(\omega \in {\mathbb {R}}\), then it holds that

$$\begin{aligned} ( 1 - \mathrm{i}) \mathrm{e}^{\frac{\pi }{2a}\left( \omega + \mathrm{i}x \right) } +(1 + \mathrm{i}) \mathrm{e}^{-\frac{\pi }{2a}\left( \omega + \mathrm{i}x \right) }&=(1 - \mathrm{i}) \mathrm{i}^k \mathrm{e}^{\frac{\pi \omega }{2a}} + ( 1 + \mathrm{i}) (-\mathrm{i})^k \mathrm{e}^{-\frac{\pi \omega }{2a}} \\&= \overline{ ( 1 + \mathrm{i}) (-\mathrm{i})^k \mathrm{e}^{\frac{\pi \omega }{2a}} +( 1 - \mathrm{i}) \mathrm{i}^k \mathrm{e}^{-\frac{\pi \omega }{2a}} } \\&= (-1)^k \cdot \overline{ ( 1 + \mathrm{i}) \mathrm{i}^k \mathrm{e}^{\frac{\pi \omega }{2a}} + ( 1 - \mathrm{i}) (-\mathrm{i})^k \mathrm{e}^{-\frac{\pi \omega }{2a}}} \\&= (-1)^k \cdot \overline{ ( 1 + \mathrm{i}) \mathrm{e}^{\frac{\pi }{2a} \left( \omega + \mathrm{i}x \right) } + ( 1 - \mathrm{i}) \mathrm{e}^{-\frac{\pi }{2a} \left( \omega + \mathrm{i}x \right) } }. \end{aligned}$$

It follows that

$$\begin{aligned} \left|{{\mathcal {V}}_\phi f_+(x,\omega )}\right| = \left|{{\mathcal {V}}_\phi f_-(x,\omega )}\right|, \end{aligned}$$

for \(x \in a {\mathbb {Z}}\) and \(\omega \in {\mathbb {R}}\). \(\square \)

Remark 3

According to the preceding proof, it holds that

$$\begin{aligned} {\mathcal {V}}_\phi f_{\pm }(x,\omega )= & {} \frac{\mathrm{e}^{-\frac{\pi }{8a^2}}}{\sqrt{2}} \mathrm{e}^{-\pi \mathrm{i}x\omega } \mathrm{e}^{-\frac{\pi }{2}\left( x^2 + \omega ^2\right) }\\&\left( \cosh \left( \frac{\pi }{2a} \left( \omega + \mathrm{i}x \right) \right) \mp \mathrm{i}\sinh \left( \frac{\pi }{2a} \left( \omega +\mathrm{i}x \right) \right) \right) , \qquad x,\omega \in {\mathbb {R}}. \end{aligned}$$

To generalise Lemma 2, we can use the fractional Fourier transform as well as time shifts and modulations to rotate and shift the functions \(f_\pm \) in the time frequency plane. In this way, we construct the functions

$$\begin{aligned} f_{\pm }^{\alpha ,\lambda } := \hbox {T}_{x_0} \hbox {M}_{\omega _0} {\mathcal {F}}_{-\alpha } f_{\pm }, \end{aligned}$$
(4)

for \(\alpha \in {\mathbb {R}}\) and \(\lambda = (x_0,\omega _0) \in {\mathbb {R}}^2\). We may now make use of well-known properties of the Gabor transform to show the following result:

Theorem 1

(Main theorem) Let \(a > 0\), \(\alpha \in {\mathbb {R}}\) and \(\lambda = (x_0,\omega _0) \in {\mathbb {R}}^2\). Let furthermore \(f_{\pm }^{\alpha ,\lambda } \in L^2({\mathbb {R}})\) be defined as in Eq. (4). Then, it holds that \(f_+^{\alpha ,\lambda }\) and \(f_-^{\alpha ,\lambda }\) do not agree up to global phase and yet

$$\begin{aligned} \left|{{\mathcal {V}}_\phi f_+^{\alpha ,\lambda }}\right| = \left|{{\mathcal {V}}_\phi f_-^{\alpha ,\lambda }}\right| \text{ on } R_\alpha (a {\mathbb {Z}}\times {\mathbb {R}}) + \lambda . \end{aligned}$$

Furthermore, it holds that for all \(\epsilon > 0\), there exists a constant \(C_\epsilon \ge 1\) (that additionally depends on a and \(\lambda \)) such that

$$\begin{aligned} \left|{{\mathcal {V}}_\phi f_{\pm }^{\alpha ,\lambda }(x,\omega )}\right| \le C_\epsilon \mathrm{e}^{-\left( \frac{\pi }{2}-\epsilon \right) \left( x^2 + \omega ^2 \right) }, \qquad x,\omega \in {\mathbb {R}}. \end{aligned}$$

Remark 4

It is immediate that the above theorem implies that

$$\begin{aligned} \left|{{\mathcal {V}}_\phi f_+^{\alpha ,\lambda }}\right| = \left|{{\mathcal {V}}_\phi f_-^{\alpha ,\lambda }}\right| \end{aligned}$$

continues to hold on the lattice \(S = R_\alpha (a {\mathbb {Z}}\times b{\mathbb {Z}}) + \lambda \) no matter how small one chooses \(b > 0\).

Proof of Theorem 1

We directly compute that

$$\begin{aligned} \left|{{\mathcal {V}}_\phi f_{\pm }^{\alpha ,\lambda }(x,\omega ) }\right|&=\left|{{\mathcal {V}}_\phi \hbox {T}_{x_0} \hbox {M}_{\omega _0} {\mathcal {F}}_{-\alpha } f_{\pm } (x,\omega ) }\right| = \left|{ {\mathcal {V}}_\phi {\mathcal {F}}_{-\alpha } f_{\pm } (x-x_0,\omega -\omega _0) }\right| \nonumber \\&= \left|{ {\mathcal {V}}_{{\mathcal {F}}_{-\alpha } \phi } {\mathcal {F}}_{-\alpha } f_{\pm } (x-x_0,\omega -\omega _0) }\right| = \left|{ {\mathcal {V}}_{\phi } f_{\pm } \left( R_{-\alpha }(x-x_0,\omega -\omega _0)\right) }\right|, \end{aligned}$$
(5)

for \(x,\omega \in {\mathbb {R}}\), where we have used the covariance property of the Gabor transform (see [2, Lemma 3.1.3 on p. 41]) in the second step, the invariance of the Gaussian under the fractional Fourier transform in the third step and Lemma 1 in the fourth and final step. It follows immediately from the above consideration and Lemma 2 that

$$\begin{aligned} \left|{{\mathcal {V}}_\phi f_+^{\alpha ,\lambda }}\right| = \left|{{\mathcal {V}}_\phi f_-^{\alpha ,\lambda }}\right| \text{ on } R_\alpha (a {\mathbb {Z}}\times {\mathbb {R}}) + \lambda . \end{aligned}$$

Additionally, we may remember the proof of Lemma 2 and estimate that

$$\begin{aligned} \left|{{\mathcal {V}}_\phi f_{\pm }(x,\omega ) }\right|&=\frac{\mathrm{e}^{-\frac{\pi }{8a^2}}}{2 \sqrt{2}} \left|{ ( 1 \mp \mathrm{i}) \mathrm{e}^{\frac{\pi }{2a} \left( \omega + \mathrm{i}x \right) } + ( 1 \pm \mathrm{i}) \cdot \mathrm{e}^{-\frac{\pi }{2a}\left( \omega + \mathrm{i}x \right) } }\right| \mathrm{e}^{-\frac{\pi }{2}\left( x^2 + \omega ^2\right) } \\&\le \mathrm{e}^{-\frac{\pi }{8a^2}} \mathrm{e}^{\frac{\pi }{2a} \left|{\omega }\right|} \cdot \mathrm{e}^{-\frac{\pi }{2}\left( x^2 + \omega ^2\right) }, \end{aligned}$$

for \(x,\omega \in {\mathbb {R}}\). It follows that

$$\begin{aligned} \left|{{\mathcal {V}}_\phi f_{\pm }^{\alpha ,\lambda }(x,\omega ) }\right|&=\left|{{\mathcal {V}}_{\phi } f_{\pm } \left( R_{-\alpha } (x-x_0,\omega -\omega _0)\right) }\right| \\&\le \mathrm{e}^{-\frac{\pi }{8a^2}} \mathrm{e}^{\frac{\pi }{2a} \left|{(x-x_0) \sin \alpha + (\omega -\omega _0) \cos \alpha }\right|} \cdot \mathrm{e}^{-\frac{\pi }{2}\left( (x-x_0)^2 + (\omega -\omega _0)^2\right) }\\&\le \mathrm{e}^{-\frac{\pi }{8a^2}} \mathrm{e}^{\frac{\pi }{2a} \left( \left|{x-x_0}\right| + \left|{\omega -\omega _0}\right| \right) } \cdot \mathrm{e}^{-\frac{\pi }{2}\left( (x-x_0)^2 + (\omega -\omega _0)^2\right) }. \end{aligned}$$

Let us now consider \(\epsilon > 0\) arbitrary but fixed. It is then readily seen that there exists \(C_\epsilon \ge 1\) depending on \(\epsilon \) as well as a, \(x_0\) and \(\omega _0\) such that

$$\begin{aligned} \left|{{\mathcal {V}}_\phi f_{\pm }^{\alpha ,\lambda }(x,\omega )}\right| \le C_\epsilon \cdot \mathrm{e}^{-\left( \frac{\pi }{2} -\epsilon \right) \left( x^2 + \omega ^2 \right) }, \qquad x,\omega \in {\mathbb {R}}. \end{aligned}$$

\(\square \)

Remark 5

The reader might note that we could have directly constructed the functions \(f_\pm ^{\alpha ,\lambda }\) using the Hadamard factorisation theorem as well as the relation between the Gabor and the Bargmann transform. This is indeed how we first constructed the examples \(f_\pm ^{\alpha ,\lambda }\). The formulation involving the fractional Fourier transform was suggested by the first reviewer and it has allowed for a much shorter and more elegant presentation of the paper.