Idempotent Fourier multipliers acting contractively on $H^p$ spaces

Abstract

We describe the idempotent Fourier multipliers that act contractively on $H^p$ spaces of the d-dimensional torus $\mathbb {T}^d$ for $d\ge 1$ and $1\le p \le \infty$. When p is not an even integer, such multipliers are just restrictions of contractive idempotent multipliers on $L^p$ spaces, which in turn can be described by suitably combining results of Rudin and Andô. When $p=2(n+1)$, with n a positive integer, contractivity depends in an interesting geometric way on n, d, and the dimension of the set of frequencies associated with the multiplier. Our results allow us to construct a linear operator that is densely defined on $H^p(\mathbb {T}^\infty )$ for every $1 \le p \le \infty$ and that extends to a bounded operator if and only if $p=2,4,\ldots ,2(n+1)$.

1 Introduction

This paper grew out of an attempt to clarify the precise scope and nature of certain contractive inequalities that have proven useful in the study of the Hardy spaces $H^p(\mathbb {T}^d)$ when $d\ge 1$ and $1\le p \le \infty$. The inequalities in question can best be seen as instances of idempotent Fourier multipliers that act contractively on $H^p(\mathbb {T}^d)$, and our main purpose will therefore be to describe such multipliers.

Since any Fourier multiplier on $L^p(\mathbb {T}^d)$ induces a Fourier multiplier on $H^p(\mathbb {T}^d)$, it is natural to begin with the easier problem of describing idempotent Fourier multipliers acting contractively on $L^p(\mathbb {T}^d)$. To this end, we represent functions f in $L^p(\mathbb {T}^d)$ by their Fourier series $f(z) \sim \sum _{\alpha \in \mathbb {Z}^d} \widehat{f}(\alpha )\,z^\alpha$, where

$$\begin{aligned} \widehat{f}(\alpha ) := \int _{\mathbb {T}^d} f(z) \,\overline{z^\alpha }\,dm_d(z) \end{aligned}$$

and $m_d$ denotes the Haar measure of the d-dimensional torus $\mathbb {T}^d$. For $\Lambda$ a non-empty subset of $\mathbb {Z}^d$, we consider the operator $P_{\Lambda }$ that is densely defined on $L^p(\mathbb {T}^d)$ by the rule

$$\begin{aligned} P_\Lambda f(z) := \sum _{\alpha \in \Lambda } \widehat{f}(\alpha ) z^\alpha . \end{aligned}$$

The operator $P_\Lambda$ is an idempotent Fourier multiplier, since it corresponds to pointwise multiplication of the Fourier coefficients $\widehat{f}(\alpha )$ by the characteristic function of $\Lambda$. We will say that $\Lambda$ is a contractive projection set for $L^p(\mathbb {T}^d)$ when $P_\Lambda$ extends to a contraction on $L^p(\mathbb {T}^d)$. Following Rudin [Rud90], we say that a subset $\Lambda$ of $\mathbb {Z}^d$ is a coset in $\mathbb {Z}^d$ if $\Lambda$ is equal to the coset of a subgroup of $(\mathbb {Z}^d,+)$. The following result can be deduced by suitably combining arguments and results due to Rudin [Rud90] and Andô [And66]. Note that the case $p=2$ is omitted in the statement, since every non-empty subset of $\mathbb {Z}^d$ is trivially a contractive projection set for $L^2(\mathbb {T}^d)$.

Theorem 1.1

   Let d be a non-negative integer and fix $1 \le p \le \infty$, $p\ne 2$. A subset $\Lambda$ of $\mathbb {Z}^d$ is a contractive projection set for $L^p(\mathbb {T}^d)$ if and only if $\Lambda$ is a coset in $\mathbb {Z}^d$.

Theorem 1.1 has a striking bearing on the question of when $P_\Lambda$ extends to a bounded operator on $L^1(\mathbb T^d)$. Indeed, results of Helson [Hel53] in dimension 1 and Rudin [Rud59] in higher dimensions show that $P_\Lambda$ defines a bounded linear operator on $L^1(\mathbb {T}^d)$ if and only if $\Lambda = \bigcup _{k=1}^n \Lambda _k$, where $\Lambda _1,\ldots ,\Lambda _n$ are cosets of $\mathbb {Z}^d$. By a celebrated paper of Cohen [Coh60], this result extends to $L^1(G)$ for G a compact abelian group. It remains however a difficult open problem to describe the sets $\Lambda$ that yield bounded operators $P_{\Lambda }$ on $L^p(\mathbb {T}^d)$ when $p\ne 1,2$.

We mention two examples of frequently encountered inequalities that are covered by Theorem 1.1. The first of these is an inequality of F. Wiener that appeared already in Bohr’s classical work on what later became known as the Bohr radius [Boh14]. In our terminology, this is just the case $d=1$ of Theorem 1.1. See [MSUV15, Section 1.7] for a recent function theoretic application and [BK97] for a d-dimensional version of it. The second example inequality deals with the restriction to the m-homogeneous terms of a power series in d variables. This is again a special case of Theorem 1.1, with the dimension of the coset being strictly smaller than the dimension of the ambient space $\mathbb {Z}^d$. We refer to [BQS16, BS16] and [CG86, Section 9] for respectively an operator, number, and function theoretic application of the corresponding contractive inequality.

Our main theorem shows that there are contractive projection sets for $H^p(\mathbb {T}^d)$ that are not covered by Theorem 1.1 when p is an even integer $\ge 4$. To state this result, we recall first that $H^p(\mathbb {T}^d)$ is the subspace of $L^p(\mathbb {T}^d)$ comprised of functions f such that $\widehat{f}(\alpha )=0$ for every $\alpha$ in $\mathbb {Z}^d \setminus \mathbb {N}_0^d$, where $\mathbb {N}_0 := \{0,1,2,\ldots \}$. We will say that a subset $\Gamma$ of $\mathbb {N}_0^d$ is a contractive projection set for $H^p(\mathbb {T}^d)$ if $P_\Gamma$ extends to a contraction on $H^p(\mathbb {T}^d)$. Since $H^p(\mathbb {T}^d)$ is a subspace of $L^p(\mathbb {T}^d)$, we get the following immediate consequence of Theorem 1.1. If $\Lambda$ is a coset in $\mathbb {Z}^d$, then $\Lambda \cap \mathbb {N}_0^d$ is a contractive projection set for $H^p(\mathbb {T}^d)$. We are interested in knowing if there are other contractive projection sets for $H^p(\mathbb T^d)$. It turns out that the dimension of the affine span of $\Gamma$, henceforth called $\dim (\Gamma )$ or the dimension of $\Gamma$, plays a nontrivial role in this problem, and we therefore make the following definition.

Definition

Suppose that $1\le k \le d$. We say that $H^p(\mathbb {T}^d)$ enjoys the contractive restriction property of dimension k if every k-dimensional contractive projection set for $H^p(\mathbb {T}^d)$ is of the form $\Lambda \cap \mathbb {N}_0^d$ with $\Lambda$ a coset in $\mathbb Z^d$.

Now our main result reads as follows.

Theorem 1.2

   Suppose that $1\le p \le \infty$.

• (a) If $d=2$ or $k=1$, then $H^p(\mathbb {T}^d)$ enjoys the contractive restriction property of dimension k if and only if $p\ne 2$.

• (b) If either $d=k=3$ or $d\ge 3$ and $k=2$, then $H^p(\mathbb {T}^d)$ enjoys the contractive restriction property of dimension k if and only if $p\ne 2, 4$.

• (c) If $d\ge 4$ and $k\ge 3$, then $H^p(\mathbb {T}^d)$ enjoys the contractive restriction property of dimension k if and only if p is not an even integer.

One may think suggestively of the case $d\ge 4$ and $k\ge 3$ as exhibiting higher-dimensional behavior. We will see that the hardest part of the theorem is item (b) which can be thought of as representing the two cases of intermediate dimension, namely $d=k=3$ and $d\ge 3$, $k=2$.

As regards the variation in p, the simplest part of the proof of Theorem 1.2 is the case $p=\infty$, because we can construct explicit examples demonstrating that any contractive projection set must be the restriction of a coset to $\mathbb {N}_0^d$. This is made possible by the fact that the norm of $H^\infty (\mathbb {T}^d)$ is easy to understand. In the case $1 \le p < \infty$, we will by contrast reformulate the problem using duality arguments (see e.g. Shapiro’s monograph [Sha71, Section 4.2]). In this approach, it is crucial to understand the Fourier coefficients of

$$\begin{aligned} |f|^{p-2} f \end{aligned}$$

in terms of the Fourier coefficients of f. It is clear that this problem takes on a completely different character when p is an even integer, in which case we have an interesting geometric description of the contractive projection sets that depend crucially on p.

Suppose that $\Gamma$ is a non-empty subset of $\mathbb {N}_0^d$, and let $\Lambda (\Gamma )$ denote the coset in $\mathbb {Z}^d$ generated by $\Gamma$. We can represent every $\lambda$ in $\Lambda (\Gamma )$ as a finite linear combination

$$\begin{aligned} \lambda = \gamma + \sum _{\begin{array}{c} \alpha \in \Gamma \\ \alpha \ne \gamma \end{array}} m_{\gamma ,\alpha } (\alpha -\gamma ) , \end{aligned}$$

(1.1)

where $\gamma$ is any element in $\Gamma$ and $m_{\gamma ,\alpha }$ are integers.

Definition

Let $\Gamma$ be a non-empty subset of $\mathbb {N}_0^d$ and suppose that $\lambda$ is in $\Lambda (\Gamma )$. The distance from $\Gamma$ to $\lambda$ is

$$\begin{aligned} d(\Gamma ,\lambda ) := \inf \max \left( \sum _{m_{\gamma ,\alpha }>0} m_{\gamma ,\alpha }, -\sum _{m_{\gamma ,\alpha }<0} m_{\gamma ,\alpha }\right) \end{aligned}$$

where the infimum is taken over all possible representations (1.1) of $\lambda$. For a non-negative integer n, the n-extension of $\Gamma$ is

$$\begin{aligned} E_n(\Gamma ) := \{\lambda \in \Lambda (\Gamma )\cap \mathbb {N}_0^d\,:\,d(\Gamma ,\lambda ) \le n \}. \end{aligned}$$

Fig. 1

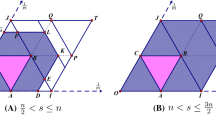
Points $\lambda$ which satisfy $d(\Gamma ,\lambda )=1$ and $d(\Gamma ,\lambda )=2$ for $\Gamma =\{(3,0,0),(0,3,0),(1,1,1)\}$, represented in the projected plane defined by $z=3-x-y$. The shaded triangle represents the intersection of this plane and the narrow cone. Note that (0, 0, 3) is in $E_2(\Gamma )$, so $E_2(\Gamma )=\Lambda (\Gamma )\cap \mathbb {N}_0^3$. However (0, 0, 3) is not in $E_1(\Gamma )$, so $E_1(\Gamma )=\Gamma$.

Clearly, $\Lambda (E_n(\Gamma ))=\Lambda (\Gamma )$ for every $n\ge 1$. Moreover, we find that $\Gamma = \Lambda \cap \mathbb {N}_0^d$ for a coset $\Lambda$ in $\mathbb {Z}^d$ if and only if

$$\begin{aligned} \Gamma = \bigcup _{n=1}^\infty E_n(\Gamma ). \end{aligned}$$

See Figure 1 for an example illustrating the possibility that $E_2(\Gamma ) \ne E_1(\Gamma )=\Gamma$.

The proof of Theorem 1.2 in the case that p is an even integer, which is the most difficult case, is based on the following result.

Theorem 1.3

   Let d be a positive integer and n be a non-negative integer. A set $\Gamma$ in $\mathbb {N}_0^d$ is a contractive projection set for $H^{2(n+1)}(\mathbb {T}^d)$ if and only if $E_n(\Gamma )=\Gamma$.

Theorem 1.3 gives rise to an effective algorithm for checking whether a finite subset $\Gamma$ of $\mathbb {N}_0^d$ is a contractive projection set for $H^{2(n+1)}(\mathbb {T}^d)$.

The d and k dependence of Theorem 1.2 appears when we operationalize the condition of Theorem 1.3. Inspired by a suggestive terminology introduced by Helson [Hel06], we will sometimes refer to $\mathbb {N}_0^d$ as the narrow cone in $\mathbb {Z}^d$ to visualize how the geometry changes when d increases: $\mathbb {N}_0^d$ becomes narrower in $\mathbb {Z}^d$, and this permits more sets $\Gamma$ to enjoy the crucial property that $E_n(\Gamma )=\Gamma$.

Two of our examples reflecting the kind of narrowness just alluded to, has an interesting application in the limiting case $d=\infty$. To state this final result of the present paper, we first define $\mathbb {T}^\infty$ as the countably infinite product of the torus $\mathbb {T}$ and equip it with its Haar measure $m_\infty$. The dual group of $\mathbb {T}^\infty$ is

$$\begin{aligned} \mathbb {Z}^{(\infty )} = \bigcup _{d=1}^\infty \mathbb {Z}^d \end{aligned}$$

in view of the natural inclusion $\mathbb {Z}^d \subseteq \mathbb {Z}^{d+1}$. Fix $1 \le p \le \infty$. Every f in $L^p(\mathbb {T}^\infty )$ can be represented as a Fourier series $f(z) \sim \sum _{\alpha \in \mathbb {Z}^{(\infty )}} \widehat{f}(\alpha )\,z^\alpha$, where

$$\begin{aligned} \widehat{f}(\alpha ) = \int _{\mathbb {T}^\infty } f(z)\,\overline{z^\alpha }\,dm_\infty (z). \end{aligned}$$

The Hardy space $H^p(\mathbb {T}^\infty )$ is the subspace of $L^p(\mathbb {T}^\infty )$ comprised of functions f such that $\widehat{f}(\alpha )=0$ for every $\alpha$ in $\mathbb {Z}^{(\infty )} \setminus \mathbb {N}_0^{(\infty )}$. It is not hard to see that Theorems 1.1, 1.2, and 1.3 extend to the infinite-dimensional torus.

Bayart and Mastyło [BM19] have recently demonstrated that there are no variants of the classical real and complex interpolation theorems for $H^p(\mathbb {T}^\infty )$ in contrast to the finite dimensional case. The following result strikingly exemplifies the impossibility of interpolating between Hardy spaces on the infinite-dimensional torus.

Theorem 1.4

   Fix an integer $n\ge 1$. There is a linear operator $T_n$ which is densely defined on $H^p(\mathbb {T}^\infty )$ for every $1 \le p \le \infty$, and which does not extend to a bounded operator on $H^p(\mathbb {T}^\infty )$ unless $p=2,4,\ldots ,2(n+1)$.

Our main interest in Theorem 1.4 stems from the Bohr correspondence, which allows us to translate results from Hardy spaces on the infinite-dimensional torus to Hardy spaces of Dirichlet series. Readers familiar with that field of study will immediately notice the partial analogy between Theorem 1.4 and the local embedding problem (see [SS09, Section 3] or Section 4 below). However, it should be stressed that the construction of Theorem 1.4 is purely multiplicative, while the local embedding problem concerns the interplay between the additive and multiplicative structure of the integers.

We close this introduction by giving a brief overview of the contents of the three additional sections of this paper. Section 2 contains an exposition of the proof of Theorem 1.1 and the proof of Theorem 1.2 in the case $p=\infty$. The body of the paper is Section 3 which deals with contractive projection sets for $H^p(\mathbb {T}^d)$ and contains the proof of Theorems 1.2 and 1.3 for $p<\infty$. In the final Section 4, we establish Theorem 1.4 and discuss our results in the context of Hardy spaces of Dirichlet series.

2 Contractive Projection Sets for $L^p(\mathbb {T}^d)$

2.1 Proof of Theorem 1.1.

The purpose of this section is to present a self-contained proof of Theorem 1.1. As mentioned above, this can be achieved by combining arguments and results due to Rudin [Rud90] and Andô [And66]. For expositional reasons, we have nevertheless chosen to furnish a complete proof.

Suppose that $\Lambda$ is a non-empty subset of $\mathbb {Z}^d$. We begin by noting that we may assume without loss of generality that 0 is in $\Lambda$. Indeed, suppose that this is not the case. Fix some $\lambda$ in $\Lambda$ and consider the translated set

$$\begin{aligned} \Lambda -\lambda := \left\{ \alpha \in \mathbb {Z}^d \,:\, \alpha +\lambda \in \Lambda \right\} \end{aligned}$$

which clearly contains 0. Define $M_\lambda$ on $L^p(\mathbb {T}^d)$ by $M_\lambda f(z) := z^\lambda f(z)$. Evidently, $M_\lambda$ is an isometric isomorphism on $L^p(\mathbb {T}^d)$. Note also that

$$\begin{aligned} P_{\Lambda } M_\lambda = M_\lambda P_{\Lambda -\lambda }, \end{aligned}$$

(2.1)

which implies at once that $\Lambda$ is a contractive projection set for $L^p(\mathbb {T}^d)$ if and only if $\Lambda -\lambda$ is a contractive projection set for $L^p(\mathbb {T}^d)$.

The following part of the proof is from Section 3.1.2 and Section 3.2.4 in Rudin’s monograph [Rud90], where the analogous statement is established for $L^1(G)$ with G a compact abelian group. This part of Rudin’s argument extends to $1< p \le \infty$, $p\ne 2$, without modification.

Proof of Theorem 1.1: Sufficiency

As noted above, we may restrict our attention to the case that $\Lambda$ is a subgroup of $\mathbb {Z}^d$ by translating a coset if necessary.

We will require some preliminary results regarding $\mathbb {T}^d$ and $\mathbb {Z}^d$. Recall that $\mathbb {T}^d$ is a compact abelian group whose dual group is $\mathbb {Z}^d$. Suppose that $\Lambda$ is a subgroup of $\mathbb {Z}^d$. The annihilator

$$\begin{aligned} \Lambda ^\perp := \left\{ z \in \mathbb {T}^d \,:\, z^\alpha =1 \text { for every } \alpha \text { in } \Lambda \right\} \end{aligned}$$

is the dual group of the coset group $\mathbb {Z}^d/\Lambda$ (see e.g. [Rud90, Theorem 2.1.2]). Since $\Lambda ^\perp$ is a closed subgroup of $\mathbb {T}^d$, it is a compact abelian group whose Haar measure we shall denote by $\mu$. By the duality relations between $\mathbb {Z}^d/\Lambda$ and $\Lambda ^\perp$, we may represent the characteristic function of $\Lambda$ in $\mathbb {Z}^d$ as

$$\begin{aligned} \mathbf {1}_\Lambda (\alpha ) = \int _{\Lambda ^\perp } \zeta ^\alpha \,d\mu (\zeta ). \end{aligned}$$

For any f in $L^p(\mathbb {T}^d)$, set $f_\zeta (z) := f(\zeta _1 z_1, \zeta _2 z_2, \ldots , \zeta _d z_d)$. We now find that

$$\begin{aligned} P_\Lambda f(z) = \sum _{\alpha \in \Lambda } \widehat{f}(\alpha )\, z^\alpha = \sum _{\alpha \in \mathbb {Z}^d} \mathbf {1}_\Lambda (\alpha ) \widehat{f}(\alpha ) \, z^\alpha = \int _{\Lambda ^\perp } f_\zeta (z)\,d\mu (\zeta ). \end{aligned}$$

(2.2)

Taking the $L^p(\mathbb {T}^d)$ norm on both sides and combining Minkowski’s inequality and the fact that $\Vert f_\zeta \Vert _p=\Vert f\Vert _p$ for every $\zeta$ in $\mathbb {T}^d$, we see that

$$\begin{aligned} \Vert P_\Lambda f \Vert _p \le \Vert f\Vert _p \left( \mu (\Lambda ^\perp )\right) ^\frac{1}{p}= \Vert f\Vert _p, \end{aligned}$$

since $\mu$ is the Haar measure of $\Lambda ^\perp$. $\square$

Observe that (2.2) says that any projection with respect to a subgroup $\Lambda$ is in fact an averaging operator in $L^1(\mathbb {T}^d)$. Douglas [Dou65] proved that any projection in $L^1$ that fixes the constants, is in fact a conditional expectation with respect to a sigma-algebra.

Before we proceed with the proof that every contractive projection set in $L^p(\mathbb {T}^d)$ for $1 \le p \le \infty$, $p\ne 2$, is necessarily a coset in $\mathbb {Z}^d$, let us explain how F. Wiener’s projection and the m-homogeneous projection mentioned in the introduction fit into the framework of the proof presented above. Note that by Theorem 1.1, we see that Example 2.1 and Example 2.2 contain all the contractive projection sets for $L^p(\mathbb {T})$, since the only cosets in $\mathbb {Z}$ are the arithmetic progressions and the singletons.

Example 2.1

The contractive projection sets that correspond to F. Wiener’s projection, are the arithmetic progressions $\Lambda := r +k\mathbb {Z}$ for integers $k>1$ and $0 \le r < k$. The associated subgroup of $\mathbb {Z}$ is $k\mathbb {Z}$ and clearly

$$\begin{aligned} (k\mathbb {Z})^\perp = \big \{\omega _k^j \,:\, j=0,1,\ldots ,{k-1}\big \}, \end{aligned}$$

where $\omega _k = \exp (2\pi i /k)$. The Haar measure of $(k\mathbb {Z})^\perp$ is the normalized counting measure. Combining (2.1) and (2.2), we get the well-known formula

$$\begin{aligned} P_\Lambda f(z) = \frac{1}{k}\sum _{j=0}^{k-1} f(\omega _k^jz) \,\omega _k^{-jr} \end{aligned}$$

for f in $L^p(\mathbb {T})$.

Example 2.2

Fix $d\ge 1$. For an integer m, the m-homogeneous projection on $L^p(\mathbb {T}^d)$ corresponds to the contractive projection set

$$\begin{aligned} \Lambda _m := \big \{\alpha \in \mathbb {Z}^d \,:\, \alpha _1+\alpha _2+\cdots + \alpha _d = m\big \}. \end{aligned}$$

The associated subgroup of $\mathbb {Z}^d$ is $\Lambda _0$, so $\Lambda _0^\perp =\big \{z=(w,\ldots , w) \,:\, w\in \mathbb {T}\big \}$, and the Haar measure is $m_1$ on $\mathbb T$. Combining (2.1) and (2.2), we get

$$\begin{aligned} P_{\Lambda _m} f(z) = \int _{\mathbb {T}} f(z_1w,z_2w,\ldots ,z_d w) \,w^{-m}\,dm_1(w) \end{aligned}$$

for f in $L^p(\mathbb {T}^d)$.

By results in Section 1.4.1 and Section 3.2.3 in Rudin’s monograph [Rud90], it follows that if $\Gamma$ is a contractive projection set for $L^1(\mathbb {T}^d)$, then $\Gamma$ is necessarily a coset in $\mathbb {Z}^d$. This part of Rudin’s argument does not work for $p>1$. However, we can appeal to a general result of Andô [And66, Theorem 1] which states that any contractive projection on $L^p$ for $1<p<\infty$, $p\ne 2$, which fixes the constants, extends to a contractive projection on $L^1$. Hence any contractive projection set for $L^p(\mathbb {T}^d)$, for $1<p<\infty$, $p\ne 2$, must be a coset in $\mathbb {Z}^d$. The case $p=\infty$ is handled by Riesz–Thorin interpolation, since the linear operator $P_\Lambda$ is contractive on $L^p$ for $2<p<\infty$ when it is contractive on $L^2$ and $L^\infty$. These considerations also apply if $\mathbb {T}^d$ is replaced by a compact abelian group G.

To highlight the new difficulties that arise when we later treat the corresponding problem for $H^p(\mathbb {T}^d)$, we will present a direct proof of the necessity part of Theorem 1.1 below. We shall require two preliminary estimates. We note in passing that it is possible to obtain similar estimates if $\mathbb {T}^d$ is replaced by a compact abelian group G, thereby sidestepping the need for Andô’s theorem and Riesz–Thorin interpolation.

Lemma 2.3

Fix $1 \le p \le \infty$, $p\ne 2$, and set $c_p := 2/p-1$. Then

$$\begin{aligned} \Vert c_p \varepsilon \overline{z}+1+\varepsilon z \Vert _p < \Vert 1+\varepsilon z \Vert _p \end{aligned}$$

(2.3)

for every sufficiently small $\varepsilon >0$.

Proof

Let c be a real number and compute

$$\begin{aligned} |c \varepsilon \overline{z}+1+\varepsilon z|^2 = 1 + \varepsilon (1+c) (z+\overline{z}) + \varepsilon ^2 \left( (1+c^2) + c(z^2+{\overline{z}^2}) \right) . \end{aligned}$$

(2.4)

Using the binomial expansion, we find that

$$\begin{aligned} |c \varepsilon \overline{z}+1+\varepsilon z|^p = 1&+ \varepsilon \,\frac{p}{2}(1+c) (z+\overline{z}) \\&+ \varepsilon ^2 \left( \frac{p}{2}\left( (1+c^2) + c(z^2+{\overline{z}^2})\right) + \left( {\begin{array}{c}p/2\\ 2\end{array}}\right) (1+c)^2 (z+\overline{z})^2\right) \\&+O(\varepsilon ^3) \end{aligned}$$

for every sufficiently small $\varepsilon >0$. Integrating over $\mathbb {T}$ and simplifying, we get

$$\begin{aligned} \Vert c \varepsilon \overline{z}+1+\varepsilon z\Vert _p^p = 1 + \left( \frac{p^2}{4}(c+1-2/p)^2+p-1 \right) \varepsilon ^2 + O(\varepsilon ^3). \end{aligned}$$

If $1 \le p < \infty$ and $\varepsilon >0$ is sufficiently small, then the minimum is attained at $c=2/p-1$, which yields (2.3). It remains to deal with the case $p=\infty$. Inspecting (2.4) with $c=c_\infty =-1$, we find that the supremum is attained at $z = \pm i$. Consequently, (2.3) reduces in this case to

$$\begin{aligned} \sqrt{1+4\varepsilon ^2}<1+\varepsilon , \end{aligned}$$

which holds for all sufficiently small $\varepsilon >0$. $\square$

Lemma 2.4

Fix $1 \le p < \infty$, $p\ne 2$, and set $c_p := 1-p/2$. Then

$$\begin{aligned} \Vert 1+ \varepsilon (z_1+z_2) + c_p \,\varepsilon ^2 z_1 z_2\Vert _p&< \Vert 1+ \varepsilon (z_1+z_2)\Vert _p \end{aligned}$$

(2.5)

for every sufficiently small $\varepsilon >0$. Moreover,

$$\begin{aligned} \Vert 1+z_1+z_2-z_1z_2\Vert _\infty&< \Vert 1+z_1+z_2\Vert _\infty . \end{aligned}$$

(2.6)

Proof

Let c be a fixed real number. For sufficiently small $\varepsilon >0$, expand

$$\begin{aligned} \big (1+ \varepsilon (z_1+z_2) + c \,\varepsilon ^2 z_1 z_2\big )^{p/2} = \sum _{j=0}^\infty \left( {\begin{array}{c}p/2\\ j\end{array}}\right) \big (\varepsilon (z_1+z_2) + c \,\varepsilon ^2 z_1 z_2\big )^j. \end{aligned}$$

(2.7)

In this expansion, any monomial of degree m will have $\varepsilon ^m$ in front of it. Hence we can rearrange in terms of m-homogeneous polynomials to obtain

$$\begin{aligned} \big (1+\varepsilon (z_1+z_2)+c\varepsilon ^2z_1 z_2\big )^{p/2} = \sum _{m=0}^\infty \varepsilon ^m P_m(z). \end{aligned}$$

(2.8)

Here $P_m$ is an m-homogeneous polynomial whose coefficients do not depend on $\varepsilon$. Since $P_m \perp P_n$ in $L^2(\mathbb {T}^2)$ for $m \ne n$, we get from (2.8) that

$$\begin{aligned} \Vert 1+\varepsilon (z_1+z_2)+c \varepsilon ^2z_1 z_2\Vert _p^p = \sum _{m=0}^\infty \varepsilon ^{2m} \Vert P_m\Vert _2^2. \end{aligned}$$

(2.9)

We need the first three terms, which we can read off from (2.7). They are

$$\begin{aligned} P_0(z)&= 1, \\ P_1(z)&= \frac{p}{2}(z_1+z_2), \\ P_2(z)&= \frac{p}{2}(c+p/2-1)z_1z_2 + \left( {\begin{array}{c}p/2\\ 2\end{array}}\right) (z_1^2+z_2^2). \end{aligned}$$

Inserting this into (2.9) we find that

$$\begin{aligned} \Vert 1+\varepsilon (z_1+z_2)+c \varepsilon ^2z_1 z_2\Vert _p^p = 1&+ \frac{p^2}{2} \varepsilon ^2 \\&+ \frac{p^2}{4} \left( (c+p/2-1)^2 + \frac{(p-2)^2}{8}\right) \varepsilon ^4 +O(\varepsilon ^6). \end{aligned}$$

Hence if $1 \le p < \infty$, $p\ne 2$, and $\varepsilon >0$ is sufficiently small, then the minimum is attained at $c=1-p/2$, and (2.5) follows.

It remains to establish (2.6). The right-hand side is clearly equal to 3. For the left-hand side, we rewrite $1+z_1+z_2-z_1z_2 = 1+z_2 + z_1(1-z_2)$ which implies that

$$\begin{aligned} \Vert 1+z_1+z_2-z_1z_2\Vert _\infty = \sup _{z_2 \in \mathbb {T}} \left( |1+z_2|+|1-z_2|\right) = 2\sqrt{2}. \end{aligned}$$

Hence (2.6) holds since the right-hand side equals 3. $\square$

Proof Theorem 1.1: Necessity

Fix $1 \le p < \infty$, $p\ne 2$, and suppose that $\Lambda$ is a contractive projection set for $L^p(\mathbb {T}^d)$. As above, we may assume without loss of generality that 0 is in $\Lambda$, and we are therefore required to prove that $\Lambda$ is a subgroup of $\mathbb {Z}^d$. If $\Lambda =\{0\}$, there is nothing to prove, so we shall assume that there is at least one element $\ne 0$ in $\Lambda$ and use this to establish that $\Lambda$ must be closed under the group operations.

Suppose that $\alpha$ is in $\Lambda \setminus \{0\}$. By substituting $z = z^\alpha$ in Lemma 2.3 and using that $P_\Lambda$ is a contraction on $L^p(\mathbb {T}^d)$, we conclude at once that $-\alpha$ must be in $\Lambda$. Suppose next that $\alpha$ and $\beta$ are two (not necessarily distinct) elements in $\Lambda \setminus \{0\}$. We need to show that $\alpha +\beta$ is in $\Lambda$. There are two cases.

If $j \alpha \ne k \beta$ for every pair of integers $j,k\ne 0$, then we may substitute $z_1 = z^\alpha$ and $z_2 = z^\beta$ in Lemma 2.4. The fact that $P_\Lambda$ is a contraction on $L^p(\mathbb {T}^d)$ implies at once that $\alpha +\beta$ is in $\Lambda$, since $z_1 z_2 = z^{\alpha +\beta }$.

If $j \alpha = k \beta$ for integers $j,k\ne 0$, then we may write $\alpha = a \gamma$ and $\beta = b\gamma$, where a, b are integers and $\gamma$ in $\mathbb {Z}^d$ satisfies $\gcd (\gamma _1,\gamma _2,\ldots ,\gamma _d)=1$. We will prove that if $P_\Lambda$ is a contraction on $L^p(\mathbb {T}^d)$, then $\Lambda$ must contain all integer multiples of $\gcd (a,b)\gamma$. In particular, $\alpha +\beta = (a+b)\gamma$ will be in $\Lambda$.

If $n\gcd (a,b)\gamma$ and $(n+1)\gcd (a,b)\gamma$ are in $\Lambda$, then we may appeal to Lemma 2.3 to see that $(n+2) \gcd (a,b)\gamma$ and $(n-1) \gcd (a,b)\gamma$ must be in $\Lambda$. Hence it is sufficient to establish that $\gcd (a,b) \gamma$ is in $\Lambda$.

To prove this, we use a modified Euclidean algorithm. We identify the integer n with the point $n \gcd (a,b) \gamma$ and start with the integers $a_1=a/\gcd (a,b)$ and $b_1=b/\gcd (a,b)$. We may assume without loss of generality that $0<a_1<b_1$, since if $a_1=b_1$, there is nothing to do. By Lemma 2.3, we know that $c_1 = 2a_1 - b_1$ is in $\Lambda$. We also see that $\gcd (a_1,b_1)=\gcd (a_1,c_1)$ and $0 \le |c_1|<b_1$. If $c_1=0$, then $a_1|b_1$ and $\gcd (a,b)=a$. If $|c_1|>0$, then $\max (a_1,b_1)>\max (a_1,|c_1|)$ and we repeat the procedure starting with $a_1$ and $|c_1|$. $\square$

2.2 Proof of Theorem 1.2 for $p=\infty$.

Since $H^p(\mathbb {T}^d)$ is a subspace of $L^p(\mathbb {T}^d)$, we know from Theorem 1.1 that if $\Gamma$ is the restriction of a coset in $\mathbb {Z}^d$ to $\mathbb {N}_0^d$, then $\Gamma$ is a contractive projection set for $H^p(\mathbb {T}^d)$. In this case, $\Gamma = \Lambda (\Gamma ) \cap \mathbb {N}_0^d$, where we recall that $\Lambda (\Gamma )$ denotes the coset generated by $\Gamma$.

Let us take a look at how Lemmas 2.3 and 2.4 can be applied in the context of $H^p(\mathbb {T}^d)$. Pick three affinely independent points $\alpha ,\beta ,\gamma$ from $\Gamma$. Consider the function $f(z) = c \varepsilon \overline{z}+1+\varepsilon z$ from Lemma 2.3. By replacing f by

$$\begin{aligned} g(z) := z^\beta f\left( z^{\alpha -\beta }\right) = c \varepsilon z^{2\beta -\alpha } + z^\beta + \varepsilon z^\alpha , \end{aligned}$$

we see that Lemma 2.3 implies that if $\Gamma$ is a contractive projection set for $H^p(\mathbb {T}^d)$ and the point $2\beta -\alpha$ is in $\mathbb {N}_0^d$, then it must be included in $\Gamma$. Geometrically, $2\beta -\alpha$ is the point obtained by linear reflection of $\alpha$ through $\beta$. By similar considerations starting from Lemma 2.4, we also find that if the point $\alpha + (\beta -\alpha ) + (\gamma -\alpha )$ is in $\mathbb {N}_0^3$, then it must be included in $\Gamma$ whenever $\Gamma$ is a contractive projection set. Geometrically, this new point is obtained by triangular reflection of $\alpha$ through $\beta$ and $\gamma$.

Figure 2 contains all the points obtained by linear and triangular reflections starting from the set $\Gamma = \{(3,0,0),(0,3,0),(1,1,1)\}$. From the figure, we see that the necessary conditions derived from Lemmas 2.3 and 2.4 provide no insight into whether this $\Gamma$ is a contractive projection set for $H^p(\mathbb {T}^3)$.

Moreover, when comparing Figures 1 and 2 (which are based on the same initial set $\Gamma$), we see that the linear and triangular reflections in Figure 2 correspond precisely to the points in $E_1(\Gamma )$. This is not a coincidence. It is easy to verify that every 1-extension is the same as a linear reflection or a triangular reflection. In the latter case, we can see this by rewriting

$$\begin{aligned} \alpha + (\beta -\alpha ) + (\gamma -\alpha )=\beta +(\beta -\alpha )-(\beta -\gamma ). \end{aligned}$$

Is it therefore possible to prove Theorem 1.2 (a) using Lemmas 2.3 and 2.4.

To see what additional estimates are required to handle case (b) and (c) of Theorem 1.2, recall that every $\lambda$ in $\Lambda (\Gamma )$ can be represented as

$$\begin{aligned} \lambda = \gamma _0 + \sum _{j=1}^n m_j (\gamma _j-\gamma _0), \end{aligned}$$

(2.10)

where $m_j$ are integers and $\{\gamma _0,\gamma _1,\ldots ,\gamma _n\}$ is an affinely independent subset in $\Gamma$ for $n = \dim (\Lambda (\Gamma ))$. If we hope to prove Theorem 1.2 by the same approach as Theorem 1.1, we would require estimates for every representation (2.10).

In the case $p=\infty$, we may actually establish the additional estimates in one fell swoop. This is especially fortunate since the duality techniques that we will employ in the next section to study the case $1 \le p < \infty$, $p\ne 2$, do not apply when $p=\infty$.

Fig. 2

The points $\lambda$ obtained by linear and triangular reflection starting from the set $\Gamma =\{(3,0,0),(0,3,0),(1,1,1)\}$, represented in the projected plane defined by $z=3-x-y$. The shaded triangle represents the intersection of this plane and the narrow cone. Note that none of the points obtained are in $\mathbb {N}_0^3$ and that the point (0, 0, 3) is not obtained.

Lemma 2.5

Fix any $\alpha$ in $\mathbb {Z}^d$. Then

$$\begin{aligned} \Bigg \Vert d + \sum _{j=1}^d z_j - \varepsilon z^\alpha \Bigg \Vert _\infty < \Bigg \Vert d + \sum _{j=1}^d z_j\Bigg \Vert _\infty \end{aligned}$$

(2.11)

for every sufficiently small $\varepsilon >0$.

Proof

The right-hand side of (2.11) is plainly equal to 2d, so it suffices to show that the left-hand side is strictly less than 2d for some sufficiently small $\varepsilon >0$. By the triangle inequality, we find that

$$\begin{aligned} \Bigg |d + \sum _{j=1}^d z_j - \varepsilon z^\alpha \Bigg | \le 2(d-1)+|1+z_j|+\varepsilon \end{aligned}$$

for any $j=1,2,\ldots ,d$. Suppose that the supremum on the left-hand side of (2.11) may be attained for $|1+z_j| \le 2(1-\varepsilon )$ for some j. Then, clearly, the left-hand side is equal to $2d-\varepsilon$, and we are done. Suppose therefore that

$$\begin{aligned} \Bigg \Vert d + \sum _{j=1}^d z_j - \varepsilon z^\alpha \Bigg \Vert _\infty = \sup _{\begin{array}{c} z \in \mathbb {T}^d \\ |1+z_j|\ge 2(1-\varepsilon ) \end{array}}\Bigg |d + \sum _{j=1}^d z_j - \varepsilon z^\alpha \Bigg |. \end{aligned}$$

To handle this case, we first estimate

$$\begin{aligned} \sup _{\begin{array}{c} z \in \mathbb {T}^d \\ |1+z_j|\ge 2(1-\varepsilon ) \end{array}}\Bigg |d + \sum _{j=1}^d z_j - \varepsilon z^\alpha \Bigg | \le 2(d-1) + \sup _{\begin{array}{c} z \in \mathbb {T}^d \\ |1+z_j|\ge 2(1-\varepsilon ) \end{array}} \left| 1+z_1 - \varepsilon z^\alpha \right| . \end{aligned}$$

Hence we are done if we can prove that

$$\begin{aligned} \sup _{\begin{array}{c} z \in \mathbb {T}^d \\ |1+z_j|\ge 2(1-\varepsilon ) \end{array}} \left| 1+z_1 - \varepsilon z^\alpha \right| < 2 \end{aligned}$$

(2.12)

for some sufficiently small $\varepsilon >0$. To this end, we see that when $0<\varepsilon <1$, we have

$$\begin{aligned} |1+z_j| \ge 2(1-\varepsilon ) \qquad \Longleftrightarrow \qquad |\theta _j| \le 2\arccos (1-\varepsilon ). \end{aligned}$$

Hence, if $|1+z_j| \ge (2-\varepsilon )$, then certainly $|\theta _j| \le 4 \sqrt{\varepsilon }$. If this estimate holds for every $j=1,2,\ldots ,d$ and $z^\alpha = e^{i\vartheta }$, then $|\vartheta | \le 4|\alpha | \sqrt{\varepsilon }$. By expanding and using Taylor’s theorem, we find that

$$\begin{aligned} \left| 1+z_j - \varepsilon z^\alpha \right| ^2&= (1+\cos {\theta _j}-\varepsilon \cos {\vartheta })^2 + (\sin {\vartheta _j}-\varepsilon \sin {\vartheta })^2 \\&= 2 + 2\cos (\theta _j) + \varepsilon ^2 -2 \varepsilon \big ((1+\cos {\theta _j})\cos {\vartheta }-\varepsilon \sin {\theta _j}\sin {\vartheta }\big ) \\&= 4 - 4\varepsilon - \theta _j^2 + O(\varepsilon ^2), \end{aligned}$$

which establishes (2.12) for every sufficiently small $\varepsilon >0$. $\square$

Proof of Theorem 1.2

for $p=\infty$. Suppose that $\Gamma$ is not the restriction of a coset in $\mathbb {Z}^d$ to $\mathbb {N}_0^d$. Hence we can find $\lambda$ in $\left( \Lambda (\Gamma ) \cap \mathbb {N}_0^d\right) \setminus \Gamma$. By (2.10) we write

$$\begin{aligned} \lambda = \gamma _0 + \sum _{j=1}^n m_j (\gamma _j-\gamma _0), \end{aligned}$$

where $m_j$ are integers and $\{\gamma _0,\gamma _1,\ldots ,\gamma _n\}$ is an affinely independent set in $\Gamma$. Let

$$\begin{aligned} f_1(z) = n + \sum _{j=1}^n z_j -\varepsilon z^{\alpha },\qquad f_2(z) =n + \sum _{j=1}^n z_j \end{aligned}$$

be the functions from Lemma 2.5 with $\alpha =(m_1,m_2,\ldots ,m_n)$ and define

$$\begin{aligned} g_i(z) = z^{\gamma _0} f_i\left( z^{\gamma _1-\gamma _0},\,z^{\gamma _2-\gamma _0},\,\ldots ,\,z^{ \gamma _n-\gamma _0}\right) , \quad i=1,2. \end{aligned}$$

Since $\{\gamma _0,\gamma _1,\ldots ,\gamma _n\}$ is an affinely independent set, the estimates of Lemma 2.5 imply that $\Vert g_1\Vert _\infty < \Vert g_2\Vert _\infty$. Hence $\Gamma$ is not a contractive projection set for $H^\infty (\mathbb {T}^d)$.

$\square$

3 Contractive Projection Sets for $H^p(\mathbb {T}^d)$ with $1\le p<\infty$

3.1 Overview.

This section is devoted to the proof of Theorem 1.2 for $p < \infty$. We begin in the next subsection by reformulating the problem in terms of duality. We then record some immediate consequences, which include the proof of Theorem 1.3 and the verification of Theorem 1.2 when $k=1$ and when p not even integer.

Section 3.2 sets the stage for the most substantial part of the proof of Theorem 1.2 which splits naturally into three parts:

• Section 3.3: The necessity of the conditions in part (b) and (c);

• Section 3.4: The sufficiency of the case $d\ge 3$ and $k=2$;

• Section 3.5: The sufficiency of the cases $d=k=2$ and $d=k=3$.

The necessity part requires four examples, while the two sufficiency parts rely on making appropriate extensions of a given subset of $\mathbb N_0^d$ in terms of a sequence of 1- or 2-extensions. Both constructions are quite intricate in the case of 2-extensions, and they also differ substantially. The arguments used in the case $d\ge 3$ and $k=2$ combine geometric and arithmetic considerations, while those used in the case $d=k=3$, relying on linear algebra, are more of a combinatorial nature. Another notable distinction between the two cases is that the first deals primarily with finite sets, while the second is concerned with extensions of finite sets to infinite sets.

3.2 Duality reformulation with some immediate consequences.

The main tool for the case $p<\infty$ of Theorem 1.2 is the following result.

Lemma 3.1

Fix $1 \le p < \infty$ and $d\ge 1$. A set of frequencies $\Gamma$ in $\mathbb {N}_0^d$ is a contractive projection set for $H^p(\mathbb {T}^d)$ if and only if

$$\begin{aligned} \int _{\mathbb {T}^d} |f(z)|^{p-2} f(z) \, \overline{z^\lambda }\,dm_d(z) = 0 \end{aligned}$$

(3.1)

for every $f(z) = \sum _{\gamma \in \Gamma } a_\gamma z^\gamma$ in $H^p(\mathbb {T}^d)$ and every $\lambda$ in $\left( \Lambda (\Gamma ) \cap \mathbb {N}_0^d\right) \setminus \Gamma$.

Proof

A function f in $L^p(\mathbb T^d)$ is said to be orthogonal to a closed subspace Y of $L^p(\mathbb T^d)$ if

$$\begin{aligned} \Vert f\Vert _p \le \Vert f+h\Vert _p \end{aligned}$$

for every h in Y. We will use the following characterization of orthogonality due to Shapiro (see [Sha71, Theorems 4.2.1 and 4.2.2]): a function f is orthogonal to Y if and only if

$$\begin{aligned} \int _{\mathbb {T}^d} |f(z)|^{p-2} f(z) \, \overline{h(z)}\,dm_d(z) = 0, \end{aligned}$$

for every h in Y. When $p = 1$, this holds if in addition the zero set $\{f = 0\}$ has measure 0, which will be the case because the functions f that we consider are in $H^1(\mathbb T^d)$, and thus $\log |f|$ will be in $L^1(\mathbb T^d)$ (see [Rud69, Theorem 3.3.5]). We begin by proving the necessity of (3.1). Consider $f(z) = \sum _{\gamma \in \Gamma } a_\gamma z^\gamma$ in $H^p(\mathbb {T}^d)$ and for any $\lambda$ in $\left( \Lambda (\Gamma ) \cap \mathbb {N}_0^d\right) \setminus \Gamma$ take Y to be the one-dimensional space spanned by $z^\lambda$. Since $\Gamma$ is a contractive projection set, $\Vert f\Vert _p \le \Vert f+ c z^\lambda \Vert _p$ for any complex number c, thus f is orthogonal to Y, and (3.1) holds.

To prove the reverse implication, we start by noting that since $\Lambda (\Gamma )$ is a coset, $P_{\Lambda (\Gamma )}$ is a contraction on $L^p(\mathbb T^d)$ by Theorem 1.1. Thus writing $P_{\Gamma } = P_\Gamma P_{\Lambda (\Gamma )}$, we see that to prove that $P_\Gamma$ is a contraction on $H^p(\mathbb {T}^d)$, we just need to show that for any h in $H^p(\mathbb T^d)$ with Fourier coefficients supported on $\Lambda (\Gamma ) \cap \mathbb {N}_0^d$, we have $\Vert P_{\Gamma }h\Vert _p \le \Vert h\Vert _p$. In fact, since the polynomials form a dense subset of $H^p(\mathbb T^d)$ and $P_{\Lambda (\Gamma )} g$ is a polynomial whenever g is a polynomial, it suffices to prove this for an arbitrary polynomial h. If we define Y as the finite-dimensional subspace of $H^p(\mathbb {T}^d)$ spanned by $\{z^\lambda \}$ for $\lambda$ in the spectrum of h minus $\Gamma$, we may decompose h as $h=P_\Gamma h+r$, where r belongs to Y. By (3.1), $P_\Gamma h$ is orthogonal to Y, thus $\Vert P_{\Gamma }h\Vert _p \le \Vert P_{\Gamma }h+r \Vert _p$. $\square$

Proof of Theorem 1.2

for $p<\infty$ not an even integer If $\Gamma$ is not the restriction of a coset in $\mathbb {Z}^d$ to $\mathbb {N}_0^d$, there is some $\lambda$ in $\left( \Lambda (\Gamma ) \cap \mathbb {N}_0^d\right) \setminus \Gamma$. Set $n=\dim (\Lambda (\Gamma ))\ge 1$. There is an affinely independent subset $\{\gamma _0,\gamma _1,\ldots ,\gamma _n\}$ of $\Gamma$ which generates $\Lambda (\Gamma )$. In particular, we may write

$$\begin{aligned} \lambda = \gamma _0 + \sum _{j=1}^n m_j (\gamma _j-\gamma _0), \end{aligned}$$

where $m_j$ are integers. Since $\lambda$ is not in $\Gamma$, we may assume without loss of generality that $m_1>0$ by reordering $\{\gamma _0,\gamma _1,\ldots ,\gamma _n\}$ if necessary. Similarly, we may assume that there is some $1\le k_0 \le n$ such that $m_1,\ldots , m_{k_0} \ge 0$ and $m_{k_0+1},\ldots , m_n<0$. We set

$$\begin{aligned} m_+:= \sum _{j=1}^n \max (m_j,0), \qquad m_-:= -\sum _{j=1}^n \min (m_j,0) \qquad \text {and} \qquad M:=m_++m_-. \end{aligned}$$

Our assumptions imply that $m_+\ge 1$. Set

$$\begin{aligned} f(z) := z^{\gamma _0} + \varepsilon \sum _{j=1}^n z^{\gamma _j} \end{aligned}$$

for $0<\varepsilon <1/n$ and define $g(z) = \sum _{j=1}^n z^{\gamma _j-\gamma _0}$. By the binomial series, we obtain

$$\begin{aligned} |f(z)|^{p-2} = \sum _{k_1,k_2=0}^\infty \left( {\begin{array}{c}p/2-1\\ k_1\end{array}}\right) \left( {\begin{array}{c}p/2-1\\ k_2\end{array}}\right) \varepsilon ^{k_1+k_2} g(z)^{k_1} g(\overline{z})^{k_2}. \end{aligned}$$

Since p is not an even integer, none of the binomial coefficients vanish. Writing

$$\begin{aligned} f(z) = (1+\varepsilon g(z)) z^{\gamma _0}, \end{aligned}$$

we see that

$$\begin{aligned} F(\varepsilon ) := \int _{\mathbb {T}^d} |f(z)|^{p-2} f(z)\,\overline{z^\lambda }\,dm_d(z), \end{aligned}$$

is a non-trivial power series in $\varepsilon$. Indeed, we observe that

$$\begin{aligned} F(\varepsilon )=\sum _{k=M}^\infty c_k \varepsilon ^{k}, \end{aligned}$$

where

$$\begin{aligned} c_M= \left( {\begin{array}{c}p/2-1\\ m_-\end{array}}\right) \left( {\begin{array}{c}m_+\\ m_1,\ldots ,m_{k_0}\end{array}}\right) \left( {\begin{array}{c}m_-\\ |m_{k_0+1}|,\ldots ,|m_n|\end{array}}\right) \left( \left( {\begin{array}{c}p/2-1\\ m_+\end{array}}\right) +\left( {\begin{array}{c}p/2-1\\ m_+-1\end{array}}\right) \right) \end{aligned}$$

which evidently is nonzero. Consequently, there is some $0<\varepsilon <1/n$, such that $F(\varepsilon )\ne 0$. We invoke Lemma 3.1 to conclude that $\Gamma$ is not a contractive projection set. $\square$

It remains to deal with the most difficult case, which is when $p=2(n+1)$ for some non-negative integer n. We begin by establishing Theorem 1.3, which is a geometric reformulation of Lemma 3.1.

Proof of Theorem 1.3

We will use Lemma 3.1. Let $\Gamma _0$ be any finite subset of $\Gamma$ and consider the polynomial

$$\begin{aligned} f(z) = \sum _{\alpha \in \Gamma _0} z^\alpha . \end{aligned}$$

We fix some $\gamma$ in $\Gamma _0$ and study the Fourier coefficients of $z^\gamma |f(z)|^{2n}$. By the binomial theorem

$$\begin{aligned} |f(z)|^{2n} = \sum _{j,k=0}^n \left( {\begin{array}{c}n\\ j\end{array}}\right) \left( {\begin{array}{c}n\\ k\end{array}}\right) \bigg (\sum _{\alpha \in \Gamma _0 \setminus \{\gamma \}} z^{\alpha -\gamma }\bigg )^j\bigg (\sum _{\beta \in \Gamma _0 \setminus \{\gamma \}} z^{-(\beta -\gamma )}\bigg )^k. \end{aligned}$$

The binomial coefficients are strictly positive, so by expanding further we see that $|f|^{2n}$ has strictly positive Fourier coefficients for the frequencies which may be represented by

$$\begin{aligned} \sum _{\alpha \in \Gamma _0 \setminus \{\gamma \}} j_\alpha (\alpha -\gamma ) - \sum _{\beta \in \Gamma _0 \setminus \{\gamma \}} k_\beta (\beta -\gamma ) \end{aligned}$$

where the coefficients $j_\alpha$ and $k_\beta$ are non-negative integers whose individual sums do not exceed n. Equivalently, we obtain the exponents

$$\begin{aligned} \sum _{\alpha \in \Gamma _0 \setminus \{\gamma \}} m_\alpha (\alpha -\gamma ) \qquad \text {for} \qquad \max \left( \sum _{m_\alpha >0} m_\alpha , -\sum _{m_\alpha <0} m_\alpha \right) \le n. \end{aligned}$$

It is evident that no other choice of f supported on $\Gamma _0$ can give more frequencies. Returning to (3.1), we see that the only possible $\lambda$ such that the integral is non-zero are those in $E_n(\Gamma )$. The claim now follows from Lemma 3.1. $\square$

By Theorem 1.3, our task is now to clarify under which conditions on a subset $\Gamma$ of $\mathbb N_0^d$ we will have $E_n(\Gamma )=\Gamma$. To this end, the following terminology will be useful.

Definition

Let T be a subset of $\mathbb N^d_0$. Define inductively $E_{n}^{k+1}(T):=E_n(E_n^k(T))$ for all positive integers k and set

$$\begin{aligned} E_n^\infty (T):=\bigcup _{k=1}^\infty E^k_n(T). \end{aligned}$$

We will refer to the set $E_n^{\infty }(T)$ as the n-completion of T.

Clearly, $E_n^{\infty }(T)$ is the smallest set $\Gamma$ satisfying $T\subseteq \Gamma$ and $E_n(\Gamma )=\Gamma$. We close this subsection by recording two immediate consequences, both pertaining to the simplest case of 1-completions. The first of these settles the essentially trivial case $k=1$ in part (a) of Theorem 1.2.

Lemma 3.2

Let T be a subset of $\mathbb N_0^d$ with $\dim (T)=1$. Then the 1-completion of T is $\Lambda (T) \cap \mathbb N_0^d$.

Proof

The assertion is trivial if T consists of only two points, so suppose that there are at least three points in T. Choose two distinct points $\alpha$ and $\beta$ in $E_1^\infty (T)$ subject to condition that the vector $\alpha -\beta$ have minimal length. By assumption, there is at least one more point $\eta$ in $E_1^\infty (T)$. Now it is clear that $\eta =\alpha +k(\beta -\alpha )$ for some integer k since otherwise we could find a point $\tau$ in $E_1^{\infty }(\{\alpha , \beta \})$ so that the length of $\eta -\tau$ is positive and strictly smaller than that of $\alpha -\beta$. $\square$

The next lemma will be useful for the analysis of our examples in Section 3.3. It will also be instrumental in Section 3.5, for the computation of $E_1^\infty (T)$ and $E_2^\infty (T)$ for subsets T of codimension 0 in respectively $\mathbb N^2_0$ and $\mathbb N^3_0$.

Lemma 3.3

Let T be a subset of $\mathbb N^d_0$. If there are points $\alpha$ and $\beta$ in $E_n^\infty (T)$ such that $\beta -\alpha$ is in $\mathbb N^d$, then $E_n^\infty (T) = E_1^\infty (T\cup \{\alpha , \beta \}) = \Lambda (T)\cap \mathbb N^d_0$.

Proof

Let $\tau$ be any point in $\Lambda (T)\cap \mathbb N^d_0$. Then there exist a positive integer k and (not necessarily distinct) points $\gamma _1,\ldots , \gamma _k$ in T, with a choice of signs $\varepsilon _j$ such that

$$\begin{aligned} \tau =\alpha +\sum _{j=1}^k \varepsilon _j (\gamma _j-\alpha ). \end{aligned}$$

Now let r be a positive integer which is so large that for $\eta := \alpha + r(\beta -\alpha )$, we have that $\eta +\sum _{j=1}^l \varepsilon _j (\gamma _j-\alpha )$ lie in $\mathbb N_0^d$ for $l=1, \ldots , k$. This implies that $\tau +r(\beta -\alpha )$ is in $E_1^\infty (T\cup \{\alpha , \beta \})$, which in turn means that also $\tau$ is in $E_1^\infty (T\cup \{\alpha , \beta \})$. $\square$

3.3 Examples.

Our goal is now to compile a collection of examples which, in view of Theorem 1.3, collectively demonstrate the necessity part of points (b) and (c) of Theorem 1.2 in the case when p is an even integer. Two of the examples will also be used in the proof of Theorem 1.4. After each example, we will elucidate explicitly its usage in the proof of Theorem 1.2.

We will make use of the following equivalent representation of the n-extensions, which can be deduced from Lemma 3.1 similarly to how we proved Theorem 1.3. Suppose that $\Gamma = \{\gamma _1,\gamma _2,\ldots ,\gamma _k\}$. A point $\lambda$ is in $E_n(\Gamma )$ if and only if there are functions $\tau _+ :\{1,\ldots ,n+1\} \rightarrow \{\gamma _1,\ldots ,\gamma _k\}$ and $\tau _- :\{1,\ldots ,n\} \rightarrow \{\gamma _1,\ldots ,\gamma _k\}$ such that

$$\begin{aligned} \lambda = \sum _{m=1}^{n+1} \gamma _{\tau _{+}(m)} - \sum _{m=1}^n \gamma _{\tau _{-}(m)}. \end{aligned}$$

(3.2)

The formulation (3.2) is particularly useful for checking if a given $\lambda$ is in $E_n(\Gamma )$.

The following example is presented graphically in Figure 1.

Example 3.4

Consider $\Gamma := \{(3,0,0),(0,3,0),(1,1,1)\}$. We may represent every $\lambda$ in $\Lambda (\Gamma )$ as

$$\begin{aligned} \lambda = (1,1,1) + j (2,-1,-1) + k(-1,2,-1) \end{aligned}$$

(3.3)

for integers j and k. We are only interested in $\lambda$ that lie in $\mathbb {N}_0^3$. We see that this can only be achieved if $j+k \le 1$ by inspecting the third coordinate of (3.3) and $j,k\ge -1$ by inspecting the first and second coordinates of (3.3). The only choice of j and k that provides a new point in $\mathbb {N}_0^3$, is $j=k=-1$ which gives $\lambda = (0,0,3)$. Hence we conclude that

$$\begin{aligned} \Lambda (\Gamma ) \cap \mathbb {N}_0^3 = \Gamma \cup \{(0,0,3)\}. \end{aligned}$$

Returning to (3.3) with $j=k=-1$, we see that (0, 0, 3) is in $E_2(\Gamma )$, which shows that $E_2(\Gamma )=\Lambda (\Gamma )\cap \mathbb {N}_0^3$. It remains to show that $E_1(\Gamma )=\Gamma$. In view of the reformulation (3.2) and the discussion above, this is equivalent to showing that the equation

$$\begin{aligned} (0,0,3) = \gamma _1 + \gamma _2 - \gamma _3 \end{aligned}$$

does not have a solution for (not necessarily distinct) $\gamma _1,\gamma _2,\gamma _3$ in $\Gamma$. To see this, it is sufficient to note that the third coordinate of $\gamma _1 + \gamma _2 - \gamma _3$ is at most 2.

Example 3.4 extends trivially to an example for $d\ge 3$ if we retain the first three entries as above and set the jth entry to 0 for $3\le j \le d$. This means that this example yields the necessity of the case $k=2$ in part (b) of Theorem 1.2.

Example 3.5

Consider $\Gamma := \{(4,0,0),(0,4,0),(0,0,4),(1,1,1)\}$. It is clear that the only way to get $\gamma _1+\gamma _2-\gamma _3$ in $\mathbb {N}_0^3$ for (not necessarily distinct) $\gamma _1,\gamma _2,\gamma _3$ in $\Gamma$ is to set $\gamma _1=\gamma _3$ or $\gamma _2=\gamma _3$. Hence $E_1(\Gamma )=\Gamma$. However, since

$$\begin{aligned} (4,0,0)+\big ((0,4,0)-(1,1,1)\big )+\big ((0,0,4)-(1,1,1)\big )=(2,2,2) \end{aligned}$$

we conclude that (2, 2, 2) is in $E_2(\Gamma )$. Since $(2,2,2)-(1,1,1)$ is in $\mathbb {N}^3$, we get from Lemma 3.3 that $E_2^\infty (\Gamma )=\Lambda (\Gamma )\cap \mathbb {N}_0^3$.

We see that Example 3.5 settles the necessity of the case $d=k=3$ in part (b) of Theorem 1.2.

Example 3.6

Fix an integer $n\ge 2$ and consider

$$\begin{aligned} \Gamma _n := \left\{ (n,1,0,1),(n+1,0,1,0),(0,0,n+1,0),(0,0,0,n+1)\right\} . \end{aligned}$$

The generating vectors for the coset $\Lambda (\Gamma _n)$ with respect to $\alpha :=(n,1,0,1)$ are

$$\begin{aligned} v_1&:= (1,-1,1,-1), \\ v_2&:= (-n,-1,n+1,-1), \\ v_3&:= (-n,-1,0,n). \end{aligned}$$

Hence, every $\lambda$ in $\Lambda (\Gamma _n)$ may be represented as

$$\begin{aligned} \lambda = \alpha + j_1 v_1 + j_2 v_2 + j_3 v_3 \end{aligned}$$

(3.4)

for integers $j_1,j_2,j_3$. We want to check whether there are $\lambda$ in $\mathbb {N}_0^4$ that satisfy the equation (3.4). This means that we require

$$\begin{aligned} n + j_1-nj_2-nj_3&\ge 0, \end{aligned}$$

(3.5)

$$\begin{aligned} 1 - j_1-j_2-j_3&\ge 0, \end{aligned}$$

(3.6)

$$\begin{aligned} j_1 + (n+1) j_2&\ge 0, \end{aligned}$$

(3.7)

$$\begin{aligned} 1 - j_1 - j_2 +n j_3&\ge 0. \end{aligned}$$

(3.8)

We divide our analysis into four cases.

3.3.1 Case 1.

Suppose that $j_1=1$. By (3.7), we get $j_2\ge 0$. Rewriting (3.6) as $j_3 \le - j_2$ and inserting this into (3.8), we find the necessary condition $-(n+1)j_2 \ge 0$. Hence $j_2 \le 0$ and so $j_2=0$. Returning to (3.6) and (3.8) we find that $j_3=0$. We get

$$\begin{aligned} \lambda = \alpha + v_1 = (n,1,0,1). \end{aligned}$$

3.3.2 Case 2.

Suppose that $j_1=0$. By (3.7), we get $j_2\ge 0$. Rewriting (3.6) as $j_3 \le 1-j_2$ and inserting this into (3.8), we find the necessary condition $(1-j_2)(n+1)\ge 0$. Hence $j_2 \le 1$ and so either $j_2=0$ or $j_2=1$. Returning to (3.6) and (3.8), we see at once that if $j_2=0$, then $j_3=0,1$ and if $j_2=1$, then $j_3=0$. The three cases give

$$\begin{aligned} \lambda&= \alpha = (n+1,0,1,0), \\ \lambda&= \alpha +v_2 = (0,1,n,0), \\ \lambda&= \alpha +v_3=(0,0,0,n+1). \end{aligned}$$

3.3.3 Case 3.

Suppose that $j_1>1$. Rewriting (3.6) as $j_3 \le 1 - j_1 - j_2$ and inserting this into (3.8), we obtain the necessary condition

$$\begin{aligned} 0\le (1-j_1-j_2)(n+1), \end{aligned}$$

which means that $1-j_2 \ge j_1$. Since $j_1>1$ we conclude that $j_2<0$. From (3.7) we see that $j_1 \ge - (n+1) j_2$. Hence we need $j_2<0$ to satisfy

$$\begin{aligned} 1-j_2 \ge -(n+1)j_2, \end{aligned}$$

which is impossible since $n\ge 2$.

3.3.4 Case 4.

Suppose that $j_1<0$. By (3.7), we find that $j_2 \ge 1$. Inserting this into (3.5) and (3.8), we find that

$$\begin{aligned} 0&\le j_1 - nj_3, \\ 0&\le n j_3 -j_1, \end{aligned}$$

whence $j_1 = n j_3$. Returning to (3.5), we find that $n(1-j_2)\ge 0$ which means that $j_2 \le 1$ and hence $j_2=1$. Returning to (3.7), we see that $j_1 + n+1 \ge 0$ and since $j_1$ is a strictly negative multiple of n, we must have $j_1=-n$ and hence $j_3=-1$. This gives the solution

$$\begin{aligned} \lambda = \alpha - n v_1 + v_2 - v_3 = (0,n+1,1,0). \end{aligned}$$

Note that here we have used an $(n+1)$-extension, since $j_1+j_2=n+1$ and $j_3=-1$.

3.3.5 Final part.

We have demonstrated that

$$\begin{aligned} \Lambda (\Gamma _n)\cap \mathbb {N}_0^3 = \Gamma _n \cup \{(0,n+1,1,0)\} = E_{n+1}(\Gamma _n). \end{aligned}$$

It remains to establish that $E_n(\Gamma _n) = \Gamma _n$. We want to prove that it is impossible to write $\lambda =(0,n+1,1,0)$ in the representation (3.2). We begin by looking at the more general equation

$$\begin{aligned} (0,n+1,1,0)= k_1(n,1,0,1)+ k_2(n+1,0,1,0)+k_3(0,0,n+1,0)+k_4(0,0,0,n+1) \end{aligned}$$

for arbitrary integers $k_1,k_2,k_3,k_4$. The second coordinate shows that $k_1=n+1$. In the first coordinate this gives that $k_2=-n$. In the third coordinate we find that $k_3=1$ and in the fourth coordinate we find that $k_4=-1$. Hence the only solution is $k_1=n+1$, $k_2=-n$, $k_3=1$ and $k_4=-1$. However, this is not of the representation (3.2) since $k_1+k_3=n+2>n+1$. Hence $(0,n+1,1,0)$ is not in $E_n(\Gamma _n)$, which shows that $E_n(\Gamma _n)=\Gamma _n$.

Example 3.6 extends trivially to an example for $d\ge 5$ if we keep the four first entries as above and set the jth entry to 0 for $5\le j \le d$. Hence this example yields the necessity of the case $k=3$ in part (c) of Theorem 1.2.

Example 3.7

Fix an integer $n\ge 3$ and consider

$$\begin{aligned} \Gamma _n := \left\{ (n,1,0,1), (n+1,0,1,0), (0,0,n+1,0), (0,0,0,n+1), (0,n+1,0,0)\right\} . \end{aligned}$$

The first four points in $\Gamma _n$ are the same as in Example 3.6, so we know that $(0,n+1,1,0)$ is in $E_{n+1}(\Gamma _n)$. Using this point and the fifth point in $\Gamma _n$ to perform $n+2$ successive 1-extensions we conclude that

$$\begin{aligned} (n,1,0,1)+(n+2)\big ((0,n+1,1,0)-(0,n+1,0,0)\big )=(n,1,n+2,1) \end{aligned}$$

is in $E_{n+1}^\infty (\Gamma _n)$. Since $(n,1,n+2,1)-(0,0,n+1,0)=(n,1,1,1)$ is in $\mathbb {N}^4$ we can appeal to Lemma 3.3 to conclude that $E_{n+1}^\infty (\Gamma _n)=\Lambda (\Gamma _n)\cap \mathbb {N}_0^4$.

To investigate $E_n(\Gamma _n)\setminus \Gamma _n$ we look at points in $\mathbb {N}_0^d$ which may be represented as

$$\begin{aligned} k_1(n,1,0,1)+ k_2(n+1,0,1,0)+ k_3(0,0,n+1,0)+ k_4(0,0,0,n+1)+ k_5(0,n+1,0,0) \end{aligned}$$

where the integers $k_1,k_2,k_3,k_4,k_5$ must be chosen in accordance with (3.2). In particular, $-n \le k_1,k_2,k_3,k_4,k_5 \le n+1$ and $k_1+k_2+k_3+k_4+k_5=1$. By the analysis in Example 3.6 we may restrict our attention to the case that $k_5\ne 0$.

If $k_5\ge 1$, then $k_1,k_2,k_3,k_4 \le n$ which implies that $k_3,k_4\ge 0$ and $k_1+k_2\le 0$. Looking at the first coordinate we get the condition

$$\begin{aligned} k_1 n + k_2(n+1) = (k_1 + k_2)n+k_2\ge 0. \end{aligned}$$

By the requirements above, this is only possible if $k_1=-k_2$ and $k_2\ge 0$. Since now $k_1+k_2=0$ we get that $k_3=k_4=0$. The fourth coordinate is currently equal to $-k_1$, which means that $k_1=0$ and hence $k_2=0$. We get $(0,n+1,0,0)$ which is already in $\Gamma _n$.

If $k_5 \le -1$, the second coordinate shows that $k_5=-1$ and $k_1=n+1$. We now get from (3.2) that $k_2,k_3,k_4 \le 0$ and $k_2+k_3+k_4=-(n-1)<0$. By looking at the third coordinate, we find that $k_2=k_3=0$. Hence $k_4=-(n-1)$, so the fourth coordinate is

$$\begin{aligned} n+1-(n-1)(n+1)=2+n-n^2<0 \end{aligned}$$

since $n\ge 3$. Hence $E_n(\Gamma _n)=\Gamma _n$.

When $d\ge 4$, Example 3.7 allows us to settle the necessity of the case $4\le k \le d$ in part (c) of Theorem 1.2. This is immediate if $d=4$, and for $d\ge 5$ we make the following trivial extension. We retain the first four entries as above the points and put the jth entry to 0 for $5\le j \le d$, and then we extend the set by adding $d-k$ affinely independent points with only zeros in the first 4 entries.

3.4 Two-dimensional subsets of $\mathbb {N}^d_0$ for $d\ge 3$.

The purpose of this subsection is to settle the sufficiency of the case $k=2$ in part (b) of Theorem 1.2. In view of Theorem 1.3, this will be furnished by Lemma 3.9 below. We begin with the following special case of the required result.

Lemma 3.8

Let T be a set of three affinely independent points in $\mathbb {N}^d_0$ for $d\ge 3$. Then the 2-completion of T is $\Lambda (T)\cap \mathbb {N}_0^d$.

Proof

Let $\alpha _1$, $\alpha _2$, $\alpha _3$ be the points in T, and let $\beta$ be a point in $\Lambda (T)\cap \mathbb {N}_0^d$. We denote the plane of which T is a subset by P(T). We let $\ell (\gamma ,\tau )$ be the line through the two points $\gamma$ and $\tau$, and we let $\Delta (\gamma ,\tau ,\eta )$ be the triangle with corners $\gamma$, $\tau$, $\eta$. Let V and W be the two components of $P(T)\setminus \ell (\alpha _2,\beta )$. We may assume that the remaining two points $\alpha _1$ and $\alpha _3$ lie in either $\overline{V}$ or $\overline{W}$. We may also assume that $\alpha _3$ is contained in the closed strip lying between $\ell (\alpha _2,\beta )$ and the line through $\alpha _1$ parallel to $\ell (\alpha _2,\beta )$, since otherwise it could be moved into this strip by a finite number of 1-extensions. In fact, we may assume that $\alpha _3$ lies in the interior of this strip, because the problem has a trivial solution in terms of a finite number of 1-extensions should $\alpha _3$ lie on the boundary of the strip.

Now if $\alpha _3$ lies in the parallelogram with corners $\alpha _1$, $\alpha _2$, $\beta$, $\beta +\alpha _1-\alpha _2$, then it must lie inside the triangle $\Delta (\beta ,\alpha _1,\alpha _2)$, since otherwise $\beta$ would not be contained in $\Lambda (T)$. If $\alpha _3$ does not lie in this parallelogram, then we may replace $\alpha _3$ by $\alpha _1+\alpha _2-\alpha _3$ which then must lie inside $\Delta (\beta ,\alpha _1,\alpha _2)$. We may therefore assume that $\alpha _3$ lies inside $\Delta (\beta ,\alpha _1,\alpha _2)$.

Let $\eta$ be the point at which $\ell (\alpha _1,\alpha _3)$ and $\ell (\alpha _2,\beta )$ intersect. Since $\beta$ is in $\Lambda (T)$, the distance from $\alpha _2$ to $\eta$ divides the distance from $\alpha _2$ to $\beta$, whence $\beta -\alpha _2=n(\eta -\alpha _2)$ for a positive integer n. This means that

$$\begin{aligned} \alpha _3-\alpha _1 =a(\alpha _2-\alpha _1)+b(\beta -\alpha _2), \end{aligned}$$

(3.9)

where a and b are two positive rational numbers such that $b=1/m\le 1/n$ and $a=n/m$. We see that then

$$\begin{aligned} \beta =\alpha _2+ m(\alpha _3- \alpha _1)- n(\alpha _2-\alpha _1). \end{aligned}$$

(3.10)

We may assume that $(m,n)=1$ since otherwise we could replace m and n by respectively m/(m, n) and n/(m, n). Figure 3 illustrates the case when $m=5$ and $n=2$. We need to show that we can get to $\beta$ starting from $T=\{\alpha _1,\alpha _2,\alpha _3\}$ and using 2-extensions. Reformulating (3.10) to

$$\begin{aligned} \beta = \alpha _3 + (m-1)(\alpha _3-\alpha _1) - (n-1)(\alpha _2 - \alpha _1), \end{aligned}$$

we may exclude from our discussion the case when $m,n\le 3$, since we may evidently reach $\beta$ directly from $\alpha _3$ using a single 2-extension.

Our plan is now to make successive extensions so that the point that is added in each step, lies inside $\Delta (\beta ,\alpha _1,\alpha _2)$. Using (3.9), we see that the condition that a point of the form

$$\begin{aligned} \xi =\alpha _2 + j(\alpha _3 - \alpha _1) - k(\alpha _2-\alpha _1) \end{aligned}$$

(3.11)

for $j,k>0$ to be inside $\Delta (\beta ,\alpha _1,\alpha _2)$ is that $j/m\le jn/m+1-k\le 1$. This means more specifically that

$$\begin{aligned} k=\left\lceil \frac{jn}{m}\right\rceil \qquad \text {and} \qquad \left\{ \frac{jn}{m}\right\} \ge \frac{j}{m}. \end{aligned}$$

(3.12)

We will begin by identifying what will be the final extension required to reach $\beta$. The basic idea is that it suffices with one final extension once we have reached essentially half way from the base of the triangle $\Delta (\alpha _1,\alpha _2,\beta )$ to the corner at $\beta$. We make this precise by distinguishing between the following three cases: $\square$

Fig. 3

The case $m=5$ and $n=2$ in the proof of Lemma 3.8. The shaded area represents a part of the plane P(T) that must lie inside the narrow cone $\mathbb N_0^d$. We need a 2-extension to reach ${\beta }$ which is accommodated by the move ${\beta } = {\xi }-(\alpha _2-{\xi })-(\alpha _3-{\xi } )$.

3.4.1 Case 1.

If m is an even number, then it is clear by (3.12) that

$$\begin{aligned} \xi =\alpha _2+ \frac{m}{2}(\alpha _3-\alpha _1) -\frac{(n+1)}{2}( \alpha _2-\alpha _1) \end{aligned}$$

is in $\Delta (\beta ,\alpha _1,\alpha _2)$. Assuming that $\xi$ is in $E_2^k(T)$ for some k, we see that $\beta$ is in $E_2^{k+1}(T)$ by recalling (3.10) and observing that

$$\begin{aligned} \beta =\alpha _2+2(\xi -\alpha _2)-(\alpha _1-\alpha _2). \end{aligned}$$

3.4.2 Case 2.

If m and n are both odd numbers, then

$$\begin{aligned} \left\{ \frac{(m+1)n}{2m}\right\} = \left\{ \frac{1}{2}+\frac{n}{2m}\right\} =\frac{(m+n)}{2m} \ge \frac{(m+1)}{2m}, \end{aligned}$$

whence

$$\begin{aligned} \xi =\alpha _2+ \frac{(m+1)}{2}(\alpha _3-\alpha _1)-\frac{(n+1)}{2}( \alpha _2-\alpha _1) \end{aligned}$$

is in $\Delta (\beta ,\alpha _1,\alpha _2)$ by (3.12). Assuming again that $\xi$ is in $E_2^k(T)$ for some k, we now find that $\beta$ is in $E_2^{k+1}(T)$ by recalling (3.10) and observing that

$$\begin{aligned} \beta =\alpha _2+2(\xi -\alpha _2)-(\alpha _3-\alpha _2). \end{aligned}$$

3.4.3 Case 3.

The case when m is an odd number and n is an even number requires a slightly more refined analysis. To begin with, we observe that

$$\begin{aligned} \left\{ \frac{(m-1)n}{2m}\right\} = \left\{ -\frac{n}{2m}\right\} =\frac{(2m-n)}{2m} \ge \frac{(m-1)}{2m}, \end{aligned}$$

whence

$$\begin{aligned} \xi _1:=\alpha _2+\frac{(m-1)}{2}(\alpha _3-\alpha _1) -\frac{n}{2}(\alpha _2-\alpha _1) \end{aligned}$$

is in $\Delta (\beta ,\alpha _1,\alpha _2)$ by (3.12). We use next that

$$\begin{aligned} \left\{ \frac{(m \pm 3)n}{2m}\right\} = \left\{ \frac{\pm 3n}{2m}\right\} . \end{aligned}$$

We observe that if $m/n>3/2$, then at least one of the two inequalities

$$\begin{aligned} \left\{ \frac{3n}{2m}\right\} \ge \frac{m+3}{2m} \qquad \text {and}\qquad \left\{ \frac{-3n}{2m}\right\} \ge \frac{m-3}{2m} \end{aligned}$$

must hold. On the other hand, if $m/n<3/2$, then

$$\begin{aligned} \left\{ \frac{-3n}{2m} \right\} = \frac{4m-3n}{2m} \ge \frac{m-3}{2m}. \end{aligned}$$

We conclude that at least one of the three points

$$\begin{aligned} \xi _2&:= \alpha _2+\frac{(m+1)}{2} (\alpha _3-\alpha _1) - \left( \frac{n}{2}+1\right) (\alpha _2-\alpha _1), \\ \xi _3&:= \alpha _2+\frac{(m-3)}{2} (\alpha _3-\alpha _1) - \frac{n}{2}(\alpha _2-\alpha _1), \\ \xi _4&:= \alpha _2+\frac{(m-3)}{2} (\alpha _3-\alpha _1) - \left( \frac{n}{2}-1\right) (\alpha _2-\alpha _1), \end{aligned}$$

is in $\Delta (\beta ,\alpha _1,\alpha _2)$ by (3.12). Assuming first that $\xi _1$ and $\xi _2$ are in $E_2^k(T)$ for some k, we see that $\beta$ is in $E_2^{k+1}(T)$ because

$$\begin{aligned} \beta =\alpha _2+(\xi _1-\alpha _2)+(\xi _2-\alpha _2)-( \alpha _1-\alpha _2). \end{aligned}$$

Next, if $\xi _1$ and $\xi _3$ are in $E_2^k(T)$ for some k, then we find again that $\beta$ is in $E_2^{k+1}(T)$ because

$$\begin{aligned} \beta =\xi _1-(\alpha _2-\xi _1)-(\xi _3-\xi _1). \end{aligned}$$

Finally, if $\xi _1$ and $\xi _4$ are in $E_2^k(T)$ for some k, then we find as before that $\beta$ is in $E_2^{k+1}(T)$, this time because

$$\begin{aligned} \beta =\xi _1-(\alpha _1-\xi _1)-(\xi _4-\xi _1). \end{aligned}$$

3.4.4 Final part.

We are now left with the simpler problem of reaching each of the points considered above. We claim that any one of them can be reached by starting from $\alpha _1$ or $\alpha _3$ and making successive additions of multiples of the vectors $\alpha _3-\alpha _1$ and $\alpha _1-\alpha _2$. We will refer to the integers j and k in (3.11) as respectively steps and levels. Notice that a step j determines a unique point in the strip between $\alpha _1-\alpha _2+\ell (\alpha _2,\beta )$ and $\ell (\alpha _2,\beta )$, while there may in general be several points in this strip at each level. Note that $\alpha _3$ is always step 1. In Figure 3, the point $\xi$ corresponds for example to step 2 and the point $\beta$ is at level 2.

A simple geometric consideration suffices to settle the case $n<m/2$. Indeed, then for every level $k\le m/2$, there are points of the form (3.11) lying in $\Delta (\beta ,\alpha _1,\alpha _2)$, and it is clear that the points accumulated at the initial level $k=1$ can be used to connect those lying at any level $k\le m/2$ with those found at the next level $k+1$.

The case $m/2<n<m$ requires a more careful analysis. It may be helpful to bear in mind that the lead role will now be played by the steps j rather than the levels k. We begin by treating separately a special case. Suppose that m is odd and $n=(m+1)/2$. If j is odd and $j<m$, then

$$\begin{aligned} \left\{ \frac{jn}{m}\right\} =\frac{1}{2}+\frac{j}{2m} >\frac{j}{m}, \end{aligned}$$

which means that each of the points $\xi$ in (3.11) with j odd and $j<m$ will be in $\Delta (\beta ,\alpha _1,\alpha _2)$. These points are reached in an obvious way, once we have made the initial extension

$$\begin{aligned} \xi :=\alpha _3-(\alpha _1-\alpha _3)-(\alpha _2-\alpha _3). \end{aligned}$$

We now write $n=m-r$ and assume that $1\le r \le m/2-1$. The condition that the point $\xi$ in (3.11) be in $\Delta (\beta ,\alpha _1,\alpha _2)$ is that

$$\begin{aligned} \left\{ \frac{jn}{m} \right\} =\left\{ \frac{-jr}{m} \right\} \ge \frac{j}{m}. \end{aligned}$$

This means that we must have

$$\begin{aligned} \frac{(t-1)m}{r}<j\le \frac{t m}{r+1} \end{aligned}$$

(3.13)

for some t such that $1 \le t \le r/2+1$, where the latter inequality should hold because we require that $j\le m/2+1$. We now observe that, under this restriction, the interval defined by (3.13) has length

$$\begin{aligned} m \left( \frac{t}{r+1} -\frac{(t-1)}{r}\right) =\frac{m(r+1-t)}{ r(r+1)}\ge \frac{m}{2(r+1)}\ge 1, \end{aligned}$$

whence it contains at least one integer. This yields an algorithm for reaching all steps j with $j\le m/2+1$ such that $\xi$ in (3.11) is in $\Delta (\beta , \alpha _1,\alpha _2)$. Indeed, initially we go step-by-step until $j=[m/(r+1)]$. (Notice that this suffices when $r=1$.) We then observe, denoting the interval defined by (3.13) by $I_{t}$, that

$$\begin{aligned} {\text {dist}}(I_{t+1},I_{t})=\frac{t m}{r(r+1)} \le \frac{m}{2(r+1)} \end{aligned}$$

when $t \le r/2$. This means that the points corresponding to the steps $j\le [m/(r+1)]$ can be used to connect those associated with steps lying in $I_{t}$ to those lying in $I_{t+1}$.

$\square$

The general case can now be settled with a proof that requires less effort than the preceding one.

Lemma 3.9

Fix $d\ge 3$ and let T be a set in $\mathbb {N}^d_0$ with $\dim (T)=2$. Then the 2-completion of T is $\Lambda (T)\cap \mathbb {N}_0^d$.

Proof

Lemma 3.8 proves the assertion in the special case when the cardinality of T is 3. We will use this result to run what may be thought of as a kind of Euclidean algorithm. We pick three arbitrary affinely independent points $\alpha _1$, $\alpha _2$, $\alpha _3$ in T and assume that $\tau$ is a fourth point in T such that $\tau$ is not in $\Lambda (\{\alpha _1,\alpha _2,\alpha _3\})$. The crucial point will be to prove that, on this assumption, there exists a point $\beta$ in $E_2^{\infty }(\{\tau ,\alpha _1,\alpha _2,\alpha _3\})$ such that at least one of the triangles $\Delta (\alpha _1,\alpha _2,\beta )$, $\Delta (\alpha _1,\alpha _3,\beta )$, $\Delta (\alpha _2,\alpha _3,\beta )$, say $\Delta (\alpha _1,\alpha _2,\beta )$ for definiteness, is nondegenerate with area strictly smaller than that of $\Delta (\alpha _1,\alpha _2,\alpha _3)$. This argument may be iterated so that in the next step we use $\alpha _1, \alpha _2, \beta$ in place of $\alpha _1, \alpha _2, \alpha _3$. The iteration must terminate after a finite number of steps, which means that eventually there are no points in T lying outside of the coset generated by the points $\alpha _1$, $\alpha _2$, $\alpha _3$ used in this final step of the iteration.

Fig. 4

The case $k=2$ and ${\tau _1}={\tau } +(\alpha _1-\alpha _2)+k(\alpha _2-\alpha _3)$ in the proof of Lemma 3.9. The shaded area represents a part of the plane P(T) that must lie inside the narrow cone $\mathbb {N}_0^d$.

We are now in a situation similar to that considered in the preceding lemma. We have a trivial solution if $\tau$ lies on $\ell (\alpha _1,\alpha _2)$: Then the desired $\beta$ lies on the segment $[\alpha _1,\alpha _2]$ and is reached by a finite number of 1-extensions. We therefore ignore this case in what follows. We may assume that $\tau$ and $\alpha _3$ lie in the same component of the set $P(T)\setminus \ell (\alpha _1,\alpha _2)$.

We now let m be the smallest positive integer such that $\tau$ is contained in the open strip between $\ell (\alpha _1,\alpha _2)$ and $m(\alpha _3-\alpha _2)+\ell (\alpha _1,\alpha _2)$. If neither $\alpha _3$ nor any of the points $\alpha _3\pm (\alpha _2-\alpha _1)$ lie in the triangle $\Delta (\alpha _1,\alpha _2,\tau )$, then our problem has a trivial solution: For $k=m-1$ and $i=1$ or $i=2$, the point $\beta :=\tau -k(\alpha _3-\alpha _i)$ will lie in the closure of $\Delta (\alpha _1,\alpha _2,\tau )$ and have distance to $\ell (\alpha _1,\alpha _2)$ strictly smaller than that from $\alpha _3$ to $\ell (\alpha _1,\alpha _2)$. (This distance may be 0.) This point $\beta$ will therefore have the desired property, unless it lies on $\ell (\alpha _1,\alpha _2)$ in which case the solution is again trivial as we saw above.

What remains to consider is the case when $\alpha _3$ lies inside $\Delta (\alpha _1,\alpha _2,\tau )$. Let k be the smallest positive integer such that $\alpha _2+k(\alpha _3-\alpha _2)$ does not lie in the closure of $\Delta (\alpha _1,\alpha _2,\tau )$. If $k=m$, then we see that $\beta =\tau +(m-1)(\alpha _2-\alpha _3)$ solves our problem. If $k<m$, then the point

$$\begin{aligned} \tau _1:= \tau +(\alpha _1-\alpha _2) +k(\alpha _2-\alpha _3) \end{aligned}$$

is in $\Delta (\alpha _1,\alpha _2,\tau )\cap E_2^\infty (\{\alpha _1,\alpha _2,\alpha _3,\tau \})$. See Figure 4. Now $\tau _1$ lies in the open strip between $\ell (\alpha _1,\alpha _2)$ and $(m-k)(\alpha _3-\alpha _2)+\ell (\alpha _1,\alpha _2)$ or on $\ell (\alpha _1,\alpha _2)$. We may thus iterate the argument with $\tau _1$ in place of $\tau$. It is clear that after a finite number of such iterations, we will reach a point $\tau _j$ in $E_2^\infty (\{\alpha _1,\alpha _2,\alpha _3,\tau \})$ such that the desired $\beta$ can be reached in any of the trivial ways described in the preceding discussion. $\square$

3.5 Subsets of $\mathbb {N}^2_0$ and $\mathbb {N}^3_0$ of codimension 0.

It remains to establish the case $d=k=2$ in part (a) and to finish the case $d=k=3$ in part (b) of Theorem 1.2. In either case, we will be dealing with sets of codimension 0 in the ambient space.

We begin with the easiest case $d=k=2$. By Theorem 1.3, we need to show that $E_1^\infty (T)=\Lambda (T)\cap \mathbb N_0^2$ when T is a subset of $\mathbb N^2_0$ with $\dim (T)=2$. In view of Lemma 3.3, this is accomplished by means of the following lemma.

Lemma 3.10

Let T be a set of three affinely independent points in $\mathbb {N}_0^2$. Then for every $\alpha$ in T there exists a point $\beta$ in $E^{\infty }_1(T)\setminus \{x\}$ such that $\beta -\alpha$ is in $\mathbb {N}^2$.

We will in the proof of this lemma and later, in its more elaborate 3-dimensional counterpart, make use of the following quantity.

Definition

Given a set U of d linearly independent vectors $u = (u_1,\ldots ,u_d)$ in $\mathbb {Z}^d$, we define the negativity index of U as

$$\begin{aligned} {\mathrm{ind}}(U):=\sum _{j=1}^d \min \big (0, \min _{u\in U}u_j\big ). \end{aligned}$$

The vectors u will be assumed to relate to a fixed point $\alpha$ in $\mathbb {N}^d_0$ by the condition that $\alpha +u$ be in $\mathbb {N}_0^d$ as well. When this holds, we say that u is $\alpha$-admissible. Our goal will be to successively change U by making 1- or 2-extensions of $\alpha +U$ to get to new vectors with a larger negativity index. It will be crucial that linear independence of the vectors of U be preserved during the course of this iteration.

Proof of Lemma 3.10

We begin by noting that it suffices to find a point $\beta$ in $E_1^{\infty }(T) \setminus T$ with $\beta -\alpha$ in $\mathbb N_0^2$. Indeed, should one of the entries of $\beta -\alpha$ be 0, we may replace $\beta$ by either $\alpha +m(\beta -\alpha )+(\tau -\alpha )$ or $\alpha +m(\beta -\alpha )-(\tau -\alpha )$ for a sufficiently large m, where $\tau$ is one of the two other points in T. Since $\dim (T)=2$, both entries of either $m(\beta -\alpha )+(\tau -\alpha )$ or $\alpha +m(y-\alpha )-(\tau -\alpha )$ will be positive for at least one such $\tau$. It is plain that the corresponding point $\alpha +m(\beta -\alpha )\pm (\tau -\alpha )$ will lie in $E_1^\infty (T)$.

Now fix a point $\alpha$ in T, and let $v_1$, $v_2$ be the vectors going from $\alpha$ to the other two points in T. It will be helpful to represent an entry in any of the two vectors $v_1$, $v_2$ symbolically by $+$ if it is nonnegative and − if it is negative. If one of the $v_j$, say $v_1$, is of the form $(+,+)$, then we may choose $\beta =\alpha +v_1$. Similarly, if $v_1$ is of the form $(-,-)$, then we choose $\beta =\alpha -v_1$. It remains therefore only to consider the two combinations $(+,-)$, $(+,-)$ and $(+,-)$, $(-,+)$, where we in either case may assume that all plus signs correspond to positive entries.

In the first case, at least one of the two vectors $v_1-v_2$ and $v_2-v_1$ will be $\alpha$-admissible. If, say, $v_1-v_2$ is $\alpha$-admissible, then we observe that ${\mathrm{ind}}(v_1, v_1-v_2)>{\mathrm{ind}}(v_1,v_2)$. In the second case, we have plainly ${\mathrm{ind}}(v_1, v_1+v_2)>{\mathrm{ind}}(v_1,v_2)$.

After this initial iteration, we have two new linearly independent $\alpha$-admissible vectors with a larger negativity index. We are done if one of the vectors is of the form $(+,+)$ or $(-,-)$. Otherwise we repeat the iteration. Since the negativity index increases in each step, this iteration will eventually terminate with one of the vectors being of the form $(+,+)$ or $(-,-)$. This vector is necessarily nonzero because the two vectors are linearly independent. $\square$

We turn to the final and most difficult case $d=k=3$. By Theorem 1.3 and Example 3.5, it remains to show that $E_2^\infty (T)=\Lambda (T)\cap \mathbb N_0^3$ when T is a subset of $\mathbb N^3_0$ with $\dim (T)=3$. Again appealing to Lemma 3.3, we see that this follows from the following lemma.

Lemma 3.11

Let T be a set of four affinely independent points in $\mathbb {N}^3_0$. Then for every $\alpha$ in T there exists a point $\beta$ in $E_2^\infty (T)\setminus \{\alpha \}$ such that $\beta -\alpha$ is in $\mathbb {N}^3$.

Proof

We begin as in the preceding case by noting that it suffices to find a $\beta$ in $E_2^{\infty }(T) \setminus T$ with $\beta -\alpha$ in $\mathbb N_0^3$. Should only one of the entries be 0, we may make a similar adjustment as in the proof of Lemma 3.10. Should two of the entries be 0, then we make the following elaboration of this argument. Since $\dim (T)=3$, we can find two points $\tau _1$ and $\tau _2$ in T such that $\beta -\alpha$ is not in the plane spanned by $\tau _1-\alpha$ and $\tau _2-\alpha$. We now claim that we may replace $\beta$ by $\alpha +m(\beta -\alpha )+k(\tau _1-\alpha )+\ell (\tau _2-\alpha )$ for a large positive integer m and suitable integers k and $\ell$. We see that this can be achieved by applying Lemma 3.10 to the two entries of $\alpha , \tau _1, \tau _2$ for which $\beta -\alpha$ is 0.

We now turn to the sequence of 2-extensions needed to reach the desired point $\beta$, starting from any of the points $\alpha$ in T. Our plan is to act in the same way as was done in the case $d=2$. Hence we wish to prove that there exists a k such that at least one of the two assertions is true:

• (i) There is a nonzero vector in $E^k_2(T)-\alpha$ with only nonnegative entries.

• (ii) There are three linearly independent vectors $v_1'$, $v_2'$, $v_3'$ in $E^k_2(T)-\alpha$ such that

  $$\begin{aligned} {\mathrm{ind}}(v_1',v_2',v_3')<{\mathrm{ind}}(v_1,v_2,v_3). \end{aligned}$$

We are done if (i) is true, and if (ii) holds, then the argument can be iterated, starting with the $\alpha$-admissible vectors $v_1'$, $v_2'$, $v_3'$ in place of $v_1$, $v_2$, $v_3$. Our algorithm will be such that the initial assumption that $v_1$, $v_2$, $v_3$ be linearly independent will automatically guarantee that $v_1'$, $v_2'$, $v_3'$ be linearly independent. It is clear that this iteration will eventually produce a nonzero vector in $E^k_2(T)-\alpha$ for some k.

We begin by identifying combinations of signs of the entries of the vectors $v_j$ that immediately lead to the desired $\beta$. To this end, we represent again an entry symbolically by $+$ if it is nonnegative and − if it is negative. If one of the $v_j$, say $v_1$, is of the form $(+,+,+)$, then we may choose $\beta =\alpha +v_1$. Similarly, if $v_1$ is of the form $(-,-,-)$, then we choose $\beta =\alpha -v_1$. We assume therefore that neither of the vectors $v_j$ are of these kinds.

We have found it convenient to group our treatment of the remaining nontrivial combinations of signs into seven cases. The first three cases deal only with combinations of two vectors; we are then either able to reach the desired increase of the negativity index or we are led to consider a combination of signs of three vectors which is then treated later. $\square$

3.5.1 Case 1: $(+,-,+)$ and $(+,+,-)$.

Suppose that $v_1$ is of the form $(+,-,+)$ and $v_2$ is of the form $(+, +,-)$. Then plainly $v_1+v_2$ is again $\alpha$-admissible. We may assume that at least one of the two entries $v_{1,3}$ and $v_{2,2}$ is nonzero. Indeed, if this were not the case, then at least one of the vectors $v_1-v_2$ and $v_2-v_1$ would be $\alpha$-admissible, and then we could replace $v_1$ by $v_1-v_2$ or $v_2$ by $v_2-v_1$ to force one of the entries in question to be nonzero. If, say $v_{1,3}\ne 0$, then we will increase the minimal value of the third entry if we replace $v_2$ by $v_1+v_2$. If the new vector $v_1+v_2$ is of the form $(+,+,+)$, then we are plainly done; if it is of the form $(+,+,-)$, then we may iterate the same argument, now applying it to the two vectors $v_1$ and $v_1+v_2$. If it is of the form $(+,-,+)$ or $(+,-,-)$, then we bring in $v_3$ and note that we have increased ${\mathrm{ind}}(\{v_1,v_2,v_3\})$ unless $v_{3,3}<0$. If $v_3$ is either of the form $(+,+,-)$ or $(-,+,-)$, we would then achieve the desired increase of the negativity index by replacing $v_3$ by $v_3+v_1$. If both $v_1+v_2$ and $v_3$ are of the form $(+,-,-)$, then we obtain the desired increase by replacing $v_3$ by one of the vectors $\pm (v_3-v_1-v_2)$. The only remaining case to be considered is therefore that $v_1+v_2$ is of the form $(+,-,+)$ and $v_3$ is of the form $(+,-,-)$. We will treat it as Case 6 below.

3.5.2 Case 2: $(+,-,+)$ and $(-,+,-)$.

Suppose next that $v_1$ is of the form $(+,-,+)$ and $v_2$ is of the form $(-,+,-)$. We have a nontrivial situation if both $v_{2,2}>0$ and at least one of the two entries $v_{1,1}$ and $v_{1,3}$ is positive. Assume, say, that $v_{1,3}>0$. We may assume that $v_{1}+v_2$ is not of the form $(-,+,-)$, since otherwise $v_1$ and $v_1+v_2$ are two vectors of the same form as the initial ones, and thus we may iterate the argument. Now if $v_1+v_2$ is of one of the forms $(-,+,+)$ or $(+,+,-)$, then we are back to the preceding case and may proceed accordingly. The remaining possibilities are that $v_1+v_2$ is of one of the forms $(-,-,+)$, $(+,-,-)$, $(+,-,+)$. We bring again in $v_3$ which must be of the form $(+,-,-)$ unless we already achieved the desired increase of the negativity index. Should $v_1+v_2$ be of the form $(+,-,-)$, then we may $v_3$ replace by one of the vectors $\pm (v_3-v_1-v_2)$. The two remaining cases will be dealt with as respectively Case 6 and Case 7 below.

3.5.3 Case 3: $(+,-,-)$ and $(+,-,-)$.

If we have a combination with $v_1$ of the form $(+,-,-)$ and $v_2$ of the form $(+,-,-)$, then it is plain that at least one of the two vectors $v_1-v_2$ and $v_2-v_1$ is $\alpha$-admissible. Should the new vector u be of the same form, we may iterate the argument with $v_2$ replaced by u. Then after a finite number of iterations, we either reach a vector of the desired form $(+,+,+)$ or we end up with a combination like $(+,-,-)$ and $(+,-,+)$. This situation is covered by Case 6 and Case 7 below.

Up to inessential permutations, it now remains to check the following possible combinations of signs:

$$\begin{aligned}&\begin{pmatrix} v_1 \\ v_2 \\ v_3 \end{pmatrix} = \begin{pmatrix} - &{} - &{} + \\ + &{} - &{} - \\ - &{} + &{} - \end{pmatrix} ; \end{aligned}$$

(3.14)

$$\begin{aligned}&\begin{pmatrix} v_1 \\ v_2 \\ v_3 \end{pmatrix} = \begin{pmatrix} + &{} - &{} + \\ + &{} - &{} + \\ + &{} - &{} + \end{pmatrix} ; \end{aligned}$$

(3.15)

$$\begin{aligned}&\begin{pmatrix} v_1 \\ v_2 \\ v_3 \end{pmatrix} = \begin{pmatrix} - &{} - &{} + \\ + &{} - &{} + \\ + &{} - &{} + \end{pmatrix} ; \end{aligned}$$

(3.16)

$$\begin{aligned}&\begin{pmatrix} v_1 \\ v_2 \\ v_3 \end{pmatrix} = \begin{pmatrix} - &{} - &{} + \\ + &{} - &{} - \\ + &{} - &{} + \end{pmatrix} . \end{aligned}$$

(3.17)

3.5.4 Case 4: The combination. (3.14)

If a nonnegative entry, in absolute value, is less than or equal to the two other entries in the same column, then we may replace the corresponding vector by v by $-v$ without changing the negativity index of the three vectors $v_1$, $v_2$, $v_3$. That leads us to (3.17) (see below), that will be treated later. Otherwise, $v_1+v_2+v_3$ is $\alpha$-admissible, and we increase the negativity index if we replace the three vectors $v_1$, $v_2$, $v_3$ by $v_1$, $v_2$, $v_1+v_2+v_3$. Notice that $\alpha +v_1+v_2+v_3$ is indeed in $E_2(\{\alpha ,\alpha +v_1,\alpha +v_2, \alpha +v_3\})$ because

$$\begin{aligned} \alpha +v_1+v_2+v_3=(\alpha +v_1)+(v_2-v_1)+(v_3-v_1)-(-v_1). \end{aligned}$$

3.5.5 Case 5: The combination (3.15).

We may assume that $2v_{i,2}<\min _{j} v_{j,2}$ since otherwise we may add $v_i$ to $v_i$ as many times as needed to achieve this. These operations will not change the negativity index of the three vectors. Suppose that the largest value in the first column is $v_{1,1}$. In this case, if $v_{1,3}\ge v_{i,3}$ for $i\ne 1$, we then get a larger value in the second entry by replacing $v_1$ by $v_1-v_i$. Iterating this argument, we see that we may assume that $v_{1,3}<v_{i,3}$ for $i\ne 1$. Assume similarly that the maximum in the third column is $v_{2,3}$ and that $v_{2,1}<v_{i,1}$ for $i\ne 2$. Assume first that $v_{1,2}=v_{2,2}=v_{3,2}$. Then $v_4:=v_{1}+v_2-v_3$ has the same second entry but with $v_{2,1} \le v_{4,1}<v_{1,1}$ and $v_{1,3} \le v_{4,3}<v_{2,3}$. If we have equality in any of the two inequalities to the left, then $v_2-v_4$ or $v_1-v_4$ will be of the form $(+,+,+)$ so that we have reached the desired $\beta$. Otherwise we replace $v_1$ by $v_4$, which implies that we have decreased the first entry and increased the third entry of the first vector. Iterating, we see that we will then reach our desired $\beta$ in a finite number steps.

Hence we may assume in what follows that $v_{i,2}$ is not the same for all $i=1,2,3$. If now $v_{3,2}< \max (v_{1,2},v_{2,2})$, then $v_4:=v_{1}+v_2-v_3$ is $\alpha$-admissible, and its second entry is $> \min (v_{2,2}, v_{1,2})$. Hence, if say $v_{1,2}=\max (v_{1,2}, v_{2,2})$, then the negativity index of the vectors $v_1$, $v_3$, $v_{4}$ is strictly larger than that of $v_1$, $v_2$, $v_3$. If $v_{3,2}= \max (v_{1,2},v_{2,2})$, then still $v_4$ is $\alpha$-admissible and $v_{4,2}=\min (v_{2,2}, v_{1,2})$. If, say, again $v_{1,2}=\max (v_{1,2}, v_{2,2})$, then we may replace $v_2$ by $v_4$ and iterate the arguments just given. To simplify the notation, let $v_2$ denote the replacement found for $v_2$ at any stage of the iteration. If eventually $v_{2,3}=v_{3,1}$, then the iteration will terminate because $v_1-v_2$ will be of the form $(+,+,+)$. Otherwise, since $v_{2,3}$ will be strictly decreasing as long as $v_{2,3}>v_{3,3}$, we see that $v_{2,3}$ will eventually be smaller than or equal to $v_{3,3}$. If also $v_{3,1}\ge v_{2,1}$, then $v_3-v_2$ will now be of the form $(+,+,+)$. Should this not be the case, then we may interchange the roles of $v_2$ and $v_3$ and eventually obtain that $v_{3,2}< \max (v_{1,2},v_{2,2})$, as in the preceding case.

It remains to consider the case when both $v_{3,2}> v_{1,2}$ and $v_{3,2} > v_{2,2}$. If both $v_{1,1}\ge 2v_{3,1}$ and $v_{2,3}\ge 2v_{3,3}$, then we see that $v_4:=v_1+v_2-2v_3$ will be $\alpha$-admissible. Indeed, since by assumption $2v_{3,2}<\min (v_{1,2},v_{2,2})$, wee see that $v_{4,2}>\max (v_{1,2},v_{2,2})$. If, say, $v_{1,2}<v_{2,2}$, then the negativity index of $v_4$, $v_2$, $v_3$ will exceed that of $v_1$, $v_2$, $v_3$. Otherwise, if $v_{1,2}=v_{2,2}$, then we replace $v_1$ by $v_4$ and return to the starting point of the argument, noting that our gain in this first step is a strict increase of the second entry of the vector $v_1$.

Finally, if we have $v_{1,1}< 2v_{3,1}$, then the vector $v_4:=2v_3-v_1$ will satisfy $v_{4,2}>\min (v_{1,2}, v_{2,2})$, and if we have $v_{2,3}<2v_{3,3}$, then $v_4:=2v_3-v_2$ will satisfy the same inequality. We may in either case proceed in exactly the same way as when both $v_{1,1}\ge 2v_{3,1}$ and $v_{2,3}\ge 2v_{3,3}$.

3.5.6 Case 6: The combination (3.16).

We may assume that the largest value in the first column is $v_{2,1}$. If $v_{2,3}\ge v_{1,3}$, then we see that either $v_2-v_1$ is of the form $(+,+,+)$ or we reach Case 5 by replacing $v_1$ by the $\alpha$-admissible vector $v_2-v_1$. So we may assume that $v_{2,3}< v_{1,3}$. If instead $v_{3,3}\ge v_{1,3}$, then in a similar fashion $v_3-v_1$ is of the form $(+,+,+)$ or we may replace $v_1$ by $v_3-v_1$ to once again return to Case 5. We may therefore assume that both $v_{1,3}>v_{2,3}$ and $v_{1,3}>v_{3,3}$. If now $v_{2,3}\ge v_{3,3}$, then $v_2-v_3$ is $\alpha$-admissible; if it is not of the form $(+,+,+)$, then we may replace $v_2$ by $v_2-v_3$ and repeat the reasoning just made. This iteration will either produce a vector of the form $(+,+,+)$ or a situation in which $v_{2,3}$ is maximal in the first column and $v_{2,3}<v_{3,3}<v_{1,3}$. From this point on, we may follow word for word the reasoning in the preceding Case 5, now with the roles of $v_1$ and $v_2$ interchanged.

3.5.7 Case 7: The combination (3.17).

Assume first that $v_{3,3}$ is the largest value in the third column. Then we may replace $v_1$ by $v_3-v_1$ so that either $v_3-v_1$ is of the form $(+,+,+)$ or we have reduced our problem to the preceding Case 6. Similarly, if $v_{3,1}$ is the largest value in the first column, then either $v_3-v_2$ is of the form $(+,+,+)$ or we reduce our problem to Case 6 by replacing $v_2$ by $v_3-v_2$. We consider the final possibility that $v_{2,1}$ is maximal in the first column and $v_{1,3}$ is maximal in the third column. Hence we may assume that $v_{2,1}>v_{3,1}$ and $v_{1,3}>v_{3,3}$. We have now plainly that $v_{1,1}$ is minimal in the first column and that $v_{2,1}$ is minimal in the third column. This allows us to follow word for word the reasoning in Case 5, again with the roles of $v_1$ and $v_2$ interchanged. $\square$

4 $H^p(\mathbb {T}^\infty )$ and Applications to Hardy Spaces of Dirichlet Series

4.1 Hardy spaces on the infinite-dimensional torus.

Since $\mathbb T^\infty$ is a compact abelian group, Theorem 1.1 remains true for $d=\infty$ if we use the Haar measure $m_{\infty }$ of $\mathbb T^\infty$ to define $L^p(\mathbb T^\infty )$. To this end, we may as before either rely on combining the results of Rudin [Rud90] and Andô [And66] as indicated above or simply repeat our proof in Section 2.1 word for word. It is also plain that Theorems 1.2 and 1.3 remain valid when we set $d=\infty$. In the latter case, it should be noted that all subsets $\Gamma$ of $\mathbb {N}_0^{(\infty )}$ will consist of points with finitely many nonzero entries and that $E_n(\Gamma )$ can be defined in exactly the same way as in the finite-dimensional case. We refer to [BBSS19] and to [QQ21, Ch. 6] for further information about the spaces $H^p(\mathbb T^\infty )$.

Proof of Theorem 1.4

We will apply Theorem 1.3 with Example 3.4 for $n=1$ and Example 3.6 for $n\ge 2$. We go through the details only in the latter case, since the former is completely analogous. Consider

$$\begin{aligned} \Gamma _n := \left\{ (n,1,0,1),(n+1,0,1,0),(0,0,n+1,0),(0,0,0,n+1)\right\} \end{aligned}$$

for $n\ge 2$. By Theorem 1.3, we know that $\Gamma _n$ is a contractive projection set for $H^p(\mathbb {T}^4)$ if and only if $p=2,4,\ldots , 2(n+1)$. Decompose $\mathbb {T}^\infty$ into a infinite cartesian product of four-dimensional tori,

$$\begin{aligned} \mathbb {T}^\infty = \mathbb {T}_1^4 \times \mathbb {T}_2^4 \times \mathbb {T}_3^4 \times \cdots , \end{aligned}$$

where $\mathbb {T}_j^4$ contains the variables $z_{4j-3},z_{4j-2},z_{4j-1}$, and $z_{4j}$.

For $m\ge 1$, let $T_{m,n}$ be the operator defined by letting the projection $P_{\Gamma _n}$ act on each of the m four-dimensional tori $\mathbb {T}_{(m-1)m/2+1}^4,\,\ldots ,\, \mathbb {T}_{m(m+1)/2}^4$ independently. Clearly,

$$\begin{aligned} \Vert T_{m,n}\Vert _{H^p(\mathbb {T}^\infty )\rightarrow H^p(\mathbb {T}^\infty )} = \Vert P_{\Gamma _n}\Vert _{H^p(\mathbb {T}^4)\rightarrow H^p(\mathbb {T}^4)}^m. \end{aligned}$$

(4.1)

Define the operator $T_n$ by

$$\begin{aligned} T_n f = \sum _{m=1}^\infty \frac{T_{m,n} f}{m^2}. \end{aligned}$$

(4.2)

The operator (4.2) is well-defined for f in $H^p(\mathbb {T}^d)$ for every finite d, since in this case $T_{m,n} f = 0$ for every sufficiently large m. From this we conclude that $T_n$ is densely defined on $H^p(\mathbb {T}^\infty )$ (see e.g. [BBSS19, Theorem 2.1]).

We first consider the case when $p=2k$ for some integer $1 \le k \le n+1$. Since $\Vert P_{\Gamma _n}\Vert _{H^p(\mathbb {T}^4)\rightarrow H^p(\mathbb {T}^4)}=1$ by Theorem 1.3, we get from (4.1) and the triangle inequality that

$$\begin{aligned} \Vert T_n f\Vert _p \le \frac{\pi ^2}{6} \Vert f\Vert _p, \end{aligned}$$

so the operator (4.2) is well-defined on $H^p(\mathbb {T}^\infty )$ with norm at most $\pi ^2/6$.

Consider next the case when $1 \le p \le \infty$, $p\ne 2n$, for $1 \le k \le n+1$. Since $P_{\Gamma _n}$ is not a contraction on $H^p(\mathbb {T}^4)$ we have

$$\begin{aligned} \Vert T_{m,n}\Vert _{H^p(\mathbb {T}^\infty )\rightarrow H^p(\mathbb {T}^\infty )} = (1+\delta _p)^m \end{aligned}$$

for some $\delta _p>0$. Since each $T_{m,n}$ acts on separate variables, we get from (4.2) that

$$\begin{aligned} \Vert T_n\Vert _{H^p(\mathbb {T}^\infty )\rightarrow H^p(\mathbb {T}^\infty )} \ge \frac{(1+\delta _p)^m}{m^2} \end{aligned}$$

for every positive integer m and, consequently, $T_n$ is unbounded on $H^p(\mathbb {T}^\infty )$. $\square$

Problem 4.1

Is there a linear operator T that is densely defined on $H^p(\mathbb {T}^\infty )$ for $1 \le p \le \infty$ and extends to a bounded operator on $H^p(\mathbb {T}^\infty )$ if and only if p is an even integer or $p=\infty$?

4.2 Hardy spaces of Dirichlet series.

For $1 \le p < \infty$, the Hardy space of Dirichlet series $\mathscr {H}^p$ can be defined as the closure of the set of Dirichlet polynomials $f(s) = \sum _{n=1}^N a_n n^{-s}$ in the Besicovitch norm

$$\begin{aligned} \Vert f\Vert _{\mathscr {H}^p}^p = \lim _{T\rightarrow \infty } \frac{1}{2T} \int _{-T}^T |f(it)|^p\,dt. \end{aligned}$$

The endpoint case $\mathscr {H}^\infty$ is comprised of somewhere convergent Dirichlet series that may be analytically continued to bounded analytic functions in the half-plane ${\mathrm{Re}}{s}>0$, and we set

$$\begin{aligned} \Vert f\Vert _{\mathscr {H}^\infty } := \sup _{{\mathrm{Re}}{s}>0}|f(s)|. \end{aligned}$$

Let $(p_j)_{j\ge 1}$ denote the increasing sequence of prime numbers. By the fundamental theorem of arithmetic, every positive rational number is uniquely represented as

$$\begin{aligned} q = \prod _{j=1}^d p_j^{\alpha _j} \qquad \longleftrightarrow \qquad \alpha (q) = (\alpha _1,\alpha _2,\ldots ,\alpha _d,0,0,0,\ldots ). \end{aligned}$$

This representations associates to each q in $\mathbb {Q}_+$ a unique multi-index $\alpha$ in $\mathbb {Z}^{(\infty )}$. It follows that the groups $(\mathbb {Z}^{(\infty )},+)$ and $(\mathbb {Q}_+,\times )$ are isomorphic. Note that the subset $\mathbb {N}_0^{(\infty )}$ of $\mathbb {Z}^{(\infty )}$ is identified with the subset $\mathbb {N}$ of $\mathbb {Q}_+$.

The Bohr correspondence

$$\begin{aligned} \mathscr {B}f(z) := \sum _{n=1}^\infty a_n z^{\alpha (n)} \end{aligned}$$

defines an isometric isomorphism from $\mathscr {H}^p$ to $H^p(\mathbb {T}^\infty )$. In the range $1 \le p < \infty$ this can be established either by the ergodic theorem (see [Bay02, Section 2]) or by a simple argument using the Weierstrass approximation theorem (see [SS09, Section 3]). For $p=\infty$ we can prove the isometric isomorphism by taking the limit $p\rightarrow \infty$ and using Bohr’s theorem [Boh13], which guarantees that Dirichlet series in $\mathscr {H}^\infty$ are uniformly convergent in the half-plane ${\mathrm{Re}}{s}\ge \delta$ for every $\delta >0$.

A set $\Gamma \subseteq \mathbb {N}$ is called a contractive projection set for $\mathscr {H}^p$ if the projection $P_\Gamma f(s) := \sum _{n \in \Gamma } a_n n^{-s}$ is a contraction on $\mathscr {H}^p$. In view of the discussion in Section 4.1, we may then translate Theorem 1.2 for the special case $d=\infty$ into a corresponding assertion about $\mathscr {H}^p$. We refrain from carrying out the details, noting only that we will then be dealing with restrictions of sets and cosets in $\mathbb {Q}_+$ to $\mathbb {N}$.

In this context, computations with contractive project sets for $\mathscr {H}^p$ will frequently involve arithmetic functions. A useful example, alluded to in the introduction and employed in [BS16], is the set

$$\begin{aligned} \Gamma _m := \left\{ n \in \mathbb {N}\,:\,\Omega (n)=m\right\} , \end{aligned}$$

where $\Omega (n)$ denotes the number of prime factors of n (counting multiplicities). As in Example 2.2, the formula for the projection is

$$\begin{aligned} P_{\Gamma _m}f(s) = \int _{\mathbb {T}} \left( \sum _{n=1}^\infty a_n w^{\Omega (n)} n^{-s} \right) \,w^{-m}\,dm_1(w) \end{aligned}$$

for $f(s) = \sum _{n\ge 1} a_n n^{-s}$ in $\mathscr {H}^p$.

We may reformulate Theorem 1.4 to obtain the following result.

Corollary 4.2

Fix an integer $n\ge 1$. There is a linear operator $T_n$ which is densely defined on $\mathscr {H}^p$ for every $1 \le p \le \infty$, and which does not extend to a bounded operator on $\mathscr {H}^p$ unless $p=2,4,\ldots ,2(n+1)$.

Perhaps the most important open problem in the study of the spaces $\mathscr {H}^p$ is the local embedding problem [SS16, Prob. 2.1], which asks whether there is a constant $C_p>0$ such that

$$\begin{aligned} \int _{-1}^1 |f(1/2+it)|^p\,dt \le C_p \Vert f\Vert _{\mathscr {H}^p}^p \end{aligned}$$

(4.3)

for every f in $\mathscr {H}^p$. The answer to the embedding problem is known to be positive if p is an even integer (see e.g. [SS09, Section 3]) and negative if $p < 2$ as a corollary to a recent result of Harper [Har20].

The work of Bayart and Mastyło [BM19], which we discussed in the introduction, demonstrates that the standard interpolation techniques cannot be employed to extend the positive conclusion for the embedding problem from even integers p to general $p>2$. Based on this and the analogy with the Hardy–Littlewood majorant principle (elucidated in [Mon94, Section 7.3]), it is conjectured in [QQ21, p. 274] that the local embedding should hold only for even integers p (and, trivially, for $p=\infty$).

The local embedding problem can be restated in terms of the boundedness of a densely defined linear operator. Consider the composition operator defined on $\mathscr {H}^p$ by $\mathscr {C}_\varphi f := f \circ \varphi$ for

$$\begin{aligned} \varphi (s) := \frac{1}{2} + \frac{1-2^{-s}}{1+2^{-s}}. \end{aligned}$$

The operator is well-defined and bounded on $\mathscr {H}^\infty$ by Bohr’s theorem, so it is densely defined on $\mathscr {H}^p$ for every $1 \le p \le \infty$. We know from [BB19, Theorem 3] that $\mathscr {C}_\varphi$ is bounded on $\mathscr {H}^p$ if and only if the local embedding (4.3) holds. We note in passing that if p is an even integer or $p=\infty$, then actually $\Vert \mathscr {C}_\varphi \Vert _{\mathscr {H}^p\rightarrow \mathscr {H}^p} = 2^{1/p}$ by results in [Bre17] and [QQ21, Section 8.11].

The operator $\mathscr {C}_\varphi$ is unbounded for $p<2$ by Harper’s result. Hence, if the local embedding (4.3) holds for $p>2$ only if p is an even integer, then $\mathscr {C}_\varphi$ is the operator enquired after in Problem 4.1. In this context, Corollary 4.2 does not render it implausible that the local embedding may hold only for even integers (and $p=\infty$).