Half-dimensional collapse of ends of manifolds of nonpositive curvature

Abstract

This paper accomplishes two things. First, we construct a geometric analog of the rational Tits building for general noncompact, complete, finite volume n-manifolds M of bounded nonpositive curvature. Second, we prove that this analog has dimension less than $\lfloor n/2\rfloor$.

1 Introduction

Let M be a noncompact, complete Riemannian n-manifold with bounded nonpositive sectional curvature $-1 < K\le 0$ and finite volume. We also assume that Mdoes not have arbitrarily small geodesic loops, that is, there is a positive lower bound to the length of any geodesically embedded circle. Good examples to think about are locally symmetric spaces of noncompact type, such as hyperbolic manifolds, products of surfaces, and the usual beloved $K\backslash G/\Gamma$. Sometimes taking $G = {{\,\mathrm{SL}\,}}_m{\mathbb {R}}$ and $K = {{\,\mathrm{SO}\,}}_m$ can be as satisfactory as any other semisimple Lie groups. This sentiment holds true in terms of examples to keep in mind as one reads since our approach throughout this paper is purely geometric/topological but can be demonstrated by thinking about these concrete examples the right way.

The condition that M has no arbitrarily small geodesic loops holds when M is negatively curved, i.e. $-1<K<0$, or when M is locally symmetric. One reason we need this condition in the general setting of bounded nonpositive curvature is in order to ensure, by a theorem of Gromov–Schroeder, that M is tame in the sense that the thin part $M_{< \varepsilon }$ has finitely many components and each component is topologically a product of a closed $(n-1)$-manifold with a ray. The mechanism for tameness is that the injectivity radius function on M does not have any critical point outside a compact set which can be taken to be the thick part $M_{> \varepsilon }$ for some small$\varepsilon >0$ (see also Appendix 2 of [BGS85] for a generalization). Let $\widetilde{M}_{<\varepsilon }$ be the preimage of the thin part $M_{<\varepsilon }$ under the universal covering map. We will call $\widetilde{M}_{<\varepsilon }$ the thin part of $\widetilde{M}$. It is the topology of $\widetilde{M}_{<\varepsilon }$ that we would like to describe.

When M is locally symmetric (and arithmetic), $\widetilde{M}_{<\varepsilon }$ is homotopy equivalent to the rational Tits building, which is a $(k-1)$-dimensional complex, where k is the rational rank of M. The rational Tits building of M can be realized as a subset of the visual boundary $\partial _\infty$ of $\widetilde{M}$ and can be thought of as the set of points at infinity that can be reached if one moves only within $\widetilde{M}_{<\varepsilon }$. The rank k is at most n / 2 with $k=n/2$ when M is a product of non-compact surfaces. The main purpose of this paper is to show that the n / 2 bound on the dimension of the rational Tits building is no arithmetic coincidence but in a slightly weaker sense.

In the general nonpositively curved setting, for an n-dimensional manifold M satisfying the conditions described above, we define a map

$$\begin{aligned} \rho :\partial \widetilde{M}_{<\varepsilon } \rightarrow \partial _\infty \end{aligned}$$

that is an analog of a rational Tits building in the sense that $\rho$ encodes all the directions to infinity necessary to push any topological feature (e.g. homology cycles, maps) in $\widetilde{M}_{<\varepsilon }$ without it leaving $\widetilde{M}_{<\varepsilon }$. We then prove that the image of $\rho$ has dimension at most $(\lfloor n/2 \rfloor -1)$, where $\lfloor n/2 \rfloor$ is the greatest integer less than or equal to n / 2.

Theorem 1

   Let M be a noncompact, complete, Riemannian manifold with bounded nonpositive sectional curvature $-1 < K\le 0$ and finite volume. Assume that M has no arbitrarily small geodesic loops. Let $\varepsilon > 0$ be smaller than the Margulis constant and small enough so that $M_{<2\varepsilon }$ is topologically a product with a ray. Then there is a $\pi _1(M)$-equivariant, Lipschitz map $\rho :\partial \widetilde{M}_{<\varepsilon } \rightarrow \partial _\infty$, defined on a triangulation of $\partial \widetilde{M}_{<\varepsilon }$, with the following properties.

• (a) For each $x\in \partial \widetilde{M}_{<\varepsilon }$, the unique unit speed geodesic ray $[x,\rho (x))$ connecting x to $\rho (x)$ stays in $\widetilde{M}_{<2\varepsilon }$. Moreover, the projection of $[x,\rho (x))$ to M escapes every compact set in M.

• (b) If $\sigma$ is a simplex in $\partial \widetilde{M}_{<\varepsilon }$, then $\rho (\sigma )$ has dimension less than $\lfloor n/2\rfloor$.

We can use $\rho$ to show that any polyhedron in $\widetilde{M}_{<\varepsilon }$ can be homotoped within $\widetilde{M}_{<\varepsilon }$ to one with dimension at most $(\lfloor n/2 \rfloor -1)$.

Theorem 2

   Assume the hypotheses of Theorem 1. Let P be a finite polyhedron and let $\varphi :P \rightarrow \widetilde{M}_{<\varepsilon }$ be a continuous map. Then $\varphi$ can be homotoped within $\widetilde{M}_{<\varepsilon }$ to a map ${\widehat{\varphi }} :P \rightarrow \widetilde{M}_{<\varepsilon }$ whose image has dimension $\le \lfloor n/2\rfloor -1$.

This is done by pushing P toward $\rho (P)$ until it is deep enough in $\widetilde{M}_{<\varepsilon }$ that we can “collapse” P onto a close-by copy of $\rho (P)$. The following corollary is an almost immediate consequence.

Corollary 3

The map ${\widehat{\varphi }}$ in Theorem 2 can be homotoped in ${\widetilde{M}}_{<\varepsilon }$ to factor through a polyhedron Q of dimension $\lfloor n/2\rfloor -1$. Consequently, the homology of $\widetilde{M}_{<\varepsilon }$ vanishes in dimension $\ge \lfloor n/2\rfloor$, i.e.

$$\begin{aligned} H_{\ge \lfloor n/2\rfloor }({\widetilde{M}}_{<\varepsilon })=0. \end{aligned}$$

(1)

The idea behind all of this is that we push any topological feature, such as a polyhedron P, to infinity within $\widetilde{M}_{<\varepsilon }$. Of course, we can always push anything in $\widetilde{M}_{<\varepsilon }$ to infinity since M has tame ends, but we want to push P in such a way not to stretch it more than we absolutely have to. The number of degrees of freedom in stretching P is the dimension of $\rho (P)$. This is why we build $\rho$ and why we need to make it as low dimensional as possible. In a way, the topology of $\widetilde{M}_{<\varepsilon }$ is very much determined by $\rho$.

Remark

The upper bound on the dimension of Q is sharp by the following example. If M is the product of k punctured tori $S_1\times \dots \times S_k$, each with a complete hyperbolic metric with finite volume, then M has dimension $n = 2k$, so $\lfloor n/2\rfloor -1 = k-1$. We also know that in this case $\widetilde{M}_{<\varepsilon }$ is homotopy equivalent to a wedge of $(k-1)$-spheres. One can see this explicitly by covering $\widetilde{M}_{<\varepsilon }$ with convex sets and taking the nerve of this cover. The convex sets can be chosen as follows. For each $S_i$, let $\gamma _i$ be the loop that shrinks to zero, and take the pre-image in ${\widetilde{M}}$ of the sets $U_i=\{|\gamma _i|<\varepsilon \}$ of points in M where the loop $\gamma _i$ is smaller than $\varepsilon$. For $\varepsilon$ small enough, the collection $\{p^{-1}(U_i)\}_{i=1,2,\ldots ,k}$ covers $\widetilde{M}_{<\varepsilon }$. Each connected component of $p^{-1}(U_i)$ is a convex subset of ${\widetilde{M}}$. The collection of connected components of $\{p^{-1}(U_i)\}_{i=1,2,\ldots ,k}$ is the cover that we take. It is not hard to see that the nerve of this cover is the k-fold join of infinite discrete sets, which is homotopy equivalent to an infinite wedge of $(k-1)$-spheres.

1.1 Optimal examples.

In [AN17] we build, for each n, an n-manifold M satisfying the hypotheses of Theorem 1 which has

$$\begin{aligned} {\overline{H}}_k({\widetilde{M}}_{<\varepsilon })\not =0\quad \text{ for } \text{ all } k<\lfloor n/2\rfloor . \end{aligned}$$

So, unlike in the case of locally symmetric spaces, in general there are no low dimensional homology vanishing results complementing the high dimensional homology vanishing (1).

1.2 Some other forms of collapse.

Of course in some situations we expect to be able to do better than $\lfloor n/2\rfloor$. For example, in the simple case of a finite volume hyperbolic manifold, every component of the thin part ${\widetilde{M}}_{<\varepsilon }$ collapses to a point. The feature responsible for this collapse is that the Tits boundary is discrete. In fact, the dimension of the Tits boundary $(\partial _{\infty },{{\,\mathrm{Td}\,}})$ of $\widetilde{M}$ is one of the factors that control the topology of $\widetilde{M}_{<\varepsilon }$. This is reflected in the fact that the map $\rho$ we construct is continuous (in fact, Lipschitz) in the Tits metric.

Remark

More precisely, by dimension we mean the compact topological dimension, which is defined as the maximum of the covering dimensions of compact subspaces. See [Kle99] for a comparison of different notions of dimension for the Tits boundary.

In addition, $\rho$ is constructed in such a way that it factors through a complex built out of virtual equivalence classes of certain Abelian subgroups of $\pi _1M$. So, the topology of this complex is another factor that controls the topology of ${\widetilde{M}}_{<\varepsilon }$. This leads to two additional forms of collapse via ranks of Abelian groups and dimension of the Tits boundary. To express it, let

$$\begin{aligned} d=\min \{\text{ rank }_{Ab}(\pi _1M)-1,\quad \dim (\partial _{\infty },{{\,\mathrm{Td}\,}}),\quad \lfloor n/2\rfloor -1\} \end{aligned}$$

where

• $\text{ rank }_{Ab} (\pi _1M)$ is the maximum rank of an Abelian subgroup of $\pi _1M$,

• $\dim (\partial _{\infty },{{\,\mathrm{Td}\,}})$ is the dimension of the Tits boundary, and

• $\lfloor n/2\rfloor$ still denotes the greatest integer less than or equal to n / 2.

Theorem 4

   Theorem 2 is true if we replace “$\lfloor n/2\rfloor -1$” by “d”.

Remark

If M is a noncompact, finite volume hyperbolic n-manifold, with several cusps then the fundamental group $\Gamma$ contains a parabolic Abelian subgroup of rank $n-1$. Doubling such a manifold along one of its cusps gives a non-positively curved manifold containing an Abelian subgroup of rank $n-1$ that consists of hyperbolic elements, in which case $\dim (\partial _{\infty },{{\,\mathrm{Td}\,}})\ge n-2$. So, the bounds via ranks of Abelian groups and via the dimension of the Tits boundary are situational. But, the half dimension bound $d\le \lfloor n/2\rfloor -1$ is something we always have.

1.3 Low dimensional collapse.

Now let us turn to the special situation when d is small. Notice that $d\le 1$ if

• $\pi _1M$ does not contain ${\mathbb {Z}}^3$, or

• $\dim (\partial _{\infty },{{\,\mathrm{Td}\,}})\le 1$, or

• $\dim M\le 5$.

In any of these situations we get the following immediate corollary.

Corollary 5

If $d\le 1$ then each component of the end $M_{<\varepsilon }$ is aspherical.

Once we know that each component of the end is aspherical, it is natural to ask “how bad” this aspherical manifold can be, i.e. how exotic its fundamental group is. We prove the following amplification of Corollary 5. Recall that a countable group F is locally free if every finitely generated subgroup is free.

Theorem 6

   If $d\le 1$ then for each component C of $M_{<\varepsilon }$ the fundamental group is an extension

$$\begin{aligned} 1\rightarrow F\rightarrow \pi _1 C\rightarrow \pi _1M \end{aligned}$$

of a subgroup of $\pi _1M$ by a locally free group F.

In proving the main theorems we obtain the following.

Technical byproduct of independent interest. Let G be a group that acts on a Hadamard n-manifold $\widetilde{M}$ via covering space transformations. Note that the sectional curvatures of ${\widetilde{M}}$ need not be bounded from below. Suppose that G preserves horospheres centered at $\{z_i\}_{i = 0,\ldots , k} \subset \partial _\infty$. We ask the following questions.

• 1. Can one connect in $\partial _{\infty }$ the $z_i$’s through points the horospheres centered at which are preserved by G?

• 2. If so, then the $z_i$’s can be filled by a k-simplex $\Delta ^k$. That is, one gets a map

  $$\begin{aligned} \sigma :\Delta ^k \rightarrow \partial _\infty , \end{aligned}$$

  such that horospheres centered at each point in $\sigma (\Delta ^k)$ are preserved. How nice (e.g. continuous, Hoelder, Lipschitz, etc) can this map be?

• 3. Let ${{\,\mathrm{Fix}\,}}^0(G)$ be the set points in $\partial _\infty$ whose horospheres are preserved by G. What is the relation between the dimension of ${{\,\mathrm{Fix}\,}}^0 (G)$ and the dimension of G?

We answer these questions in the case when the vertices $z_i$ are mutually a Tits distance $\le \pi /2$ apart in Sections 9 and 12. In short, the answer to the first question is yes, the answer to the second question is Lipschitz—we construct such a map $\sigma$, which we call a Busemann simplex (defined in 9.2)—and the answer to the third question is the following.

Theorem 7

   If the vertices $z_i$ span a non-degenerate Busemann k-simplex, then the homological dimension of G is less than $(n-k)$.

On Section 2and Subsection 12.1. We would like to warn the readers about the unorthodox way these sections are written and that they are written not to sketch the proof of the main theorems but to communicate what is not captured in the proof. The purpose of Section 2 and Subsection 12.1 is to discuss the problems, that is, to point the readers to where the difficulties lie. Their role is complementary to the proof. The proof of the main theorem in this paper consists of a mixture of steps and lemmas, some of which are trivial, some of which are just technicalities and some of which deal with actual difficulties. Section 2 and Subsection 12.1 are our attempt to pin-point where the difficulties lie in a coherent, though imprecise, way.

We “motivate” the proof of Theorem 2 in Section 2. Theorem 1 will be attained along the way. We will try to explain why things are done the way they are through an iteration of “what is the simplest thing to do?” and “what are the problems to overcome?” until there are no more problems. Good examples to think about are locally symmetric spaces, in particular ${{\,\mathrm{SO}\,}}_3\backslash {{\,\mathrm{SL}\,}}_3{\mathbb {R}}/{{\,\mathrm{SL}\,}}_3{\mathbb {Z}}$ and products of surfaces.

Some readers might find Section 2 and Subsection 12.1 “madness”, in which case they are encouraged to skip them (or read them afterwards for perspective) and proceed to the precise formulation given in the rest of the paper.

2 Problems and Solutions

Let P be as in Theorem 2. One can naively take a length minimizing geodesic ray $\gamma$ in M starting at a point in $\varphi (P)$, take a lift $\widetilde{\gamma }$ of $\gamma$, and then push P toward $\widetilde{\gamma } (\infty ) \in \partial _\infty$ with unit speed. Then the diameter of P will stay bounded, so once it is far enough to infinity it will be contained in a ball that is contained in $\widetilde{M}_{<\varepsilon }$. We then can contract P to a point within this ball. However, there is a problem with this approach, which is that as we push P toward $\widetilde{\gamma }(\infty )$ it might slide off $\widetilde{M}_{<\varepsilon }$ for some time during this process. This problem does not have a solution for otherwise one could contract any such P to a point within $\widetilde{M}_{<\varepsilon }$, which is not true if M is a product of noncompact surfaces.

So we need to find a way to push P to infinity without it leaving $\widetilde{M}_{<\varepsilon }$. The strategy is that we push different points of P to different points in the visual boundary $\partial _\infty$ along geodesics and we keep track of the amount of directions to infinity we need. The set of points in $\partial _\infty$ to which we push P tells us how much P “expands” as we push it to infinity. It also gives a complex $c_t(P)$ in $\widetilde{M}_{<\varepsilon }$ to which we can “collapse” P onto. We then bound the dimension of this complex to be less than $\lfloor n/2\rfloor$ by trying to make this process as efficient (in terms of how many degrees of freedom are needed as P expands) as possible.

Keeping the homotopy within the thin part$\widetilde{M}_{<\varepsilon }$. For each point x of the polyhedron P, we find in $\partial _\infty$ a point $\rho (x)$ to which we push x with unit speed along the geodesic connecting x with $\rho (x)$ as illustrated in Figure 1. We call this homotopy

$$\begin{aligned} \varphi _t :P \rightarrow \widetilde{M}_{<\varepsilon }, \quad \text {for} \ t\in [0,\infty ), \ \text {with} \ \varphi _0 = \varphi . \end{aligned}$$

We will define $\rho :P \rightarrow \partial _\infty$ systematically, skeleton by skeleton. Start with the vertices of P and suppose that x is a vertex of P. Since $\varphi (x)$ is in $\widetilde{M}_{<\varepsilon }$, there is a parabolic isometry $\gamma _x$ that moves $\varphi (x)$ by a small amount, where small means less than $\varepsilon$, so that the group $\Gamma _x$ generated by such $\gamma _x$ is virtually nilpotent by the Margulis lemma. Therefore, a natural choice for $\rho (x)$ is the center of a horosphere preserved by $\Gamma _x$ because if we push x to $\rho (x)$ along a geodesic $\varphi _t(x)$, then the small elements in $\Gamma _x$ will remain small along $\varphi _t(x)$, so $\varphi _t(x)$ will stay in $\widetilde{M}_{<\varepsilon }$.

Fig. 1

Pushing to infinity.

Next, we extend $\rho$ to the edges and higher dimensional simplices of P. Just like for the vertices, the way to go to infinity is to “follow the shrinking small loops”. Let e be the edge connecting vertices $x_0$ and $x_1$ of P. Clearly a problem is that there is no clear “transition” in terms of small loops at $\varphi (x_0)$ to small loops at $\varphi (x_1)$. But there is a solution, which is to take a fine enough subdivision of P at the beginning. That is, we take a subdivision of P in which the diameter of each simplex is tiny enough so that if $\sigma$ is a k-simplex of P with vertices $x_0, x_1,\ldots , x_k$, then for each point $y \in \sigma$, some parabolic isometry that is small at $\varphi (x_i)$ is still small at $\varphi (y)$. We can always take such a subdivision of P, so we can harmlessly assume that P is triangulated in such a way at the beginning.

This gives us a way to assign to each simplex a nontrivial nilpotent group as follows. Let $\Gamma = \pi _1(M)$. For a vertex x of P, let

$$\begin{aligned} S_x = \{ \gamma \in \Gamma \; |\; d(x,\gamma (x)) <\varepsilon \} \end{aligned}$$

be the set of $\varepsilon$-small parabolic isometries at $\varphi (x)$. Then by the Margulis lemma, the group

$$\begin{aligned} \Gamma _x = \langle \gamma \; |\; \gamma \in S_x \rangle , \end{aligned}$$

has a nilpotent subgroup of index less than a constant $I_n$ that depends only on n. We assign to x the following nontrivial nilpotent subgroup

$$\begin{aligned} N_x = \langle \gamma ^{I_n!} \; |\; \gamma \in \Gamma _x \rangle \end{aligned}$$

of $\Gamma _x$. Note that $N_x$ is characteristic and thus normal in $\Gamma _x$. One might worry with this choice of nilpotent group at x the group $N_x$ may not contain any small parabolic isometry. This can easily be fixed by making $\varepsilon$ small enough at the beginning. For a k-simplex $\sigma = x_0*x_1*\cdots *x_k$, let

$$\begin{aligned} \Gamma _\sigma = \langle \Gamma _{x_0}, \ldots , \Gamma _{x_k} \rangle . \end{aligned}$$

We assign to $\sigma$ the nilpotent group

$$\begin{aligned} N_\sigma = \langle \gamma ^{I_n!} \; |\; \gamma \in \Gamma _\sigma \rangle . \end{aligned}$$

Let $Z_\sigma = Z_{N_\sigma }$ be the center of $N_\sigma$. Note that $Z_\sigma$ is normal in $\Gamma _\sigma$.

Since nilpotent groups are at times harder to deal with than Abelian groups—life is hard enough already—we try to make things as easy as we can by assigning to the simplex $\sigma$ the Abelian group $A_\sigma = Z_\sigma$. Again, if one is worried, one can pick $\varepsilon$ to be small enough at the beginning so that $A_\sigma$ has small elements.

Now the problem with this is that this does not quite give us a way to define $\rho$ on an edge e connecting $x_0$ and $x_1$ because what we get from $A_e$ is the center of a horosphere preserved by $A_e$ to which we can push e without it leaving $\widetilde{M}_{<\varepsilon }$. However, this center is only one point while what we are looking for is a path connecting $\rho (x_0)$ and $\rho (x_1)$. Nevertheless, what we have obtained is a way to define $\rho$ on the vertices of the first barycentric subdivision $P_1$ of P. Note that in this assignment of Abelian groups adjacent vertices in $P_1$ have commuting Abelian groups.

There will be a solution to the above problem if the distance between adjacent vertices of $P_1$ in the Tits metric ${{\,\mathrm{Td}\,}}$ on $\partial _\infty$ is less than $\pi$ because then there will be a unique geodesic in $(\partial _\infty , {{\,\mathrm{Td}\,}})$ connecting them, so we can use this to define $\rho$ on the edges of $P_1$. This turns out to be true if we are picky enough when we pick where $\rho$ sends vertices of $P_1$. In fact, we can, for each simplex, make $\rho$ send all of its vertices to a set of Tits-diameter $\le \pi /2$ in $\partial _\infty$.

For each Abelian group $A_x$, where x is a vertex of $P_1$, let ${{\,\mathrm{Fix}\,}}(A_x)$ be the set of fixed points of $A_x$ in $\partial _\infty$. There is a canonical way (see Section 5) to define a unique “Center of Mass” $\xi _{A_x} \in {{\,\mathrm{Fix}\,}}(A_x)$ such that

• any isometry $\gamma$ that normalizes $A_x$ fixes $\xi _{A_x}$, and

• all points in ${{\,\mathrm{Fix}\,}}(A_x)$ are within a Tits distance of $\pi /2$ from $\xi _{A_x}$.

Define $\rho (x) = \xi _{A_x}$. Then by the first property above, adjacent Abelian groups in $P_1$ fix each other’s Centers of Mass. By the second property, they are within a Tits distance of $\pi /2$ from each other. It follows that any two adjacent vertices $x_0$ and $x_1$ in $P_1$ can be connected by a unique geodesic $\rho (e)$ in $\partial _\infty$ connecting $\rho (x_0)$ and $\rho (x_1)$. Parametrize both e and $\rho (e)$ by constant speed and use this to define $\rho$ on e the obvious way. We can extend $\rho$ to higher dimensional skeleta via geodesic triangles in the obvious way.

Now that we have found a way to define $\rho$ on $P_1$, we need to check that the homotopy $\varphi _t$ does not push P off the thin part $\widetilde{M}_{<\varepsilon }$. For each k-simplex $\sigma$ in $P_1$, we have a chain $\Gamma _{x_0} \le \cdots \le \Gamma _{x_k}$. The “bottom” group $\Gamma _{x_0}$ normalizes $A_{x_0},\ldots , A_{x_k}$ and therefore fixes $\rho (x_i) = \xi _{A_{x_i}}$ for all $i =0, 1,\ldots ,k$. It follows that $\Gamma _{x_0}$ fixes $\rho (\sigma )$pointwise. Remember that there is an element $\gamma$ of $\Gamma _{x_0}$ that is small at $x_0$ and that is still small at all points $y \in \sigma$. Since $\gamma$ fixes $\rho (y)$, it will stay small on $\varphi _t(y)$ for all $t >0$, and therefore, the homotopy $\varphi _t$ does not move P off $\widetilde{M}_{<\varepsilon }$. Note that this shows we did not have to go back and manually make $\varepsilon$ smaller at the beginning as one might have worried before. Now, we can move on to the next task.

“Collapsing”Pwithin$\widetilde{M}_{<\varepsilon }$. Now that we have defined $\rho$ of P and made sure that pushing P to $\rho (P)$ does not leave $\widetilde{M}_{<\varepsilon }$, we want to find a copy of $\rho (P)$ in $\widetilde{M}$ to which we can “collapse” P within $\widetilde{M}_{<\varepsilon }$. Take a point $c_0\in {\widetilde{M}}$ and take the geodesic cone on $\rho (P)$ with cone point $c_0$. For $t \ge 0$ and $x\in P$, let $c_t(x)$ be the point obtained by flowing for time t along the geodesic ray from $c_0$ to $\rho (x)$. Then $c_t(P)$ homeomorphic to $\rho (P)$ because geodesic retractions are homeomorphisms. Also, it is not hard to see that the distance between $\varphi _t(P)$ and $c_t(P)$ is bounded by some number R that does not depend on $t\ge 0$ (but depends on P and $c_0$). Thus, we can “collapse” $\varphi _t(P)$ onto $c_t(P)$ in an R-neighborhood of $\varphi _t(P)$.

There is a problem, which is that the “collapse” might leave $\widetilde{M}_{<\varepsilon }$, which could happen if the R-neighborhood of $\varphi _t(P)$ is large enough that it contains points outside $\widetilde{M}_{<\varepsilon }$. But there is a solution if we can show that for t large enough, $\varphi _{t_{\text {large}}}(P)$ is deep enough in $\widetilde{M}_{<\varepsilon }$ that an R-neighborhood of $\varphi _{t_{\text {large}}}(P)$ is contained in $\widetilde{M}_{<\varepsilon }$, so when we collapse $\varphi _{t_{\text {large}}}(P)$ to $c_{t_{\text {large}}}(P)$ it will not leave $\widetilde{M}_{<\varepsilon }$ during this process. Therefore, in addition to making sure that $\varphi _t(\sigma )$ stays in $\widetilde{M}_{<\varepsilon }$ for all $t >0$, we also need its projection under the covering space projection $p :\widetilde{M} \rightarrow M$ to be divergent in M. That is, $p(\varphi _t(P))$ leaves all compact sets in M as $t\rightarrow \infty$ (Figure 2). This is true by the following key lemma.

Fig. 2

Divergent ray.

Lemma 8

(Divergent Geodesic Ray). Let A be a free Abelian group of isometries. Suppose the centralizer $C_A$ preserves each horosphere centered at a point $\xi$ in $\partial _\infty \widetilde{M}$. Then for any geodesic ray $r :[0,\infty )\rightarrow \widetilde{M}$ with end point $r(\infty ) = \xi$ the projection p(r(t)) is divergent.

More generally, if $r(\infty )=\eta$ for some $\eta$ fixed by $C_A$ and ${{\,\mathrm{Td}\,}}(\eta ,\xi )<\pi /2$ then p(r(t)) is also divergent.

Lemma 8 takes care of the above problem if for each Abelian group $A_x$ above the horospheres centered at the Center of Mass$\xi _{A_x}$are preserved by the centralizer$C_{A_x}$. We prove that this is true in Section 5. If one is concerned that Lemma 8 might apply to only one single ray $\varphi _t(x)$ at a time but not uniformly to a family $\varphi _t(P)$ of rays, then one is absolutely right, but we take care of this in Proposition 14, which says that one needs not worry if P is bounded (and P is indeed bounded).

Bounding the dimension of$\rho (P)$. That the dimension of $\rho (P)$ is at most $\lfloor n/2 \rfloor -1$ is due to two factors.

• First, for each simplex $\sigma =x_0*x_1*\cdots *x_k$ in $P_1$, we get a “biggest” Abelian group $A^\sigma = \langle A_{x_0}, \ldots , A_{x_k}\rangle$. The group $A^\sigma$ is Abelian because the groups $A_{x_i}$’s commute with each other. Also, $A^\sigma$ preserves horospheres centered at $\rho (x_i) = \xi _{A_{x_i}}$ for $i = 0,\ldots , k$ and therefore preserves their intersection. If $\rho (x_i)$’s span an l-dimensional simplex at infinity (for $l \le k$), then the dimension of the intersection of the horospheres should be $n-(l+1)$. This should mean that the rank of $A^\sigma$ is less than or equal to $n-(l+1)$.

• Second, if $\sigma$ is a simplex in $P_1$, we expect the dimension of $\rho (\sigma )$ to be less than the rank of $A^\sigma$. One reason is because virtually equivalent Abelian groups are too similar to demand different treatments, in particular, they should be assigned the same point at infinity.

Putting these two factors together we get that if $A^\sigma$ has rank r, then

$$\begin{aligned} r \le n - (l+1) \quad \text {and} \quad r \ge l +1. \end{aligned}$$

Therefore, $l+1 \le \lfloor n/2 \rfloor$. So the dimension of $\rho (P)$ is at most $\lfloor n/2 \rfloor -1$.

There are, of course, problems to overcome in both claims. There are two problems in the second claim. One is that virtually equivalent Abelian groups $A_x$ and $A_y$ need not have the same Centers of Mass, in which case the complex $\rho (P)$ might be higher dimensional than it should be. Even with little optimism one expects that if $A_x$ and $A_y$ share a finite index subgroup, there should be a point at infinity whose horospheres are preserved by both $A_x$ and $A_y$. The solution is to construct, for each such Abelian group, a Center of Mass that is invariant under virtual equivalence and that has all the metric and invariance properties we mentioned above. This can be done and is done in Section 5.

The other problem in the second claim is that the rank of $A^\sigma$ could be strictly less than the number of virtual equivalence classes of Abelian groups at the vertices. For example, $\sigma$ is a triangle and the group at each vertex of $\sigma$ is isomorphic to ${\mathbb {Z}}$ and no two of them share a finite index subgroup, yet $A^\sigma$ could be ${\mathbb {Z}}^2$. A solution is to work with the second barycentric subdivision $P_2$ of P, instead of $P_1$, right from the beginning. So we need to assign Abelian groups to vertices of $P_2$. Each vertex x in $P_2$ that is not in $P_1$ is a point in the interior of a simplex $\tau$ of $P_1$. Assign to x the Abelian group $A^\tau$ generated by the Abelian groups at the vertices of $\tau$ (i.e. let $A_x = A^\tau$). The pay off for working with $P_2$ is that for each k-simplex $\sigma$ in $P_2$, the Abelian groups at the vertices of $\sigma$ form a chain $A_0\le \cdots \le A_k$. Another nice consequence is that the group generated by vertex groups is the biggest group $A_k$ in the chain (so one can forget the upper index). It follows that the rank of $A_k$ is greater than or equal to number of the number of virtual equivalence classes of Abelian groups at the vertices, which takes care of the problem.

The problem with the first claim is that it is not clear if the intersection of horospheres described above is a manifold of dimension $n-(l+1)$. For example, it is unclear (to us) how to rule out the following situation (Figure 3).

Suppose that $h_0$, $h_1$ and $h_2$ are Busemann functions on $\widetilde{M}$. Let $z_i\in \partial _\infty$, for $i = 0,1,2$, be the center of the horosphere $S_i$ defined as $h_i = 0$. Now, the intersection $S = S_1 \cap S_2 \cap S_3$ of three horospheres is an $(n-3)$-dimensional manifold if $S_1$, $S_2$, and $S_3$ intersect transversely, i.e. the gradient vectors $\nabla h_0$, $\nabla h_1$ and $\nabla h_2$ at each point in S are linearly independent. Suppose that $z_0$, $z_1$ and $z_2$ are not co-linear in $\partial _\infty$, i.e. none of the three points is on the geodesic connecting the other two, so they span a triangle in $\partial _\infty$. Since $\nabla h_0$, $\nabla h_1$ and $\nabla h_2$ “point toward” $z_0$, $z_1$ and $z_2$ respectively, this strongly suggests that they should be linearly independent. However, there is no reason to relate the linear structure at a point to what happens at infinity, which is something obtained via a limiting process in terms of the metric. We are not sure if this is a real problem or the problem lies in our inability.

Fig. 3

Colinear gradients.

But we find a way around this problem and this is a solution, which requires a modification to how $\rho$ is defined. This is the last modification we will make to $\rho$. We define $\rho$ on the vertices of $P_2$ exactly as we did, but we will not use geodesics in $(\partial _\infty , {{\,\mathrm{Td}\,}})$ to extend $\rho$ to edges and higher dimensional simplices. Instead, we construct what we call Busemann paths and Busemann simplices and we use them in place of geodesics in the above process of defining $\rho$. A Busemann k-simplex

$$\begin{aligned} \sigma :\Delta ^k \rightarrow \partial _\infty \end{aligned}$$

is a singular k-simplex in $\partial _\infty$ with vertices $z_0, z_1, \ldots , z_k$ and has the property (by construction) that if a parabolic isometry preserves the horospheres centered at $z_i$ for $i =0,1,\ldots , k$, then it will preserve horospheres centered at $\sigma (x)$ for all$x\in \Delta ^k$. The construction of Busemann simplices uses convex combinations of Busemann functions, which explains the name, and is given in Section 9. The incentive for constructing Busemann simplices is to create more points at infinity whose horospheres are preserved so that we can use them in the case when the horospheres centered at the vertices do not intersect transversely.

It turns out, however, that even with a whole nondegenerate k-simplex of points at infinity whose horospheres are preserved by an Abelian group $A_x$ we are unable to even prove existence of $(k+1)$ points whose Busemann functions have linearly independent gradient vectors everywhere. Nevertheless, Busemann simplices are too good to waste and we manage to use them to show that the first claim is true if geodesic simplices are replaced by these. Busemann simplices are constructed as pointwise limits of singular simplices

$$\begin{aligned} \sigma _{R_i} :\Delta ^k \rightarrow S(x_0, R_i) \subset \widetilde{M} \end{aligned}$$

on larger and larger spheres centered at some fixed point $x_0\in {\widetilde{M}}$. So for R large enough, $\sigma _R$ “approximates” the Busemann simplex $\sigma$ at infinity so well that nondegeneracy at infinity implies nondegeneracy of $\sigma _R(\Delta ^k)$. The union of all $\sigma _R(\Delta ^k)$ is called the “Busemann cone”, which is itself not a geodesic cone, serves as a parametrization space of intersections of horospheres centered at the vertices $z_i$, for $i =0,1,\ldots , k$. We show that if an Abelian group A of rank r preserves horospheres centered at $z_i$’s, and if the Busemann simplex with vertices $z_i$’s is non-degenerate, then when we line up these intersections of horospheres over C the union has dimension at least $r+k+1$, which gives the first claim. This is discussed in Section 12 and is hard enough to have its own “problems and solutions”.

Last but not least, all of the above effort will go to naught if Busemann simplices are space filling, in which case the Hausdorff dimension of a Busemann l-simplex could be greater than l. However, we show that Busemann simplices are Lipschitz and thus do not increase Hausdorff dimension. It follows that $\rho (P)$ has dimension at most $\lfloor n/2 \rfloor -1$, and since $c_t(P)$ is homeomorphic to $\rho (P)$, the dimension of $c_t(P)$ is also at most $\lfloor n/2 \rfloor -1$. This explains Theorems 1 and 2.

Finally, we can approximate $c_t(P)$ by a polyhedron Q of dimension at most $\lfloor n/2 \rfloor -1$ in some small neighborhood of $c_t(P)$. So when we “collapse” $\varphi _t(P)$ to $c_t(P)$, we can “collapse” it to Q instead and not have to worry that the collapse will not leave $\widetilde{M}_{<\varepsilon }$ because Q is pointwise close to $c_t(P)$. This gives a map ${\widehat{\varphi }}$ that factors through Q as in the statement of Corollary 3.

There are no more problems.

3 Setup and Notation

3.1 Setup.

In the rest of the paper, M is a complete, finite volume n-dimensional manifold of bounded non-positive curvature $(-1\le K\le 0)$ with fundamental group $\Gamma :=\pi _1M$ and universal cover ${\widetilde{M}}\rightarrow M$. Moreover, we assume that there are no arbitrarily small closed geodesics.

3.2 Margulis lemma.

There are constants $\mu _n$ and $I_n$, depending only on the dimension n, for which the group $\left\langle \gamma \in \Gamma \mid d(x,\gamma x)<\mu _n\right\rangle$ generated by elements that move x less than $\mu _n$ is virtually nilpotent and contains a nilpotent subgroup of index $\le I_n$. The constant $\mu _n$ is called the Margulis constant ( [BGS85]).

3.3 Small $\varepsilon$.

We fix a constant $\varepsilon >0$ to be less than the Margulis constant and the length of the smallest closed geodesic in M. Then elements $\gamma \in \Gamma$ which have displacement $<\varepsilon$ at some point are parabolic. The “$\varepsilon$-thin part”

$$\begin{aligned} {\widetilde{M}}_{<\varepsilon }:=\{x\in {\widetilde{M}}\mid d(x,\gamma x)<\varepsilon \text{ for } \text{ some } \gamma \in \Gamma \backslash \{1\}\} \end{aligned}$$

is topologically (see [Gro78, BGS85]) a product $\partial {\widetilde{M}}_{<\varepsilon }\times [0,\infty )$. For each $x\in {\widetilde{M}}_{<\varepsilon }$, let

$$\begin{aligned} S_x:= & {} \{\gamma \in \Gamma \mid d_{\gamma }(x)<\varepsilon \},\\ \Gamma _x:= & {} \left\langle S_x\right\rangle ,\\ N_x:= & {} \left\langle \gamma ^{I_n!}\mid \gamma \in \Gamma _x\right\rangle . \end{aligned}$$

By the Margulis lemma, the group $\Gamma _x$ is virtually nilpotent and $N_x$ is a nilpotent subgroup of $\Gamma _x$. Moreover, $N_x$ is normal in $\Gamma _x$ and since $\Gamma _x$ contains parabolic elements, so does $N_x$ (Lemma 6.6 of [BGS85]).

3.4 Tiny $\delta$.

Fix another constant $\delta >0$ so that $\varepsilon +2\delta$ is still less than the Margulis constant and the length of the shortest closed geodesic in M. If $\sigma =x_0*\dots *x_k$ is a k-simplex in ${\widetilde{M}}$ of diameter $<\delta$, then at any point $x\in \sigma$ all the elements in the set

$$\begin{aligned} S_{\sigma }:=S_{x_0}\cup \dots \cup S_{x_k} \end{aligned}$$

have displacement $<\varepsilon +2\delta$. This is less than the Margulis constant, so

$$\begin{aligned} \Gamma _{\sigma }:=\left\langle S_{\sigma }\right\rangle =\left\langle \Gamma _{x_0},\dots ,\Gamma _{x_k}\right\rangle \end{aligned}$$

is a virtually nilpotent group and

$$\begin{aligned} N_{\sigma }:=\left\langle \gamma ^{I_n!}\mid \gamma \in \Gamma _{\sigma }\right\rangle \end{aligned}$$

is a normal nilpotent subgroup of $\Gamma _{\sigma }$ containing all the groups $N_{\tau }$ for $\tau \subset \sigma$. Since $N_{\sigma }$ contains parabolic elements, its center $Z_{\sigma }$ does as well. (Section 7.6 of [BGS85].)

4 The Abelianization Map or “Mostly Abstract Nonsense with Little or No Content”

The goal of this section is to define a map $\mu$ from a triangulation of the boundary $\partial {\widetilde{M}}_{\le \varepsilon }$ of ${\widetilde{M}}_{\le \varepsilon }$ to an abstract complex $\Delta _{\lfloor pAb\rfloor }$ of virtual equivalence classes of Abelian subgroups of $\Gamma$. The existence of such a triangulation is addressed in “Appendix E”. Note that $\partial {\widetilde{M}}_{\le \varepsilon }$ is the ordinary boundary, not the ideal boundary. Recall that two subgroups $A,B<\Gamma$ are virtually equivalent if they share a finite index subgroup.

The map $\mu$ is the zeroth step in defining a map $\rho :\partial {\widetilde{M}}_{\le \varepsilon } \rightarrow \partial _\infty$. Then in the next section, we will construct for each virtual equivalence class of such Abelian subgroups a canonical center of mass in $\partial _\infty$ and use it to define $\rho$ on the vertices of $\partial {\widetilde{M}}_{\le \varepsilon }$.

4.1 Complexes of Abelian and nilpotent groups.

Let

$$\begin{aligned} pAb:=\{A<\pi _1M\mid A \text{ is } \text{ an } \text{ Abelian } \text{ group } \text{ containing } \text{ a } \text{ parabolic } \text{ element }\} \end{aligned}$$

be the set of Abelian groups in $\Gamma$ containing parabolics. Also, let $\lfloor pAb\rfloor$ be the set of virtual equivalence classes of such things. Denote by $\Delta _{pAb}$ the complex whose vertices are elements of pAb and whose simplices are chains $A_0<\dots < A_k$ of distinct such subgroups and define $\Delta _{\lfloor pAb\rfloor }$ similarly. In the same way, we define pNil to be the set of nilpotent subgroups of $\Gamma$ containing a parabolic element and we form a complex $\Delta _{pNil}$. The group $\Gamma$ acts on all these complexes by conjugation.

Remark

Note that the simplices of $\Delta _{pAb}$ come with a natural ordering of vertices corresponding to inclusions of subgroups. When we take barycentric subdivisions, which we will do below, the barycentric subdivision also gets the standard ordering.

4.2 Labeling the thin part with Abelian groups.

We assemble consequences of the Margulis lemma at points in the thin part in three steps. Let P be a $\Gamma$-equivariant triangulation of $\partial {\widetilde{M}}_{\le \varepsilon }$ that is $\delta$-fine, i.e. every simplex in the triangulation has diameter $<\delta$. Let $P_1$ be its barycentric subdivision.

• (1) Assign to each vertex$\tau$ of $P_1$ the nilpotent group

  $$\begin{aligned} \mu '(\tau ):=N_{\tau }. \end{aligned}$$

  This extends to a map

  $$\begin{aligned} \mu ':P\rightarrow \Delta _{pNil} \end{aligned}$$

  because adjacent vertices in $P_1$ give inclusions of nilpotent groups. The nilpotent groups $N_{\tau }$ in the image contain parabolics because $\varepsilon$ is small. Note that $\mu '$ is determined by the isometric $\Gamma$-action once we fix the $\Gamma$-equivariant triangulation P, so $\mu '$ is $\Gamma$-equivariant and

  $$\begin{aligned} \Gamma _{\tau } \text{ fixes } \mu '(\tau ). \end{aligned}$$

• (2) Each vertex of the barycentric subdivision of $\Delta _{pNil}$ corresponds to a chain of nilpotent subgroups $N_0<\dots <N_k$. Assign to each vertex $(N_0<\dots <N_k)$ of the barycentric subdivision of $\Delta _{pNil}$ the group generated by the centers$Z_i$ of $N_i$,

  $$\begin{aligned} \zeta (N_0<\dots <N_k):=\left\langle Z_0,\dots ,Z_k\right\rangle . \end{aligned}$$

  These groups are Abelian (because each $Z_i$ centralizes the subgroup $\left\langle Z_0,\dots ,\right. \left. Z_{i-1}\right\rangle$ of $N_i$) and contain parabolic elements. The assignment extends to a continuous map

  $$\begin{aligned} \zeta :\Delta _{pNil}\rightarrow \Delta _{pAb}, \end{aligned}$$

  because adding more groups to $N_0<\dots <N_k$ makes $\left\langle Z_0,\dots ,Z_k\right\rangle$ bigger.

• (3) Pass to virtual equivalence classes via

  $$\begin{aligned} \nu :\Delta _{pAb}\rightarrow \Delta _{\lfloor pAb\rfloor }. \end{aligned}$$

Abelianization map. We call the composition $\mu :=\nu \circ \zeta \circ \mu '$,

$$\begin{aligned} \mu :\partial {\widetilde{M}}_{\le \varepsilon }\rightarrow \Delta _{\lfloor pAb\rfloor }. \end{aligned}$$

the Abelianization map.

Fig. 4

Labeling P$_2$.

Remark

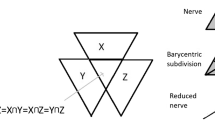
In summary, the map $\mu$ was described on each simplex in terms of the second barycentric subdivision$P_2$ of P (Figure 4). The reason is that we can connect nilpotent groups $N_0$ and $N_1$ corresponding to vertices of a simplex in P by inclusions of nilpotent groups via

$$\begin{aligned} N_0\le N_{01}\ge N_1, \end{aligned}$$

(2)

which is a path in the barycentric subdivision $P_1$, and we can connect the centers $Z_0$ and $Z_1$ by inclusions of Abelian groups

$$\begin{aligned} Z_0\le \left\langle Z_0,Z_{01}\right\rangle \ge Z_{01}\le \left\langle Z_{01},Z_1\right\rangle \ge Z_1, \end{aligned}$$

(3)

which is a path in the second barycentric subdivision $P_2$. It is necessary to pass from $P_1$ to $P_2$ when we go Abelian because unlike the situation with nilpotent subgroups, it is in general not true that $Z_0 \le Z_{01} \ge Z_1$.

4.3 For later use (to stay thin).

Let $\sigma =(\tau _0\subset \dots \subset \tau _k)$ be an ordered k-simplex in the barycentric subdivision $P_1$, where the order is by inclusion of simplices in the original complex. We noted above that $\Gamma _{\tau _i}$ fixes the vertex $\mu '(\tau _i)$. Since $\mu =\nu \circ \zeta \circ \mu '$ and the maps $\nu$ and $\zeta$ are obviously $\Gamma$-equivariant, we see that the “bottom” group $\Gamma _{\tau _0}$ in the chain $\Gamma _{\tau _0}<\dots <\Gamma _{\tau _k}$ fixes the entire simplex $\mu (\sigma )=\nu \circ \zeta \circ \mu '(\tau _0\subset \dots \subset \tau _k)$. Moreover, there is an element in $\Gamma _{\tau _0}$ that is $(\varepsilon +2\delta )$-small everywhere on $\sigma$. This is because $\sigma$ is in the subdivision of a simplex of P whose diameter is $\le \delta$ and at least one of whose vertices x has an non-trivial element $\gamma \in S_x<\Gamma _{\tau _0}$ with $d_{\gamma }(x)\le \varepsilon$. Thus $d_{\gamma }\le \varepsilon +2\delta$ everywhere on $\sigma$. In summary,

$$\begin{aligned}&\text{ for } \text{ every } x\in \partial {\widetilde{M}}_{\le \varepsilon } \text{ there } \text{ is } 1\not =\gamma \in \Gamma \text{ such } \text{ that }\\&\quad d_{\gamma }(x)\le \varepsilon +2\delta \text{ and } \gamma (\mu (x))=\mu (x). \end{aligned}$$

5 Center of Mass for an Abelian Group with Parabolics

In this section we will build a map $\beta$ on the set of vertices of the complex $\Delta _{\lfloor pAb\rfloor }$

$$\begin{aligned} \beta :\Delta _{\lfloor pAb\rfloor }^{(0)}\rightarrow (\partial _{\infty },{{\,\mathrm{Td}\,}}) \end{aligned}$$

(4)

such that

• the map $\beta$ is $\Gamma$-equivariant,

• horospheres centered at $\beta ([A])$ are preserved by the centralizer $C_{A'}$ for any Abelian group $A'$ virtually equivalent to A, and

• for any simplex $\sigma$ in $\Delta _{\lfloor pAb\rfloor }$ we have in the Tits metric

  $$\begin{aligned} \text{ diam } (\beta (\sigma ^{(0)}))<\pi /2, \end{aligned}$$

  (5)

where $\sigma ^{(0)}$ is the set of vertices of $\sigma$. Then in later sections, we will discuss how to correctly fill in $\beta$ with simplices at infinity in order to finally obtain a map $\rho :\partial \widetilde{M}_{\le \varepsilon } \rightarrow \partial _\infty$.

Every Abelian group A containing a parabolic isometry has a nonempty fixed set ${{\,\mathrm{Fix}\,}}(A)$ at infinity with a canonical center of mass$\xi _A$. This construction can be found in Appendix 3.B of [BGS85] and a variation is in 3.5 of [Ebe96]. We review it in “Appendix B” of this paper. It is, however, not invariant under virtual equivalences, so we cannot use it to define $\beta$. The plan for this section is to first recall properties of the classical center of mass, and then, inspired by this, construct a canonical center of mass that depends only on the virtual equivalence class of the parabolic Abelian group. We will prove similar properties for this new center of mass and use it to define $\beta$.

5.1 The classical center of mass for a parabolic Abelian group A

The center of mass $\xi _A$ has the crucial property that for every $y\in {{\,\mathrm{Fix}\,}}(A)$,

$$\begin{aligned} {{\,\mathrm{Td}\,}}(\xi _A,y)\le \pi /2. \end{aligned}$$

Also, since the construction of $\xi _A$ is canonical, $\xi _A$ is fixed by the normalizer of A. This implies that for a simplex $\sigma =(A_0<\dots <A_k)$ in $\Delta _{pAb}$ each group $A_i$ fixes all the points $\xi _{A_j}$, and from this the first property gives

$$\begin{aligned} {{\,\mathrm{Td}\,}}(\xi _{A_i},\xi _{A_j})\le \pi /2. \end{aligned}$$

In addition, the following feature of $\xi _A$ is fundamental and is crucial in the next section.

Proposition 9

(Preserved horospheres). The centralizer $C_A$ preserves horospheres centered at $\xi _A$.

Proof

Let h be a Busemann function centered at $\xi _A$. We need to show that h is $\gamma$-invariant under isometries $\gamma \in C_A$. Since $|\nabla h|=1$ we have

$$\begin{aligned} {|h(\gamma ^nx)-h(x)|\over n}\le {d(\gamma ^nx,x)\over n}. \end{aligned}$$

Since $\gamma \in C_A$ we already know it fixes $\xi _A$, so the quantity on the left is independent of n and x and is equal to $|h(\gamma x)-h(x)|$. Letting $n\rightarrow \infty$ and using the well known formula for the infimum displacement of an isometry (Lemma 6.6.(2) in [BGS85])

$$\begin{aligned} |\gamma |:=\inf _{x\in {\widetilde{M}}}d(\gamma x,x)= \lim _{n\rightarrow \infty }{d(\gamma ^nx,x)\over n} \end{aligned}$$

we get

$$\begin{aligned} |h(\gamma x)-h(x)|\le |\gamma |. \end{aligned}$$

So we see that h is $\gamma$-invariant whenever $|\gamma |=0$.

Now, suppose that $|\gamma |>0$. Then, according to Karlsson-Margulis ( [KM99], see also “Appendix C”), there are geodesic rays $r_{\pm }=[x,\eta ^{\pm })$ sublinearly tracking the positive and negative $\gamma$-orbits, i.e.

$$\begin{aligned} \lim _{n\rightarrow \infty } {d(\gamma ^nx,r_+(n|\gamma |))\over n}=0, \end{aligned}$$

and

$$\begin{aligned} \lim _{n\rightarrow \infty } {d(\gamma ^{-n}x,r_-(n|\gamma |))\over n}=0. \end{aligned}$$

It follows from this and the formula for $|\gamma |$ that

$$\begin{aligned} 2|\gamma |=\lim _{t\rightarrow \infty }{d(r_+(t|\gamma |),r_-(t|\gamma |))\over t}. \end{aligned}$$

Reparametrizing and using the $\angle$-metric description on p. 36 of [BGS85] we get

$$\begin{aligned} 1=\lim _{t\rightarrow \infty }{d(r_+(t),r_-(t))\over 2t}=\sin \left( {\angle (\eta ^+,\eta ^-)\over 2}\right) . \end{aligned}$$

Therefore $\angle (\eta ^+,\eta ^-)=\pi$ which implies that

$$\begin{aligned} {{\,\mathrm{Td}\,}}(\eta ^+,\eta ^-)\ge \pi . \end{aligned}$$

On the other hand, since A commutes with $\gamma$ it fixes the limit points $\lim _{n\rightarrow \infty }\gamma ^nx=\eta ^+$ and $\lim _{n\rightarrow \infty }\gamma ^{-n}x=\eta ^-$. Therefore

$$\begin{aligned} {{\,\mathrm{Td}\,}}(\eta ^{\pm },\xi _A)\le \pi /2. \end{aligned}$$

Putting these two inequalities together we get

$$\begin{aligned} \pi \le {{\,\mathrm{Td}\,}}(\eta ^+,\eta ^-)\le {{\,\mathrm{Td}\,}}(\eta ^+,\xi _A)+{{\,\mathrm{Td}\,}}(\xi _A,\eta ^-)\le \pi \end{aligned}$$

and consequently

$$\begin{aligned} {{\,\mathrm{Td}\,}}(\eta ^{\pm },\xi _A)=\pi /2. \end{aligned}$$

This implies that $\nabla h\cdot \dot{r}_+\rightarrow 0$ along the geodesic ray $r_+$ (see 4.2 in [BGS85]) and consequently

$$\begin{aligned} {h(r_+(n|\gamma |))-h(x)\over n}={1\over n}\int _0^{n|\gamma |}|\nabla h\cdot \dot{r}_+|dt\rightarrow 0 \end{aligned}$$

as $n\rightarrow \infty$. Putting this together with

$$\begin{aligned} {|h(\gamma ^nx)-h(r_{+}(n|\gamma |))|\over n}\le {d(\gamma ^nx,r_+(n|\gamma |))\over n}\rightarrow 0 \end{aligned}$$

we get that ${h(\gamma ^n x)-h(x)\over n}\rightarrow 0$. Since this quantity is actually constant and equal to $h(\gamma x)-h(x)$, we conclude that h is $\gamma$-invariant. $\square$

5.2 Dealing with finite index issues.

Centers of mass of virtually equivalent Abelian groups might be different. Our goal in this subsection is to pick a single point at infinity that will play the role of the center of mass for the whole virtual equivalence class [A] of A. We will do this by constructing a center of mass for the union of fixed point sets of all the groups virtually equivalent to A, which is also equal to

$$\begin{aligned} F_A:=\bigcup _{n\in {\mathbb {N}}}{{\,\mathrm{Fix}\,}}(n!A), \end{aligned}$$

since every group virtually equivalent to A contains some n!A as a subgroup. It is easy to see and occasionally useful to remember that

$$\begin{aligned}{}[A]=[A']&\implies&F_A=F_{A'}, \text{ and } \end{aligned}$$

(6)

$$\begin{aligned} B\le A&\implies&F_B\supseteq F_A. \end{aligned}$$

(7)

A two-step center of mass construction. Now we construct a center of mass for $F_A$ that depends only on the virtual equivalence class of A. We do this in two steps.

(Step 1) First, we will show that there is a point $\xi$ in $F_A$ so that any other point of $F_A$ is within $\pi /2$ of $\xi$. To show this, let

$$\begin{aligned} B_{n,A}:=\{x\in {{\,\mathrm{Fix}\,}}(A)\mid {{\,\mathrm{Td}\,}}(x,y)\le \pi /2 \text{ for } \text{ all } y\in {{\,\mathrm{Fix}\,}}(n!A)\}. \end{aligned}$$

The sets $B_{n,A}$ are closed in the sphere topology (by the lower semicontinuity of Td, see “Appendix B”) and nested:

$$\begin{aligned} B_{0,A}\supseteq B_{1,A}\supseteq B_{2,A}\supseteq \cdots . \end{aligned}$$

They are also non-empty because the center of mass $\xi _{n!A}$ of the fixed point set of n!A is fixed by A and therefore $\xi _{n!A}\in B_{n,A}$. So there is a point $\xi$ contained in the intersection $\cap _{n}B_{n,A}$. For this $\xi \in {{\,\mathrm{Fix}\,}}(A)$ we have ${{\,\mathrm{Td}\,}}(\xi ,y)\le \pi /2$ for all $y\in F_A$. This finishes the first step.

(Step 2) The point $\xi$ constructed in Step 1 may not be unique, and we denote the set of all such points by

$$\begin{aligned} B_{[A]}:=\{x\in F_A\mid {{\,\mathrm{Td}\,}}(x,y)\le \pi /2 \text{ for } \text{ all } y\in F_A\}. \end{aligned}$$

This set is our collection of potential centers of mass. The second step is to pick in a canonical way a single point from this set.

It is clear that $B_{[A]}$ has Tits diameter $\le \pi /2$, so if it was closed in the sphere topology then one way to pick a unique point would be to take the center of $B_{[A]}$ (in the sense of “Appendix B”). Unfortunately, the set $B_{[A]}$ may not be closed in the sphere topology, so we first replace it by its closure in the sphere topology ${\overline{B}}_{[A]}$. It is easy to see (again, using lower semicontinuity of ${{\,\mathrm{Td}\,}}$) that this closure is equal to

$$\begin{aligned} \overline{B}_{[A]}=\{x\in {\overline{F}}_A\mid {{\,\mathrm{Td}\,}}(x,y)\le \pi /2 \text{ for } \text{ all } y\in {\overline{F}}_A\}, \end{aligned}$$

where $\overline{F}_A$ is the closure of $F_A$ in the sphere topology. In particular, ${\overline{B}}_{[A]}$ still has Tits diameter $\le \pi /2$. Therefore, the function

$$\begin{aligned} \tau (\cdot ):=\sup _{x\in {\overline{B}}_{[A]}}{{\,\mathrm{Td}\,}}(\cdot ,x) \end{aligned}$$

has infimum

$$\begin{aligned} \inf \tau <\pi /2-\alpha \end{aligned}$$

for a positive constant $\alpha =\alpha _n>0$ that only depends on the dimension n. This infimum is attained at a unique point in $\partial _{\infty }$ which we will denote by $\xi _{[A]}$. In other words, there is a unique ball of smallest radius containing ${\overline{B}}_{[A]}$. This ball is centered at $\xi _{[A]}$ and has radius $\tau (\xi _{[A]})$. See “Appendix B” for everything in this paragraph. We call the point $\xi _{[A]}$ the center of mass of [A].

What remains to be shown is that $\xi _{[A]}$ is actually contained in $B_{[A]}$. We prove this in the remainder of the subsection. We begin with

Lemma 10

The set $B_{[A]}$ is convex.

Proof

Let $x_0,x_1\in B_{[A]}$ and let $x_t$ be a point on the geodesic segment in $\partial _{\infty }$ connecting them. There are virtually equivalent groups $A_0,A_1\in [A]$ fixing $x_0$ and $x_1$, so the entire geodesic segment is fixed by the group $(A_0\cap A_1)\in [A]$. Moreover, since $\partial _{\infty }$ is CAT(1) we see for any $y\in F_A$ that ${{\,\mathrm{Td}\,}}(x_t,y)\le \pi /2$ by comparison with the round sphere. Thus $x_t\in B_{[A]}$. $\square$

We will use this to show that $\xi _{[A]}$ is contained in ${\overline{B}}_{[A]}$. If the closure ${\overline{B}}_{[A]}$ was convex, then this would follow easily (see “Appendix B”). But, we only know that ${\overline{B}}_{[A]}$ is the closure in the sphere topology of a${{\,\mathrm{Td}\,}}$-convex set. So, we need the following lemma.

Lemma 11

Fix $\alpha >0$. Suppose C is a convex set of diameter $\le \pi /2$. Let ${\overline{C}}$ be its closure in the sphere topology. Let $\xi \in \partial _{\infty }$ be a point for which

$$\begin{aligned} {{\,\mathrm{Td}\,}}(\xi ,y)\le \pi /2-\alpha \quad \text{ for } \text{ every } y\in C. \end{aligned}$$

Then there is a point $x\in {\overline{C}}$ so that

$$\begin{aligned} {{\,\mathrm{Td}\,}}(x,y)\le {{\,\mathrm{Td}\,}}(\xi ,y) \quad \text{ for } \text{ all } y\in C. \end{aligned}$$

Proof

First, let $r=\inf _{y\in C}{{\,\mathrm{Td}\,}}(\xi ,y)$. Then there is a sequence of points $x_i\in C$ so that ${{\,\mathrm{Td}\,}}(\xi ,x_i)\rightarrow r$. After passing to a subsequence, we may assume that in the sphere topology $x_i\rightarrow x\in {\overline{C}}$. Now, pick a point $y\in C$. Since C is convex, the geodesic segment $[x_i,y]$ is contained in C. On this segment there is a unique closest point $y_i$ to $\xi$. Since it is the closest point to $\xi$ on the segment $[x_i,y]$, at this point the angles $\angle _{y_i}(x_i,\xi )$ and $\angle _{y_i}(\xi ,y)$ are both obtuse (that is, greater or equal to $\pi /2$). Therefore, triangle comparison with obtuse triangles on the round sphere gives

$$\begin{aligned} {{\,\mathrm{Td}\,}}(y_i,y)\le {{\,\mathrm{Td}\,}}(\xi ,y), \end{aligned}$$

and also

$$\begin{aligned} {{\,\mathrm{Td}\,}}(x_i,y_i)\le \cos ^{-1}\left( {\cos ({{\,\mathrm{Td}\,}}(x_i,\xi ))\over \cos ({{\,\mathrm{Td}\,}}(y_i,\xi ))}\right) . \end{aligned}$$

As $i\rightarrow \infty$ the right hand side of this tends to zero because the denominator

$$\begin{aligned} \cos ({{\,\mathrm{Td}\,}}(y_i,\xi ))\ge \cos (\pi /2-\alpha )>0 \end{aligned}$$

doesn’t approach zero and

$$\begin{aligned} r\le {{\,\mathrm{Td}\,}}(y_i,\xi )\le {{\,\mathrm{Td}\,}}(x_i,\xi )\rightarrow r. \end{aligned}$$

Therefore, using lower semicontinuity of ${{\,\mathrm{Td}\,}}(\cdot ,y)$ we get

$$\begin{aligned} {{\,\mathrm{Td}\,}}(x,y)\le & {} \liminf _{i}{{\,\mathrm{Td}\,}}(x_i,y)\\\le & {} \liminf _i({{\,\mathrm{Td}\,}}(x_i,y_i)+{{\,\mathrm{Td}\,}}(y_i,y))\\\le & {} {{\,\mathrm{Td}\,}}(\xi ,y). \end{aligned}$$

$\square$

So, since $B_A$ is a convex set of diameter $\le \pi /2$ and $\xi _{[A]}$ is the unique point at which $\rho$ attains its infimum, we conclude that

$$\begin{aligned} \xi _{[A]}\in {\overline{B}}_A. \end{aligned}$$

Therefore

$$\begin{aligned} {{\,\mathrm{Td}\,}}(\xi _{[A]},y)\le & {} \pi /2\quad \text{ for } \text{ all } y\in F_A, \text{ and } \end{aligned}$$

(8)

$$\begin{aligned} {{\,\mathrm{Td}\,}}(\xi _{[A]},y)\le & {} \pi /2-\alpha \quad \text{ for } \text{ all } y\in B_{[A]}. \end{aligned}$$

(9)

The set $F_A$ is preserved by A so its center of mass $\xi _{[A]}$ is fixed by A, and therefore

$$\begin{aligned} \xi _{[A]}\in B_{[A]}, \end{aligned}$$

which is what we needed to show. This finishes the second step.

Remark

At this point the reader can safely forget about the closures ${\overline{B}}_{[A]}$. While they appeared in the construction of $\xi _{[A]}$ they will never appear again.

5.3 The map $\beta :\Delta ^{(0)}_{\lfloor pAb\rfloor }\rightarrow (\partial _\infty ,{{\,\mathrm{Td}\,}}).$

We set

$$\begin{aligned} \beta ([A]):=\xi _{[A]}. \end{aligned}$$

Let us verify that it has all the properties we promised at the beginning of Section 5. First, it follows from the construction that $\xi _{[\gamma A\gamma ^{-1}]}=\gamma \xi _{[A]}$ so the map $\beta$ is $\Gamma$-equivariant. Second, for any $A'$ virtually equivalent to A, the centralizer $C_{A'}$ of $A'$ fixes $\xi _{[A']}=\xi _{[A]}$, so the proof of Proposition 9 applies word-for-word and shows that $C_{A'}$ preserves horospheres centered at $\xi _{[A]}$. To prove the third bullet we proceed as follows. For any simplex $\sigma =([A_0]<\cdots <[A_k])$ in $\Delta _{\lfloor pAb\rfloor }$ we can pick representatives $A_i$ so that $A_0<\cdots <A_k$. Then

$$\begin{aligned} F_{A_0}\supseteq \cdots \supseteq F_{A_k}, \end{aligned}$$

so by (8) if $i\le j$ we get ${{\,\mathrm{Td}\,}}(\xi _{[A_i]},y)\le \pi /2$ for all $y\in F_{A_j}$. Since for all i, j each group $A_j$ fixes all the points $\xi _{[A_i]}$ we also have $\xi _{[A_i]}\in F_{A_j}$. In summary

$$\begin{aligned} \xi _{[A_i]}\in B_{[A_j]}\quad \text{ for } \text{ all } i\le j. \end{aligned}$$

The upshot of these gymnastics is that (9) implies that for all i, j

$$\begin{aligned} {{\,\mathrm{Td}\,}}(\xi _{[A_i]},\xi _{[A_j]})\le \pi /2-\alpha . \end{aligned}$$

In other words, the diameter of $\beta (\sigma ^{(0)})$ is strictly less than $\pi /2$, which is what we wanted to show.

6 A Criterion for and the Necessity of Being Divergent

Now that we have defined $\beta$ (and thus $\rho :=\beta \circ \mu$) on vertices, we need to extend it to each simplex. The extension must be canonical and satisfy a divergence property. The goal of this section is to carefully discuss this notion of a divergent simplex at infinity, give a criterion for when a simplex is divergent, and illustrate how it is useful in the context of the main theorem.

In this section we will need the observation that $M_{\ge \varepsilon }$ is compact. It is immediate that $M_{\ge \varepsilon }$ is closed. It is bounded because if not, one can pack infinitely many disjoint $\varepsilon$-balls into M, which means that M has infinite volume, but the volume of M is finite. So M is closed and bounded, and therefore compact.

6.1 Divergent rays, divergent simplices and divergent maps

6.1.1 Divergent rays.

Recall that a geodesic ray in $\widetilde{M}$ is divergent if its projection under the covering map p leaves all compact sets. It turns out, as we will see, that parabolic Abelian subgroups $A<\Gamma$ give geodesic rays $[x,\xi _A)$ which project to divergent rays in M, and thus determine distinguished directions to go to infinity in M.

Proposition 12

Any ray $[x,\xi _{[A]})$ in ${\widetilde{M}}$ projects to a divergent ray in M.

The key to obtaining results of this sort is the strong invariance of $\xi _A$ established in Proposition 9. The centralizer $C_A$ preserves horospheres centered at $\xi _{[A]}$, so Proposition 12 follows from Lemma 13 below. This is a way to produce divergent rays in M.

Lemma 13

Suppose A is a subgroup of $\Gamma$. If $C_A$ preserves horospheres centered at $\xi$ and A fixes $\xi$, then any geodesic ray $r:[0,\infty )\rightarrow {\widetilde{M}}$ with endpoint $r(\infty )=\xi$ projects to a divergent ray in M.

Proof

We prove the contrapositive. If the projection of the geodesic ray r to M does not diverge then there is a sequence of times $t_i\rightarrow \infty$ and elements $g_i\in \Gamma$ so that $\{g_ir(t_i)\}$ converges to a point $x_0$ in ${\widetilde{M}}$. We will construct out of this an element in $C_A$ that does not preserve a Busemann function h centered at $\xi$. This will prove the Proposition. Let $D:=\sup _{i}d(x_0,g_ir(t_i))$.

Claim

After passing to a subsequence of $\{g_i\}$, we have $g_j^{-1}g_i\in C_A$.

Recall that for any isometry $\rho$, it follows from triangle inequality that

$$\begin{aligned} |d_{\rho }(x)-d_{\rho }(y)|\le 2d(x,y). \end{aligned}$$

This implies that for any element $\gamma$,

$$\begin{aligned} |d_{g_i\gamma g_i^{-1}}(x_0)-d_{g_i\gamma g_i^{-1}}(g_ir(t_i))|\le & {} 2d(x_0,g_ir(t_i)) \end{aligned}$$

(10)

$$\begin{aligned}\le & {} 2D. \end{aligned}$$

(11)

If $\gamma$ fixes $r(\infty )=\xi$, we also get

$$\begin{aligned} d_{g_i\gamma g_i^{-1}}(g_ir(t_i))= & {} d_{\gamma }(r(t_i)), \end{aligned}$$

(12)

$$\begin{aligned}\le & {} d_{\gamma }(r(0)), \end{aligned}$$

(13)

so that $\{d_{g_i\gamma g^{-1}_{i}}(x_0)\}_{i=1}^{\infty }$ is bounded. Thus, there are only finitely many different conjugates in the sequence $\{g_i\gamma g_i^{-1}\}_{i=1}^{\infty }$. After passing to a subsequence, we may assume that all the conjugates are the same, i.e. that

$$\begin{aligned} g_1\gamma g_1^{-1}=g_2\gamma g_2^{-1}=\cdots , \end{aligned}$$

(14)

and consequently that $g^{-1}_jg_i$ commutes with $\gamma$.

In the special case when $A=\left\langle \gamma _1,\dots ,\gamma _r\right\rangle$ is a finitely generated group fixing $\xi$ we can do the above argument for each one of the generators. So, after passing to subsequences finitely many times, we get a sequence $\{g_i\}$ for which $g_j^{-1}g_i$ commutes with the entire group $A=\left\langle \gamma _1,\dots ,\gamma _r\right\rangle$.

In general, A is countable so we get the same result via diagonal argument.

Claim

For large enough j, the element $g_j^{-1}g_i$ does not preserve h.

Note that $d(g_j^{-1}g_ir(t_i),r(t_j))=d(g_ir(t_i),g_jr(t_j))$ is bounded by 2D, so

$$\begin{aligned} |h(g_j^{-1}g_ir(t_i))-h(r(t_j))|\le 2D. \end{aligned}$$

On the other hand, as $j\rightarrow \infty$ we have

$$\begin{aligned} h(r(t_j))=(h(r(0))-t_j)\quad \rightarrow -\infty . \end{aligned}$$

(15)

Therefore $\lim _{j\rightarrow \infty }h(g_j^{-1}g_ir(t_i))=-\infty$. This implies that h is not $g_j^{-1}g_i$-invariant for a fixed i and large enough j.

So we’ve found an element $g_j^{-1}g_i\in C_A$ that does not preserve horospheres centered at $r(\infty )$. This proves the proposition. $\square$

6.2 Wiggle room in the divergent ray argument.

It is good to notice that the divergent ray argument is not delicate. There is quite a bit of “wiggle room” in the argument. If one looks through the proof, one sees that the assumptions can be weakened. We only need to know that

• (1) the group A fixes the point at infinity $r(\infty )$,

• (2) there is some point$\eta$ such that $C_A$ preserves horospheres at $\eta$, and

• (3) there is a positive constant $\alpha >0$ such that

  $$\begin{aligned} {{\,\mathrm{Td}\,}}(\eta ,r(\infty ))\le \pi /2-\alpha . \end{aligned}$$

In other words, we can separate the point $\eta$ from the endpoint of the geodesic ray $r(\infty )$ in the argument as illustrated in the figure above. The point $r(\infty )$ just needs to be fixed by A as long as the (much stronger) condition that horospheres are preserved by the entire centralizer is satisfied by some nearby point $\eta$. Having phrased things in this way, we note that we can vary the endpoint$r(\infty )$of the geodesic ray, as long as all the rays we use satisfy (1) and (3) for a$\underline{single\, point\, \eta \,and \,a \,single \,constant \,\alpha >0}$. Finally, note that we can vary the startpoint of the geodesic ray r in a bounded set. So, we arrive at the following Proposition, which produces divergent sectors.

Proposition 14

Suppose A is a subgroup of $\Gamma$, B is a bounded subset of ${\widetilde{M}}$, and h is a $C_A$-invariant Busemann function centered at a point $\eta \in \partial _{\infty }$. Then for every $\varepsilon >0$ there is a constant $T:=T_{A,\varepsilon ,\eta ,\alpha ,B}$ so that any geodesic ray $r:[0,\infty )\rightarrow {\widetilde{M}}$ with $r(0)\in B$ and $r(\infty )$ satisfying (1) and (3) has

$$\begin{aligned} r(t)\in {\widetilde{M}}_{\le \varepsilon }\quad \text{ for } \text{ all } t\ge T. \end{aligned}$$

Proof

Suppose the conclusion is not true. Then there are times $t_i\rightarrow \infty$, elements $g_i\in \Gamma$, and rays $r_i$ with $r_i(0)\in B$ and $r_i(\infty )$ satisfying (1) and (3) such that $\{g_ir_i(t_i)\}$ converges to a point $x_0\in {\widetilde{M}}$. As before, using (1) we show that after passing to a subsequence we can assume $g_j^{-1}g_i\in C_A$ for all i, j. As before, h is a Busemann function whose level sets are horospheres centered at $\eta$ and $|h(g_j^{-1}g_ir_i(t_i))-h(r_j(t_j))|\le 2D$. Condition (3) implies that $r_j'(t)$ and the tangent to the geodesic ray from $r_j(t)$ to $\eta$ is at an angle at most $\pi /2-\alpha$ for all t, which implies that

$$\begin{aligned} h(r_j(t_j))\le & {} h(r_j(0))-t_j\cdot \sin \alpha ,\\\rightarrow & {} -\infty . \end{aligned}$$

So we again conclude that $\lim _{j\rightarrow \infty }h(g_j^{-1}g_ir(t_i))\rightarrow -\infty$. This contradicts the assumption that h is $C_A$-invariant, so it proves the proposition. $\square$

6.2.1 Divergent maps and divergent simplices.

In order to state our main application of Proposition 14, we introduce the following terminology. A family of maps $\{\varphi _t:X\rightarrow {\widetilde{M}}\}_{t\in {\mathbb {R}}^+}$diverges overM if for any $\varepsilon >0$ there is T so that

$$\begin{aligned} {{\,\mathrm{Im}\,}}(\varphi _t)\subset {\widetilde{M}}_{\le \varepsilon }\quad \text{ for } \text{ all } t\ge T. \end{aligned}$$

Two families $\{\varphi _t,\psi _t:X\rightarrow {\widetilde{M}}\}_{t\ge 0}$ are asymptotic if for every compact set $K\subset X$, the distance $\sup _{x\in K,t\ge 0}d(\varphi _t(x),\psi _t(x))$ is finite. Next, fix a basepoint $z\in {\widetilde{M}}$, let $S_z(t)$ be the sphere of radius t centered at z, and let

$$\begin{aligned} c_t=c_t^z:\partial _{\infty }\rightarrow S_z(t) \end{aligned}$$

be the geodesic retraction that sends $\xi \in \partial _{\infty }$ to the point $[z,\xi )_t$ obtained by flowing for a time t along the geodesic ray from z to $\xi$. We say that a singular simplex $\lambda :\Delta ^k\rightarrow \partial _{\infty }$diverges overM if the family $c_t\circ \lambda$ diverges over M. Whenever it doesn’t cause confusion, we will omit “over M” and just say that the simplex $\lambda$ diverges. A direct corollary of Proposition 14 is the following criterion for finding divergent simplices.

Corollary 15

Suppose horospheres centered at $\eta \in \partial _{\infty }$ are $C_A$-invariant. For $\alpha >0$, any simplex contained in ${{\,\mathrm{Fix}\,}}(A)\cap B_{\pi /2-\alpha }(\eta )$ diverges over M.

It is easy to see that the definition of divergence for simplices does not depend on the choice of basepoint z. The underlying reason is that for different basepoints z and $z'$ the cone homotopies $c^z_t\circ \lambda$ and $c^{z'}_t\circ \lambda$ are asymptotic. Somewhat more generally we have the following lemma which will be useful in the next subsection.

Lemma 16

Suppose that two families $\{\varphi _t,\psi _t:X\rightarrow {\widetilde{M}}\}_{t\ge 0}$ are asymptotic. If $\varphi _t$ diverges then for any compact subset $K\subset X$

• for sufficiently large t, the geodesic homotopy between $\varphi _t\mid _K$ and $\psi _t\mid _K$ is inside${\widetilde{M}}_{\le \varepsilon }$, and in particular

• $\psi _t\mid _K$ diverges.

Proof

Let $D:=\sup _{x\in K,t\ge 0}d(\varphi _t(x),\psi _t(x))$. This is finite because $\varphi _t$ and $\psi _t$ are asymptotic. We claim that since $\varphi _t$ diverges in M and the injectivity radius function on M is proper, there is a time T so that for $t\ge T$ the closed D-neighborhood of $\varphi _t\mid _K$ is contained in ${\widetilde{M}}_{\le \varepsilon }$. To see this, note that the injectivity radius being proper implies that there is $\varepsilon '<\varepsilon$ such that $d(M_{\ge \varepsilon },M_{\le _{\varepsilon '}})>D$. Then also $d({\widetilde{M}}_{\ge \varepsilon },{\widetilde{M}}_{\le \varepsilon '})>D$ and therefore once t is large enough so that $\varphi _t$ is in ${\widetilde{M}}_{\le \varepsilon '}$ its D-neighborhood will be in ${\widetilde{M}}_{\le \varepsilon }$.

Since the geodesic homotopy between $\varphi _t\mid _K$ and $\psi _t\mid _K$ is in this D-neighborhood, we get the first bullet point. The second follows immediately from the first. $\square$

6.2.2 Filling $\beta$ in with divergent simplices.

We are now almost ready to establish our basic collapse result, Theorem 18 below. In order to do this, we will need to extend the “center of mass” map $\beta$ to the entire complex $\Delta _{\lfloor pAb\rfloor }$ by filling it in with divergent simplices in a natural way. The resulting $\beta :\Delta _{\lfloor pAb\rfloor }\rightarrow (\partial _{\infty },{{\,\mathrm{Td}\,}})$ should be continuous, of course, and it should

• (1) be $\Gamma$-equivariant,

• (2) send a vertex [A] to its center of mass $\xi _A$, and

• (3) for each simplex $\sigma$ of $\Delta _{\lfloor pAb\rfloor }$, the simplex $\beta (\sigma )$ should diverge.

We will express (3) by saying “$\beta$ diverges on simplices”. Because of condition (2) and by Proposition 12, the vertices of a simplex $\sigma$ are mapped to the endpoints of divergent rays by $\beta$. The extra condition (3) says that for all points in a simplex $p\in \sigma$ all the rays $[z,\beta (p))$ diverge, and they do so uniformly. In practice, if the map $\beta$ doesn’t distort things too much one can get (3) from (1) and (2):

Lemma 17

Suppose $\beta$ satisfies (1) and (2), and let $\alpha >0$. If $\beta (\sigma )$ is in the $(\pi /2-\alpha )$-neighborhood of the vertex set $\beta (\sigma ^{(0)})$, then $\beta (\sigma )$ diverges.

Proof

Let $\sigma$ be a simplex in $\Delta _{\lfloor pAb\rfloor }$ represented by a chain of Abelian groups $A_0<\cdots <A_k$. Then $\sigma$ is fixed pointwise by each group $A_i$ since all the $A_i$ commute. Since $\beta$ is equivariant, $\beta (\sigma )$ is fixed by $A_i$ as well. Moreover, the group $C_{A_i}$ preserves horospheres centered at $\beta ([A_i])$. Therefore Corollary 15 implies

$$\begin{aligned} \beta (\sigma ) \text{ diverges } \text{ if } \text{ for } \text{ some } \text{ vertex } v \text{ we } \text{ have } \beta (\sigma )\subset B_{\pi /2-\alpha }(v). \end{aligned}$$

(16)

Even if the entire simplex is not contained in the $(\pi /2-\alpha )$-neighborhood of a single vertex, applying Corollary 15 to a vertex shows that the portion of the simplex that lies in the $(\pi /2-\alpha )$-neighborhood of that vertex diverges. Doing this for each one of the vertices of $\sigma$ proves the lemma.$\square$

We will describe different versions of $\beta$ in Section 8 and use the lemma to check that for each of these versions all simplices $\beta (\sigma )$ diverge.

6.3 The perks of being a divergent simplex.

Suppose we have, one way or another, got our hands on such a “divergent simplex” map $\beta$. Let us explain how it can be used, together with the Abelianization map $\mu$ constructed in section 4, to understand the topology of the thin part. The idea is that the composition $\rho :=\beta \circ \mu$

$$\begin{aligned} \partial {\widetilde{M}}_{\le \varepsilon }{\mathop {\rightarrow }\limits ^{\mu }}\Delta _{\lfloor pAb\rfloor }{\mathop {\rightarrow }\limits ^{\beta }}(\partial _{\infty },{{\,\mathrm{Td}\,}}) \end{aligned}$$

tells us how to push topological features to infinity while staying in the thin part. To make this precise, denote by

$$\begin{aligned} (\beta \circ \mu )_t:\partial {\widetilde{M}}_{\le \varepsilon }\rightarrow & {} {\widetilde{M}}\\ x\mapsto & {} [x,\beta \circ \mu (x))_t \end{aligned}$$

the map which sends a point $x\in \partial {\widetilde{M}}_{\le \varepsilon }$ to the point obtained by going for a time t along the geodesic ray $[x,\beta \circ \mu (x))$. Note that it is $\Gamma$-equivariant and that it “approaches $\beta \circ \mu$” in the sense that

$$\begin{aligned} (\beta \circ \mu )_t \text{ is } \text{ asymptotic } \text{ to } \text{ the } \text{ cone } \text{ homotopy } c_t\circ \beta \circ \mu . \end{aligned}$$

Two additional key features of this map (proved below) is that it stays in the thin part for all t and pushes further into the thin part for large t. This lets us collapse any compact subset in ${\widetilde{M}}_{\le \varepsilon }$ to a subset of topological dimension less than or equal to $\dim ({{\,\mathrm{Im}\,}}(\beta \circ \mu ),\angle _x).$

Theorem 18

Let $\mu :\partial {\widetilde{M}}_{\le \varepsilon }\rightarrow \Delta _{\lfloor pAb\rfloor }$ be the Abelianization map. Suppose there is a $\Gamma$-equivariant map $\beta :\Delta _{\lfloor pAb\rfloor }\rightarrow (\partial _{\infty },{{\,\mathrm{Td}\,}})$ which sends vertices [A] to their centers of mass $\xi _{[A]}$ and which diverges on simplices. Then

• $(\beta \circ \mu )_t:\partial {\widetilde{M}}_{\le \varepsilon }\rightarrow {\widetilde{M}}$ is in ${\widetilde{M}}_{\le \varepsilon +2\delta }$ for all $t\ge 0$, and

• $(\beta \circ \mu )_t$ diverges over M.

Denote the dimension of the image of $\beta \circ \mu$ in the sphere topology by

$$\begin{aligned} d:=d_{\beta }=\dim ({{\,\mathrm{Im}\,}}(\beta \circ \mu ),\angle _x). \end{aligned}$$

Then the inclusion of any compact subset $\varphi :K\hookrightarrow \partial {\widetilde{M}}_{\le \varepsilon }$ can be homotoped in ${\widetilde{M}}_{\le \varepsilon +2\delta }$ to a map ${\hat{\varphi }}$ with image of dimension $\le d$.

We will prove this theorem at the end of this section. Next, we present several topological consequences of Theorem 18.

Corollary 19

Assume the hypotheses of Theorem 18. Then

$$\begin{aligned} H_{>d}({\widetilde{M}}_{\le \varepsilon })=0. \end{aligned}$$

Proof

Let $\varphi :F\rightarrow \partial {\widetilde{M}}_{\le \varepsilon }$ be a homology cycle of dimension $k>d$. By the previous theorem, it can be homotoped in ${\widetilde{M}}_{\le \varepsilon +2\delta }$ to a map ${\hat{\varphi }}$ with d-dimensional image. Since M is tame, we can push the homotopy a little along the product direction of ${\widetilde{M}}_{\le \varepsilon +2\delta }=\partial {\widetilde{M}}_{\le \varepsilon +2\delta }\times [0,\infty )$ so that it stays in the $\varepsilon$-thin part ${\widetilde{M}}_{\le \varepsilon }$. By a standard argument (recalled in “Appendix D”) we can further homotope the map ${\hat{\varphi }}$ in ${\widetilde{M}}_{\le \varepsilon }$ to a map $\overline{\varphi }$ whose image lands in the d-skeleton ${\widetilde{M}}_{\le \varepsilon }^{(d)}$ of a triangulation of ${\widetilde{M}}_{\le \varepsilon }$. Since $d<k$, we conclude that $\varphi$ is zero on k-dimensional homology. $\square$

Corollary 20

Assume the hypotheses of Theorem 18. If $d\le 1$ then each component of ${\widetilde{M}}_{\le \varepsilon }$ is aspherical.

Proof

If $d\le 1$ then, arguing as in the previous corollary, any map $\varphi :S^k\rightarrow {\widetilde{M}}_{\le \varepsilon }$ can be homotoped in ${\widetilde{M}}_{\le \varepsilon }$ to factor through a graph. Therefore each component of ${\widetilde{M}}_{\le \varepsilon }$ is aspherical. $\square$

In order for these results to mean anything, we need some control over the dimension d. The first observation is that d is also equal to the dimension of the image of $\rho =\beta \circ \mu$in the Tits metric.

Proposition 21

Assume the hypotheses of Theorem 18. Then

$$\begin{aligned} d=\dim ({{\,\mathrm{Im}\,}}\rho ,\angle _x)=\dim ({{\,\mathrm{Im}\,}}\rho ,{{\,\mathrm{Td}\,}})\le \dim (\partial _{\infty },{{\,\mathrm{Td}\,}}). \end{aligned}$$

Proof

As a continuous image of a compact set, $\rho (\sigma )$ is compact in the Tits metric. Therefore, the identity map $(\rho (\sigma ),{{\,\mathrm{Td}\,}})\rightarrow (\rho (\sigma ),\angle _x)$ is a homeomorphism (since it is a continuous bijection from a compact space to a Hausdorff space) and thus it preserves topological dimensions, i.e. $\dim (\rho (\sigma ),\angle _x)=\dim (\rho (\sigma ),{{\,\mathrm{Td}\,}})$. Now, since ${{\,\mathrm{Im}\,}}(\rho )$ is a countable union of the images of simplices $\rho (\sigma )$, its dimension is equal, in either the $\angle _x$ or the ${{\,\mathrm{Td}\,}}$-metric, to the supremum of the dimensions of the simplices by the countable sum theorem in dimension theory (see III.2 in [HW48]). We conclude that

$$\begin{aligned} \dim ({{\,\mathrm{Im}\,}}\rho ,\angle _x)=\sup _{\sigma }\dim (\rho (\sigma ),\angle _x)=\sup _{\sigma }\dim (\rho (\sigma ),{{\,\mathrm{Td}\,}})=\dim ({{\,\mathrm{Im}\,}}\rho ,{{\,\mathrm{Td}\,}}) \end{aligned}$$

which proves the proposition. $\square$

Remark

We initially defined d via the sphere topology on $\partial _{\infty }$ because this is the topology for which the cone map $c_t$ is a homeomorphism onto its image. This is unsatisfying because the sphere topology does not reflect in any way the geometry of the universal cover. After all, the metric space $(\partial _{\infty },\angle _x)$ is just a round $(n-1)$-sphere. Proposition 21 is useful because the topological dimension of the Tits boundary is a geometrically meaningful quantity that can be (and often is) much smaller than $n-1$. For instance, for symmetric spaces it is one less than the dimension of a maximal flat.

We end this section by giving the proof of Theorem 18.

Proof of Theorem 18

The proof consists of several steps. First we prove the two properties of the homotopy $(\beta \circ \mu )_t$ mentioned in the bullets and then we explain how to use these properties to collapse K to a d-dimensional subset.

Claim

The homotopy $(\beta \circ \mu )_t$ is in the $(\varepsilon +2\delta )$-thin part ${\widetilde{M}}_{\le \varepsilon +2\delta }$ for all t.

Recall from 4.3 that for every point $x\in \partial {\widetilde{M}}_{\le \varepsilon }$ there is a non-trivial element $\gamma \in \Gamma$ that is $(\varepsilon +2\delta )$-small at x and fixes $\mu (x)$. Because $\beta$ is $\Gamma$-equivariant $\gamma$ also fixes $\beta \circ \mu (x)$, so $\gamma$ is $(\varepsilon +2\delta )$-small on the entire geodesic ray $[x,\beta \circ \mu (x))$. Since $(\beta \circ \mu )_t$ is defined by flowing along these geodesic rays for a time t, its image is in ${\widetilde{M}}_{\le \varepsilon +2\delta }$.

Claim

The homotopy $(\beta \circ \mu )_t$ diverges.

Let F be a compact fundamental domain for the $\Gamma$-action on ${\widetilde{M}}_{\le \varepsilon }$. Since $\mu (F)$ is contained in a finite union of simplices of $\Delta _{\lfloor pAb\rfloor }$ and $\beta$ diverges on simplices, we conclude that $c_t\circ \beta \circ \mu \mid _F$ diverges. It is asymptotic to $(\beta \circ \mu )_t\mid _F$ so Lemma 16 that $(\beta \circ \mu )_t\mid _F$ diverges. But since $(\beta \circ \mu )_t$ is $\Gamma$-equivariant and F is a fundamental domain, this actually implies that the entire $(\beta \circ \mu )_t$ diverges.

Claim

Collapsing K to dimension d in the thin part.

Since $(\beta \circ \mu )_t$ diverges and is asymptotic to $c_t\circ \beta \circ \mu$, for any compact subset K and large enough t the straight-line homotopy between $(\beta \circ \mu )_t\mid _K$ and $c_t\circ \beta \circ \mu \mid _K$ is inside${\widetilde{M}}_{\le \varepsilon }$ by Lemma 16. Thus for a compact K we can go along $(\beta \circ \mu )_t$ for a sufficiently large time and then take the straight line homotopy to $c_t\circ \beta \circ \mu$, and during this process the image of the set K will stay inside the $(\varepsilon +2\delta )$-thin part ${\widetilde{M}}_{\le \varepsilon +2\delta }$. Since $c_t$ is a diffeomorphism, the topological dimension of the image of $c_t\circ \beta \circ \mu$ is equal to d. This finishes the proof of the theorem. $\square$

7 The Importance of being Lipschitz

As pointed out in the previous section, we need some control over the dimension $d =\dim ({{\,\mathrm{Im}\,}}(\beta \circ \mu ),\angle _x)$. The inconvenient truth that continuous maps can be space-filling means that if $\beta$ is only continuous, then d can be as high as $(n-1)$ and all information on the topology of $\partial \widetilde{M}_{\le \varepsilon }$ will be lost. Therefore, we need $\beta$ to be Lipschitz because Lipschitz maps do not raise dimensions, so that we will have

$$\begin{aligned} d\le \dim (\Delta _{\lfloor pAb\rfloor })\le \text{ rank }_{Ab}(\pi _1M)-1. \end{aligned}$$

(17)

To get further constraints on the dimension d, it turns out to be important to understand non-degenerate simplices. A simplex $\lambda :\Delta ^k\rightarrow X$ is non-degenerate if $\lambda (\Delta ^k)\not = \lambda (\partial \Delta ^k)$. Since ${{\,\mathrm{Im}\,}}(\beta )$ is the union of all the non-degenerate simplices $\beta (\sigma )$, Lipschitzness of $\beta$ will imply that

$$\begin{aligned} d\le \dim ({{\,\mathrm{Im}\,}}(\beta ),\angle _x)\le \max \{k\mid \text{ there } \text{ is } \text{ a } \text{ non-degenerate } k\text{-simplex } \beta (\sigma )\}, \end{aligned}$$

so understanding non-degenerate simplices may tell us something about d.

Some simplices are better adapted for this than others. We will discuss three possibilities in the next section. Of course, the third one is always the one to be chosen in the end. It will be named after Busemann.

8 Intermission and Flyers on Various Types of Simplices

8.1 Summary of previous sections.

We have found a systematic way (given by the map $\beta$) of sending vertices of a sufficiently fine enough triangulation of $\partial \widetilde{M}_{\le \varepsilon }$ to $\partial _\infty$. We need to fill in $\beta$ with simplices in $\partial _\infty$ that are Lipschitz and satisfy the criterion for divergence explained above.

So let us now turn to the problem of actually constructing divergent simplices for the map $\beta$. There are at least three different ways to do it. The easiest method is to use geodesic simplices so we will mention it first.

8.2 Geodesic simplices in $(\partial _{\infty },{{\,\mathrm{Td}\,}})$.

To reassure the reader that the present discussion is not devoid of content, we note that one way to build $\beta$ is using geodesic simplices. Recall that a geodesic simplex $\sigma _k$ with (ordered set of) vertices $v_0,\ldots ,v_k$ that are mutually $\le \pi /2$ apart is defined inductively as the iterated geodesic join $\sigma _k=\sigma _{k-1}*v_k$. So, by definition, a geodesic simplex is contained in the convex hull of its vertices. If the set of vertices has diameter $<\pi /2-\alpha$ then the geodesic simplex $\sigma _k$ is inside the ball $B_{\pi /2-\alpha }(v_i)$ centered at any vertex. Therefore, by (16), if we form $\beta$ using geodesic simplices, then the resulting simplices with diverge. It is also easy to see from the definition that that the resulting map $\beta$ will be Lipschitz and $\Gamma$-equivariant. So, this $\beta$ will have all the properties listed in Subsection 6.1.3 and all the results of Subsection 6.2 and Section 7 apply to it. In particular, $\underline{\hbox {geodesic simplices are sufficient to establish the rank}_{Ab}(\pi _1M)\hbox {and }\dim (\partial _{\infty },{{\,\mathrm{Td}\,}})}$$\underline{\hbox {versions of Theorem 4}}$. However it is difficult to say anything about non-degenerate geodesic simplices and we do not know how to get the half-dimensional bound of Theorems 1 and 2 using geodesic simplices.

8.3 Barycentric simplices in $(\partial _{\infty },{{\,\mathrm{Td}\,}})$.

These simplices were introduced in Section 4 of [Kle99]. Suppose the diameter of the set $\{v_0,\ldots ,v_k\}$ is $<\pi /2-\alpha$. For each $t\in \Delta ^k$, let $\lambda (t)$ be the unique minimum (see Lemma 4.22 of [Kle99]) of the function

$$\begin{aligned} f_t(\cdot ):=\sum _it_i{{\,\mathrm{Td}\,}}(\cdot ,v_i)^2. \end{aligned}$$

This defines a map $\lambda :\Delta ^k\rightarrow \partial _{\infty }$ that is called the barycentric simplex with vertices$v_0\dots ,v_k$. Points x with ${{\,\mathrm{Td}\,}}(x,v_i)\ge \pi /2-\alpha$ for all i, are not on the barycentric simplex $\lambda$. This is because any function of the form $f_t$ has

$$\begin{aligned} f_t(x)\ge (\pi /2-\alpha )^2>f_t(v_i) \end{aligned}$$

so it does not have a minimum at x. Therefore $\lambda$ is contained in the $(\pi /2-\alpha )$-neighborhood of its vertex set $N_{\pi /2- \alpha }(\lambda ^{(0)})$. Barycentric simplices are Lipschitz and defined in an equivariant way, so we can use them to construct a “divergent simplex” map $\beta$. These simplicies are well adapted to understanding the Tits boundary with the Tits metric. Their key feature is that non-degenerate barycentric k-simplices must have $k\le \dim (\partial _{\infty },{{\,\mathrm{Td}\,}})$. In particular, we get from this that $d\le \dim (\partial _{\infty },{{\,\mathrm{Td}\,}})$, but we already knew that.

8.4 Busemann simplices in $(\partial _{\infty },{{\,\mathrm{Td}\,}})$.

The main focus of the rest of this paper is to introduce a new way of constructing simplices at infinity which we call Busemann simplices and which can also be used to build a “divergent simplex” map $\beta$. In this subsection, we give an informal account of Busemann simplices and their utility.

For a set of Busemann functions $h_0,\dots ,h_k$ centered at vertices $v_0,\dots ,v_k\in \partial _{\infty }$ with ${{\,\mathrm{Td}\,}}(v_i,v_j)<\pi /2-\alpha$, and a basepoint $x\in {\widetilde{M}}$ we let $\sigma _R(t)$ be the unique minimum of the function

$$\begin{aligned} f_t(\cdot )=\sum _it_ih_i(\cdot ) \end{aligned}$$

on the sphere $S_R(x)$. This defines for each radius R a map $\sigma _R:\Delta ^k\rightarrow S_R(x)$. Doing this for all the simplices in $\Delta _{\lfloor pAb\rfloor }$ gives a map

$$\begin{aligned} \beta _R:\Delta _{\lfloor pAb\rfloor }\rightarrow S_R(x). \end{aligned}$$

As we will see in Section 9, this map is Lipschitz in the $\angle _x$-metric with a Lipschitz constant that does not depend onRorx. This allows us to find a convergent subsequence $\beta _{R_i}\rightarrow \beta :\Delta ^k\rightarrow \partial _{\infty }$ converging to a Lipschitz map $\beta$. Such a limit map $\beta$ is called “the” Busemann map and its restriction to each simplex $\sigma$ is called a Busemann simplex.

Remark

The map $\beta$ depends on a sequence of scales $\{R_i\rightarrow \infty \}$ that we choose once and for all.

The limit map $\beta$does not depend on the choice of basepointx and it follows from this that $\beta$ is $\Gamma$-equivariant and Lipschitz in the Tits metric. The basepoint independence also leads, via (16), to divergence for Busemann simplices. Therefore, this $\beta$ constructed out of Busemann simplices serves as a “divergent simplex” map and the results of Subsection 6.2 and Section 7 apply to it.

Busemann simplices are particularly well-adapted to studying the topology of the end. Let us say a bit about why this is the case. Let G be a discrete group which preserves horospheres at the vertices of the simplex $\sigma$. Busemann simplices are constructed so that the group G preserves horospheres on the entire simplex. One also has a good understanding of non-degenerate Busemann simplices in terms of the finite approximations $\beta _{R_i}(\sigma )$. These are the key features that lead to a bound

$$\begin{aligned} hdim(G)+k+1\le n \end{aligned}$$

for a non-degenerate Busemann k-simplex $\beta (\sigma )$. This dimension bound is our main technical result. If $\sigma$ is a k-simplex in $\Delta _{\lfloor pAb\rfloor }$ then the group preserving horospheres at the vertices is at least${\mathbb {Z}}^{k+1}$ so if $\beta (\sigma )$ is non-degenerate we get from the dimension bound that $2(k+1)\le n$ and therefore

$$\begin{aligned} k\le \lfloor n/2\rfloor -1. \end{aligned}$$

Since $\beta$ is Lipschitz and its image ${{\,\mathrm{Im}\,}}(\beta )$ is the union of the non-degenerate $\beta (\sigma )$, we get the half-dimensional collapse phenomenon

$$\begin{aligned} d\le \lfloor n/2\rfloor -1. \end{aligned}$$

9 Busemann Simplices (Mostly Metric Properties)

We now construct the Busemann simplices introduced at the end of the last section. These are limits of singular simplices on spheres centered at a fixed point x of finite radius $R_i$, i.e.

$$\begin{aligned} \lim _{R_i\rightarrow \infty }\sigma _{R_i,x}:\Delta ^k\rightarrow (\partial _{\infty },\angle _x). \end{aligned}$$

Since Busemann simplices are defined as limits, we need to make sure that such limits exist and must also be Lipschitz and divergent. Therefore, we will first give some preliminary estimates on the finite radius approximations.

For reasons that will be clear by the end of this section, Busemann simplices can be defined whenever the vetices $z_0,\dots ,z_i$ are pairwise at an angle $\le \pi /2$ from each other. Therefore, we will consider in this section only Busemann functions $h_0,\dots ,h_k$ whose gradients are pairwise at an angle $\le \pi /2$ everywhere.

9.1 Preliminary estimates.

Let $\Delta ^k=\{(t_0,\dots ,t_k)\mid t_0+\dots +t_k=1 \text{ and } t_i\ge 0 \text{ for } \text{ each } i\}$. For each $t \in \Delta ^k$, take the convex combination

$$\begin{aligned} f_t :=t_0h_0+\cdots +t_kh_k. \end{aligned}$$

9.1.1 Infinitesmal Lipschitz estimate.

Since $\nabla h_0,\dots ,\nabla h_k$ are unit vectors that pairwise make an angle $\le \pi /2$, the Hölder inequality gives

$$\begin{aligned} {1\over \sqrt{k+1}}\le \sum _{i=0}^kt_i^2 \le |\nabla f_t| \le 1. \end{aligned}$$

Therefore the radial projection from the convex hull of the $\nabla h_i$ to the unit sphere is at most $\sqrt{k+1}$-Lipschitz, so we get

$$\begin{aligned} \angle (\nabla f_t,\nabla f_{t'})\le \sqrt{k+1}|t-t'|_2. \end{aligned}$$

9.1.2 Radius-R Lipschitz estimate.

Fix a basepoint $x\in {\widetilde{M}}$. Since $f_t$ is convex with no critical points as $|\nabla f_t|>0$, the minima of $f_t$ on the R-ball $B_x(R)$ form a convex subset of its boundary sphere $S_x(R)$, and strict convexity of the R-ball implies that this subset is a point. Denote it by $\sigma _R(t)$. This defines a map

$$\begin{aligned} \sigma _R:\Delta ^k\rightarrow S_x(R). \end{aligned}$$

Lemma 22

For each $R >0$, the map

$$\begin{aligned} \sigma _R :\Delta ^k \rightarrow (S_x(R), \measuredangle _x) \end{aligned}$$

is $2\sqrt{k+1}$-Lipschitz in the $L^2$-metric on $\Delta ^k$.

Proof

The main idea of this proof is in Figure 5, which might be necessary for the purpose of following what is written next.

Let $p_1 = \sigma _R (t)$ and $p_2 = \sigma _R(t+\delta )$. Let $\alpha = \measuredangle _x(p_1,p_2)$. Our goal is to bound $\alpha$ in terms of $\delta$. For each $i = 1,2$,

• let $\beta _i$ be the angle at $p_i$ between $-\nabla f_t$ and $-\nabla f_{t+\delta }$,

• let $\alpha _i = \measuredangle _{p_i} (x, p_{i+1})$, where addition in i is taken mod 2,

• let $\mu _1$ be the angle at $p_1$ between the $-\nabla f_{t+\delta }$ and the tangent to the geodesic from $p_1$ to $p_2$, and

• let $\mu _2$ be the angle at $p_2$ between the $-\nabla f_{t}$ and the tangent to the geodesic from $p_2$ to $p_1$.

Fig. 5

Lipschitz bound.

Then

$$\begin{aligned} \alpha _1 + \mu _1 + \beta _1 \ge \pi \end{aligned}$$

since at $p_1$ the vector $-\nabla f_t$ is parallel to the tangent vector to the geodesic from x to $p_1$ because they are both orthogonal to the level set $f_t = f_t(p_1)$. Similarly,

$$\begin{aligned} \alpha _2 + \mu _2 + \beta _2 \ge \pi . \end{aligned}$$

Therefore,

$$\begin{aligned} \beta _1 +\beta _2 \ge (\pi - \alpha _1 -\alpha _2) + (\pi - \mu _1 - \mu _2). \end{aligned}$$

Now, $\alpha$, $\alpha _1$ and $\alpha _2$ are the three angles of the triangle $\triangle xp_1p_2$. Thus,

$$\begin{aligned} \alpha +\alpha _1 +\alpha _2 \le \pi , \quad \text {so}\quad \alpha \le \pi - \alpha _1 -\alpha _2. \end{aligned}$$

Hence,

$$\begin{aligned} \beta _1 +\beta _2 \ge \alpha + (\pi - \mu _1 - \mu _2). \end{aligned}$$

Next, we show that $\mu _1 \le \pi /2$. Observe that $p_1$ does not belong to the sublevel set $f_{t+\delta } \le f_{t+\delta }(p_2)$ since the sphere $S_x(R)$ lies on the other side of the level set $f_{t+\delta } = f_{t+\delta }(p_2)$. Therefore, $f_{t+\delta }(p_1) > f_{t+\delta }(p_2)$, so $p_2$ is contained in the sublevel set $f_{t+\delta } \le f_{t+\delta }(p_1)$. Since at $p_1$ the vector $-\nabla f_{t+\delta }$ is orthogonal to the level set $f_{t+\delta } = f_{t+\delta }(p_1)$ it follows that $\mu _1 \le \pi /2$. Similarly, we see that $\mu _2 \le \pi /2$ and we obtain that

$$\begin{aligned} \alpha \le \beta _1 +\beta _2. \end{aligned}$$

Since each $\beta _i\le \sqrt{k+1}|\delta |_2$ by 9.1.1, it follows that $\alpha \le 2\sqrt{k+1}|\delta |_2$. $\square$

9.2 Definition of Busemann simplices.

The approximations $\sigma _R:\Delta ^k\rightarrow \ S_{x}(R)$ depend on the choice of basepoint x. For the moment, let us emphasize this dependence and denote them by $\sigma _{R,x}$. Let us identify all the $(S_x(R),\angle _x)$ with $(\partial _{\infty },\angle _x)$ via geodesic retraction. Then for each $R>0$ we get a map

$$\begin{aligned} \sigma _{R_i,x}:\Delta ^k\rightarrow (\partial _{\infty },\angle _x), \end{aligned}$$

and all these maps are Lipschitz with the same Lipschitz constant $2\sqrt{k+1}$. Therefore, by Arzela-Ascoli, there is a sequence of radii $R_i\rightarrow \infty$ so that $\sigma _{R_i,x}$ converge to a $2\sqrt{k+1}$-Lipschitz map

$$\begin{aligned} \sigma :=\lim _{R_i\rightarrow \infty }\sigma _{R_i,x}:\Delta ^k\rightarrow (\partial _{\infty },\angle _x). \end{aligned}$$

We call any such map $\sigma$ a Busemann simplex.

9.3 Properties of Busemann simplices

9.3.1 Independence of basepoint.

Next we will show that $\sigma$ does not depend on the choice of basepoint x but only on the sequence of radii $R_i$. The (easy) estimate we need for this is

$$\begin{aligned} d_{{\widetilde{M}}}(\sigma _{R,x}(t),\sigma _{R,y}(t))\le D+\sqrt{2DR+D^2} \end{aligned}$$

(18)

where $D:=d(x,y)$. The key point is that R appears under the square root in the estimate (18). It follows from this (by Section 16.2) that $\{\sigma _{R_i,x}\}$ converges if and only if $\{\sigma _{R_i,y}\}$ converges, and that both converge to the same $\sigma$.

Remark

Here is what we are using: If $x_i\rightarrow \xi$ and ${d(y_i,x_i)\over d(x_0,x_i)}\rightarrow 0$ then $y_i\rightarrow \xi$.

Proof of estimate (18)

We will use the following notation. Fix $c_1,c_2\in {\mathbb {R}}$. Denote by $x_i$ and $y_i$ the closest point projections of x and y onto the sublevel set $\{f_t\le c_i\}$, respectively. Suppose that $d(x,x_1)=R$ and $d(y,y_2)=R$. In other words, $x_1=\sigma _{R,x}(t)$ and $y_2=\sigma _{R,y}(t)$. Without loss of generality $c_2\le c_1$.

We need to bound $d(x_1,y_2)$ in terms of D and R. First, note that

$$\begin{aligned} d(x_1,y_2)\le & {} d(x_1,x_2)+d(x_2,y_2)\\\le & {} d(x_1,x_2)+d(x,y)\\= & {} d(x_1,x_2)+D, \end{aligned}$$

because closest point projection to $\{f_t\le c_2\}$ is a semicontraction, i.e. a 1-Lipschitz map. It remains to bound $d(x_1,x_2)$. To do this, note that $c_2\le c_1$ implies $\angle _{x_1}(x,x_2)\ge \pi /2$, so

$$\begin{aligned} d(x_1,x_2)^2+R^2= & {} d(x_1,x_2)^2+d(x,x_1)^2\\\le & {} d(x,x_2)^2\\\le & {} d(x,y_2)^2\\\le & {} (D+R)^2, \end{aligned}$$

where the first inequality is by triangle comparison with an obtuse triangle in Euclidean space, the second inequality is because $x_2$ is the closest point to x on $\{f_t\le c_2\}$ while $y_2$ is just some point on this sublevel set, and the third is the triangle inequality. Simplifying, we get $d(x_1,x_2)\le \sqrt{2DR+D^2}$. $\square$

9.3.2 Busemann simplices are Lipschitz in the Tits metric.

A consequence of the basepoint independence is that $\sigma :\Delta ^k\rightarrow \partial _{\infty }$ is $2\sqrt{k+1}$-Lipschitz in the $\angle _y$ metric for any point $y\in {\widetilde{M}}$, since we can use finite approximations $\{\sigma _{R_i,y}\}$ based at y to get the limit simplex $\sigma$, and for these Lemma 22 gives the $2\sqrt{k+1}$-Lipschitz estimate. Therefore, Busemann simplices are $2\sqrt{k+1}$-Lipschitz in the $\angle$-metric $\angle =\sup _{y\in {\widetilde{M}}}\angle _y$. Since for distances $<\pi$ the Tits metric agrees with the $\angle$-metric (in the sense that $\angle =\min ({{\,\mathrm{Td}\,}},\pi )$, see “Appendix B”) Busemann simplices are also locally $2\sqrt{k+1}$-Lipschitz in the Tits metric. Since the Tits metric is a path metric, this implies they are $2\sqrt{k+1}$-Lipschitz in the Tits metric.

9.3.3 Diameter bound.

For each Busemann function $h_i$, denote by ${\overline{h}}_i$ the center of the horosphere $h_i^{-1}(0)$. Busemann simplices are small in the following sense.

Lemma 23

If the set of vertices $\sigma ^{(0)}$ has ${{\,\mathrm{Td}\,}}$-diameter $<\pi /2-\alpha$ then the entire Busemann simplex $\sigma$ is contained in a ball of radius $\pi /2-\alpha$ centered at any one of the vertices, i.e.

$$\begin{aligned} {{\,\mathrm{Td}\,}}({\overline{h}}_i,{\overline{h}}_j)<\pi /2-\alpha \quad \text{ for } \text{ all } i,j\implies {{\,\mathrm{Td}\,}}({\overline{h}}_i,\sigma (t))\le \pi /2-\alpha . \end{aligned}$$

Proof

Fix a basepoint $x_0$ and let $\sigma _R(t):=\sigma _{R,x_0}(t)$ be the finite approximation based at $x_0$. Extend the geodesic segment $[x_0,\sigma _R(t)]$ to a geodesic ray $[x_0,\xi _R)$ with endpoint $\xi _R\in \partial _{\infty }$. Then, by looking at the ideal triangle with vertices $x_0$, $\sigma _R(t)$, and ${\overline{h}}_i$, we see that by nonpositive curvature we have

$$\begin{aligned} \angle _{x_0}(\sigma _R(t),{\overline{h}}_i)\le \angle _{\sigma _R(t)}(\xi _R,{\overline{h}}_i). \end{aligned}$$

(19)

Now, let $f_t=t_0h_0+\cdots +t_kh_k$. At the point $\sigma _R(t)$ the negative of the gradient $-\nabla f_t$ points at $\xi _R$. The gradient $\nabla f_t$ is a convex combination of gradients of the Busemann functions $h_i$ and in general is not a unit vector, but we can rescale it to be a unit vector $\nabla f_t/|\nabla f_t|$, which is a non-negative linear combination of the $\nabla h_i$. Now, the visual boundary $(\partial _\infty , \angle _{\sigma _R(t)})$ with the angle metric $\angle _{\sigma _R(t)}$ can be identified with the unit sphere of the tangent space $T_{\sigma _R(t)}\widetilde{M}$. With respect to this identification, the normalized vector $\nabla f_t/|\nabla f_t|$ lies on the intersection of the unit sphere of $T_{\sigma _R(t)}\widetilde{M}$ and the “positive quadrant” of the vector subspace spanned by $\nabla h_i$’s. It follows that in the $\angle _{\sigma _R(t)}$-metric the point $\xi _R$ is in the convex hull of the set $\{{\overline{h}}_0,\dots ,{\overline{h}}_k\}$. Since this set has diameter $<\pi /2-\alpha$ in the $\angle _{\sigma _R(t)}$-metric, its convex hull is contained in an $\angle _{\sigma _R(t)}$-metric $(\pi /2-\alpha )$-ball around each vertex ${\overline{h}}_i$, and therefore

$$\begin{aligned} \angle _{\sigma _R(t)}(\xi _R,{\overline{h}}_i)<\pi /2-\alpha . \end{aligned}$$

Using the earlier inequality (19) and taking the limit as $R_i\rightarrow \infty$ we get

$$\begin{aligned} \angle _{x_0}(\sigma (t),\overline{h_i})\le \pi /2-\alpha . \end{aligned}$$

Since this holds for every basepoint $x_0$, we get the same bound in the Tits metric. $\square$

9.3.4 Invariance of horospheres on a Busemann simplex.

Let

$$\begin{aligned} f=t_0h_0+\dots +t_kh_k \end{aligned}$$

be a convex combination of Busemann functions with ${{\,\mathrm{Td}\,}}(h_i,h_j)\le \pi /2$. Then f is a convex function that does not attain its infimum. If we denote

$$\begin{aligned} s_i:=f(\sigma _{R_i}(t)), \end{aligned}$$

then, by definition, $\sigma _{R_i}(t)$ is the closest point projection of the basepoint $x_0$ to the sublevel set $\{f\le s_i\}$. It follows from 3.9 of [BGS85] that the limit

$$\begin{aligned} {\hat{f}}(x):=\lim _{i\rightarrow \infty }d(x,\{f\le s_i\})-d(x_0,\{f\le s_i\}) \end{aligned}$$

(20)

exists and is equal to a Busemann function centered at $\sigma (t)$. If the Busemann functions $h_i$ are G-invariant then f is also (obviously) and inspecting the formula (20) we see that ${\hat{f}}$ is, as well. In summary, we get

Lemma 24

If G preserves horospheres at all the vertices ${\overline{h}}_i$ of a Busemann simplex $\sigma :\Delta \rightarrow \partial _{\infty }$, then G preserves horospheres at every point $\sigma (t)$ of $\sigma$.

Remark

We do not know whether the same is true for geodesic or barycentric simplices. For those simplices, we only know that points on the simplex are fixed by G but we do not know that horospheres centered at those points are G-invariant.

10 The Busemann Map

In this section, we will construct a Lipschitz map $\beta$ such that $\beta$ satisfies the properties (1)–(3) of Subsection 6.1.3 and the restriction of $\beta$ to each simplex $\sigma$ in $\Delta _{\lfloor pAb\rfloor }$ is a Busemann simplex.

10.1 Construction.

Define $\beta$ on the vertices of $\Delta _{\lfloor pAb\rfloor }$ as in 5.3 by

$$\begin{aligned} \beta ([A]):=\xi _{[A]}. \end{aligned}$$

Fix a basepoint x. Doing the construction from 9.1.2 of the finite approximations $\sigma _R$ on each simplex of $\Delta _{\lfloor pAb\rfloor }$ gives a map

$$\begin{aligned} \beta _R:\Delta _{\lfloor pAb\rfloor }\rightarrow S_x(R). \end{aligned}$$

This map is 3k-Lipschitz in the $\angle _x$-metric: It is enough to check this on paths, where it follows from the fact (Lemma 22) that it is 3k-Lipschitz (note that $2\sqrt{k+1}\le 3k$) on each simplex. Since $\Delta _{\lfloor pAb\rfloor }$ has countably many simplices, by Arzela-Ascoli we can take a sequence of radii $R_i\rightarrow \infty$ for which $\beta _{R_i}$ converge to a 3k-Lipschitz map

$$\begin{aligned} \beta :\Delta _{\lfloor pAb\rfloor }\rightarrow (\partial _{\infty },\angle _x). \end{aligned}$$

(21)

Since the Lipschitz constant does not depend on x, this map is also Lipschitz in the Tits metric. We call it “the” Busemann map.

10.2 Equivariance.

For any $\gamma \in \Gamma$ and simplex $\tau$ in $\Delta _{\lfloor pAb\rfloor }$, the Busemann simplices $\beta :\gamma \tau \rightarrow \partial _{\infty }$ and $\gamma \beta :\tau \rightarrow \partial _\infty$ have the same ordered set of vertices, so they are equal, i.e. $\gamma \beta =\beta \gamma$. Therefore $\beta$ is $\Gamma$-equivariant.

10.3 Divergence.

If $\sigma$ is a simplex in $\Delta _{\lfloor pAb\rfloor }$ with vertices $[A_0]<\dots <[A_k]$, then the Busemann simplex $\beta (\sigma )$ is fixed pointwise by $A_k$ because $\beta$ is $\Gamma$-equivariant, and contained in a $(\pi /2-\alpha )$-neighborhood of a vertex $\beta ([A_k])$ by Lemma 23. The group $C_{A_k}$ preserves horospheres at this vertex by Proposition 9, so we get by Corollary 15 that the Busemann simplex $\beta (\sigma )$ diverges in M.

Remark

Here is a slightly different way to see that the Busemann simplices diverge: Since $\beta$ is continuous, the image $\beta (\sigma )$ is compact in the Tits metric. Cover it with finitely many $(\pi /2-\alpha )$-balls. Since $C_{A_k}$ preserves horospheres on the entire Busemann simplex (Lemma 24) we can apply Proposition 14 to the centers of each of these balls and conclude that the portion of $\sigma$ contained in each one of the finitely many $(\pi /2-\alpha )$-balls diverges. Therefore, the entire Busemann simplex $\sigma$ diverges.

11 (Non)-degeneracy and Consequences

We saw earlier how it is important to have control over the dimension $d =\dim ({{\,\mathrm{Im}\,}}(\beta \circ \mu ),\angle _x)$. This d is bounded by the maximum of the dimensions of non-degenerate Busemann simplices in $\beta$. Thus, it would be good to know, especially if one wants to be efficient, when a Busemann simplex is degenerate and what we can do with non-degenerate ones. The goal of this section is to address these and to set things up for the next sections, where we will bound the number of vertices of non-degenerate simplices of $\beta$ by $\lfloor n/2\rfloor$. Since Busemann simplices are Lipschitz, this will bound the dimension d from above by $\lfloor n/2\rfloor -1$.

11.1 Non-degenerate simplices and linearly independent vectors.

A simplex $\lambda :\Delta \rightarrow X$ is non-degenerate if the image $\lambda (\Delta )$ is not contained in the image of the boundary $\lambda (\partial \Delta )$. Any point $x\in \lambda (\Delta )\backslash \lambda (\partial \Delta )$ is called a non-degenerate point of$\lambda$. The meaning of non-degeneracy for the finite approximations $\sigma _R$ is, partly, explained by the following simple lemma.

Lemma 25

Suppose $\sigma$ is a Busemann simplex and let $\sigma _R$ be a finite approximation of it. If $x\in \sigma _R(\Delta )$ is non-degenerate, then the gradient vectors $\{\nabla h_0,\dots ,\nabla h_k\}$ are linearly independent at x.

Proof

Note that $x=\sigma _R(t)$ for some $t=(t_0,\dots ,t_k)\in \Delta$, and look at the convex combination $f_t=t_0h_0+\dots +t_kh_k$. At the point x, the gradient

$$\begin{aligned} \nabla f_t=t_0\nabla h_0+\dots +t_k\nabla h_k \end{aligned}$$

is perpendicular to the sphere $S_{x_0}(R)$. Suppose the $\{\nabla h_i\}$ are linearly dependent at x, and write down a linear dependence relation as

$$\begin{aligned} \rho :=s_0\nabla h_0+\dots +s_k\nabla h_k=0, \end{aligned}$$

where we can assume that at least one of the coefficients $s_j$ is positive. So, there is a smallest $\varepsilon \ge 0$ such that $t_i-\varepsilon s_i=0$ for some i. After reordering the indices, we may assume this happens for $i=0$. Then $t_0-\varepsilon s_0=0$ and $t_i-\varepsilon s_i\ge 0$ for all i, so at x we have

$$\begin{aligned} \nabla f_t= & {} \nabla f_t-\varepsilon \rho \\= & {} (t_1-\varepsilon s_1)\nabla h_1+\dots +(t_k-\varepsilon s_k)\nabla h_k\\= & {} a_1\nabla h_1+\dots +a_k\nabla h_k \end{aligned}$$

for some non-negative constants $\{a_i\}_{i=1}^k$. Setting

$$\begin{aligned} t':=\left( 0,{a_1\over |a|_1},\dots ,{a_k\over |a|_1}\right) \in \partial \Delta , \end{aligned}$$

the above equation can be rewritten as

$$\begin{aligned} \nabla f_t=|a|_1\nabla f_{t'} \end{aligned}$$

at the point x, which implies that $x=\sigma _R(t')$. So, x is a degenerate point. $\square$

Remark

The proof of this lemma is less delicate than it may appear at first glance. All we are doing is finding an intersection point a of the line $t+\mathbb Rs$ with the boundary of the positive “octant” $\partial (({\mathbb {R}}_+)^{k+1})$ and observing that the boundary point $a/|a|_1\in \partial \Delta$ defined by this is mapped to $\sigma _R(t)$.

The map $\sigma _R:\Delta \rightarrow {\widetilde{M}}$ may be very far from an embedding. However, we will see next that the situation is better if we restrict to the preimages of non-degenerate points. Putting these together for all R forms the set

$$\begin{aligned} ({\mathbb {R}}^+\times \Delta )^{nd}_{\sigma }:=\{(R,t)\in {\mathbb {R}}^+\times \Delta \mid \sigma _R(t) \text{ is } \text{ non-degenerate }\}. \end{aligned}$$

(22)

This set is open because being non-degenerate is an open condition. Here, there is a slight abuse of notation since $({\mathbb {R}}^+\times \Delta )^{nd}_{\sigma }$ depends only on the vertices of $\sigma$ and the basepoint $x_0$, but not on the actual choice of $\sigma$. That is, one considers the vertex set $\{{\overline{h}}_0,\dots ,{\overline{h}}_k\}$ of $\sigma$ and associates to each ${\overline{h}}_i$ a Busemann function $h_i$ normalized so that $h_i(x_0)=0$ and then, for every $t=(t_0,\dots ,t_k)$, lets $f_t=\sum _{i=0}^kt_ih_i$ and lets $\sigma _R(t)$ be the minimum of $f_t$ on the R-sphere about $x_0$.

Corollary 26

The map

$$\begin{aligned} ({\mathbb {R}}^+\times \Delta )^{nd}_{\sigma }\rightarrow & {} {\widetilde{M}}, \end{aligned}$$

(23)

$$\begin{aligned} (R,t)\quad\mapsto & {} \sigma _R(t) \end{aligned}$$

(24)

is injective.

Proof

Note that $\sigma _R(t)=x=\sigma _R(t')$ gives the linear relation

$$\begin{aligned} t_0\nabla h_0+\dots +t_k\nabla h_k=c(t'_0\nabla h_0+\dots +t'_k\nabla h_k) \end{aligned}$$

at the point x. If x is non-degenerate, the previous lemma implies this relation is trivial. So we much have $t=ct'$. Since $\sum t_i=1=\sum t'_i$, this implies $c=1$ and $t=t'$. This proves the corollary. $\square$

11.2 Busemann cone.

In section 12 it will often be useful to put all the (images of) Busemann simplices $\sigma _R$ based at a single point $x_0$ together. The Busemann cone of $\sigma$ (based at $x_0$) is the set

$$\begin{aligned} \sigma _{>0}:=\bigcup _{R>0}\sigma _R(\Delta ) \end{aligned}$$

of all points in ${\widetilde{M}}$ that lie on $\sigma _R=\sigma _{R,x_0}$ for some radius R. Sometimes it is convenient to also include the basepoint $x_0$. The result is then a closed set

$$\begin{aligned} \sigma _{\ge 0}:=\sigma _{> 0}\cup \{x_0\}. \end{aligned}$$

A point on the Busemann cone is degenerate if it is a degenerate point of $\sigma _R$ for some R. As a matter of convention, we declare that $x_0$ is also a degenerate point. That is, a point on the Busemann cone is degenerate if it is not in the image of the map in Corollary 26.

11.3 A sequential criterion for degeneracy.

Suppose $\sigma _{R_i}\rightarrow \sigma$ is a Busemann simplex. Since the sequence of radii $\{R_i\}$ is chosen somewhat non-canonically, sometimes we cannot avoid dealing with points on the Busemann cone that are not on $\sigma _{R_i}$. Therefore, it will be useful later to have the following lemma which gives a criterion for degeneracy of a point $\sigma (t)$ in terms of a sequence of points on the Busemann cone $\{q_i\}$ converging to $\sigma (t)$. Note that the $q_i$’s need not belong to $\sigma _{R_i}$.

Lemma 27

Let $\sigma :\Delta \rightarrow \partial _{\infty }$ be a Busemann simplex. Then, a point $\sigma (t)$ is degenerate if there is a sequence $\{q_i\}_{i=1}^{\infty }$ of degenerate points on the Busemann cone $q_i\in \sigma _{\ge 0}$ with

$$\begin{aligned} \lim _{i\rightarrow \infty }{d(q_i,\sigma _{R_i}(t))\over R_i}=0. \end{aligned}$$

(25)

Proof

The sublinearity (25) implies that $\angle _{x_0}(q_i,\sigma _{R_i}(t))\rightarrow 0$, so $q_i\rightarrow \sigma (t)$, but this by itself does not yet mean that $\sigma (t)$ is degenerate. To prove degeneracy, we need to find a point $t'\in \partial \Delta$ satisfying $\sigma (t)=\sigma (t')$. We will now do this.

Fig. 6

Comparison triangle.

Since $q_i$ are degenerate points on the Busemann cone, we have

$$\begin{aligned} q_i=\sigma _{R_i'}(t'_i) \end{aligned}$$

for $t'_i\in \partial \Delta$ and radii $R_i'\rightarrow \infty$. Passing to a subsequence, we may assume

$$\begin{aligned} t'_i\rightarrow t'\in \partial \Delta . \end{aligned}$$

Now, the sublinearity (25) and the triangle inequality imply that ${|R_i'-R_i|\over R_i}\rightarrow 0$. Therefore we can write

$$\begin{aligned} R_i'=(1+\delta _i)R_i\quad \text{ for } \text{ a } \text{ sequence } \delta _i\rightarrow 0. \end{aligned}$$

Since both $\sigma _{R_i}(t')$ and $\sigma _{R'_i}(t')$ are obtained as closest point projections of $x_0$ to (different) sublevel sets of the same convex function $f_{t'}:=t_0'h_0+\dots +t_k'h_k$, comparison of the triangle with vertices $x_0$, $\sigma _{R_i}(t')$ and $\sigma _{R'_i}(t')$ (depicted in Figure 6) with an obtuse Euclidean triangle (see 15.2) gives

$$\begin{aligned} {d(\sigma _{R_i'}(t'),\sigma _{R_i}(t'))\over R_i}\le \sqrt{2\delta _i+\delta _i^2}\rightarrow 0. \end{aligned}$$

Therefore the sequence $\{q_i\}=\{\sigma _{R'_i}(t')\}$ converges to the same point as the sequence $\{\sigma _{R_i}(t')\}$, and that point is

$$\begin{aligned} \sigma (t)=\lim q_i=\sigma (t')\in \partial \Delta . \end{aligned}$$

$\square$

12 A Dimension Bound

Busemann simplices provide a way to connect points at infinity whose horospheres are preserved. Our goal in this section is to relate the dimension of a group G that acts on $\widetilde{M}$ preserving a collection of horospheres and the dimension of the Busemann simplex with vertices at the centers of those horospheres. One expects these two dimensions to be complementary. Theorem 28 gives the expected bounds on these dimensions. This is responsible for the n / 2 bound in the main theorems and is the climax of this paper. We will end this section by giving the proof of Theorem 7 in the introduction.

Recall that ${{\,\mathrm{Fix}\,}}^0(G)$ is the set of points in $\partial _{\infty }$ the horospheres centered at which are preserved by G.

Theorem 28

If ${{\,\mathrm{Fix}\,}}^0({\mathbb {Z}}^r)$ contains the image of a non-degenerate Busemann k-simplex $\sigma$, then

$$\begin{aligned} \dim {\widetilde{M}}\ge k+1+r. \end{aligned}$$

(26)

Remark

The method of proof of Theorem 28 applies to any subgroup $G<\Gamma$ that preserves horospheres on a non-degenerate Busemann k-simplex (see 12.6). But, for now it is helpful to focus on the case $G={\mathbb {Z}}^r$. This is all we need for half-dimensional collapse.

The proof of Theorem 28 is not quite a natural argument, so before giving the technical proof, we will explain why it is the way it is in Section 12.1. Readers who did not like Section 2 should definitely skip this Subsection.

12.1 Problems and solutions.

A natural approach to obtaining the bound $\dim {\widetilde{M}}\ge r+k+1$ is to show that each intersection of horospheres has dimension $\ge r$ and that there is a $(k+1)$-dimensional family of such intersections of horospheres. Consider the following parameter space for intersections of horospheres.

Pick representatives $h_i$ for the vertices of the non degenerate Busemann simplex $\sigma :\Delta ^k\rightarrow {{\,\mathrm{Fix}\,}}^0({\mathbb {Z}}^r)$, such that $h_i(x_0)=0$, and look at the “horospherical coordinates” map

$$\begin{aligned} \vec {h}:{\widetilde{M}}\rightarrow & {} {\mathbb {R}}^{k+1}, \end{aligned}$$

(27)

$$\begin{aligned} x\mapsto & {} (h_0(x),\dots ,h_k(x)). \end{aligned}$$

(28)

The map $\vec {h}$ is (obviously) ${\mathbb {Z}}^r$-invariant, and its image $\vec {h}({\widetilde{M}})$ in ${\mathbb {R}}^{k+1}$ is the parameter space for all possible intersections of horospheres $\cap _{i=0}^k\{h_i=b_i\}$.

Let $T_b$ be the intersection of horospheres $\vec {h}^{-1}(b)$. One can hope to show that each intersection of horospheres $T_b$ has dimension $\ge r$ by letting ${\mathbb {Z}}^r$ act on it. Ideally, $T_b$ is an $(n-k-1)$-dimensional submanifold that is contractible. It will then follow that $r\le (n-k-1)$, so we obtain $\dim \widetilde{M} = n \ge r+1+k$.

However, in order for this intersection of horospheres to be an $(n-k-1)$-dimensional submanifold, the gradients of the corresponding Busemann functions need to be linearly independent everywhere on the submanifold. This leads us to the main problem: these gradients need not be linearly independent (even on just the intersection of the horospheres). So we cannot show that $T_b$ has dimension $(n-k-1)$. Neither can we bound its dimension from below by r. The map $\vec {h}$ is ${\mathbb {Z}}^r$-invariant, so the group ${\mathbb {Z}}^r$ acts on each $T_b$, but this by itself is not enough to bound the dimension of $T_b$ from below by r. Pessimistically speaking, $T_b$ could be discrete. So we will not try to prove anything about$T_b$. Instead, we will show that the complement $(\widetilde{M}-T_o)$ has dimension at least $(k+r+1)$. Note that $T_o$ is a closed subset of $\widetilde{M}$, so $(\widetilde{M}-T_o)$ is a manifold of dimension n and thus, we will obtain $n \ge k+r+1$.

Recall that in algebraic topology, there are two ways to show that ${\mathbb {R}}^m$ has dimension m. One way is to remove a point o from it and to show that a sphere centered at o is nontrivial in the $(m-1)$-homology of the complement $({\mathbb {R}}^m - o)$. The second way is to let ${\mathbb {Z}}^m$ act on ${\mathbb {R}}^m$ the standard way and to show that the quotient is an m-torus, which has nontrivial m-homology. We will do something that is a combination of both ways in order to show that $(\widetilde{M}-T_o)$ is a manifold of dimension at least $(k+r+1)$.

That is, we will try to bound the dimension of

$$\begin{aligned} (\widetilde{M}-T_o)/{\mathbb {Z}}^r, \end{aligned}$$

for some fixed $b =o\in {\mathbb {R}}^{k+1}$.

So this problem has a topological solution if we can show $(\widetilde{M}-T_o)/{\mathbb {Z}}^r$ has a nontrivial homology class in dimension $(k+r)$ because it will imply that $n\ge (k+r+1)$ since $(\widetilde{M}-T_o)/{\mathbb {Z}}^r$ is noncompact.

Finding a$(k+r)$-homology class in$(\widetilde{M}-T_o)/{\mathbb {Z}}^r$. One can attempt to define a map ${\mathbb {S}}^k\times {\mathbb {T}}^r \rightarrow (\widetilde{M} - T_o)/{\mathbb {Z}}^r$ as follows. First, take a ${\mathbb {Z}}^r$-equivariant map $f :{\mathbb {R}}^r\rightarrow \widetilde{M}$ that takes $0 \mapsto x_0$, where $x_0$ is a fixed basepoint at which we will take the Busemann cone later. Then for each $T_b\ne \emptyset$, compose f with the closest point projection to $T_b$. If we can do this for b taking values in a k-sphere in $(\vec {h}(\widetilde{M})-o)$, then we obtain a map ${\mathbb {S}}^k\times {\mathbb {T}}^r \rightarrow (\widetilde{M} - T_o)/{\mathbb {Z}}^r$. Specifically, if $\vec {h}(\widetilde{M})$ has nonempty interior (as a subset of ${\mathbb {R}}^{k+1}$), then we can take o to be an interior point and let b take value in a k-sphere surrounding o. A problem with this approach is that $T_b$ needs not be convex so closest point projection is not well-defined. Nevertheless, intersections of horoballs are convex, so the solution is to project $f({\mathbb {R}}^r)$ onto

$$\begin{aligned} \widehat{T}_b:= \{x \in \widetilde{M}\; |\; h_i(x) \le b_i, \; i =0,1,\ldots , k\} \end{aligned}$$

instead. However, the price we pay for this is that the projection of $f({\mathbb {R}}^r)$ needs not land in $T_b$. Neither should it even be close to $T_b$. This is a problem.

But there is a solution, which is to use the magic of the Busemann cone$\sigma _{>0}$. We will show later in this Section 5 (in Lemma 30) that if $b\in \vec {h}(\sigma _{>0})$, then the closest-point projection $p(b,x_0)$ of $x_0 = f(0)$ onto the intersection $\widehat{T}_b$ of horoballs is actually contained in the intersection of horospheres $T_b$, or in other words, $\vec {h}(p(b,x_0)) = b$. It follows that the projection of $f({\mathbb {R}}^r)$ is contained in an L-neighborhood of $T_b$. This is because the action of ${\mathbb {Z}}^r$ is cocompact on $f({\mathbb {R}}^r)$ and closest-point projections are distance non-increasing. A result of this is that L is independent of b once we fix f, which suggests the following: if $\vec {h}(\sigma _{>0})$ contains a ball of radius larger than L, then the above attempt to define a map ${\mathbb {S}}^k\times {\mathbb {T}}^r \rightarrow (\widetilde{M}-T_o)/{\mathbb {Z}}^r$ can be realized, with o the center of the ball. Since L is arbitrarily large, it is not enough to show that $\vec {h}(\widetilde{M})$ has nonempty interior; we need to show that the subset $\vec {h}(\sigma _{>0})$contains arbitrarily large balls. Before we explain this, we also need to check that the homology class obtained is nontrivial.

Showing the$(k+r)$-homology class is nontrivial. Note that having such a map ${\mathbb {S}}^k\times {\mathbb {T}}^r \rightarrow (\widetilde{M}-T_o)/{\mathbb {Z}}^r$ is not enough, we also need this map to be nontrivial in homology, which holds if there is a map

$$\begin{aligned} (\widetilde{M} -T_o)/{\mathbb {Z}}^r \rightarrow {\mathbb {S}}^k\times {\mathbb {T}}^r \end{aligned}$$

such that the composition

$$\begin{aligned} {\mathbb {S}}^k\times {\mathbb {T}}^r \rightarrow (\widetilde{M} -T_o)/{\mathbb {Z}}^r \rightarrow {\mathbb {S}}^k\times {\mathbb {T}}^r \end{aligned}$$

has non-zero degree. There is a natural candidate for $(\widetilde{M} -T_o)/{\mathbb {Z}}^r \rightarrow {\mathbb {T}}^r$, which is the composition

$$\begin{aligned} (\widetilde{M} -T_o)/{\mathbb {Z}}^r \hookrightarrow \widetilde{M}/{\mathbb {Z}}^r \simeq {\mathbb {T}}^r. \end{aligned}$$

In fact, this is a good candidate because the restriction ${\mathbb {T}}^r\rightarrow {\mathbb {T}}^r$ is a homotopy equivalence. A natural candidate for $(\widetilde{M} -T_o)/{\mathbb {Z}}^r \rightarrow {\mathbb {S}}^k$ is to take $\vec {h} :(\widetilde{M} -T_o) \rightarrow ({\mathbb {R}}^{k+1}-o) \simeq {\mathbb {S}}^k$ and then quotient out by the action of ${\mathbb {Z}}^r$ using the fact that $\vec {h}$ is ${\mathbb {Z}}^r$-invariant. This is also a good candidate.

In summary, what we are left to explain is how to show that the set of horospherical coordinates $\vec {h}(\sigma _{>0})$ of the Busemann cone $\sigma _{>0}$ contains arbitrarily large balls. This is where we need $\sigma$ to be non-degenerate.

How to show that$\vec {h}(\sigma _{>0})$contains arbitrarily large balls. First, let us comment on why $\vec {h}(\sigma _{>0})$ has nonempty interior as a subset of ${\mathbb {R}}^{k+1}$. The reason is because $\vec {h}$ maps non-degenerate points in $\sigma _{>0}$ to interior points of the image $\vec {h}(\sigma _{>0})$. This is an Invariance-of-Domain argument. Recall that one obtains the Busemann cone $\sigma _{>0}$ by mapping in

$$\begin{aligned} \sigma _{>0} :{\mathbb {R}}^+\times \Delta \rightarrow \widetilde{M} \end{aligned}$$

as explained in Section 11. Since $\sigma$ is non-degenerate, the approximation $\sigma _{R_i}$ has non-degenerate points if i is large enough, and since being non-degenerate is an open condition, this implies that the set $({\mathbb {R}}^+\times \Delta )^{nd}$ of non-degenerate (R, t)-coordinates of $\sigma _{>0}$ is open in ${\mathbb {R}}^+\times \Delta$ and therefore is a $(k+1)$-dimensional manifold. Note that $\vec {h}\circ \sigma _{>0}$ maps $({\mathbb {R}}^+\times \Delta )^{nd}$ into ${\mathbb {R}}^{k+1}$, so if one can show that it is injective on $({\mathbb {R}}^+\times \Delta )^{nd}$, then one can use Invariance of Domain to show it is an open map and obtain that $\vec {h}(\sigma _{>0})$ has nonempty interior. To see that $\vec {h}\circ \sigma _{>0}$ is injective on $({\mathbb {R}}^+\times \Delta )^{nd}$, we need the maps $\vec {h}$ and $\sigma _{>0}$ to be injective (when restricted to the relevant domains). The map $\sigma _{>0}$ restricted to $({\mathbb {R}}^+\times \Delta )^{nd}$ is injective by Corollary 26. The restriction of $\vec {h}$ to the Busemann cone $\sigma _{>0}$ has an inverse $p( \cdot , x_0 )$ since (see Corollary 31) $\vec {h}(p(x_0,b)) = b$ for all $b \in \sigma _{>0}$, and therefore is injective.

To see that $\vec {h}(\sigma _{>0})$ contains arbitrarily large balls, we suppose for contradiction that it does not, which implies that $\vec {h}(\sigma _{>0})$ has an L-net Q of boundary points (in the sense of point set topology) of $\vec {h}(\sigma _{>0})$. Since $\vec {h}$ maps non-degenerate points in $\sigma _{>0}$ to interior points of the image $\vec {h}(\sigma _{>0})$, the points in Q belong to $\vec {h}(\sigma _{>0}({\mathbb {R}}^+\times \partial \Delta ))$. Take $p( Q, x_0)$ to get a subset of degenerate points of $\sigma _{>0}$ and if this gives an L-net in $\sigma _{>0}$, then this will imply that all points of $\sigma$ are degenerate, which contradicts the assumption that $\sigma$ is non-degenerate. However, $p( Q, x_0)$ needs not give a net in $\sigma _{>0}$ because $p(\cdot , x_0)$ might stretch distance between points in a nonuniform way. Nevertheless, a quantitative estimate on how $p(\cdot , x_0)$ distorts distance, as in the proof of Lemma 35, implies that $p(Q,x_0)$ is a $L\sqrt{R}$-net, by which we mean any point in $\sigma _{>0}$ that is a distance R from $x_0$ is $L\sqrt{R}$-close to a point in $p(Q,x_0)$. Since $\sqrt{R}$ is sublinear, this implies (by Lemma 27) all points in $\sigma$ are degenerate, contradicting the hypothesis that $\sigma$ is non-degenerate.

12.2 The setup.

Let us now begin setting up the proof. Fix a basepoint $x_0\in {\widetilde{M}}$ and let $h_i$ be Busemann functions representing the vertices of the non-degenerate Busemann simplex $\sigma :\Delta ^k\rightarrow {{\,\mathrm{Fix}\,}}^0({\mathbb {Z}}^r)$, normalized such that $h_i(x_0)=0$. Putting these Busemann functions together gives the horospherical coordinates map

$$\begin{aligned} \vec {h}:{\widetilde{M}}\rightarrow & {} {\mathbb {R}}^{k+1}, \end{aligned}$$

(29)

$$\begin{aligned} x\mapsto & {} (h_0(x),\dots ,h_k(x)). \end{aligned}$$

(30)

The map $\vec {h}$ is ${\mathbb {Z}}^r$-invariant because its coordinates are. It is a semicontraction in the sup norm $|\cdot |_{\infty }$ on ${\mathbb {R}}^{k+1}$ because $|\nabla h_i|=1$.

In the course of the argument, we will need to project various points to various (intersections of) horoballs. Define $\{\vec {h}\le b\}$ as the $\vec {h}$-preimage of $(-\infty ,b]$, so it is an intersection of horoballs. To keep track of all this, let p(b, x) be the closest point projection of the pointxto the intersection of horoballs$\{\vec {h}\le b\}$. This defines a map

$$\begin{aligned} p:{\mathbb {R}}^{k+1}\times {\widetilde{M}}\rightarrow {\widetilde{M}}. \end{aligned}$$

For a fixed b the map $p(b,\cdot )$ is a semicontraction, since it is the closest point projection to a convex set. It is ${\mathbb {Z}}^r$-equivariant since ${\mathbb {Z}}^r$ preserves the Busemann functions $h_i$ and thus also preserves the intersection of horoballs $\{\vec {h}\le b\}$.

The “error”. A central role in the proof is played by the difference

$$\begin{aligned} \vec {h}(p(b,\cdot ))-b, \end{aligned}$$

which measures the extent to which the closest point projection to the intersection of horoballs $\{\vec {h}\le b\}$ fails to land in the intersection of horospheres $\{\vec {h}=b\}$. We will call it the “error”.

Lemma 29

$\vec {h}(p(b,\cdot ))-b$ is a ${\mathbb {Z}}^r$-invariant semicontraction in the sup norm.

Proof

This follows directly from what we have said about $p(b,\cdot )$ and $\vec {h}$. $\square$

12.3 Some key properties of the Busemann cone.

Now let us turn to the Busemann cone $\sigma _{\ge 0}$. The key property of the Busemann cone is that the horospherical coordinates embed it in ${\mathbb {R}}^{k+1}$.

Lemma 30

For a Busemann simplex $\sigma$, the restriction

$$\begin{aligned} \vec {h}\mid _{\sigma _{\ge 0}}:\sigma _{\ge 0}\rightarrow {\mathbb {R}}^{k+1} \end{aligned}$$

is a homeomorphism onto its image, with inverse $p(\cdot ,x_0)$.

Proof

Let $b=(b_0,\dots ,b_k):=\vec {h}(\sigma _R(t))$ be the image of a point on the Busemann cone. We need to show that

$$\begin{aligned} p(b,x_0)=\sigma _R(t). \end{aligned}$$

The intersection of horoballs $\bigcap _{i}\{h_i\le b_i\}$ contains $\sigma _R(t)$ and is contained in the sublevel set $\{h_0t_0+\dots +h_kt_k\le b_0t_0+\dots +b_kt_k\}$. We claim that $\sigma _R(t)$ is the unique closest point to $x_0$ in this sublevel set. Therefore, it is also the unique closest point to $x_0$ on the intersection of horoballs. This proves that $p(b,x_0)=\sigma _R(t)$.

To see that $\sigma _R(t)$ is the unique closest point to $x_0$ on the sublevel set $\{h_0t_0+\dots +h_kt_k\le b_0t_0+\dots +b_kt_k\}$, note that $b_i=h_i(\sigma _R(t))$ implies $\sigma _R(t)$ lies on the boundary of this sublevel set. Any given point of ${\widetilde{M}}$ lies on the boundary of only one sublevel set of $h_0t_0+\dots +h_kt_k$, and by definition $\sigma _R(t)$ is on the boundary of the unique sublevel set of $h_0t_0+\dots +h_kt_k$ whose distance to $x_0$ is R. So the claim follows. $\square$

Denote the image of the Busemann cone in horospherical coordinates by

$$\begin{aligned} W:=\vec {h}(\sigma _{\ge 0}). \end{aligned}$$

Lemma 30 has several important consequences. The first is an estimate for the error in terms of the distance to the orbit of the basepoint ${\mathbb {Z}}^rx_0$. To get it, note first that the lemma immediately implies the error vanishes at $x_0$.

Corollary 31

For points $b\in W$ we have $\vec {h}(p(b,x_0))=b.$

It follows that the error is bounded by the distance to the orbit ${\mathbb {Z}}^rx_0$.

Proposition 32

For any $b\in W$ we have $|\vec {h}(p(b,x))-b|_{\infty }\le d(x,{\mathbb {Z}}^rx_0)$.

Proof

We’ve shown that the error is a ${\mathbb {Z}}^r$-invariant semicontraction that vanishes at $x_0$, so this is clear. $\square$

The second is a topological regular value theorem for Busemann simplices.

Lemma 33

If $x\in \sigma ^{nd}_{>0}$ is a non-degenerate point on the Busemann cone, then $\vec {h}(x)$ is an interior point of W.

Proof

By Corollary 26 and Lemma 30 the composition

$$\begin{aligned} ({\mathbb {R}}^+\times \Delta )^{nd}_{\sigma }&\hookrightarrow \,\sigma _{>0}^{nd}\,\,\hookrightarrow&W\quad \subset \;{\mathbb {R}}^{k+1}, \end{aligned}$$

(31)

$$\begin{aligned} (R,t)&\mapsto \sigma _R(t)\mapsto&\vec {h}(\sigma _R(t)) \end{aligned}$$

(32)

is injective. Since $({\mathbb {R}}^+\times \Delta )^{nd}_{\sigma }$ is an open subset of ${\mathbb {R}}^{k+1}$, Invariance of Domain implies that the image of this composition is also an open subset of ${\mathbb {R}}^{k+1}$ and thus is contained in the interior of W. $\square$

The third says that boundary points of W come from degenerate points.

Corollary 34

For every $b\in \partial W$ there is degenerate $q\in \sigma _{\ge 0}$ with $\vec {h}(q)=b$.

Proof

First, we show that $b\in W$. To see this, note that if $b^i\in W$ converges to b then $p(b^i,x_0)\in \sigma _{\ge 0}$ converges to a point $q:=p(b,x_0)\in \sigma _{\ge 0}$ because $p(\cdot ,x_0)$ is a continuous map on all of ${\mathbb {R}}^{k+1}$ and $\sigma _{\ge 0}$ is closed. Since $q\in \sigma _{\ge 0}$, Lemma 30 implies that $b=\vec {h}(q)\in W$. Since b is a boundary point, Lemma 33 implies that q is a degenerate point. $\square$

12.4 Finding large balls in W.

In Lemma 33 we showed that if $\sigma$ is non-degenerate then W contains open balls. In this subsection we will show that when $\sigma$ is non-degenerate then W contains arbitrarily large balls. To do this, we will need to control how much the map $p(\cdot ,x)$ distorts things.

Lemma 35

Suppose that $a,b\in {\mathbb {R}}^{k+1}$ with $b\le a$, which means $b_i\le a_i$ for all $0\le i\le k$. Let $x\in {\widetilde{M}}$. Then

$$\begin{aligned} d(p(a,x),p(b,x))\le \sqrt{2d(x,p(a,x))|a-b|_1+|a-b|_1^2}. \end{aligned}$$

Proof

We use the short hand notation $x_a:=p(a,x)$. In other words, $x_a$ is the closest point to x on the intersection of horoballs $\{\vec {h}\le a\}$. In this notation, what we need to prove is

$$\begin{aligned} d(x_a,x_b)\le \sqrt{2d(x,x_a)|a-b|_1+|a-b|_1^2}. \end{aligned}$$

(33)

First, note that since $b\le a$ the point $x_b$ lies in the intersection of horoballs $\{\vec {h}\le a\}$ and therefore we have

$$\begin{aligned} \angle _{x_a}(x,x_b)\ge \pi /2. \end{aligned}$$

Therefore

$$\begin{aligned} d(x,x_a)^2+d(x_a,x_b)^2\le & {} d(x,x_b)^2\\\le & {} d(x,x_{ab})^2\\\le & {} (d(x,x_a)+d(x_a,x_{ab}))^2, \end{aligned}$$

where the first inequality follows by triangle comparison with an appropriate obtuse Euclidean triangle, the second inequality is because $x_b$ is the closest point to x in the intersection of horoballs $\{\vec {h}\le b\}$ while the projection $x_{ab}$ of $x_a$ to $\{\vec {h}\le b\}$ is also in this intersection, and the third is the triangle inequality.

In order to get (33) from this, it is enough to prove

$$\begin{aligned} d(x_a,x_{ab})\le |a-b|_1. \end{aligned}$$

(34)

Proof of (34)

Starting at $x_a=:p^0$ go for a time $|a_0-b_0|$ along $-\nabla h_0$ to arrive at a point which we call $p^1$, then go for time $|a_1-b_1|$ along $-\nabla h_1$ to arrive at a point denoted $p^2$, and continue this way, going from $p^i$ for time $|a_i-b_i|$ along $-\nabla h_i$ to arrive at $p^{i+1}$. We obtain a piecewise geodesic path

$$\begin{aligned} {[}p^0,p^1]\cup \cdots \cup [p^k,p^{k+1}] \end{aligned}$$

of length $|a-b|_1$ starting at $x_a$. Along this path all the Busemann functions $h_i$ are monotone non-increasing since we assumed that $\angle (-\nabla h_i,-\nabla h_j)\le \pi /2$ (see beginning of Section 9). Moreover, each $h_i$ decreases by $|a_i-b_i|$ on the segment $[p^i,p^{i+1}]$ and therefore at the endpoint $p^{k+1}$ we get $h_i(p^{k+1})\le b_i$ for all i. Thus, the endpoint $p^{k+1}$ is contained in the intersection of horoballs $\{h_0\le b_0,\dots , h_k\le b_k\}$. Since $x_{ab}$ is the closest point to $x_a$ in this intersection of horoballs, we get

$$\begin{aligned} d(x_a,x_{ab})\le & {} d(x_a,p^{k+1})\\\le & {} |a-b|_1, \end{aligned}$$

which is what we wanted to show. $\square$

Now we are ready to prove the main result of this subsection.

Proposition 36

If $\sigma :\Delta \rightarrow \partial _{\infty }$ is a non-degenerate Busemann simplex, then W contains arbitrarily large $(k+1)$-balls.

Proof

Fix $L>0$. Let

We will show that W contains a set of the form for some a, which will imply that W contains a ball of radius $L/(2k+2)$ because is a right angled triangle/simplex in ${\mathbb {R}}^{k+1}$ with side length L. Since L is arbitrary, this implies that W contains arbitrarily large balls.

Suppose that W does not contain any set of the form . From the definition of Busemann simplices, we have a sequence $R_{i}\rightarrow \infty$ so that the maps $\sigma _{R_i}$ converge to $\sigma$. In particular $\sigma _{R_i}(t)\rightarrow \sigma (t)$. Let $a^i:=\vec {h}(\sigma _{R_i}(t))$. We are indexing the sequence $\{a^i\}$ with superscripts instead of subscripts to avoid possible confusion with the coordinates $a_i$ and $b_i$ of a and b. Since is not contained in W, there is a point . By Corollary 34, we get a sequence of degenerate points $q_i\in \sigma _{\ge 0}$ on the Busemann cone for which $\vec {h}(q_i)=b^i$. We claim the distance $d(q_i,\sigma _{R_i}(t))$ grows sublinearly as a function of $R_i$. In fact, since $q_i=p(b^i,x_0)$ and $\sigma _{R_i}(t)=p(a^i,x_0)$, by Lemma 35, we get

$$\begin{aligned} d(q_i,\sigma _{R_i}(t))\le \sqrt{2R_iL+L^2}. \end{aligned}$$

(By letting $a=a^i,b=b^i,x=x_0$ in Lemma 35 and noting that $|a^i-b^i|_1\le L$ and $d(x_0,p(a^i,x_0))=R_i$.)

Thus, by Lemma 27, $\sigma (t)$ is a degenerate point. Since this is true for every $t\in \Delta$, we see that $\sigma$ is a degenerate simplex. This contradicts the assumption that $\sigma$ is non-degenerate. Thus W contains a set of the form . $\square$

12.5 Proof of Theorem 28.

We are now ready for the proof of the dimension bound. Given a non-degenerate Busemann k-simplex $\sigma$, we will use the projection family $p(\cdot ,\cdot )$ to build a $(k+r)$-dimensional homology cycle $S^k\times {\mathbb {T}}^r\rightarrow ({\widetilde{M}}-\vec {h}^{-1}(s))/{\mathbb {Z}}^r$ in the subset obtained by cutting out an appropriately chosen intersection of horospheres, and then show that the cycle is non-zero in the homology of the manifold $({\widetilde{M}}-\vec {h}^{-1}(s))/{\mathbb {Z}}^r$. This will imply that the dimension of the manifold is greater than $k+r$ and will finish the proof of Theorem 28. The proof uses Propositions 32 and 36 that we established in the previous subsections.

12.5.1 Building the homology cycle.

Since ${\widetilde{M}}$ is contractible, the quotient ${\widetilde{M}}/{\mathbb {Z}}^r$ is homotopy equivalent to the r-torus ${\mathbb {R}}^r/{\mathbb {Z}}^r$. Any homotopy equivalence $g:{\mathbb {T}}^r\rightarrow {\widetilde{M}}/{\mathbb {Z}}^r$ is covered by a ${\mathbb {Z}}^r$-equivariant map ${\tilde{g}}:{\mathbb {R}}^r\rightarrow {\widetilde{M}}$. Form the Busemann cone $\sigma _{\ge 0}$ based at ${\tilde{g}}(0)$ and let $W=\vec {h}(\sigma _{\ge 0})$. Proposition 32 tells us that for all points $b\in W$ we have the uniform error bound

$$\begin{aligned} |\vec {h}(p(b,{\widetilde{g}}(\cdot )))-b|_{\infty }\le & {} \text{ diameter } \text{ of } {\widetilde{g}}([0,1]^r). \end{aligned}$$

(35)

Since $\sigma$ is a non-degenerate Busemann k-simplex, the image of its Busemann cone in horospherical coordinates W contains arbitrarily large balls by Proposition 36. So W contains a closed L-ball about s whose radius L (in the sup metric) is greater than the diameter of ${\widetilde{g}}([0,1]^r)$. Let $S^k_s$ be its boundary sphere. Then the map

$$\begin{aligned} S^k_s\times {\mathbb {R}}^r\rightarrow & {} {\widetilde{M}}, \end{aligned}$$

(36)

$$\begin{aligned} (b,z)\mapsto & {} p(b,{\tilde{g}}(z)). \end{aligned}$$

(37)

will miss the intersection of horospheres $\{\vec {h}=s\}$ because for every $b\in S^k_s$ the distance $|s-b|_{\infty }=L$ while the distance $|\vec {h}(p(b,{\widetilde{g}}(\cdot )))-b|_{\infty }$ is strictly less than L. Thus, quotienting out by the ${\mathbb {Z}}^r$-action we get a homology cycle

$$\begin{aligned} S_s^k\times {\mathbb {T}}^r\rightarrow ({\widetilde{M}}-\vec {h}^{-1}(s))/{\mathbb {Z}}^r. \end{aligned}$$

(38)

12.5.2 The homology cycle is non-trivial in the homology of $({\widetilde{M}}\backslash \vec {h}^{-1}(s))/{\mathbb {Z}}^r.$

Look at the composition

$$\begin{aligned} \begin{array}{ccccc} S_s^k\times {\mathbb {R}}^r&{}\rightarrow &{}{\widetilde{M}}-\vec {h}^{-1}(s)&{}\rightarrow &{}({\mathbb {R}}^{k+1}\backslash \{s\})\times {\widetilde{M}},\\ (b,z)&{}\mapsto &{} p(b,{\widetilde{g}}(z))&{}\mapsto &{}(\vec {h}(p(b,{\widetilde{g}}(z))),p(b,{\widetilde{g}}(z))). \end{array} \end{aligned}$$

(39)

We can homotope the second factor of this composition via the straight line homotopy in ${\widetilde{M}}$ to the map $(b,z)\mapsto {\widetilde{g}}(z)$. We can also homotope the first factor of this composition via the (Euclidean) straight line homotopy to the map $(b,z)\mapsto b$. As we travel along this straight line, the sup distance to b is monotone decreasing, so the inequality (35) is preserved, and therefore the straight line avoids $s\in {\mathbb {R}}^{k+1}$. Both of these homotopies are ${\mathbb {Z}}^r$-equivariant. In summary, we can ${\mathbb {Z}}^r$-equivariantly homotope the composition (39) to $(b,z)\mapsto (b,{\widetilde{g}}(z))$ which covers the homotopy equivalence $id\times g$ of the ${\mathbb {Z}}^r$-quotients $S_s^k\times {\mathbb {T}}^r\rightarrow ({\mathbb {R}}^{k+1}\backslash \{s\})\times {\widetilde{M}}/{\mathbb {Z}}^r$, so the original map (39) also defines a homotopy equivalence of the ${\mathbb {Z}}^r$-quotients. But, this original map factors through the map (38) representing the homology cycle, so that cycle is non-zero in homology.

12.5.3 Finishing the proof of Theorem 28.

Since $({\widetilde{M}}-\vec {h}^{-1}(s))/{\mathbb {Z}}^r$ is a non-compact n-manifold, it deformation retracts to an $(n-1)$-complex. We showed that this $(n-1)$-complex has non-zero $(r+k)$-homology which implies that $r+k\le n-1$. This finishes the proof of Theorem 28.

12.6 Proof of Theorem 7 (replacing ${\mathbb {Z}}^r$ by a general group G).

In the proof of the dimension bound (Theorem 28), the Abelian nature of the group ${\mathbb {Z}}^r$ only played a role in subsection 12.5, an even there the specifics of the group ${\mathbb {Z}}^r$ played only a minor role. In this subsection we will phrase the argument given in 12.5 in a way that applies to any subgroup $G<\Gamma$. The topological conclusion is that we get the same result as before for any group G if we replace the rank of the Abelian group ${\mathbb {Z}}^r$ by the homological dimension of the discrete group G. This is expressed in Corollary 38 below, which is a reformulation of Theorem 7 from the introduction. We stated it here in a slightly different, but equivalent, form. The main technical step is the following proposition which combines 12.5.1 and 12.5.2.

Proposition 37

Suppose that $\sigma :\Delta ^k\rightarrow {{\,\mathrm{Fix}\,}}^0(G)$ is non-degenerate Busemann k-simplex. Then the inclusion of any compact subset of $S^k\times {\widetilde{M}}/G$ factors up to homotopy through $({\widetilde{M}}-\vec {h}^{-1}(s))/G$ for an appropriately chosen intersection of horospheres $\vec {h}^{-1}(s)$.

Proof

It is clearly enough to prove the proposition for subsets of the form $S^k\times K$, where K is compact. Let $K\hookrightarrow {\widetilde{M}}/G$ be the inclusion of a subset of diameter $<L$, and let ${\widetilde{K}}\hookrightarrow {\widetilde{M}}$ be its inverse image in ${\widetilde{M}}$. It is a G-equivariant inclusion. Pick a point $x_0\in {\widetilde{K}}$ and form the Busemann cone $\sigma _{\ge 0}$ based at this point. Since $\sigma$ is a non-degenerate k-simplex, the image of the Busemann cone in horospherical coordinates contains a closed ball ${\overline{B}}_s(L)\subset W$ of radius L (in the sup metric) centered at some point $s\in W$. Let $S_s^k$ be its boundary sphere and denote by

$$\begin{aligned} i:S_s^k\times {\widetilde{K}}\hookrightarrow {\mathbb {R}}^{k+1}\times {\widetilde{M}} \end{aligned}$$

the standard inclusion. Let

$$\begin{aligned} f:S_s^k\times {\widetilde{K}}\rightarrow {\mathbb {R}}^{k+1}\times {\widetilde{M}} \end{aligned}$$

be the map given by

$$\begin{aligned} f(b,z):=(\vec {h}(p(b,z)),p(b,z)), \end{aligned}$$

and denote by $f_t$ the straight line homotopy (along the Euclidean straight lines $(1-t)b+t\vec {h}(p(b,z))$ in the first factor and geodesic lines from z to p(b, z) in the second factor) starting at i and ending at f. Since points $b\in S_s^k\subset W$ are in the image of the Busemann cone, we have

$$\begin{aligned} \vec {h}(p(b,x_0))=b \quad \text{ for } \text{ all } b\in S_s^k. \end{aligned}$$

K has diameter $<L$ so every point z in ${\widetilde{K}}$ is a distance $<L$ from a point of the orbit $Gx_0$. Since $\vec {h}(p(b,\cdot ))$ is a G-invariant semicontraction we get

$$\begin{aligned} |\vec {h}(p(b,z))-b|_{\infty }= & {} |\vec {h}(p(b,z))-\vec {h}(p(b,Gx_0))|_{\infty }\\\le & {} d(z,Gx_0)\\< & {} L \end{aligned}$$

for all points $(b,z)\in S^k_s\times {\widetilde{K}}$. Therefore the straight line homotopy $f_t$ between f and i avoids $s\times {\widetilde{M}}$, i.e. it stays in $({\mathbb {R}}^{k-1}\backslash s)\times {\widetilde{M}}$. Finally, note that the map $f=f_1$ factors as

$$\begin{aligned} S_s^k\times {\widetilde{K}}{\mathop {\longrightarrow }\limits ^{p(\cdot ,\cdot )}}{\widetilde{M}}-\vec {h}^{-1}(s){\mathop {\longrightarrow }\limits ^{\vec {h}\times id}}({\mathbb {R}}^{k+1}\backslash s)\times {\widetilde{M}}. \end{aligned}$$

Quotienting out by the G-action, we see that $S_s^k\times K\hookrightarrow ({\mathbb {R}}^{k+1}\backslash s)\times {\widetilde{M}}/G$ can be homotoped to factor through the proper open subset $({\widetilde{M}}-\vec {h}^{-1}(s))/G$ of ${\widetilde{M}}/G$. $\square$

Corollary 38

(Theorem 7) Suppose $\sigma :\Delta ^k\rightarrow {{\,\mathrm{Fix}\,}}^0(G)$ is a non-degenerate Busemann k-simplex. Then

$$\begin{aligned} hdim(G)+k\le n-1. \end{aligned}$$

Proof

Let $\Sigma$ be a non-zero r-dimensional homology class (with any system of coefficients) in ${\widetilde{M}}/G$. Then $S^k\times \Sigma$ is a non-trivial $(r+k)$-dimensional homology class in $S^k\times {\widetilde{M}}/G$. It is supported on a compact subset $S^k\times K$, so the proposition implies that it defines a non-trivial homology class on the open manifold $({\widetilde{M}}\backslash \vec {h}^{-1}(s))/G$. Since this manifold is homotopy equivalent to an $(n-1)$-complex we conclude that $r+k\le n-1$. $\square$

13 Finishing the Proofs of Theorems 1, 2, and 4

Our main application of Theorem 28 is the following corollary. It is the last ingredient we need in order to finish the proofs of Theorems 1,2, and 4.

Corollary 39

Let $\beta :\Delta _{\lfloor pAb\rfloor }\rightarrow (\partial _{\infty },{{\,\mathrm{Td}\,}})$ be the Busemann map. Then

$$\begin{aligned} \dim ({{\,\mathrm{Im}\,}}\beta )\le \lfloor n/2\rfloor -1. \end{aligned}$$

Proof

Let $\sigma =([A_0]<\dots <[A_k])$ be a k-simplex in $\Delta _{\lfloor pAb\rfloor }$ and note that, because we are using virtual equivalence classes,

$$\begin{aligned} \text{ rank }(A_k)\ge k+1. \end{aligned}$$

Note that the top Abelian group $A_k$ preserves horospheres on the entire Busemann simplex $\beta (\sigma )$. So, if $\beta (\sigma )$ is a non-degenerate, Theorem 28 gives

$$\begin{aligned} n\ge k+1+\text{ rank }(A_k). \end{aligned}$$

The right hand side is $\ge 2(k+1)$ so we conclude

$$\begin{aligned} k\le \lfloor n/2\rfloor -1. \end{aligned}$$

Since $\beta$ is Lipschitz, Lipschitz maps do not raise Hausdorff dimension, and topological dimension is less than or equal to Hausdorff dimension, we get for any non-degenerate Busemann simplex $\beta (\sigma )$ that

$$\begin{aligned} \dim (\beta (\sigma ))\le \text{ Hausdorff- }\dim (\beta (\sigma ))\le \dim (\sigma )\le \lfloor n/2\rfloor -1. \end{aligned}$$

The image ${{\,\mathrm{Im}\,}}(\beta )$ is a countable union of non-degenerate Busemann simplices, so its topological dimension has the same upper bound. $\square$

Now, let $\beta$ be the Busemann map. The above corollary implies that

$$\begin{aligned} d=\dim ({{\,\mathrm{Im}\,}}(\beta \circ \mu ))\le \dim ({{\,\mathrm{Im}\,}}\beta )\le \lfloor n/2\rfloor -1. \end{aligned}$$

So, Theorem 18 applied to the Busemann map $\beta$ proves Theorem 2. We saw in Section 7 and Proposition 21 that $d\le \text{ rank }_{Ab}(\pi _1M)-1$ and $d\le \dim (\partial _{\infty },{{\,\mathrm{Td}\,}})$ so it also proves Theorem 4. Inspecting Theorem 18 we see that Theorem 1 (a) follows from the two bullets in Theorem 18 (in 3.4 we can pick $\delta <\varepsilon /2$) and that Theorem 1 (b) follows from $d\le \lfloor n/2\rfloor -1$.

14 Low Dimensional Collapse: $\dim ({{\,\mathrm{Im}\,}}\rho )\le 1$

In this section we will explain the more specific consequences we get when our analogue of the rational Tits building has one dimensional image, i.e. when $d:=\dim ({{\,\mathrm{Im}\,}}\rho )\le 1$. This happens if one of the following is true.

• The fundamental group $\pi _1M$ does not contain ${\mathbb {Z}}^3$, or

• $\dim (\partial _{\infty },{{\,\mathrm{Td}\,}})\le 1$, or

• $\dim M\le 5$.

We have seen in Corollary 20 that if $d\le 1$ then each component of $M_{\le \varepsilon }$ is aspherical. Let $\partial$ be a component of $\partial M_{\le \varepsilon }$. Next we ask “how bad can the fundamental group of $\partial$ be?” Notice it is an extension of a subgroup of $\pi _1M$ by the fundamental group of a component ${\hat{\partial }}$ of $\partial {\widetilde{M}}_{\le \varepsilon }$, i.e. it fits into an exact sequence

$$\begin{aligned} 1\rightarrow \pi _1({\hat{\partial }})\rightarrow \pi _1\partial \rightarrow \pi _1M. \end{aligned}$$

(40)

The main theorem of this section is that if $d\le 1$ then every finitely generated subgroup of$\pi _1({\hat{\partial }})$is free. Such a group is called a locally free group.

Theorem 40

If $d\le 1$ then $\pi _1({\hat{\partial }})$ is locally free.

The moral of the theorem is that the fundamental group of the aspherical manifold $\partial$ is built out of two ingredients that we understand, namely locally free groups and fundamental groups of nonpositively curved manifolds, so it is “not too exotic”.

14.1 Proof of Theorem 40 (Theorem 6 of the introduction).

Let $G<\pi _1{\widetilde{M}}_{\le \varepsilon }$ be a finitely generated subgroup. Fix a presentation with finitely many generators for G, let $BG^{(2)}$ be its presentation 2-complex, (a single vertex, one edge for each generator, one 2-cell for each relation) and $BG^{(1)}$ the 1-skeleton of this 2-complex. Since ${\widetilde{M}}_{\le \varepsilon }\cong \partial {\widetilde{M}}_{\le \varepsilon }\times [0\infty )$ is aspherical, the inclusion of groups is induced by a map

$$\begin{aligned} BG^{(2)}{\mathop {\rightarrow }\limits ^{\varphi }}\partial {\widetilde{M}}_{\le \varepsilon }. \end{aligned}$$

(41)

First, we will explain the proof in the simpler case when G is finitely presented. In this case, the complex $BG^{(2)}$ is finite, so $\varphi$ can be homotoped in ${\widetilde{M}}_{\le \varepsilon }$ to a map $\overline{\varphi }$ whose image $\overline{\varphi }(BG^{(2)})$ is contained in a graph (see the proof of Corollary 19). Thus the inclusion of $G<\pi _1({\hat{\partial }})$ factors through a free group, implying G is free.

In general, we only know that G is finitely generated, i.e. that $BG^{(1)}$ is finite. So, if we try to homotope the map $\varphi$ to factor through a graph then the finitely many generators $BG^{(1)}$ do not cause any problems but the infinitely many relations $BG^{(2)}$ might. They may “stick out” into the thick part in the course of the homotopy. The key idea is that this is not problematic because the images of the relations are one-dimensional at the end of the homotopy and we can simply attach them to the thin part as “strands” sticking out into the thick part without breaking the argument.

Let us now make precise sense of this idea. Think of $\varphi$ as a map of pairs

$$\begin{aligned} (BG^{(2)},BG^{(1)}){\mathop {\rightarrow }\limits ^{\varphi }}({\widetilde{M}},{\widetilde{M}}_{\le \varepsilon }). \end{aligned}$$

(42)

Claim

We claim that the map of pairs $\varphi$ can be homotoped inside $({\widetilde{M}},{\widetilde{M}}_{\le \varepsilon })$ to a map of pairs $\overline{\varphi }$ whose image is in the 1-skeleton of a triangulation of $({\widetilde{M}},{\widetilde{M}}_{\le \varepsilon })$, i.e.

$$\begin{aligned} (BG^{(2)},BG^{(1)}){\mathop {\rightarrow }\limits ^{\overline{\varphi }}}({\widetilde{M}}^{(1)},{\widetilde{M}}_{\le \varepsilon }^{(1)}). \end{aligned}$$

This is the main technical step in the proof of the theorem. It will follow from a relative version of the collapse argument given in the proof of Theorem 18. We will state it as a separate proposition and, since for this collapse argument it is not important that $d\le 1$, we state it for general d.

Proposition 41

Suppose K is a compact subset of $\partial {\widetilde{M}}_{\le \varepsilon }$. Then the standard inclusion $i:(\partial {\widetilde{M}}_{\le \varepsilon },K)\hookrightarrow ({\widetilde{M}},{\widetilde{M}}_{\le \varepsilon })$ is homotopic as a map of pairs in $({\widetilde{M}},{\widetilde{M}}_{\le \varepsilon })$ to a map

$$\begin{aligned} {\overline{f}}:(\partial {\widetilde{M}}_{\le \varepsilon },K)\rightarrow ({\widetilde{M}}^{(d)},{\widetilde{M}}^{(d)}_{\le \varepsilon } ) \end{aligned}$$

whose image is contained in the d-skeleton of some triangulation of $({\widetilde{M}},{\widetilde{M}}_{\le \varepsilon })$.

Proof

In the proof of Theorem 18 we homotoped the inclusion of a compact subset $K\hookrightarrow \partial {\widetilde{M}}_{\le \varepsilon }$ inside ${\widetilde{M}}_{\le \varepsilon }$ to a map with d-dimensional image. But, the proof really gave us a bit more. We constructed a homotopy between the inclusion $\partial {\widetilde{M}}_{\le \varepsilon }\hookrightarrow {\widetilde{M}}_{\le \varepsilon }$ and $c_t\circ \beta \circ \mu$ whose restriction to a compact subset K had, for large enough t, the additional property that the set K stayed inside ${\widetilde{M}}_{\le \varepsilon }$. Since the image of $c_t\circ \beta \circ \mu$ is d-dimensional, one can deform it (not just its restriction to K, but the entire map $c_t\circ \beta \circ \mu$) by a $\delta$-small deformation into a d-skeleton of a sufficiently fine triangulation of ${\widetilde{M}}$. This is done in two steps. First, one deforms the map by a $\delta$-small deformation to a map $f'$ whose image has Hausdorff dimension $\le d$ (not just topological dimension $\le d$). Second one deforms $f'$ into a d-skeleton of a sufficiently fine triangulation. The triangulation can be taken to be a triangulation of pairs $({\widetilde{M}},{\widetilde{M}}_{\le \varepsilon })$ and this second deformation can be done in a way that preserves simplices of the triangulation, i.e. a point inside a closed simplex stays inside that simplex (see “Appendix D” for more details on these two steps). $\square$

Now we return to our $d\le 1$ situation and let $K=\varphi (BG^{(1)})$. Since the map of pairs $\varphi$ factors through the inclusion i, we can apply Proposition 41 to get the desired homotopy of pairs $F:(BG^{(2)},BG^{(1)})\times I\rightarrow ({\widetilde{M}},{\widetilde{M}}_{\le \varepsilon })$ from $i\circ \varphi$ to ${\overline{f}}\circ \varphi$. This proves the claim. Next, note that the restriction of F to $BG^{(2)}\times \{0\}\cup BG^{(1)}\times I\cup BG^{(2)}\times \{1\}$ has image contained in ${\widetilde{M}}^{(1)}\cup {\widetilde{M}}_{\le \varepsilon }$. Since this image is aspherical, we can extend this restriction across every (2-cell)$\times I$ in $BG^{(2)}\times I$ to get a map

$$\begin{aligned} {\hat{F}}:BG^{(2)}\times I\rightarrow {\widetilde{M}}^{(1)}\cup {\widetilde{M}}_{\le \varepsilon }. \end{aligned}$$

This is a homotopy between the two maps

$$\begin{aligned} \varphi :BG^{(2)}\rightarrow {\widetilde{M}}^{(1)}\cup {\widetilde{M}}_{\le \varepsilon } \end{aligned}$$

(43)

and

$$\begin{aligned} {\overline{f}}\circ \varphi :BG^{(2)}\rightarrow {\widetilde{M}}^{(1)}\cup {\widetilde{M}}_{\le \varepsilon }. \end{aligned}$$

(44)

The first map (43) is $\pi _1$-injective (the original map (41) is $\pi _1$-injective by definition, and attaching the one dimensional “strands” ${\widetilde{M}}^{(1)}$ to the thin part ${\widetilde{M}}_{\le \varepsilon }$ does not change this) while the image of the second map (44) is contained in a graph. Since these two maps are homotopic, we conclude that G is a free group. This proves that $\pi _1({\hat{\partial }})$ is locally free.

Appendices

Appendix A: A Useful Comparison

In this paper we repeatedly use the following standard comparison geometry argument.

1.1 Comparison with obtuse Euclidean triangle.

Let $C\subset {\widetilde{M}}$ be a convex set and $p_C:{\widetilde{M}}\rightarrow C$ the closest point projection. Let $x_0\not \in C,y\in C$ and let $x=p_C(x_0)$ be the closest point to $x_0$ in C. Since C is convex and x is the closest point to $x_0$ in C, we observe (see figure above) that

$$\begin{aligned} \measuredangle _x(x_0,y)\ge \pi /2. \end{aligned}$$

(45)

Because of this, the Euclidean triangle with sides $[x_0,x]$ and [x, y] meeting at an angle $\angle _x(x_0,y)$ has $d(x_0,y)^2\ge d(x_0,x)^2+d(x,y)^2$. Triangle comparison implies that the same is true for our triangle in ${\widetilde{M}}$. Consequently,

$$\begin{aligned} d(x,y)\le \sqrt{d(x_0,y)^2-d(x_0,x)^2}. \end{aligned}$$

(46)

By comparison the sum of angles in any triangle is $\le \pi$ so (45) also implies

$$\begin{aligned} \angle _{x_0}(x,y)<\pi /2. \end{aligned}$$

(47)

Next is a typical example of how this triangle comparison is used.

1.2 Distance dependence of projections to sublevel sets.

Suppose $f:{\widetilde{M}}\rightarrow {\mathbb {R}}$ is a convex function that does not attain its infimum. Pick a basepoint $x_0$. Then for every $R\ge 0$ there is a unique constant t(R) so that the sublevel set $\{f\le t(R)\}$ meets the sphere $S_{x_0}(R)$ at a single point $\lambda _R$. Comparing with Euclidean triangles, we see how $\lambda _R$ can vary with R.

Lemma 42

$d(\lambda _{R(1\pm \delta )},\lambda _R)\le \sqrt{2\delta +\delta ^2}R$.

Proof

The sublevel set $\{f\le t(R)\}$ is convex, and $\lambda _{R}$ is the point on it that is closest to $x_0$. Since $t(R+\varepsilon R)\le t(R)$, the point $\lambda _{R(1+\delta )}$ is also in the sublevel set $\left\{ f\le t(R)\right\}$. So, we can apply inequality (46) with $C=\{f\le t(R)\}$, $x=\lambda _{R}$ and $y=\lambda _{R(1+\delta )}$ to get $d(\lambda _{R},\lambda _{R(1+\delta )})\le \sqrt{2\delta +\delta ^2}R$. A similar argument with $C=\{f\le t(R-\delta R)\}, x=\lambda _{R(1-\delta )}$ and $y=\lambda _R$ shows that $d(\lambda _{R(1-\delta )},\lambda _{R})\le \sqrt{2\delta -\delta ^2}R$. $\square$

Appendix B: The Metrics $\angle _x,\angle$ and ${{\,\mathrm{Td}\,}}$ on $\partial _{\infty }$

In this “Appendix” we collect some results about metrics on $\partial _{\infty }$. Everything except for 16.7 can be found in Section 4 and Appendix 3 of [BGS85]. See also 3.5 of [Ebe96].

1.1 Angle metric.

For every point $x\in {\widetilde{M}}$ we have the round metric $(\partial _{\infty },\angle _x)$ which identifies the boundary at infinity with the unit sphere $T^1_x{\widetilde{M}}$ in the tangent space at x. Taking the supremum over all $x\in {\widetilde{M}}$ we get the angle metric

$$\begin{aligned} \angle (\xi ,\eta ):=\sup _{x\in {\widetilde{M}}}\angle _x(\xi ,\eta ). \end{aligned}$$

1.2 Description via distance in ${\widetilde{M}}.$

This metric has the following alternative description. Fix a basepoint $x_0$ in ${\widetilde{M}}$ and denote by $r_{\xi }=[x_0,\xi )$ the unit speed geodesic ray starting at $x_0$ and going to $\xi \in \partial _{\infty }$. Then

$$\begin{aligned} \sin \left( {\angle (\xi ,\eta )\over 2}\right) =\lim _{t\rightarrow \infty }{d(r_{\xi }(t),r_{\eta }(t))\over 2t}. \end{aligned}$$

1.3 Tits metric.

By construction, the space $(\partial _{\infty },\angle )$ has diameter $\pi$. So, in order to study large scale features of $\partial _{\infty }$ one takes the induced path metric. This is called the Tits metric and denoted $(\partial _{\infty },{{\,\mathrm{Td}\,}})$. Then

$$\begin{aligned} \angle =\min ({{\,\mathrm{Td}\,}},\pi ), \end{aligned}$$

so for small scale purposes there is no difference between ${{\,\mathrm{Td}\,}}$ and $\angle$.

1.4 Relation between sphere and ${{\,\mathrm{Td}\,}}$ topology.

The topology obtained from the metric $(\partial _{\infty },{{\,\mathrm{Td}\,}})$ is generally very different from the usual sphere topology $(\partial _{\infty },\angle _x)$. But, we have the following relation, which is usually called lower semicontinuity of ${{\,\mathrm{Td}\,}}$ in the sphere topology: If $x_i\rightarrow x$ in the sphere topology then

$$\begin{aligned} {{\,\mathrm{Td}\,}}(x,y)\le \liminf _{i}{{\,\mathrm{Td}\,}}(x_i,y). \end{aligned}$$

Here is a typical application. Let C be a subset of $\partial _{\infty }$ and ${\overline{C}}$ its closure in the sphere topology. Then

$$\begin{aligned} {{\,\mathrm{Td}\,}}\text{-diameter }(C)={{\,\mathrm{Td}\,}}\text{-diameter }({\overline{C}}). \end{aligned}$$

1.5 Curvature bounded above.

A key feature of ${{\,\mathrm{Td}\,}}$ is that any points x, y with ${{\,\mathrm{Td}\,}}(x,y)<\pi$ are connected by a unique ${{\,\mathrm{Td}\,}}$-geodesic. Moreover, ${{\,\mathrm{Td}\,}}$ is CAT(1), which means that for three points x, y, z mutually a distance $\le \pi /2$ the geodesic triangle $\Delta _{xyz}$ is thinner than the corresponding comparison triangle with the same side lengths in the round sphere.

1.6 Sets of ${{\,\mathrm{Td}\,}}$-diameter $\le \pi /2$ have canonical centers.

If K is a set in $\partial _{\infty }$ that has ${{\,\mathrm{Td}\,}}$-diameter $\le \pi /2$ and is closed in the sphere topology, then there is a unique point $\xi \in \partial _{\infty }$ at which the function

$$\begin{aligned} \tau (\cdot ):=\sup _{\eta \in K}{{\,\mathrm{Td}\,}}(\eta ,\cdot ) \end{aligned}$$

attains its infimum. This point $\xi =\xi _K$ is called the center of K. See 3.5.4–3.5.7 of [Ebe96].

1.7 Convex sets contain their centers.

In general, the center $\xi _K$ may not be in the set K. However, if K is convex in the ${{\,\mathrm{Td}\,}}$-metric then $\xi _K\in K$. To see this, note that for any point $\xi '$ with $\tau (\xi ')\le \pi /2$ we can take a sequence of points $x_i\in K$ with

$$\begin{aligned} {{\,\mathrm{Td}\,}}(x_i,\xi ')\rightarrow & {} \inf _{y\in K}{{\,\mathrm{Td}\,}}(y,\xi ') \end{aligned}$$

Passing to a subsequence, we can assume $x_i$ converges in the sphere topology to some point $x\in K$, since by assumption K is closed in the sphere topology. Then, by lower semicontinuity of ${{\,\mathrm{Td}\,}}$, the point x is a closest point to $\xi '$ in the set K and comparison with the round sphere gives $\tau (x)\le \tau (\xi ')$. Since the center $\xi _K$ is the unique infimum of $\tau$, it must be contained in K.

Remark

In Section 5 we show that if $K={\overline{C}}$ is the closure (in the sphere topology) of a ${{\,\mathrm{Td}\,}}$-convex set C, then we still get the conclusion $\xi _K\in K$.

1.8 Centers of mass for fixed sets of parabolics.

One application of this is to finding canonical centers of mass in fixed sets of parabolic elements. Suppose $\gamma \in \Gamma$ is a parabolic element, and let ${{\,\mathrm{Fix}\,}}(\gamma )$ in $\partial _\infty$ be its fix set. This set is non-empty, and one can find a canonical center of mass inside of it by the following process.

• First, find a point $\xi \in {{\,\mathrm{Fix}\,}}(\gamma )$ so that ${{\,\mathrm{Td}\,}}(\xi ,\eta )\le \pi /2$ for all $\eta \in {{\,\mathrm{Fix}\,}}(\gamma )$. Such a point exists by Appendix 3, Lemma 3 of [BGS85].

• Second take the set of all such points

  $$\begin{aligned} B_{\gamma }=\{\xi \in {{\,\mathrm{Fix}\,}}(\gamma )\mid {{\,\mathrm{Td}\,}}(\gamma ,\eta )\le \pi /2 \text{ for } \text{ all } \eta \in {{\,\mathrm{Fix}\,}}(\gamma )\}. \end{aligned}$$

  This set is non-empty, has diameter $\le \pi /2$ and is closed in the sphere topology. Therefore it has a unique center, which we denote $\xi _{\gamma }$.

• Since $B_{\gamma }$ has diameter $\le \pi /2$, any two points $\xi ,\xi '\in B_{\gamma }$ are connected by a unique geodesic $[\xi ,\xi ']$. The endpoints of this geodesic are fixed by $\gamma$ so uniqueness implies that the entire geodesic $[\xi ,\xi ']$ is fixed pointwise by $\gamma$. Moreover, CAT(1) comparison shows that for any point $\xi ''$ on this geodesic $[\xi ,\xi ']$ we have ${{\,\mathrm{Td}\,}}(\xi '',\eta )\le \pi /2$ for all $\eta \in {{\,\mathrm{Fix}\,}}(\gamma )$. Therefore $B_{\gamma }$ is convex and hence

  $$\begin{aligned} \xi _{\gamma }\in B_{\gamma }. \end{aligned}$$

1.9 Centers of mass for fixed sets of Abelian groups.

Since $\xi _{\gamma }$ is the center of mass of ${{\,\mathrm{Fix}\,}}(\gamma )$, it is fixed by anything that preserves this fixed set. So, it is fixed by the anything that commutes with $\gamma$. In particular, for any Abelian group A containing a parabolic element $\gamma$, the point $\xi _{\gamma }$ is contained in the set

$$\begin{aligned} B_A:=\{\xi \in {{\,\mathrm{Fix}\,}}(A)\mid {{\,\mathrm{Td}\,}}(\xi ,\eta )\le \pi /2 \text{ for } \text{ all } \eta \in {{\,\mathrm{Fix}\,}}(A)\}. \end{aligned}$$

This set is ${{\,\mathrm{Td}\,}}$-convex, has ${{\,\mathrm{Td}\,}}$-diameter $\le \pi /2$ and is closed in the sphere topology for the same reasons as $B_{\gamma }$. So, it has a unique center which we denote by $\xi _A\in B_A$. In this way we have constructed a center of mass $\xi _A\in {{\,\mathrm{Fix}\,}}(A)$ for any Abelian group A containing a parabolic element.

Remark

In Section 5 we take this construction one step further and obtain a unique center of mass for any virtual equivalence class of Abelian groups [A] containing a parabolic by replacing the fix set ${{\,\mathrm{Fix}\,}}(A)$ in this construction with the countable union of fixed sets

$$\begin{aligned} \bigcup _{n\in {\mathbb {N}}}{{\,\mathrm{Fix}\,}}(n!A) \end{aligned}$$

of finite index subgroups $n!A=\{\gamma ^{n!}\mid \gamma \in A\}$. The added difficulties involved are that this union may not be fixed by any single element and also that it is, possibly, no longer closed in the sphere topology. These difficulties are dealt with in Section 5.

Appendix C: The Karlsson-Margulis Lemma (Isometries of Positive Infimum Displacement)

In this “Appendix” we describe a special case (Proposition 43 below) of Theorem 2.1 of [KM99] which is the “nonpositively curved geometry” part of their paper (as opposed to the “ergodic theory part”). There is nothing new here, but we found it comforting to know that the proof of this special case is elementary and does not resort to any ergodic theory.

1.1 Geodesic rays sublinearly tracking $\gamma$-orbits.

Let $\gamma$ be an isometry, pick a basepoint y, and let $y_n:=\gamma ^ny$. The infimum displacement of $\gamma$ can computed as the limit

$$\begin{aligned} A:=\lim _{n\rightarrow \infty }{d(y,y_n)\over n}. \end{aligned}$$

(48)

Proposition 43

Suppose $A>0$. Then there is a geodesic ray c for which

$$\begin{aligned} \lim _{k\rightarrow \infty } {d(y_k,c(Ak))\over k}=0. \end{aligned}$$

(49)

In other words, the Proposition says that if the infimum displacement of $\gamma$ is positive, then there is a geodesic ray sublinearly tracking the positive $\gamma$-orbit $y,\gamma y,\gamma ^2y,\dots$. It follows that the positive $\gamma$-orbit converges to a unique limit point

$$\begin{aligned} \lim _{n\rightarrow \infty }\gamma ^ny=c(\infty ), \end{aligned}$$

but the sublinear tracking is stronger that just this statement alone. Also note that there is another (different) geodesic ray $c'$ that sublinearly tracks the negative $\gamma$-orbit $y,\gamma ^{-1}y,\gamma ^{-2}y,\dots$. In general the rays c and $c'$ do not form a bi-infinite geodesic.

Remark

When $\gamma$ is a hyperbolic element, then the proposition is easy. If $y\in {\widetilde{M}}$ is a point at which $\gamma$ has minimum displacement then the positive $\gamma$-orbit of y spans a geodesic ray c and its negative $\gamma$-orbit spans a geodesic ray $c'$. The union of these rays is a bi-infinite geodesic which is an axis of $\gamma$. The point of the proposition is that some aspects of this nice situation are still true for parabolic $\gamma$ as long as the infimum displacement of $\gamma$ is positive.

1.2 Finding good orbit points.

Fix $\varepsilon >0$. By the displacement formula (48), there is $K=K_{\varepsilon }$ such that for all $k\ge K$

$$\begin{aligned} (A-\varepsilon )k\le d(y,y_k)\le (A+\varepsilon ) k. \end{aligned}$$

(50)

Since the sequence $\{d(y,y_n)-(A-\varepsilon )n\}_n$ is unbounded above, there are $\underline{\hbox {arbitrarily}} \underline{\hbox {large }n}$ such that the nth term of this sequence is larger than all its predecessors, i.e. for $0\le k\le n$

$$\begin{aligned} d(y,y_{n-k})-(A-\varepsilon )(n-k)\le d(y,y_n)-(A-\varepsilon )n. \end{aligned}$$

Since $\gamma$ is an isometry $d(y,y_{n-k})=d(y_k,y_n)$, so this can be rewritten as

$$\begin{aligned} (A-\varepsilon )k\le d(y,y_n)-d(y_k,y_n). \end{aligned}$$

(51)

The right-hand side is $\le d(y,y_k)$ because of the triangle inequality. Thus, for $K\le k\le n$ we get

$$\begin{aligned} (A-\varepsilon )k\le d(y,y_n)-d(y_k,y_n)\le (A+\varepsilon )k \end{aligned}$$

(52)

if n satisfies (51). Call $y_n$ an $\varepsilon$-good orbit point if n satisfies (51). We emphasize that $\underline{\hbox {there are infinitely many } \varepsilon \hbox {-good orbit points}}$, so we can always find a sequence $\{y_{n_i}\}$ of such points converging to a point at infinity.

1.3 Finite segments.

The heart of the proof is the following lemma. It says that for $\varepsilon$-good orbit points $y_n$ the geodesic segments $[y,y_n]$ sublinearly track a large segment of the $\gamma$-orbit $y_K,y_{K+1},\dots ,y_n$ up to an error determined by $\varepsilon$.

Lemma 44

For $\varepsilon >0$ pick $K_{\varepsilon }$ satisfying (50) and $n=n_{\varepsilon }$ satisfying (51). Let $c_n=[y,y_n]$ be the geodesic segment from y to $y_n$ and $c_n(Ak)$ the point obtained by going for a distance Ak along $c_n$. Then for any $K_{\varepsilon }\le k\le n$

$$\begin{aligned} {d(y_k,c_n(Ak))\over k}\le 2\sqrt{A\varepsilon }+\varepsilon . \end{aligned}$$

(53)

Proof

Let $R:=d(y,y_n)-d(y_k,y_n)$. Notice that

$$\begin{aligned} \angle _{c_n(R)}(y,y_k)\ge \pi /2 \end{aligned}$$

because the geodesic segment $[c_n(R),y_k]$ is contained in the convex ball $\{d(\cdot ,y_n)\le d(y_k,y_n)\}$ and the segment $[c_n(R),y]$ is perpendicular to this ball. So, comparing with the corresponding obtuse Euclidean triangle gives

$$\begin{aligned} d(y_k,c_n(R))\le & {} \sqrt{d(y,y_k)^2-R^2}\\\le & {} \sqrt{(A+\varepsilon )^2k^2-(A-\varepsilon )^2k^2}\\= & {} 2\sqrt{A\varepsilon }k. \end{aligned}$$

Inequality (52) implies $|R-Ak|\le \varepsilon k$ so we conclude that

$$\begin{aligned} d(y_k,c_n(Ak))\le & {} d(y_k,c_n(R))+d(c_n(R),c_n(Ak))\\\le & {} (2\sqrt{A\varepsilon }+\varepsilon )k. \end{aligned}$$

$\square$

1.4 Limits.

What remains is to take limits as $n\rightarrow \infty$ and as $\varepsilon \rightarrow 0$ to get the desired geodesic ray c. We need to take some care in how we do this.

Fix $\varepsilon >0$ and let $\{y_{n_i}\}$ be a convergent sequence of $\varepsilon$-good orbit points. Then the segments $c_{n_i}$ converge to a geodesic ray

$$\begin{aligned} c^{\varepsilon }:=\lim _{i\rightarrow \infty }c_{n_i}. \end{aligned}$$

The lemma implies that inequality (53) holds for $n=n_i$ and all $K_{\varepsilon }\le k\le n_i$. Therefore, taking the limit of (53)$_{n=n_i}$ as $i\rightarrow \infty$, we get for all $k\ge K_{\varepsilon }$ that

$$\begin{aligned} {d(y_k,c^{\varepsilon }(Ak))\over k}\le 2\sqrt{A\varepsilon }+\varepsilon . \end{aligned}$$

(54)

Now we vary $\varepsilon$. By the triangle inequality we get from (54) that

$$\begin{aligned} {d(c^{\varepsilon }(Ak),c^{\varepsilon '}(Ak))\over k}\le (2\sqrt{A\varepsilon }+\varepsilon )+(2\sqrt{A\varepsilon '}+\varepsilon ') \end{aligned}$$

(55)

when $k\ge \max \{K_{\varepsilon },K_{\varepsilon '}\}$. Therefore, any sequence $\{c^{\varepsilon }(\infty )\}_{\varepsilon \rightarrow 0}$ is Cauchy in the $\angle _y$-metric, which implies that $c^{\varepsilon }$ converges to a geodesic ray

$$\begin{aligned} c:=\lim _{\varepsilon \rightarrow 0}c^{\varepsilon }. \end{aligned}$$

Next, notice that because the distance function $d(\cdot ,\cdot )$ is convex, knowing (55) for arbitrarily large k implies it for all k. So

$$\begin{aligned} (55) \text{ holds } \text{ for } \underline{all} \, k>0. \end{aligned}$$

Taking the limit as $\varepsilon '\rightarrow 0$ of inequality (55), we get that for all $k>0$

$$\begin{aligned} {d(c^{\varepsilon }(Ak),c(Ak))\over k}\le 2\sqrt{A\varepsilon }+\varepsilon . \end{aligned}$$

(56)

Finally, putting this together with (54) gives

$$\begin{aligned} {d(y_k,c(Ak))\over k}\le 2(2\sqrt{A\varepsilon }+\varepsilon ). \end{aligned}$$

for all $k\ge K_{\varepsilon }$. This proves the proposition.

Appendix D: $\delta$-Deforming Subsets to Subcomplexes

Let $K\subset {\widetilde{M}}$ be a compact subset of Hausdorff dimension d. Let $\delta$ be greater than zero. A $\delta$-deformation $K\times I\rightarrow {\widetilde{M}}$ is a homotopy of the inclusion $K\rightarrow \widetilde{M}$ during which each point of K at each point in time $t \in I$ is moved by at most $\delta$ from the original position. For any $\delta >0$ we can $\delta$-deform it to a d-dimensional subcomplex. In this “Appendix” we will recall this argument and also explain why it applies when instead of a compact set we have a countable union of compact sets $\cup _i K_i$. Then, we will explain how to get the same conclusion only assuming that K has topological dimension d (instead of Hausdorff dimension d).

The argument is by induction on skeleta of a fine triangulation of ${\widetilde{M}}$. In the course of the induction the inclusion $i:K\hookrightarrow {\widetilde{M}}$ will be $\delta$-deformed to maps $f:K\rightarrow {\widetilde{M}}$ that are not necessarily inclusions. So, it is better to state the result like this.

Recall that P is a $\delta$-fine triangulation of ${\widetilde{M}}$ if every simplex of P has diameter $\le \delta$.

Proposition 45

Let K be a compact set and suppose that $f:K\rightarrow {\widetilde{M}}$ is a map whose image f(K) has Hausdorff dimension d. Then for every $\delta >0$ the map f can be $\delta$-deformed to a map ${\hat{f}}$ whose image is contained in a d-dimensional subcomplex of ${\widetilde{M}}$.

More generally, the same is true if $K=\cup _iK_i$ is a countable union of compact sets.

Let P be a smooth, $\delta$-fine triangulation of ${\widetilde{M}}$. The main step is to show, for every $k>d$, that if f(K) is contained in the k-skeleton $P^{(k)}$ then we can deform via a family $f_t:K\rightarrow P^{(k)}$ to a map $f_1:K\rightarrow P^{(k-1)}$ to the $(k-1)$-skeleton in such a way that during the deformation points of each closed simplex $\sigma$ of $P^{(k)}$ remain in that simplex, i.e.

$$\begin{aligned} f_t(\sigma )\subset \sigma , \end{aligned}$$

and

$$\begin{aligned} \dim (f_1(K))\le \dim (f(K))=d. \end{aligned}$$

Once one proves this main step, iterating it proves the Proposition.

Now we prove the main step. Note that since k is greater than the Hausdorff dimension of the image f(K), for every k-simplex $\sigma$ in $P^{(k)}$ there is a point $x\in \text{ Interior }(\sigma )-f(K)$ of the interior of $\sigma$ that is not contained in the image f(K). First let’s deal with the case when $\underline{K\hbox { is compact}}$. In this case there is a $\varepsilon _x$-neighborhood of x that is disjoint from f(K). Using the linear structure of $\sigma$, we can radially project away from x on the simplex $\sigma$ (and not do anything outside $\sigma$) and get a map

$$\begin{aligned} r^{\sigma }_1:(P^{(k)}-\{x\})\rightarrow (P^{(k)}-\text{ Interior }(\sigma )) \end{aligned}$$

that is Lipschitz on f(K) since $\varepsilon _x>0$. Since this map is Lipschitz, it not increase Hausdorff dimension, i.e.

$$\begin{aligned} \dim (r_1^{\sigma }\circ f(K))\le \dim (f(K))=d. \end{aligned}$$

This map is part of an obvious radial projection homotopy $r^{\sigma }_t$ that is the identity outside the interior of $\sigma$. Doing such a deformation on each k-simplex $\sigma$ of $P^{(k)}$ gives the desired deformation of $f_t$ of f into the $(k-1)$-skeleton $P^{(k-1)}$. This deformation preserves simplices and does not increase Hausdorff dimension of f(K) because this is true for all the individual deformations $r^{\sigma }_t$. This finishes the proof of the main step when K is compact.

Next, we explain why the same argument applies in general when K is a countable union of compact sets $\cup _i K_i$. We will use the fact that Hausdorff dimension of a countable union of compact sets is the supremum of the Hausdorff dimensions of the individual sets in union. This fact follows directly from the definition of Hausdorff dimension of a set as the infimum of numbers $d'$ for which the $d'$-dimensional Hausdorff measure of the set is zero, since measures are countably additive. As before, we conclude that the radial projection $r^{\sigma }_1$ is Lipschitz on each compact set $f(K_i)$, but the Lipschitz constant might depend on i. However, this doesn’t matter because we still get for each individual compact set that

$$\begin{aligned} \dim (r_1^{\sigma }\circ f(K_i))\le \dim (f(K_i))\le d \end{aligned}$$

and therefore we get the same bound

$$\begin{aligned} \dim (r_1^{\sigma }\circ f(\cup _iK_i))\le d \end{aligned}$$

for the countable union. Therefore, the main step works for countable unions of compact sets $\bigcup _iK_i$.

1.1 A topological version.

There is also a topological version of this, which says that if the topological dimension of K is $\le d$ then we can $\delta$-deform K to a d-dimensional subcomplex of ${\widetilde{M}}$. The simplest way to arrive at this version is to first $\delta$-deform K to a map $f'$ whose image has Hausdorff dimension $\le d$ and then apply the proposition to $f'$. So, all we need is the following lemma.

Lemma 46

Suppose that $f:S\hookrightarrow {\widetilde{M}}$ is the inclusion of a subset of topological dimension $\le d$. For any $\delta >0$, we can $\delta$-deform it to a map $f':S\rightarrow {\widetilde{M}}$ whose image has Hausdorff dimension $\le d$.

Proof

Start with a cover of S by $\delta$-balls in ${\widetilde{M}}$. Since S has topological dimension $\le d$, this cover has a refinement whose nerve N has dimension $\le d$ (by Theorem V.8 of [HW48]). Build a map $S\rightarrow N$ to this nerve using a partition of unity (as in Theorem V.9 of [HW48]) and a map from the nerve $N\rightarrow {\widetilde{M}}$ using geodesic simplices in ${\widetilde{M}}$.

In more detail, the second map is constructed as follows. First, take the barycentric subdivision of the nerve and call it $N_1$. Second, send each vertex of the barycentric subdivision to a point in the corresponding intersection of elements of the cover. Third, join adjacent points by geodesics to extend the map to the 1-skeleton of $N_1$. Fourth, use the standard order on the vertices of each 2-simplex in the barycentric subdivision to extend the map to the 2-skeleton of $N_1$ by forming geodesic simplices. Continue in this fashion to produce a map $N\rightarrow {\widetilde{M}}$. Note that since balls are convex, each simplex of $N_1$ is mapped into a $\delta$-ball. It follows that the composition $S\rightarrow N\rightarrow {\widetilde{M}}$ is $\delta$-close to the original map f. Moreover, its image has Hausdorff dimension $\le d$ because N is d-dimensional and the map $N\rightarrow {\widetilde{M}}$ built using geodesic simplices is Lipschitz. $\square$

Remark

One can try to prove the topological version directly by mimicking the proof of Proposition 45 without first deforming to a map with Hausdorff dimension $\le d$. The difficultly with doing this direct argument is that it is not clear that the map $r^{\sigma }_1$ does not raise topological dimensions of subsets of $P^{(k)}-\{x\}$.

Appendix E: Triangulating the Thick Thin Decomposition

In this “Appendix” we describe how to topologically isotope $\partial M_{\le \varepsilon }$ to a smooth submanifold $S\subset M_{\le \varepsilon }$. This implies that $\partial M_{\le \varepsilon }$ has a triangulation. The procedure consists of two parts. We construct the smooth manifold S and specify a vector field V on $M_{\le \varepsilon }$ which guides the isotopy.

Let us start with the vector field. For this, we need the following fact, which is established during the proof of Lemma 4 in Appendix 2 of [BGS85]. For every $x\in {\widetilde{M}}_{\le \varepsilon }$ there is a vector $v_x$ such that for every covering translation $\gamma$ with $d_{\gamma }(x)\le \varepsilon$ we have $\left\langle v_x,\nabla d_{\gamma }\right\rangle \le 0$ and the inequality is strict for at least one such $\gamma$. Since this property is preserved under convex combinations of vectors, we can use partitions of unity to define a smooth vector field V on $M_{\le \varepsilon }$ whose lift ${\widetilde{V}}$ to ${\widetilde{M}}_{\le \varepsilon }$ satisfies this property at every point.

To produce the smooth manifold, we pick a smooth function $g:{\mathbb {R}}^+\rightarrow {\mathbb {R}}$ with $g(r)=0$ for $r\ge \varepsilon$, $g'(r)<0$ on $(0,\varepsilon )$ and $\lim _{r\rightarrow 0^+}g(r)=\infty$. The following function was used in [BGS85]:

$$\begin{aligned} {\widetilde{F}}(x):=\sum _{\gamma \not =1}g\circ d_{\gamma }(x). \end{aligned}$$

This function is $\Gamma$-invariant and thus descends to a function $F:M\rightarrow [0,\infty )$ on the quotient. This function is proper, smooth, and has no critical points outside a compact set (see Appendix 2 of [BGS85]). So, for a large enough constant c the level set $S:=F^{-1}(c)$ is a smooth, separating submanifold in $M_{\le \varepsilon }$.

The gradient of ${\widetilde{F}}$ is

$$\begin{aligned} \nabla {\widetilde{F}}=\sum _{\gamma \not =1}g'\nabla d_{\gamma } \end{aligned}$$

and therefore by the definition of V we have

$$\begin{aligned} \left\langle V,\nabla F\right\rangle =\langle {\widetilde{V}},\nabla {\widetilde{F}}\rangle >0. \end{aligned}$$

(57)

Therefore the integral curves of V meet S exactly once, so flowing along them from $\partial M_{\le \varepsilon }$ to S (and stopping once one reaches S) defines a topological isotopy from $\partial M_{\le \varepsilon }$ to S.