Abstract
In this article we address a number of features of the moduli space of spherical metrics on connected, compact, orientable surfaces with conical singularities of assigned angles, such as its non-emptiness and connectedness. We also consider some features of the forgetful map from the above moduli space of spherical surfaces with conical points to the associated moduli space of pointed Riemann surfaces, such as its properness, which follows from an explicit systole inequality that relates metric invariants (spherical systole) and conformal invariant (extremal systole).



















Similar content being viewed by others
References
Lars V. Ahlfors, Lectures on quasiconformal mappings, second ed., University Lecture Series, vol. 38, American Mathematical Society, Providence, RI, (2006), With supplemental chapters by C. J. Earle, I. Kra, M. Shishikura and J. H. Hubbard.
Enrico Arbarello, Maurizio Cornalba, and Phillip A. Griffiths, Geometry of algebraic curves. Volume II, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 268, Springer, Heidelberg, (2011), With a contribution by Joseph Daniel Harris.
D. Bartolucci and G. Tarantello, Liouville type equations with singular data and their applications to periodic multivortices for the electroweak theory, Comm. Math. Phys. (1)229 (2002), 3–47
Daniele Bartolucci, Francesca De Marchis, and Andrea Malchiodi, Supercritical conformal metrics on surfaces with conical singularities, Int. Math. Res. Not. IMRN (24)(2011), 5625–5643
Melvyn S. Berger, Riemannian structures of prescribed Gaussian curvature for compact 2-manifolds, J. Differential Geometry 5 (1971), 325–332
Haïm Brezis and Frank Merle, Uniform estimates and blow-up behavior for solutions of \(-\Delta u=V(x)e^u\) in two dimensions, Comm. Partial Differential Equations (8–9)16 (1991), 1223–1253
Alessandro Carlotto, On the solvability of singular Liouville equations on compact surfaces of arbitrary genus, Trans. Amer. Math. Soc. (3)366 (2014), 1237–1256
Chiun-Chuan Chen and Chang-Shou Lin, Mean field equation of Liouville type with singular data: topological degree, Comm. Pure Appl. Math. (6)68 (2015), 887–947
Subhadip Dey, Spherical metrics with conical singularities on 2-spheres, Geometriae Dedicata (2017), 1–9
Alexandre Eremenko, Co-axial monodromy, preprint arXiv:1706.04608.
Alexandre Eremenko, Metrics of positive curvature with conic singularities on the sphere, Proc. Amer. Math. Soc. (11)132 (2004), 3349–3355 (electronic)
Alexandre Eremenko and Andrei Gabrielov, On metrics of curvature 1 with four conic singularities on tori and on the sphere, Illinois J. Math. (4)59 (2015), 925–947
Alexandre Eremenko, Andrei Gabrielov, and Vitaly Tarasov, Metrics with four conic singularities and spherical quadrilaterals, Conform. Geom. Dyn. 20 (2016), 128–175
Alexandre Eremenko and Vitaly Tarasov, Fuchsian equations with three non-apparent singularities, SIGMA Symmetry Integrability Geom. Methods Appl. 14 (2018), 058, 12 pages.
Lisa R. Goldberg, Catalan numbers and branched coverings by the Riemann sphere, Adv. Math. (2)85 (1991), 129–144
W. K. Hayman, Meromorphic functions, Oxford Mathematical Monographs, Clarendon Press, Oxford, (1964).
John Hamal Hubbard, Teichmüller theory and applications to geometry, topology, and dynamics. Vol. 1, Matrix Editions, Ithaca, NY, (2006), Teichmüller theory, With contributions by Adrien Douady, William Dunbar, Roland Roeder, Sylvain Bonnot, David Brown, Allen Hatcher, Chris Hruska and Sudeb Mitra, With forewords by William Thurston and Clifford Earle.
Michael Kapovich, Branched covers between spheres and polygonal inequalities in simplicial trees, preprint available at https://www.math.ucdavis.edu/~kapovich/EPR/covers.pdf.
Paul Koebe, Über die Uniformisierung beliebiger analytischer Kurven, Göttinger Nachrichten (1907), 191–210
Paul Koebe, Über die Uniformisierung beliebiger analytischer Kurven (Zweite Mitteilung), Göttinger Nachrichten (1907), 633–669
Chang-Shou Lin and Chin-Lung Wang, Elliptic functions, Green functions and the mean field equations on tori, Ann. of Math. (2) (2)172 (2010), 911–954
Fu Liu and Brian Osserman, The irreducibility of certain pure-cycle Hurwitz spaces, Amer. J. Math. (6)130 (2008), 1687–1708
Feng Luo, Monodromy groups of projective structures on punctured surfaces, Invent. Math. (3)111 (1993), 541–555
Feng Luo and Gang Tian, Liouville equation and spherical convex polytopes, Proc. Amer. Math. Soc. (4)116 (1992), 1119–1129
Rafe Mazzeo and Xuwen Zhu, Conical metrics on Riemann surfaces, I: the compactified configuration space and regularity, preprint arXiv:1710.09781.
Robert C. McOwen, Point singularities and conformal metrics on Riemann surfaces, Proc. Amer. Math. Soc. (1)103 (1988), 222–224
Gabriele Mondello and Dmitri Panov, Spherical metrics with conical singularities on a 2-sphere: angle constraints, Int. Math. Res. Not. IMRN (16)(2016), 4937–4995
J. Moser, A sharp form of an inequality by N. Trudinger, Indiana Univ. Math. J. 20 (1970/71), 1077–1092
Anton Petrunin, Puzzles in geometry which I know and love, preprint arXiv:0906.0290.
Henri Poincaré, Sur l’uniformisation des fonctions analytiques, Acta Math. (1)31 (1908), 1–63.
Irina Scherbak, Rational functions with prescribed critical points, Geom. Funct. Anal. (6)12 (2002), 1365–1380.
Dirk Siersma, Voronoi diagrams and morse theory of the distance function, Geometry in Present Day Science, World Scientific, World Scientific, 1999, pp. 187–208
Kurt Strebel, Bemerkungen über quadratische Differentiale mit geschlossenen Trajektorien, Ann. Acad. Sci. Fenn. Ser. A I No. 405 (1967), 12
Marc Troyanov, Les surfaces euclidiennes à singularités coniques, Enseign. Math. (2) (1–2)32 (1986), 79–94.
Marc Troyanov, Metrics of constant curvature on a sphere with two conical singularities, Differential geometry (Peñíscola, 1988), Lecture Notes in Math., vol. 1410, Springer, Berlin, 1989, pp. 296–306
Marc Troyanov, Prescribing curvature on compact surfaces with conical singularities, Trans. Amer. Math. Soc. (2)324 (1991), 793–821
Acknowledgements
We would like to thank Daniele Bartolucci and Misha Kapovich for fruitful discussions and Francesca De Marchis for helpful explanations on [BMM11]. We are particularly grateful to Alexandre Eremenko for a number of valuable remarks that allowed us to improve the exposition. We also thank an anonymous referee for carefully reading the paper and for useful expository suggestions. G.M.’s research was partially supported by FIRB 2010 Italian grant “Low-dimensional geometry and topology” (code RBFR10GHHH_003) and by GNSAGA INdAM research group. D.P. was supported by a Royal Society University Research Fellowship and partially supported by grant RGF\(\backslash \)EA\(\backslash \)180221.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
On the Extremal Length
On the Extremal Length
In this appendix we will recall the definition of extremal length of an essential simple closed curve in a Riemann surface and of extremal systole, and we will list some basic facts about them.
Definition A.1
(Extremal length). Let \(\Sigma \) be a Riemann surface and let \(\gamma \subset \Sigma \) be an essential simple closed curve. The extremal length of \(\gamma \) in \(\Sigma \) is
where the inf is taken over all \(\check{\gamma }\) freely homotopic to \(\gamma \) and the sup is taken over all conformal metrics \(\rho \) on \(\Sigma \) of finite area. If C is a cylinder and \(\gamma \) is its waist, then the modulus of C is \(M(C)=1/\mathrm {Ext}_\gamma (C)\).
It is a fact that all cylinders with finite positive extremal length are isomorphic to a standard annulus as in the below example.
Example A.2
(Modulus of a standard plane annulus). For every \(0<r'<r''\), the modulus of the annulus \(C=\{z\in \mathbb {C}\,|\,r'<|z|<r''\}\) is \(M(C)=\frac{1}{2\pi }\log (r''/r')\) and it is attained at Euclidean metrics homothetic to \(\frac{|dz|^2}{|z|^2}\).
Since cylinders are biholomorphic to standard annuli of Example A.2, their extremal length is attained at the standard flat metric. Moreover, the following well-known variational characterization holds.
Lemma A.3
(Modulus and height of a cylinder). Let C be a cylinder with metric \(\rho '\) of area \(\mathrm {Area}(C)\) and such that the distance between the two boundary components is H. Then \(M(C)\ge H^2/\mathrm {Area}(C)\). Moreover, equality holds if and only if \((C,\rho ')\) is a flat straight cylinder.
The following standard subadditivity property of modulus directly descends from its definition and is used to estimate the modulus of a Voronoi cylinder.
Lemma A.4
(Subadditivity of modulus). Suppose that a cylinder C is cut into two cylinders \(C'\) and \(C''\) by a homotopically nontrivial simple loop. Then \(M(C)\ge M(C')+M(C'')\).
In order to understand what metric on a general punctured surface realizes the extremal length of a given simple closed curve \(\gamma \), let us first recall the relation between \(\mathrm {Ext}_\gamma (\dot{S})\) and modulus of subcylinders C homotopic to \(\gamma \).
Remark A.5
(Modulus and extremal length). It is well-known that the extremal length can be characterized as
where the infimum is taken over all annuli \(C\subset \Sigma \) homotopic to \(\gamma \). It follows that, if \(\Sigma \subset \Sigma '\) is a conformal embedding, then \(\mathrm {Ext}_\gamma (\Sigma )\ge \mathrm {Ext}_\gamma (\Sigma ')\).
Using the above remark, it can be shown that on a general punctured surface \(\dot{S}\) the sup in the definition of extremal length is achieved at the flat metric  with conical singularities associated to the Strebel differentials
with conical singularities associated to the Strebel differentials  on \(\dot{S}\) introduced in the below proposition (see, for instance, Strebel’s book [Str67]).
on \(\dot{S}\) introduced in the below proposition (see, for instance, Strebel’s book [Str67]).
Proposition A.6
(Strebel differentials). Let (S, J) be a Riemann surface with marked points \(\varvec{x}\) and let \(\gamma \subset \dot{S}\) be an essential simple closed curve. Then there exists a non-zero holomorphic quadratic differential  on \(\dot{S}\) (unique up to positive multiples) such that
on \(\dot{S}\) (unique up to positive multiples) such that
-
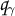 has at worst simple poles at \(\varvec{x}\),
has at worst simple poles at \(\varvec{x}\), -
every horizontal trajectory of
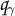 is either smooth, closed and freely homotopic to \(\gamma \) or it is an arc with endpoints in
is either smooth, closed and freely homotopic to \(\gamma \) or it is an arc with endpoints in 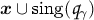 , where
, where 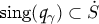 is the zero locus of
is the zero locus of 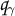 .
.
Moreover, the union \(C_\gamma \) of all smooth closed horizontal trajectories of \(\gamma \) is the complement of finitely many arcs.
In view of Remark A.5, Strebel’s study of the extremal properties of the cylinder \(C_\gamma \) leads to the following characterization of the extremal length.
Corollary A.7
(Extremal length and embedded cylinders). Let \(\gamma \) be a simple closed essential curve in \(\dot{S}\) and let \(C\subset \dot{S}\) be a cylinder that retracts by deformation onto \(\gamma \). Then \(\mathrm {Ext}_{\gamma }(\dot{S},J)\le 1/M(C)\). Equality is attained if and only if both the following conditions hold:
-
the metric \(\rho \) is
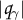 , where
, where 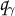 is a Strebel differential associated to \(\gamma \);
is a Strebel differential associated to \(\gamma \); -
the cylinder C is \(C_\gamma \).
Now we introduce a quantity associated to a punctured Riemann surface \(\Sigma \) which is invariant under biholomorphisms. Such quantity measures how close \(\Sigma \) is to be conformally degenerate (see Lemma 6.3).
Definition A.8
(Extremal systole). Let \(\Sigma \) be a connected punctured Riemann surface. The extremal systole\(\mathrm {Ext}\mathrm {sys}(\Sigma )\) is the minimum of \(\mathrm {Ext}_{\gamma }(\Sigma )\) as \(\gamma \) ranges over all essential simple closed curves on \(\Sigma \).
Finally, we show how the extremal length of a simple closed curve \(\gamma \) inside a punctured spherical surface \(\dot{S}\) provides a non-trivial upper bound for the length of shorter curves homotopic to \(\gamma \) inside \(\dot{S}\).
Proposition A.9
(Extremal length bounds length from above). Let S be a surface with spherical metric and conical singularities at \(\varvec{x}\) of angles \(2\pi \varvec{\vartheta }\) and assume \(\chi (\dot{S})<0\). For every essential, simple closed curve \(\gamma \) on \(\dot{S}\) there exists a simple closed curve \(\check{\gamma }\subset \dot{S}\) freely homotopic to \(\gamma \) of length
Proof
By definition A.1 of extremal length, \(\mathrm {Area}(S)\cdot \mathrm {Ext}_{\gamma }(\dot{S})\ge \inf _{\gamma '}\ell (\gamma ')^2\), where \(\gamma '\) ranges over all simple closed curves in \(\dot{S}\) freely homotopic to \(\gamma \). By Corollary A.7, the sup in the definition of \(\mathrm {Ext}_{\gamma }(\dot{S})\) is not attained at a spherical metric, and so there exists \(\varepsilon >0\) such that \(\mathrm {Area}(S)\cdot \mathrm {Ext}_{\gamma }(\dot{S})>2\varepsilon +\inf _{\gamma '}\ell (\gamma ')^2\). Furthermore, there exists \(\check{\gamma }\simeq \gamma \) such that \(\ell (\check{\gamma })^2\le \varepsilon +\inf _{\gamma '}\ell (\gamma ')^2\), and so \(\mathrm {Area}(S)\cdot \mathrm {Ext}_{\gamma }(\dot{S})>\varepsilon +\ell (\check{\gamma })^2\). In other words, \(\ell (\check{\gamma })<\sqrt{\mathrm {Area}(S)\cdot \mathrm {Ext}_{\gamma }(\dot{S})}\). The conclusion then follows, since \(\mathrm {Area}(S)=2\pi \left( \chi (\dot{S})+\Vert \varvec{\vartheta }\Vert _1\right) < 2\pi \Vert \varvec{\vartheta }\Vert _1\) by Gauss–Bonnet. \(\square \)
As a consequence, combining Proposition A.9 and Lemma 3.11, we obtain the following bound from above for the systole in terms of the extremal systole.
Corollary A.10
(Extremal systole bounds systole from above). In a spherical surface S with conical singularities at \(\varvec{x}\) of angles \(2\pi \varvec{\vartheta }\), the systole satisfies \(\mathrm {sys}(S,\varvec{x})\le \sqrt{(\pi /2) \mathrm {Ext}\mathrm {sys}(\dot{S})\Vert \varvec{\vartheta }\Vert _1}\).
1.1 Peripheral regions in 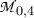 .
.
We recall that the moduli space  of Riemann surfaces of genus 0 with 4 distinct marked points is isomorphic to \(\mathbb {C}\mathbb {P}^1{\setminus }\{0,1,\infty \}\).
of Riemann surfaces of genus 0 with 4 distinct marked points is isomorphic to \(\mathbb {C}\mathbb {P}^1{\setminus }\{0,1,\infty \}\).
For every \(1\le i\le 3\) denote by  the subset of
the subset of  consisting of isomorphism classes of Riemann surfaces \((S,J,\varvec{x})\) such that there exists a simple closed curve \(\gamma \subset \dot{S}\) with \(\mathrm {Ext}_{\gamma }(\dot{S},J)<2\) such that a connected component of \(S{\setminus } \gamma \) contains \(\{x_i,x_4\}\).
consisting of isomorphism classes of Riemann surfaces \((S,J,\varvec{x})\) such that there exists a simple closed curve \(\gamma \subset \dot{S}\) with \(\mathrm {Ext}_{\gamma }(\dot{S},J)<2\) such that a connected component of \(S{\setminus } \gamma \) contains \(\{x_i,x_4\}\).
In this subsection we want to prove the following result.
Lemma A.11
(Peripheral regions of  ). The subsets
). The subsets  ,
,  ,
,  of
of  are non-empty, open, connected and disjoint.
are non-empty, open, connected and disjoint.
We begin by exhibiting an explicit construction of Riemann surfaces of genus 0 with marked points \(x_1,x_2,x_3,x_4\) endowed with a Strebel differential  associated to a simple closed curve \(\gamma \) that separates \(x_1,x_2\) from \(x_3,x_4\).
associated to a simple closed curve \(\gamma \) that separates \(x_1,x_2\) from \(x_3,x_4\).
Example A.12
Let \(r>0\) and consider a flat cylinder \(\mathcal {C}_r=(\mathbb {R}/2r\mathbb {Z})\times [0,\frac{1}{r}]\) of waist 2r and height \(\frac{1}{r}\), which can be obtained from the strip \(\{z\in \mathbb {C}\,|\,\mathrm {Im}(z)\in [0,\frac{1}{r}]\}\) by identifying \(z\sim z+2r\). Given \(\phi \in \mathbb {R}/\mathbb {Z}\), let \(S_{r,\phi }\) be the flat surface obtained from \(\mathcal {C}_r\) by identifying \((u,0)\sim (-u,0)\) and \((u-2r\phi ,\frac{1}{r})\sim (2r\phi -u,\frac{1}{r})\), and then marking the conical points \([0,0],[r,0],[2r\phi ,\frac{1}{r}],2r(\phi +\frac{1}{2}),\frac{1}{r}]\) by \(x_1,x_2,x_3,x_4\). The quadratic differential \(dz^2\) on the strip descends to a quadratic differential  on \(S_{r,\phi }\) and
on \(S_{r,\phi }\) and  agrees with the induced flat metric on \(S_{r,\phi }\). Note that the only two horizontal non-periodic trajectories of
agrees with the induced flat metric on \(S_{r,\phi }\). Note that the only two horizontal non-periodic trajectories of  have length r: they are the arc \(\alpha _{12}\) between \(x_1,x_2\) induced by the boundary curve \(\{\mathrm {Im}(z)=0\}\) of \(\mathcal {C}_r\) and the arc \(\alpha _{34}\) between \(x_3,x_4\) induced by the boundary curve \(\{\mathrm {Im}(z)=\frac{1}{r}\}\) of \(\mathcal {C}_r\).
have length r: they are the arc \(\alpha _{12}\) between \(x_1,x_2\) induced by the boundary curve \(\{\mathrm {Im}(z)=0\}\) of \(\mathcal {C}_r\) and the arc \(\alpha _{34}\) between \(x_3,x_4\) induced by the boundary curve \(\{\mathrm {Im}(z)=\frac{1}{r}\}\) of \(\mathcal {C}_r\).
In the next lemma we show that all surfaces in  endowed with Strebel differentials are of the type seen above.
endowed with Strebel differentials are of the type seen above.
Lemma A.13
(Strebel differentials that separate \(x_1,x_2\) from \(x_3,x_4\)). Let  . Let \(\gamma \) be a simple closed curve in \(\dot{S}\) that separates \(x_1,x_2\) from \(x_3,x_4\) and let
. Let \(\gamma \) be a simple closed curve in \(\dot{S}\) that separates \(x_1,x_2\) from \(x_3,x_4\) and let  be the associated Strebel differential of area 2. Then
be the associated Strebel differential of area 2. Then  is isomorphic to a
is isomorphic to a  constructed in Example A.12 for some \(r>0\) and \(\phi \in \mathbb {R}/\mathbb {Z}\). As a consequence, \(\mathrm {Ext}_{\gamma }(S_{r,\phi })=2r^2\).
constructed in Example A.12 for some \(r>0\) and \(\phi \in \mathbb {R}/\mathbb {Z}\). As a consequence, \(\mathrm {Ext}_{\gamma }(S_{r,\phi })=2r^2\).
Proof
Since  has simple poles at \(\varvec{x}\), there is a unique horizontal trajectory outgoing from each \(x_i\). It follows that the complement of the cylinder \(C_\gamma \) is the union of two segments joining \(x_1\) to \(x_2\) and \(x_3\) to \(x_4\). It is now easy to see that
has simple poles at \(\varvec{x}\), there is a unique horizontal trajectory outgoing from each \(x_i\). It follows that the complement of the cylinder \(C_\gamma \) is the union of two segments joining \(x_1\) to \(x_2\) and \(x_3\) to \(x_4\). It is now easy to see that  must be of the type produced in Example A.12. The last claim follows by noting that a geodesic loop homotopic to \({\gamma }\) has length 2r. \(\square \)
must be of the type produced in Example A.12. The last claim follows by noting that a geodesic loop homotopic to \({\gamma }\) has length 2r. \(\square \)
In the lemma below we show that there can be at most one simple closed curve with extremal length smaller than 2 on a Riemann surface in  . This is a special case of a more general lower bound for the product the extremal lengths of two simple closed curves in terms of their geometric intersection product. We include a short proof for completeness.
. This is a special case of a more general lower bound for the product the extremal lengths of two simple closed curves in terms of their geometric intersection product. We include a short proof for completeness.
Lemma A.14
(Small extremal systole is realized at one curve). For every Riemann surface (S, J) of genus 0 with 4 marked points there exists at most one (essential) simple closed curve \(\gamma \subset \dot{S}\) such that \(\mathrm {Ext}_\gamma (\dot{S},J)<2\).
Proof
Up to relabelling the marked points, we can assume that \(\gamma \) separates \(x_1,x_2\) from \(x_3,x_4\). Up to rescaling, we can also assume that  has area 2. By Lemma A.13, the couple
has area 2. By Lemma A.13, the couple  is isomorphic to a couple
is isomorphic to a couple  constructed in Example A.12.
constructed in Example A.12.
If \(\beta \) is any other essential simple closed curve in \(\dot{S}\) not homotopic to \(\gamma \), then any geodesic representative \(\bar{\beta }\) of \(\beta \) must cross both the arcs \(\alpha _{12}\) and \(\alpha _{34}\). Hence, \(\bar{\beta }\) must have length at least \(\frac{2}{r}\) and so \(\mathrm {Ext}_\beta (\dot{S},J)\ge \frac{1}{2}\left( \frac{2}{r}\right) ^2=\frac{2}{r^2}\). It follows that \(\mathrm {Ext}_\gamma (\dot{S},J)\cdot \mathrm {Ext}_\beta (\dot{S},J)\ge 4\). As a consequence, if \(\mathrm {Ext}_\gamma (\dot{S},J)<2\), then \(\mathrm {Ext}_\beta (\dot{S},J)>2\). \(\square \)
We can now prove the main result of this subsection.
Proof of Lemma A.11
In view of Lemma A.14, the above regions are disjoint. Since their union is \(\mathrm {Ext}\mathrm {sys}^{-1}(0,2)\) and  is continuous by Lemma 6.3, it follows that each region is open.
is continuous by Lemma 6.3, it follows that each region is open.
Let us prove that  is non-empty and connected. The cases (1, 4) and (2, 4) will be analogous.
is non-empty and connected. The cases (1, 4) and (2, 4) will be analogous.
Consider the map  that sends \(z=re^{2\pi i\phi }\) to the Riemann surface \((S_{r,\phi },\varvec{x})\) constructed in Example A.12. It is not difficult to see that such map is continuous.
that sends \(z=re^{2\pi i\phi }\) to the Riemann surface \((S_{r,\phi },\varvec{x})\) constructed in Example A.12. It is not difficult to see that such map is continuous.
Since the curve \(\gamma \) inside \(S_{r,\phi }\) that separates \(x_1,x_2\) from \(x_3,x_4\) satisfies \(\mathrm {Ext}_{\gamma }(S_{r,\phi })=2r^2\), it follows that  is the image of the punctured unit disk \(\Delta ^*=\{z=re^{2\pi i\phi }\in \mathbb {C}^*\,|\,r<1\}\) via \(\Psi \). Hence,
is the image of the punctured unit disk \(\Delta ^*=\{z=re^{2\pi i\phi }\in \mathbb {C}^*\,|\,r<1\}\) via \(\Psi \). Hence,  is non-empty and connected. \(\square \)
is non-empty and connected. \(\square \)
1.2 Comparing \(\mathrm {sys}\) and \(\mathrm {Ext}\mathrm {sys}\) in a sequence of explicit examples.
The content of Theorem C can be rephrased as an upper bound for \(\mathrm {Ext}\mathrm {sys}\) as in Corollary A.15 below. The aim of this section is to show that, in the case of spherical surfaces with small systole, such an upper bound for \(\mathrm {Ext}\mathrm {sys}\) is reasonably optimal, and more precisely it is optimal up to a factor 3.
Corollary A.15
(Bound for \(\mathrm {Ext}\mathrm {sys}\) in terms of \(\mathrm {sys}\)). Let S be a surface with spherical metric and conical singularities at \(\varvec{x}\) of angles \(2\pi {\varvec{\vartheta }}\). Assume that \(\chi =\chi (\dot{S})<0\) and that \(\dot{S}\) is not a 3-punctured sphere. Then
provided \(\mathrm {sys}(S,\varvec{x})\le \left( \frac{1}{4\pi \Vert \varvec{\vartheta }\Vert _1}\min \left\{ \frac{1}{2},\,\mathrm {NB}_{\varvec{\vartheta }}(S,\varvec{x})\right\} \right) ^{1-3\chi }\). In particular, if \(\chi (\dot{S})\) and \(\varvec{\vartheta }\) are fixed, then
as \(\mathrm {sys}(S,\varvec{x})\rightarrow 0\).
Proof
Let \(\varepsilon =4\pi \Vert \varvec{\vartheta }\Vert _1\mathrm {sys}(S,\varvec{x})^{\frac{1}{1-3\chi }}\), so that the last inequality in the statement of Theorem C becomes an equality. The assumption on \(\mathrm {sys}(S,\varvec{x})\) implies that \(\varepsilon <\frac{1}{2}\) and \(\mathrm {NB}_{\varvec{\vartheta }}(S,\varvec{x})\ge \varepsilon \). By Theorem C,
and the conclusion follows. \(\square \)
In particular, we will produce an explicit sequence of surfaces of genus 0 with an increasing number of marked points and we will estimate their systole and extremal systole, thus proving the following statement.
Proposition A.16
(Bound for \(\mathrm {Ext}\mathrm {sys}\) in terms of \(\mathrm {sys}\) in some examples). There exist spherical surfaces S of genus 0 with conical singularities at \(\varvec{x}\) of angles \(2\pi \varvec{\vartheta }\) and \(\chi =\chi (\dot{S})<-1\) and \(\mathrm {NB}_{\varvec{\vartheta }}(S,\varvec{x})=\frac{1}{2}\) such that the ratio
can be made as close to 1 as desired.
Incidentally, we recall that the extremal systole can be always bounded from below in terms of the systole as in Corollary A.10.
The construction of such sequence of spherical surfaces proceeds as follows.
1.2.1 Construction of the examples.
Fix positive integers m and \(N\ge 1\) and a real parameter \(\varepsilon \in (0,\frac{1}{2})\). Let \(\varvec{\vartheta }=(2N+\frac{1}{2},\frac{1}{2},\frac{1}{2},1^{m+1})\) and denote by \(\epsilon \) the quantity \(\frac{\varepsilon }{4\pi \Vert \varvec{\vartheta }\Vert _1}\).
Consider the surface S obtained by doubling a spherical triangle with vertices \(x_1,x_2,x_3\) and angles \(2\pi \cdot (2N+\frac{1}{2},\frac{1}{2},\frac{1}{2})\). Such an S comes with a natural orientation-reversing involution.
Along the geodesic arc \(\alpha _{12}\) that goes from \(x_1\) and \(x_2\), mark by \(y_i\) the point that sits at distance \(\epsilon ^i\) from \(x_1\) for \(i=0,\ldots ,m\). Thus, S is a spherical surface of genus 0 with \(4+m\) conical points \(\varvec{x}=(x_1,x_2,x_3,y_0,y_1,\ldots ,y_m)\) of angles \(2\pi \varvec{\vartheta }\). Denote by \(\dot{S}\) the punctured surface \(S{\setminus } \varvec{x}\). For simplicity, we will use the shorter notation \(\mathrm {NB}(S)\) and \(\mathrm {sys}(S)\) with the obvious meaning.
For all \(i=1,\ldots ,m\) define \(\gamma _i\) to be the simple closed curve in \(\dot{S}\) consisting of points at distance \(\epsilon ^{i-\frac{1}{2}}\) from \(x_1\), which in particular separates \(x_1,y_m,\ldots ,y_i\) from all the other punctures.
Certainly, the systole is \(\mathrm {sys}(S)=\epsilon ^m\) and \(\mathrm {NB}(S)=\frac{1}{2}\). Also, \(\Vert \varvec{\vartheta }\Vert _1=2N+m+2+\frac{1}{2}\).
Since the ratio \(\frac{-\chi -2}{-\chi }\) can be made close to 1 by choosing m large, Proposition A.16 will then be a consequence of the following statement.
Lemma A.17
(Comparison between \(\mathrm {Ext}\mathrm {sys}\) and \(\mathrm {sys}\) for S). For the surfaces S constructed in Subsection A.2.1, we have \(\mathrm {NB}(S)=\frac{1}{2}>\varepsilon \) and
Moreover, choosing \(N,\varepsilon \) such that \(N\gg m\) and \(\varepsilon <\exp \left[ -8(4N+1)^2\right] \), the ratio
can be made as close to 1 as desired.
The systole of our surface S was easily computed above. To understand the extremal systole, we consider the surfaces \(\dot{S}_k\) obtained from \(\dot{S}\) by filling the punctures \(y_{k+1},\ldots ,y_m\) for all \(k=1,\ldots ,m\). We begin by estimating the extremal length of \(\gamma _k\) inside \(\dot{S}_k\) and we will show that in fact \(\gamma _k\) realizes the extremal systole inside \(\dot{S}_k\) proceeding by induction on k.
1.2.2 Planar model.
In order to reduce the problem to some well-known estimates of conformal moduli of plane annular domains, we will use the following description of the complement in S of the geodesic arc \(\alpha _{23}\) between \(x_2\) and \(x_3\).
Lemma A.18
(Planar model for \(S{\setminus }\alpha _{23}\)). There is a biholomorphism between \(S{\setminus }\alpha _{23}\) and the unit disk \(S':=\Delta \) such that
-
(a)
the points \(x_1\), \(x_2\), \(x_3\) in S correspond to \(x'_1=0\), \(x'_2=1\), \(x'_3=-1\) in \(S'\),
-
(b)
the point \(y'_j=\tan (\epsilon ^j/2)^{1/\vartheta _1}\) in \((0,1)\subset S'\) corresponds to \(y_j\) for all j,
-
(c)
the orientation-reversing involution of \(S{\setminus }\alpha _{23}\) corresponds to the conjugation, the two shores of the cut in \(S{\setminus }\alpha _{23}\) correspond to the two arcs on \(\partial S'\) between 1 and \(-1\), and the arc \(\alpha _{12}\subset S\) corresponds to \([0,1]\subset S'\).
Proof of Lemma A.18
Let \(\mathbb {C}\) with the natural coordinate w be endowed with the standard spherical metric \(\left( \frac{2 |dw|}{1+|w|^2}\right) ^2\), for which \(\{|w|=1\}\) is a maximal circle. A (multivalued) developing map from \(\iota :S{\setminus }\alpha _{23}\rightarrow \mathbb {C}\) that sends \(x_1\) to the origin has image equal to the open unit disk and it has order \(\vartheta _1\) at \(x_1\). Thus, there exists a biholomorphism \(\psi :S{\setminus }\alpha _{23}\rightarrow S'\) that sends \(x_1\) to 0 and such that \(\iota =\iota '\circ \psi \), where \(\iota '(z)=z^{\vartheta _1}\). Moreover \(\psi \) can be uniquely chosen so that \(x_2\) corresponds to \(x'_2=1\).
Since \([0,1)\subset S'\) running from \(x'_1=0\) to \(x'_2=1\) is sent to a geodesic by \(\iota '\), such segment corresponds to \(\alpha _{12}\subset S\). Thus the orientation-reversing involution of \(S{\setminus }\alpha _{23}\) that fixes \(\alpha _{12}\) must correspond to the conjugation in \(S'\) and so \(x_3\in S\) corresponds to \(x'_3=-1\).
Finally, the point \(w_j=\tan (\epsilon ^j/2)\) in \(\mathbb {C}\) is at distance \(\epsilon ^j\) from 0. Hence, the point \(y'_j=\tan (\epsilon ^j/2)^{1/\vartheta _1}\) in \((0,1)\subset S'\) is at distance \(\epsilon ^j\) from \(x'_1=0\), and so \(y'_j\in S'\) corresponds to \(y_j\in S\). \(\square \)
We denote by \(\dot{S}'_k\) the punctured domain \(S'{\setminus } \{x'_1,x'_2,x'_3,y'_0,\ldots ,y'_k\}\) and by \(\dot{S}'=\dot{S}'_m\).
1.2.3 The Strebel differential 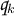 on \(\dot{S}_k\).
on \(\dot{S}_k\).
In order to estimate the extremal lengths in \(\dot{S}_k\), consider the Strebel differential  on \(\dot{S}_k\) associated to \(\gamma _k\), such that the total area of
on \(\dot{S}_k\) associated to \(\gamma _k\), such that the total area of  is exactly \(\mathrm {Ext}_{\gamma _k}(\dot{S}_k)\).
is exactly \(\mathrm {Ext}_{\gamma _k}(\dot{S}_k)\).
Lemma A.19
The couple  is isomorphic to a doubled rectangle of vertices \(x_1,y_k,y_{k-1},x_3\) with base \(x_1 y_k\) of length \(\frac{1}{2}\mathrm {Ext}_{\gamma _k}(\dot{S}_k)\) and height \(x_1 x_3\) of length 1. The horizontal trajectories of
is isomorphic to a doubled rectangle of vertices \(x_1,y_k,y_{k-1},x_3\) with base \(x_1 y_k\) of length \(\frac{1}{2}\mathrm {Ext}_{\gamma _k}(\dot{S}_k)\) and height \(x_1 x_3\) of length 1. The horizontal trajectories of  are parallel to the base. The points \(y_{k-1},\ldots ,y_0,x_2\) lie in this order on the horizontal trajectory running from \(y_{k-1}\) to \(x_3\).
are parallel to the base. The points \(y_{k-1},\ldots ,y_0,x_2\) lie in this order on the horizontal trajectory running from \(y_{k-1}\) to \(x_3\).
Proof
The curve \(\gamma _k\) is essential inside \(\hat{S}_k=S_k{\setminus }\{x_1,y_k,y_{k-1},x_3\}\). Consider the quadratic differential  associated to \(\gamma _k\) inside \(\hat{S}_k\) such that
associated to \(\gamma _k\) inside \(\hat{S}_k\) such that  has total area \(\frac{1}{2}\mathrm {Ext}_{\gamma _k}(\dot{S}_k)\) (see Figure 21 on the right, for the case \(k=m\)). The analysis contained in Example A.12 shows that \(\hat{S}_k\) is isomorphic to \(S_{r,\phi }\) with \(\phi =0\) and \(r^2=\frac{1}{2}\mathrm {Ext}_{\gamma _k}(\dot{S}_k)\), and so
has total area \(\frac{1}{2}\mathrm {Ext}_{\gamma _k}(\dot{S}_k)\) (see Figure 21 on the right, for the case \(k=m\)). The analysis contained in Example A.12 shows that \(\hat{S}_k\) is isomorphic to \(S_{r,\phi }\) with \(\phi =0\) and \(r^2=\frac{1}{2}\mathrm {Ext}_{\gamma _k}(\dot{S}_k)\), and so  is isometric to a doubled rectangle with corners \(x_1,y_k,y_{k-1},x_3\). Moreover, the orientation-reversing involution of \(\dot{S}_k\) is an isometry and so conformal; hence, it fixes the metric
is isometric to a doubled rectangle with corners \(x_1,y_k,y_{k-1},x_3\). Moreover, the orientation-reversing involution of \(\dot{S}_k\) is an isometry and so conformal; hence, it fixes the metric  and so it is the natural involution of the doubled rectangle. In particular, \(\alpha _{12}\) is fixed by the involution of the doubled rectangle and so it is the union of the horizontal segments \(x_1 y_k\) and \(y_{k-1}x_3\) and the vertical segment \(y_k y_{k-1}\). It is easy now to check that
and so it is the natural involution of the doubled rectangle. In particular, \(\alpha _{12}\) is fixed by the involution of the doubled rectangle and so it is the union of the horizontal segments \(x_1 y_k\) and \(y_{k-1}x_3\) and the vertical segment \(y_k y_{k-1}\). It is easy now to check that  and the conclusion easily follows. \(\square \)
and the conclusion easily follows. \(\square \)
We call  the corresponding quadratic differential on \(\dot{S}'_k\) and \(\gamma '_k\) the curve in \(\dot{S}'_k\) that corresponds to \(\gamma _k\).
the corresponding quadratic differential on \(\dot{S}'_k\) and \(\gamma '_k\) the curve in \(\dot{S}'_k\) that corresponds to \(\gamma _k\).
1.2.4 Estimate for the extremal length of \(\gamma _k\) in \(\dot{S}_k\).
The extremal length of \(\gamma _k\subset \dot{S}_k\) is estimated from above using the spherical metric and superadditivity of the modulus. The bound from below uses the plane model of \(\dot{S}{\setminus }\alpha _{23}\) and a classical estimate stating that the modulus of the annulus obtained from \(\mathbb {C}\) by removing the two segments \([-1,0]\) and \([t-1,+\infty )\) is at most \(\frac{1}{2\pi }\log (16t)\) for all real \(t>1\) (see [Ahl06, Chap.3B]).
Lemma A.20
(Extremal length of \(\gamma _k\)). The extremal length of \(\gamma _k\) inside \(\dot{S}_k\) satisfies
and so in particular \(\displaystyle \mathrm {Ext}_{\gamma _k}(\dot{S}_k)-\frac{2\pi \vartheta _1}{\log (1/\epsilon )}=O\left( \frac{\vartheta _1^2}{\log ^2(1/\epsilon )}\right) \).
Proof
In order to bound \(\mathrm {Ext}_{\gamma _k}(\dot{S}_k)\) from below, consider the locus \(C_k\subset \dot{S}_k\) of points at distance between \(\epsilon ^k\) and \(\epsilon ^{k-1}\) from \(x_1\). By Lemma 5.5 we immediately have \(M(C_k)>\frac{1}{2\pi \vartheta _1}\log (1/\epsilon )\) and so \(\mathrm {Ext}_{\gamma _k}(\dot{S}_k)<\frac{2\pi \vartheta _1}{\log (1/\epsilon )}\).
In order to bound \(\mathrm {Ext}_{\gamma _k}(\dot{S}_k)\) from above, consider the quadratic differential  described in Lemma A.19. Since \(\alpha _{23}\) is a horizontal segment, \(\mathrm {Ext}_{\gamma _k}(\dot{S}_k)=\mathrm {Ext}_{\gamma _k}(\dot{S}_k{\setminus }\alpha _{23})= \mathrm {Ext}_{\gamma '_k}(\dot{S}'_k)\) and it is achieved at the metric
described in Lemma A.19. Since \(\alpha _{23}\) is a horizontal segment, \(\mathrm {Ext}_{\gamma _k}(\dot{S}_k)=\mathrm {Ext}_{\gamma _k}(\dot{S}_k{\setminus }\alpha _{23})= \mathrm {Ext}_{\gamma '_k}(\dot{S}'_k)\) and it is achieved at the metric  . Thus,
. Thus,  . Since \(\Omega _k=\mathbb {C}{\setminus } \Big ([0,y'_k]\cup [y'_{k-1},+\infty )\Big )\) is biholomorphic to \(\mathbb {C}{\setminus } \left( [-1,0]\cup [\frac{y'_{k-1}}{y'_k}-1,+\infty )\right) \), it follows that
. Since \(\Omega _k=\mathbb {C}{\setminus } \Big ([0,y'_k]\cup [y'_{k-1},+\infty )\Big )\) is biholomorphic to \(\mathbb {C}{\setminus } \left( [-1,0]\cup [\frac{y'_{k-1}}{y'_k}-1,+\infty )\right) \), it follows that

and so \(\displaystyle \mathrm {Ext}_{\gamma _k}(\dot{S}_k)\ge \frac{2\pi \vartheta _1}{\vartheta _1\log (16)+\log (1/\epsilon )+O(\epsilon )}\). The last assertion is a straightforward calculation. \(\square \)
1.2.5 Estimate for the extremal systole of \(\dot{S}_k\).
Now we inductively show that the extremal systole of \(\dot{S}_k\) is realized at the closed curve \(\gamma _k\).
Lemma A.21
(Extremal systole of \(\dot{S}_k\)). Suppose that \(\varepsilon <\exp \left[ -8(4N+1)^2\right] \). Then the extremal systole of the punctured surface \(\dot{S}_k\) is achieved at \(\gamma _k\) only.
Proof
Preliminarly observe that the total area of S for the spherical metric is \(2\pi \vartheta _1\) and that our assumption on \(\varepsilon \) implies that \(\log \left( \frac{1}{\epsilon }\right)>8(4N+1)^2> \left( \frac{2\pi \vartheta _1}{\pi -2}\right) ^2\).
Now, \(\mathrm {Ext}_{\gamma _k}(\dot{S}_k)<\frac{2\pi \vartheta _1}{\log (1/\epsilon )}\) by Lemma A.20. We claim that, if \(\gamma \subset \dot{S}_k\) is a simple closed curve not homotopic to \(\gamma _k\), then \(\mathrm {Ext}_\gamma (\dot{S}_k)\ge \frac{2\pi \vartheta _1}{\log (1/\epsilon )}\). It will follow that \(\mathrm {Ext}\mathrm {sys}(\dot{S}_k)\) is attained at \(\gamma _k\) only.
Denote by \(\dot{S}^+_k\) the region of \(\dot{S}_k\) consisting of points at  -distance less than \(\frac{1}{2}\) from the segment \(x_1 y_k\), by \(\dot{S}^-_k\) the region of points at
-distance less than \(\frac{1}{2}\) from the segment \(x_1 y_k\), by \(\dot{S}^-_k\) the region of points at  -distance less than \(\frac{1}{2}\) from the segment \(y_{k-1}x_3\) (see Figure 21 on the right in the case \(k=m\)).
-distance less than \(\frac{1}{2}\) from the segment \(y_{k-1}x_3\) (see Figure 21 on the right in the case \(k=m\)).
Let us prove the above claim by induction on \(k\ge 1\).
Consider the case \(k=1\). The surface \(\dot{S}_1\) has 5 punctures \(x_1,x_2,x_3,y_0,y_1\) and the only closed curve in \(\dot{S}^+_1\) is \(\gamma _1\). A closed curve \(\gamma \subset \dot{S}_1\) that cannot be deformed inside \(\dot{S}^+_1\) or \(\dot{S}^-_1\) must cross both segments \(y_1 x_1\) and \(y_0 x_3\), and so it must have  -length at least 2. Hence,
-length at least 2. Hence,
where the first inequality on the left follows from the very definition of extremal length using the metric  , the second inequality relies on Lemma A.20 and the third inequality is a rephrasing of \(\epsilon <\exp (-\vartheta _1\pi )\), which follows from our assumption on \(\varepsilon \).
, the second inequality relies on Lemma A.20 and the third inequality is a rephrasing of \(\epsilon <\exp (-\vartheta _1\pi )\), which follows from our assumption on \(\varepsilon \).
Finally, a closed curve \(\gamma \) contained in \(\dot{S}^-_1\) must be homotopic either to \(\gamma _{23}\) that separates \(x_2,x_3\), or to \(\gamma _{0,2}\) that separates \(y_0,x_2\) or to \(\gamma _{0,3}\) that separates \(y_0,x_3\) from the other points.
Any curve homotopic to \(\gamma _{2,3}\) (resp. \(\gamma _{0,2}\), \(\gamma _{0,3}\)) has spherical length at least 2 (resp. at least \(\pi -2\), at least \(\pi \)). Hence, \(\mathrm {Ext}_\gamma (\dot{S}_1)\ge \frac{(\pi -2)^2}{2\pi \vartheta _1}\), which is larger than \( \frac{2\pi \vartheta _1}{\log (1/\epsilon )}\) by our observation at the very beginning of the proof.
Consider now the case \(k>1\). Again, every simple closed curve in \(\dot{S}^+_k\) is homotopic to \(\gamma _k\). Analogously to the case \(k=1\), a simple closed curve \(\gamma \subset \dot{S}_k\) that is not homotopic to a curve in \(\dot{S}^+_k\) or in \(\dot{S}^-_k\) must have  -length at least 2 and so \(\mathrm {Ext}_\gamma (\dot{S}_k)>\frac{2\pi \vartheta _1}{\log (1/\epsilon )}\). Finally, if \(\gamma \subset \dot{S}^-_k\) is a simple closed curve, then \(\mathrm {Ext}_{\gamma }(\dot{S}_k)\ge \mathrm {Ext}_{\gamma }(\dot{S}_{k-1})\ge \frac{2\pi \vartheta _1}{\log (1/\epsilon )}\) by induction. \(\square \)
-length at least 2 and so \(\mathrm {Ext}_\gamma (\dot{S}_k)>\frac{2\pi \vartheta _1}{\log (1/\epsilon )}\). Finally, if \(\gamma \subset \dot{S}^-_k\) is a simple closed curve, then \(\mathrm {Ext}_{\gamma }(\dot{S}_k)\ge \mathrm {Ext}_{\gamma }(\dot{S}_{k-1})\ge \frac{2\pi \vartheta _1}{\log (1/\epsilon )}\) by induction. \(\square \)
We can now prove the main result of this section.
Proof of Lemma A.17
First note that \(\mathrm {Ext}\mathrm {sys}(\dot{S})=\mathrm {Ext}_{\gamma _m}(\dot{S})\) by Lemma A.21, because \(\dot{S}=\dot{S}_m\). By taking N / m large enough, the ratio \(\frac{\Vert \varvec{\vartheta }\Vert _1}{\vartheta _1}>1\) can be made as close to 1 as desired. Moreover, our assumption on \(\varepsilon \) implies that \(\frac{\vartheta _1}{\log (1/\epsilon )}<\frac{1}{2(4N+1)}\) and so this ratio can be made as small as desired by taking N large enough. Lemma A.20 then ensures that \(\mathrm {Ext}_{\gamma _m}(\dot{S})\) is as close to \(\frac{2\pi \vartheta _1}{\log (1/\epsilon )}\), and so to \(\frac{2\pi \Vert \varvec{\vartheta }\Vert _1}{\log (1/\epsilon )}\), as we wish.
\(\square \)
Rights and permissions
About this article
Cite this article
Mondello, G., Panov, D. Spherical surfaces with conical points: systole inequality and moduli spaces with many connected components. Geom. Funct. Anal. 29, 1110–1193 (2019). https://doi.org/10.1007/s00039-019-00506-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00039-019-00506-3




 has at worst simple poles at
has at worst simple poles at  is either smooth, closed and freely homotopic to
is either smooth, closed and freely homotopic to 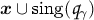 , where
, where 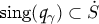 is the zero locus of
is the zero locus of 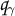 .
.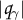 , where
, where 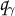 is a Strebel differential associated to
is a Strebel differential associated to 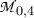 .
.

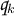 on
on 