Introduction

Cervical cancer represents a substantial disease burden, with an estimated 530,000 new cases and 275,000 deaths each year worldwide (Ferlay et al. 2010). Screening techniques such as cytology and testing for human papillomavirus (HPV) infection are available and vaccination against HPV now offers a promising additional strategy for management of cervical cancer.

HPV infection is closely associated with cervical cancer (zur Hausen 1996; Walboomers et al. 1999; Bosch et al. 2002). One hundred and twenty types of HPV have been identified (Trottier and Franco 2006), classified into high-risk (oncogenic) types that can lead to pre cervical cancer lesions [low-grade intraepithelial neoplasia (CIN) lesions (CIN 1) and high-grade CIN (CIN2/3)] and cervical cancer and low-risk (non-oncogenic) types that can produce genital warts or CIN 1 but not CIN 2/3 nor cervical cancer (Munoz et al. 2006). Two oncogenic HPV types, HPV-16 and HPV-18, are responsible for 70% of detected cervical cancer cases worldwide (WHO/ICO 2010). Clinical studies have shown that the currently available bivalent vaccine targeting HPV 16/18 is effective against these types but also even beyond these and well tolerated in preventing infections and cervical intraepithelial neoplasia (CIN) (Harper et al. 2006; Paavonen et al. 2009). Addition of HPV vaccination at an early age (12 years) to screening offers a potentially cost-effective method of reducing cervical cancer incidence (Kim et al. 2008; Marra et al. 2009).

As the clinical benefits of vaccination accrue in the future, long-term clinical data will take some decades to collect. In the meantime, modelling studies can integrate currently available clinical data with country-specific epidemiological data to evaluate the potential long-term impact of adding vaccination to screening. Models can also test different scenarios to investigate the effect of uncertainty around some of the input parameters. Several models of HPV vaccination have been published, with varying degrees of complexity and transparency (Kim et al. 2008). In general, sophisticated models lead to more accurate results but are likely to be more difficult to understand. Moreover, detailed input data are not available for all countries, and simpler models may be more widely applicable (Debicki et al. 2008). We developed a succinct model, based on an existing model (Goldie et al. 2004) and close to the one developed by Kulsingam and Myers (2003) that allows transparent estimation of the cost-effectiveness of HPV vaccination using a data set that is easily accessible for most countries. It can be used to provide a rapid preliminary assessment of various vaccination and screening scenarios, such as vaccination with or without screening (opportunistic or organised), at various ages and with or without catch-up vaccination. The model has been described in detail and its performance compared with a more complex modelling approach elsewhere (Debicki et al. 2008). In the present paper we describe its application to evaluating the cost-effectiveness of HPV vaccination in a specific country, France.

Methods

Model design

The model is a lifetime Markov cohort model developed in Microsoft Excel, based on a previously published model (Debicki et al. 2008) with some simplifications to facilitate its transposition to different settings (Debicki et al. 2008). The model consists of three modules.

  • Natural history, with nine health states (no HPV, oncogenic HPV, CIN stage 1, CIN stage 2/3, persistent CIN stage 2/3, cervical cancer, cancer cured, cervical cancer death, death from other cause)

  • Screening, with two additional health states (detected CIN stage 1, detected CIN stage 2/3)

  • Vaccination, which alters the transition probability for moving from the ‘no HPV’ health state to the ‘oncogenic HPV’ health state, based on vaccine efficacy data

The screening module allows the modelling of different screening patterns, such as opportunistic screening (irregular) or organised (national program with a fixed screening interval within a given age range) screening at different ages and intervals.

The model has a cycle time of 1 year and is run over a maximum of 96 cycles, representing the lifetime of the cohort of 11 years girls modelled. The 1-year cycle time facilitates the use of country specific available statistical data most frequently reported on an annual basis.

Each health state has an associated cost and utility score [between 0 and 1, quality-adjusted life-years (QALY)]. At the end of the model (96 cycles) the total costs and total QALYs over each year are summed to estimate lifetime outcomes (life-years, cervical cancer cases, cervical cancer deaths, and QALYs) for the cohort.

Input data

The model inputs for the base case are summarised in Table 1, together with the values used for the univariate deterministic sensitivity analyses. Input data were obtained from published literature and/or official reports where possible, and were further validated by a panel of four French experts to insure applicability to the French settings especially for data reported for other countries whenever no French data were available (Table 1).

Table 1 Input data values for base case and sensitivity analyses
Full size table

Transition probabilities

The probability for the transition from persistent CIN stage 2/3 to cervical cancer was estimated by calibrating the model to the observed cancer incidence data (see section on Model calibration and validation). Other transition probabilities were based on published literature, national statistics, current guidelines and expert opinion (Table 1).

Costs

The costs associated with events in the model were estimated from a limited societal perspective (all direct healthcare costs) at 2007 values, and are listed in Table 1. Some of the event costs were based on a treatment algorithm supplied by the experts panel, to which unit costs were applied. For positive detected CIN lesion, it was assumed that most treatment costs would fall in the first year, and costs in subsequent years would only consist of follow-up costs such as more frequent pap smear tests.

Disutility values

A utility value of 1 (no disutility) was assigned to the following health states: no HPV, oncogenic HPV, CIN 1 and CIN 2/3, as the model assumes that no disutility occurs from competing illnesses. A utility value of 0 was assigned to death and death from cervical cancer by definition. The disutility values, estimated over a 1 year period, for the other health states (detected CIN, cervical cancer and cured cervical cancer) were taken from published sources (Gold et al. 1998; Institute of Medicine 2000; Goldie et al. 2004; Myers et al. 2004; Insinga et al. 2005) and based both on the disutility experienced by the women and the duration of the disease in order to adjust to the 1 year cycle. They are listed in Table 1.

Vaccine efficacy

Vaccine efficacy data were taken from clinical trials and include cross protection (vaccine efficacy against non vaccine HPV types i.e., non HPV 16 and 18) assuming a reduction only in new infections (from no HPV to HPV) and no effect on existing infections or lesions. Vaccine efficacy was differentiated for females in pre- (HPV naïve) versus post-HPV exposure condition (Total Vaccinated Cohort DNA negative irrespective of HPV sero-status data (TVC DNA neg)). A cut-off date of 17 years of age was selected to differentiate between pre- and post exposure based on the average age of sexual debut in France (Wellings et al. 2006). That info was combined with data on the proportion of HPV due to these HPV types (WHO/ICO 2010) (and data on cross-protection (protection beyond HPV 16/18) to calculate the overall reduction in cervical cancer and CIN cases, corrected for the lower proportion of CIN cases caused by oncogenic HPV (Debicki et al. 2008), The values used are listed in Table 1.

Discount rate

In the base case scenario, costs were discounted at a rate of 3% and outcomes at a rate of 1.5% (Table 1). The discount rate of 1.5% for outcomes was selected for ethical reasons, as a higher discount rate would undervalue clinical benefits felt by future generations and this was considered unacceptable by the authors. This parameter was tested in sensitivity analysis (Table 1). Differential discount for cost and effect is also applicable in other countries such as Belgium and the Netherlands (ISPOR 2010).

Model calibration and validation

The model was calibrated to the cancer incidence rates reported in the French national registry (Exbrayat 2002), by adjusting the transition probability for persistent CIN 2/3 to cervical cancer. This transition probability was selected for calibration as no data are available about this transition probability and therefore had to be assumed.

The model was tested against the criteria published by the International Society for Pharmacoeconomics and Outcomes Research (ISPOR) (Weinstein et al. 2003). External validity was tested by entering the input data for models previously published by Goldie et al. (1999, 2004; Kohli et al. 2007), and Kulasingam and Myers (2003), and comparing the results.

Analysis

The base case analysis compared the costs and outcomes of a girls cohort receiving screening according to current practice in France with those of a cohort receiving screening plus vaccination at age 12 years. We calculated the incremental cost-effectiveness ratio (ICER), expressed as the incremental cost per QALY gained or per life-year gained for the vaccinated cohort compared with the non-vaccinated cohort.

Specific scenarios such as age at vaccination and the effects of implementing a catch-up programme with vaccination of additional cohorts up to 25 years of age were also investigated assuming constant efficacy across ages.

Sensitivity analysis

Univariate deterministic sensitivity analyses were conducted to assess the effect of uncertainty around the input values on the model output. The values used are listed in Table 1. Most parameters were varied by ±20% from the base case values, with the exception of the vaccine cross-protection rate (minimum of 0%), the vaccine efficacy rates (maximum of 100%), and the screening frequency (±2 years). As the vaccine coverage rate does not affect the ICER (for any change in coverage, the changes in costs and outcomes are proportional so the ICER does not change), this parameter was not varied (Suárez et al. 2008).

A probabilistic sensitivity analysis was performed using @Risk version 5.0 (Palisade Corporation, Ithaca, New York, USA). Distributions were assigned to transition probabilities, costs, utility and vaccine-related data using normal distributions (limited between 0 and 1 for transition probabilities) when confidence intervals were available, and beta distributions ranging from 20% below the base case value to 20% above the base case value otherwise. A total of 5,000 replicates were obtained using these distributions and used to derive a confidence interval (CI) around the ICER and to conduct a multivariate stepwise linear regression analysis. This analysis identifies the variables in the probabilistic analysis that have the largest impact on the ICER result. The regression coefficients measured were normalised and a value of 0 corresponds to no significant relationship between the input variable and the output result. A value of +1 or −1 indicates that a change of +1 or −1 standard deviation in the input variable results in an equivalent change in the output result (Suárez et al. 2008).

Results

Model validation

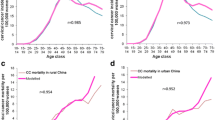
As shown in Fig. 1, the model results closely matched the incidence and mortality data for invasive cervical cancer reported by the French national cancer registry (Exbrayat 2002) for women aged 60–65 years or less, although the model tends to underestimate cancer incidence and mortality at older ages.

Fig. 1
figure 1

Incidence (top) and mortality (bottom) of invasive cervical cancer in France predicted by the model (squares) and observed by the French national cancer registry (Exbrayat 2002) (diamonds)

Full size image

It fully met all the ISPOR criteria except that the model does not account for the time spent in one health state before transition to another state. The model was also able to replicate the results of a previously published model when run with the input data used for this model, further supporting our model’s validity.

Single cohort analysis

Table 2 shows the base case estimated costs, outcomes and ICER for vaccination of a single cohort of 100,000 girls at age 12 years plus current screening compared with current screening alone. Addition of vaccination at age 12 years to current screening would avoid 749 cases of cervical cancer and 244 deaths from cervical cancer and would gain 5,819 life-years and 6,723 QALYs, compared with screening alone. The estimated discounted ICER was €9,706/QALY. Discounting had a major effect on the results. Without discounting, the estimated ICER would be €309/QALY Table 2.

Table 2 Cost-effectiveness in a single cohort of 100,000 girls vaccinated at age 12 years, base case
Full size table

Effect of age at vaccination

Figure 2 shows the effect of age at vaccination on the ICER and on the numbers of cervical cancer cases avoided and life-years saved. It can be clearly seen that the estimated benefits of adding vaccination to screening were greatest with vaccination at younger ages (before sexual debut), although substantial benefits still accrue even for vaccination at later ages. Approximately 85% of deaths from invasive cervical cancer would be avoided by vaccination at age 12 years, and for vaccination at age 40 years the corresponding value would be approximately 34%. The estimated ICER was also most favourable when vaccination was carried out at age 12, and this was true regardless of discounting (Fig. 2). At a cost-effectiveness threshold of 50,000€/QALY, vaccination would remain cost effective up to the age of 40 years.

Fig. 2
figure 2

Effect of age at vaccination on incremental cost-effectiveness ratio (ICER) both discounted (DISC) and non discounted (NDISC) (top) and number of life-years (LY) saved and number of cervical cancer cases (CC) prevented (bottom) with vaccination compared to without

Full size image

Multiple cohort analysis

The effects of a catch-up vaccination programme for women up to the age of 25 years were also explored in a multiple cohort analysis. For a one-year vaccination campaign covering girls and women aged 12–25 years, the ICER for adding vaccination to screening was estimated at €13,079 per QALY. For a 20-year campaign, including all new cohorts of 12-year-old girls over the total campaign, the ICER was estimated at €10,465 across the entire multiple cohort.

Sensitivity analysis

Figure 3 shows the results of the univariate sensitivity analysis as a Tornado plot, with each parameter being varied according to the limits shown in Table 1. The discount rate was the most influential parameter. Most other parameters had only a small effect on the ICER.

Fig. 3
figure 3

One-way sensitivity analysis on discounted ICER (€/QALY). CC cervical cancer; CIN cervical intraepithelial neoplasia; HPV human papillomavirus

Full size image

The 95% confidence intervals for the ICER, determined from the probabilistic sensitivity analysis, ranged from €2,376/QALY to €33,978/QALY. Figure 4 shows the regression coefficient for all significant results determined from the multivariate stepwise analyses, displaying the level of impact of each on the discounted ICER. These results showed that the most influential parameters were those related to the disease history: progression and regression from HPV, CIN1 and CIN2/3.

Fig. 4
figure 4

Regression coefficient obtained from multivariate stepwise regression analysis against discounted ICER (R 2 = 82%). CC cervical cancer; CIN cervical intraepithelial neoplasia; HPV human papillomavirus

Full size image

Discussion

Healthcare authorities and policymakers need to evaluate the economic impact of healthcare interventions to decide on the allocation of scarce resources. But not all national or regional authorities have access to detailed information on HPV epidemiology, age-specific sexual behaviour or the patterns of cervical cancer screening and treatment, and this lack of data may make it difficult to investigate the potential impact of cervical cancer vaccines. The model presented here has despite several limitations, important advantages. It requires a limited amount of input data that should be readily available in most countries and regions. It represents a generally applicable tool that can help answer key economic questions on cervical cancer vaccination, such as the effects of age at vaccination, catch-up programmes, or different screening practices. These evaluations may be useful when assessing the potential public health impact of different policy options.

The model showed good agreement with cervical cancer incidence and mortality data reported by the French national cancer registry for women aged <60–65 years, but underestimated both parameters for women in older age groups (Fig. 1). This may be because the registry data reflect current incidence and mortality based on past screening practice, whereas the model projects current screening practice into the future. Improvements in screening practice would be expected to reduce the future incidence of cervical cancer, but this may not yet be fully reflected in current observed data in older age groups who would have been screened according to past practice. We were able to replicate the findings of previously published models when our model was run with their input data, and the present model has been shown to produce results similar to those from a more detailed cohort model when tested with data from four countries (Canada, Italy, Taiwan and UK) (Debicki et al. 2008). The findings therefore indicate that the current model is robust and they give confidence in the cost-effectiveness results of HPV vaccination plus screening compared with screening alone.

The model results presented here show that the addition of vaccination with a bivalent HPV vaccine to current cervical screening practice in France would substantially reduce the incidence of and mortality from cervical cancer, at an estimated ICER of €9,706/QALY from a direct healthcare cost perspective. The greatest benefits and most favourable cost-effectiveness would be obtained with vaccination at younger ages (before sexual debut), but substantial benefits would still be obtained with vaccination at older ages. For example, vaccination at age 40 years would still prevent an estimated 35% of cases of invasive cervical cancer, compared with screening alone. These benefits account for a decrease in vaccine efficacy in previously infected women. As expected for a preventive intervention where benefit occurs many years after the intervention, the results are most sensitive to the discount rate and the parameters related to the natural history of the disease.

Our model has a number of limitations. It is not a dynamic transmission model and therefore does not take into account the benefits of herd protection. It would thus underestimate the true benefit of vaccination in that respect. Other published models of cervical cancer have considered this aspect, but these models require much more detailed data than is readily available in France and more computational power. Also, given a succinct model was used, a trade off had to be made between the complexity of the scenarios investigated and their feasibility. For instance our model does not include HPV type specific health states, therefore complex screening pattern such as including HPV DNA testing (Rogoza et al. 2008) or the effect of HPV type specific lesions could not be investigated. Furthermore, we did not account for type replacement or specifically investigate the effect of vaccination on co-infection. One of the uncertainties about HPV vaccination is indeed whether other HPV types will replace the HPV types targeted by the vaccines. To date this question cannot be answered, but available evidence suggests that niche competition is unlikely (Stanley et al. 2006). On the other hand by including only one HPV health state we do not face the problem of increasing susceptibility to non protected HPV types with the vaccine as encountered with other models (Goldie et al. 2004). Finally, our analysis focuses on cost-effectiveness analysis. This, however, does not account for issue of budget impact and therefore affordability that can be assessed by the model but is at the end a decision to be taken by the local health authorities.

A recently published study also investigated the cost-effectiveness of HPV vaccination in France, using a quadrivalent HPV vaccine (Bergeron et al. 2008). This study was an adaptation of the model previously published by Kulasingam and Myers (2003), and compared screening plus vaccination at age 14 years with screening alone. The ICER for the addition of vaccination to screening was €13,809/QALY when considering all direct healthcare costs (Bergeron et al. 2008). This is somewhat higher than our finding of €9,706/QALY for the bivalent vaccine, although it should be noted that no study undertook a direct head-to-head comparison of the two products and the results may therefore not be directly comparable.

This paper describes a succinct cohort model that can be used to investigate key economic issues in HPV vaccination for the prevention of cervical cancer. The model results agreed well with observed data in France, as shown here, and indicate that HPV vaccination would be a cost-effective policy option. As the model uses data that are readily available in most countries and regions, it should be generally applicable to the evaluation of the cost effectiveness of HPV vaccination in a variety of settings.