On the Resistance Distance and Kirchhoff Index of $K_n$-chain(Ring) Network

Abstract

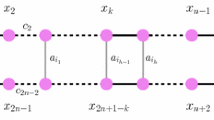
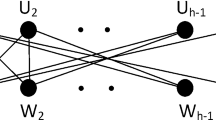
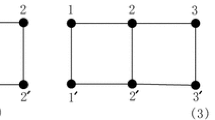
The resistance distance $r_{G}(u,v)$ between two vertices u and v of a graph G is defined as the net effective resistance between them in the electric network constructed from G by replacing each edge with a unit resistor. The Kirchhoff index Kf(G) is defined as the sum of resistance distances between all pairs of vertices. Let $L^{m}_{n}$ be a $K_n$-chain network with m complete graphs. Then identifying the opposite lateral edges of $L^{m}_{n}$ in an order way yields the $K_n$-ring, denoted by $C^{m}_{n}$. In this paper, we first construct a new equivalent network transformation on complete graphs. Then utilize combinatorial and electrical network approaches, we give explicit formula for the resistance distances between any two vertices in $L^{m}_{n}$ and $C^{m}_{n}$. Further, the closed-form formulas of the Kirchhoff index for $L^{m}_{n}$ and $C^{m}_{n}$ are also obtained. In addition, our results contain the main results of [Symmetry. 15(5) (2023) 1122] and [Phys. Scr. 98(4) (2023) 045222] as special cases.

Appendices

Appendix A Proof of Case 5 in Theorem 3.1

Proof

By principle of elimination, we have

$$\begin{aligned} r(u,v)&=r_{L^*}(v,u)=r_{L^*}(v,u_{j})+r_{L^*}(u_{j},v_{i-1})+r_{L^*}(v_{i-1},u)\nonumber \\&=r_{L^*}(v,u_{j})+\sum \limits _{\ k=j}^{i-2} r_{L^*}(u_{k},w_k)+r_{L^*}(u_{i-1},v_{i-1})\\&\quad +\sum \limits _{\ k=j}^{i-2}r_{L^*}(w_{k},u_{k+1})+r_{L^*}(v_{i-1},u) \nonumber \\&=\frac{3}{4(n-1)}-\frac{i-j-1}{n(n-1)}-\frac{1}{2n(n-1)}+\frac{i-j-1}{n-1}+\frac{1}{n} \nonumber \\&=\frac{i-j}{n}+\frac{3n-2}{4n^{2}-4n}.\nonumber \end{aligned}$$

The proof is complete. $\square$

Appendix B Proof of Case 5 in Theorem 3.2

Proof

By carrying out series and parallel principles to simplify network $C^*$, we obtain the isomorphic equivalent network $H^{*}$ as shown in Fig. 11a, where

$R_{H^{*}}(u,v_{i})=\frac{1}{n}; R_{H^{*}}(u_j,x_j)= R_{H^{*}}(u_j,y_j)=R_{H^{*}}(x_j,w_{j-1})=R_{H^{*}}(y_j,w_{j-1})=\frac{1}{n-1};$

$R_{H^{*}}(v_{i},u_j)=\frac{i-j}{n}-\frac{1}{2n^{2}-2n}$; $R_{H^{*}}(v_{i},w_{j-1})=\frac{m-i+j-1}{n}-\frac{1}{2n^{2}-2n}$.

Without loss of generality, let $v=x_j$. Then we replace the path $u_{j}y_{j}w_{j-1}$ by a new edge $u_{j}w_{j-1}$ of weight $\frac{2}{n-1}$. Since $\{x_{j},u_{j},w_{j-1}\}$ form a $\triangle$-network in Fig. 11a, we make $\triangle -Y$ transformation to it by replacing the $\triangle$-network $\{x_{j},u_{j},w_{j-1}\}$ with a Y-network with center $o_j$, then we obtain the final network $H^{\star }$, see Fig. 11b, where

$R_{H^{\star }}(u,v_{i})=\frac{1}{n}$; $R_{H^{\star }}(o_j,x_j)=\frac{1}{4n-4};$

$R_{H^{\star }}(v_{i},u_j)=\frac{i-j}{n}-\frac{1}{2n^{2}-2n}$; $R_{H^{\star }}(v_{i},w_{j-1})=\frac{m-i+j-1}{n}-\frac{1}{2n^{2}-2n}$;

$R_{H^{\star }}(u_j,o_j)=R_{H^{\star }}(w_{j-1},o_j)=\frac{1}{2n-2}$.

By simple calculation, we have

$$\begin{aligned} r(u,v)&=r_{H^{\star }}(u,v)=r_{H^{\star }}(u,v_{i})+r_{H^{\star }}(v_i,o_{j})+r_{H^{\star }}(o_j,x_j)\nonumber \\&=\frac{1}{n}+\frac{1}{4n-4}+\frac{[2(m-i+j-1)+1][2(i-j)+1]}{4mn}.\nonumber \end{aligned}$$

The proof is complete. $\square$