One-Bit DOA Estimation Using Cross-Dipole Array

Abstract

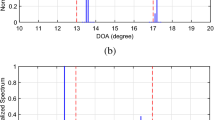
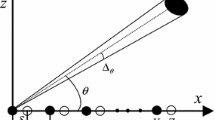
In this paper, we devise an effective algorithm for direction-of-arrival (DOA) estimation using the cross-dipole array via one-bit quantization. Firstly, we theoretically prove that after one-bit quantization, two circular complex Gaussian random processes with different variance still satisfy the arcsine law and calculate the normalized covariance matrix of the cross-dipole array output based on this property. Subsequently, we reconstruct the noise-free normalized covariance matrix by subtracting the normalized noise matrix. Finally, we apply the TLS-ESPRIT algorithm to the reconstructed noise-free normalized covariance matrix to extract the DOAs of sources. Numerical results demonstrate the validity of the proposed algorithm.

Appendix A: Proof of (17)

Assume that X and Y are two real-value zero-mean Gaussian random variables with variances $\sigma ^2_X$ and $\sigma ^2_Y$, respectively. The joint probability density function of X and Y is given by

$$\begin{aligned} f_{XY}(x,y)=\frac{1}{2\pi \sigma _X\sigma _Y\sqrt{1-\rho ^2}} e^{-\frac{1}{2(1-\rho ^2)}\left( \frac{x^2}{\sigma ^2_X}-2\rho \frac{xy}{\sigma _X\sigma _Y} +\frac{y^2}{\sigma ^2_Y}\right) } \end{aligned}$$

(28)

where $\rho =E\{XY\}/\sigma _X\sigma _Y$ denotes the cross-correlation coefficient. With one-bit quantization, the amplitudes of X and Y are $X^{[1b]}=\textrm{sign}(X)$ and $Y^{[1b]}=\textrm{sign}(Y)$, and then the cross-correlation function is expressed as

$$\begin{aligned} R=\frac{1}{2\pi \sigma _X\sigma _Y\sqrt{1-\rho ^2}} \int _{-\infty }^{+\infty }\int _{-\infty }^{+\infty }X^{[1b]}Y^{[1b]} e^{\alpha }\,dx\,dy \end{aligned}$$

(29)

where

$$\begin{aligned} \alpha =-\frac{1}{\sqrt{1-\rho ^2}}\left[ \frac{x^2}{\sigma ^2_X} -2\rho \frac{xy}{\sigma _X\sigma _Y}+\frac{y^2}{\sigma ^2_Y}\right] . \end{aligned}$$

(30)

Introducing ellipse polar coordinates $X=\sigma _Xr\cos (\phi )$ and $Y=\sigma _Yr\sin (\phi )$, (29) can be simplified as [17]:

$$\begin{aligned} R=\frac{2}{\pi }\textrm{arcsin}\rho . \end{aligned}$$

(31)

Next, we consider two zero-mean CCGPs $\tilde{X}(t)$ and $\tilde{Y}(t)$ with variances $\sigma ^2_{\tilde{X}}$ and $\sigma ^2_{\tilde{Y}}$, respectively. Denoting $\tilde{X}^{[1b]}(t)$ and $\tilde{Y}^{[1b]}(t)$ as the result of $\tilde{X}(t)$ and $\tilde{Y}(t)$ after one-bit quantization, the cross-correlation function of $\tilde{X}^{[1b]}(t)$ and $\tilde{Y}^{[1b]}(t)$ is computed as

$$\begin{aligned}&R_{\tilde{X}\tilde{Y}}(\tau )^{[1b]}\nonumber \\&\quad =E\{\tilde{X}^{[1b]}(t)[\tilde{Y}^{[1b]}(t+\tau )]^*\}\nonumber \\&\quad =E\bigg \{\frac{1}{\sqrt{2}}\big (\tilde{X}^{[1b]}_c(t) +j\tilde{X}^{[1b]}_s(t)\big )\nonumber \\&\qquad \cdot \frac{1}{\sqrt{2}}\big (\tilde{Y}^{[1b]}_c(t+\tau ) -j\tilde{Y}^{[1b]}_s(t+\tau )\big )\bigg \}\nonumber \\&\quad =\frac{1}{2}\big (R_{\tilde{X}_c,\tilde{Y}_c}^{[1b]}(\tau ) +R_{\tilde{X}_s,\tilde{Y}_s}^{[1b]}(\tau )\big )\nonumber \\&\qquad +\frac{1}{2}j\big (R_{\tilde{X}_s,\tilde{Y}_c}^{[1b]}(\tau ) -R_{\tilde{Y}_c,\tilde{Y}_s}^{[1b]}(\tau )\big ). \end{aligned}$$

(32)

Each term in the last row of (32) satisfies the arcsine law. Thus, we have

$$\begin{aligned}&R_{\tilde{X}\tilde{Y}}^{[1b]}(\tau )\nonumber \\&\quad =\frac{1}{2}\Bigg (\frac{2}{\pi }\textrm{arcsin} \bigg (\frac{R_{\tilde{X}_c,\tilde{Y}_c}(\tau )}{\tfrac{1}{2} \sigma _{\tilde{X}}\sigma _{\tilde{Y}}}\bigg ) +\frac{2}{\pi }\textrm{arcsin}\bigg (\frac{R_{\tilde{X}_s, \tilde{Y}_s}(\tau )}{\tfrac{1}{2}\sigma _{\tilde{X}} \sigma _{\tilde{Y}}}\bigg )\Bigg )\nonumber \\&\qquad +\frac{1}{2}j\Bigg (\frac{2}{\pi }\textrm{arcsin} \bigg (\frac{R_{\tilde{X}_s,\tilde{Y}_c}(\tau )}{\tfrac{1}{2} \sigma _{\tilde{X}}\sigma _{\tilde{Y}}}\bigg )-\frac{2}{\pi } \textrm{arcsin}\bigg (\frac{R_{\tilde{X}_c,\tilde{Y}_s}(\tau )}{\tfrac{1}{2}\sigma _{\tilde{X}}\sigma _{\tilde{Y}}}\bigg )\Bigg ). \end{aligned}$$

(33)

For two CCGPs, the following equations hold:

$$\begin{aligned} R_{\tilde{X}_c,\tilde{Y}_c}(\tau )&= R_{\tilde{X}_s,\tilde{Y}_s}(\tau ) \end{aligned}$$

(34)

$$\begin{aligned} R_{\tilde{X}_s,\tilde{Y}_c}(\tau )&= -R_{\tilde{X}_c,\tilde{Y}_s}(\tau ) \end{aligned}$$

(35)

Substituting (34) and (35) into (33) yields

$$\begin{aligned}&R_{\tilde{X}\tilde{Y}}^{[1b]}(\tau )\nonumber \\&\quad =\frac{2}{\pi }\textrm{arcsin}\bigg (\frac{2R_{\tilde{X}_c, \tilde{Y}_c}(\tau )}{\sigma _{\tilde{X}}\sigma _{\tilde{Y}}}\bigg ) +j\frac{2}{\pi }\textrm{arcsin}\bigg (\frac{2 R_{\tilde{X}_s, \tilde{Y}_c}(\tau )}{\sigma _{\tilde{X}}\sigma _{\tilde{Y}}}\bigg )\nonumber \\&\quad =\frac{2}{\pi }\textrm{arcsin}\bigg (\frac{R_{\tilde{X}_c,\tilde{Y}_c} (\tau )+R_{\tilde{X}_s,\tilde{Y}_s}(\tau )}{\sigma _{\tilde{X}} \sigma _{\tilde{Y}}}\bigg )\nonumber \\&\quad +j\frac{2}{\pi }\textrm{arcsin}\bigg (\frac{ R_{\tilde{X}_s, \tilde{Y}_c}(\tau )-R_{\tilde{X}_c,\tilde{Y}_s}(\tau )}{\sigma _{\tilde{X}}\sigma _{\tilde{Y}}}\bigg )\nonumber \\&\quad =\frac{2}{\pi }\textrm{arcsin}\bigg (\frac{\Re \big (R_{\tilde{X},\tilde{Y}}(\tau )\big )}{\sigma _{\tilde{X}} \sigma _{\tilde{Y}}}\bigg )+j\frac{2}{\pi }\textrm{arcsin} \bigg (\frac{\Im \big (R_{\tilde{X},\tilde{Y}}(\tau ) \big )}{\sigma _{\tilde{X}}\sigma _{\tilde{Y}}}\bigg ) \end{aligned}$$

(36)

Evidently, two CCGPs with different variance also satisfy the arcsine law.