1 Introduction

The prevalence of smart devices in our daily lives has pushed for an unprecedented demand on audio communication systems. As such, the need for a seamless speech communication system on such devices especially in noisy environments is highly sought after. An effective way to enhance noisy speech is via single channel speech enhancement techniques [1, 6, 7]. From the ideas of spectral subtraction by Boll [1], more optimal methods were developed that optimize MMSE and log MMSE errors [6, 7]. Those methods have highlighted the two main tasks associated with single channel processing which are noise suppression and speech preservation. However, it is a challenge to achieve both tasks optimally as suppression and distortion are conflicting measures, which results in a natural trade-off [13, 14, 19, 20]. For instance, if the noise estimator makes an erroneous estimation in the noise statistics, it will cause a mismatch in the noise suppression function. This in turn generates annoying musical artefacts, which reduce the overall perceptual quality of the enhanced speech [1, 12, 18]. An efficient way to combat the musical noise problem is to improve the noise spectrum estimation [3, 8, 12]. By using a soft voice activity detector idea based on the speech presence probability (SPP), significant improvement of the noise spectrum estimation was achieved. Yong et al. [22] further improved upon those results by using a modified sigmoid function which incorporates an a-priori SNR estimate to reduce the latency of the real-time SNR estimation. The modified decision directed approach [23] overcomes the one-frame delay problem when estimating the a-priori SNR by matching the estimated clean speech spectrum with the a-priori SNR as opposed to the previous frame. The reduction in SNR estimation’s latency results in greater noise suppression and generates less musical noise.

While [22, 23] outlined a means to improve the SNR estimation, the method still employed the a-priori SNR estimate which was computationally complex and often gave large variations in the estimate for non-stationary background noise. Enzner [4] addressed the a-priori SNR problem by using a Bayesian Marginalization technique, but this required a lot of pre-training. In addition, it required the estimation of the global a-priori SNR of the speech data for each SNR. The result from this is a look up table that can be related to the posteriori SNR. Enzner did not device a way to address the noise estimation problem.

In this paper, we propose to overcome the aforementioned problems by using the modified sigmoid function to approximate both the speech presence probability (SPP) and the speech enhancement gain function and illustrated through the Wiener filter. The benefit is twofold. First, by applying an approximation via the sigmoid functions it is shown that only the posteriori estimate of SNR is needed, resulting in a lower complexity system which does not require the a-priori SNR estimation. Secondly, since only the posteriori information is needed, the proposed method can directly measure the variations in non-stationary noise scenarios, thereby reducing its sensitivity to large variations typically observed in non-stationary noise. The sigmoid function is designed with four parameters to be optimized. This paper further employs an efficient optimization algorithm, which optimizes the parameters of the sigmoid function with respect to speech quality measures. By incorporating speech quality measures in the optimization, the set of optimized parameters yield the best possible perceptually enhanced and intelligible speech. The optimization algorithm is based on the idea that the solution obtained for a given problem should move towards the best solution and avoid the worst solution. The proposed algorithm requires minimal control parameters and does not require any algorithm specific parameters.

Simulation results shows the comparison in performance of several speech quality measures, namely the perceptual evaluation of speech quality (PESQ) measure [17], the short-time objective intelligibility (STOI) measure [21] and the log-likelihood ratio (LLR) [15] for (i) the decision directed, (ii) modified decision directed, (iii) and the system with the sigmoid functions for both the gain function and the speech present probability. The proposed method is tested on some of the common types of noise, namely the babble, factory, pink and white noise. The set of sigmoid function coefficients are optimized with 0 dB SNR and the system is tested for various SNR. The results demonstrate that the proposed sigmoid functions achieve better results in terms of PESQ, STOI and LLR when compared with existing methods, namely the decision directed and modified decision directed with low complexity. In addition, a trade-off between PESQ, STOI and LLR performance can be achieved between the two proposed optimized sigmoid gain functions.

The paper is organized as follows: The system mode and the gain function are discussed in Sect. 2. The a-priori SNR estimation and the speech present probability are investigated in Sect. 3. The proposed system with the sigmoid function model for both the SPP and the gain function is given in Sect. 4. The optimization procedure is given in Sect. 5. Simulation results are given in Sect. 6, and finally, the conclusions are in Sect. 7.

2 System Model and the Gain Function

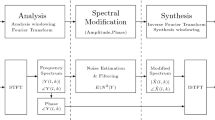
The goal of speech enhancement scheme is to estimate the enhanced speech signal \({\hat{x}}(n)\), given a noisy signal \(y(n)=x(n)+v(n)\), where x(n) and v(n) denote the clean speech signal and the noise, respectively. By applying the short-time Fourier transform (STFT) to the time data, the STFT of the noisy signal is given as

$$\begin{aligned} Y\left( k,m\right) =X\left( k,m\right) +V\left( k,m\right) \end{aligned}$$
(1)

where \(X\left( k,m\right) \) and \(V\left( k,m\right) \) denote the STFT of the clean speech signal \(x\left( n\right) \) and the uncorrelated additive noise \(v\left( n\right) \), respectively [6, 7]. Here, k is the frequency bin index and m is the frame index. The estimated clean speech spectrum \({\hat{X}}(k,m)\) is then obtained as

$$\begin{aligned} {\hat{X}}(k,m)=G(k,m)Y(k,m) \end{aligned}$$
(2)

where G(k, m) is a spectral gain function. Our objective is to obtain an efficient and low complexity method to estimate the gain function G(k, m). In the following, we discuss the methods to estimate G(k, m).

The gain function G(k, m) is often derived from MMSE or Log-MMSE optimization criteria [6, 7], which requires the estimation of the a-priori SNR. One popular MMSE method results in the Wiener filter [19], where the again function can be computed as

$$\begin{aligned} G_{\text {WF}}(k,m)=\frac{\xi (k,m)}{1+\xi (k,m)} \end{aligned}$$
(3)

and \(\xi (k,m)\) is the a-priori SNR, obtained as

$$\begin{aligned} \xi (k,m)=\frac{\lambda _{x}(k,m)}{\lambda _{v}(k,m)}. \end{aligned}$$
(4)

Here, \(\lambda _{x}(k,m)\) and \(\lambda _{v}(k,m)\) represent the clean speech power spectral density and the noise power spectral density, respectively, which are unknown in practice and hence required to be estimated.

The gain function derived using the Log-MMSE criteria also requires the estimation of the a-priori SNR [24]. In [2, 24], the sigmoid function was investigated as the function of the a-priori SNR to model the gain function G(k, m). However, the estimation of the a-priori SNR is often computationally complex [2]. In the following, we will discuss the estimation of the a-priori SNR and the speech presence probability that is used to estimate the noise power spectral density in (4).

3 A-priori SNR Estimation and the Speech Presence Probability

In [5], the a-priori SNR is estimated using the decision direction (DD) method,

$$\begin{aligned} {\hat{\xi }}_{DD}(k,m)=\max \left\{ \beta \frac{|{{\hat{X}}}(k,m-1)|^2}{\hat{\lambda _{v}}(k,m)} + (1-\beta )P[\gamma (k,m)-1],\epsilon _0 \right\} \end{aligned}$$
(5)

where \({\hat{X}}(k,m-1)\) and \(\hat{\lambda _{v}}(k,m)\) denote, the estimated clean speech spectrum and the estimated noise PSD, respectively. In addition, the parameter \(\beta \) denotes the smoothing factor, \(P[\cdot ]\) denotes the half-wave rectification and \(\epsilon _o\) is the SNR floor. Here, \({\gamma }(k,m)\) is the \(\textit{a-posteriori}\) SNR obtained as

$$\begin{aligned}{\gamma }(k,m)=\dfrac{|Y(k,m)|^{2}}{{\lambda _{v}}\left( k,m\right) }.\end{aligned}$$

The modified decision direction method (MDD) was developed in [24] for the estimation of the a-priori SNR to improve further the speech quality of the DD method. The main difference between the MDD and DD methods is the estimation of the a-priori SNR which requires the use of the gain function \(G(k,m-1)\) in the previous iteration to estimate \({\hat{X}}(k,m-1)\),

$$\begin{aligned} {\hat{\xi }}_{MDD}(k,m)=\max \left\{ \beta \frac{|G(k,m-1)Y(k,m)|^2}{\hat{\lambda }_v(k,m)} + (1-\beta )P[\gamma (k,m)-1],\epsilon _0 \right\} . \end{aligned}$$
(6)

In addition, the estimations in (5) and (6) require the estimation of the a-posteriori SNR and the noise power spectral density \(\lambda _{v}(k,m)\). One common method of estimating \({\lambda }_{v}(k,m)\) is applying a temporal recursive smoothing to the noisy observation using the speech presence probability (SPP) p(k, m) [3, 11],

$$\begin{aligned} {\lambda }_{v}\left( k,m\right)&=p(k,m){\lambda }_{v}\left( k,m-1\right) +\left( 1-p(k,m)\right) ||Y(k,m)||^2. \end{aligned}$$
(7)

Assuming both \(X\left( k,m\right) \) and \(V\left( k,m\right) \) have Gaussian distributions, then the SPP is given by [3],

$$\begin{aligned} p(k,m)=\left\{ 1+\left( 1+\xi (k,m)\right) Q\exp \left( -{\gamma \left( k,m\right) }\frac{\xi \left( k,m\right) }{1+\xi \left( k,m\right) }\right) \right\} ^{-1} \end{aligned}$$
(8)

where \(Q=\dfrac{P\left( {\mathcal {H}}_{0}\right) }{P\left( {\mathcal {H}}_{1}\right) }\) is the ratio between \(P\left( {\mathcal {H}}_{0}\right) \) the \(\textit{a-priori}\) probability for speech absence and \(P\left( {\mathcal {H}}_{1}\right) \) the probability for speech presence.

It can be seen that the speech presence probability p(k, m) yields a value that is close to one when \({\gamma }(k,m)\) is sufficiently large and is small otherwise. In between zero and one, a soft transition for SPP is desired. As such, a sigmoid function is employed for the SPP in Eq. (8) [23] as a function of the estimated a-posteriori SNR \({\gamma }(k,m)\) and fixed coefficients

$$\begin{aligned} p_{\text {sig}}(k,m)=\frac{1}{1+e^{-c_{\text {sig}}\left( {\gamma }(k.m)-d_{\text {sig}}\right) }} \end{aligned}$$
(9)

where \(c_{\text {sig}}\) and \(d_{\text {sig}}\) indicate, respectively, the slope and the mean of the sigmoid function, given by

$$\begin{aligned} c_{\text {sig}}=\frac{\xi _{{{\mathcal {H}}}_{1}}}{1+\xi _{{{\mathcal {H}}}_{1}}},\;\;d_{\text {sig}}=\log \left( Q\left( 1+\xi _{{{\mathcal {H}}}_{1}}\right) \right) \frac{1+\xi _{{{\mathcal {H}}}_{1}}}{\xi _{{{\mathcal {H}}}_{1}}}. \end{aligned}$$
(10)

The value \(\xi _{{{\mathcal {H}}}_{1}}\) denote the a-priori SNR when speech is present.

The estimations of the a-priori SNR \(\xi \left( k,m\right) \) and the speech presence probability in (5), (6), (8) are computational expensive and can be sensitive to large variations in the noise estimate. From (8), it is evident that if only the a-posteriori SNR \(\gamma (k,m)\) is used, it is easier to control the variations in the noise power. Thus, we propose to model \(G\left( k,m\right) \) estimation based on the a-posteriori SNR \(\gamma \left( k,m\right) \) for each frequency bin k and time instance m. This will result in a lower complexity estimator as only the noise and noisy speech are required to be estimated. In addition, a general sigmoid function is proposed for the SPP in (9) and the sigmoid function coefficient will be optimized to improve the performance.

4 The Proposed Gain Function and Speech Presence Probability

In this section, we propose to approximate the gain function and the speech presence probability as general sigmoid functions of the a-posteriori SNR \(\gamma \left( k,m\right) \). The gain function for each frequency bin k and instant time m can be obtained as

$$\begin{aligned} G_{\text {SIG}}(k,m)=\max \left\{ \frac{2}{1+e^{-a({\gamma }(k,m)-b)}}-1,0\right\} . \end{aligned}$$
(11)

where a and b are some constants. In addition, the speech presence probability can also be modelled as a general sigmoid function

$$\begin{aligned} p_{\text {SIG}}(k,m)=\frac{1}{1+e^{-c\left( \gamma (k,m)-d\right) }}. \end{aligned}$$
(12)

where c and d are constant parameters, which can be optimized. This will result in lower complexity for the estimation as the a-posterior SNR \(\gamma (k,m)\) is much easier to estimate.

It has been reported in [23] that if the SPP estimate p(k, m) is used directly in Eq. (8), then the noise estimate becomes more noisy due to large variations in p(k, m) which modulates the noise estimate. One way to reduce this variability is to smooth \(\gamma (k,m)\) or p(k, m). However, the smoothing results in extra delay, which reduces its noise tracking capability. Here, we quantize \(p_{\text {appr}}(k,m)\) into four different regions, i.e.,

$$\begin{aligned} p'={\left\{ \begin{array}{ll} \text {noise only presence},\mathcal{P}_{1}, &{} p_{\text {appr}}\le p_{1}\\ \text {likely speech presence},\mathcal{P}_{2}, &{} p_{1}<p_{\text {appr}}\le p_{2}\\ \text {more likely speech presence},\mathcal{P}_{3}, &{} p_{2}<p_{\text {appr}}\le p_{3}\\ \text {most likely speech presence},\mathcal{P}_{4}, &{} p_{\text {appr}}\ge p_{3} \end{array}\right. } \end{aligned}$$
(13)

where \(0<p_{1}<p_{2}<p_{3}\le 1\) are different values of the sigmoid function, they correspond to an instantaneous estimate of the SPP. These quantized values are mapped to different averaging smoothing constant. For the region where speech is less likely to present, i.e. when \({\gamma }\approx 1\) (this means 0 dB), the averaging constant for the noise estimation should be fast. The result is an even smoothed estimate compared to the original noise PSD estimate when \({\gamma }\) is small, which reduces the likelihood of noise being overestimated and underestimated locally. For the regions where speech is either more likely or most likely to present, the soft transitions of \(p_{\text {appr}}\) might not be sufficient for the noise PSD estimate to change from using the previous noise PSD estimates to tracking the current noisy observations and vice versa. Accordingly, to avoid those pitfalls, quantized decisions are imposed on \(p_{\text {appr}}\) to realize an improved posterior SPP estimate.

Now we have replaced the a-priori SNR with the posterior SNR through our approximation. How well the approximation works for the Wiener filter (3) and the SPP in Eq. (8) is shown in an example, by choosing the coefficients \(\textbf{x}=[a~b~c~d]=[1 ~1~1~1]\) and \(Q=0.5\), see Figs. 1 and 2. It can be seen that the approximation is very close for the SPP and relatively close for the Wiener filter approximation with the sigmoid approximation being slightly more aggressive for \(a=1\).

Fig. 1
figure 1

Approximation of the Wiener filter using Eq. (11) with \(a=1\) and \(b=1\)

Full size image
Fig. 2
figure 2

Approximation of the speech presence probability \(q=0.5\) in Eq. (8) using Eq. (12) with \(a=1\) and \(b=1\)

Full size image

However, the main benefit is that we can optimize these coefficients based on data which generalizes them to a more flexible data based functions. Hence, we investigate on how to optimize the coefficient vector for unknown, \(\textbf{x}=[a~b~c~d]\). It is proposed that the optimization is made with respect to the maximum achievable speech quality measures as that will naturally provide the best objective evaluated enhanced speech. In general, the speech quality assessment can be classified in terms of subjective and objective measures. Subjective evaluation involves subjective listening test by some listeners while objective evaluation measures the numerical distance between the reference signal and the processed signal. One established method of evaluating the enhanced signal is using perceptual evaluation of speech quality (PESQ). PESQ is an automatic computation algorithm to replace human subjects in the evaluation of the mean opinion score (MOS). The PESQ model considers how human perceive speech and it has been widely used in the evaluation of speech quality. Another popular measure is the short-time objective intelligibility (STOI) measure, which highly correlates with the intelligibility of speech. By optimizing with respect to both PESQ and STOI, the parameters are optimized to give the speech an overall quality improvement and speech intelligibility. Thus, a multi-objective optimization problem can be formulated with PESQ and STOI as the objective measure,

$$\begin{aligned} \left\{ \begin{array}{lll} \max ~~ f(\textbf{x})=\text {PESQ}(\textbf{x})+\alpha \text {STOI}(\textbf{x})\\ \text{ subject } \text{ to } ~~~\textbf{x}_{l}\le \textbf{x}\le \textbf{x}_{u} \end{array}\right. \end{aligned}$$
(14)

where \(\textbf{x}_{l}\) and \(\textbf{x}_{u}\) are the lower and the upper bounds for the coefficient vector \(\textbf{x}\), respectively, and \(\alpha \) is the weighting constant. Different value of \(\alpha \) results in different optimal solution for the Pareto optimality, allowing the trade-off between the two objective measures.

5 Optimization Procedure

In this paper, the Jaya method [16] with a modified stopping criteria is employed to obtain the optimal solution to the optimization problem (14). At any iteration k, we have N number of candidate solutions. Let the best candidate obtain the best value of \(f(\textbf{x})\) and the worst candidate obtain the worse value of \(f(\textbf{x})\),

$$\begin{aligned} \begin{array}{lll} \textbf{x}_{best,k} &{} =\text{ arg }\max \limits _{i}f(\textbf{x}_{k,i})\\ \textbf{x}_{worse,k} &{} =\text{ arg }\min \limits _{i}f(\textbf{x}_{k,i}). \end{array} \end{aligned}$$
(15)

The coefficient vectors of the \(k+1\) iteration are given as

$$\begin{aligned} \textbf{x}_{k+1,i}=\textbf{x}_{k,i}+r_{1,k,i}\left( \textbf{x}_{best,k}-|\textbf{x}_{k,i}|\right) +r_{2,k,i}\left( \textbf{x}_{worst,k}-|\textbf{x}_{k,i}|\right) \end{aligned}$$
(16)

where \(r_{1,k,i}\) and \(r_{2,k,i}\) are random numbers in the range [0, 1]. The first term in Eq. (16) indicates the tendency for the solution to move closer to the best solution while the second term indicates the tendency to avoid the worst solution. \(\textbf{x}_{k+1,i}\) is accepted if it gets a better solution. The algorithm stops if the difference in the optimal objective function between the two consecutive iterations is small. The steps for the optimization algorithm are summarized in Procedure 1.

Procedure 1: Optimization algorithm

  • Step 1: Initialize the coefficient vector \(\textbf{x}_{0,i},~1\le i\le N\) for the 0\(^{\text {th}}\) iteration. Set \(k=0\).

  • Step 2: Calculate the objective function \(f(\textbf{x}_{k,i})\). Obtain the best and the worse solutions \(\textbf{x}_{best,k}\) and \(\textbf{x}_{worst,k}\) as in (15).

  • Step 3: Obtain the new set of coefficient vectors for the \(k+1\) iteration as in (16). For all the value \(1\le i\le N\), if \(f(\textbf{x}_{k+1,i})<f(\textbf{x}_{k,i})\), then set \(\textbf{x}_{k+1,i}=\textbf{x}_{k,i}\). Otherwise, \(\textbf{x}_{k+1,i})\) remains the same as before.

  • Step 4: The algorithm converges if there is no improvement in the maximum objective function or the maximum number of iterations is reached. Otherwise, set \(k:=k+1\) and return to Step 2.

6 Experimental Results

For the objective evaluation, the noisy speech corpus NOIZEUS with 30 IEEE speech sequences were employed [9, 10]. The database was chosen as it was developed to facilitate for algorithm comparison purpose. More information about the NOIZEUS can be found in [9]. The noisy speech was corrupted with babble, factory, pink and white noise for a wide range of SNRs. All the results are generated with \(K=256\) frequency bins with a sampling frequency of \(f_{s}=8000\). A square-root Hanning window was used with 50% overlap. Simulations are evaluated with

$$\begin{aligned} p'={\left\{ \begin{array}{ll} {{\mathcal {P}}}_{1}, &{} \,p_{\text {appr}}\le 0.55\\ {{\mathcal {P}}}_{2}, &{} \,0.55<p_{\text {appr}}\le 0.7\\ {{\mathcal {P}}}_{3}, &{} \,0.7<p_{\text {appr}}<0.8\\ {{\mathcal {P}}}_{4} &{} p_{\text {appr}}>0.8 \end{array}\right. } \end{aligned}$$

where \({{\mathcal {P}}}_{i}=\exp \left( -2.2R\right) /\left( t_{i}f_{{{\mathcal {s}}}}\right) \) indicates the exponential smoothing constant, with \(i=[1,2,3,4]\). Here, R indicates the STFT frame rate, \(t_{i}\) denotes the averaging time constant, with \(t_{1}<t_{2}<t_{3}\ll t_{4}\). This means that the averaging time is mapped to the speech presence probability but the averaging times and thresholds can be modified.

To evaluate the performance of the proposed sigmoid gain function and proposed SPP, the problem (14) is optimized for the different type of noise, namely the babble, factory, pink and white noise, with signal-to-noise ratio of 0 dB. For each type of noise, the optimal set of coefficient is then tested for different levels of SNR. The SNR level is increased from −5 dB to 10 dB. The results are compared with those obtained from the decision directed method and the modified decision directed method. As mentioned earlier, the proposed method has significantly lower complexity than both the decision directed and modified decision directed methods as it does not require the estimation of the a-priori SNR.

Table 1 PESQ, STOI and LLR performance for different SNR with babble noise and \(K=256\)
Full size table

6.1 Performance Comparison Between the Proposed Method, The Decision Direct Method and the Modified Decision Directed Method

Table 1 shows the PESQ, STOI and LLR results for different speech enhancement methods: (i) the decision directed; (ii) the modified decision directed [22] and (iii) the result with the optimized gain function \(G_{\text {SIG}}\) and the weighting constant \(\alpha =0\). The coefficients for the gain function \(G_{\text {SIG}}\) are optimized with SNR\(=0\) dB and the results are tests for different SNR levels and babble noise. It can be seen from the table that the modified decision direct improves the PESQ, STOI and LLR results over the decision directed method. In addition, the optimized sigmoid gain function together with the sigmoid SPP improves the PESQ, STOI and LLR values further over the modified decision directed method. For example, at \(-5\) dB SNR level, the optimized method with gain function \(G_{\text {SIG}}\) improves 0.2158 dB for PESQ over the decision directed method and 0.2041 dB over the modified decision directed method. For STOI measure, the optimized method improves 0.0575 dB and 0.0469 dB, respectively, over the decision directed and the modified decision directed methods. For the LLR measure, the optimized method is 0.24 dB and 0.168 dB lower than the decision directed and the modified decision directed methods, which means that the optimized method performs better than the other two methods. For other SNRs, the optimized method with sigmoid gain functions \(G_{\text {SIG}}\) also has significant improvement for PESQ, STOI and LLR over the decision directed and modified decision directed methods.

Table 2 PESQ, STOI and LLR performance for different SNR with factory noise and \(K=256\)
Full size table
Table 3 PESQ, STOI and LLR performance for different SNR with pink noise and \(K=256\)
Full size table
Table 4 PESQ, STOI and LLR performance for different SNR with white noise and \(K=256\)
Full size table

Tables 2, 3 and 4 show the results for the factory noise, pink noise and white noise for different SNR and different gain function methods. It can be seen that the optimized gain functions \(G_{\text {SIG}}\) have significant improvement for PESQ, STOI and LLR over the results obtained using the decision directed and the modified decision directed methods. For example, with SNR=\(-5\) dB and white noise, the optimized method with the gain function \(G_{\text {SIG}}\) improves 0.2528 dB and 0.1643 dB for PESQ, respectively, over the decision direct method and the modified decision directed method. For the STOI measure, the optimized method improves 0.0272 dB and 0.0204 dB, respectively, over the decision directed and the modified decision directed methods. For the LLR measure, the optimized method improves 0.09 dB over the decision directed and the modified decision directed methods. For all the cases, the optimization algorithm converges quickly which requires only a few iterations for convergence.

Fig. 3
figure 3

PESQ for different speech enhancement methods with babble noise and different SNR for \(\alpha =0\)

Full size image
Fig. 4
figure 4

STOI for different speech enhancement methods with babble noise and different SNR for \(\alpha =0\)

Full size image
Fig. 5
figure 5

LLR for different speech enhancement methods with babble noise and different SNR for \(\alpha =0\)

Full size image

Figures 3, 4 and 5 show PESQ, STOI and LLR values for different speech enhancement methods with the babble noise and different SNRs. It can be seen that proposed method with the gain function \(G_{\text {SIG}}\) improve the results over the decision directed and the modified decision directed methods.

6.2 Trade-Off Investigation Between Perceptual Measures PESQ, STOI and LLR for Different Weighting Constants \(\alpha \) and Different SNR

We now investigate the Pareto trade-off for different weighting factor \(\alpha \) on the perceptual measures PESQ, STOI and LLR. Table 5 shows the trade-off between PESQ, STOI and LLR values for different weighting constraint \(\alpha \) and the babble noise. The SNR level increases from \(-5\) dB to 10 dB and the weighting constant \(\alpha \) increases from 0 to 15. It can be seen from the table that there is a trade-off between the PESQ and STOI values. The PESQ values decrease when \(\alpha \) increases while the STOI values increase. This is to be expected as the weighting provides an engineering choice between quality and intelligibility through the PESQ and STOI measures, respectively. The LLR values are approximately the same for all the cases with the babble noise. When compared to the decision directed and modified decision directed performance in Table 1, the optimized sigmoid gain function has better PESQ, STOI and LLR performance than the decision directed method and the modified decision directed method.

Table 5 Trade-off between PESQ, STOI and LLR for different weighting function \(\alpha \) with different SNR and babble noise
Full size table
Table 6 Trade-off between PESQ, STOI and LLR for different weighting function \(\alpha \) with different SNR and factory noise
Full size table
Table 7 Trade-off between PESQ, STOI and LLR for different weighting function \(\alpha \) with different SNR and pink noise
Full size table
Table 8 Trade-off between PESQ, STOI and LLR for different weighting function \(\alpha \) with different SNR and white noise
Full size table

Tables 6, 7 and 8 show the PESQ, STOI and LLR results for different SNRs and different weighting constant \(\alpha \) with factory noise, pink noise and white noise, respectively. Similar to the case with the babble noise, when \(\alpha \) increases, the PESQ value decreases while the STOI value increases. It can be seen that the weighting \(\alpha \) provides a trade-off between PESQ and STOI in the objective measures [see Eq. (14)]. As \(\alpha \) increases, more weighting is emphasized towards STOI as opposed to PESQ, which results in a higher value of STOI. The role of \(\alpha \) serves as a trade-off between the two performance measures, which provides flexibility to the user to trade-off between the two measures. The increased of LLR in tandem with alpha shows that LLR is more correlated to STOI, which is related to the measure of speech intelligibility.

In addition, the LLR values improves slightly with a higher value of \(\alpha \). Similar to the babble noise case, the optimized sigmoid gain function achieves good trade-off performance when compared with the decision direct and modified decision directed methods. In addition, the proposed gain function has a lower complexity when compared with existing methods as it does not require the estimation of the a-priori SNR.

Fig. 6
figure 6

Winner filter and optimized Sigmoid function for the gain function with different type of noise. The sigmoid functions are optimized from data at 0 dB

Full size image
Fig. 7
figure 7

Optimized sigmoid function for speech presence probability with different type of noise. The sigmoid functions are optimized from data at 0 dB

Full size image

6.3 Approximation of the Gain Function and the Speech Present Probability using the Sigmoid Function for different Type of Noise

Figures 6 and 7 show the optimal sigmoid functions for the gain function and the speech present probability for different a-posteriori SNR. The optimal sigmoid functions for the gain function and the speech present probably are optimized together from data at 0 dB SNR for different type of noise, namely the babble noise, factory noise, pink and white noises. It can be seen from the figures that the optimized sigmoid function for the gain function and the speech present probability approximations follow the shape of the Wiener filter in Eq. (11) and the speech present probability in (8). In addition, the sigmoid functions for the factory and babble noises are slightly more aggressive than the sigmoid functions for the white and pink noises. The sigmoid functions are then tested for different SNR levels from −5 dB to 10 dB. It can be seen in Sects. 6.1 and 6.2 that the sigmoid models achieve good results for all the cases with a lower computational complexity as it does not require the estimation of the a-priori SNR.

7 Conclusions

This paper proposes the use of sigmoid function for both the speech presence probability (SPP) and the overall gain function of a speech enhancement system as a means to achieve low complexity and efficient implementation. The former serves to better the SNR estimation and the latter provides an overall perceptually smooth gain function. The advantage of the proposed system is that it avoids the estimation the a-priori SNR resulting in an improved noise estimate. An efficient optimization algorithm is employed to solve the optimization problem, which optimizes the parameters of the sigmoid functions with respect to the speech quality measures. The optimization algorithm is based on the idea that the solution obtained for a given problem should move towards the best solution and avoid the worst solution. The presented algorithm requires minimal control parameters and does not require any algorithm specific parameters. Simulation results show that the proposed sigmoid functions achieve improved performance when compared with existing methods with low complexity.