Coarray Polarization Smoothing for DOA Estimation with Coprime Vector Sensor Arrays

Abstract

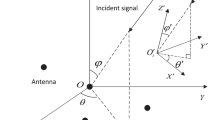
In this paper, the problem of direction-of-arrival (DOA) estimation of multiple sources using a coprime electromagnetic vector sensor (EMVS) array is addressed. Each EMVS consists of three mutually orthogonal electric dipoles and three mutually orthogonal magnetic loops, all collocated at a single point in space. By exploiting the polarization diversities embedded in the vector sensors, the coarray polarization smoothing (COPS) is presented to increase the degrees of freedom (DOFs) from the polarization coarray domain. In contrast to the widely used spatial smoothing technique, the COPS offers the following insights: (1) it is source polarization-dependent and is proved to offer 20 DOFs at most, (2) it does not reduce the efficient spatial coarray aperture of the coprime array so that it enables the use of all virtual coarray sensors without resorting to the nontrivial sparse recovery or array interpolation operations, and (3) it can be synthesized with the spatial smoothing to get the DOFs multiplied. Finally, the efficacy of the COPS scheme is verified by numerical examples.

Appendices

Appendix A: Proof of Theorem 1

Using the following three matrix prosperities given in [11]

$$\begin{aligned}{} & {} {{\varvec{A}}} \odot ({{\varvec{B}}} \odot {{\varvec{C}}}) = ({{\varvec{A}}} \odot {{\varvec{B}}}) \odot {{\varvec{C}}}, \end{aligned}$$

(22)

$$\begin{aligned}{} & {} {{\varvec{U}}}_{P \times Q} ({{\varvec{A}}} \odot {{\varvec{B}}}) = ({{\varvec{B}}} \odot {{\varvec{A}}}), \end{aligned}$$

(23)

$$\begin{aligned}{} & {} ({{\varvec{A}}} \otimes {{\varvec{B}}})({{\varvec{C}}} \odot {{\varvec{D}}}) = {{\varvec{A}}C} \odot {{\varvec{B}}D}, \end{aligned}$$

(24)

we have

$$\begin{aligned} ({{\varvec{U}}}_{6 \times L} \otimes {{\varvec{I}}}_{6L} ) [({{\varvec{Q}}} \odot {{\varvec{C}}})^*\odot ({{\varvec{Q}}} \odot {{\varvec{C}}})]= & {} {{\varvec{U}}}_{6 \times L} ({{\varvec{Q}}}^*\odot {{\varvec{C}}}^*) \odot {{\varvec{I}}}_{6L} ({{\varvec{Q}}} \odot {{\varvec{C}}}) \nonumber \\ {}= & {} ({{\varvec{C}}}^*\odot {{\varvec{Q}}}^*) \odot ({{\varvec{Q}}} \odot {{\varvec{C}}}) \end{aligned}$$

(25)

and

$$\begin{aligned} ({{\varvec{I}}}_6 \otimes {{\varvec{U}}}_{6 \times L^2}) ({{\varvec{C}}}^*\odot {{\varvec{Q}}}^*) \odot ({{\varvec{Q}}} \odot {{\varvec{C}}})= & {} {{\varvec{I}}}_6 {{\varvec{C}}}^*\odot {{\varvec{U}}}_{6 \times L^2}[ ({{\varvec{Q}}}^*\odot {{\varvec{Q}}}) \odot {{\varvec{C}}}] \nonumber \\ {}= & {} ({{\varvec{C}}}^*\odot {{\varvec{C}}}) \odot ({{\varvec{Q}}}^*\odot {{\varvec{Q}}}). \end{aligned}$$

(26)

Let ${{\varvec{P}}} = ({{\varvec{I}}}_6 \otimes {{\varvec{U}}}_{6 \times L^2}) ({{\varvec{U}}}_{6 \times L} \otimes {{\varvec{I}}}_{6\,L})$. The relationship (9) is established.

Appendix B: Proof of Theorem 2

The DOFs obtained from the polarization coarray equal to the rank of $\bar{{\varvec{C}}}$, which relies on the linear dependence of the polarization coarray steering vector $\bar{{\varvec{c}}} \triangleq {{\varvec{c}}}^*\odot {{\varvec{c}}}$. In fact, the ith element of $\bar{{\varvec{c}}}$, denoted by $\bar{c}_i$, is the product of the mth element of ${{\varvec{c}}}^*$ and the nth element of ${{\varvec{c}}}$, where the mapping between m, n, and i is

$$\begin{aligned} m = \left\lceil i/6 \right\rceil , \ n = i - 6 \left\lfloor (i - \textrm{eps})/6 \right\rfloor . \end{aligned}$$

(27)

With the notations mentioned above, the 36 elements of $\bar{{\varvec{c}}}$ can be computed and are listed in Table 1.

Table 1 Entries in the $36 \times 1$ Vector ${{\varvec{c}}}^*\otimes {{\varvec{c}}}$

From Table 1, it is easy to check that

$$\begin{aligned}{} & {} \bar{c}_7 - \bar{c}_2 = e_y^*e_x - e_x^*e_y = 0, \\{} & {} \bar{c}_{10} - \bar{c}_5 = e_y^*m_x - e_x^*m_y = 0, \\{} & {} \bar{c}_{21} - \bar{c}_{16} = m_x^*e_z - e_z^*m_x = 0,\\{} & {} \bar{c}_{24} + \bar{c}_{13} = m_x^*m_z + e_z^*e_x = 0,\\{} & {} \bar{c}_{25} - \bar{c}_{20} = m_y^*e_x - m_x^*e_y = 0,\\{} & {} \bar{c}_{26} + \bar{c}_{19} + \bar{c}_{18} = m_y^*e_y + m_x^*e_x + e_z^*m_z = 0,\\{} & {} \bar{c}_{27} - \bar{c}_{17} = m_y^*e_z - e_z^*m_y = 0,\\{} & {} \bar{c}_{28} - \bar{c}_{23} = m_y^*m_x - m_x^*m_y = 0,\\{} & {} \bar{c}_{29} + \bar{c}_{22} - \bar{c}_{15} = m_y^*m_y + m_x^*m_x - e_z^*e_z = 0,\\{} & {} \bar{c}_{30} + \bar{c}_{14} = m_y^*m_z + e_z^*e_y = 0,\\{} & {} \bar{c}_{31} - \bar{c}_{6} = m_z^*e_x - e_x^*m_z = 0,\\{} & {} \bar{c}_{32} - \bar{c}_{12} = m_z^*e_y - e_y^*m_z = 0,\\{} & {} \bar{c}_{33} + \bar{c}_{4} + \bar{c}_{11} = m_z^*e_z + e_x^*m_x + e_y^*m_y = 0,\\{} & {} \bar{c}_{34} + \bar{c}_{3} = m_z^*m_x + e_x^*e_z = 0,\\{} & {} \bar{c}_{35} + \bar{c}_{9} = m_z^*m_y + e_y^*e_z = 0,\\{} & {} \bar{c}_{36} - \bar{c}_{1} - \bar{c}_{8} = m_z^*m_z - e_x^*e_x - e_y^*e_y = 0, \end{aligned}$$

Therefore, the 7th, 10th, 21st, and 24-36th rows of ${\bar{{\varvec{C}}}}$ are linearly dependent on the remaining 20 rows. For sources of pairwise distinct auxiliary polarization angles and pairwise distinct polarization phase differences, the rank of ${\bar{{\varvec{C}}}}$ is up to 20 at most. That is, $\textrm{rank} ({\bar{{\varvec{C}}}}) \le \textrm{min}(20, K)$. Since the spatial coarray manifold $\tilde{{\varvec{Q}}}$ and the diagonal matrix ${{\varvec{R}}}_s$ are always full rank, the rank of the signal part of ${{\varvec{R}}}_\textrm{cops}$ would equal to $\textrm{rank} (\tilde{{\varvec{Q}}} {{\varvec{R}}}_s \bar{{\varvec{C}}})$ and satisfy

$$\begin{aligned} \textrm{rank} (\tilde{{\varvec{Q}}} {{\varvec{R}}}_s \bar{{\varvec{C}}}) \le \textrm{min}(20, K, \tilde{L}) \le \textrm{min}(20, K). \end{aligned}$$

(28)

For the use of the subspace-based techniques, it is required that

$$\begin{aligned} \textrm{rank}({{\varvec{R}}}_\textrm{cops}) = \textrm{rank} (\tilde{{\varvec{Q}}} {{\varvec{R}}}_s \bar{{\varvec{C}}}) = K. \end{aligned}$$

(29)

The requirement in (29) together with the limitation in (28) imply that $K \le 20$. In addition, to guarantee that a signal subspace is available, it is required that $K \le \tilde{L} - 1$. Combining these two constraints yields

$$\begin{aligned} K \le \textrm{min}(\tilde{L} - 1, K). \end{aligned}$$

(30)

Therefore, applying the subspace-based techniques directly to ${{\varvec{R}}}_\textrm{cops}$, the maximum number of identifiable sources is $K = \min \{\tilde{L} - 1, 20\}$. The proof is thus complete.

Appendix C: Proof of Corollary 1

For $\gamma _1 = \gamma _2 = \cdots = \gamma _K = \gamma$, we have

$$\begin{aligned}{} & {} \cos ^2 \gamma \bar{c}_{15} - \sin ^2 \gamma (\bar{c}_{1} + \bar{c}_{8}) = 0,\\{} & {} \cos ^2 \gamma \bar{c}_{16} + \sin ^2 \gamma \bar{c}_{6} = 0,\\{} & {} \cos ^2 \gamma \bar{c}_{17} + \sin ^2 \gamma \bar{c}_{12} = 0,\\{} & {} \cos ^2 \gamma \bar{c}_{22} - \sin ^2 \gamma \bar{c}_{1} = 0,\\{} & {} \cos ^2 \gamma \bar{c}_{23} - \sin ^2 \gamma \bar{c}_{2} = 0. \end{aligned}$$

Combining with the results obtained in Appendix 5, we can conclude that for $\gamma _1 = \gamma _2 = \cdots = \gamma _K$, the 7th, 10th, 15-17th, and 21-36th rows of $\bar{{\varvec{C}}}$ are linearly dependent on the remaining 15 rows.

For $\eta _1 = \eta _2 = \cdots = \eta _K = \eta$, we have

$$\begin{aligned}{} & {} e^{j \eta } \bar{c}_{13} - e^{-j\eta } \bar{c}_{3} = 0,\\{} & {} e^{j \eta } \bar{c}_{14} - e^{-j\eta } \bar{c}_{9} = 0,\\{} & {} e^{j \eta } \bar{c}_{18} + e^{-j \eta } (\bar{c}_{4} + \bar{c}_{11}) = 0,\\{} & {} e^{j \eta } \bar{c}_{19} - e^{-j\eta } \bar{c}_{4} = 0,\\{} & {} e^{j \eta } \bar{c}_{20} - e^{-j\eta } \bar{c}_{5} = 0. \end{aligned}$$

Combining with the results obtained in Appendix 5, we can conclude that for $\eta _1 = \eta _2 = \cdots = \eta _K$, the 7th, 10th, 13rd, 14th, 18-21st, and 24-36th rows of $\bar{{\varvec{C}}}$ are linearly dependent on the remaining 15 rows. For the preceding two cases, we have $\textrm{rank} ({\bar{{\varvec{C}}}}) \le \textrm{min}(15, K)$. Following the same routine as we did in Appendix 5, the result in Corollary 1 can be thus established.

Appendix D: Proof of Corollary 2

For $\gamma _1 = \gamma _2 = \cdots = \gamma _K = \gamma$ and $\eta _1 = \eta _2 = \cdots = \eta _K = \eta$, we have

$$\begin{aligned}{} & {} e^{-j \eta } \cos \gamma \bar{c}_{4} - \sin \gamma \bar{c}_{1} = 0,\\{} & {} e^{-j \eta } \cos \gamma \bar{c}_{5} - \sin \gamma \bar{c}_{2} = 0,\\{} & {} e^{j \eta } \sin \gamma \bar{c}_{6} + \cos \gamma \bar{c}_{3} = 0,\\{} & {} e^{-j \eta } \cos \gamma \bar{c}_{11} - \sin \gamma \bar{c}_{8} = 0,\\{} & {} e^{j \eta } \sin \gamma \bar{c}_{12} + \cos \gamma \bar{c}_{9} = 0. \end{aligned}$$

Together with the results obtained in Appendices 5 and 5, we can conclude that for $\gamma _1 = \gamma _2 = \cdots = \gamma _K$ and $\eta _1 = \eta _2 = \cdots = \eta _K$, only the first three, the 8th, and the 9th rows of $\bar{{\varvec{C}}}$ are linear independent. Thus, $\textrm{rank} ({\bar{{\varvec{C}}}}) \le \textrm{min}(5, K)$, and the result in Corollary 2 can be established.

Appendix E: Proof of Corollary 3

It follows directly from (16) and (19) that the rank of $\bar{{\varvec{R}}}_\textrm{cops}$ satisfies

$$\begin{aligned} \textrm{rank} (\bar{{\varvec{R}}}_\textrm{cops})\le & {} \textrm{rank}\left( \sum _{p = 1}^P {{\varvec{F}}}_p {{\varvec{R}}}_\textrm{cops} {{\varvec{F}}}_p^H\right) \nonumber \\ {}\le & {} \textrm{min}(PJ, PK). \end{aligned}$$

(31)

Constraints (29) and (31) together yield $K \le PJ$. To apply the subspace-based techniques, it is required that $K \le L^{\prime } - 1$. Combining these two constraints leads to

$$\begin{aligned} K \le \textrm{min}(L^{\prime } - 1, PJ). \end{aligned}$$

(32)

Therefore, applying the subspace-based techniques directly to $\bar{{\varvec{R}}}_\textrm{cops}$, the maximum number of identifiable sources is $K = \min \{L^{\prime } - 1, PJ\}$, completing the proof.